ЭКОНОМЕТРИКА Лекция 12 Прогнозирование с помощью моделей Проверка адекватности модели

Прогнозирование значений эндогенной переменной Имеем оценку линейной модели множественной регрессии (12. 1) Параметры модели получены по выборке {y, X} и предполагаем, что все предпосылки теоремы Гаусса. Маркова выполнены Обозначим символом z 0 «точку» , в котрой необходтмо вычислить прогнозное значение эндогенной переменной Это значение обозначим y(z 0)=y 0 При этом:

Прогнозирование значений эндогенной переменной Элементы выборки связаны между собой системой уравнений наблюдений с неколлинеарной матрицей коэффициентов Х 1. Точечный прогноз Согласно теореме Гаусса – Маркова наилучший точечный прогноз эндогенной переменной вычисляется по формуле: (12. 2) Стандартная ошибка прогноза (СКО) есть (12. 3)

Прогнозирование значений эндогенной переменной Пример 1 Исходная выборка ВНП С I (млрд. долл) 14, 00 8, 00 1, 65 16, 00 9, 50 1, 80 18, 00 11, 00 20, 00 12, 00 2, 10 23, 00 13, 00 2, 20 23, 50 14, 00 2, 40 25, 00 15, 00 2, 65 26, 50 16, 50 2, 85 28, 50 17, 00 3, 20 30, 50 18, 00 3, 55 Задача Построить модель и получить прогнозные значения ВВП при С=14. 5 ; i=4. 0

Прогнозирование значений эндогенной переменной В результате применения МНК оценка модели приняла вид: Подставляя в оценку модели значения С=14. 5 ; i=4. 0, получим

Прогнозирование значений эндогенной переменной Оценка стандартной ошибки прогноза соответственно есть: С I (млрд. дол (млрд. до л) лл) Х= 1 1 1 1 1 8, 00 9, 50 11, 00 12, 00 13, 00 14, 00 15, 00 16, 50 17, 00 18, 00 1, 65 1, 80 2, 00 2, 10 2, 20 2, 40 2, 65 2, 85 3, 20 3, 55 q 0=8. 74 σy=2. 06 Точечный прогноз – ВНП=25. 3 σВВП=2. 06

Прогнозирование значений эндогенной переменной Прогнозирование в условиях гетероскедастичности В условиях гетероскедастичности исходной модели (12. 1) оценка параметров модели осуществляется ВМНК Что, в частности, может быть сведено к модели вида: (12. 4) Имея точку z 0=(1, z 2, …)Т, в которой нужно получить прогнозное значение переменной y, необходимо преобразовать исходную точку z 0, получить прогнозное значение y* оценить стандартную ошибку ε

Прогнозирование значений эндогенной переменной Имея значения y* σε , легко получить значения прогноза для переменной y и σu (12. 5) Соотношения (12. 5) представляют собой точечную оценку эндогенной переменной y исходной модели

Прогнозирование значений эндогенной переменной 2. Интервальное прогнозирование В отличие от точечного метода прогнозирования интервальный позволяет в качестве прогноза получить числовой интервал, внутри которого может лежать прогнозное значение эндогенной переменной Для построения такого прогноза образуется дробь Стьюдента в виде: (12. 4) Знаем, что в схеме Гаусса-Маркова дробь (12. 4) имеет закон распределения Стьюдента с числом степеней свободы η=n-к-1 где к – количество регрессоров в модели

Прогнозирование значений эндогенной переменной Задав уровень доверительной вероятности Рдов (α=1 Рдов), легко оценить границы интервала (y-0: y+0), внутри которого с вероятностью Рдов лежат значения прогноза (12. 5) Значение ошибки прогноза рассчитывается по формуле (12. 3) В примере 1 интервальный прогноз получает вид: При tкрит(0. 05, 7)=2. 36 имеем

Проверка адекватности модели Определение. Адекватность – возможность получения результата с удовлетворительной точностью Применительно к построению эконометрических моделей следует сказать, под точностью результата понимается абсолютное значение разности между прогнозом, полученным с помощью модели и реальным значением эндогенной переменной Тогда модель считается адекватной, если эта разность не превосходит некоторого наперед заданного значения Отсюда вытекает алгоритм процедуры проверки адекватности

Проверка адекватности модели Алгоритм процедуры проверки адекватности 1. Вся имеющаяся в распоряжении выборка наблюдений делится на две неравные части: обучающую и контролирующую Обучающая выборка включает основную (большую) часть наблюдений Контролирующая выборка содержит до 5% от общего объема выборки 2. По обучающей выборке оценивается модель (рассчитываются оценки параметров модели и их стандартные ошибки)

Проверка адекватности модели 3. Задается значение доверительной вероятности Рдов =1 -α и определяется критическое значение дроби Стьюдента tкрит 4. Для каждой «точки» из контролирующей выборки по известным значениям экзогенных переменных строится доверительный интервал прогнозного значения эндогенной переменной (12. 5) 5. Проверяется попадает ли соответствующее значение эндогенной переменной внутрь полученного интервала

Проверка адекватности модели Пункты 5 и 6 проводятся для каждой точки выборки персонально! Вывод. Если все значения эндогенных переменных из контрольной выборки накрываются соответствующими доверительными интервалами, то полученная модель с вероятностью Рдов считается адекватной, т. е. пригодной для дальнейшего использования в целях решения экономических задач

Проверка адекватности модели Пример Исходная выборка ВНП С I (млрд. долл) 14, 00 8, 00 1, 65 16, 00 9, 50 1, 80 18, 00 11, 00 20, 00 12, 00 2, 10 23, 00 13, 00 2, 20 23, 50 14, 00 2, 40 25, 00 15, 00 2, 65 26, 50 16, 50 2, 85 28, 50 17, 00 3, 20 30, 50 18, 00 3, 55 Точки для проверки адекватности
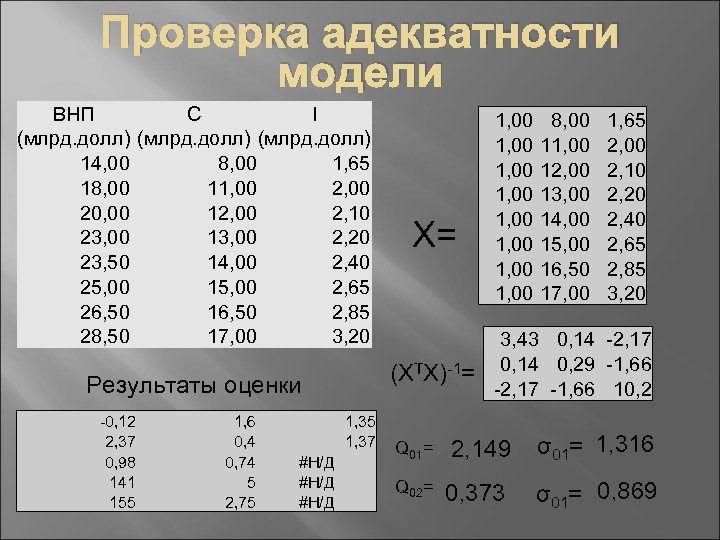
Проверка адекватности модели ВНП С I (млрд. долл) 14, 00 8, 00 1, 65 18, 00 11, 00 20, 00 12, 00 2, 10 23, 00 13, 00 2, 20 23, 50 14, 00 2, 40 25, 00 15, 00 2, 65 26, 50 16, 50 2, 85 28, 50 17, 00 3, 20 (ХТХ)-1= Результаты оценки -0, 12 2, 37 0, 98 141 155 1, 6 0, 4 0, 74 5 2, 75 1, 37 #Н/Д Х= Q 01= Q 02= 1, 00 1, 00 8, 00 11, 00 12, 00 13, 00 14, 00 15, 00 16, 50 17, 00 1, 65 2, 00 2, 10 2, 20 2, 40 2, 65 2, 85 3, 20 3, 43 0, 14 -2, 17 0, 14 0, 29 -1, 66 -2, 17 -1, 66 10, 2 2, 149 σ01= 1, 316 0, 373 σ01= 0, 869

Проверка адекватности модели Адекватность в т. Z 01 Прогноз в точке Z 01 1. Точечная проверка адекватности Доверительный интервал Вывод Модель в т. Z 1 адекватна

Процедура построения модели 1. Спецификация модели 2. Подготовка исходной информации 3. Оценивание параметров модели 4. Тестирование качества параметров модели: — гомоскедастичность — автокорреляция 5. Проверка адекватности
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Бабешко Л.О.
1
1 ФГБОУ ВО «Финансовый университет при Правительстве РФ»
Данная статья посвящена вопросам методики проверки адекватности модели прогнозирования спроса на электроэнергию Фишера – Кайсена (F.M. Fisher, C. Kaysen) в Excel. Выбор табличного процессора MS Excel обусловлен тем, что он является наиболее доступным средством для числовой обработки экономической информации и особенно эффективен на этапе изучения эконометрических методов. Реализация матричных методов построения доверительных интервалов для проверки адекватности модели множественной линейной регрессии в Excel при помощи функций МУМНОЖ, МОБР, ТРАНСП занимает большую часть времени, отведённого на изучение темы. В работе приводится пример реализации метода Салкевера (Salkever), позволяющего оптимизировать процедуру вычисления стандартных ошибок прогнозов, используемую для построения доверительных интервалов значений эндогенной переменной на интервале прогнозирования. Процедура Салкевера состоит в добавлении в спецификацию модели множественной линейной регрессии фиктивных переменных. В работе, на примере спецификации модели с фиктивной переменной, показано, что оценки параметров при фиктивных переменных и их стандартные ошибки представляют собой ошибки прогнозов и стандартные ошибки прогнозов соответственно. Метод Салкевера легко реализуем в Excel, например при помощи функции ЛИНЕЙН.
фиктивные переменные
прогнозы
ошибки прогнозирования
доверительные интервалы
стандартные ошибки прогнозирования
ковариационная матрица
1. Цаплина М.Г. Страхование рисков на рынке электроэнергии с применением фьючерсных стратегий // Экономика устойчивого развития. 2015. № 2 (22). С. 296–300.
2. Фёдорова Е.А., Афанасьев Д.О. Исследование взаимосвязи цены и спроса на российском рынке электроэнергии // Известия РАН. Энергетика. 2015. № 3. С. 3–17.
3. Zachmann G. A stochastic fuel switching model for electricity prices. Energy Economics. 2013. Vol. 35. P. 5–13. DOI: 10.1016/j.eneco.2012.06.019.
4. Берндт Э.Р. Практика эконометрики: классика и современность. М.: ЮНИТИ-ДАНА, 2012. 863 с.
5. Григорьева А.Л., Григорьев Я.Ю. Эконометрика для экономистов // Международный журнал прикладных и фундаментальных исследований. 2011. № 7. С. 134–135.
6. Бабешко Л.О. Эконометрическое прогнозирование по разнородной информации. М.: Вега-Инфо, 2016. 232 с.
7. Бабешко Л.О., Бич М.Г., Орлова И.В. Эконометрика и эконометрическое моделирование. М.: Вузовский учебник: ИНФРА-М, 2017. 400 с.
8. Salkever D. The Use of Dummy Variables to Compute Predictions, Prediction Errors, and Confidence Intervals. Journal of Econometrics, 1976. № 4. P. 393–397.
9. Dufour J.M. Dummy variables and predictive test for structural change. Economic Letter. 1980. № 6 (3). P. 241–247.
10. Магнус Я.Р., Катышев П.К., Пересецкий А.А., Головань С.В. Сборник задач к начальному курсу эконометрики. М.: Дело, 2007. 368 с.
11. Доугерти К. Введение в эконометрику. М.: ИНФРА-М, 2009. 465 с.
Необходимым условием устойчивого развития государства является стабильность электроэнергетической сферы, составляющей основу функционирования экономики. Надёжное и доступное электроснабжение – неотъемлемая часть успешного конкурентного развития производства и качества жизни современного общества. Необходимость моделирования и прогнозирования спроса на электроэнергию состоит в значительных издержках, связанных с недостаточным или избыточным строительством электростанций. В условиях ужесточения экологических требований, решение о строительстве новых электростанций должно быть эмпирически обосновано [1].
Моделированию спроса на электроэнергию посвящено множество работ [2, 3]. Подробный обзор мировой эконометрической практики приведен в книге Э.Р. Берндта «Практика эконометрики: классика и современность». Автор обсуждает технику выбора инструментов эконометрических исследований на разнообразных классических и современных статистических данных. В частности, для моделирования спроса на электроэнергию приводятся данные временных рядов по США за 1951–1984 гг., заимствованные из работы Нельсона – Пека (Nelson, Peck) [4]. В книге предлагается приобрести навыки построения и исследования эконометрических моделей, опираясь на опыт авторов статьи.
Данная статья посвящена вопросам методики проверки адекватности модели прогнозирования спроса на электроэнергию Фишера – Кайсена (F.M. Fisher, C. Kaysen) в Excel. Выбор табличного процессора MS Excel обусловлен тем, что он является наиболее доступным средством для числовой обработки экономической информации и особенно эффективен на этапе изучения эконометрических методов [5].
Материалы и методы исследования
В качестве модели прогнозирования спроса на электроэнергию выбрана спецификация множественной линейной регрессии:
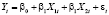 ,
, 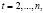 (1)
(1)
с переменными:
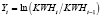 ,
,
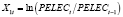 ,
,
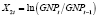 ,
,
где KWH – общее количество электроэнергии, используемой всеми потребителями за год (в млн киловатт-часов); PELEC – средняя цена электроэнергии за 1 кВТ•час (в центах); GNP – валовой национальный продукт США (в млн долл.). Формирование переменных в форме процентных изменений позволяет решить проблему мультиколлинеарности. Уравнения наблюдений модели (1) в матричной форме:
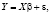
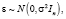
где Y – (n×1) – вектор-столбец значений эндогенной переменной, X – (n×k)-матрица регрессоров, ε – (n×1)-вектор-столбец возмущений, β – (k×1)-вектор-столбец параметров модели, σ2 – дисперсия возмущений, In – (n×n)-единичная матрица, n – объем выборки, k – число параметров модели. Модель оценивается методом наименьших квадратов (значок «Т» означает операцию транспонирования):
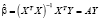 (2)
(2)
– МНК-оценки параметров,
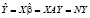 (3)
(3)
– оценки (прогнозы) вектора значений эндогенной переменной.
Точное совпадение фактических данных и прогнозных значений – явление маловероятное. Оценки и прогнозы эндогенных переменных не совпадают с их истинными значениями в силу разных причин: ограниченность выборочных данных, ошибки спецификации (пропуск существенных регрессоров, неправильный выбор уравнения регрессии), ошибки измерений. Обозначим [6]: вектор остатков регрессии (отклонений на интервале оценивания, t ≤ n)
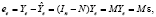
где 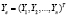 ,
, 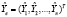 ,
, 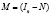 идемпотентная матрица, вектор ошибок прогнозов (отклонений на интервале прогнозирования, например, для t > n)
идемпотентная матрица, вектор ошибок прогнозов (отклонений на интервале прогнозирования, например, для t > n)
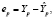
где
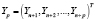 ,
, 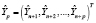 ,
,
p – период упреждения. Автоковариационная матрица вектора отклонений 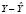 для любого интервала:
для любого интервала:
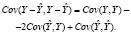 (4)
(4)
На интервале оценивания:
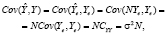 (5)
(5)
поэтому автоковариационная матрица вектора остатков (4), с учетом (5), принимает вид:
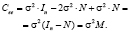 (6)
(6)
На интервале прогнозирования:
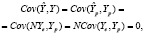 (7)
(7)
в силу некоррелированности возмущений в различных наблюдениях, поэтому автоковариационная матрица вектора ошибок прогнозов, с учетом (4)–(7) равна
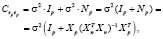 (8)
(8)
где Xp – матрица регрессоров на интервале прогнозирования, Xn – матрица регрессоров на интервале оценивания. Несмещенная оценка дисперсии возмущений, вычисляемая через вектор остатков регрессионной модели
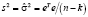 , (9)
, (9)
позволяет оценить автоковариационные матрицы всех случайных векторов.
Проверка адекватности модели по выборочным данным базируется на построении интервальных оценок. Для построения интервальной оценки эндогенной переменной на интервале прогнозирования, применяется процедура трансформации дроби Стьюдента
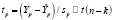
в интервальную оценку
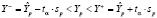 , (10)
, (10)
где 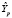 – прогноз значения эндогенной переменной для момента t = p > n, tα – квантиль уровня значимости α, Yp – истинное значение эндогенной переменной на момент t = p, sp – стандартная ошибка прогноза,
– прогноз значения эндогенной переменной для момента t = p > n, tα – квантиль уровня значимости α, Yp – истинное значение эндогенной переменной на момент t = p, sp – стандартная ошибка прогноза, 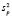 – оценка дисперсии ошибки прогноза – диагональный элемент оценки матрицы (8) (
– оценка дисперсии ошибки прогноза – диагональный элемент оценки матрицы (8) (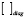 – диагональный элемент матрицы):
– диагональный элемент матрицы):
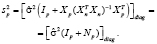 (11)
(11)
Алгоритм проверки адекватности модели состоит из следующих шагов [7]:
1) результаты наблюдений разделяют на две части: обучающую (90–95 % наблюдений) и контролирующую выборки (оставшиеся наблюдения);
2) по обучающей выборке выполняется оценка параметров модели (по формуле (2));
3) по оцененной модели строится прогноз значений эндогенной переменной из контролирующей выборки и доверительные интервалы для их истинных значений (формулы: (3), (9), (11), (10));
4) выполняется проверка: если значения эндогенной переменной из контролирующей выборки накрываются доверительными интервалами – модель признается адекватной, в противном случае подлежит доработке.
Результаты исследования и их обсуждение
Для оценки модели использованы ежегодные данные временных рядов по данным США за 1951–1984 гг. В качестве обучающей выборки в работе [4] предлагается использовать наблюдения с 1951 по 1973 г. (n = 22), контролирующей – с 1974 г. по 1984 г. (p = 11).
Результаты оценивания модели по обучающей выборке в Excel при помощи функции ЛИНЕЙН приведены в табл. 1.
Таблица 1
Результат функции ЛИНЕЙН
|
0,45043 |
–0,41043 |
0,049294 |
|
0,216209 |
0,162311 |
0,008312 |
|
0,473976 |
0,020244 |
#Н/Д |
|
8,560016 |
19 |
#Н/Д |
|
0,007016 |
0,007786 |
#Н/Д |
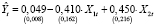 ,
,
s = 0,02, R2 = 0,474, F = 8,560. (12)
Прогноз эндогенной переменной по значениям регрессоров из контролирующей выборки по формуле (12) приведен в табл. 2.
Таблица 2
Точечный прогноз эндогенной переменной
|
Год |
Вектор значений эндогенной переменной Y |
Матрица регрессоров Xp |
Прогноз эндогенной переменной |
||
|
1974 |
–0,004 |
1 |
0,155 |
–0,006 |
–0,017 |
|
1975 |
0,024 |
1 |
0,071 |
–0,012 |
0,015 |
|
1976 |
0,060 |
1 |
0,004 |
0,053 |
0,071 |
|
1977 |
0,049 |
1 |
0,046 |
0,054 |
0,055 |
|
1978 |
0,035 |
1 |
0,004 |
0,049 |
0,070 |
|
1979 |
0,026 |
1 |
–0,004 |
0,028 |
0,064 |
|
1980 |
0,011 |
1 |
0,083 |
–0,004 |
0,014 |
|
1981 |
0,025 |
1 |
0,051 |
0,019 |
0,037 |
|
1982 |
–0,029 |
1 |
0,059 |
–0,015 |
0,018 |
|
1983 |
0,030 |
1 |
–0,014 |
0,036 |
0,071 |
|
1984 |
0,058 |
1 |
0,000 |
0,066 |
0,079 |
Для построения доверительных интервалов значений эндогенной переменной, необходимо вычислить стандартные ошибки прогнозов по формуле (11). Для вычисления Np в Excel используются функции ТРАНСП, МУМНОЖ и МОБР категорий «Ссылки и массивы» и «Математические» соответственно. В табл. 3 представлены значения диагональных элементов проекционной матрицы Np, значения стандартных ошибок прогнозов, левая и правая границы доверительных интервалов и истинные значения эндогенной переменной.
Таблица 3
Интервальные оценки эндогенной переменной
|
Год |
Np |
sp |
Y- |
Y+ |
Yp |
|
1974 |
1,816579 |
0,033974 |
–0,08828 |
0,053936 |
–0,00409 |
|
1975 |
0,591807 |
0,025541 |
–0,03884 |
0,068078 |
0,023847 |
|
1976 |
0,162967 |
0,021831 |
0,025557 |
0,116943 |
0,060068 |
|
1977 |
0,481826 |
0,024643 |
0,002932 |
0,106088 |
0,048969 |
|
1978 |
0,14264 |
0,021639 |
0,02443 |
0,115013 |
0,035079 |
|
1979 |
0,067088 |
0,020912 |
0,0198 |
0,107338 |
0,026013 |
|
1980 |
0,678001 |
0,026223 |
–0,04112 |
0,068647 |
0,011211 |
|
1981 |
0,361146 |
0,023618 |
–0,01261 |
0,086253 |
0,024827 |
|
1982 |
0,507091 |
0,024852 |
–0,03383 |
0,070201 |
–0,02866 |
|
1983 |
0,053016 |
0,020773 |
0,027746 |
0,114705 |
0,030455 |
|
1984 |
0,237543 |
0,02252 |
0,031869 |
0,126139 |
0,057546 |
Как следует из табл. 3, значения эндогенных переменных из контролирующей выборки накрываются доверительными интервалами для всех рассматриваемых наблюдений. Это подтверждает адекватность модели Фишера – Кайсена спроса на электроэнергию.
Реализация матричного алгоритма в Excel затратна по времени. Поэтому для вычисления стандартных ошибок прогнозов на практических занятиях рекомендуется использовать легко реализуемый метод Салкевера (Salkever) [8, 9].
В методе Салкевера, для оценки стандартной ошибки прогноза на момент t = n + 1, в матрицу регрессоров добавляется строка значений регрессоров Xt и столбец фиктивных переменных
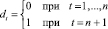 , (13)
, (13)
в вектор-столбец значений эндогенной переменной добавляется значение Yn+1. По сформированным таким способом данным, при помощи функции ЛИНЕЙН, оценивается модель, проверяемая на адекватность. Если исходная спецификация включает свободный член, то он учитывается параметром КОНС = 1. Стандартный протокол функции ЛИНЕЙН включает ошибку прогноза на момент t = n + 1 – оценка параметра при фиктивной переменной (13) и стандартную ошибку прогноза – стандартная ошибка параметра при фиктивной переменной. Справедливость этого утверждения можно показать на модели с фиктивной переменной [10]:
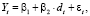
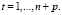 (14)
(14)
Упорядочим наблюдения таким образом, что, dt = 0 при t = 1,…,n, dt = 1, при, 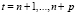 . Обозначим
. Обозначим
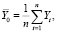
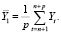
В соответствии с (2)
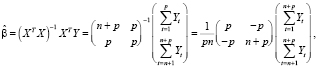
где
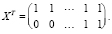
Таким образом, оценка свободного члена модели (14) равна
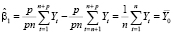 , (15)
, (15)
оценка параметра при фиктивной переменной:
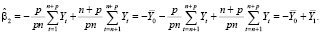 (16)
(16)
Автоковариационная матрица оценок параметров:
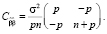
С учетом структуры вектора Y в методе Салкевера, для периода упреждения p = 1:
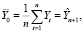
где 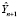 – прогноз значения эндогенной переменной модели;
– прогноз значения эндогенной переменной модели;
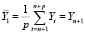
– значение эндогенной переменной на интервале прогнозирования. Таким образом, оценка параметра (16) при фиктивной переменной равна ошибке прогноза эндогенной переменной:
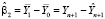 , (17)
, (17)
и, следовательно, дисперсия оценки параметра при фиктивной переменной равна дисперсии ошибки прогноза (с учетом некоррелированности ошибок):
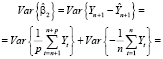
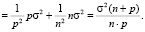 (18)
(18)
В соответствии с (11), дисперсия ошибки прогноза вычисляется по формуле
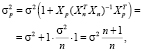 (19)
(19)
где 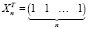 ,
, 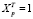 . С учетом значения p = 1, формула (18) дисперсии оценки параметра при фиктивной переменной для модели (14) принимает вид (19) и совпадает с дисперсией ошибки прогноза. Этот же результат подтверждается эмпирической проверкой. Сформируем вспомогательную матрицу регрессоров с блочной структурой [11]:
. С учетом значения p = 1, формула (18) дисперсии оценки параметра при фиктивной переменной для модели (14) принимает вид (19) и совпадает с дисперсией ошибки прогноза. Этот же результат подтверждается эмпирической проверкой. Сформируем вспомогательную матрицу регрессоров с блочной структурой [11]:
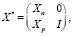
где Xn – (n×k)-матрица значений регрессоров из обучающей выборки (n = 22), Xp – (p×k)-матрица значений регрессоров из контролирующей выборки (p = 3), 0 – (n×p) – нулевая матрица, I – (p×p)-единичная матрица. В табл. 4 приведены элементы вспомогательной матрицы X* для контролирующей выборки, включающей три наблюдения.
Таблица 4
Вспомогательная матрица регрессоров
|
t |
Xt1 |
Xt2 |
Xt3 |
dt1 |
dt2 |
dt3 |
|
|
1 |
0,0758 |
–0,0097 |
0,0363 |
0 |
0 |
0 |
|
|
2 |
0,1065 |
–0,0262 |
0,0372 |
0 |
0 |
0 |
|
|
3 |
0,0683 |
–0,0134 |
–0,0121 |
0 |
0 |
0 |
|
|
4 |
0,1589 |
–0,0770 |
0,0650 |
0 |
0 |
0 |
|
|
5 |
0,0940 |
–0,0523 |
0,0212 |
0 |
0 |
0 |
|
|
6 |
0,0535 |
–0,0154 |
0,0180 |
0 |
0 |
0 |
|
|
7 |
0,0206 |
0,0078 |
–0,0043 |
0 |
0 |
0 |
|
|
8 |
0,0956 |
–0,0354 |
0,0582 |
0 |
0 |
0 |
|
|
9 |
0,0629 |
0,0583 |
0,0212 |
0 |
0 |
0 |
|
|
10 |
0,0482 |
–0,0076 |
0,0260 |
0 |
0 |
0 |
|
|
11 |
0,0733 |
–0,0309 |
0,0562 |
0 |
0 |
0 |
|
|
12 |
0,0683 |
–0,0319 |
0,0394 |
0 |
0 |
0 |
|
|
13 |
0,0729 |
–0,0371 |
0,0514 |
0 |
0 |
0 |
|
|
14 |
0,0627 |
–0,0385 |
0,0586 |
0 |
0 |
0 |
|
|
15 |
0,0815 |
–0,0584 |
0,0580 |
0 |
0 |
0 |
|
|
16 |
0,0600 |
–0,0329 |
0,0267 |
0 |
0 |
0 |
|
|
17 |
0,0904 |
–0,0591 |
0,0451 |
0 |
0 |
0 |
|
|
18 |
0,0883 |
–0,0468 |
0,0275 |
0 |
0 |
0 |
|
|
19 |
0,0577 |
–0,0270 |
–0,0018 |
0 |
0 |
0 |
|
|
20 |
0,0545 |
0,0054 |
0,0333 |
0 |
0 |
0 |
|
|
21 |
0,0816 |
0,0108 |
0,0550 |
0 |
0 |
0 |
|
|
22 |
0,0713 |
–0,0054 |
0,0561 |
0 |
0 |
0 |
|
|
23 |
–0,0041 |
0,1549 |
–0,0064 |
1 |
0 |
0 |
|
|
24 |
0,0238 |
0,0715 |
–0,0119 |
0 |
1 |
0 |
|
|
25 |
0,0601 |
0,0043 |
0,0527 |
0 |
0 |
1 |
В табл. 5 приводится протокол оценки модели спроса на электроэнергию (1) при помощи функции ЛИНЕЙН методом Салкевера.
Таблица 5
Вспомогательная матрица регрессоров
|
–0,01118 |
0,009226 |
0,013084 |
0,45043 |
–0,41043 |
0,049294 |
|
0,021831 |
0,025541 |
0,033974 |
0,216209 |
0,162311 |
0,008312 |
|
0,66172 |
0,020244 |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
|
7,433304 |
19 |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
|
0,015231 |
0,007786 |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
Заключение
Сравнение результатов оценивания с табл. 1 и 3 (третий столбец) показывает, что оценки параметров и их стандартные ошибки при регрессорах [ ]diag исходной модели и вспомогательной модели Салкевера совпадают. Стандартные ошибки оценок параметров при фиктивных переменных (отмеченные жирным шрифтом в табл. 5) равны стандартным ошибкам прогнозов, приведенных в табл. 3, используемым для построения интервальных оценок в алгоритме проверки адекватности, но их вычисление намного эффективнее матричного метода при реализации в Excel.
Библиографическая ссылка
Бабешко Л.О. ЭКОНОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ СПРОСА НА ЭЛЕКТРОЭНЕРГИЮ: ПРОВЕРКА АДЕКВАТНОСТИ // Фундаментальные исследования. – 2018. – № 12-1.
– С. 47-52;
URL: https://fundamental-research.ru/ru/article/view?id=42350 (дата обращения: 31.01.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Подборка по базе: Историческое значение теории и практики общественного призрения , Конституция Российской Федерации.docx, Организация работы органов и учреждений социальной защиты населе, Конституция Российской Федерации.docx, Система образования в Российской Федерации.pdf, Бюджетная система Российской Федерации.docx, Организация государственной статистики в Российской Федерации.do, Терроризм как угроза национальной безопасности Российской Федера, Министерство образования и науки Российской Федерации.docx, Практическое занятие БЮДЖЕТНАЯ СИСТЕМА РОССИЙСКОЙ ФЕДЕРАЦИИ.docx
……………………………………….
Пример 5.7.
На основании данных (табл. 5.1) по 40 наблюдениям была построена модель зависимости Количества безработных от Индекса реального объема промышленного производства:  ,
,  ,
,  ,
,  ,
,
Используя прогнозную оценку Индекса реального объема промышленного производства (табл. 5.7), построить точечный и интервальный прогноз ожидаемого Количества безработных на ближайшие 8 кварталов.
Решение
Подставив прогнозные значения IP в модель  , получим точечный прогноз Количества безработных, затем построим интервальную оценку значения эндогенной переменной — Количества безработных. Формула для вычисления ошибки прогноза в случае модели парной регрессии может быть записана в виде:
, получим точечный прогноз Количества безработных, затем построим интервальную оценку значения эндогенной переменной — Количества безработных. Формула для вычисления ошибки прогноза в случае модели парной регрессии может быть записана в виде: ,
,
Для построения границ доверительного интервала вычислим:
прогноз значения эндогенной переменной
 ;
;

…………………………………….
 .
.
стандартную ошибку прогноза значения эндогенной переменной


……………………………………………………………………………………

- доверительный интервал


………………………………………………

Результаты вычислений запишем в таблицу 5.8.
Таблица 5.8.
Вычисление доверительных интервалов прогноза Количества безработных
| год | квартал | t | Прогноз IP (из табл.6.6) | Прогноз U |  |
Верхняя граница | Нижняя граница |
| 2017 | 1 | 41 | 148,184 | 4,641 | 0,889 | 5,530 | 3,752 |
| 2017 | 2 | 42 | 150,402 | 4,509 | 0,890 | 5,399 | 3,619 |
| 2017 | 3 | 43 | 154,794 | 4,249 | 0,895 | 5,144 | 3,353 |
| 2017 | 4 | 44 | 166,602 | 3,548 | 0,929 | 4,477 | 2,619 |
| 2018 | 1 | 45 | 149,589 | 4,557 | 0,889 | 5,447 | 3,668 |
| 2018 | 2 | 46 | 151,807 | 4,426 | 0,891 | 5,317 | 3,535 |
| 2018 | 3 | 47 | 156,199 | 4,165 | 0,898 | 5,063 | 3,268 |
| 2018 | 4 | 48 | 168,007 | 3,465 | 0,935 | 4,399 | 2,530 |
Полученные результаты прогнозирования представим на двух графиках.
На рис. 5.10 приведен прогноз Количества безработных по модели  .
.
На рис. 5.11 приведен график динамики Количества безработных в зависимости от номера наблюдения.
 Рис. 5.10. Построение прогноза по модели
Рис. 5.10. Построение прогноза по модели

Рис. 5.11. График динамики количества безработных.
Приложение 1. Значения статистик Дарбина-Уотсона при 5%-ном уровне значимости
Значения статистик Дарбина-Уотсона при 5%-ном уровне значимости*
(n– число наблюдений, k– число объясняющих переменных без учета
постоянного члена; d– статистика Дарбина-Уотсона: dL и dU.)
| n | k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | ||||||
| d1 | d2 | d1 | d2 | d1 | d2 | d1 | d2 | d1 | d2 | d1 | d2 | |
| 6 | 0,610 | 1,400 | — | — | — | — | — | — | — | — | — | — |
| 7 | 0,700 | 1,356 | 0,467 | 1,896 | — | — | — | — | — | — | — | — |
| 8 | 0,763 | 1,332 | 0,559 | 1,777 | 0,368 | 2,287 | — | — | — | — | — | — |
| 9 | 0,824 | 1,320 | 0,629 | 1,699 | 0,455 | 2,128 | 0,296 | 2,588 | — | — | — | — |
| 10 | 0,879 | 1,320 | 0,697 | 1,641 | 0,525 | 2,016 | 0,376 | 2,414 | 0,243 | 2,822 | — | — |
| 11 | 0,927 | 1,324 | 0,658 | 1,604 | 0,595 | 1,928 | 0,444 | 2,283 | 0,320 | 2,645 | 0,203 | 3,005 |
| 12 | 0,971 | 1,331 | 0,812 | 1,579 | 0,658 | 1,864 | 0,512 | 2,177 | 0,379 | 2,506 | 0,268 | 2,832 |
| 13 | 1,010 | 1,340 | 0,861 | 1,562 | 0,715 | 1,816 | 0,574 | 2,094 | 0,445 | 2,390 | 0,328 | 2,692 |
| 14 | 1,045 | 1,350 | 0,905 | 1,551 | 0,767 | 1,779 | 0,632 | 2,030 | 0,505 | 2,296 | 0,389 | 2,572 |
| 15 | 1,077 | 1,361 | 0,946 | 1,543 | 0,814 | 1,750 | 0,685 | 1,977 | 0,562 | 2,220 | 0,447 | 2,472 |
| 16 | 1,106 | 1,371 | 0,982 | 1,539 | 0,857 | 1,728 | 0,734 | 1,935 | 0,615 | 2,157 | 0,502 | 2,388 |
| 17 | 1,133 | 1,381 | 1,015 | 1,536 | 0,897 | 1,710 | 0,779 | 1,900 | 0,664 | 2,104 | 0,554 | 2,318 |
| 18 | 1,158 | 1,391 | 1,046 | 1,535 | 0,933 | 1,696 | 0,820 | 1,872 | 0,710 | 2,060 | 0,603 | 2,257 |
| 19 | 1,180 | 1,401 | 1,074 | 1,536 | 0,967 | 1,685 | 0,859 | 1,849 | 0,752 | 2,023 | 0,649 | 2,206 |
| 20 | 1,201 | 1,411 | 1,100 | 1,537 | 0,998 | 1,676 | 0,984 | 1,828 | 0,792 | 1,991 | 0,692 | 2,162 |
| 21 | 1,222 | 1,420 | 1,125 | 1,538 | 1,026 | 1,669 | 0,927 | 1,812 | 0,829 | 1,964 | 0,732 | 2,124 |
| 22 | 1,239 | 1,429 | 1,147 | 1,541 | 1,053 | 1,664 | 0,958 | 1,797 | 0,863 | 1,940 | 0,769 | 2,090 |
| 23 | 1,257 | 1,437 | 1,168 | 1,543 | 1,078 | 1,660 | 0,986 | 1,785 | 0,895 | 1,920 | 0,804 | 2,061 |
| 24 | 1,273 | 1,446 | 1,188 | 1,546 | 1,101 | 1,656 | 1,013 | 1,775 | 0,925 | 1,902 | 0,837 | 2,035 |
| 25 | 1,288 | 1,454 | 1,206 | 1,550 | 1,123 | 1,654 | 1,038 | 1,767 | 0,953 | 1,886 | 0,868 | 2,012 |
| 26 | 1,302 | 1,461 | 1,224 | 1,553 | 1,143 | 1,652 | 1,062 | 1,759 | 0,979 | 1,873 | 0,897 | 1,992 |
| 27 | 1,316 | 1,469 | 1,240 | 1,556 | 1,162 | 1,651 | 1,084 | 1,753 | 1,004 | 1,861 | 0,925 | 1,974 |
| 28 | 1,328 | 1,476 | 1,255 | 1,560 | 1,181 | 1,650 | 1,104 | 1,747 | 1,028 | 1,850 | 0,951 | 1,958 |
| 29 | 1,341 | 1,483 | 1,270 | 1,563 | 1,198 | 1,650 | 1,124 | 1,743 | 1,050 | 1,841 | 0,975 | 1,944 |
| 30 | 1,352 | 1,489 | 1,284 | 1,567 | 1,214 | 1,650 | 1,143 | 1,739 | 1,071 | 1,833 | 0,998 | 1,931 |
| 31 | 1,363 | 1,496 | 1,297 | 1,570 | 1,229 | 1,650 | 1,160 | 1,735 | 1,090 | 1,825 | 1,020 | 1,920 |
| 32 | 1,373 | 1,502 | 1,309 | 1,574 | 1,244 | 1,650 | 1,177 | 1,732 | 1,109 | 1,819 | 1,041 | 1,909 |
| 33 | 1,383 | 1,508 | 1,321 | 1,577 | 1,258 | 1,651 | 1,193 | 1,730 | 1,127 | 1,813 | 1,061 | 1,900 |
| 34 | 1,393 | 1,514 | 1,333 | 1,580 | 1,271 | 1,652 | 1,028 | 1,728 | 1,144 | 1,808 | 1,080 | 1,891 |
| 35 | 1,402 | 1,519 | 1,343 | 1,584 | 1,283 | 1,653 | 1,222 | 1,726 | 1,160 | 1,803 | 1,097 | 1,884 |
| 36 | 1,411 | 1,525 | 1,354 | 1,587 | 1,295 | 1,654 | 1,236 | 1,724 | 1,175 | 1,799 | 1,114 | 1,877 |
| 37 | 1,419 | 1,530 | 1,364 | 1,590 | 1,307 | 1,655 | 1,249 | 1,723 | 1,190 | 1,795 | 1,131 | 1,870 |
| 38 | 1,427 | 1,535 | 1,373 | 1,594 | 1,318 | 1,656 | 1,261 | 1,722 | 1,204 | 1,792 | 1,146 | 1,864 |
| 39 | 1,435 | 1,540 | 1,382 | 1,597 | 1,328 | 1,658 | 1,273 | 1,722 | 1,218 | 1,789 | 1,161 | 1,859 |
| 40 | 1,442 | 1,544 | 1,391 | 1,600 | 1,338 | 1,659 | 1,285 | 1,721 | 1,230 | 1,786 | 1,175 | 1,854 |
| 45 | 1,475 | 1,566 | 1,430 | 1,615 | 1,383 | 1,666 | 1,336 | 1,720 | 1,287 | 1,776 | 1,238 | 1,835 |
| 50 | 1,503 | 1,585 | 1,462 | 1,628 | 1,421 | 1,674 | 1,378 | 1,721 | 1,335 | 1,771 | 1,291 | 1,822 |
| 55 | 1,528 | 1,601 | 1,490 | 1,641 | 1,452 | 1,681 | 1,414 | 1,724 | 1,374 | 1,768 | 1,334 | 1,814 |
| 60 | 1,549 | 1,616 | 1,514 | 1,652 | 1,480 | 1,689 | 1,444 | 1,727 | 1,408 | 1,767 | 1,372 | 1,808 |
| 65 | 1,567 | 1,629 | 1,536 | 1,662 | 1,503 | 1,696 | 1,471 | 1,731 | 1,438 | 1,767 | 1,404 | 1,805 |
| 70 | 1,583 | 1,641 | 1,554 | 1,672 | 1,525 | 1,703 | 1,494 | 1,735 | 1,464 | 1,768 | 1,433 | 1,802 |
| 75 | 1,598 | 1,652 | 1,571 | 1,680 | 1,543 | 1,709 | 1,515 | 1,739 | 1,487 | 1,770 | 1,458 | 1,801 |
| 80 | 1,611 | 1,662 | 1,586 | 1,688 | 1,560 | 1,715 | 1,534 | 1,743 | 1,507 | 1,772 | 1,480 | 1,801 |
| 85 | 1,624 | 1,671 | 1,600 | 1,696 | 1,575 | 1,721 | 1,550 | 1,747 | 1,525 | 1,774 | 1,500 | 1,801 |
| 90 | 1,635 | 1,679 | 1,612 | 1,703 | 1,589 | 1,726 | 1,566 | 1,751 | 1,542 | 1,776 | 1,518 | 1,801 |
| 95 | 1,645 | 1,687 | 1,623 | 1,709 | 1,602 | 1,732 | 1,579 | 1,755 | 1,557 | 1,778 | 1,535 | 1,802 |
| 100 | 1,654 | 1,694 | 1,634 | 1,715 | 1,613 | 1,736 | 1,592 | 1,758 | 1,571 | 1,780 | 1,550 | 1,803 |
| 150 | 1,720 | 1,746 | 1,706 | 1,760 | 1,693 | 1,774 | 1,679 | 1,788 | 1,665 | 1,802 | 1,651 | 1,817 |
* Источник: Суслов В.И; Ибрагимов Н.М, Талышева Л.П.; Цыплаков А.А. Эконометрия: Учебник. — Новосибирск: Из-во СО РАН, 2005. «—» обозначена невозможность получения оценки статистики dw из-за отсутствия автокорреляции остатков с помощью данного критерия при соответствующих комбинациях значений объема выборки n и числа объясняющих переменных k в модели.
Источник: Суслов В.И; Ибрагимов Н.М, Талышева Л.П.; Цыплаков А.А. Эконометрия: Учебник. — Новосибирск: Из-во СО РАН, 2005. «—» обозначена невозможность получения оценки статистики dw из-за отсутствия автокорреляции остатков с помощью данного критерия при соответствующих комбинациях значений объема выборки n и числа объясняющих переменных k в модели.
1Реальный объем промышленного производства по ОКВЭД (IP_EA_Q) в России цепной индекс, где за базу (100%) взят уровень 2002 года. Количество безработныхв среднем за период в млн. чел(UNEMPL_Q). Данные с сайта http://sophist.hse.ru
- 2Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
- Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
- Если массив1 и массив2 имеют различное количество точек данных, то функция КОРРЕЛ возвращает значение ошибки #Н/Д.
- Если массив1 либо массив2 пуст, или если σ (стандартное отклонение) их значений равно нулю, то функция КОРРЕЛ возвращает значение ошибки #ДЕЛ/0!.
3 В более ранних версиях СТЬЮДРАСПРОБР.
1 Если надстройка Анализ данных не установлена, то установить, выполнив следующее: Файл-Параметры-Надстройки-Надстройки Excel-Перейти. В диалоговом окне доступных надстроек отметить флажками Пакет анализа и Поиск решения.
2 Модель строим по 39 наблюдениям. Последнее наблюдение будет использовано при проверке адекватности модели.
2)
вектору наблюдённых значений эндогенной
переменной,
![]() ;
;
3)
вектору
![]() ;
;
4)
вектору случайных возмущений,
![]() .
.
46.
Для каких целей используется F
статистика?
1)
для проверки адекватности модели;
2)
для прогнозирования значений эндогенной
переменной;
3)
для тестирования гомоскедастичности
случайных возмущений;
4)
для исследования качества спецификации
модели.
47.
Что вычисляется по следующей формуле

?
1)
коэффициент детерминации;
2)
статистика теста Голдфелда-Квандта;
3)
величина
![]() ;
;
4)
статистика теста Дарбина-Уотсона.
48.
В
рамках модели

уравнения
наблюдений
1)
образуют схему Гаусса-Маркова;
2)
не образуют схему Гаусса-Маркова;
3)
образуют схему Дарбина-Уотсона;
4)
образуют схему Голдфелда-Квандта.
49.
Что нужно знать для построения
интервального прогноза значения
эндогенной переменной, [y0—,
y0+]
?
1)
точечный прогноз значения эндогенной
переменной,
![]() ;
;
2)
величину Fкрит;
3)
значение эндогенной переменной, y0;
4)
коэффициент детерминации R2.
50.
Коэффициент детерминации, R2
является
1)
константой;
2)
случайной переменной;
3)
экзогенной переменной;
4)
предопределённой переменной.
51.
На какой этап возвращается экономист,
если оценённая модель признана
неадекватной?
1)
первый этап схемы построения модели;
2)
второй этап схемы построения модели;
3)
третий этап схемы построения модели;
4)
четвёртый этап схемы построения модели.
52.
Количество
текущих эндогенных переменных
эконометрической модели совпадает с:
1)
количеством экзогенных переменных;
2)
количеством предопределённых переменных;
3)
количеством уравнений;
4)
количеством тождеств.
53.
Практически
достоверным называется событие,
вероятность которого:
1)
равна 1;
2)
равна 0,5;
3)
расположена в промежутке [0,95; 1);
4)
расположена в промежутке [0; 0,5).
54.
Согласно утверждению теоремы Гаусса-Маркова
оценка
![]()
коэффициента
![]()
функции регрессии обладает
1)
нулевой дисперсией;
2)
нулевым математическим ожиданием;
3)
наименьшей дисперсией;
4)
наименьшим математическим ожиданием.
55.
Для каких целей предназначена статистика
![]()
?
1)
для проверки адекватности модели
 ;
;
2)
для исследования значимости коэффициента
детерминации;
3)
для исследования качества спецификации
модели
 ;
;
4)
для тестирования предпосылок теоремы
Гаусса-Маркова.
56.
В каких случаях используются константы
dL
и dU
?
1)
при оценивании модели;
2)
при тестировании предпосылки теоремы
Гаусса-Маркова;
3)
в процессе проверки адекватности модели;
4)
при прогнозировании значений эндогенной
переменной.
57.
Чему
будет равна величина
![]()
при
оценивании модели

методом наименьших квадратов?
1)
минимуму;
2)
величине
![]() ;
;
3)
величине
![]() ;
;
4) Нулю
58.
Для каких целей предназначена статистика
![]()
?
1)
для оценивания модели;
2)
для тестирования предпосылки теоремы
Гаусса-Маркова;
3)
для проверки адекватности модели;
4)
для прогнозирования значений эндогенной
переменной.
59.
Что нужно знать для построения
интервального прогноза значения
эндогенной переменной, [y0—,
y0+]
?
1)
ср. кв. ошибку прогноза значения
эндогенной переменной,
![]() ;
;
2) величину
Fкрит;
3) значение
эндогенной переменной, y0;
4) коэффициент
детерминации R2.
60.
Что следует изменить, если в спецификации
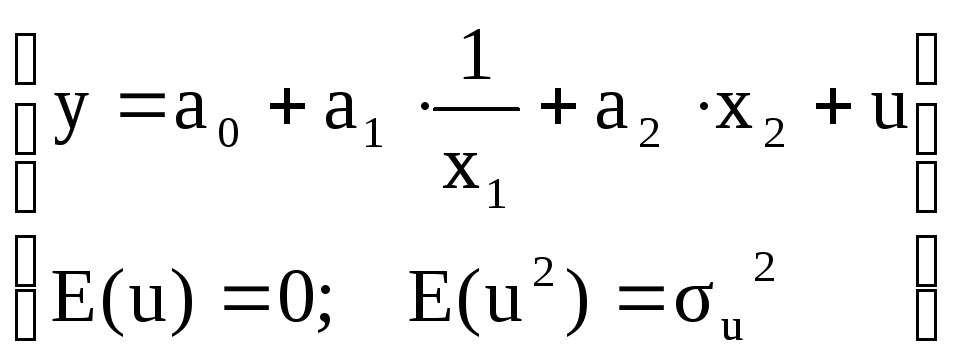
предпосылка
![]()
неадекватна?
1)
вид функции регрессии;
2)
величину
![]() ;
;
3)
коэффициент
![]() ;
;
4)
коэффициент
![]()
![]() .
.
61.
Чему равносилен пропуск значащей
объясняющей переменной в модели?
1)
гетероскедастичности случайных
возмущений;
2)
неверному виду функции регрессии;
3)
неверному выбору эндогенной переменной;
4)
гомоскедастичности случайных возмущений.
62.
В какой из следующих форм может быть
представлена эконометрическая модель?
1)
открытой и закрытой;
2)
линейной и нелинейной;
3)
макроэкономической и микроэкономической;
4)
структурной и приведённой.
63.
Как называется выражение
![]() ?
?
1)
нормальными уравнениями;
2)
уравнениями наблюдений;
3)
поведенческим уравнением;
4)
экономическим тождеством.
64.
Где используются константы dL
и dU
?
1)
в тесте Голдфелда- Квандта;
2)
в процедуре прогнозирования эндогенной
переменной;
3)
в процессе проверки адекватности модели;
4)
в тесте Дарбина-Уотсона.
65.
Для
оценивания модели

методом наименьших квадратов
1)
не требуется её преобразование к
линейному виду;
2)
требуется преобразование к линейному
виду;
3)
требуется логарифмическое преобразование;
4)
требуется преобразование переменной
x1.
66.
Что нужно знать для оценки точности
прогноза значения эндогенной переменной
![]()
в рамках модели

?
1)
значения экзогенных переменных, (x1,
x2);
2)
значение случайного возмущения u;
3)
значение эндогенной переменной y0;
4)
значение прогноза эндогенной переменной,
![]() .
.
67.
Чему должна быть равна величина (![]()
—![]() ),
),
если
![]()
— оптимальный прогноз значения
![]()
в рамках адекватной модели
 ?
?
1)
равна нулю;
2)
имеет нулевую дисперсию;
3)
имеет нулевое ожидаемое значение;
4)
равна величине u.
68.
На каком этапе построения модели
используется обучающая выборка
![]() ?
?
1)
на первом этапе схемы построения модели;
2)
на втором этапе схемы построения модели;
3)
на третьем этапе схемы построения
модели;
4)
на четвёртом этапе схемы построения
модели.
69. Для каких целей
предназначена приведённая форма
эконометрической модели
?
1)
прогнозирования предопределённых
переменных;
2)
прогнозирования текущих экзогенных
переменных;
3)
прогнозирования значений текущих
эндогенных переменных;
4)
прогнозирования лаговых переменных.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #