ОБЕСПЕЧЕНИЕ
КАЧЕСТВА НА АНАЛИТИЧЕСКОМ ЭТАПЕ.
Качество на аналитическом этапе
обеспечивается системой контроля
качества
Контроль
качества
Терминология контроля качества.
Термин «контроль качества» — не совсем
удачный перевод английского выражения
‘quality control’. Если
слово ‘quality’
обозначает «качество» и употребляется
в положительном смысле, то слово
‘control’ скорее
равнозначно русским словам «проверка»,
«контроль», «надзор», которые
справедливо могут вызвать определенную
настороженность в связи с возможными
репрессивными мерами. Однако
Оксфордский словарь английского языка
дает и другие значения:
‘control’ — это также
«управление» или «определение
неполадок путем сравнения». Во всяком
случае американский статистик
W.Shewhart, заложивший теоретические
основы контроля качества, подразумевал
под контролем качества «способ
управления серийным производством
путем выявления и предотвращения
возможных неполадок (ошибок)». В 1931
году он изложил некоторый способ для
улучшения индустриального производства
продукции в больших сериях. Уже отсюда
идея контроля качества, как одного из
способов управления производством,
распространилась на другие
профессиональные сферы, включая
лабораторную медицину. В настоящее
время контроль качества — это система,
разработанная для проверки и подтверждения
того, что процесс измерения проходит в
соответствии со сделанными предположениями,
а также чтобы убедиться, что образцы
пациентов измеряются правильно. В
Международном Стандарте под «качеством»
понимается — совокупность свойств и
характеристик изделия или услуги,
обеспечивающая удовлетворение
обусловленных или предполагаемых
потребностей. Термин «качество» не
применяется ни для выражения превосходной
степени в сравнительном смысле, ни
в количественном смысле при проведении
технических оценок. Обеспечение
качества — совокупность планируемых
и систематически проводимых мероприятий,
необходимых для создания уверенности
в том, что изделие или услуга удовлетворяет
определенным требованиям качества.
На предприятии обеспечение качества
служит инструментом управления.
Контроль качества — методы и
деятельность, используемые для
удовлетворения требований качества.
Контроль качества включает методы и
виды деятельности, направленные
одновременно на управление процессом
и устранение причин неудовлетворительных
результатов. Система качества —
совокупность организационной структуры,
ответственности, процедур и ресурсов,
направленных на внедрение административного
контроля качеством. Масштабы системы
качества должны соответствовать задачам
обеспечения качества. Программа
качества — документ, регламентирующий
конкретные меры в области качества.
Проверка качества — систематический
и независимый анализ, позволяющий
определить соответствие деятельности
и результатов в области качества
запланированным мероприятиям, а также
эффективность их внедрения и соответствие
поставленным целям. Проверки качества
проводятся лицами, которые не несут
непосредственной ответственности за
проверяемые участки. При этом
желательно взаимодействие с персоналом
проверяемых участков. Одной из целей
проверки качества является оценка
необходимости проведения корректирующих
мероприятий.
Надзор за качеством — постоянное
наблюдение и проверка состояния процедур,
методов, условий исполнения, процессов,
а также анализ полученных результатов
в сравнении с установленными
показателями. Надзор за качеством может
осуществляться заказчиком или от его
имени с целью проверки выполнения
договорных обязательств.
Контроль — мероприятия, включающие
проведение измерений, испытаний, проверки
одной или нескольких характеристик
изделия или услуги и их сравнение с
установленными требованиями с целью
определения соответствия.
Надежность — способность изделия
выполнить требуемые функции в заданных
условиях в течение заданного периода
времени. Термин «надежность» также
используется как характеристика
вероятности успеха.
Несоответствие — невыполнение
установленных требований, т.е. отсутствие
одной или нескольких характеристик
качества
Техническое условие — документ,
устанавливающий требования, которым
должны соответствовать изделие или
услуга.
Основы теории контроля качества.
Критерии качественного измерения имеют
общий характер для многих видов
деятельности. ГОСТ 16263-70 определяет эти
критерии качества измерений. Статистический
анализ вероятных ошибок можно
проиллюстрировать на хорошо известном
примере мишени, в которую некий
стрелок пускает свои стрелы (рис.3).
В лабораторной практике это будет
равнозначно повторению анализа из одной
и той же пробы. Здесь могут возникнуть
несколько ситуаций.
Если стрелок всякий раз попадал близко
к середине мишени, то никаких серьезных
ошибок не было (рис 4). В этом случае имела
место правильная стрельба.
Точность измерений — качество
измерений, отражающее близость их
результатов к истинному значению
измеряемой величины, при котором малы
все виды погрешностей систематические
и случайные (правильность и воспроизводимость
близки к идеальным). Если все стрелы
легли рядом, но достаточно далеко от
центра мишени. В этом случае имеет место
плохая правильность стрельбы при хорошей
воспроизводимости.
Правильность — качество измерений,
отражающее близость к нулю систематических
погрешностей в их результатах, то
есть соответствие среднего значения
результатов измерений с истинной
величиной измеряемого параметра.
Причиной отклонения от правильного
результата был один и тот же фактор,
который называют систематической
ошибкой;
Если стрелы летели в целом в правильном
направлении, но при этом попадали в
самые разные части мишени. Такая ситуация
характеризуется плохой
сходимостью/воспроизводимостью при
достаточной правильности.
Сходимость — качество измерений,
отражающее близость друг к другу
результатов измерений, выполненных в
одинаковых условиях (стрельба по одной
мишени в одно время из одного лука)
(рисунок 6).
Воспроизводимость — качество
измерений, отражающее близость друг к
другу результатов измерений,
выполненных в разных условиях (стрельба
по разным мишеням в разное время) (рисунок
7). Различают воспроизводимость в серии
(сходимость), во времени (день ото дня)
и межлабораторную воспроизводимость.
Причин плохой воспроизводимости больше,
чем плохой сходимости, но в том и другом
случае их может быть несколько, а все
вместе их определяют термином случайная
ошибка.
Стрелы вообще не попали в мишень (рисунок
7). Такие, так называемые грубые
ошибки, в целом свойственны
человеческой натуре и их никак нельзя
полностью исключить, но, используя
соответствующие организационные меры,
можно попытаться свести их к минимуму.
Главными аналитическими характеристиками
являются воспроизводимость и правильность.
По рекомендации Международной федерации
клинической химии (IFCC)
воспроизводимость выражается в виде
стандартного отклонения или коэффициента
вариации результатов повторных измерений
одной и той же пробы, а правильность — в
виде разности между средним значением
серии повторных измерений и истинным
значением.
Основные статистические понятия, используемые в контроле качества.
Статистика случайных величин использует
так называемое нормальное распределение
(рис. 8). Нормальное распределение
характеризуется тем, что среднее
арифметическое значение (получается
делением суммы всех значений на количество
измерений (уравнение 1), совпадает с
модой (наиболее часто повторяющееся
значение) и медианой (центр, от которого
половина значений будет меньше, а
половина больше медианы).
Для оценки качества исследований
рассчитываются следующие статистические
показатели:
1. Среднее арифметическое значение или
средняя арифметическая (Хср )
SXi
Хср = ———— (уравнение 1) п
В уравнении 1 Xi — значения
конкретных измерений, n —
число измерений
2. Отклонение от правильного значения,
то есть разница между истинной величиной
(i) (центр мишени)
и средней арифметической будет отражает
величину систематической ошибки (Ь) и,
соответственно, точность определений
(d %):
b (абсолютная величина) =
Хср — ^ (уравнение 2 ) или
(Xep-^l)
d (отклонение в %%) =
————— х 100% (уравнение 3 ) ^
Если при проведении контроля качества
используется контрольная сыворотка с
исследованным содержанием вещества,
то контроль правильности целесообразно
проводить в условиях хорошей сходимости
результатов, то есть при минимальном
отклонении (d). Если все полученные
значения укладываются в пределы
допустимых отклонений, имеющихся в
паспорте сыворотки, то правильность
удовлетворительная
3. Стандартное отклонение (ст
— «сигма», SD
стандартная девиация, дисперсия).
/
£(Xi-Xep)2
/ ————— (уравнение 4 ) ст= ^/
п — 1
Стандартное отклонение отражает величину
случайной ошибки, то есть воспроизводимость
конкретного измерения в абсолютной
величине. Как показано на рисунке 9, в
диапазон ± 1 ст вокруг среднего попадает
около 68,3 % измеренных значений, в диапазон
± 2 а — около 95 % , в диапазон ± 3 от — около
99,7 % измеренных значений. Иными словами
— в среднем только 1 результат из 3
может отклоняться от среднего значения
более чем на 1 ст, только 1 результат из
20 последовательных может отклоняться
от среднего значения более чем на 2 от
и только 1 из 333 последовательньпс
результатов может отклоняться от
Xq, более чем на 3 от.
4. Коэффициент вариации (V или
CV)
ст
V=
—— х 100 % (уравнение 5 )
Хср
Коэффициент вариации отражает
воспроизводимость в относительном
значении (процентах). Его легко можно
использовать для характеристики и
сравнения различных лабораторных
показателей. Чем меньше коэффициент
вариации, тем выше воспроизводимость
и сходимость результатов. Коэффициент
вариации, характеризующий сходимость,
всегда меньше, чем коэффициент
вариации, характеризующий воспроизводимость
изо дня в день.
5. Допустимый предел ошибки (ДПО)
При оценке результатов лабораторных
исследований встает задача не только
сравнить разные методы (способы, подходы
и т.д.), но и сопоставить получаемые
результаты с возможными биологическими
вариациями. Допустимая ошибка связана
с тем диапазоном, который свойственен
исследуемой величине здоровых людей.
Для этого коэффициент вариации
сопоставляют с допустимым пределом
ошибки (ДПО), который рассчитывается по
формуле Тонкса (уравнение б):
(диапазон нормальной области) ДПО = 1/4 х
—————————————— х 100% (уравнение
6)
среднее значение нормальной области
Вопрос о медицинских допустимых пределах
ошибок является сложным и окончательно
нерешенным. При установлении ДПО
необходимо ориентироваться на референтные
величины. Однако эти величины
определены не для всех компонентов, они
зависят от многих факторов, в том числе
от уровня лабораторной оснащенности.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
Used in algorithmic trading, the standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
Предположим, мы измеряем вес 10 разных черепах.
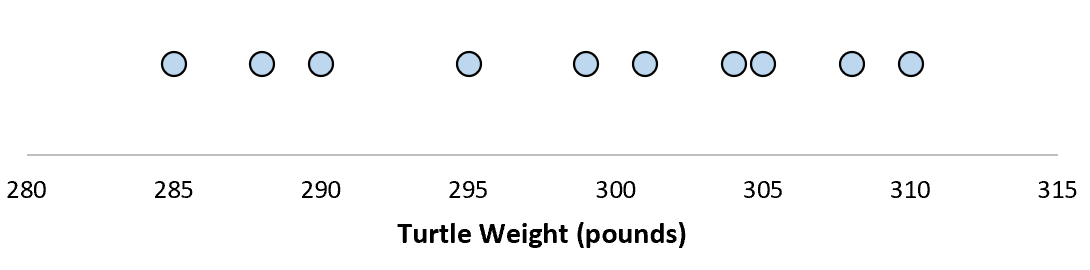
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
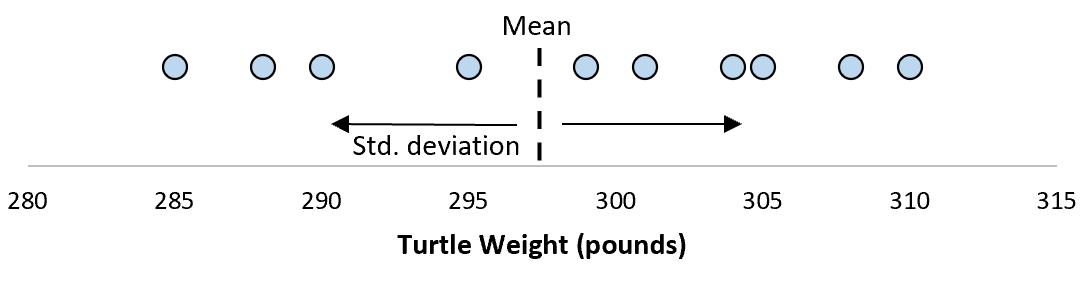
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
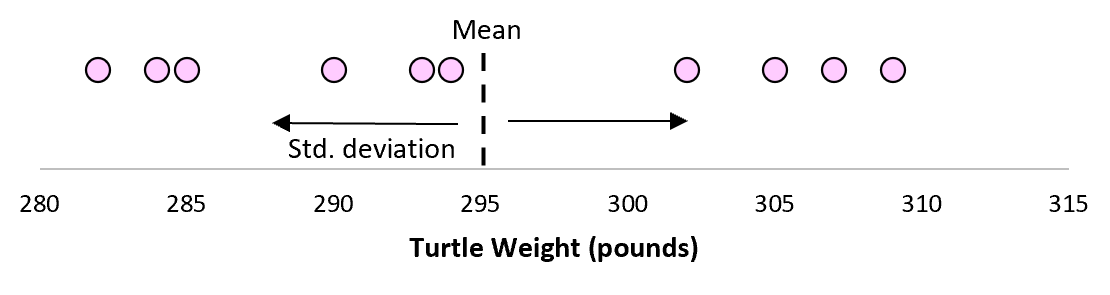
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
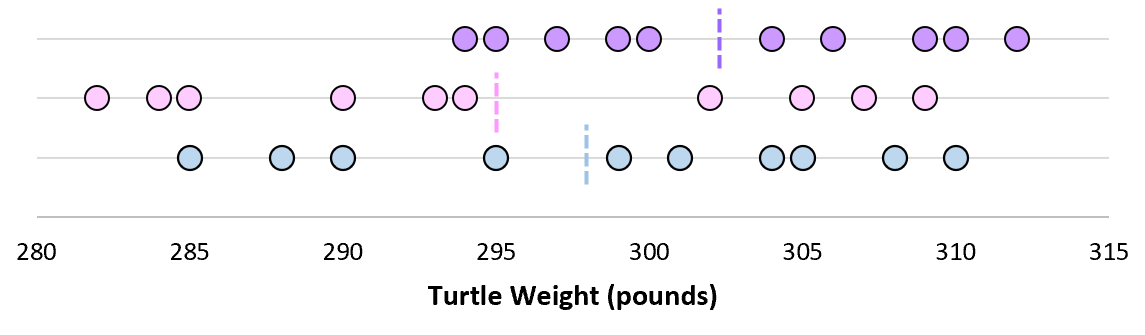
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
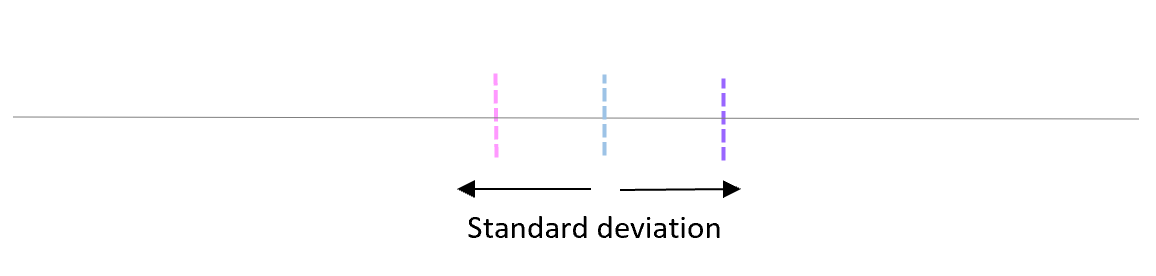
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.


Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
Термин «статистика» означает практику анализа и сбора числовых данных, которые предоставляются в больших количествах. Есть несколько статистических исследований, в том числе биология, финансы, психология, инженерия и многие другие.
Статистические исследования полезны для сбора и анализа любых данных в числовой форме.
Стандартное отклонение и стандартная ошибка являются двумя наиболее распространенными показателями, которые используются в области статистики. Основной мотив стандартного отклонения и стандартной ошибки — показать результаты статистического анализа и характеристики выборочных данных.
Стандартное отклонение и стандартная ошибка немного сбивают с толку, но они отличаются друг от друга во многих терминах.
Основные выводы
- Стандартное отклонение измеряет разброс точек данных вокруг среднего значения, а стандартная ошибка оценивает изменчивость среднего значения выборки.
- Чем больше размер выборки, тем меньше стандартная ошибка, но размер выборки не влияет на стандартное отклонение.
- Стандартное отклонение подходит для анализа отдельных точек данных, а стандартная ошибка используется для оценки точности выборочных средних.
Стандартное отклонение против стандартной ошибки
Разница между стандартным отклонением и стандартной ошибкой заключается в том, что они оба различаются по своим статистическим помехам. Стандартное отклонение помогает рассредоточить отдельные значения данных. Он показывает точность среднего значения, которое представляет выборочные данные. В то время как стандартная ошибка основана на статистических помехах данных выборки.

Хотите сохранить эту статью на потом? Нажмите на сердечко в правом нижнем углу, чтобы сохранить в свой собственный блок статей!
В статистике стандартное отклонение выражает количество членов определенной группы, которое отличается от значения среднего значения той же группы. Карл Пирсон был первым, кто использовал стандартное отклонение в письменной форме для своих лекций.
Этот термин был впервые использован в 1894 году. Термин «стандартное отклонение» использовался для замены альтернативных названий, использовавшихся ранее для тех же идей.
В статистике стандартная ошибка называется приблизительным стандартным отклонением, которое включается в статистическую выборку. Вариация, включенная в стандартную ошибку, находится между средним значением, рассчитанным на основе совокупности, и другим точным значением, которое принято.
Если расчет среднего включает больше точек данных, то стандартная ошибка будет меньше.
Сравнительная таблица
| Параметры сравнения | Стандартное отклонение | Стандартная ошибка |
|---|---|---|
| Смысл | Мера дисперсии от среднего по набору данных. | Мера оценки посредством ее статистической точности. |
| Обозначает изменчивость | В пределах выборки. | В популяции, среди нескольких выборок. |
| Тип | Описательная статистика. | Выведенный статистика. |
| Распределение | Наблюдение касается нормальной кривой. | Оценка связана с нормальной кривой. |
| Расчет | Путем извлечения квадратного корня из дисперсии. | Деление стандартного отклонения на квадратный корень из размера выборки. |
Что такое стандартное отклонение?
Вариация указывает на отклонение значений, находящихся в среднем. В результате степень вариации обозначается мерами вариации. Что касается показателей вариации, стандартное отклонение является одним из наиболее распространенных показателей.
Для удобного математического анализа люди предпочитают стандартное отклонение, поскольку оно полностью основано на всех значениях, будь то самое высокое или самое низкое.
Стандартное отклонение называется мерой отклонения от среднего по набору данных. Его основной мотив — измерить абсолютную изменчивость любого распределения.
Если дисперсия или изменчивость выше, стандартное отклонение слишком велико. В результате величина отклонения также будет больше. Стандартное отклонение обозначается σ (сигма).
Когда дело доходит до финансовых условий, стандартное отклонение используется в таких сделках, как взаимные фонды, акции и другие. Стандартное отклонение используется для измерения рисков, связанных с инвестиционным инструментом.
Это полезно для инвесторов, потому что дает им математическую основу для принятия решений на финансовом рынке для своих инвестиций.
Стандартное отклонение можно рассчитать с помощью программного обеспечения, используемого для статистического анализа, а также вручную. Для окончательного результата вам нужно пройти несколько шагов, например найти среднее значение, а затем найти отклонение каждой оценки.
Далее квадратное отклонение и находим сумму квадратов. Затем перейдите к дисперсии и найдите ее, а затем найдите из нее квадратный корень.

Что такое стандартная ошибка?
В математике стандартная ошибка используется для измерения изменчивости статистики. SE — это его сокращенная форма. Это помогает сделать приближение стандартной ошибки в данной выборке.
Он оценивает точность, согласованность и эффективность выборки, или можно сказать, что он измеряет, как представить распределение выборки, точно представляющее совокупность.
Среднее или среднее значение рассчитывается при наличии выборочной совокупности. Стандартная ошибка помогает компенсировать любые случайные неточности, связанные со сбором образцов.
Когда собирается несколько выборок, это создает разницу между переменными, поскольку среднее значение каждой выборки немного отличается друг от друга. Разница рассчитывается как стандартная ошибка.
Стандартная ошибка полезна как в статистике, так и в экономике. Когда дело доходит до финансовых терминов, это полезно в области, связанной с эконометрикой. В этом исследователь использует стандартную ошибку для выполнения гипотеза тестирование и регрессионный анализ.
Тогда как в выведенный статистика Стандартная ошибка является основой для создания доверия интер.
Стандартная ошибка рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки. Если в расчете среднего значения больше точек данных, стандартная ошибка будет меньше.
В результате данные будут более репрезентативными для истинного среднего значения. Если в данных обнаружены заметные несоответствия, это означает, что стандартная ошибка велика.
Основные различия между стандартным отклонением и стандартной ошибкой
- Стандартное отклонение не зависит от случайной выборки, потому что это типичное отклонение от среднего. Но стандартная ошибка зависит от случайной выборки, потому что от ожидаемого значения это типичное отклонение.
- Что касается увеличения размера выборки, стандартное отклонение дает его конкретную меру. С другой стороны, в стандартной ошибке она уменьшается.
- Стандартное отклонение упоминается как выборочная статистика, поскольку его статистика включает значения, полученные из выборки. В то время как стандартная ошибка упоминается как параметр совокупности, в котором параметр является значением и описывает всю совокупность.
- Стандартное отклонение измеряет количество наблюдений, которые отличаются друг от друга, тогда как стандартная ошибка измеряет точность среднего значения выборки до Средняя численность населения.
- Когда дело доходит до расчета доверительного интервала, связанного с генеральной совокупностью, стандартное отклонение не рассчитывается через него. С другой стороны, стандартная ошибка делает это.
Рекомендации
- https://www.sciencedirect.com/science/article/pii/S0022103113000668
- https://www.jstor.org/stable/2729411

Эмма Смит имеет степень магистра английского языка в колледже Ирвин-Вэлли. Она работает журналистом с 2002 года, пишет статьи об английском языке, спорте и праве. Подробнее обо мне на ней био страница.

