Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение 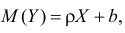
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии  неизвестны, неизвестна и величина коэффициента корреляции
неизвестны, неизвестна и величина коэффициента корреляции 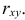 Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений:
Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений: 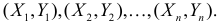 Эти результаты могут служить источником информации о неизвестных значениях
Эти результаты могут служить источником информации о неизвестных значениях 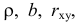 надо только уметь эту информацию извлечь оттуда.
надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии 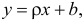 как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для
как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для  можно принять те их значения, при которых имеет минимум функция
можно принять те их значения, при которых имеет минимум функция 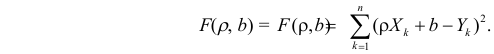
Такие значения  , согласно необходимым условиям экстремума, находятся из системы уравнений:
, согласно необходимым условиям экстремума, находятся из системы уравнений:
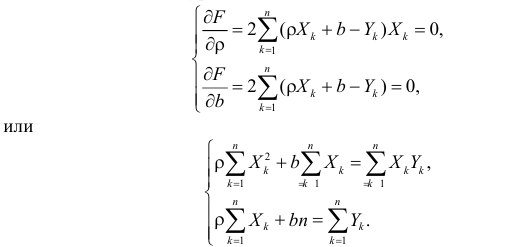
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.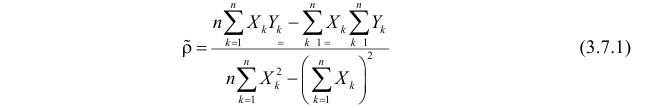
и
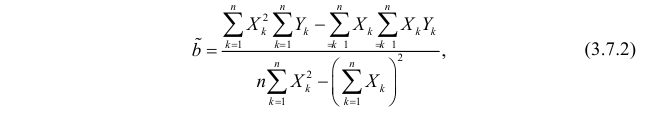
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 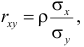 где
где 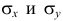 средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через
средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через 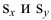 оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку
оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку 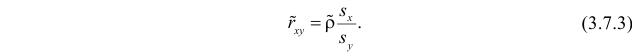
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 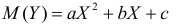 оценки параметров
оценки параметров 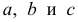 находятся из условия минимума функции
находятся из условия минимума функции
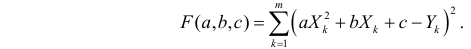
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X 
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
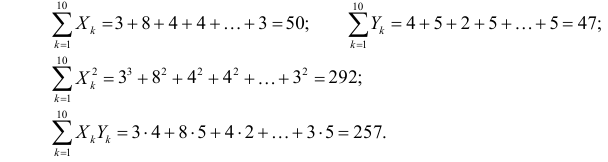
По формулам (3.7.1) и (3.7.2) получим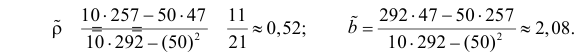
Итак, оценка линии регрессии имеет вид 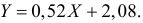 Так как
Так как 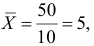 то по формуле (3.1.3)
то по формуле (3.1.3)
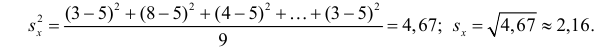
Аналогично, 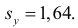 Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину
Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину 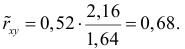
Ответ. 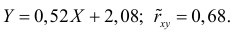
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 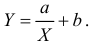 Найти оценки параметров
Найти оценки параметров 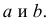
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 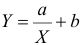 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)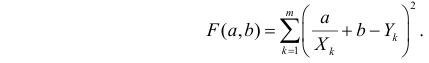
Необходимые условия экстремума приводят к системе из двух уравнений: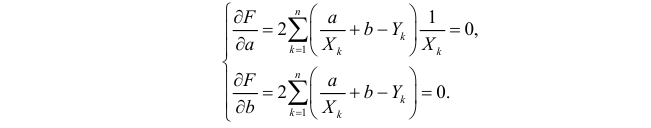
Откуда
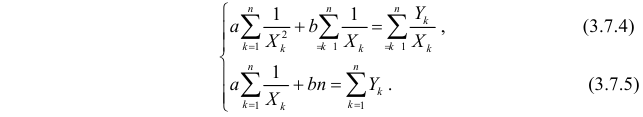
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров 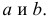
На основе опытных данных вычисляем: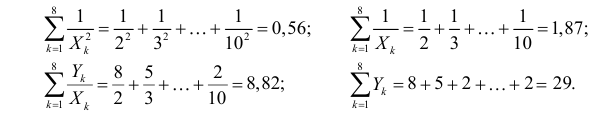
В итоге получаем систему уравнений (?????) и (?????) в виде 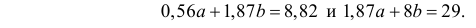
Эта система имеет решения 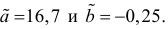
Ответ. 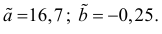
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 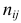 равно числу наблюдений, для которых X находится в интервале
равно числу наблюдений, для которых X находится в интервале 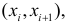 а Y – в интервале
а Y – в интервале 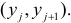 Через
Через 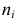 обозначено число наблюдений, при которых
обозначено число наблюдений, при которых 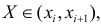 а Y произвольно. Число наблюдений, при которых
а Y произвольно. Число наблюдений, при которых 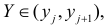 а X произвольно, обозначено через
а X произвольно, обозначено через 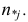
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 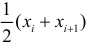 и
и 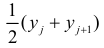 наблюдались
наблюдались 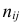 раз.
раз.
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.

Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 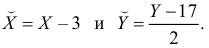 Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 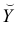 при фиксированных значениях
при фиксированных значениях 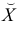 :
:
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).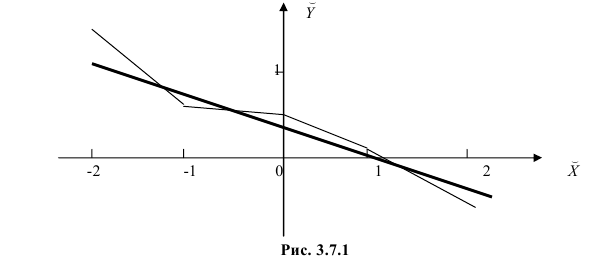
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33): 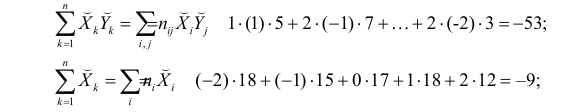
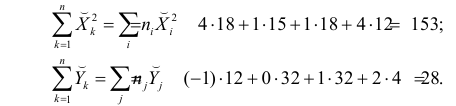
Тогда
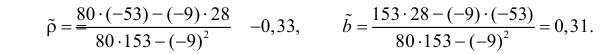
В новом масштабе оценка линии регрессии имеет вид 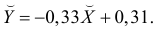 График этой прямой линии изображен на рис. 3.7.1.
График этой прямой линии изображен на рис. 3.7.1.
Для оценки 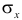 по корреляционной таблице можно воспользоваться формулой (3.1.3):
по корреляционной таблице можно воспользоваться формулой (3.1.3):
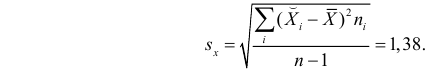
Подобным же образом можно оценить 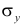 величиной
величиной 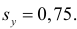 Тогда оценкой коэффициента корреляции может служить величина
Тогда оценкой коэффициента корреляции может служить величина 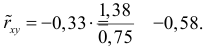
Вернемся к старому масштабу:
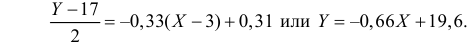
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ. 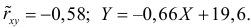
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 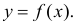 Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то
Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то 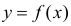 играет роль линии регрессии и все свойства линии регрессии приложимы к
играет роль линии регрессии и все свойства линии регрессии приложимы к 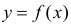 . В частности,
. В частности, 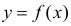 обычно находят по методу наименьших квадратов.
обычно находят по методу наименьших квадратов.
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
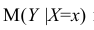 можно представить в виде
можно представить в виде 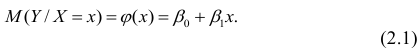
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 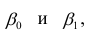 называемые коэффициентами регрессии, а также
называемые коэффициентами регрессии, а также 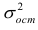 — остаточная дисперсия.
— остаточная дисперсия.
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей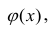 которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости
которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости 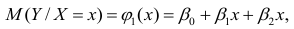
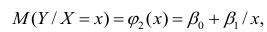
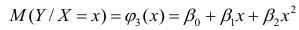 линейны относительно параметров
линейны относительно параметров 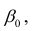
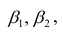 хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости
хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости 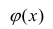 выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
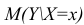 можно представить в виде (2.1).
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 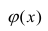 линейна и по оцениваемым параметрам, и
линейна и по оцениваемым параметрам, и
по переменным. Оценки параметров модели (2.1) 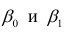 обозначил
обозначил 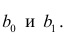 Оценку остаточной дисперсии
Оценку остаточной дисперсии 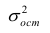 обозначим
обозначим 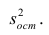 Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии
Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии 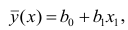 коэффициенты которого
коэффициенты которого 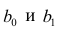 находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака
находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака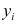 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 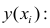
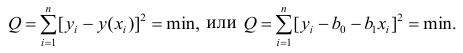
Составим систему нормальных уравнений: первое уравнение
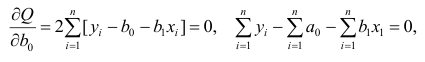
откуда 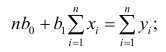
второе уравнение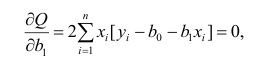
откуда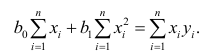
Итак,
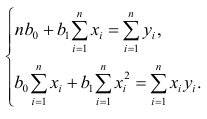
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно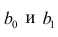 найдём оценки параметров
найдём оценки параметров 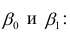
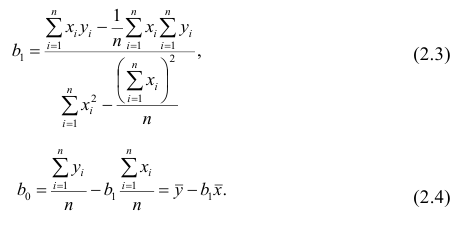
Остаётся получить оценку параметра 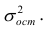 . Имеем
. Имеем
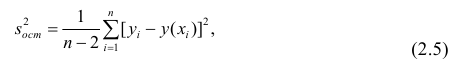
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы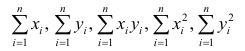 заменяют на
заменяют на
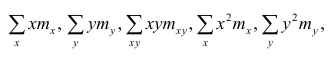
где 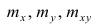 — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
— частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
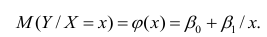
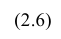
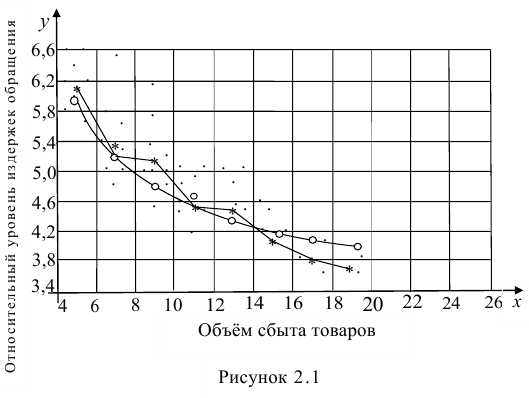
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
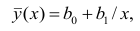
где 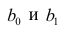 —оценки коэффициентов регрессии
—оценки коэффициентов регрессии 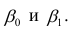
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
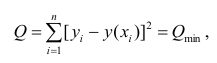
или
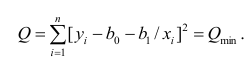
Дифференцируя последнее равенство по 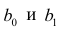 и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
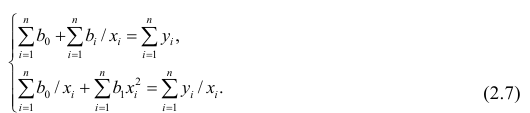
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
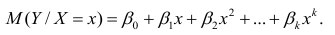
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
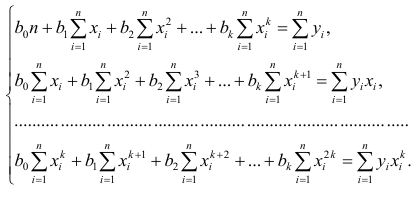
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 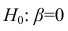 статистика
статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 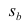 — оценка среднеквадратического отклонения
— оценка среднеквадратического отклонения
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение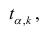 удовлетворяющее условию
удовлетворяющее условию 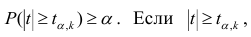 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При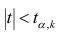 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
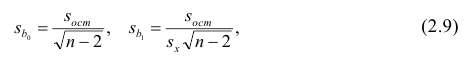
где 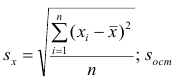 — оценка остаточной дисперсии, вычисляемая по
— оценка остаточной дисперсии, вычисляемая по
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
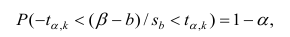
где а — уровень значимости, находим

Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 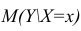 является условное среднее
является условное среднее 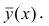 Кроме точечной оценки для
Кроме точечной оценки для 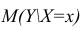 можно
можно
построить доверительный интервал в точке 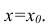
Известно, что 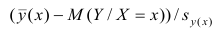 имеет распределение
имеет распределение
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания 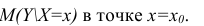
Оценку дисперсии условного среднего вычисляют по формуле
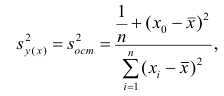
или для интервального ряда
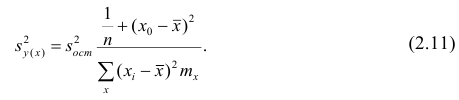
Доверительный интервал находят из условия
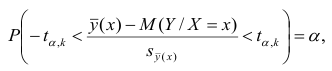
где а — уровень значимости. Отсюда
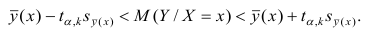
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
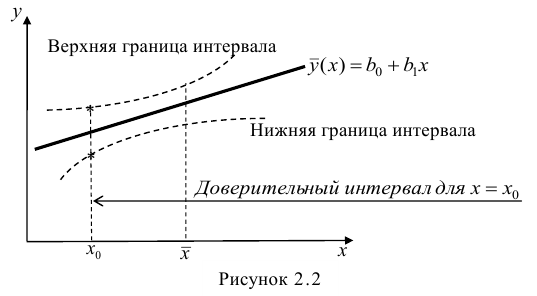
Из рис. 2.2 видно, что в точке 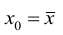 границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 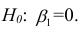 Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением
Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением 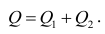 — Общая сумма квадратов отклонений результативного признака
— Общая сумма квадратов отклонений результативного признака
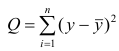 разлагается на
разлагается на 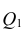 (сумму, характеризующую влияние признака
(сумму, характеризующую влияние признака
X) и 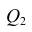 (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
(остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
Для проверки нулевой гипотезы вычисляют статистику 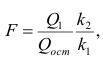 которая имеет распределение Фишера-Снедекора с А
которая имеет распределение Фишера-Снедекора с А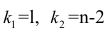 степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы
степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы 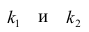 находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение
находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение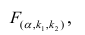 удовлетворяющее условию
удовлетворяющее условию 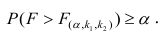 . Если
. Если 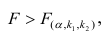 нулевую гипотезу отвергают, уравнение считают значимым. Если
нулевую гипотезу отвергают, уравнение считают значимым. Если 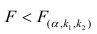 то нет оснований отвергать нулевую гипотезу.
то нет оснований отвергать нулевую гипотезу.
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 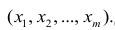 Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним
Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним 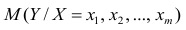 и постоянной дисперсией
и постоянной дисперсией 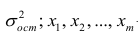 — линейно независимые векторы
— линейно независимые векторы 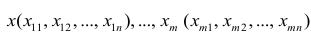 . Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
. Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
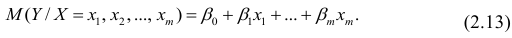
Оценке подлежат параметры 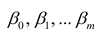 и остаточная дисперсия.
и остаточная дисперсия.
Заменив параметры их оценками, запишем уравнение регрессии
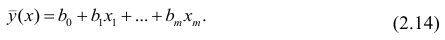
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 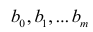 является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:
является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

Как и в двумерном случае, составляют систему нормальных уравнений
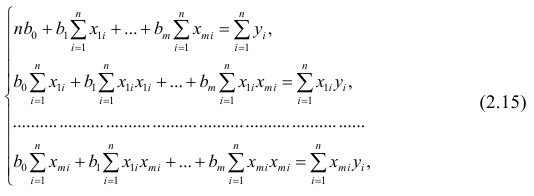
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 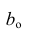 через остальные параметры:
через остальные параметры:
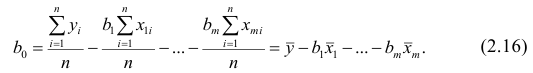
Подставим в остальные уравнения системы вместо 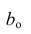 полученное выражение:
полученное выражение:
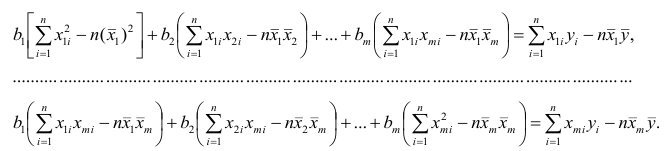
Пусть С — матрица коэффициентов при неизвестных параметрах 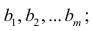
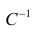 — матрица, обратная матрице С;
— матрица, обратная матрице С; 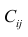 — элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы
— элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы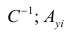 — выражение
— выражение
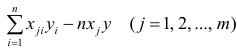 . Тогда, используя формулы линейной алгебры,
. Тогда, используя формулы линейной алгебры,
запишем окончательные выражения для параметров:
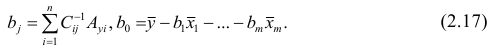
Оценкой остаточной дисперсии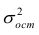 является
является
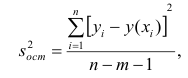
где 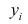 — измеренное значение результативного признака;
— измеренное значение результативного признака;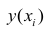 значение результативного признака, вычисленное по уравнению регрессий.
значение результативного признака, вычисленное по уравнению регрессий.
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику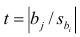 вычисляют для каждого j-го коэффициента регрессии
вычисляют для каждого j-го коэффициента регрессии
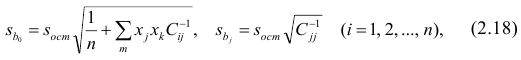
где 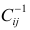 —элемент обратной матрицы, стоящий на пересечении i-й строки и j-
—элемент обратной матрицы, стоящий на пересечении i-й строки и j-
го столбца;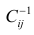 —диагональный элемент обратной матрицы.
—диагональный элемент обратной матрицы.
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 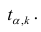 Если
Если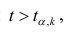 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если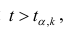 то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: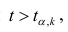
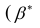 — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики
— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 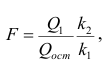 , где
, где 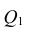 — сумма квадратов, характеризующая влияние признаков X;
— сумма квадратов, характеризующая влияние признаков X; 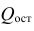 — остаточная сумма квадратов, характеризующая влияние неучтённых факторов;
— остаточная сумма квадратов, характеризующая влияние неучтённых факторов; 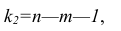
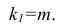 Для уровня значимости а и числа степеней свободы
Для уровня значимости а и числа степеней свободы 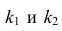 по табл. 3 приложений находят критическое значение
по табл. 3 приложений находят критическое значение 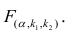 Если
Если 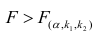 то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При
то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 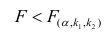 нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 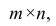 аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений
аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений 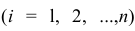 столбцы — признакам
столбцы — признакам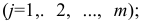 таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных
таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных 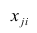 переходят к переменным
переходят к переменным 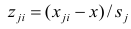 В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
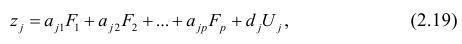
где 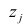 -j-й признак (величина случайная);
-j-й признак (величина случайная); 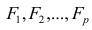 — общие факторы (величины случайные, имеющие нормальный закон распределения);
— общие факторы (величины случайные, имеющие нормальный закон распределения); 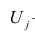 — характерный фактор;
— характерный фактор; 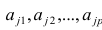 — факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);
— факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);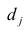 — нагрузка характерного фактора.
— нагрузка характерного фактора.
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 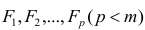 и характерного фактора
и характерного фактора 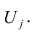
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков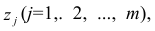 , т.е.
, т.е.
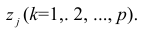
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы 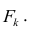
Факторные нагрузки 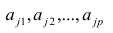 . характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
. характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
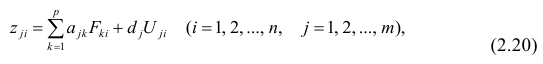
где 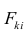 значение k-го фактора для i-го объекта.
значение k-го фактора для i-го объекта.
Дисперсию признака 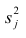 можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность
можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность 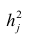 и часть, обусловленную действием j-го характера фактора, характерность
и часть, обусловленную действием j-го характера фактора, характерность 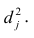 Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака
Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака 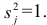 Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
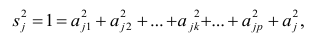
где 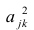 —доля дисперсии признака
—доля дисперсии признака 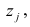 приходящаяся на k-й фактор.
приходящаяся на k-й фактор.
Полный вклад k-го фактора в суммарную дисперсию признаков
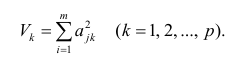
Вклад общих факторов в суммарную дисперсию 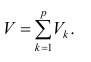
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
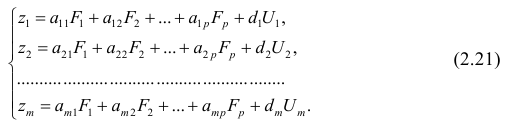
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
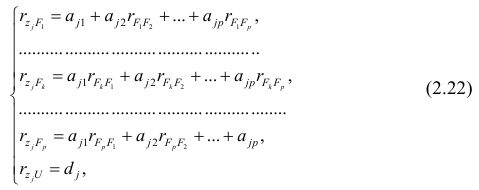
где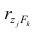 — выборочный коэффициент корреляции между j-м параметром и к-
— выборочный коэффициент корреляции между j-м параметром и к-
м фактором;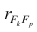 — коэффициент корреляции между к-м и р-м факторами.
— коэффициент корреляции между к-м и р-м факторами.
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
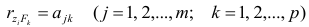 , т.е. коэффициенты отображения равны
, т.е. коэффициенты отображения равны
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам: 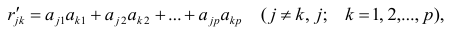
где 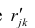 —вычисленный по отображению коэффициент корреляции между j-м
—вычисленный по отображению коэффициент корреляции между j-м
и к-м признаком. Остаточный коэффициент корреляции
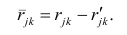
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
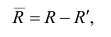
где 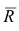 — матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
— матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
Результаты факторного анализа удобно представить в виде табл. 2.10.

Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
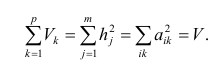
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции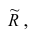 у которой на главной диагонали стоят значения общностей
у которой на главной диагонали стоят значения общностей 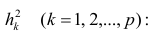 :
: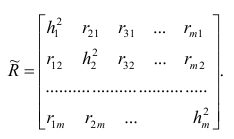
Редуцированная и полная матрицы связаны соотношением

где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 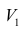 должен быть найден при условии
должен быть найден при условии
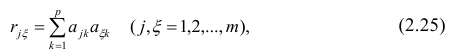
где 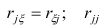 —общность
—общность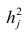 параметра
параметра
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора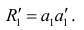 Имея эту матрицу, получают первую матрицу остатков:
Имея эту матрицу, получают первую матрицу остатков: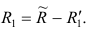
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 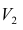 находят из условия
находят из условия
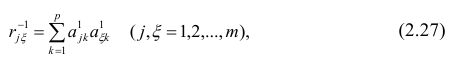
где 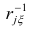 — коэффициент корреляции из первой матрицы остатков;
— коэффициент корреляции из первой матрицы остатков; 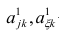 — факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков:
— факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков: 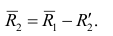
Факторный анализ учитывает суммарную общность. Исходная суммарная общность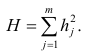 Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на
Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на 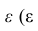 — наперёд заданное малое число).
— наперёд заданное малое число).
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных 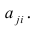
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
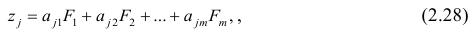
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 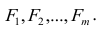 По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
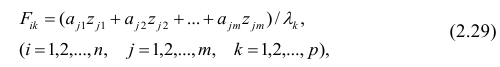
где 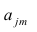 — элементы факторного решения:
— элементы факторного решения: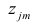 — исходные переменные;
— исходные переменные; 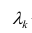 .— k-е собственное значение; р — количество оставленных главных
.— k-е собственное значение; р — количество оставленных главных
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента 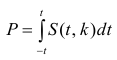
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 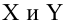 связаны линейной корреляционной зависимостью
связаны линейной корреляционной зависимостью 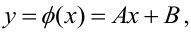 для отыскания которой проведено
для отыскания которой проведено 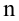 независимых измерений
независимых измерений 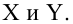
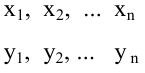
Диаграмма рассеяния (разброса, рассеивания)
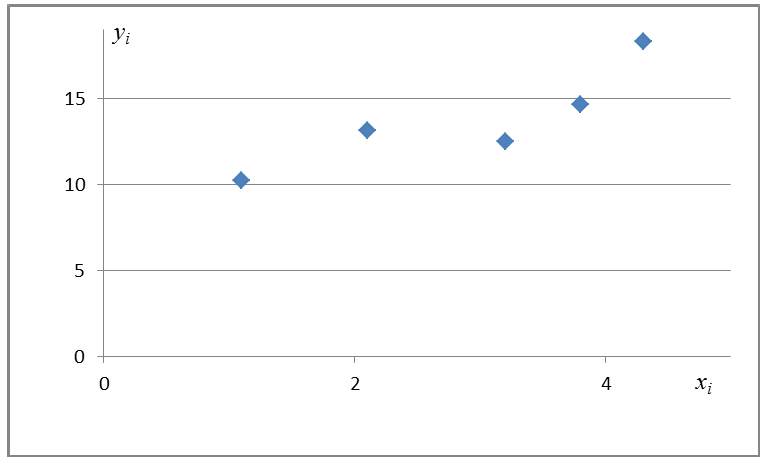
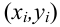 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Выборочное уравнение прямой линии регрессии 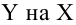 имеет вид
имеет вид
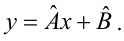
Задача: подобрать 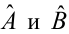 таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой
таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой 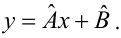
Для того, что бы провести прямую 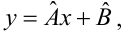 воспользуемся МНК. Потребуем,
воспользуемся МНК. Потребуем,
чтобы 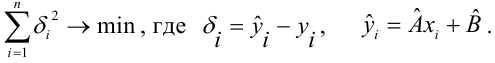
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
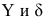 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.- Дисперсия
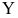 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения. - Результаты наблюдений
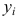 в разных точках независимы.
в разных точках независимы. - Входные переменные
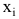 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 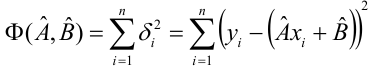 и найдём её минимальное значение
и найдём её минимальное значение
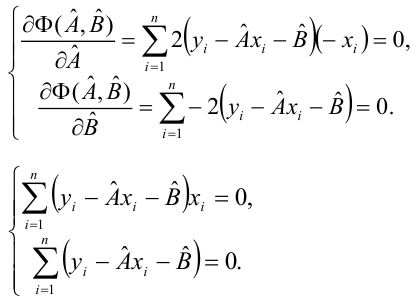
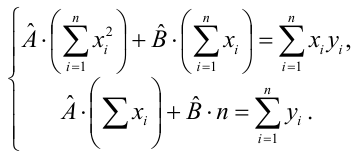
Решив систему, получим искомые значения 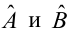
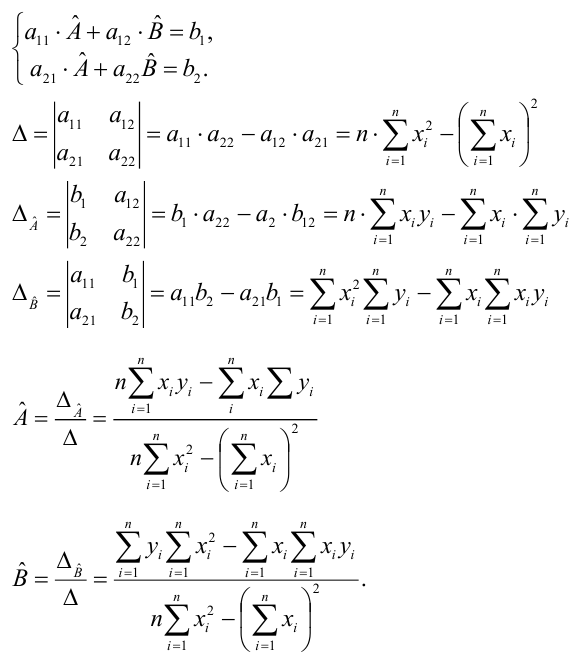
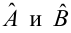 является несмещенными оценками истинных значений коэффициентов
является несмещенными оценками истинных значений коэффициентов 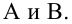
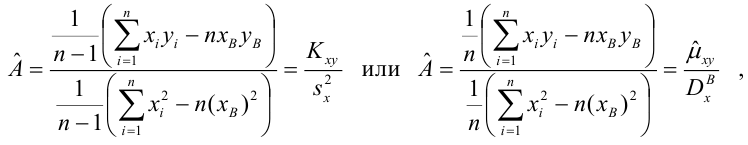 где
где
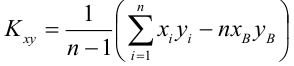 несмещенная оценка корреляционного момента (ковариации),
несмещенная оценка корреляционного момента (ковариации),
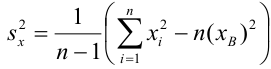 несмещенная оценка дисперсии
несмещенная оценка дисперсии 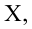
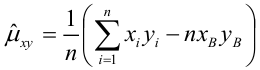 выборочная ковариация,
выборочная ковариация,
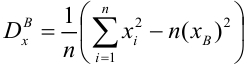 выборочная дисперсия
выборочная дисперсия 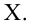
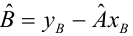
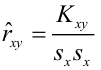 — выборочный коэффициент корреляции
— выборочный коэффициент корреляции
Коэффициент детерминации
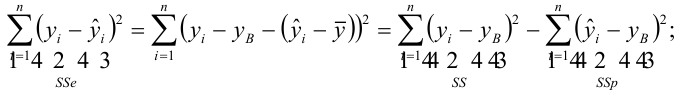
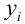 — наблюдаемое экспериментальное значение
— наблюдаемое экспериментальное значение 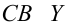 при
при 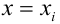
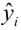 — предсказанное значение
— предсказанное значение 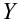 удовлетворяющее уравнению регрессии
удовлетворяющее уравнению регрессии
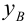 — средневыборочное значение
— средневыборочное значение 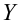
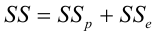
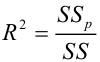 — коэффициент детерминации, доля изменчивости
— коэффициент детерминации, доля изменчивости 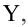 объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии
объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии 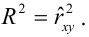
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
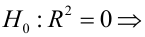 регрессия незначима
регрессия незначима
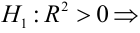 регрессия значима
регрессия значима
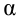 — уровень значимости
— уровень значимости
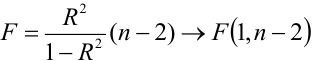 — статистический критерий
— статистический критерий
Критическая область — правосторонняя; 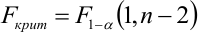
Если 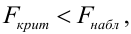 то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
Мощность статистического критерия. Функция мощности
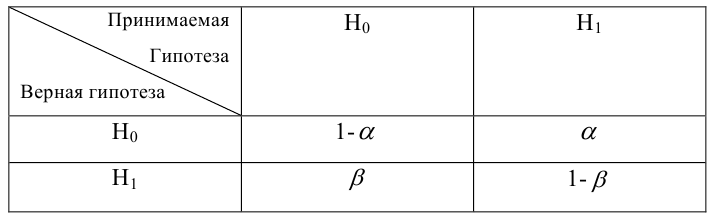
Определение. Мощностью критерия 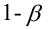 называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода 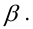
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 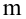 и дисперсией
и дисперсией 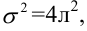 проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
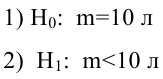
3) Уровень значимости 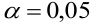
4) Статистический критерий
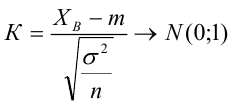
5) Критическая область — левосторонняя
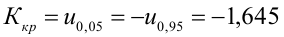
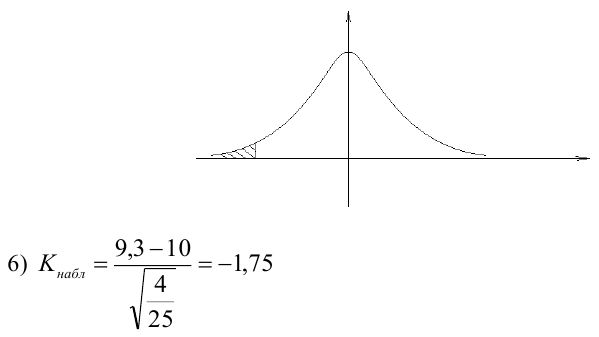
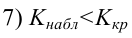 следовательно
следовательно 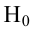 отвергается на уровне значимости
отвергается на уровне значимости 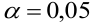
Пример:
В условиях примера 1 предположим, что наряду с 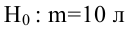 рассматривается конкурирующая гипотеза
рассматривается конкурирующая гипотеза 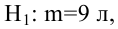 а критическая область задана неравенством
а критическая область задана неравенством 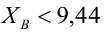 Найти вероятность ошибок I рода и II рода.
Найти вероятность ошибок I рода и II рода.
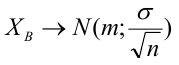
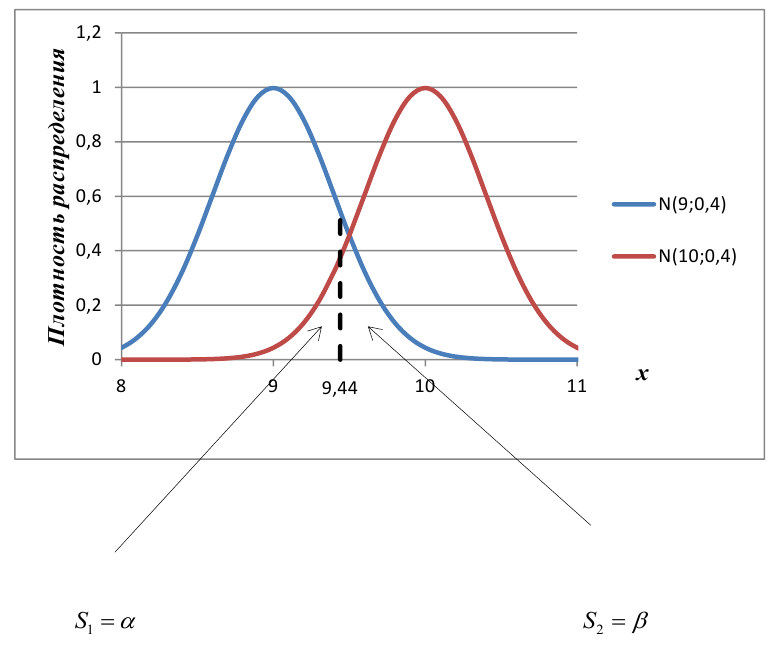
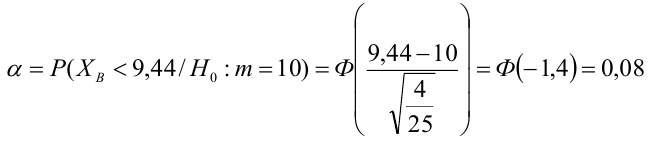
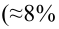 автомобилей имеют меньший расход топлива)
автомобилей имеют меньший расход топлива)
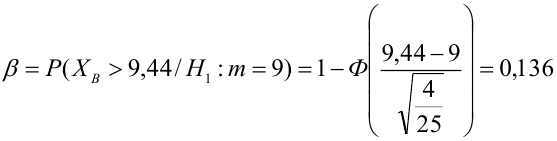
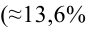 автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
Определение. Пусть проверяется 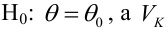 — критическая область критерия с заданным уровнем значимости
— критическая область критерия с заданным уровнем значимости 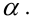 Функцией мощности критерия
Функцией мощности критерия 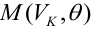 называется вероятность отклонения
называется вероятность отклонения 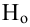 как функция параметра
как функция параметра 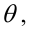 т.е.
т.е.
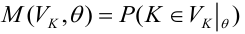
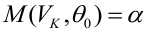 — ошибка 1-ого рода
— ошибка 1-ого рода
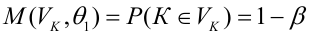 — мощность критерия
— мощность критерия
Пример:
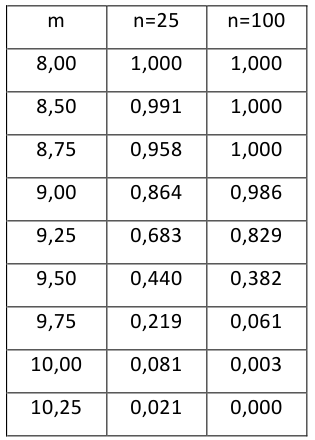
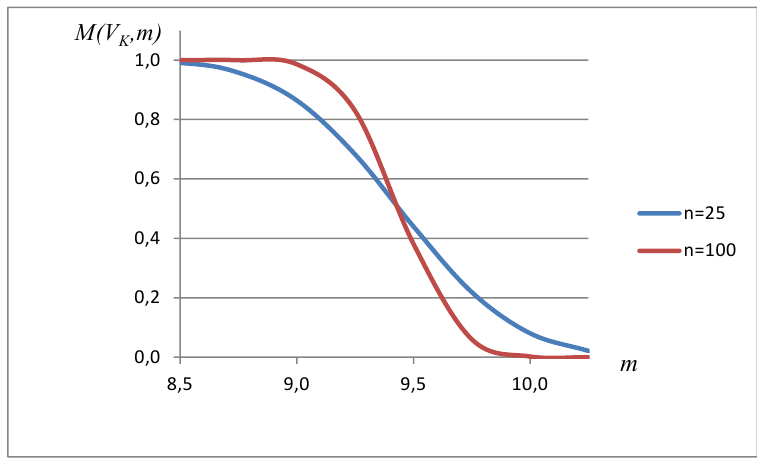
Построить график функции мощности из примера 2 для 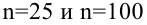
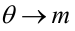
 попадает в критическую область.
попадает в критическую область.
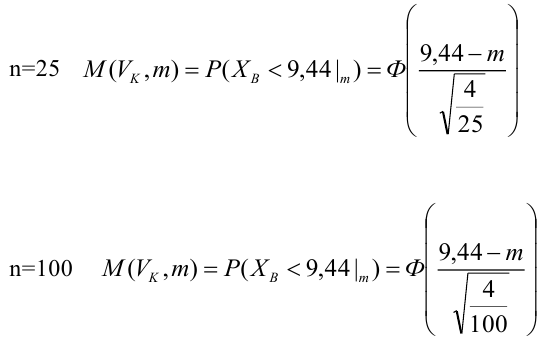
Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить 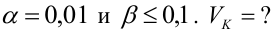
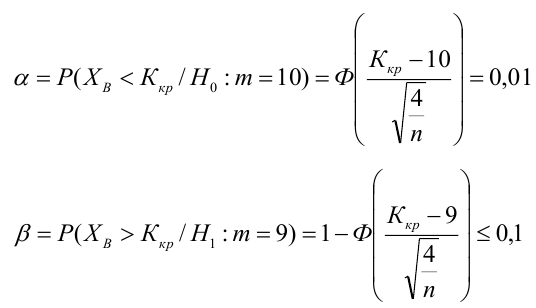
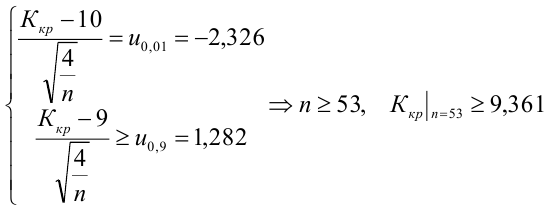
Лемма Неймана-Пирсона.
При проверке простой гипотезы 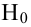 против простой альтернативной гипотезы
против простой альтернативной гипотезы 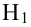 наилучшая критическая область (НКО) критерия заданного уровня значимости
наилучшая критическая область (НКО) критерия заданного уровня значимости 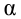 состоит из точек выборочного пространства (выборок объема
состоит из точек выборочного пространства (выборок объема 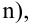 для которых справедливо неравенство:
для которых справедливо неравенство:
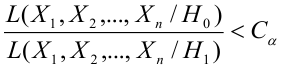
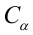 — константа, зависящая от
— константа, зависящая от 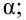
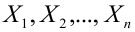 — элементы выборки;
— элементы выборки;
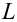 — функция правдоподобия при условии, что соответствующая гипотеза верна.
— функция правдоподобия при условии, что соответствующая гипотеза верна.
Пример:
Случайная величина 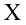 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 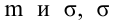 известно. Найти НКО для проверки
известно. Найти НКО для проверки 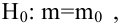 против
против 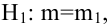 причем
причем 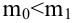
Решение:
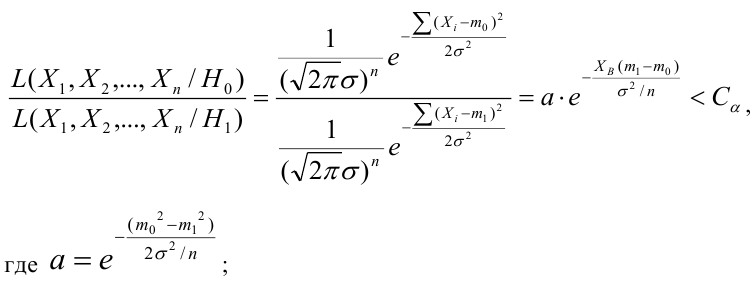
Ошибка первого рода: 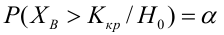
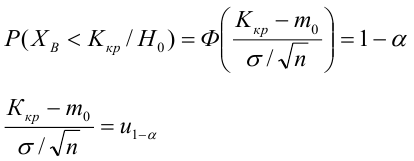
НКО: 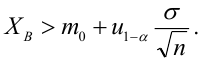
Пример:
Для зависимости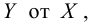 заданной корреляционной табл. 13, найти оценки параметров
заданной корреляционной табл. 13, найти оценки параметров 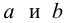 уравнения линейной регрессии
уравнения линейной регрессии 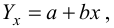 остаточную дисперсию; выяснить значимость уравнения регрессии при
остаточную дисперсию; выяснить значимость уравнения регрессии при 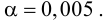
Решение. Воспользуемся предыдущими результатами
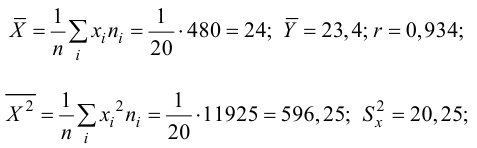
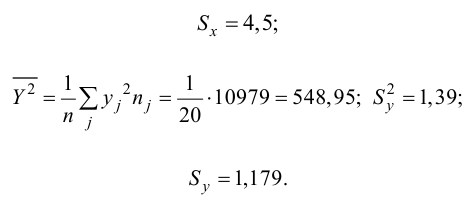
Согласно формуле (24), уравнение регрессии будет иметь вид 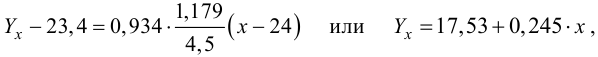 тогда
тогда 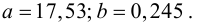
Для выяснения значимости уравнения регрессии вычислим суммы 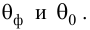 Составим расчетную таблицу:
Составим расчетную таблицу:
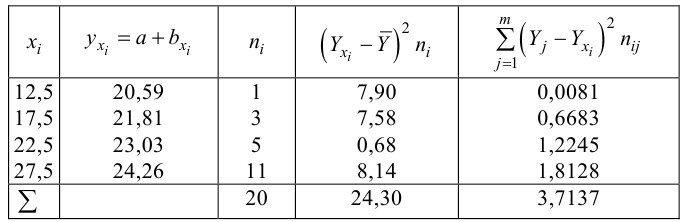
Из (27) и (28) по данным таблицы получим 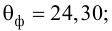
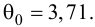
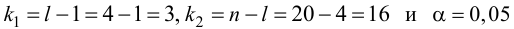 по табл. П7 находим
по табл. П7 находим 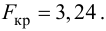
Вычислим статистику
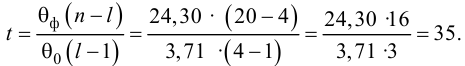
Так как 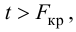 то уравнение регрессии значимо. Остаточная дисперсия равна
то уравнение регрессии значимо. Остаточная дисперсия равна 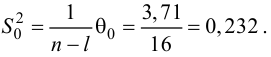
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
1.2.1. Стандартная ошибка оценки по регрессии
Обозначается как
Sy,xи вычисляется по формуле
Sy,x=![]() .
.
Стандартная ошибка
оценки по регрессии показывает, на
сколько в среднем мы ошибаемся, оценивая
значение зависимой переменной по
найденному уравнению регрессии при
фиксированном значении независимой
переменной.
Квадрат стандартной
ошибки по регрессии является несмещенной
оценкой дисперсии ![]() 2,
2,
т.е.
![]() =
=
![]() =
=![]() .
.
Дисперсия ошибок
характеризует воздействие в модели
(1.1) неучтенных факторов и ошибок.
1.2.2. Оценка
значимости уравнения регрессии
(дисперсионный анализ регрессии)
Для оценки
значимости уравнения регрессии
устанавливают, соответствует ли выбранная
модель анализируемым данным. Для этого
используется дисперсионный анализ
регрессии. Основная его посылка – это
разложение общей суммы квадратов
отклонений
![]() на
на
составляющие. Известно, что такое
разложение имеет вид
![]() =
=![]() +
+![]() .
.
Второе слагаемое
в правой части разложения – это часть
общей суммы квадратов отклонений,
объясняемая действием случайных и
неучтенных факторов. Первое слагаемое
этого разложения – это часть общей
суммы квадратов отклонений, объясняемая
регрессионной зависимостью. Следовательно,
если регрессионная зависимость между
уихотсутствует, то
общая сумма квадратов отклонений
объясняется действием только случайных
факторов или ошибок, т.е.![]() =
=![]() .
.
В случае функциональной зависимости
между уихдействие
случайных факторов и ошибок отсутствует
и тогда![]() =
=![]() .
.
Будучи отнесенными к соответствующему
числу степеней свободы, эти суммы
называются средними квадратами отклонений
и служат оценками дисперсии![]() в
в
разных предположениях.
MSE= (![]() )/(n–2)
)/(n–2)
– остаточная дисперсия, которая является
оценкой![]() в
в
предположении отсутствия регрессионной
зависимости, аMSR= (![]() )/1
)/1
– аналогичная оценка без этого
предположения. Следовательно, если
регрессионная зависимость отсутствует,
то эти оценки должны быть близкими.
Сравниваются они на основе критерия
Фишера:F=MSR/MSE.
Расчетное значение
этого критерия сравнивается с критическим
значением F(с числом степеней свободы числителя,
равным 1, числом степеней свободы
знаменателя, равнымn–2,
и фиксированным уровнем значимости![]() ).
).
ЕслиF![]() <F, то гипотеза о не значимости
<F, то гипотеза о не значимости
уравнения регрессии не отклоняется, т.
е. признается, что уравнение регрессии
незначимо. В этом случае надо либо
изменить вид зависимости, либо пересмотреть
набор исходных данных.
При компьютерных
расчетах оценка значимости уравнения
регрессии осуществляется на основе
дисперсионного анализа регрессии в
таблицах вида:
Таблица
1.1
Дисперсионный
анализ регрессии
|
Источник вариации |
Суммы квадратов |
Степени свободы |
Средние квадраты |
F-отношение |
p-value |
|
Модель |
SSR |
1 |
MSR |
MSR/MSE |
Уровень |
|
Ошибки |
SSE |
n–2 |
MSE |
значимости |
|
|
общая |
SST |
n–1 |
Здесь p-value– это вероятность выполнения неравенстваF<F![]() ,
,
т. е. того, что расчетное значениеF-статистики попало в
область принятия гипотезы. Если эта
вероятность мала (меньше![]() ),
),
то нулевая гипотеза отклоняется.
Стандартная ошибка регрессии и R-квадрат являются ценными математическими расчетами, которые можно использовать для оценки набора данных. Хотя эти два расчета похожи, между ними есть явные различия, которые делают их применение уникальным. Научившись использовать стандартную ошибку регрессии и R-квадрат, вы сможете улучшить свои аналитические способности и стать более эффективным специалистом. В этой статье мы обсудим, что такое стандартная ошибка регрессии, что такое R-квадрат и как эти два показателя сравниваются, включая ключевые различия в их применении.
Что такое стандартная ошибка регрессии?
Стандартная ошибка регрессии — это мера логической регрессии, которую можно применить к набору данных, чтобы определить, насколько далеко среднее значение в наборе данных находится от линии регрессии данных. Это дает представление о том, насколько точно ваша регрессия соответствует набору данных и насколько уверенно вы должны оценивать значение, полученное с помощью линии регрессии. При проведении анализа значений со стандартной ошибкой регрессии примерно 95% наблюдаемых данных должны находиться на расстоянии менее двух стандартных ошибок регрессии от линии регрессии.
Что означает R-квадрат?
R-квадрат — это регрессионный показатель, применяемый к набору данных и анализирующий взаимосвязь между зависимой и независимой переменными. Нахождение коэффициента R-квадрат показывает, какой процент зависимой переменной можно точно предсказать на основе значения независимой переменной. Более высокое значение R-квадрат указывает на сильную корреляцию между двумя переменными, в то время как низкое значение R-квадрат указывает на то, что между двумя переменными существует менее прямая корреляция. Это может помочь вам определить, насколько предсказуемо вы можете учесть изменения в объеме производства, изменив один из производственных факторов, например.
Стандартная ошибка регрессии против. R-квадрат
Хотя и стандартная ошибка регрессии, и R-квадрат могут дать ценную информацию при оценке набора данных, между ними есть важные различия, которые помогут вам определить, какой из них более полезен или вы можете эффективно применять оба показателя. Ключевые различия между R-квадратом и стандартной ошибкой регрессии включают:
Единицы измерения
Первое существенное различие между этими двумя расчетами заключается в единицах, в которых они возвращают значения. При расчете R-квадрат вы получаете значение в виде десятичной дроби без единиц измерения. Вы можете преобразовать это значение в процент, умножив его на 100. R-квадрат остается таким независимо от единиц, используемых для анализируемой информации.
При расчете стандартной ошибки регрессии вы получаете ответ в тех же единицах, что и ваша независимая переменная. Например, оценка максимальной скорости автомобилей в сравнении с их лошадиными силами даст R-квадрат, измеренный в процентах, и ошибку регрессии, измеренную в милях в час.
Предоставленная информация
Так же, как оба расчета используют разные единицы измерения в своих результатах, стандартная ошибка регрессии и R-квадрат также предоставляют разную информацию, когда вы их используете. Стандартная ошибка регрессии предоставляет конкретную информацию, связанную с точными показателями переменных, которые вы измеряете. Функционируя в единицах, которые вы использовали для измерения зависимой переменной, она показывает, насколько точно вы можете предсказать производительность, основываясь на знании независимой переменной.
R-квадрат не предоставляет вам непосредственно применимую информацию о том, насколько точно вы можете оценить значение на зависимом уровне. Вместо этого она позволяет проанализировать существующие результаты и определить, какую часть показателей зависимой переменной можно напрямую отнести на счет влияния независимой переменной.
Практическое применение
Эти различия в единицах измерения и информации оказывают существенное влияние на практическое применение каждого расчета. Стандартная ошибка регрессии позволяет определить предполагаемые уровни эффективности и уровень доверия к ним. Низкая стандартная ошибка регрессии означает, что ваши данные более плотно прилегают к линии регрессии, и вы можете более точно предсказать результаты на определенном уровне зависимой переменной. Это часто более понятное применение, так как получение информации в единицах, которые вы измеряете, облегчает понимание результатов стандартной ошибки регрессии.
Практическое применение R-квадрат лучше всего использовать для определения взаимосвязи между двумя переменными. Анализ корреляции между зависимой и независимой переменными может помочь вам принимать обоснованные бизнес-решения. Например, выявление сильной связи между качеством компонента и удовлетворенностью клиентов может продемонстрировать ценность инвестиций в более дорогое сырье в процессе производства. Выявление корреляции с низким R-квадрат вместо этого указывает на минимальное влияние на зависимую переменную, если вы внесете изменения в независимую переменную.
Пример стандартной ошибки регрессии против. R-квадрат
Компания проводит анализ эффективности рекламных кампаний, связанных с продажами отдельного продукта в своей линии. Компания ранее провела пять рекламных кампаний, с разными бюджетами для каждого случая. Они создают набор данных, записывая маркетинговый бюджет, выделенный на каждую кампанию, количество продаж, сгенерированных в ходе каждой кампании, и соотношение долларов на продажу для каждой кампании.
|
Маркетинговый бюджет |
Продажи |
Коэффициент ($sale) |
Стандартная ошибка |
|
|
1 |
$6,100 |
191 |
32 |
54.588 |
|
2 |
$13,600 |
470 |
29 |
|
|
3 |
$13,400 |
574 |
R-квадрат |
|
|
4 |
$13,300 |
451 |
0.92001 |
|
|
5 |
$6,700 |
221 |
92% |
Используя автоматизированные функции в своей программе электронных таблиц, компания рассчитывает стандартную ошибку регрессии и R-квадрат для маркетинговых данных. В документе получен R-квадрат 92%, что указывает на сильную связь между расходами на маркетинг и продажами, сделанными. Увеличение или уменьшение расходов оказывает значительное достоверное влияние на количество продаж. Расчет стандартной ошибки регрессии дает значение 54.588, что означает, что данные по продажам отличаются от линии регрессии в среднем на 54.588 продажи. Поэтому, оценивая продажи для установленного бюджета, компания может ожидать, что средняя ошибка составит менее 55 от общего объема продаж.
