Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения – чем стандартное отклонение отличается от стандартной ошибки, и в каких случаях, применять ту или иную статистику. А недавно в книге Искусство статистики Дэвида Шпигельхалтера я узнал про бутстрэппинг, и понял, как объяснить различия стандартного отклонения и стандартной ошибки.
Для начала зададим 100 значений стандартной нормально распределенной случайной величины. В этом контексте стандартная означает, что ее матожидание μ = 0, а среднеквадратичное отклонение σ = 1. Поскольку значения в Excel получены с помощью волатильной функции СЛМАССИВ(), после любого действия они пересчитываются. Поэтому диаграммы в заметке и в файле будут отличаться.
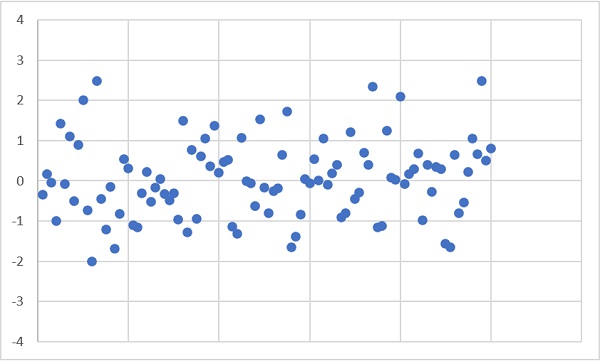
Рис. 1. Нормально распределенная случайная величина
Скачать заметку в формате Word или pdf, примеры в формате Excel
Стандартное отклонение
… является наиболее распространенным показателем рассеивания значений случайной величины относительно её среднего арифметического.
Стандартное отклонение вычисляют по формуле:
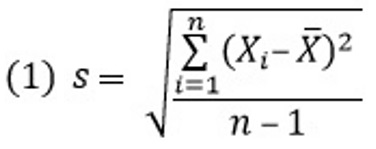
где X̅ – среднее арифметическое значений случайной величины (далее я буду называть его просто средним), Хi – отдельные значения случайной величины, n – число значений случайной величины.
Вообще термины разными авторами используются немного по-разному. Мне нравится следующий подход. Генеральную совокупность описывают параметрами, обозначаемыми греческими буквами: математическое ожидание μ и среднеквадратичное отклонение σ. Выборки описывают статистиками, обозначаемыми латинскими буквами: среднее арифметическое X̅ и стандартное отклонение s. Стандартное отклонение иначе называют оценкой среднеквадратичного отклонения. Как правило, есть генеральная совокупность с неизвестным нам среднеквадратичным отклонением σ. Извлекая выборку, и вычисляя стандартное отклонение s, мы кое-что узнаем о среднеквадратичном отклонении генеральной совокупности σ. Поэтому и говорят, что s является оценкой сигмы.
На самом деле за термином стандартное отклонение стоят две немного отличающиеся статистики. Но эта заметка о другом)) Подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?
Нанесем на диаграмму линию среднего и границы, отстоящие от среднего на расстоянии ±2s.

Рис. 2. Линия среднего и границы ±2s
Для стандартного нормального распределения за границы ±2s попадают 4,6% значений.
=(1-НОРМ.СТ.РАСП(2;ИСТИНА))*2 = 4,6%
И действительно 5 точек на рис. 2 лежат вне границ. Совпадение не обязано быть таким точным. Если вы откроете файл Excel на листе «Рис. 2» и понажимаете F9, принудительно изменяя случайные значения, то увидите, что вне границ может лежать от 2 до 8 точек. А если нажимать F9 достаточно долго, то вы получите более экстремальные числа точек вне границ. Для стандартного нормального распределения в пределах ±2s лежат приблизительно 95% значений. Поскольку s – оценка среднеквадратичного отклонения σ, которое в свою очередь равно 1, то 95% всех значений попадают в диапазон ≈ ±2.
Чем меньше s, тем кучнее значения случайной величины располагаются вокруг среднего. Итак
стандартное отклонение – мера разброса случайной величины
Среднее арифметическое выборки
Напомню, что мы задаем наши 100 значений с помощью генератора случайных чисел формулой в Excel
=НОРМ.СТ.ОБР(СЛМАССИВ(100;;0;1;ЛОЖЬ))
Хотя мы установили для генератора случайных чисел μ = 0 и σ = 1, значения X̅ и s будут немного отличаться для каждой выборки.
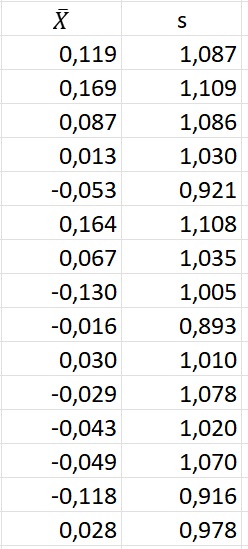
Рис. 3. Среднее и стандартное отклонение для 15 выборок размером n = 100
Теперь мы хотим узнать, что можно сказать о неизвестном математическом ожидании генеральной совокупности μ, подсчитав среднее арифметическое конкретной выборки, например, первой X̅ = 0,119?
Бутстрэп
Как пишет Евгения Поникарова, переводчик книги Дэвида Шпигельхалтера «Искусство статистики», слово bootstraps означает ремешки в виде ушка, которые прикрепляются к верхней части обуви, чтобы ее было проще натягивать. В английском языке есть выражение To pull oneself over a fence by one’s bootstraps (буквально — перетащить себя через ограду за ушки своей обуви), которое означает «выпутаться из своих проблем самому». Еще можно вспомнить барона Мюнхгаузена, который вытащил себя за волосы из болота.
Бутстрэп – компьютерный метод исследования распределения статистик, основанный на многократной генерации выборок методом Монте-Карло на базе имеющейся одной выборки. Термин ввел в 1977 году Брэдли Эфрон.
Итак, возьмем одну выборку из 100 случайных чисел и зафиксируем значения. Это наша исходная выборка (столбец А на рис. 4). Её среднее X̅(100) = 0,121, а стандартное отклонение s(100) = 0,995. 95% значений попадают в диапазон ≈ 0,121 ± 1,990.
С помощью генератора случайных чисел будем формировать из исходной выборки бутстрэп-выборки разного размера. Хитрость заключается в том, что выбирать значения мы будем с возвращением. Т.е., все значения любой бутстрэп-выборки взяты из исходной, а вот уникальность значений будет потеряна. Например, выборка в столбце С содержит два значения 0,7394. Я подсветил их с помощью условного форматирования. Опять же, если вы откроете Excel-файл, то дублей может не быть, так как бутстрэп-выборка сформирована волатильной функцией СЛМАССИВ().
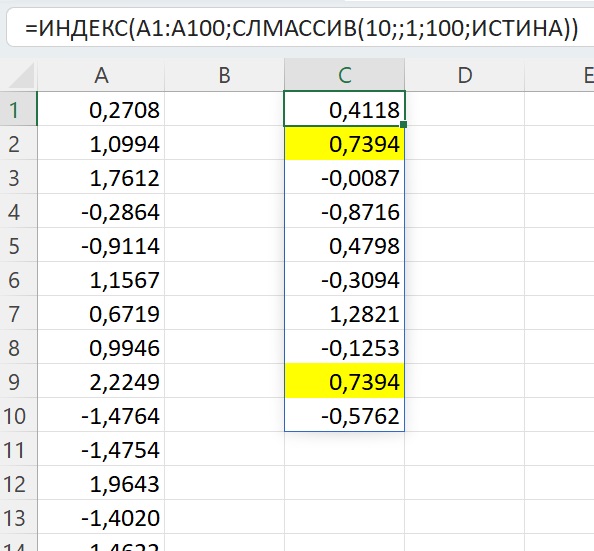
Рис. 4. Бутстрэп-выборка может содержать повторения
Для удобства последующей обработки расположим значения бутстрэп-выборки по горизонтали. Начнем со значения n = 3. Извлечем 1000 бутстрэп-выборок (рис. 5). В столбце А исходная выборка, n = 100. Столбец С содержит номер бутстрэп-выборки. В столбцах D, E и F извлеченные значения, в G – средние значения по выборкам. В ячейке G1 среднее D1:F1, в ячейке G2 – среднее D2:F2 и т.д. На диаграмме показано распределение средних значений бутстрэп-выборок для n = 3.
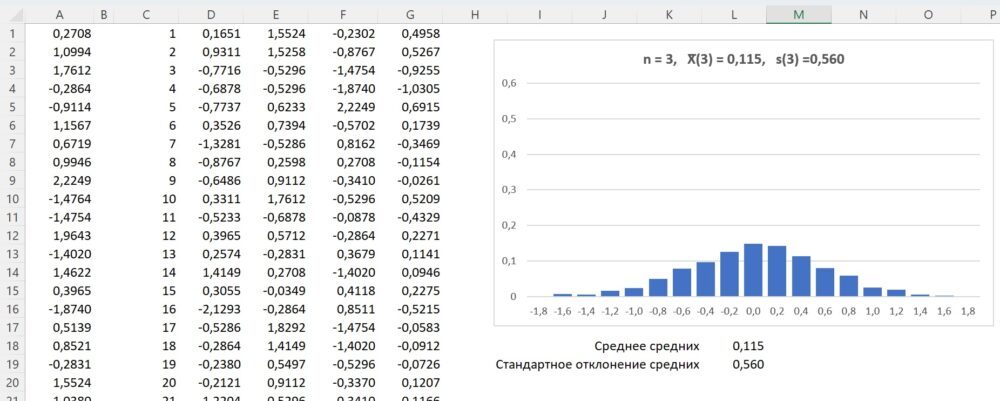
Рис. 5. Распределений средних значений 1000 бутстрэп-выборок, n = 3
Среднее средних 1000 бутстрэп-выборок = 0,115, стандартное отклонение средних значений 1000 бутстрэп-выборок = 0,560. Напоминаю, что 95% исходных значений выборки попадают в диапазон 0,12 ± 1,99. Для бутстрэп-выборок n = 3 мы только что нашли, что 95% средних попадают в диапазон 0,115 ± 1,120 (0,560*2 = 1,120). Кажется естественным, что разброс средних меньше, чем разброс отдельных значений.
Повторим моделирование для n = 5, 20, 50.
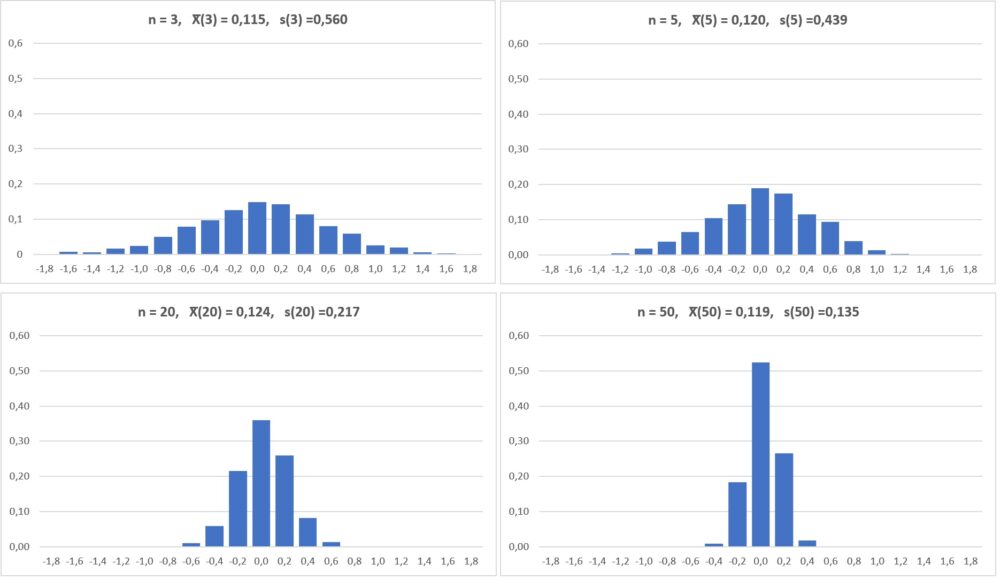
Рис. 6. С увеличением n стандартное отклонение средних значений бутстрэп-выборок уменьшается
Осмыслим, что мы получили. На рис. 6 представлены распределения средних значений бутстрэп-выборок разного размера из исходной выборки 100 случайных нормально распределенных чисел. Среднее каждого распределения близко к нулю (в нашей конкретной выборке из 100 чисел это среднее равно 0,121). А вот стандартное отклонение s(n) уменьшается по мере роста размера бутстрэп-выборок: s(3) = 0,560, s(5) = 0,439, s(20) = 0,217, s(50) = 0,135.
Стандартна ошибка
…или стандартная ошибка среднего – статистика, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности.
Ничего не напоминает!? А что за статистику s(n) мы рассчитали выше в бутстрэп-анализе!? Да, это было стандартное отклонение выборочного среднего X̅(n).
Величина стандартной ошибки зависит от дисперсии генеральной совокупности σ2 и объёма выборки n. Стандартная ошибка среднего вычисляется по формуле
![]()
где σ – величина среднеквадратического отклонения генеральной совокупности, и n – объём выборки. Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле:
![]()
где s — стандартное отклонение случайной величины.
Сведем в одной таблице рассмотренные статистики:

Рис. 7. Рассмотренные статистики
Здесь в столбцах J:L приведены статистики для одной выборки размера n, а в столбце M – статистики для бутстрэп-выборок соответствующего размера с рис. 6. Если в Excel-файле на листе «Рис. 7» понажимать F9, вы увидите, что не всегда совпадение между столбцами L и M будет таким хорошим, но тенденция будет прослеживаться.
Выше я писал, что мы исследуем неизвестное математическое ожидание генеральной совокупности μ на основе среднего арифметического выборки X̅(100) = 0,119.
Мы можем использовать статистику, именуемую стандартной ошибкой. Для нас она черный ящик – формула, выведенная на основе теории вероятностей. С другой стороны мы можем построить множество бутстрэп-выборок размера n = 100, и подсчитать стандартное отклонение средних этих бутстрэп-выборок. И мы показали, что стандартная ошибка для одной выборки и стандартное отклонение средних бутстрэп-выборок, это одно и то же! В нашем примере, получив X̅(100) = 0,119, мы можем сказать, что с вероятностью 95% математическое ожидание генеральной совокупности μ лежит в диапазоне 0,119 ± 0,212 (0,106*2=0,212). Итак
стандартная ошибка – мера оценки математического ожидания генеральной совокупности μ на основании статистик выборки
Например, 95%-ный доверительный интервал для μ
Понятно, что с увеличением размера выборки n доверительный интервал будет сужаться. В пределе при n → ∞, X̅ → μ и SE → 0.
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
Предположим, мы измеряем вес 10 разных черепах.
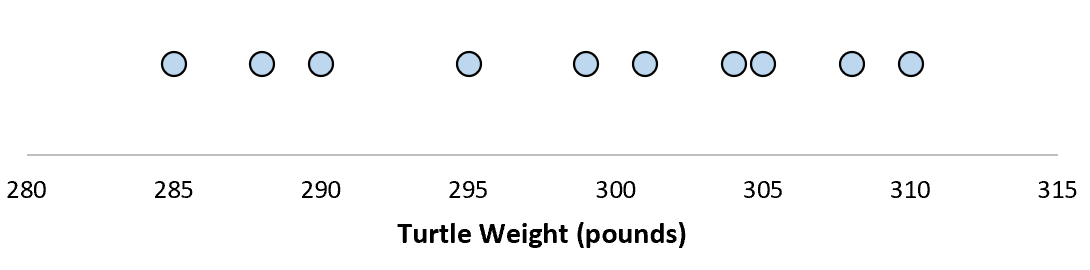
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
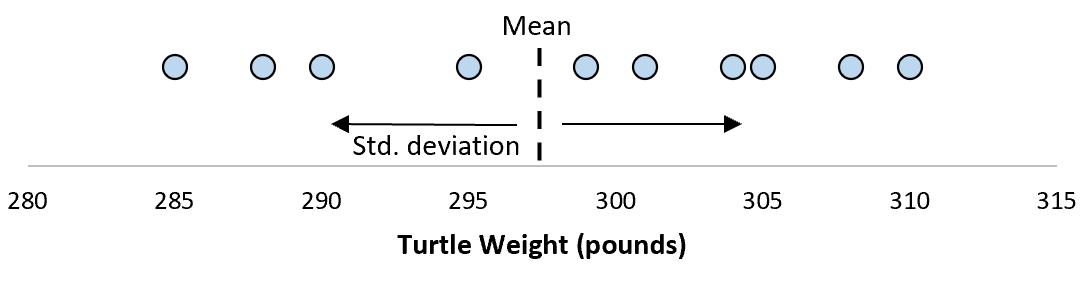
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
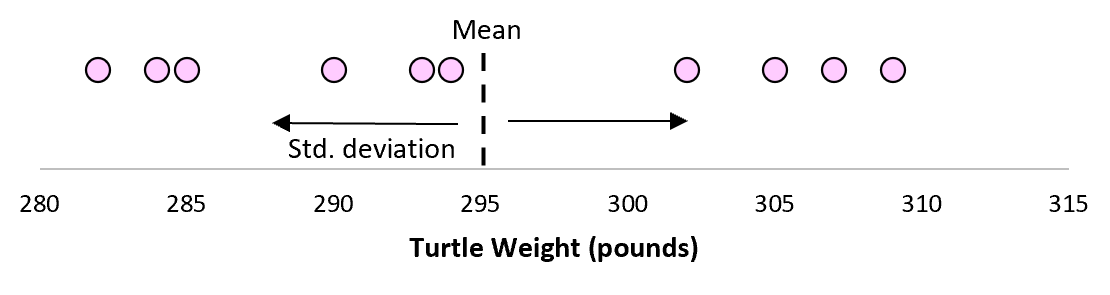
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
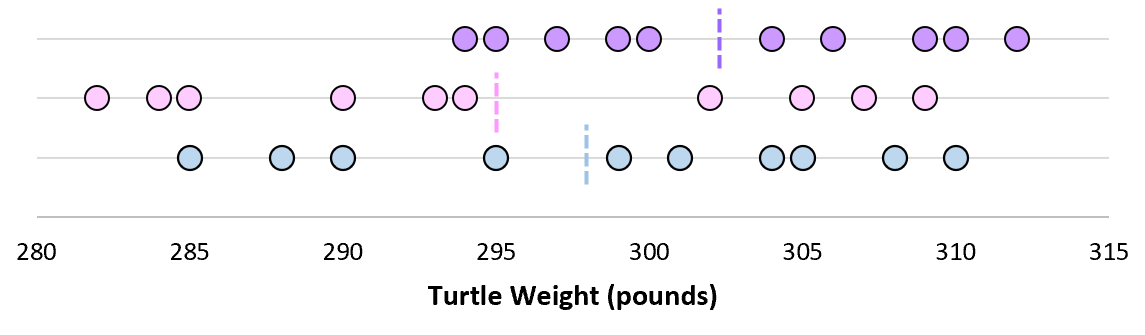
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
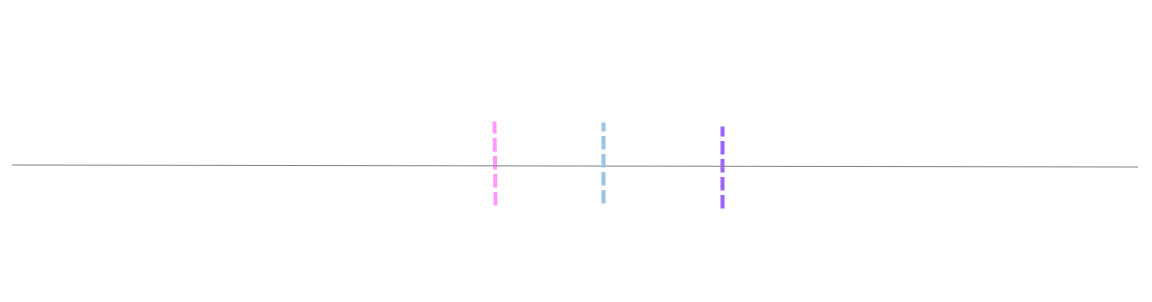
Стандартное отклонение этих средних значений известно как стандартная ошибка.
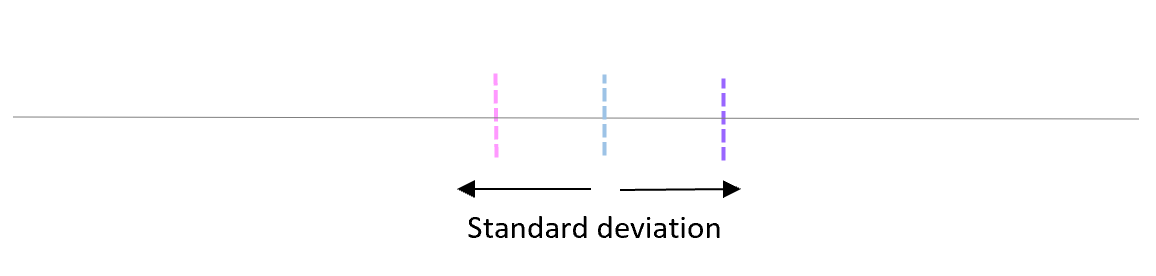
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-

1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-

2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-

3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-

4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-

5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-

6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-

2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-

3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-

4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-

5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 49 776 раз.
Была ли эта статья полезной?
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
Used in algorithmic trading, the standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Основные выводы:
-
Стандартная ошибка среднего указывает, насколько среднее значение генеральной совокупности может отличаться от среднего выборочного.
-
Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
-
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для обобщения наборов данных.
Если вы собираете данные для научных или статистических целей, стандартная ошибка среднего может помочь вам определить, насколько точно набор данных представляет фактическую совокупность. Проверка точности вашего образца подтверждает ваше клиническое исследование и помогает вам сделать правильные выводы.
В этой статье мы определяем стандартную ошибку среднего, объясняем, как она отличается от стандартного отклонения, и предлагаем формулу для ее расчета.
Какова стандартная ошибка среднего?
Стандартная ошибка среднего (SEM) используется для определения различий между более чем одной выборкой данных. Это помогает вам оценить, насколько хорошо ваши выборочные данные представляют всю совокупность, измеряя точность, с которой выборочные данные представляют совокупность, используя стандартное отклонение.
В статистике, среднеквадратичное отклонение является мерой того, насколько разбросаны числа. Иметь в виду относится к среднему числу. Стандартные функции ошибок используются для проверки точности выборки из нескольких выборок путем анализа отклонений в пределах средних значений.
Высокая стандартная ошибка показывает, что средние значения выборки широко разбросаны по среднему значению генеральной совокупности, поэтому ваша выборка может не точно представлять вашу генеральную совокупность. Низкая стандартная ошибка показывает, что средние значения выборки близко распределены вокруг среднего значения совокупности, что означает, что ваша выборка репрезентативна для вашей совокупности. Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
Например, если вы измерите вес большой выборки мужчин, их вес может варьироваться от 125 до более чем 300 фунтов. Однако, если вы посмотрите на среднее значение выборочных данных, образцы будут различаться всего на несколько фунтов. Затем вы можете использовать стандартную ошибку среднего, чтобы определить, насколько вес отличается от среднего.
Связанный: Как рассчитать стандартную ошибку в Excel (с советами)
Стандартная ошибка среднего по сравнению со стандартным отклонением
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для суммирования наборов данных.
Стандартная ошибка среднего значенияСтандартное отклонениеОценивает изменчивость в нескольких выборках генеральной совокупностиОписывает изменчивость в пределах одной выборкиВыводная статистика, которую можно оценитьОписательная статистика, которую можно рассчитатьИзмеряет, насколько вероятно, что среднее значение выборки будет отличаться от фактического среднего значения в популяции. выборка отличается от фактического среднего значенияСтандартная ошибка — это стандартное отклонение, деленное на квадратный корень размера выборкиСтандартное отклонение — это квадратный корень из дисперсии
Стандартная ошибка средней формулы
Формула для стандартной ошибки среднего выражается как:
SE = σ/√n
-
SE = стандартная ошибка выборки
-
σ = стандартное отклонение выборки
-
n = размер выборки
Обратите внимание, что σ — это греческая буква сигма, а √ — символ квадратного корня.
Формула стандартного отклонения выборки выражается следующим образом:
-
x̄ = среднее значение выборки, сначала найдите это значение
-
xᵢ = отдельные значения x
-
x = значение в наборе данных
-
n = количество точек данных
-
Σ — это сигма-обозначение для суммирования
Вот шаги, которые вы можете использовать для расчета стандартной ошибки среднего, используя выборку из пяти результатов теста SAT. Сначала рассчитайте стандартное отклонение, а затем подставьте это значение в формулу SEM.
1. Рассчитайте среднее
Сложите все образцы вместе и разделите общую сумму на количество образцов.
Пример: пять общих баллов SAT: 1000 + 1200 + 820 + 1300 + 680 = 5000.
Среднее (мк) = 5000 / 5 = 1000
2. Рассчитать отклонение от среднего
Рассчитайте отклонение каждого измерения от среднего, вычитая отдельные измерения из среднего.
Пример. Вычтите средний балл SAT, равный 1000, из каждого балла SAT.
хᵢ — мю
1000 — 1000 = 0
1200 — 1000 = 200
820 — 1000 = -180
1300 — 1000 = 300
680 — 1000 = -320
3. Возведите в квадрат каждое отклонение от среднего
Вычислите квадрат отклонения каждого измерения от среднего. Измерения, которые были отрицательными, после возведения в квадрат станут положительными.
Пример: Найдите квадратный корень отклонения каждой оценки от среднего.
(xᵢ — μ)²
0² = 0
200² = 40000
-180² = 32400
300² = 90000
-320² = 102400
4. Рассчитайте сумму квадратов отклонений
Определить сумму квадратов отклонений, сложив все числа из третьего шага.
Пример: 0 + 10 + 40000 + 32400 + 90000 + 102400 = 264810 = Σ
5. Разделите эту сумму на количество точек данных.
Возьмите сумму, которую вы подсчитали на четвертом шаге, и разделите ее на единицу меньше размера выборки. Используя приведенную выше формулу, это будет выглядеть как n-1.
Пример: 264810 / (5-1) = 66202,5
6. Вычислить квадратный корень, чтобы найти стандартное отклонение
Возьмите квадратный корень из числа, которое вы вычислили на пятом шаге. Это даст вам стандартное отклонение.
Пример: σ = √ 66202,5 = 257,298
7. Разделите стандартное отклонение на квадратный корень из размера выборки.
Используя стандартное отклонение, которое вы определили на шестом шаге, разделите это число на квадратный корень из размера выборки. Это позволит вам определить стандартную ошибку.
Пример: SE = σ/√n
SE = 257,298/√5
SE = 115,067
8. Рассчитайте стандартную ошибку среднего
Вычтите из среднего значения стандартную ошибку и запишите это число. Это стандартная ошибка ниже среднего. Затем добавьте стандартную ошибку к среднему значению и запишите число. Это стандартная ошибка выше среднего.
Пример:
SE ниже среднего: 1000 — 115,067 = 884,933
SE выше среднего: 1000 + 115,067 = 1115,067
Стандартная ошибка среднего может быть представлена следующим образом:
Средний балл SAT случайной выборки испытуемых составляет 1000 ± 115,067.
Пример СЭМ
Чтобы понять силу информации, которую вы можете получить из случайной выборки, используя стандартную ошибку среднего, рассмотрим следующий пример.
Вам дан вес при рождении 17 000 детей, рожденных в больницах Нью-Йорка. Средний вес при рождении составлял семь фунтов и три унции, а стандартное отклонение — один фунт три унции. Допустим, вы хотели узнать средний вес при рождении в этом районе, но получили веса только 30 случайных рождений по сравнению с общей численностью населения. Если бы эта выборка была взята только из всего населения, то вам лучше всего было бы предположить, что средний вес при рождении в выборке также будет равен семи фунтам и трем унциям.
Это предположение вряд ли будет точным, поскольку среднее значение выборки из 30 не будет таким точным, как среднее значение выборки из 17 000. Если бы вы продолжали брать случайные выборки из 30, вполне вероятно, что среднее значение каждой из них несколько изменилось бы.
Поскольку стандартное отклонение генеральной совокупности обычно неизвестно, вам необходимо оценить его, используя стандартное отклонение выборки. Чтобы сделать это с некоторой точностью, ваша выборка должна иметь нормальное распределение и состоять как минимум из 20 измерений. Хотя оценка может быть не совсем точной даже при большой выборке, ошибки в выборочной оценке стандартного отклонения генеральной совокупности будут уменьшены, если вы разделите его на квадратный корень из размера выборки.
Допустим, у вас есть шесть случайных выборок из 30 масс при рождении со стандартными отклонениями 1,3 фунта, 1,16 фунта, 1,14 фунта, 1,2 фунта, 1,25 фунта и 1,19 фунта, что на 0,098 фунта отличается от истинного значения стандартного отклонения населения. Эти шесть образцов приводят к оценкам стандартной ошибки, которые находятся в пределах 0,017 фунта от истинного значения. Ошибки стандартной ошибки средних оценок меньше, чем ошибки оценок стандартного отклонения, а значит, они более точные. Если бы размер выборки был больше 30, стандартная ошибка среднего была бы еще больше уменьшена.

