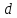Создание проблемных ситуаций через умышленно допущенные учителем ошибки - Ремонт и установка крупной бытовой техники

Создание проблемных ситуаций на уроках математики

1. Создание проблемных ситуаций через умышленно допущенные учителем ошибки.

В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение.

Пример №1.7 кл. Тема «Линейные уравнения с одной переменной».

Решаю быстро уравнение:

(3x + 7) ∙ 2 – 3 = 17,

6x + 14 – 3 = 17,

6x = 17 – 14 – 3,

6x = 0,

x = 0.

Естественно при проверке ответ не сходится, проблемная ситуация. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат — внимательность и заинтересованность на уроке.

Пример №2. Даю задачу на дом и говорю: “У меня не получается”. Попробуйте вы, обращайтесь к кому хотите за помощью. Хотя задача решается. Проблемная ситуация. На другой урок у них радостные лица – они решили.

2.Создание проблемных ситуаций через использование занимательных заданий.

Пример №1. 7 кл. Тема: «Линейная функция»

Обычная форма задания:

Функция задана формулой y = x + 5.Найдите значение функции при x = 0, 7; -5; 1.

Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано y = x + 5. На доске заготовлена таблица:

х
у

Ученик из класса называет какое-нибудь значение x. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение y. Затем другой ученик из класса называет другое значение x и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу.

Пример №2.7 кл. Тема: «Формулы сокращённого умножения»

Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения

( 2y +1)2 – 4y2 =9

y = 2

5972 = (600 – 3)2 =6002 -2 х 600 х 3 + 32 = 360000 – 3600 + 9 =356409

Пример №3. 9 кл. Тема «Сумма n-первых членов арифметической прогрессии»

Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: «Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствие он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”

Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел? Решение проблемы (1 + 100) х 50 = 5050

Последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической прогрессии.

3. Создание проблемных ситуаций через решение задач, связанных с жизнью.

Пример №1. 5 кл. Тема «Периметр прямоугольника»

Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный метр изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.

Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).

Пример №2. 5 кл. Тема: «Площадь прямоугольника»

На прошлом уроке ребята мы измеряли длину и ширину нашего класса и по формуле, нашли его периметр. Р=( а+в)х2=(6+5)х2=22м. Помните!

Посмотрите, пожалуйста, на пол. Линолеум сносился, много чёрных полос. Вам нравится? Мне тоже не нравится. Я думаю, что летом нам нужно обязательно его сменить. Давайте с вами посчитаем, сколько денег нужно будет потратить, если 1 кв.м стоит 180 рублей.

Проблемная ситуация. Для решения этой задачи нам нужно найти площадь пола (площадь прямоугольника).

Дорешав задачу до конца, делаем вывод: нам нужно беречь пол в классе и в школе.

4.Создание проблемных ситуаций через выполнение практических заданий.

Пример №1. 5 кл. Тема «Площадь квадрата»

К уроку вам было дано задание из газеты склеить 1 м2. Вы сделали это? Молодцы! Давайте посмотрим, сколько человек поместится на нём. Выясняем, что 4 человека. Как вы думаете, возможно ли на квадратной площадке со стороной 30 км поместить всё население мира ? ( 7,3 млрд.)

Проблемная ситуация: нужно найти площадь площадки (площадь квадрата)

Пример №2. 6 кл. Тема «Координатная плоскость»

На этапе активного и осознанного усвоения нового материала, а также на этапе закрепления применяю практические работы «Животные на плоскости», «Астрономия и координатная плоскость». Ребята строят точки по координатам и рисуют животных и созвездия, затем рассказывают про них. Также выполняют творческие работы, сами предлагают свои рисунки и по ним составляют задания.

5. Создание проблемных ситуаций через решение задач на внимание и сравнение.

Пример №1 Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе.

6.Создание проблемных ситуаций через противоречие нового материала старому, уже известному.

Пример №1. 7 кл. Тема «Формулы сокращённого умножения»

Вычисляем (2 х 5)²= 2² х5² = 100

(3 х 4)²= 3² х 4² = 9 х 16 = 144

(5 : 6)² = 5² : 6² = 25 : 36

(3 + 4)² = 3² + 4² = 9 + 16 = 25

Попробуйте сосчитать по-другому.

( 3 + 4)² =7² = 49

Проблемная ситуация создана. Почему разные результаты?

( 3 +4)² ≠ 3² + 4²

7. Создание проблемных ситуаций через различные способы решения одной задачи.

Пример №1. 7 кл. Тема «Решение задач»

На заправке две цистерны. В начале посевной обе цистерны заполнены. В 1 было 59 т бензина, а во 2 — 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1 цистерны ежедневно расходуется 5т, а из 2 — 2 т.

Решают с помощью уравнения (алгебраический)

59 – 5х = 44 – 2х

А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить.

Проблемная ситуация: какой способ он предложил (арифметический)

8. Создание проблемных ситуаций через выполнение небольших исследовательских заданий.

5 кл. Тема «Длина окружности»

Ещё древние греки находили длину окружности по формуле С=πD. D- это диаметр окружности.

Вопрос: а что же такое π?

Работаем в парах, выполняя необходимые измерения.

1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.

С1	С2	С3	С сред.	D	π

2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу.

3.Найдите значение π, как неизвестного множителя. Можно пользоваться калькулятором.

4.Каждой паре занести вычисленное значение π в таблицу на доске.

Полученные значения π

1 пара	2 пара	3 пара

среднее арифметическое =( 1 пара +2 пара +3 пара):3. Значение π от 3,1 до 3,2

π- это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.

π=3,1415926…

Для того, чтобы легче запомнить цифры надо сосчитать количество букв в каждом слове высказывания: «это я знаю и помню прекрасно»

В дальнейшей работе мы будем использовать значение π =3,14.

Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь принесли желаемый результат. Проблема решена.

1. Формирование у учащихся
метапредметных результатов относится
сегодня к важнейшему требованию, определенному
Федеральным государственным образовательным
стандартом второго поколения, которые
предусматривают системно-деятельностный
подход к организации процесса обучения. Он
задает другой подход к уроку, утверждает другие
ценности: урок в частности и обучение в целом
оцениваются с точки зрения деятельности каждого
ученика, учитель же в этих условиях становится
организатором процесса получения знаний, а не
источником информации.

За долгие годы своей работы в школе я
столкнулась со следующими проблемами:

— низкий уровень мотивации;

— снижение или отсутствие интереса к предмету;

— высокий уровень тревожности учащихся;

— быстрая утомляемость на уроках, перегрузка
учащихся;

Одним из путей решения данных проблем я считаю
активизацию познавательной деятельности
учащихся, как на уроках, так и во внеурочное
время.

Активная познавательная деятельность учащихся
на уроках способствует более качественному
усвоению знаний, повышает интерес к предмету,
повышает самооценку детей, что, в свою очередь,
помогает школьникам чувствовать себя в классе
более комфортно.

Активизации познавательной деятельности
учащихся можно добиться средствами современных
педагогических технологий. Одной из таких
технологий является технология проблемного
обучения.

Данная технология не нова. Эффективность
проблемного обучения доказана как в работах
отечественных (А.М. Матюшкин, М.И. Махмутов, Г.К.
Селевко) так и зарубежных (Дж.Дьюи, Э де Боно,
В.Оконь) ученых.

Для меня в процессе обучения главным является
постановка перед обучающимися небольших проблем
и стремление решить их с детьми.

Сегодня под проблемным обучением понимается
такая организация учебных занятий, которая
предполагает создание под руководством учителя
проблемных ситуаций и активную самостоятельную
деятельность учащихся по их разрешению, в
результате чего и происходит творческое
овладение знаниями, умениями, навыками и
развитие мыслительных способностей (Г.К.
Селевко).

Основная особенность технологии проблемного
обучения заключается в том, что новые знания не
даются в готовом виде. На уроках с применением
технологии проблемного обучения создаются
условия для получения учащимися опыта
формирования таких УУД как сравнение,
сопоставление, обобщение, аналогия, умение
устанавливать взаимосвязи, у учащихся
формируются умения выдвигать гипотезы,
предлагать самостоятельные доказательства.

2. Наиболее эффективны следующие три метода
организации проблемного обучения:

1. Проблемное изложение;

2. Частично-поисковый метод;

3 .Исследовательский метод.

1) Проблемное изложение представляет собой
промежуточный метод, переходный от
объяснительно-иллюстративного типа к собственно
проблемному обучению. При проблемном изложении
учитель сам формулирует проблему, выдвигает
проблемную задачу, излагает сложные пути ее
решения, как бы ведет поиск и выдает результат.
Учащиеся – активные и заинтересованные
слушатели.

2) Частично–поисковый метод предполагает
частичное вовлечение учащихся в процесс поиска.
Проблему формулирует учитель, но в процессе
изложения темы он постоянно обращается к
учащимся с просьбой сформулировать и оценить
гипотезы, предложить методы решения задач, дать
объяснение и сделать вывод по проведенному опыту
и т.д.

3) Исследовательский метод имеет в виду
наивысшую самостоятельность учащихся. Они
самостоятельно формулируют проблему и сами ее
решают.

Самостоятельно проходят все этапы
исследования:

Видение проблемы — формулировка проблемы –
принятие ее к решению как проблемной задачи –
анализ условий — выдвижение гипотезы –
разработка вариантов решения проблемы –
выполнение плана решения – проверка полученного
результата и оценка действий

3. Проблемная ситуация

Главным и характерным признаком проблемного
обучения является проблемная ситуация.

Проблемная ситуация – это ситуация конфликта
между знаниями, представляющими собой прошлый
опыт, и незнанием того, как объяснить новые
явления. Это затруднение и является условием
возникновения познавательной потребности

Виды проблемной ситуации:

Познавательные.

Решаются сравнением, выдвижением гипотез,
предположений и т.д. В результате появляются
новые законы и выводы в науке, новые понятия.

Оценочные.

Требуют критической оценки предметов и
результатов труда.

Организаторско-производственные.

Решение организаторско-производственных
проблем способствует развитию практического
мышления, а также ведёт к поиску применения
знаний на практике.

Рассмотрим подробнее некоторые проблемные
ситуации.

Создание проблемных ситуаций, через
выполнение практических заданий

Тема “Площадь треугольника” (геометрия 8
класс)

Задача: “Три маляра должны покрасить фронтон
дома в форме прямоугольного треугольника со
сторонами 3м и 4 м. Хватит ли им 1 банки
краски, если на ней написано: площадь покрытия
10г/кв.м.?”

Переведем задачу на математический язык:

“Найдите площадь S прямоугольного
треугольника, если один из катетов 3 м, а
другой – 4 м”.

Первая проблемная ситуация: как вычислить
площадь прямоугольного треугольника, зная
формулу для нахождения площади прямоугольника?”

Учащиеся предлагают различные варианты
решения: достроить данный треугольник до
прямоугольника .

Вычисляют площадь прямоугольника, а затем
находят площадь прямоугольного треугольника.

Вторая проблемная ситуация: всегда ли можем
использовать получившуюся формулу, если
треугольники бывают разной формы?

Задача: “Найти площадь любого
треугольника”.

При помощи наводящих вопросов ученики находят
способ. Они предлагают достроить треугольник до
параллелограмма.

Отвечают на вопрос задачи: площадь любого
треугольника равна половине произведения его
основания на высоту.

Создание проблемных ситуаций через решение
задач на внимание и сравнение

Тема “Сумма углов треугольника” (7 класс):

1)Построить треугольник по трем заданным углам:

2) Два угла треугольника равны 118^o и 62^o.
Найти величину третьего угла.

Создание проблемных ситуаций через умышленно
допущенные учителем ошибки

Тема “Линейные уравнения с одной
переменной” (6 класс)

Решаю быстро уравнение:

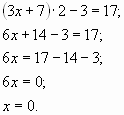
При проверке ответ не сходится. Проблемная
ситуация. Ищем ошибку. Дети решают проблему.

Создание проблемных ситуаций через
противоречие нового материала старому, уже
известному

Тема “Формулы сокращённого умножения” (7
класс)

Вычисляем

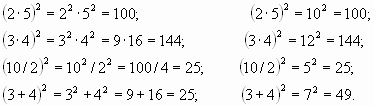
Проблемная ситуация создана. Почему разные
результаты?

Пути, которыми учитель может привести учеников
к проблемной ситуации:

Побуждающий диалог – это “экскаватор”,
который выкапывает проблему;
Подводящий диалог – “локомотив”, движущийся к
новому знанию, способу действия;
Применение мотивирующих приемов: “яркое
пятно” — сообщение интригующего материала и т.д.

Рассмотрим несколько уроков математики, где
были использованы приемы и методы проблемного
обучения.

Тема: “Координатная плоскость” (6 класс)
(подводящий диалог)

В начале урока учитель можно показать классу
хорошо знакомые предметы, например, шахматную
доску, глобус, билет в театр. Учащиеся отвечают на
вопрос: “Что объединяет все эти предметы?”.

Затем предлагается провести параллель между
объектами в географии и математике.

Как описать положение точки на плоскости? –
Ввести координаты на плоскости.
Какова же тема урока? — Координаты на плоскости.
Географические координаты (широта и долгота) –
это воображаемые окружности на поверхности
земного шара. Что можно взять на плоскости вместо
окружностей? – Прямые.
Сколько прямых и каково их взаимное
расположение? – Две пересекающиеся прямые.

В заключение диалога подводится итог: “Рене
Декарт – великий французский математик,
предложивший использовать две взаимно
перпендикулярные прямые для введения координат
на плоскости, в последствии названные –
декартовой системой координат”.

Тема: “Сумма n-первых членов
арифметической прогрессии” (9 класс) (прием
“яркое пятно)

Начать урок можно с исторической зарисовки о
детстве великого математика Карла Гаусса.

Рассказывают, что в начальной школе, где учился
мальчик Карл Гаусс, ставший потом знаменитым
математиком, учитель, чтобы занять класс на
продолжительное время самостоятельной работой,
дал детям задание — вычислить сумму всех
натуральных чисел от 1 до 100. Но маленький Гаусс
это задание выполнил почти моментально. Он
увидел, что…

На доске:

Подводящий диалог:

Что собой представляет последовательность
чисел 1, 2, …, 100? — Арифметическую прогрессию,
первый член которой равен 1, n-член равен 100, а
разность равна 1.
Что требуется найти? — Сумму 100 первых членов.
(Вводим обозначение. На доске: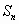 — сумма n-первых членов
арифметической прогрессии).
Какова будет тема урока? — Сумма n-первых
членов арифметической прогрессии.

На доске появляется тема урока и условие
задачи:

Дано: –
арифметическая прогрессия,

Найти: .

Вопрос: как связать числа 101 и 50 с данными
“нашей задачи”. Что интересного вы заметили?

Запишите формулу суммы n-первых членов
арифметической прогрессии.

Тема: “Построение треугольника по трем
элементам” (7 класс) (противоречие между
необходимостью и невозможностью)

В начале урока учитель объясняет способы
построения треугольников по трем элементам.

Затем учащимся предлагается ответить на
вопрос: “Всегда ли можно построить треугольник
по указанным трем элементам?”

Дается задание: построить с помощью циркуля и
линейки треугольник со сторонами:

а) 5см; 6см; 7см;

б) 1см; 2см; 3см;

Учащиеся, опираясь на описанный учителем ход
построения, дают положительный ответ в пункте а),
а в пункте б) создается проблемная ситуация с
удивлением и затруднением (между необходимостью
и невозможностью выполнить задание)

Затем учитель ведет побуждающий диалог от
проблемной ситуации:

“Вы смогли выполнить задание? В чем
затруднение?” — “Нет. Окружности не
пересекаются”.

“Почему они не пересекаются? А когда
пересекутся?”

Побуждение к выдвижению гипотез: “Какие есть
гипотезы?” — “Дело в длинах сторон. Одна сторона
много больше двух других (равна двум другим)”.
Побуждение к устной проверке гипотезы: “Согласны
с этой гипотезой? Почему?” — “Потому что для
любого треугольника верно свойство: длина
большей стороны меньше суммы длин двух других
сторон”.

В своей работе я использую следующую типологию
проблемных задач по математике

Задачи с несформулированным вопросом.
Задачи с недостающими данными.
Задачи с излишними данными.
Задачи с несколькими решениями.
Задачи с меняющимся содержанием.
Задачи на доказательство.
Задачи на соображение, логическое рассуждение.

В своей работе:

1. Применяю сочетание традиционного объяснения
с созданием проблемных ситуаций.

2. Проблемные ситуации в основном применяю при
объяснении нового материала, решении задач

Вывод: Из опыта работы по использованию
проблемного обучения на уроках математики можно
сделать вывод: подготовка проблемного урока –
занятие не простое, трудоемкое, требующее
большой подготовки от учителя к каждому уроку,
умение организовать проблемные ситуации,
активизирующие умственную деятельность
учащихся. Возникает вопрос? Все ли обучение
должно быть проблемным? Я думаю, что проблемное
обучение должно сочетаться с традиционным
усвоением знаний, а главное — обучение должно
быть развивающим!

Вадия Фаритовна Васильева

Ход мастер-класса

Приветствие. Представление. Проведение интеллектуальной разминки.

Приём «Продолжи фразу»: Я предлагаю вам первую часть высказывания, концовку вы должны спрогнозировать сами.

Учитесь сами, не ждите… (когда жизнь вас научит)

Спрашивай и узнаешь, ищи и … (найдёшь) (монгольская посл.)

Для того чтобы усовершенствовать ум, надо… (больше размышлять, чем заучивать) (Р.Декарт).

Как блохи скачут мысли с человека на человека, но … (не каждого кусают).

Если у двух человек имеется по одному яблоку, и они ими обменяются, то у каждого из них окажется опять по одному яблоку. Если у каждого человека есть по одной идее, и они обменяются ими, … (то у каждого будет уже по две идеи )(Б.Шоу).

— Я надеюсь, что сегодня каждый из нас уйдёт, обогащённый множеством идей.

Использование проблемных ситуаций на уроке

как средство формирования УУД .

Развитие педагогической мысли в последнее десятилетие достигло апогея. Многие ведущие дидакты современности говорят о безоговорочном преимуществе такого обучения, в ходе которого ученик выступает как субъект познания и наравне с учителем участвует в учебном процессе. Одним из способов достижения такого результата является проблемное обучение, в ходе которого учителем создаются такие проблемные ситуации, которые принимаются учащимися как личностно-значимые. Такая проблемная ситуация преобразуется в учебную задачу, решая которую ученик овладевает универсальными учебными действиями.

Сегодня я хочу представить некоторые приемы создания проблемной ситуации в учебной деятельности на уроках математики.

1. Создание проблемной ситуации на основе домашних заданий.

Такие задания позволяют поставить учебные проблемы на уроке, к которым учащиеся подошли самостоятельно. По характеру эти задания могут быть различны: предварительное домашнее задание, выполнение практических действий, наблюдений.

Для примера возьмем урок алгебры в 10 классе.

Тема урока: Арксинус. Решение уравнения sin x=a.

За день до урока учащиеся получили задание:

Решите уравнения: а) sin x=1/2

б) sin x =1

в) sin x=0.

г) sin x=2/7.

Решение уравнений осуществляется с помощью числовой окружности. При записи ответа для первых трёх уравнений учащиеся не испытывают трудностей, а вот в четвёртом уравнении возникает проблема – как записать ответ.

Проблемная ситуация принимается учащимися, возникшее затруднение требует своего разрешения – это уже учебная проблема. Учащиеся высказывают свои гипотезы. В дальнейшем учитель умело управляет поиском учащихся, сообщает новые факты, направленные на обоснование выдвинутой гипотезы.

2. Создание проблемной ситуации на основе постановки предварительных заданий на уроке к материалу учебника.

Такие задания ставятся перед учащимися до изучения нового материала или в начале объяснения нового материала.

Для примера возьмём урок математики в 5 классе.

Тема урока: Числовые и буквенные выражения

Изучение новой темы начинается с постановки вопроса:

На доске записаны выражения:

78 + 37; 17 – а; 23 + с; 127 – 63; а + в; 71 – 18;

— Ребята, внимательно посмотрите, на какие две группы можно разделить эти выражения? Попросить записать их в два столбика:

78 + 37; 17 – а;

127 – 63; 23 + с;

71 – 18; а + в;

— почему вы пришли к такому разделению?

— дайте название каждому столбику (числовые и буквенные).

— сформулируйте тему сегодняшнего урока.

— «Числовые и буквенные выражения»

— Сегодня мы будем учиться читать и записывать буквенные выражения.

Такая работа требует логического анализа материала, активизирует внимание и мыслительную деятельность, делает восприятие материала более целенаправленным.

3. Создание проблемных ситуаций через решение задач, связанных с жизнью.

Здесь происходит сталкивание противоречий теоретических знаний и практической деятельности.

Школьникам предлагается выполнить такое задание, для выполнения которого у них недостаточно знаний, нужно ещё что-то новое узнать, изучить. Такие задания стимулируют познавательную деятельность, дети понимают, что выполнить его можно только после определённой теоретической подготовки. Противоречие между теоретическими знаниями и практической деятельностью приводит к проблемной ситуации, а в конечном итоге, к активизации познавательной деятельности.

Для примера возьмём урок математики в 5 классе.

Тема урока: Периметр прямоугольника.

Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать, сколько потребуется штакетника, для изгороди, если на 1 погонный метр изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.

Сразу же начинается обсуждение задачи: Какой Дима? На какой улице его дом? Диме нужно помочь. Но как? Возникает затруднение. Придётся нам решать эту проблему. Проблемная ситуация создана.

Для её решения высказываются ребятами различные предположения (может, сходим на место и попробуем прикладывать по всей длине огорода рейки, но это очень долго; можно спросить у старших дома; может, сами попробуем найти в учебнике какое-то решение и т.д.). Вместе выдвигаем и формулируем основную гипотезу: «нужно найти периметр прямоугольника, он и будет длиной изгороди». Записываем формулу, используем её на практике. Затем делаем вывод: формула периметра прямоугольника нужна. Доводим решение задачи до конца: Диме помогли!

4. Создание проблемных ситуаций при решении занимательных задач.

Для примера возьмём урок математики в 7 классе.

Тема урока: Тема: «Линейная функция»

Обычная форма задания. Функция задана формулой У = Х + 5. Найдите значение функции при Х = 0, 7, -5, 1.

Занимательная форма задания. Приглашаю к доске ученика, даю ему карточку, на которой написано У = Х + 5. На доске заготовлена таблица:

Один ученик из класса называет какое-нибудь значение Х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение У. Затем другой ученик из класса называет другое значение Х и ученик у доски проделывает те же операции. Возникает проблема: “Угадать” формулу, записанную на карточке. Проблемная ситуация создана. Гипотеза: для того чтобы угадать формулу, надо найти какую-то закономерность. Продолжаем подставлять значения х и находим закономерность, и делаем вывод: зная закономерность, легко угадать формулу. В итоге выигрывает тот ученик, который первый назовет формулу.

9 кл. Тема урока «Сумма n-первых членов арифметической прогрессии»

Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа:

«Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс.

В последствие он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?»

Затруднение – как найти быстро сумму первых 100 натуральных чисел – проблемная ситуация для детей. Предположения учащихся (наверное, он выписывал все числа на листочке, а может быть взял в справочнике или знал какое-то правило и т.д.). С помощью учителя формулируют гипотезу: Гаусс знал какое-то правило (формулу) для быстрого счёта. Затем идёт поиск решений. Решение проблемы (1 + 100) × 50 = 5050.

Так как последовательность чисел 1, 2, 3,…,100 является арифметической прогрессией, то по этой формуле мы можем найти сумму любых первых членов арифметической прогрессии, поэтому выводим формулу суммы n-первых членов арифметической прогрессии.

Главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности. Они справились с проблемой!

5. Создание проблемных ситуаций через умышленно допущенные учителем ошибки.

Задачи с заведомо допущенными ошибками. Данный приём развивает внимание, активизирует мыслительную деятельность учащихся. В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение. Иногда учителю полезно предложить “найти ошибки” в заданиях, которые выполнены верно. Чтобы проанализировать готовое решение, детям необходимо сначала самим правильно решить задачу. Проанализировав, сравнив, приходят к выводу, что решение верное. Но бывает, что ребёнок сам допускает ошибку. Возникает проблемная ситуация. Тогда на помощь приходит класс или учитель.

6. Создание проблемных ситуаций через решение задач на внимание и сравнение.

«Говорят, уравнение вызывает сомнение, но итогом сомнения может быть озарение!»

Попробуйте найти хотя бы одно решение уравнения: 28k + 30n + 31m = 365

(проблема, сложность в том, что уравнение содержит 3 неизвестных, что не изучается в школе). Однако любой ученик может найти решение, обратив внимание на числа. Достаточно очевидная гипотеза о том, что речь идет о количестве дней в календарном году, легко проверяется расчетами. Можно сделать вывод о том, что иногда для решения задачи требуется мысль, озарение, а не строгий алгоритм. “Смотреть – не значит видеть!”

Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году.

Тогда: 28 ×1 + 30 ×·4 + 31 ×·7 = 365.

7. Создание проблемных ситуаций через противоречие нового материала старому, уже известному.

Здесь учитель должен подвести школьников к противоречию, вызывающему у них удивление или затруднение. Этот путь наиболее сложен, так как он в точности повторяет звено постановки проблемы в настоящем научном творчестве. Однако именно таким образом формируется творческая способность учащихся к самостоятельному осознанию противоречия и формулированию проблемы.

8. Создание проблемных ситуаций через различные способы решения одной задачи.

7 кл. Тема «Решение задач с помощью уравнений»

На заправке две цистерны. В начале посевной обе цистерны заполнены. В 1-ой было 59 т бензина, а во 2-ой – 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1-ой цистерны расходуется 5т, а из 2-ой – 2 т?

Решают с помощью уравнения (алгебраический способ решения).

59 – 5х = 44 – 2х

А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить. Ученики удивлены: как же он смог решить эту задачу? (Проблема создана). Как вы думаете, не умея решать такие уравнения, он мог решить эту задачу? Дети выдвигают гипотезы (списал, спросил у родителей, посмотрел в ГДЗ, может быть есть другой способ решить задачу, не применяя уравнение и т.д.). Проверяют гипотезы, и кто-то из ребят решает задачу по действиям. Приходим к выводу, что он мог решить эту задачу только другим способом (арифметическим). Далее с помощью учителя убеждаются, что решить данную задачу проще с помощью уравнений.

При каких педагогических условиях проблемная ситуация способствует формированию УУД?.

Учитель должен знать основные приемы создания проблемных ситуаций, четко представлять характер познавательной деятельности на каждом её этапе, понимать сущность проблемного обучения, владеть его методикой.

В работе с учащимися учитель должен использовать разнообразные приемы и методы создания проблемных ситуаций и их разрешения; типология проблемных ситуаций должна быть многообразной.

Это условие исключает возможность учителя «работать по шаблону», требует гибкости и мастерства от педагога, дает «зеленый свет» педагогическому экспромту, творческому проведению урока. Это в свою очередь, формирует у учащихся критичность мышления, творческие продуктивные приемы мыслительной деятельности. Дети всегда «начеку», они не «спят на уроке, зная что учитель скажет (сделает, попросит выполнить) дальше», учащиеся внимательны в течении всего урока, а так как учитель неординарен, многообразен, то и ребята (подражая ему) творчески подходят, к выполнению любого задания, решению любой проблемной ситуации: они ищут все возможные варианты решения, а не останавливаются на одном .

Педагогу необходимо применять на уроке все виды проблемных заданий – проблемный вопрос, проблемные задания практического характера, проблемные задачи.

Важным условием эффективности проблемного обучения для активизации познавательной деятельности является факт «принятия» учеником проблемы как своей личной, т.е. переход проблемной ситуации в учебную проблему. У любой деятельности есть мотив. У познавательной деятельности мотивом является интерес к познавательному, значимость познавательного для субъекта. Следовательно, каждый ученик должен заинтересоваться предметом изучения, проблема должна быть для него интересной, значимой, требующей решения.

Несомненно, решение проблемной ситуации должно идти по определенному, логически обусловленному плану. Должна четко соблюдаться структура, познавательной деятельности на этапе решения проблемы: актуализация прежнего опыта, поиск известных способов решения, отказ от них, формулирование гипотезы о способах решений проблемы, доказательство и проверка гипотезы.

Все этапы решения проблемы характеризуются самостоятельностью познавательной деятельности учащихся. Но это не исключает помощи учителя. Педагог обязан оказать помощь, строго дозированную и своевременную.

Как помочь на уроке? Это не в коем случае не подсказки. Вовремя заданный вспомогательный вопрос, переформулировка проблемного задания, обращение к опыту ребят, показ какого-либо объекта на картинке, организация практического действия, наблюдение из окна – вот неполный перечень того, чем владеет учитель, того, что может помочь учащимся, натолкнуть на мысль. Иногда и это не приносит успеха, тогда учитель делает вывод, что проблема учащимся не доступна (пока) и откладывает ее «на потом».

Когда это происходит на уроке впервые, некоторые ученики бывают так заинтригованы, заинтересованы настолько, что упорно ищут ответ, решение в дополнительной литературе, в интернете, у домочадцев, у старшеклассников после уроков. К следующему учебному дню треть класса уже знает ответ на вопрос. Такая ситуация повторялась у нас не раз, и с каждым разом все больше учащихся активно искали и находили самостоятельно, без задания учителя, нужную информацию. Так, даже из затруднительного положения, учитель извлекает пользу.

В заключении можно сказать, что использование проблемных ситуаций на уроках:

прежде всего формирует регулятивные универсальные учебные действия, обеспечивая выращивание умения решать проблемы. Наряду с этим происходит формирование и других универсальных учебных действий: за счёт использования диалога – коммуникативных, необходимости извлекать информацию, делать логические выводы и т.п. – познавательных.

Ребята больше думают, чаще говорят, активнее формируют мышление и речь и им очень нравится, что они сами могут объяснить увиденные явления, опыты, формулы. Это мотивирует школьников к усвоению нового материала, включая в работу практически весь класс. Диалогический поиск решения, в отличие от изложенных готовых сведений, обеспечивает понимание нового знания каждым учеником. Они учатся отстаивать собственную позицию, рискуют, проявляют инициативу.

Список использованной литературы.

Кульневич С. В., Лакоценина Т. П. Современный урок. Часть ІІІ: Проблемные уроки. — Ростов-н/Д: Изд-во «Учитель», 2005.

Куланин Е. П. Как подготовить и провести проблемную беседу. «Математика» — приложение к газете «Первое сентября»

Лернер И. Я. Проблемное обучение. – М: «Наука», 1980.

Лоповок Л. М. Тысяча проблемных задач по математике. – М: «Просвещение», 1995.

Манвелов С. Г. Основы творческой разработки урока математики. – Статьи из газеты «Математика», 1997.

Матюшкин А. М. Проблемные ситуации в мышлении и обучении. – М: «Просвещение», 1991.

Окунев А. А. Как учить не уча. – Санкт-Петербург: «Нева», 1998.

«Развитие познавательной и творческой активности учащихся через технологию проблемного обучения»

Цель: показать развитие познавательной и творческой активности учащихся через технологию проблемного диалога, создание проблемных ситуаций на уроке.

Ход занятия:

Одна из серьезных проблем современной школы — нежелание большинства учащихся учиться. Такое состояние порождает ряд других не менее катастрофических проблем:

• усиливается репрессивная, принудительная составляющая учебного процесса, что вызывает еще большее отторжение учения;
• подавляются творческие начала, разрушаются личностные качества учащихся.

Сегодня мне хотелось бы представить вам в действии технологию проблемного диалога. Она даёт возможность учителю создать условия, для того чтобы ученик сам добывал знания, учился самостоятельно решать поставленные перед ним задачи. Всё это позволяет обучать ребёнка в режиме деятельностного подхода. Что соответствует требованиям стандартов нового поколения. А учитель, как образно замечает Л.С.Выготский, “… должен быть рельсами, по которым свободно и самостоятельно движутся вагоны, получая от них только направление собственного движения».

Т.е. учитель играет роль режиссёра учебного процесса. Он мотивирует школьников к самостоятельному принятию решения. Корректирует их действия. Участвует в обсуждении и ищет способы, чтобы включить в работу каждого ученика. Это в целом ведёт к формированию УУД: личностных, коммуникативных, познавательных и регулятивных.

Эпиграфом к современному обучению может служить стихотворения Н .Рыленкова «Урок как дорога в будущее»

Пока идёшь за кем-то вслед,

Дорога не запомнится.

Зато, куда б ты не попал,

И по какой распутице

Дорога та, что сам искал

Вовек не позабудется.

К сожалению, очень часто учитель не предоставляет свободы ученику, когда он пытается ответить на вопрос. Учитель не ждёт, сразу же задаёт другой наводящий вопрос. Можно ли учить так, чтобы каждый ребёнок рассуждал над проблемой своим путём, своим темпом, но при необходимости мог сопоставить свою точку зрения с одноклассниками, может даже изменить её? Да, можно. Проанализировав ситуацию в классах, где веду математику, пришла к выводу: Математика начинается вовсе не со счета, что кажется очевидным, а с…загадки, проблемы.

Помочь ученику раскрыться, лучше использовать свой творческий потенциал помогает создание проблемных ситуаций на уроке.

Проблемное обучение – это «начальная школа» творческой деятельности.

Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.

Технологию проблемного диалога можно применять при изучении любой школьной дисциплины и на любой образовательной ступени и потому необходима каждому учителю.

Что нужно учителю для освоения технологии?

Всего две вещи нужны учителю для осознанного освоения технологии проблемного диалога: знания и желание их применять.

АВТОРОМ ЭТОЙ ТЕХНОЛОГИИ ЯВЛЯЕТСЯ Мельникова Елена Леонидовна

Из каких этапов состоит проблемно-диалогический урок?

Этапы урока по технологии проблемного диалога

1. Создание проблемной ситуации учителем и формулирование учебной проблемы учениками.

2. Выдвижение версий решения проблемы.

3. Актуализация имеющихся знаний.

4. Составление плана решения проблемы.

5. Поиск решения проблемы – открытие нового знания.

6. Выражение решения проблемы и применение нового знания на практике.

!!! Модель не жёсткая. В рамках каждой темы возможны существенные вариации при сохранении основных этапов.

Я сегодня остановлюсь на первом этапе: создание проблемной ситуации учителем и формулирование учебной проблемы учениками. Для меня в процессе обучения главным является постановка перед учащимися на уроках небольших проблем и стремление решить их вместе с детьми.

Как же создавать проблемные ситуации? Об этом мы сегодня и поговорим.

Проблемная ситуация — состояние умственного затруднения, вызванного в определенной учебной ситуации объективной недостаточностью ранее усвоенных учащимися знаний и способов умственной и практической деятельности для решения возникшей познавательной задачи.

Типы проблемной ситуации: с удивлением и с затруднением

Ученик должен сформулировать проблему. А учитель должен создать для этого условия. А делает он это с помощью двух диалогов.

Виды диалогов

 Побуждающий диалог

Вопросы учителя, побуждающие детей высказывать различные версии решения проблемы

 Подводящий диалог

Цепочка вопросов, последовательно приводящих к правильному ответу, запланированному учителем

ПО МНЕНИЮ АВТОРОВ технологии, побуждающий и подводящий диалоги имеют достоинства и недостатки.

Побуждающий диалог

 Вопросы учителя, побуждающие детей высказывать различные версии решения проблемы

 + Развивает творческое мышление.

 + Максимально близок к жизненным ситуациям.

 — Ученики могут увести в сторону от темы.

 — Невозможно рассчитать время на уроке.

Подводящий диалог

 Цепочка вопросов, последовательно приводящих к правильному ответу, запланированному учителем

 + Развивает логическое мышление.

 + Просчитывается по времени.

 + Ведет к нужному результату коротким путем.

 — В меньшей степени развивает творчество и инициативу.

Сегодня я остановлюсь на побуждающем диалоге. Чтоб создать его, учитель использует следующие приёмы (их 4)

Приёмы создания проблемной ситуации

Прием 1. Проблемная ситуация с противоречивыми положениями создается одновременным предъявлением классу противоречивых фактов, теорий, мнений. В данном случае факт понимается как единичная научная информация, теория – система научных взглядов, мнение – позиция отдельного человека. Побуждение к осознанию противоречия осуществляется репликами: «Что вас удивило? Что интересного заметили? Какое противоречие налицо?».

Прием 2. Проблемная ситуация со столкновением мнений учеников класса создается вопросом или практическим заданием на новый материал. Побуждение к осознанию противоречия осуществляется репликами: «Вопрос был один? А мнений сколько?» или «Задание было одно? А выполнили вы его как?». И далее общий текст: «Почему так получилось? Чего мы еще не знаем?».

Прием 3. Проблемная ситуация с противоречием между житейским (т.е. ограниченным или ошибочным) представлением учеников и научным фактом создается в два шага. Сначала (шаг 1) учитель выявляет житейское представление учеников вопросом или практическим заданием «на ошибку». Затем (шаг 2) сообщением, экспериментом, расчетами или наглядностью предъявляет научный факт. Побуждение к осознанию противоречия осуществляется репликами: «Вы что думали сначала? А что оказывается на самом деле?».

Прием 4. Проблемная ситуация с противоречием между необходимостью и невозможностью выполнить задание учителя создается практическим заданием, не сходным с предыдущим. Побуждение к осознанию проблемы осуществляется репликами: «Вы смогли выполнить задание? В чем затруднение? Чем это задание не похоже на предыдущее?».

Предлагаю следующие варианты создания проблемных ситуаций на уроках математики.

1. Создание проблемных ситуаций через умышленно допущенные учителем ошибки.

Пример №1. Тема «Линейные уравнения с одной переменной». (7 класс)

Решаю быстро уравнение:

(3Х + 7) • 2 – 3 = 17

6Х + 14 – 3 = 17

6Х = 17 – 14 – 3

6Х = 0

Х = 0

Естественно при проверке ответ не сходится Проблемная ситуация. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат — внимательность и заинтересованность на уроке.

Пример №2. «Обманные задачи»:

а) Постройте прямоугольник со сторонами 2, 3 и 5 см.

б) Больший угол треугольника равен 50°. Найдите остальные углы.

в) Две стороны треугольника перпендикулярны третьей. Определите вид

треугольника.

г) Внешний угол при основании равнобедренного треугольника равен 75°. Найдите

углы треугольника.

д) Диагональ ромба в два раза больше его стороны. Найдите углы ромба.

2.Создание проблемных ситуаций через использование занимательных заданий. Прием «яркое пятно» — заключается в сообщении классу интригующего материала, но при этом связанного с темой урока. Это может быть использование сказки, легенды, фрагмента из художественной литературы, случая из истории науки, культуры, повседневной жизни и т.д.

Пример №1. Тема: «Линейная функция»(7 класс)

Обычная форма задания:

функция задана формулой 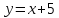. Найдите значение функции при x = 0, 7, -5, 1.

Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано .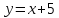

Х
У

На доске заготовлена таблица:

Ученик из класса называет какое-нибудь значение х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение у. Затем другой ученик из класса называет другое значение х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу.

Пример №2. Тема: «Формулы сокращённого умножения»(7 класс)

( 2y +1)² – 4y² =9

y = 2

597² = (600 – 3)² =6002 -2 • 600 • 3 + 3² = 360000 – 3600 + 9 =356409

Пример №3. Тема «Сумма n-первых членов арифметической прогрессии» (9 класс)

Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствие он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”

Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?

Решение проблемы (1 + 100) • 50 = 5050

3. Создание проблемных ситуаций через решение задач, связанных с жизнью. Прием «актуальность» — состоит в обнаружении смысла, значимости предлагаемой темы для самих обучающихся, лично для каждого.

Пример №1. Тема «Периметр прямоугольника»( 5 класс)

Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.

Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).

Пример №2. Тема «Проценты»( 5 класс)

Вы знаете, что в этом году я выиграла в лотерею. Размер выигрыша 10 тыс. руб. Но я получу не все деньги. Вычитают подоходный налог 13%. Я хочу, чтобы вы помогли сосчитать, какую сумму я получу.

Вопрос: «А как же мы вам поможем, если мы не знаем, что такое процент?»

Проблемная ситуация создана. Ребята с удовольствием работают в течении всего урока. В конце урока дорешивают задачу до конца. Я вижу радостные лица ребят. Они справились с проблемой!

4.Создание проблемных ситуаций через выполнение практических заданий.

Пример.№1. Тема «Площадь квадрата»(5 класс)

К уроку вам было дано задание из газеты склеить 1 м². Вы сделали это? Молодцы. Давайте посмотрим, сколько человек поместится на нём. Выясняем, что 4 человека. Как вы думаете, возможно ли на квадратной площадке со стороной 30 км. поместить всё население мира ?( 6,5 млрд.)

Проблемная ситуация: нужно найти площадь площадки (площадь квадрата)

Пример №2. Тема «Координатная плоскость»( 6 класс)

Пример № 3.Темы: «Построение треугольника по трем элементам», «Неравенство треугольника».( 7 класс)

Теорему о неравенстве треугольника вводим при изучении темы «Построение треугольника по трем элементам», решая задачу на построение треугольника по трем его сторонам. Предлагаем ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 9см; 5см; 6см;

в) 1см; 2см; 3см; г) 3см; 4см; 10см.

Ребята работают самостоятельно и приходят к тому, что построить треугольник в последних двух примерах не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи, дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему.

5. Создание проблемных ситуаций через решение задач на внимание и сравнение. Задается вопрос (задание), которое выявляет разные мнения учеников класса, сталкивая их. Какие же мнения верные?

Пример№1. Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе.

Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а, б?

Что общего в данных фигурах, а в чём различие?

Пример №2. Тема: «Площадь трапеции». (8 класс)

При выводе формулы для вычисления площади трапеции учитель предлагает учащимся воспользоваться ранее изученными формулами для вычисления площади прямоугольника, параллелограмма, треугольника, свойствами площадей.

Ребята предлагают различные способы:

а) провести диагональ и найти площадь трапеции как сумму площадей двух треугольников;

б) провести две высоты и найти площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников;

в) провести прямую, параллельную боковой стороне трапеции и найти площадь трапеции как сумму площадей параллелограмма и треугольника.

Пример №3. Тема: «Четырехугольники». ( 8 класс)

К моменту изучения темы «Квадрат» учащимся знакомы такие виды четырехугольников как прямоугольник, ромб и их свойства. Прошу учащихся сформулировать определение квадрата. На что они дают два разных определения: «Квадратом называется прямоугольник, у которого все стороны равны» или «Квадратом называется ромб, у которого все углы прямые». Оба определения верные. Обсуждаем почему имеет право быть каждое из них.

6.Создание проблемных ситуаций через противоречие нового материала старому, уже известному. Дается задание, выполнение которого вызывает затруднения при имеющемся уровне знаний и умений. Почему не смогли выполнить задание?

Пример№1. Тема «Формулы сокращённого умножения»( 7 класс)

Вычисляем (2 • 5)²= 2² •5² = 100

(3 • 4)²= 3² • 4² = 9 • 16 = 144

(5 : 6)² = 5² : 6² = 25 : 36

(3 + 4)² = 3² + 4² = 9 + 16 = 25

Попробуйте сосчитать по-другому.

( 3 + 4)² =7² = 49

Проблемная ситуация создана. Почему разные результаты?

( 3 +4)² ≠ 3² + 4²

7. Создание проблемных ситуаций через различные способы решения одной задачи.

Пример. Тема «Решение задач»( 7 класс)

На заправке села две цистерны. В начале посевной обе цистерны заполнены. В 1 было 59 т бензина, а во 2 — 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1 цистерны ежедневно расходуется 5т, а из 2 — 2 т.

Решают с помощью уравнения (алгебраический)

59 – 5х = 44 – 2х

А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить.

Проблемная ситуация: какой способ он предложил (арифметический)

8. Создание проблемных ситуаций через выполнение небольших исследовательских заданий.

Пример№1. Тема «Длина окружности»( 6 класс)

Ещё древние греки находили длину окружности по формуле 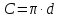, где d — это диаметр окружности.

Вопрос: а что же такое π ?

Работаем в парах, выполняя необходимые измерения.

С1	С2	С3	С сред.

2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу.

3.Найдите значение , как неизвестного множителя. Можно пользоваться калькулятором.

4.Каждой паре занести вычисленное значение в таблицу на доске.

Полученные значения

1 пара	2 пара	3 пара

среднее арифметическое =( 1 пара +2 пара +3 пара):3 Значение от 3,1 до 3,2

это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.

=3,1415926…

Для того, чтобы легче запомнить цифры надо сосчитать количество букв в каждом слове высказывания: «Это я знаю и помню прекрасно» или «Нужно только постараться и запомнить всё как есть: три, четырнадцать, пятнадцать, девяносто два и шесть!»

В дальнейшей работе мы будем использовать значение =3,14

Имея успех в небольших исследованиях на уроках, некоторые ребята вовлекаются в более серьёзные исследования, требующие много времени. Это уникальная возможность для ученика сделать своё открытие, узнать то, что до него никто не знал. Исследования помогают расширить кругозор ученика, повысить самооценку, самоутвердиться, формировать исследовательскую компетентность.

Рекомендации учителям по созданию проблемных ситуаций на уроке.

1.Подводить к противоречию с уже известным и предлагать самим находить способ разрешения.

2. Побуждать делать сравнения, обобщения, выводы.

3. Создавать ситуации включения, используя задания, связанные с их жизненным опытом.

4. Использовать задачи с заведомо допущенными ошибками.

5. Предлагать практические исследовательские задания.

6. Отыскивать различные способы решения одной и той же задачи.

7. Излагать различные точки зрения на один и тот же вопрос.

8.Учить составлять задачи по статистическим данным своего населённого пункта.

Итак, сегодня я познакомила вас с технологией проблемного диалога. Чтобы создать его я применяю различные приёмы, в частности, создание проблемной ситуации.

Преимущества технологии проблемного диалога

 Проблемный диалог является мощным источником мотивации познавательной деятельности учащихся.

 Проблемный диалог реализуется на любой ступени обучения.

 Проблемный диалог дает учителю широкие возможности выбора методов, форм и средств обучения.

 В работу включается практически весь класс, что гарантирует усвоение нового материала большинством учеников.

 Обеспечивает более качественное усвоение знаний, приучает учащихся мыслить, развивает их интеллектуальные способности и активность.

Вывод:

Сегодня я попыталась показать вам, что использование технологии проблемного диалога, в частности, создание проблемных ситуаций на уроках математики не только формирует ту систему математических знаний, умений и навыков, которая предусмотрена программой, но и самым естественным образом развивает у школьников познавательную и творческую активность. Ситуация затруднения школьника в решении задач приводит к пониманию учеником недостаточности имеющихся у него знаний, что в свою очередь вызывает интерес к познанию и установку на приобретение новых. Всякий раз при разрешении проблемной ситуации я с удовольствием наблюдаю, как ребята не только усваивают новое для себя, но и переживают этот процесс как «открытие» ещё чего-то неизвестного: кто сдержанно (старшеклассники), а кто с нетерпением и восторгом (шестиклассники), торопясь, чтобы его не опередили в «открытии», и обижаясь иногда на себя, если не сумел быть первым, а иногда на меня «почему выбрала другого, а не меня». А мне на каждом уроке приходится думать о том, как ободрить его, заставить поверить в свои силы, снова увидеть горящие глаза. Именно это заставляет меня искать что-то новое, всегда быть в поиске.

Выбор за тобой

«Это невозможно!» — сказала Причина.

«Это безрассудство!» — заметил Опыт.

«Это бесполезно!» — отрезала Гордость.

«Попробуй…» — шепнула Мечта.

Литература

1.Мельникова Е.Л. Проблемный урок, или как открывать знания с учениками: Пособие для учителя. — М., 2002.

2.Мельникова Е.Л. Технология проблемного диалога: методы, формы, средства обучения // Образовательные технологии. Сборник материалов. М., Баласс, 2008.

3. Кульневич С.В. Современный урок. Часть II Проблемные уроки. – Ростов на Дону:

Учитель,2006

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Считается, что теоретическую основу современной технологии проблемного обучения разработал Джон Дьюи. Основываясь на результатах своей деятельности в опытной школе Чикаго (США), в 1909 г. в книге «Как мы мыслим» он заявил о высокой эффективности обучения, в котором организована активная деятельность по самостоятельному решению детьми учебных проблем. Отвергая догматическое обучение, Дьюи впоследствии обосновал и психологические механизмы способности ребёнка решать проблемы.

В отечественной педагогике идеи проблемного обучения стали актуальными начиная со второй половины 1950-х гг., а в 1960-е гг. в научно-педагогической и методической литературе обосновывается богатый потенциал решения учебных проблем, и выявляются способы организации проблемного обучения.

Можно сказать, что проблемное обучение является современным уровнем развития практической педагогики и дидактики.

Цель курсовой работы – раскрыть теоретические положения, особенности содержания и методики проблемного обучения в педагогическом процессе.

Объект исследования – процесс проблемного обучения.

Предмет исследования – методы, формы, содержание проблемного обу- чения в учебной деятельности.

Актуальность данной технологии определяется развитием высокого уровня мотивации к учебной деятельности, активизации познавательных интересов учащихся, что становится возможным при разрешении возникающих противоречий, создании проблемных ситуаций на уроке. В преодолении посильных трудностей у учащихся возникает постоянная потребность в овладении новыми знаниями, новыми способами действий, умениями и навыками.

§1. Сущность проблемного обучения

Сущность проблемного обучения заключается в такой организации учебно-познавательной деятельности учащихся, при которой эта деятельность приобретает целенаправленный поисковый характер. Он начинается с их участия в постановке вопросов, с уяснения сути проблемы и проблемных задач, заложенных в учебных программах и учебниках, в проблемном изложении учебного материала педагогом и его пояснении учебной информации. Поисковый характер учебной деятельности учащихся раскрывается в процессе разрешения проблемы с использованием разнообразных видов их самостоятельной работы.

В проблемных вопросах, в отличие от непроблемных, всегда присутствует определенное скрытое противоречие. Необходимость уяснения и вскрытия этого противоречия уже является одной из характерных особенностей проблемной ситуации. При этом большое значение приобретает также мотивационная сторона проблемной ситуации. Мотивация состоит в наличии у ученика такого уровня и объема знаний, умений и навыков, который был бы достаточным для того, чтобы начать поиск неизвестного результата или способа выполнения задания. При ощущении же и осознании их недостаточности ученик самостоятельно стремится восполнить имеющиеся пробелы в своих знаниях, умениях и навыках. Иначе он не сможет воспринять суть ситуации, и она утратит для него роль учебной проблемы.

Проблемное обучение представляет собой способ развития сознания человека через самостоятельное разрешение им познавательных проблем, содержащих в себе противоречия, или через его активное участие в процессе разрешения этих проблем.

Противоречия являются важнейшей чертой содержательного аспекта проблемного обучения, закономерно возникающей и раскрывающейся в процессе познавательной деятельности ученика и являющейся источником ее движения и развития. Примерами таких противоречий могут быть:

1) противоречия между исходными знаниями и новыми, парадоксальными фактами, не укладывающимися в известную теорию и разрушающими ее;

2) противоречия между пониманием научной важности проблемы и отсутствием необходимой теоретической базы для ее решения;

3) противоречия между теоретически возможным способом решения проблемы и его практической нецелесообразностью;

4) противоречия между существованием определенного многообразия концепций и отсутствием надежной теории для объяснения данных фактов;

5) противоречия между практически доступным результатом и отсутствием его теоретического обоснования;

6) противоречия между большим количеством фактических данных и отсутствием общего метода их обработки и анализа.

Все указанные противоречия обычно возникают вследствие наличия определенного дисбаланса между теоретической и практической информацией, избытком одной из них и недостатком другой, или наоборот [Бондаренко, Пономарев и др., 2005, с. 253 – 255].

Общие функции проблемного обучения:

1) усвоение учениками системы знаний и способов умственной и практической деятельности;

2) развитие интеллекта учащихся, т. е. их познавательной самостоятельности и творческих способностей;

3) формирование диалектико-материалистического мышления школьников;

4) формирование всесторонне и гармонично развитой личности.

Специальные функции проблемного обучения:

1) воспитание навыков творческого усвоения знаний (применение системы логических приемов или отдельных способов творческой деятельности);

2) воспитание навыков творческого применения знаний (применение усвоенных знаний в новой ситуации) и умений решать учебные проблемы;

3) формирование и накопление опыта творческой деятельности (овладение методами научного исследования, решения практических проблем и художественного отображения действительности);

4)формирование мотивов учения, социальных, нравственных и познавательных потребностей [Махмутов, 1975, с. 20 – 23].

Технология проблемного обучения раскрывается через постановку (преподавателем) и разрешение (учеником) проблемного вопроса, задачи и ситуации, выступающих центральными категориями этой технологии.

Вопрос может содержать в себе скрытое противоречие, вызывать различные, порой противоположные позиции при его разрешении. Например, высказывание «завтра ожидается холодный южный ветер» содержит противоречие: южный, но холодный. Почему? Ответ: потому что циклон. Могут ли существовать горячий снег, жареный лед и т.д.? Поиски ответов на подобные вопросы стимулируют мысль, активизируют мышление, заставляют ученика думать.

Проблемная задача выступает простейшим, частным случаем проблемы, когда последняя состоит всего лишь из одной задачи. Она представляет собой учебно-познавательную задачу, вызывающую стремление к самостоятельному поиску путей, способов и средств рационального ее решения. В основе проблемной задачи обычно лежит противоречие между существующими знаниями. Пример проблемной задачи: «Возможна ли привязка типового проекта к определенной местности»? Для решения этой задачи требуется провести специальный поиск способа действий или найти какие-то недостающие данные: провести разведку местности, сделать ее геодезическую съемку, исследовать в лаборатории характеристики грунта, определить розу ветров и т.п.

Проблемные задачи принципиально отличаются от тренировочных, цель которых состоит не в поиске нового способа решения, а закрепление у учеников навыка применения определенного известного метода [Бондаренко, Пономарев и др., 2005, с. 255 – 257].

Важным является то, что формой реализации принципа проблемности в обучении является учебная проблема. Учебная проблемная ситуация представляет собой психическое состояние мыслительного взаимодействия ученика или класса с некоторой проблемой под руководством преподавателя. Для такой ситуации характерным является психологическое состояние интеллектуального затруднения. Иными словами, человек, воспринимая проблему, осознает, что ему недостает, например, знаний для ее решения, он не может выполнить задачу известными ему способами и поэтому должен найти новые способы. У него возникает потребность активно мыслить, чтобы ответить на вопрос «почему»? Потребность, как известно, рождает мотив, побуждающий человека думать и действовать.

Проблемная ситуация является начальным моментом мышления, вызывающая познавательную потребность ученика и создающая внутренние условия для активного усвоения новых знаний и способов деятельности [Дышинский, Лурье, Людмилов, 1975, с. 56].

Проблемные ситуации можно подразделять по нескольким основаниям:

1) по области научных знаний или учебной дисциплине (русскому языку, математике и тому подобное);

2) по направленности на поиск недостающего нового (новых знаний, способов действия, выявления возможности применения известных знаний и способов в новых условиях);

3) по уровню проблемности (очень острые противоречия, средней остроты, слабо или неявно выраженные противоречия);

4) по типу и характеру содержательной стороны противоречий (например, между житейскими представлениями и научными знаниями, неожиданным фактом и неумением его объяснить и тому подобное) [Кудрявцев, 1991, с. 18].

Серия проблемных вопросов должна преобразовать проблемную ситуацию в проблемную задачу, то есть в модель поиска решения, где известно, что «дано», что «требуется доказать» и планомерно рассмотреть различные пути, средства и методы решения.

Различается четыре основных типа проблемных ситуаций:

1) ситуация нехватки знаний (учащиеся не могут решить задачу, ответить на вопрос из-за отсутствия необходимых знаний);

2) ситуация новых условий (необходимые знания у детей, однако им предстоит придумать, как применить имеющиеся знания и умения в новых условиях);

3) ситуация противоречия между теоретической возможностью и практической осуществимостью (например, ученику надо выбрать из нескольких известных ему способов решения самый рациональный);

4) ситуация противоречия между полученным практическим результатом и отсутствием знаний для того, чтобы объяснить, как и почему получен именно такой результат [Матюшкин, 2008, с. 87 – 90].

В проблемном обучении главное – не мгновенный выход на решение проблемы, а своеобразная «путепроходческая» работа. Преподаватель, зная оптимальный путь решения, ориентирует поисковую деятельность учащихся, постоянно подводя их к «разгадке».

§2. Система методов проблемного обучения

Система общих методов:

1) объяснительно иллюстративный;

2) репродуктивный;

3) проблемное изложение;

4) частично-поисковый;

5) исследовательский метод.

Система методов проблемного обучения представляет собой органическое сочетание общих и бинарных методов.

В целом можно говорить о пяти дидактических способах организации процесса проблемного обучения (то есть общих методах), представляющих собой три вида изложения учебного материала учителем и три вида организации им самостоятельной учебной деятельности учащихся:

1) монологическом;

2) рассуждающем;

3) диалогическом;

4) эвристическом;

5) исследовательском [Лернер, 1981, с. 94 – 104].

Монологический метод – предполагает изложение обучающим учебного материала с целью объяснения учащимся готовых выводов науки в форме рассказа или школьной лекции с применением аудиовизуальных средств и формирования у учащихся знаний и умений на уровне их восприятия и понимания.

На первый взгляд кажется, что использовать монологический метод довольно просто: рассказал, показал, прочитал, объяснил, повторил. Однако каждому учителю известно, как это трудно сделать. Трудно удержать внимание учащихся на учебном материале, поддержать их интерес к нередко неинтересным для них явлениям и фактам. Поэтому при монологическом методе необходимо обращать особое внимание на приёмы, усиливающие его возможности.

Приём проблемного изложения – применительно к монологическому методу характеризуется спорадическим возникновением проблем.

Прием нахождения аналогии – формирует готовность восприятия учебного материала путем концентрации внимания учащихся на конечной цели — нахождении аналогии изучаемому событию, явлению, процессу, личности и т. п.

Приём обнаружения противоречий – активизирует способность анализировать, выделять главное.

Рассуждающий (показательный) метод – предполагает объяснение учебного материала путём постановки проблемы и показа учащимся логики научного исследования, формирование у них способов поисковой деятельности. Деятельность учащихся носит репродуктивный характер, но возможности побуждения к учебной деятельности шире, чем при монологическом методе.

Приём логического изложения – формирует у учащихся понятие о логике и способах решения научной или практической проблемы. В монолог преподавателя вводятся элементы рассуждения, порядок следования сообщаемых фактов выбирается таким образом, чтобы объективные противоречия содержания были представлены особенно подчёркнуто и возбуждали познавательный интерес учащихся и желание их разрешить.

Приём предположения – в нём в отличие от приёма логического изложения учащимся предлагается после постановки учителем проблемного вопроса, предположить на какие факты опираются, доказывая свою правоту, сторонники той или иной точки зрения. Использование этого приёма возможно как индивидуально, так и в варианте парного и группового взаимодействия. В качестве подсказки можно предложить опорные слова и выражения. Последующее сопоставления собственного варианта с объяснением учителя способствует формированию у учащихся способов поисковой деятельности [Котова, Шиянов, 2000, с. 134 – 136 ].

Диалогический метод – предполагает проведение сообщающей беседы с целью объяснения учебного материала учителем, усвоения его учащимися. Ученики при этом методе активно участвуют в постановке проблемы и её решении путём выдвижения предположений и самостоятельного доказательства своих гипотез, что способствует формированию у них умений речевого общения, самостоятельной деятельности и коллективной мыслительной деятельности.

В беседе преподаватель привлекает учащихся к ответам на такие вопросы, которые обращены к имеющимся у них знаниям и умениям. Доля их самостоятельности в учебной деятельности определяется количеством вопросов репродуктивного характера.

Особенно привлекательным в данном методе является его динамичность, он может перейти и в эвристический, и при необходимости в монологический, кроме того, может применяться практически на любом этапе урока.

Из приёмов, соответствующих этому методу, назовем следующие:

Приём создания проблемной ситуации – в нём, в отличие от приёма проблемного изложения, проблемные вопросы вызывают удивление, создают познавательное затруднение, вызывают эмоции. Решаются они самими детьми при помощи учителя следующим образом: уяснение и постановка проблемы; формулирование вариантов решения; оценка их предпочтительности; выбор средств оптимального решения [Махмутов, 1987, с. 84 – 90].

Следует отметить, что данный приём может использоваться и в эвристическом, и в исследовательском методах.

Эвристический метод – предполагает проведение эвристической беседы с решением познавательных задач. Открытие нового закона, правила и тому подобное совершается не учителем при участии учащихся, а самими учащимися под руководством и с помощью учителя.

Для проведения уроков с использованием данного метода используются следующие приёмы:

Приём альтернативной ситуации – предполагает выбор вариантов исторического развития реально существовавших в истории. Проблемный вопрос в данной ситуации начинается со слов: Что было бы, если…[Лернер, 1981, с. 106 – 108].

Исследовательский метод – предполагает организацию учителем самостоятельной работы учащихся по решению проблемных заданий с целью усвоения ими новых понятий и способов действий и развития у них интеллектуальной и других сфер [Махмутов, 1987, с. 84 – 90].

§3. Структура проблемного урока

Принято различать три основных звена в технологии проблемного обучения:

1) осознание общей проблемной ситуации, ее анализ;

2) формулировка конкретной проблемы, решение проблемы (выдвижение, обоснование гипотез, последовательная проверка их);

3) проверка правильности решения проблемы.

В зависимости от того, какие и сколько звеньев задействованы в учебном процессе, можно выделить три уровня реализации технологии проблемного обучения. При традиционной технологии обучения учитель сам формулирует и решает проблему (выводит формулу, доказывает теорему и т.д.). Ученик же должен понять и запомнить чужую мысль, запомнить формулировку, принцип решения, ход рассуждения. Первый уровень технологии проблемного обучения характеризуется тем, что учитель ставит проблему, формулирует ее, указывает на конечный результат и направляет самостоятельные поиски ученика [Котова, Шиянов, 2000, с. 149].

После проведенного анализа переход идет на этап формулирования проблемы, преобразования задачи, сравнения, поиска аналогов и др. В результате проделанной работы ученики выдвигают вариант или варианты решения проблемы. Затем выбранный вариант (варианты) проверяются, исключаются неверные заключения уточняются и развиваются достоверные положения [Богданова, 2011, с. 58].

У ученика воспитывается способность самостоятельно и формулировать, и решать проблему, а учитель только указывает на нее, не формулируя конечного результата.

И, наконец, на третьем уровне учитель даже не указывает на проблему: ученик должен увидеть ее самостоятельно, а увидев, сформулировать и исследовать возможности и способы ее решения.

В итоге воспитывается способность самостоятельно анализировать проблемную ситуацию и видеть проблему, находить правильный ответ. Если учитель чувствует, что учащиеся затрудняются выполнить то или иное задание, то он может ввести дополнительную информацию, снизить тем самым степень проблемности и перевести учащихся на более низкий уровень технологии проблемного обучения. Трехуровневая технология проблемного обучения применима при постановке задачи на «открытие» простого математического закона, правила правописания, исторической или биологической закономерности [Котова, Шиянов, 2000, с. 149].

Также не стоит забывать, что на таких уроках следует ставить акцент на устное изложение, а точнее диалог, который может быть как живое общение преподавателя с учениками, либо как внутренний диалог [Богданова, 2011, с. 61].

§4. Опыт проведения проблемных уроков в начальной школе

Л.В. Иванова, учитель начальных классов МОУ «Лицей №2» г. Воронежа и С.Г. Студенцова, учитель начальных классов МБОУ «Гимназия №5» г. Воронежа используют следующие варианты создания проблемных ситуаций на уроках математики:

1) создание проблемных ситуаций через умышленно допущенные учителем ошибки;

2) создание проблемных ситуаций через использование занимательных заданий;

3) создание проблемных ситуаций через решение задач, связанных с жизнью;

4) создание проблемных ситуаций через решение задач на внимание и сравнение;

5) создание проблемных ситуаций через различные способы решения одной задачи;

6) создание проблемных ситуаций через выполнение небольших исследовательских заданий.

Они приводят следующие примеры.

Пример №1. Ввести скобки как средство обозначения порядка действий.

Учащиеся выполняют вычисления по двум различным программам, приводящим к одинаковым выражениям, но различным результатам.

1 программа. Из числа 56 вычесть 15. К полученной разности прибавить 23.

56-15+23=64

2 программа. К числу 15 прибавить 23. Из числа 56 вычесть полученную сумму.

56-15+23=18.

— Что вы замечаете?

Выражения в левой части обоих равенств одинаковые, а их значение, разные. (Предъявление двух противоречивых фактов – создание проблемной ситуации).

— Почему получились разные ответы?

(Дети устанавливают, что разные ответы получились из-за порядка действий, необходимы скобки.)

Проблемное обучение невозможно без учебного диалога. Ученики должны быть поставлены в ситуацию интеллектуального затруднения, из которого сами должны найти выход. Они считают, что эффективность выбранной технологии доказывают стабильные результаты нашего совместного с ребятами труда. Проблемные ситуации можно использовать на различных этапах урока: при объяснении, закреплении, контроле.

При обучении математике на решение задач отводится большая часть учебного времени. Проблемные текстовые задачи ставят ученика в ситуацию, в которой у него должно появиться удивление и ощущение трудности, которое ученик намерен преодолеть.

При работе над задачами они пытаются использовать разные типы задач.

Пример №2. Задачи без вопроса: « В парке 32 берёзы, а остальные сосны…»

«У белочки 7 орехов, а грибов в 5 раз больше…»

При решении таких задач перед учеником стоит проблема. Какой задать к задаче вопрос? Ведь в зависимости от поставленного вопроса будет меняться решение задачи.

Пример №3. Задачи с недостающими данными:

«В классе 29 мальчиков и девочек. Сколько в классе девочек?»

«На тарелке 5 яблок. 3 груш, остальные мандарины. Сколько мандаринов на тарелке?»

Пример № 4. Задачи с излишними данными:

«У белочки в дупле 25 грибов, 23 орешка и 17 шишек. На сколько больше у белочки грибов, чем шишек?»

Пример №5. Задачи на логическое мышление:

«На фотографии две мамы, две дочки и бабушка с внучкой. Сколько человек на фотографии?»

В ходе решения проблемы учащийся преодолевает все трудности, его активность и самостоятельность достигают высокого уровня.

Результаты обучения достаточно высокие и устойчивые. Учащиеся легче применяют полученные знания в новых ситуациях и одновременно развивают свои умения и творческие способности.

Проблемное обучение вызывает со стороны учащихся живые споры, обсуждения. Проблемное обучение вызывает к жизни эмоции учеников, создается обстановка увлеченности, раздумий, поиска. Это плодотворно сказывается на отношении школьника к учению.

Рассмотрим проблемное обучение на уроке Русского языка.

Пример приводит учитель начальных классов Шохтина Ирина Владимировна, МАОУ «Средняя общеобразовательная школа №1» г. Тобольск.

Проблемный урок она строит по следующей структуре:

Этапы урока	Учитель	Ученик
Орфографическая зарядка (комплексное повторение, развитие умений с элементами актуализации изученного).	Предлагает учащимся записать предложения, слова, выполнить комплекс заданий (группировка и объяснение орфограмм, разные виды разбора и т.д.)	Вариант: ученики сами формулируют задания к данному предложению и затем выполняют их.
Актуализация изученного.	Воспроизведение понятий и алгоритмов, необходимых для «открытия» нового знания; фиксирование затруднения в деятельности	Выполняют упражнение.
Постановка учебной проблемы.	Варианты:1. Создание проблемной ситуации. 1.1. Предлагает практическое задание на новый материал, чтобы возник разброс мнений учащихся (фронтально, в группах или в парах) или разные варианты уже выполненного задания. 1.2. Одновременно предлагает противоречивые факты или теории. 2. Подводящий к теме диалог (система вопросов и заданий, выводящая на формулирование темы урока).	Вступают в диалог с учителем, выполняя задание, выявляют, осознают и проговаривают противоречие.
Формулирование проблемы, планирование деятельности.	Какой же возникает вопрос? Что предстоит выяснить? Как будем действовать? Записывает на доске основную проблему, вопрос или тему, план.	Формулируют учебную проблему (вопрос или тему), называют этапы работы.
Поиск решения (открытие нового знания), формулирование правила (определения)	Варианты:1. Предлагает ученикам выдвинуть гипотезы: — Какие есть предложения, версии? (Все версии принимаются с одобрением). Фиксирует на доске версии в виде схем, ключевых слов и т.д., организует обсуждение. 2. Предлагает материал для наблюдения и систему вопросов, которые подводят детей к формулировке правила или определения.	Предлагают свои версии (фронтально или в группах). По окончании работы сверяют свой результат с правилом (определением учебника). Отвечают на вопросы, формулируют правило или определение, сверяют с учебником.
Развитие умений, применение нового знания.	1. Просит детей прочитать про себя задание к упражнению, объяснить, что нужно сделать (с проговариваем, коллективно, по ходу выполнения упражнения).2. Предлагает самостоятельно выполнить упражнение.	Читают, объясняют и выполняют с проговариванием. Выполняют индивидуально или в парах, по окончании работы объясняют, проговаривают, как действовали.
Итог урока.	— Какая была проблема (вопрос, тема)? — Какой ответ (решение) мы нашли? К какому выводу пришли? — Что получилось на уроке? — Что вызвало затруднение? — Как оцениваете свою работу? и т.д.	Обобщают, делают выводы. Рефлексия. Самоанализ, самооценка. Обсуждение.
Домашнее задание.	Комментирование д/з.	Вопросы по ходу комментирования.

Прежде чем запланировать проблемное изучение определенной темы, необходимо установить возможность и дидактическую целесообразность создания проблемных ситуаций при её изучении. При этом надо учитывать специфику содержания изучаемого материала, его сложность, характер (описательный материал или требующий обобщений, анализа, выводов). Большое внимание должно быть уделено выявлению внутренних условий мышления учащихся и предварительной работе:

1) выявить уровень знаний и представлений учащихся по данной теме (установить каков реальный запас их знаний и жизненный опыт, а также учесть типичные ошибки, допускаемые школьниками);

2) необходимо предусмотреть, какие новые сведения понадобятся учащимся для разрешения системы проблемных ситуаций при проблемном изучении темы, а также продумать способы сообщения этих необходимых сведений;

3) надо выявить интеллектуальные возможности учащихся, уровень их развития, наличие собственного мнения.

В зависимости от выявленного уровня внутренних условий мышления учащихся разрабатывается соответствующая система конкретных заданий и рассчитанных на то, чтобы обнаружить противоречие на пути движения школьников от незнания к знанию и тем самым создать проблемные ситуации.

ЗАКЛЮЧЕНИЕ

По результатам проделанной работы можно выделить следующие преимущества проблемного обучения: это, во-первых, наибольшие возможности для развития внимания, наблюдательности, активизации мышления и познавательной деятельности учащихся; во-вторых, развитие самостоятельности, ответственности, критичности и самокритичности, инициативности, нестандартности мышления, осторожности и решительности.

Проблемное обучение связано с исследованием и поэтому предполагает растянутое во времени решение задачи. Ученик попадает в ситуацию подобно деятелю, решающему творческую задачу или проблему. Он постоянно думает над ней и не выходит из этого состояния, пока её не решит.

К трудностям проблемного обучения можно отнести то, что оно всегда вызывает затруднение у учащихся в учебном процессе, поэтому на его осмысление и поиски путей решения уходит значительно больше времени, чем при традиционном обучении. Кроме того, разработка технологии проблемного обучения требует от учителя большого педагогического мастерства и много времени. На мой взгляд, зная уровень интеллектуального развития учащихся своего класса и работая в системе, этих трудностей можно избежать.

Проблемные уроки очень эффективны и нравятся детям. Поэтому можно проводить по такой структуре уроки по любым предметам. Конечно, работа трудоёмка, так как к каждому уроку надо подбирать необходимые и достаточные упражнения для актуализации знаний и создания проблемной ситуации, продумывать постановку проблемы и выбор путей её решения в соответствии с принципом рациональности

Проблемное изучение просто необходимо, так как оно формирует гармонически развитую творческую личность, способную логически мыслить, находить решения в различных проблемных ситуациях, систематизировать и накапливать знания, умеющую делать самоанализ, стремящуюся к саморазвитию и самокоррекции.

Постоянная постановка перед ребенком проблемных ситуаций приводит к тому, что он не «пасует» перед проблемами, а стремится их разрешить, тем самым мы имеем дело с творческой личностью всегда способной к поиску.

СПИСОК ЛИТЕРАТУРЫ

1. Абушкин Х.Х. Проблемное обучение. – Саранск: Морд, 1996. – 174 с.

2. Баксанский O.E., Чистова М.В. Проблемное обучение, обоснование и реализация // Наука и школа. – 2000. – № 1. – С. 19 – 25.

3. Богданова В. Ю. Педагогика и психология // Вестник Адыгейского государственного университета. – 2011. – № 1. – С. 56 – 61.

4. Бондаревский В.Б. Воспитание интереса к занятиям и потребности к самообразованию. – М.: Просвещение, 1985. – 144 с.

5. Бондаренко В. В., Пономарев А.С., Романовский А. Г., Товажнянский Л. Л., Черванева З. А. Основы педагогики высшей школы: начальное пособие. – Харьков: НТУ «ХПИ», 2005. – 601 с.

6. Дышинский Е. А., Лурье A. M., Людмилов Д. С. Некоторые вопросы проблемного обучения математике: пособие для учителей. – Пермь: Звезда, 1975. – 116 с.

7. Задоя С.Э. Технология проблемного обучения // Сидоров С.В. Сайт педагога — исследователя. – 2012. URL: http://si-sv.com/publ/14-1-0-84 (дата обращения 01.11. 2013).

8. Кудрявцев Т. В. Проблемное обучение: истоки, сущность, перспективы. – М.: 3нание, 1991. – 80 с.

9. Коджаспиров А. Ю., Коджаспирова Г.М. Педагогический словарь. – М.: Академия, 2000. – 176 с.

10. Котова И. Б., Е. Н. Шиянов. Развитие личности в обучении: Учеб. пособие для студ. пед. вузов. – М.: Академия, 2000. – 288 с.

11. Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. – 186 с.

12. Лернер И.Я. Проблемное обучение. – М.: Знание, 1974. – 64 с.

13. Лернер И.Я. Процесс обучения и его закономерности. – М.: Знание,

1980. – 96 с.

14. Матюшкин А. М. Проблемные ситуации в мышлении и обучении. – М.: Директ-Медиа, 2008. – 392 с.

15. Матюшкин А. М. Психология мышления. Мышление как разрешение проблемных ситуаций: учебное пособие / под ред. канд. психол. наук А. А. Матюшкиной. – М.: КДУ, 2009. – 190 с.

16. Махмутов М.И. Организация проблемного обучения в школе. – М.: Педагогика, 1987. – 156 с.

17. Махмутов М.И. Проблемное обучение. Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.

18. Махмутов М. И. Теория и практика проблемного обучения. – Казань: Таткнигоиздат, 1972. – 365 с.

19. Мельникова Е.Л. Технология проблемного обучения. Школа 2100. – М.: Баласс, 1999. – 60с.

20. Оконь В.В. Основы проблемного обучения. – М.: Просвящение, 1986. – 208 с.

21. Психологический словарь / под ред. Зинченко В.П., Мещерякова Б.Г. – М.: Астрель, 2010 – 666 с.

22. Сафиуллина И.А. Проблемное обучение как средство реализации творческого потенциала будущего специалиста. – Нижнекамск: НМИ «Чишмэ», 2000. – 68 с. 23. Селиванов В.С. Основы общей педагогики: теория и методика воспитания / под ред. В.А. Сластенина. – М.: Академия, 2000. – 208 с.

24. Смолкин A.M. Методы активного обучения: научно-методическое пособие. – М.: Высшая школа, 1991. – 175 с.

25. Федоряк Л.М. Формирование исследовательских умений у учащихся в проблемно-модульном обучении. – Тюмень, 1997. – 148 с.

26. Чуричков А., Снегирев В. Головоломки и занимательные задачи в тренинге. – СПб.: Речь, 2006. – 208 с.

ПРИЛОЖЕНИЕ

Приемы, которые можно использовать на уроках при создании проблемной ситуации.

Автор: Будянская Лариса Аркадьевна, учитель начальных классов

МОУ «Пролетарская средняя общеобразовательная школа №1»

Цель: заинтересовать детей, удивить, разобраться, дойти до истины.

Это составные компоненты проблемного обучения.

На традиционном уроке ребята слушают учителя, следят за его мыслью, запоминают готовое определение. Такая учебная деятельность – «пришел, услышал, заучил» – называется репродуктивной.

А при построении проблемной ситуации идёт творческое усвоение знаний.

Имитационная игра.

Приём: «Найди верное решение».

Цель: создать проблемную ситуацию, и направить учащихся на её решение, организуя поиск.

На доске записываю 2 примера.

6+2 х 3=12 6+2 х 3 =24

— Вижу вы удивлены? Почему?

-Но если отличаются правые части, то…

-Над каким вопросом подумаем?

-Ну и чем же отличаются левые части? Есть идеи?

-Какой порядок действий в первом примере?

— а во втором?

— В каком примере мы действовали по правилам?

— А во втором мы нарушили правило!

Как же нам догадаться, что здесь сначала сложение?

— Молодцы! Есть такой знак! (дописываю скобки во второй пример.)

Он называется «скобки». Так что же обозначают скобки? (скобки обозначают действие, которое выполняется в первую очередь).

Данный приём помогает ей заинтересовать детей, заставить думать, опираясь на ранее полученные знания.

Приём «Лови верное решение».

Цель: научить сравнивать, видеть различие, уметь аргументировать правильное решение.

Дана задача: золушка разложила в 4 корзинки по 3 орешка. Сколько всего орешков разложила Золушка?

На доске записано 2 примера:

4 х 3 =12

3 х 4 = 12

Вижу вы удивлены. Почему? (Правые части равны, левые тоже, т. к. пользуясь переместительным свойством мы знаем, что 4 х 3 = 3 х 4)

Какие есть идеи? (Второй пример верен, т. к. по 3 орешка взяли 4 раза).

А какую задачу вы можете составить, чтобы её решением был первый пример?

Данный приём учит рассуждать над поставленной проблемной задачей, находить верное решение и доказывать свой выбор.

Приём «Найди лишнее».

Цель: формировать у учащихся умения классифицировать учебный материал, данный с избыточными данными.

На слайде показаны картинки с дикими животными и собакой.

Проблема: Все ли эти животные дикие?

Если на традиционном уроке мы бы просто перечислили представителей дикой природы, то с точки зрения проблемного подхода, ребята должны доказать, какие животные относятся к диким и почему собака к ним не относится.

Данные приёмы: «Найди верное решение», «Лови верное решение»,

«Найди лишнее», «Услышь ошибку» я применяю на образовательных областях при фронтальной работе.

Трудность управления проблемным обучением состоит в том, что возникновение проблемной ситуации – акт индивидуальный, вот именно поэтому она и использует индивидуальный подход.

Приём «Составление кластера»

Цель: Систематизировать знания учащихся по данной проблеме.

Кластер – это графическая организация материала, показывающая смысловые поля того или иного понятия. Составление кластера позволяет учащимся свободно и открыто думать по поводу какой — либо темы. Ученик записывает в центре листа ключевое понятие, а от него рисует стрелки – лучи в разные стороны, которые соединяют это слово с другими, от которых в свою очередь лучи расходятся далее и далее.

Всем раздаётся кластер, ниже приведены ключевые слова, но одно из понятий ошибочно.

Проблема: Составьте схему классификации животных и их отличительных признаков?

Данный приём стимулирует мыслительную деятельность, на стадии осмысления позволяет учащимся самостоятельно структурировать учебный материал, ну и, как правило, использую при проверке знаний.

Каждая новая проблема не всегда вызывает интерес у учащихся. В таком случае нужна задача, которая на первый взгляд, кажется простой, а на деле требует нестандартного подхода, который создаёт проблему. При поиске этой проблемы ученик сталкивается с её исследованием и обобщением.

Муниципальное бюджетное образовательное учреждение

«Шуруповская основная общеобразовательная школа»

Фроловского района Волгоградской области

Обобщение педагогического опыта:

«Создание проблемных ситуаций на уроках математики»

(мастер – класс)

подготовила

учитель начальных классов

Карпухина Марина Анатольевна

2013

Информационная карта

Ф.И.О. автора – Карпухина Марина Анатольевна
Район – Фроловский
Образовательное учреждение – МБОУ «Шуруповская ООШ»
Занимаемая должность – учитель начальных классов
Педагогический стаж и квалификационная категория – 9 лет, первая

квалификационная категория

Тема педагогического опыта: «Создание проблемных ситуаций на уроках математики».
Уровень опыта – творческий, новизна в комбинации известных методик:

— проблемно-диалогичских методов (подводящий диалог, побуждающий диалог),

информационный метод, деятельностный метод обучения.

Цель педагогического опыта:

— учить детей самостоятельно добывать знания, учить учиться;

— создание мотивации к дальнейшей успешной учебной деятельности;

— формирование интереса к образованию;

— создание условий в процессе обучения для максимального раскрытия способностей каждого ученика;

— создание ситуации комфортности на уроке;

— развитие личности ребенка;

— развитие речи учащихся;

— развитие умения применять приобретённые знания, умения и навыки в практической деятельности;

9. Краткое описание опыта:

Основные компоненты системы работы:

— организация подводящего диалога;

— организация побуждающего диалога;

— организация деятельности на уроке;

Методы, формы, средства и виды деятельности, используемые в данном опыте, последовательность их применения и обоснование выбора:

Проблемно-диалогический метод, деятельностный метод обучения.

Виды деятельности — исследовательская, поисковая, моделирование отношений и структур, конструирование, критический анализ, творческие работы.

Уроки, на которых дети сами определяют тему урока, выявляют трудности, обозначают проблемы, самостоятельно делают выводы, составляют правила – доставляют удовольствие учителю, радость открытия детям.

Приемы стимулирования, контроля, взаимоконтроля и самоконтроля:

Организация проблемных диалогов оживляет работу учащихся и предоставляет учащимся большую возможность «самостоятельно» прийти к «открытиям» новых знаний на уроках, что обеспечивает ситуацию успеха практически для каждого ребенка.

Условия, обеспечивающие наибольшую эффективность:

Четкое следование методике в организации проблемных диалогов, системность в работе приводит к тому, что дети привыкают идти к знаниям самостоятельно, им становится скучно, если это начинает делать учитель.

Проблемные методы отличаются эффективностью, т.к. постановка проблемы обеспечивает познавательную мотивацию учеников, а поиск решения – понимание материала большинством учащихся класса.

Результативность:

— повышается интерес к учебе;

— обеспечивается развивающий эффект и мотивация учения;

— не допускается переутомления на уроке;

— обеспечивается атмосфера сотрудничества учителя и ученика;

— развитие речи, логического мышления;

— развитие личности ребенка, его творческих способностей и интереса к предметам;

— вырабатывается активная позиция детей;

— дети показывают высокий уровень обученности.

Преимущество этого опыта:

— умение добывать знания;

— воспитывает самостоятельность;

— делает работу на уроках ОНЗ интересной для учеников и учителя;

— высокая мотивация способствует формированию интереса к учебе;

— обеспечивают на уроках подлинно творческую деятельность, как учащихся, так и учителя.

10. Проблемные методы эффективнее традиционных, т.к. постановка проблемы обеспечивает познавательную мотивацию учеников, а поиск решения – понимание материала большинством учащихся класса.

Ход мастер-класса

Организация учебного пространства (расположение столов по группам).
Индивидуальная работа у доски (во время встречи участников мастер-класса):

Выскажите свою точку зрения. Какой предмет на ваш взгляд является самым трудным для учащихся? Русский язык? Математика? Литературное чтение? ИЗО? (прикрепите магнит возле выбранной вами карточки) слайд 1

Приветствие. Представление. Разогрев учебной группы. Проведение интеллектуальной разминки.

Приём «Продолжи фразу»: Я предлагаю вам первую часть высказывания, концовку вы должны спрогнозировать сами.

Учитесь сами, не ждите… (когда жизнь вас научит)
Спрашивай и найдешь, старайся … (и узнаешь) (монгольская посл.)
Для того чтобы усовершенствовать ум, надо… (больше размышлять, чем заучивать )(Р.Декарт).
Как блохи скачут мысли с человека на человека, но … (не каждого кусают).
Если у двух человек имеется по одному яблоку, и они ими обменяются, то у каждого из них окажется опять по одному яблоку. Если у каждого человека есть по одной идее, и они обменяются ими, … (то у каждого будет уже по две идеи )(Б.Шоу).

— Я надеюсь, что мысли, которые будут высказываться по теме занятия сегодня, не будут вами восприниматься равнодушно. Каждый из нас уйдёт, обогащённый множеством идей.

— Давайте вернёмся к началу встречи, когда каждый из вас определил самый трудный учебный предмет в школе для обучающихся.(ответы : большинство назвали «математика»)

— Как вы думаете с чем это связано? В чём проблема?

Помашите рукой. Кто любил в школе = математику?

Помашите рукой. Кто помнит, как звали учителя математики?

Чему вас учили на уроках математики? (ответы: считать, решать задачи…)

Китайская притча, гласит: Скажи мне – и я забуду;

Покажи мне – и я запомню;

Дай сделать – и я пойму.

Китайцы считают математику высшей наукой – ее основы должен знать каждый… там нет разделения на сильных и слабых учеников – есть способные и не очень… а научить должны всех (как и мы!!!!)

Впервые я узнала о новаторстве в методике начального обучения встретив учебник математики Л.Г.Петерсон, в очередной раз убедилась: создание проблемных ситуаций, организация «затруднения в деятельности», постановка учебной задачи и т.д. методически правильно организованные учителем на уроке, это возможность, предоставленная учителю: учить детей учиться.

В сельской местности, в отличие от городской, родители гораздо меньше уделяют времени детям при подготовке домашних заданий. Учителю приходится максимально рассчитывать только на работу, организованную на уроке. Возникает необходимость в организации процесса обучения таким образом, чтобы ребенок максимально усваивал новый материал на уроке. Использование технологии проблемно-диалогического обучения дает такую возможность. Учащиеся самостоятельно открывают новые знания, а знания открытые детьми самостоятельно, запоминаются лучше, таким образом, нет необходимости дома зазубривать правила, которые детям не всегда понятны.

В начале педагогической деятельности постоянно задавала себе вопросы:

— Как изучение нового материала сделать интересным и захватывающим для детей?

— Как сделать активным участником учебного процесса каждого ребенка?

— Как не допустить перегрузки детей, не смотря на большой объем знаний?

— Как максимально развить способности каждого ребенка?

— Как добиваться максимального усвоения знаний на уроке?

слайд 2 Из многочисленных проблем жизни самая «человеческая» — это проблема выбора. Свой выбор 7 лет назад я остановила на математике Петерсон Л.Г. Чем руководствовалась я, делая свой выбор? На первом плане стоял мотив «мне самой должно быть интересно». Таким образом, с 2005 учебного года обучение учащихся я осуществляю по УМК «Школа 2000 — Школа 2100». ».Было страшно начинать первой, но любопытство и стремление сделать рывок вперёд взяли верх, так как данная программа соответствует всем требования ФГОС второго поколения. Разработана программа на основе дидактических принципов деятельностного метода обучения.

Главная задача каждого учителя сегодня — не только обеспечить прочное и осознанное усвоение знаний, умений и навыков, но и развитие способностей учащихся, приобщение их к творческой деятельности.

слайд 3Проблемное обучение – это «начальная школа» творческой деятельности.

Проблемное обучение основывается на теоретических положениях американского философа, психолога, педагога Дж. Дьюи (1859-1952). В России дидактику проблемного обучения разработал И.Я. Лернер.

Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.

Для меня в процессе обучения главным является постановка перед учащимися на уроках небольших проблем и стремление решить их вместе с детьми.

Как же создавать проблемные ситуации? Об этом мы сегодня и поговорим!

слайд 4 Я хотела бы сегодня поделиться своим опытом работы по использованию в учебном процессе технологии проблемного обучения на уроках математики.

слайд 5, 6 В отличии от традиционного, проблемный урок характеризует творческая, а не репродуктивная деятельность учеников, которая обеспечивает более глубокое усвоение знаний, развитие интеллекта и творчества, воспитание активной позиции, не вызывая при этом перегрузок. Для ребят действительно «учение с увлечением», значительно снижающее нервные нагрузки. Постановка перед ребенком проблемных ситуаций приводит к тому, что он не боится проблем, а стремится их разрешить. Войдя в жизнь, ребенок буде защищен от стрессов.

слайд 7

Деятельность учителя и учащихся в условиях проблемного метода обучения

Деятельность учителя Деятельность учащихся

— создаёт проблемную ситуацию — осознаёт противоречия

— организует размышление над проблемой — формулирует проблему

и её формулировкой — выдвигают гипотезы

— организует поиск гипотез — проверяют гипотезы в эксперименте

— организует проверку гипотез — анализируют результаты, делают выводы

— организует обобщение результатов — применяют полученные знания

и применение полученных знаний

слайд 8, 9

Типы проблемных ситуаций

Проблемная ситуация возникает при условии, если уч-ся не знают способа решения поставленной задачи, не могут ответить на проблемный вопрос, дать объяснение новому факту, т.е. определяется недостаточность прежних знаний для объяснения нового факта.
Проблемная ситуация возникает при столкновении учащихся с необходимостью использовать ранее усвоенные знания в новых практических условиях, однако очевиден факт недостаточности этих знаний.
Проблемная ситуация возникает в том случае, если имеется противоречие между теоретически возможным путем решения задачи и практической неосуществимостью избранного способа.
Проблемная ситуация возникает тогда, когда имеется противоречие между практически достигнутым результатом выполнения учебного задания и отсутствием у учащихся знаний для его теоретического обоснования.

слайд 10

Приёмы создания проблемной ситуации

« с удивлением» « с затруднением»

Противоречивые факты, точки зрения 1) задание невыполнимо вообще
Разные мнения учеников 2) задание не сходное с предыдущим
Противоречие между житейскими и научными фактами

слайд 11 Проблемные ситуации, возникшие «с удивлением»

Прием 1. Учитель одновременно предъявляет классу противоречивые факты, научные теории или взаимоисключающие точки зрения.

Математика, 2 класс. слайд 12
Учитель делает на доске запись 2 + 5 * 3 = 17 и 2 + 5 * 3 = 21. Учитель: Вижу, вы удивлены (реакция удивления). Почему?

Ученики: Примеры одинаковые, а ответы разные! Учитель: Значит, над каким вопросом подумаем?
Ученики: Почему же в одинаковых примерах получились разные ответы?

Прием 2. Учителю требуется столкнуть разные мнения учеников, а не предъявлять ребятам чужие точки зрения. Для этого классу предлагается вопрос или практическое задание на новый материал. Возникший в результате этого разброс мнений обычно вызывает у школьников удивление.

Математика, 3 класс. слайд 13
Учитель: Решите примеры. Вспомните алгоритм. Один ученик у доски, остальные выполняют задание в тетради. (Решают примеры, проговаривают алгоритм. Примеры: 367 — 143,534 — 216,328-174. Далее следует практическое задание на новый учебный материал.) Решите следующий пример, работайте на листочках. (Фронтально решают пример: 400 — 172.) Решили пример? (Побуждение к осознанию противоречия.)
Ученики: Да, решили.
Учитель: Какие получились ответы? (Называют разные ответы.) Я вам предложила решить одинаковый пример? (Ответ: да.) А ответы получились какие? Ученики: Разные. Учитель: Почему?
Ученики: Мы еще не решали такие примеры.
Учитель: Чем этот пример отличается от тех, которые мы только что решали? Ученики: В уменьшаемом отсутствуют единицы и десятки. Учитель: Значит, какие примеры будем учиться решать?
Ученики: Примеры на вычитание трехзначных чисел, где в уменьшаемом отсутствуют единицы и десятки.
Учитель: Верно. Тему фиксируем на доске.

слайд 14
Проблемные ситуации, возникшие «с затруднением»

Прием 1.Учитель предлагает задание, не выполнимое вообще. Оно вызывает у школьников явное затруднение.
Математика, 2 класс. слайд 15
Обучающимся предлагается ряд заданий, решение которых сводится к вычислению одинаковых слагаемых, например: 2 + 2 + 2 + 2 = 8. Затем дается задача: «На одну рубашку пришивают 9 пуговиц. Сколько пуговиц надо пришить на 970 рубашек?» — практическое задание, не выполнимое второклассниками вообще.
Прием 2. Учитель дает практическое задание, с которым ученики до настоящего момента не сталкивались, т. е. задание, не похожее на предыдущее.
Математика, 2 класс. слайд 16
Учитель: На доске дан ряд чисел. Что это за числа? Выпишите в столбик однозначные числа и умножьте их на 7. (Обучающиеся легко справляются с заданием, способ выполнения которого уже известен.) Выпишите в другой столбик двузначные числа и тоже умножьте их на 7. (Обучающиеся испытывают затруднение.) Вы смогли выполнить мое задание? Почему же это задание не получилось? Чем оно отличается от предыдущего? (Побуждение к осознанию противоречия.) Какова же будет тема нашего урока?
Ученики: Умножение двузначного числа на однозначное.
слайд 17

Деление двузначного числа на двузначное.

Учитель:

Ученики:

Найдите значение данных выражений и разделите их на группы.

24:2 70:5 66:6

78:6 78:13

24:2=12 78: 6=13

66:6=11 70:5=14

I столбик: делимое заменяем суммой разрядных слагаемых.

II столбик: делимое заменяем суммой удобных слагаемых.

78:13 – не смогли найти значение, т.к. еще не умеют делить на двузначное число

слайд 18-19

Математика, 3 класс.
Учитель: Сравните углы. (На доске изображение прямого, острого и тупого углов. Обучающиеся легко выполняют задание.) А каким способом вы сейчас сравнивали углы? (Ответ: на глаз. Далее -шаг 1. На доске два примерно равных угла — практическое задание, сходное с предыдущим.) Теперь сравните такие углы.
Ученики: Они одинаковые. (Выполняют задание, применив известный способ.)
Учитель: Каким способом сравнивали? (Ответ: на глаз.) Можете ли вы утверждать, что это точный способ? (Ответ: нет.) Тогда можно ли утверждать, что эти углы равны? (Ответ: нет. Далее -шаг 2. Обучающиеся осознают, что задание не выполнено, возникает реакция затруднения.) Итак, что вы хотели сделать?
Ученики: Сравнить углы.
Учитель: Какой способ применили? (Ответ: визуальный.) Получилось выполнить задание? Ученики: Выполнили, но не можем утверждать, что этот способ точный. (Побуждение к осознанию противоречия.)
Учитель: Какой будет тема урока? (Побуждение к формулированию проблемы.)
Ученики: Сравнение углов.

слайд 20

Приём 3. Столкнуть разные мнения учеников вопросом или практическим заданием.

На уроке математики по теме: «Метр». Я прошу двух учеников измерить длину нашего класса шагами. У одного получается 16 шагов, а у другого 14.

Проблема: почему получились разные ответы? Кто из учеников прав? Значит, нужна какая – то единица измерения длины, чтобы мы получили один правильный ответ.

Предлагаю варианты творческого подхода к созданию проблемных ситуаций на уроках математики.

1. Создание проблемных ситуаций через умышленно допущенные учителем ошибки.

слайд 21 Пример №1

612 3

12 24

Пример №2. Даю задачу на дом и говорю: “У меня не получается”. Попробуйте вы, обращайтесь к кому хотите за помощью. Хотя задача решается. Проблемная ситуация. На другой урок у них радостные лица – они решили.

слайд 22

2.Создание проблемных ситуаций через использование занимательных заданий.

3.Создание проблемных ситуаций через решение задач, связанных с жизнью.

слайд 23

Пример №1 Тема «Периметр прямоугольника»

Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.

Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).

слайд 24

4.Создание проблемных ситуаций через выполнение практических заданий.

Пример №1 Тема «Площадь квадрата»

Проблемная ситуация: нужно найти площадь площадки (площадь квадрата)

5. Создание проблемных ситуаций через решение задач на внимание и сравнение.

слайд 25

Учитель предлагает вниманию первоклассников плакат, на котором изображены несколько четырёхугольников и пятиугольников. Все эти фигуры никак не сгруппированы, но четырёхугольники окрашены в красный цвет, а пятиугольники в зелёный. Учитель сообщает, что все красные фигуры можно назвать четырёхугольниками, а зелёные – пятиугольниками. После этого перед классом ставится проблемный вопрос «Почему?». Для решения данной проблемы дети должны провести ряд наблюдений, сопоставлений, сравнений. Они должны мысленно сравнить термины «четырёхугольник» и «пятиугольник». Анализируя эти слова, они должны расчленить их, выделить в них знакомые слова, являющиеся частями новых терминов – «четыре» и «угол», «пять» и «угол». Проверить правильность возникших предположений они смогут, обратившись к внимательному рассматриванию предложенных фигур. Они должны убедиться, что действительно все красные фигуры содержат по четыре угла, а зелёные по пять углов. Подметив эту особенность, дети должны прийти к выводу, который и будет ответом на поставленный проблемный вопрос.

6.Создание проблемных ситуаций через противоречие нового материала старому, уже известному.

Слайд 26

Даны фигуры прямоугольника и треугольника. Найдите периметр и площадь фигур.

На первый взгляд задание не представляет для учащихся 4 класса никаких трудностей. Они легко находят периметр. Учащимся известно правило нахождение площади прямоугольника. Применив формулу S=a*b, они легко находят площадь прямоугольника. По этой же формуле они пытаются найти площадь треугольника, долго обсуждая где у треугольника длина и ширина. Проблема имеет место в данной теме урока.

слайд 27

7. Создание проблемных ситуаций с использованием мультимедийной презентации. «Собери урожай»

слайд 28

8. Создание проблемных ситуаций с использованием задач с недостающими данными, нереальными, лишними. 1 класс

Давайте потренируемся.

слайд 29

Практическая работа в группах(3)

Группа: Определите приём по предложенному конспекту
Смоделируйте проблемную ситуацию по теме: уравнения, объём, дециметр, 1 класс

Рекомендации учителям по созданию проблемных ситуаций на уроке.

1.Подводить к противоречию с уже известным и предлагать самим находить способ разрешения.

2. Побуждать делать сравнения, обобщения, выводы.

3. Создавать ситуации включения, используя задания, связанные с их жизненным опытом.

4. Использовать задачи с заведомо допущенными ошибками.

5. Предлагать практические исследовательские задания.

6. Отыскивать различные способы решения одной и той же задачи.

7. Излагать различные точки зрения на один и тот же вопрос.

8.Учить составлять задачи по статистическим данным своего населённого пункта.

9.Использовать тесты с выбором правильного ответа.

слайд 30

— Ответьте мне на вопрос:

А вы знаете, сколько будет 2 умножить на 2? Думаете 4? Я докажу, что вы сильно ошибаетесь.

25-20-5=20-16-4
5(5-4-1)=4(5-4-1)
5=4
5=2*2

Итак, вы согласны, что 2*2 = 5? Тогда докажите , что я не права.

Это пример софизмов. Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Любой софизм содержит одну или несколько замаскированных ошибок. Разбор софизмов прежде всего развивает логическое мышление. Обнаружить ошибку в софизме это значит осознать ее, а осознание ошибки предупреждает повторение ее в дальнейшем в других математических рассуждениях.

слайд 31-32

Рассмотрим софизм про генерала и сапоги: Один отставной генерал решил продать свои сапоги. Он позвал своего денщика и велел ему продать сапоги за 15 рублей. Денщик встретил на базаре двух одноногих ветеранов и продал каждому сапог за 7,5 рублей. Узнав об этом, генерал заявил, что с инвалидов можно было взять и поменьше. Он дал ему 5 рублей и велел отдать инвалидам. По дороге на базар денщик прогулял 3 рубля в трактире и вернул каждому ветерану по рублю.

А теперь давайте посчитаем: каждый ветеран заплатил по 6,5 рублей. 6,5 * 2 = 13 рублей, да еще 3 рубля которые денщик прогулял в трактире, получается 16 рублей. Откуда взялся лишний рубль?

На самом деле нельзя прибавлять к 13 рублям 2 рубля. 13 рублей – это 10, которые остались у генерала и 3 рубля, которые денщик прогулял в трактире.

слайд 33

Каждый из вас сейчас на минутку занял место своих учеников: думал как найти выход, рассуждал. Как интересно наблюдать этот процесс нам, учителям со стороны, когда этим занимаются дети. Каков наш восторг, когда дети приходят к разрешению предложенной им проблемы. Часто бывает, что учащиеся предлагают несколько вариантов разрешения проблемной ситуации. Я этому только рада.

слайд 34

Приём «Яркое пятно»

слайд 35

Умножение «палочками»

Для умножения чисел без таблиц умножения, достаточно иметь карандаш и бумагу…

Умножим 21х34 =

Посчитайте столбиком… А теперь посмотрите, новый для вас способ…

Ответ совпал. Можете проверить. Попробуйте выполнить умножение чисел 11 и 13 (Ответ 143)

слайд 36

Умножение в уме

Для детей не знающих таблицу умножения – это большое подспорье в выполнении заданий (А кто сказал, что мы должны учить детей считать только столбиком? в стандартах об этом ни слова!!!!)

слайд 37

Таблица умножения на 9 на пальцах

слайд 38

Работа в группах

Определите достоинства и недостатки проблемного обучения: (обоснуйте, дополните)

Требует больших затрат времени для усвоения одного и того же объёма знаний, чем другие типы обучения.
Способствует формированию определенного мировоззрения учащихся, поскольку высокая самостоятельность усвоения знаний обуславливает возможность трансформации их в убеждения.
Формирует личностную мотивацию учащегося, его познавательные интересы.
Развивает мыслительные способности учащихся.
Помогает формированию и развитию диалектического мышления учащихся, обеспечивает выявление ими новых связей в изучаемых явлениях и закономерностях.
Развитие внимания, наблюдательности учащегося
Активизация познавательной деятельности, мышления
Воспитание самостоятельности, инициативности, ответственности, нестандартности мышления
Обеспечивает прочные знания, которые добываются самостоятельно
Преподаватель должен хорошо владеть материалом, постоянно совершенствовать своё профессиональное мастерство
Необходимо научиться формулировать проблемные вопросы и учителю, и учащимся
Предъявляет высокие требования к учителю. Это касается не только его культуры, интеллекта, но и той нравственной атмосферы, которая непроизвольно возникает и должна поддерживаться.
Усвоение становится творческим
Самостоятельное добывание знаний путем собственной творческой деятельности.
Высокий интерес к предметам
Развитие продуктивного мышления

слайд 39

Технология проблемного обучения позволяет добиться положительной динамики качества обучения. В течение 7 лет уровень обученности класса, который обучался по УМК «Школа 2000 — Школа 2100» с 2005 учебного года, составляет 100 % , качество знаний – от 60 % до 83% .

Результативность по математике :

Вывод:

Сегодня я попыталась показать вам, что создание проблемных ситуаций на уроках математики не только формирует ту систему математических знаний, умений и навыков, которая предусмотрена программой, но и самым естественным образом развивает у школьников творческую активность. Ситуация затруднения школьника в решении заданий приводит к пониманию учеником недостаточности имеющихся у него знаний, что в свою очередь вызывает интерес к познанию и установку на приобретение новых. Нельзя заставлять ребёнка слепо штудировать предмет в погоне за общей успеваемостью. Необходимо давать ему возможность экспериментировать и не бояться ошибок, воспитывать у учащихся смелость быть не согласным с учителем.

Использованные материалы и Интернет-ресурсы

htt://images.jndex.ru

http://tehnologi.su

Мельникова Е.Л. Технология проблемного обучения // Школа 2100. Образовательная программа и пути ее реализации. Вып. 3.-М., Баласс, 1999.

Мельникова Е.Л. Технология проблемно-диалогического обучения // Образовательная система «Школа 2100». Сборник программ . – М, 2004

Мельникова Е.Л. Проблемный урок в начальной школе, или как открывать знания вместе с детьми // Начальная школа:плюс-минус.1999. №5, 6, 7, 8.

Мельникова Е.Л. Анализ уроков изучения нового материала.// Школа 2100. Вып. 4-М.: Баласс, 2000.

Образовательная система «Школа 2100»: Сб. программ/Под науч. ред. А.А. Леонтьева. –М: Баласс, 2004.

Образовательная система «Школа 2100»: Сб. программ/Под науч. ред. Д.И. Фельдштейна. –М: Баласс, 2008.

Петерсон Л.Г. Деятельностный метод обучения.// Школа 2000…, Москва 2007.

Петерсон Л.Г., М.А.Кубышева и др. Что значит «уметь учиться» //Москва 2008.

«Школа 2000…» Непрерывность образования: дидактическая система деятельностного метода. Выпуск 5, Москва, 2005

«Школа 2000…» Математика для каждого: технология, дидактика, Мониторинг. Выпуск 4. Издание второе, Москва, 2004

Петерсон Л.Г. Математика 1-4 классы.- М.: Издательство «Ювента», 2011

Источник

Муниципальное
бюджетное общеобразовательное учреждение

средняя
школа №2 г. Пошехонье

Методическая
разработка

на тему: «Проблемное
обучение на уроках математики в 5-9 классах»

Работу выполнила:

учитель математики

МБОУ СШ №2

Носкова Елена
Викторовна

Пошехонье, 2016

Содержание

Введение	3
1	Сущность технологии проблемного обучения	5
2	Опыт применения технологии проблемного обучения в процессе обучения математике в 5-9 классах	8
Заключение	15
Список литературы	16
Приложение 1 Конспект урока по теме: «Сравнение дробей» (математика 5 класс)	17
Приложение 2 Конспект урока по теме: «Отношение чисел» (математика 6 класс)	23
Приложение 3 Примеры приемов создания проблемных ситуаций на уроке: стихотворение «Треугольник и квадрат»	33
Приложение 4 Практическая задача по математике по теме: «Четырехугольники» (геометрия 8 класс)	34
Приложение 5 Ситуационное задание по математике по теме: «Натуральные числа» (математика 5 класс) «Поездка к бабушке»	36

Введение

Замечено, чем
больше учитель учит своих учеников и чем меньше предоставляет им
возможностей самостоятельно
приобретать знания,
мыслить, действовать, тем менее энергичным и плодотворным становится процесс
обучения.

И. Лернер [4]

На современном этапе модернизации образования перед школой встают новые
задачи, а именно формирование опыта самостоятельной деятельности учащихся и
целостной системы универсальных учебных действий. Требования к формированию
метапредметных результатов определены Федеральным государственным
образовательным стандартом второго поколения. В
основе Стандарта лежит системно — деятельностный подход, который в частности
обеспечивает активную учебно-познавательную деятельность учеников. Согласно
Стандарту, творческая деятельность учащихся должна стать основным видом их
деятельности, т.е. большую часть знаний ученики должны усваивать не со слов
учителя, а в процессе самостоятельного поиска информации и способов решения
задач. Учителю же отводится роль организатора процесса открытия и получения
новых знаний учениками. [101]

Математика, как учебный предмет
имеет огромный потенциал для развития познавательной и творческой активности
учащихся. Согласно Концепции
развития математического образования в России, математическое образование
должно: обеспечивать каждого обучающегося развивающей
интеллектуальной деятельностью на доступном уровне, используя присущую
математике красоту и увлекательность. Изучение математики развивает
познавательные способности человека, в том числе к логическому мышлению, влияя
на преподавание других дисциплин. Качественное математическое образование
необходимо каждому для его успешной жизни в современном обществе. [1]

«Развивает и формирует ученика не столько само
знание, сколько метод его приобретения. Если учебная деятельность протекает
только в рамках воспроизведения усвоенных знаний, то это не способствует
развитию человека». Именно поэтому традиционные методы обучения и формы организации
учебного процесса лишь частично способствуют реализации в полном объеме целей и
задач современного образовательного процесса. Традиционный арсенал методов и
форм обучения необходимо дополнять современными средствами обучения,
позволяющими максимально активизировать деятельность учеников. В сложившейся
ситуации становится актуальным применение активных форм обучения и
соответствующих образовательных технологий. Одна из таких технологий – это
технология проблемного обучения. [14]

В
данной работе представлен опыт применения технологии проблемного обучения на
уроках математики.

Ведущей
педагогической идей опыта является создание
условий для повышения познавательной и творческой активности учащихся на уроках
математики, посредством применения технологии проблемного обучения.

Необходимость
применения технологии проблемного обучения на уроках математики возникла из
проблемы преемственности на ступени начальная – основная школа. Одной из
программ, по которым ведется обучение в начальных классах МБОУ СШ №2 г. Пошехонье,
является система развивающего обучения Л.В. Занкова. Реализацию принципов
развивающего обучения необходимо продолжать и в основной школе. Этому
способствует и УМК под ред. Г.В. Дорофеева, по которому изучается математика в
5-6 и алгебра в 7-9 классах. Линия УМК отражает современные
методические и педагогические тенденции преподавания математики. В учебниках
реализовано целенаправленное обучение приёмам и способам рассуждений, что
позволяет обогатить интеллектуальный багаж школьников, активизировать развитие
мышления, создание условий для формирования навыков исследовательской
деятельности, самостоятельности мышления, творческих способностей.[15]

Актуальность
данной технологии определяется развитием высокого уровня мотивации к учебной
деятельности, активизации познавательных интересов учащихся, что становится
возможным при разрешении возникающих противоречий, создании проблемных ситуаций
на уроке. В преодолении посильных трудностей у учащихся возникает постоянная
потребность в овладении новыми знаниями, новыми способами действий, умениями и
навыками.

1.
Сущность
технологии проблемного обучения

«Всякий
мыслительный процесс является по своему внутреннему строению действием,
направленным на разрешение определенной задачи. Задача эта заключает в себе
цель для мыслительной деятельности индивида, соотнесенную с условиями, которыми
она задана… Начальным моментом мыслительного процесса обычно является
проблемная ситуация. Мыслить человек начинает, когда у него появляется
потребность что-то понять. Мышление обычно начинается с проблемы или вопроса, с
удивления или недоумения, с противоречия». [10]

Умение действовать по готовым алгоритмам и
выученным правилам, решать стандартные задачи – лишь часть того содержания
образования, который должен усвоить ученик. Реальные жизненные ситуации, как
правило, отличаются от учебных заданий и требуют от человека умений
самостоятельно находить решение, выбирать для него оптимальный способ. Поэтому
среди противоречий современного учебного процесса часто называют разрыв между
усвоенными знаниями и умениями с одной стороны и готовностью ученика применять
их на практике для решения учебных и практических задач – с другой. На
преодоление этого противоречия направлена одно из наиболее известных современных
педагогических технологий: технология проблемного обучения проблемного обучения,
которая предполагает поиск резервов умственного развития учащихся: способности
к творческому мышлению и самостоятельной познавательной деятельности.

Идеи проблемного обучения в отечественной педагогике
стали актуальными начиная со второй половины 1950-х гг., а в 1970-е гг. Вопросами
проблемного обучения в разное время занимались ученые — педагоги и психологи:
Дж. Брунер – США, В. Оконь – Польша, в нашей стране М.Н. Скаткин, И.Я.
Лернер, М.И. Махмутов, А.М. Матюшкин, Т.В. Кудрявцев и др.

Существует
несколько взглядов на понятие проблемного обучения.

Так
польский ученый-педагог Виценты Оконь понимает проблемное обучение как
«совокупность таких действий, как организация проблемных ситуаций,
формулирование проблем, оказание ученикам необходимой помощи в решении проблем,
проверка этих решений и, наконец, руководство процессом систематизации и закрепления
приобретенных знаний.[7]

И.
Я. Лернер видит сущность проблемного обучения в том, что «учащийся под
руководством учителя принимает участие в решении новых для него познавательных
и практических проблем в определенно системе, соответствующей образовательно — воспитательным
целям школы» .[4]

Т.
В. Кудрявцев суть процесса проблемного обучения видит в выдвижении перед
учащимися дидактических проблем, в их решении и овладении учащимися обобщенными
знаниями и принципами проблемных задач.

На
основе обобщения практики и анализа результатов теоретических исследований М.
И. Махмутов дает следующее определение понятия «проблемное обучение»:
«Проблемное обучение — это тип развивающего обучения, в котором сочетаются
систематическая самостоятельная поисковая деятельность учащихся с усвоением ими
готовых выводов науки, а система методов построена с учетом целеполагания и
принципа проблемности; процесс взаимодействия преподавания и учения
ориентирован на формирование познавательной самостоятельности учащихся,
устойчивости мотивов учения и мыслительных (включая и творческие) способностей
в ходе усвоения ими научных понятий и способов деятельности, детерминированного
системой проблемных ситуаций».[6]

Проблемное
обучение, в отличие от любого другого, способствует не только приобретению
учащимися необходимой системы знаний, умений и навыков, но и достижению
высокого уровня их умственного развития, формированию у них способности к
самообучению, самообразованию. Обе эти задачи могут быть реализованы с большим
успехом именно в процессе проблемного обучения, поскольку усвоение учебного
материала происходит в ходе активной поисковой деятельности учащихся, в
процессе решения ими системы проблемно-познавательных задач. Нужно отметить еще
одну из важных целей проблемного обучения: формирование особого стиля
умственной деятельности, исследовательской активности и самостоятельности
учащихся.[14]

Проблемное
обучение
– это обучение, при котором учитель, создавая проблемные ситуации и организуя
деятельность учащихся по решению учебных проблем, обеспечивает оптимальное
сочетание их самостоятельной поисковой деятельности с усвоением готовых выводов
науки.

Цель
проблемного обучения: развитие интеллекта и творческих
способностей учащихся; формирование прочных знаний; повышение мотивации через
эмоциональную окраску урока; воспитание активной личности.

Суть
проблемного обучения состоит в организации педагогом для учащихся проблемных
ситуаций, осознании этих ситуаций, их принятия и решения в процессе совместной
взаимодействия учащихся и учителя при максимальной самостоятельности учеников и
общем направляющем руководстве педагога. (табл.1)

Таблица1 Деятельность учителя и ученика в условиях
проблемного обучения

Деятельность учителя

Деятельность ученика

-создает
проблемную ситуацию

-организует
размышление над проблемой и ее формулировкой

-организует
поиск гипотезы

-организует
проверку гипотезы

-организует
обобщение результатов и применение полученных знаний

-осознают
противоречия

-формирует
проблему

-выдвигают
гипотезы, объясняющие явления

-проверяют
гипотезу в эксперименте, решении задач

-анализируют
результаты, делают выводы

-применяют
полученные знания

В структуре урока при проблемном обучении принято
выделять четыре основных этапа:

1) осознание проблемной ситуации («ситуация
требует разрешения, потому что…»);

2) анализ ситуации и формулировка проблемы
(«проблема состоит в том, что…»;

3) решение проблемы: выдвижение гипотез и
обоснование путей решения, отбор наиболее логичных гипотез и их
последовательная проверка;

4) проверка правильности решения («противоречие
устранено, потому что…»). [16]

Основным звеном
проблемного обучения является проблемная ситуация.

Проблемные ситуации возникают, например, в таких
случаях:

— если обнаруживается несоответствие между уже
известными учащимся фактами и новыми знаниями;

— если учащиеся сталкиваются с новыми для них
условиями использования уже имеющихся знаний, умений и навыков;

— если необходимо выбрать из известных ученику
способов решения учебно-познавательной задачи единственный правильный или
наилучший и т.д.

При создании проблемных ситуаций учителю следует
руководствоваться правилами:

— каждое задание должно основываться на тех
знаниях и умениях, которыми уже владеет ученик;

— то неизвестное, которое нужно «открыть» ученику
при разрешении проблемной ситуации, должно подлежать усвоению, способствовать
формированию действительно важных знаний и умений;

— выполнение проблемного задания должно вызывать
у ученика интерес, потребность в усваиваемом знании. [16]

Десять
способов создания проблемной ситуации по М.И. Махмутову

•
Побуждение
учащихся к теоретическому объяснению явлений, фактов, внешнего несоответствия
между ними.

•
Использование
учебных и жизненных ситуаций, возникающих при выполнении учащимися практических
заданий в школе, дома или на производстве, в ходе наблюдений за природой.

•
Постановка
учебных практических заданий на объяснение явления или поиск путей его
практического применения.

•
Побуждение
учащихся к анализу фактов и явлений действительности, порождающему противоречия
между житейскими представлениями и научными понятиями об этих фактах.

•
Выдвижение
предположений (гипотез), формулировка выводов и их опытная проверка.

•
Побуждение
учащихся к сравнению, сопоставлению и противопоставлению фактов, явлений,
правил, действий, в результате которых возникает проблемная ситуация.

•
Побуждение
учащихся к предварительному обобщению новых фактов.

•
Ознакомление
учащихся с фактами, носящими как будто бы необъяснимый характер и приведшими в
истории науки к постановке учебной проблемы.

•
Организация
межпредметных связей.

Варьирование
задачи, переформулировка вопроса[5]

Технология
проблемного обучения позволяет учащимся самостоятельно «открывать» знания. Она
представляет собой детальное описание методов обучения, а также их
взаимосвязей с формами и средствами обучения. Методы составляют центральную
часть технологии, поскольку определяют выбор форм и средств обучения. Методы
проблемного обучения – это способы деятельности учителя на этапе введения
знаний. Они (методы) обеспечивают постановку и решение учебных проблем
школьниками и представляют собой определенные сочетания приемов, вопросов, заданий.
Применение технологии проблемного обучения дает широкие возможности
варьирования форм обучения (фронтальной, групповой, парной, индивидуальной). Средства
обучения (опорные сигналы, учебники, наглядные и технические средства) в
процессе проблемного обучения служат вспомогательными инструментами творческого
усвоения знаний.

Проблемное
обучение строится на основе принципа проблемности, реализуемого через различные
типы учебных проблем и через сочетание репродуктивной, продуктивной и
творческой деятельности ученика. Наличие различных типов учебных проблем
обеспечивает поисковую, или частично-поисковую, или
конструкторско-изобретательскую деятельность ученика, или их сочетание в ходе
выполнения теоретических и практических самостоятельных работ, при изложении
учебного материала учителем на уроке. [17]

2.
Опыт
применения технологии проблемного обучения в процессе обучения математике

Целью представленного педагогического
опыта является развитие познавательной и творческой активности учащихся вследствие
применения технологии проблемного обучения, и как результат — формирование
глубоких и прочных знаний, рост мотивации учащихся в процессе обучения
математике.

Для достижения
поставленной цели необходимо решение следующих задач:

1)
использовать
на уроках технологии проблемного обучения и ее элементы,

2)
учить
детей аргументировать, находить и выделять главное, рассуждать, доказывать,
находить рациональные пути выполнения задания

3)
развивать
у учащихся такие мыслительные операции, как анализ, сравнение и сопоставление
фактов и явлений;

4)
формировать
навыки поисковой и исследовательской деятельности;

5)
повышать
уровень самостоятельности и активности учащихся

6)
формировать
чувства уверенности в своих силах, удовлетворение от умственной деятельности;

7)
создавать
ситуацию успеха в процессе деятельности учащихся;

развивать
коммуникативные умения; воспитывать у учащихся чувство коллективизма и
взаимопомощи;

9)
развивать
межпредметные связи.

Эти задачи могут
быть реализованы с большим успехом именно в процессе проблемного обучения,
поскольку усвоение учебного материала происходит в ходе активной поисковой
деятельности учащихся, в процессе решения ими системы проблемно-познавательных
задач.

Проблемное
обучение существенно отличается от традиционного. При проблемном обучении
учитель либо не даёт готовых знаний, либо даёт их на особом предметном
содержании – новые знания, умения и навыки школьники приобретают самостоятельно
при решении особого рода задач и вопросов, называемых проблемными. При
традиционном обучении упор делается на мотивы непосредственного побуждения
(учитель интересно рассказывает, показывает), при проблемном же обучении
ведущими мотивами познавательной деятельности становятся интеллектуальные
(учащиеся самостоятельно ищут знания, испытывая удовлетворение от процесса
интеллектуального труда, от преодоления сложностей и найденных решений,
догадок, озарений). [14]

На уроке,
проводимом с применением технологии проблемного обучения, можно наблюдать
следующие этапы (Приложение 1):

1.
Мотивация
к учебной деятельности

2.
Актуализация
имеющихся знаний и умений учащихся

3.
Создание
проблемной ситуации.

4.
Построение
проекта выхода из затруднения (выдвижение и фиксирование гипотез)

5.
Реализация
построенного проекта

·
исследование,
обмен информацией при работе в группах, парах

·
представление
результатов исследования,

·
формулировка
выводов, подтверждение или опровержение выдвинутых ранее гипотез

6.
Первичное
закрепление нового материала с проговариванием во внешней речи

7.
Самостоятельная
работа с самопроверкой по образцу (или взаимопроверкой)

8.
Включение
в систему знаний и повторение

9.
Рефлексия
учебной деятельности

Данная
структура урока развивает навыки самостоятельной работы. обеспечивает повышение
познавательной активности и мотивации учащихся, формирует умения применять
ранее усвоенные знания в новой ситуации, творчески их преобразовывать,
способствует развитию интеллектуальных способностей школьников. Создание
проблемных ситуаций, их анализ, активное участие учеников в поиске путей
решения поставленной учебной проблемы возбуждает мыслительную активность
учащихся, поддерживает глубокий познавательный интерес.

Моя
личная концепция, состоит в сочетании традиционных и проблемных методов
и форм обучения предусматривающих применение элементов современных
образовательных технологий.

В
своей работе использую разнообразные методы и приемы работы: работа по
алгоритму, самостоятельная работа с учебником, работа в парах переменного
состава, работа по тестам, фронтальная работа, работа в группах, индивидуальная
работа, взаимопроверка, самопроверка, применение дифференцированных заданий, в
том числе домашних, специальные задания по конкретной теме, в т.ч. компетентностно-ориентированные,
инструкции и памятки по работе, тренировочные упражнения.

А
так же применяю разнообразные формы организации урока: традиционный урок, урок
с использованием активных способов обучения, с применением элементов
технологии проблемного обучения (приложение 1), урок-путешествие,
урок-исследование, урок-практикум, деловые игры.

Организацию
учебного процесса в своей работе стараюсь выстраивать по принципу проблемности,
чтобы отношение учащихся к возникающим проблемным ситуациям было вдумчивым и
осмысленным.

На
уроках математики использую следующие варианты создания проблемных ситуаций
через:

1)
умышленно
допущенные учителем ошибки;

2)
использование
занимательных задач

3)
решение
задач, связанных с жизнью;

4)
решение
задач на внимание и сравнение;

5)
различные
способы решения одной задачи;

6)
выполнение
небольших исследовательских заданий.

Рассмотрим примеры заданий, ситуаций, применяемых в каждом
случае.

1)
Создание проблемных ситуаций через умышленно
допущенные учителем ошибки.

По мнению
учеников, учитель все знает и никогда не ошибается. Все утверждения,
доказательства, объяснения учителя практически никогда не подвергаются
сомнениям со стороны учеников. Именно на этом факте основана данная проблемная
ситуация.

Пример 1. Тема: «Линейные уравнения»
(алгебра 7 класс)

Решить уравнение и выполнить проверку

Прописываю решение уравнения на доске,
проговаривая процесс решения. на доске:

2х-6=-34

2х=-34+6

2х=-28

х=-28:2

х=-14

Классу предлагается выполнить проверку. В процессе решения
найденное решение не является корнем уравнения. Возникает проблемная ситуация.
В процессе исследования выясняется, что корень уравнения найден неверно.
УЧИТЕЛЬ ОШИБСЯ!!! Ситуация вызывает удивление. Ученики находят выход из сложившейся проблемной ситуации.
Дальнейшая работа на уроке проходит при повышенным внимании и
заинтересованности.

Пример 2. Подготовка
к ОГЭ по математике в 9 классе.

Вычислите

121^-5 ٠121^-6 1)11 2)
3)121 4)

121^-10

Ответ___________________

Прописываю решение уравнения на доске,
проговаривая процесс решения. на доске. В процессе решения получаю 121³⁰:121^-10=121²⁰

При выборе
номера правильного ответа выясняется, что такого варианта ответа нет.
Поступают предложения, что среди предложенных нет правильного ответа. Затем
решают проверить ход решения. Находят ошибку, решают данное задание верно,
определяют номер ответа. В результате созданной проблемной ситуации
активизируется внимание, мыслительная активность, совершенствуются навыки
самоконтроля, взаимопроверки.

2) Создание проблемных ситуаций через использование
игровых ситуаций и занимательных задач

Пример1. Игровая
ситуация «Математические предсказания»

Тема: «Формулы
сокращенного умножения» (алгебра 7 класс)

Предлагаю ученикам придумать
задания на возведение в квадрат разности или суммы двух выражений, произведения
суммы и разности двух выражений. Предложенные задания решаются учениками на
доске с применением правила умножения многочленов. Учитель выступает в роли
предсказателя ответов придуманных заданий: не глядя на доску, предсказывает
будущие ответы. Результаты учеников и «предсказания» учителя прописываются на
доску. Ответы действительно одинаковые. Ученики удивлены. В результате решения
проблемной ситуации, выясняется, что секрет данного математического фокуса
кроется в формулах сокращенного умножения.

Пример 2. Тема «Сумма n-первых членов арифметической прогрессии»

(алгебра 9 класс)

Изучение вопроса о сумме n–первых членах
арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет
тому назад в одной из школ Германии на уроке математики учитель предложил
ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд
складывать числа, а один ученик почти сразу же дал правильный ответ.

Имя этого ученика Карл Фридрих Гаусс. В
последствии он стал великим математиком. Как удалось Гауссу так быстро
подсчитать эту сумму

Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?

Решение проблемы (1 + 100) х 50 = 5050

Последовательность чисел 1, 2, 3,…,100 является
арифметической прогрессией. Теперь выводим формулу суммы n-первых членов арифметической
прогрессии.

Главный фактор занимательности – это приобщение
учащихся к творческому поиску, активизация их самостоятельной исследовательской
деятельности, так как уникальность занимательной задачи служит мотивом к
учебной деятельности, развивая и тренируя мышление вообще и творческое, в
частности.

Пример 3.
Использование ребусов (приложение 2),загадок , стихов (приложение 3, басен,
сказок и других занимательных приемов.

3) Создание проблемных
ситуаций через решение задач, связанных с жизнь (приложение 3,4) [8]

Пример 1. Тема: «масштаб» (математика 6 класс)

Ситуационное задание:

«Вычисление количества денежных средств на перевозку учащихся на
автобусе».

Задачная формулировка. Три раза в
день, шесть раз в неделю учеников отдаленной территории забирает автобус и
отвозит в школу. Сколько денежных средств необходимо выделить школе на бензин,
чтобы дети не пропускали учебные занятия в школе? Необходимо рассчитать
километраж маршрута по карте города. По данным источникам вычислить расходы на
бензин.

Источник (содержит
информацию, необходимую для успешной деятельности учащегося по выполнению
задания):

1. Карта города.

2. Примерный расход бензина на километр автобуса (ПАЗ).

31,6 л/100 км.

3. Стоимость бензина: 28,30 рублей.

Длина пути: 16,1 см на карте.

Масштаб карты: 1 : 700 (1 см = 700 метров).

Измерить:

1. Длину пути 16, 1 см.

2. Выразить его в километрах: 16,1 × 700 = 11,27 км.

3. Найти сколько километров в день проходит автобус:

11, 27 × 6 = 67,62 км.

4. В неделю: 67,62 × 6 = 405,72 км.

5. В месяц: 405,72 × 4 = 1622,88 км.

6. Количество бензина: 1622,88 × 31,6/100 = 512,83 литра на месяц.

7. Стоимость всего бензина: 512,83 × 28,3 = 14512,81 рублей.
4.Создание проблемных ситуаций через выполнение
практических заданий.

Пример 1. Тема:
«Функция у=ах², её графики свойства». (алгебра 9 класс) [18]
Учащимся
предлагается построить попарно графики функций у=2х² и у= -2х²и, опираясь на непосредственное изображение графиков, заполнить таблицу:

Свойства функции	у=2х² (у=ах², а>0)	у= -2х²(у=ах², а<0)
1.Область определения функции
2.Область значения функции
3.Нули функции
4.График функции и его расположение
5.Промежутки возрастания и убывания функции

После заполнения таблицы учащиеся делают
окончательные выводы и формулируют основные свойства.

5. Создание проблемных ситуаций через решение
задач на внимание и сравнение.
Тема: «Сумма углов треугольника» (геометрия 7 класс)

Учитель читает условие задачи, ученики
анализируют его и выявляют ошибки, тем самым мы можем проверить учеников на
внимательность. В данных задачах следует вспомнить теорему о сумме углов
треугольника, полагаясь на данную теорему, мы придем к выводу, что не все
условия задач поставлены корректно, тем самым некоторые треугольники не
существуют.

Пример
1. Построить треугольник по трем заданным углам [19]

Пример 2. Два угла треугольника
равны 121º и 59º. Найти величину третьего угла. [19]

Пример 3. В треугольнике АВС найдите
неизвестные углы,

если на больше , а .

Пример 4. Дан треугольник АВС, где . Найти .
[19]

6.Создание проблемных
ситуаций через противоречие нового материала старому, уже известному.
Пример 1. Тема: «Формулы сокращённого умножения» (алгебра 7
класс)

Учитель
дает задание, пытаясь запутать учеников. Вычислите:

(3٠4)²=3²٠4²=9٠16=144

(5٠6)²=5²٠6²=25٠36=900

(8:2)²=8²:2²=64:4=16

(3:9)²=3²:9²=
=

(5+6)²=5²+6²=25+36=61

Решим
последний пример, соблюдая порядок действий в вычислениях: (5+6)²=11²=121

Имеем:
(5+6)²≠(5+6)²

Почему
в итоге получились разные результаты? И какой из результатов верный?

Ученики обращают
внимание на знак в последнем примере и понимают, что данный пример решается
по-другому (применяя формулу для квадрата суммы).

7. Создание проблемных ситуаций через различные способы решения
одной задачи.
Тема:
«Распределительный закон умножения относительно сложения» (математика 5 класс)

На
данном уроке учащимся предлагается решить следующие задачи:

Задача 1. В
школьном саду посажены фруктовые деревья в 10 рядов. В каждом ряду посажено
по 5 груш и по 7 яблонь. Сколько всего деревьев посажено в саду?

Решение.

1
способ. 2 способ.

(7 + 5) ٠10 = 120 7 ٠10 + 5 ٠10 = 120

Ответ: 120
деревьев.

Задача 2. Две
автомашины одновременно выехали навстречу друг другу из двух пунктов.
Скорость первой автомашины 80 км в час, скорость второй 60 км в час. Через
3 часа автомашины встретились. Какое расстояние между пунктами, из
которых выехали автомашины?

Решение.

1
способ. 2 способ.

(80 + 60) ٠3 = 420 80 ٠ 3 + 60 ٠3 = 420

Ответ: 420 км

В результате
такого сравнения учащиеся пришли к следующим выводам:

·
1-й
способ решения всех задач одинаков, 2-й – тоже.

·
выражения,
полученные при решении задач отличаются друг от друга только числовыми
данными;

·
выражения,
полученные при решении задачи №1 и № 2 1-м и 2-м способами, отличаются
друг от друга числом арифметических действий и порядком действий;

·
числовые
значения выражений, полученные при решении задачи №1 2-мя способами,
одинаковы, а, значит, можно сделать такую запись:

(7 + 5) ٠8 = 7 ٠8 + 5 ٠8.

(80 + 60) ٠3 = 80 ٠3 + 60 ٠3.

(5 + 3) ٠4 = 5 ٠4 + 3 ٠4.

Далее
предлагается ученикам заменить одинаковые цифры в полученных

выражениях одинаковыми буквами. В
результате получены три одинаковых выражения, а именно: (а + в) ٠с = ас + вс.

Ученики с помощью
учителя формулируют этот закон словесно и на примерах новый закон умножения:
распределительный закон умножения относительно сложения.

Убеждаются в
целесообразности усвоения и запоминания этого закона: он облегчает
вычисления.

8. Создание проблемных ситуаций через выполнение
небольших исследовательских заданий.

Пример 1. Тема «Длина окружности» (математика 5
класс)
Ещё древние греки находили длину окружности по формуле С=πd, d — это диаметр
окружности.
Вопрос: а что же такое ?
Работаем в парах, выполняя
необходимые измерения.
1.Опоясать стакан ниткой, распрямить
нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить
более точный результат, нужно это проделать несколько раз. Занесите данные в
следующую таблицу.

№ опыта	Длина окружности	Диаметр
1	С ₁	d ₁
2	С ₂	d ₂
3…	С _3…	d ₃

2.Измерьте диаметр стакана линейкой. Данные
занесите в таблицу.
3.Найдите значение π, как неизвестного
множителя. Можно пользоваться калькулятором
4.Каждой паре занести вычисленное значение π в
таблицу.
π- это бесконечная дробь, современные машины
могут определить до миллиона знаков после запятой.
π≈3,1415926…
Для того, чтобы легче запомнить цифры надо
сосчитать количество букв в каждом слове высказывания: «это я знаю и помню
прекрасно»
В дальнейшей работе мы будем использовать
значение П ≈3,14
Исследование проведено. На уроке, кроме
исследовательской работы удачно использовалась работа в парах. Сотрудничество и
взаимопомощь принесли желаемый результат. Проблема решена.

Имея успех в небольших исследованиях на уроках,
некоторые ребята вовлекаются в более серьёзные исследования, требующие много
времени. Это уникальная возможность для ученика сделать своё открытие, узнать
то, что до него никто не знал. Исследования помогают расширить кругозор
ученика, повысить самооценку, самоутвердиться, формировать исследовательскую
компетентность.

Заключение.

В процессе изучения принципов развивающего обучения, применения
его элементов на уроках, я пришла к выводу, что создание проблемных ситуаций в
процессе обучения математике позволяет развивать мышление учеников,
активизирует их деятельность на уроке, способствует их интеллектуальному
развитию. Создание проблемных ситуаций на уроках
математики способствует формированию системы универсальных учебных
действий учащихся. Цели и задачи технологии проблемного
обучения полностью соответствуют требованиям ФГОС.

Ситуация затруднения школьника в решении задач
приводит к пониманию учеником недостаточности имеющихся у него знаний, что в
свою очередь вызывает интерес к познанию и установку на приобретение новых.
Необходимо давать ученику возможность
экспериментировать и не бояться
ошибок, учить отстаивать собственное мнение, воспитывать смелость быть не
согласным с учителем.

Преимущества
проблемного обучения: это наибольшие возможности для развития внимания,
наблюдательности, активизации мышления и познавательной деятельности учащихся, развитие
самостоятельности, ответственности, критичности и самокритичности,
инициативности, нестандартности мышления, осторожности и решительности.

К
трудностям проблемного обучения можно отнести то, что на осмысление проблемной
ситуации и поиски путей решения выхода из нее уходит значительно больше
времени, чем при традиционном обучении. Проблемное обучение связано с
исследованием и поэтому предполагает растянутое во времени решение задачи.

Кроме
того, разработка технологии проблемного обучения требует от учителя большого
педагогического мастерства и много времени. Конечно, работа трудоёмка, так как
к каждому уроку надо подбирать необходимые и достаточные упражнения для
актуализации знаний и создания проблемной ситуации, продумывать постановку
проблемы и выбор путей её решения в соответствии с принципом рациональности.

Но
проблемные уроки очень эффективны и нравятся детям. Проблемное изучение просто
необходимо, так как оно формирует гармонически развитую творческую личность,
способную логически мыслить, находить решения в различных проблемных ситуациях,
систематизировать и накапливать знания, умеющую анализировать, планировать, делать
выводы, стремящуюся к саморазвитию и самокоррекции. Постоянная постановка перед
ребенком проблемных ситуаций приводит к тому, что он не «пасует» перед проблемами,
а стремится их разрешить. Таким образом, применение технологии проблемного
обучения на уроках математики способствует воспитанию творческой личности, способной
к поиску и исследованию.

Хоть выйди ты не в
белый свет,

А в поле за
околицей

Пока идёшь за
кем-то вслед

Дорога не
запомнится.

Зато куда б ты ни
попал

И по какой распутице,

Дорога та, что сам
искал,

Вовек не
позабудется.

(Н. Рыленков)

Список
литературы

1.
Концепция развития математического
образования в Российской Федерации.[Электронный ресурс].– Режим доступа: http://www.firo.ru/wp-content/uploads/2014/12/Concept_mathematika.pdf

2.
Крупич В.И. Дидактический механизм
возникновения проблемной ситуации в обучении математике. — М.:МГПИ,1984.

3.
Кудрявцев
Т. В. Проблемное обучение: истоки, сущность, перспективы. — М.: Знание, 1991.

4.
Лернер И.Я. Проблемное обучение. Серия
«Педагогика и психология», №7, — М., 1974.

5.
Махмутов
М. И. Организация проблемного обучения в школе. Книга для учителей. — М.:
Просвещение, 1977.

6.
Махмутов
М. И. Проблемное обучение. Основные вопросы теории. — М.: Педагогика, 1975.

7. Оконь В.
Основы проблемного обучения. — М.:Просвещение, 1968 г.

8.
Пашкевич,
А.В. Оцениваем метапредметные результаты. Стратегия и методы
оценивания.Проектирование заданий, тестов, задач. Электронное приложение с
презентациями и мониторинговыми материалами/ А.В,Пашкевич.- Волгоград: Учитель,
2016 г.

9.
Полтавская
Г.Б. Математика. 5-11 классы: проблемно-развивающие задания, конспекты уроков,
проекты .-изд.3-е перераб.-Волгоград: Учитель, 2013 г.

10.
Рубинштейн
С.Л. Основы общей психологии. – М., 1973.

11. Федеральный
государственный образовательный стандарт основного общего образования / М-во
образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с. –
(Стандарты второго поколения).

12.
Шафигулина
Л.Р.Математика. 5-9 классы. Проблемное и игровое обучение -Волгоград: Учитель,
2013 г.

13.
Юрко
О.А. Уроки профессионального мастерства. Математика. 5-8 классы:
технологические карты, презентации уроков в электронном приложении. —
Волгоград: Учитель, 2016

14.
Проблемное
обучение на уроках математики .[Электронный
ресурс].– Режим доступа: http://festival.1september.ru/articles/211680/

15. Линия УМК по
математике под ред. Г.В. Дорофеева .[Электронный
ресурс].– Режим доступа: http://edvisrb.ru/education/programs/?id=440824

16. Концепция
проблемного обучения [Электронный ресурс] // Сидоров С.В. Сайт
педагога-исследователя. – URL: http://si-sv.com/publ/1/14-1-0-171 (дата
обращения: 18.10.2016)

17. Проблемное
обучение на уроках математики [Электронный ресурс].– Режим доступа: http://nsportal.ru/shkola/obshchepedagogicheskie-tekhnologii/library/2012/04/22/problemnoe—obuchenie—na—urokakh

18. Технология
проблемного обучения на уроках математики. [Электронный ресурс].– Режим
доступа: https://infourok.ru/vistuplenie—na—pedagogicheskom—sovete—tehnologiya—problemnogo—obucheniya—na—urokah—matematiki-570537.html

19. Проблемное
обучение на уроках математики в средней школе [Электронный ресурс]. http://eduherald.ru/ru/article/view?id=13857

ПРИЛОЖЕНИЕ
1

Конспект урока

по теме:
«Сравнение дробей»

1.
Предмет математика

2.
Класс 5

3.
Тема и номер урока в теме «Сравнение
обыкновенных дробей», 13-ый урок

4.
Базовый учебник Дорофеев,
Г.В., Шарыгин, И.Ф. Математика: учебник для 5 класса общеобразовательных
учреждений / Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова, Е.А. Бунимович и др. –
М.: Просвещение, 2014.

5.
Цель урока: исследовать
5 возможных случаев сравнения обыкновенных дробей; на основе полученных
результатов исследований сформулировать общее правило сравнения обыкновенных
добей.

6.
Планируемые результаты:

Предметные:
выделяют основные типы заданий на сравнение
обыкновенных дробей, имеют представление о классификации обыкновенных
дробей, формулируют и применяют при решении задач и примеров правила
сравнения дробей сравнивают

·
дроби с одинаковыми знаменателями

·
дроби с одинаковыми числителями

·
правильные (неправильные) дроби с 1

·
правильную дробь с неправильной

·
дроби с разными числителями и разными знаменателями

Метапредметные: проводят
простейшие исследования, подтверждает результаты исследований примерами
из жизни, выбирают наиболее эффективные способы решения задач в
зависимости от конкретных условий; осуществляют контроль и оценку
процесса и результата деятельности; анализируют, строят логические цепи
рассуждений; самостоятельно формулируют тему и цель урока; работают
в группе и участвуют в коллективном обсуждении

Личностные:
сотрудничают с учителем и сверстниками в процессе
поиска средств и методов реализации поставленной цели; оценивают
свою деятельность и деятельность одноклассников по заданным критериям.

7.
Тип урока: урок
изучения нового материала

8.
Структура и ход урока

Структура
урока

1.
Мотивация к учебной деятельности

2.
Актуализация имеющихся знаний и умений учащихся

3.
Создание проблемной ситуации, мотивация.

4.
Построение проекта выхода из затруднения

5.
Реализация построенного проекта

6.
Первичное закрепление нового материала с проговариванием во внешней речи

7.
Самостоятельная работа с самопроверкой по образцу

8.
Включение в систему знаний и повторение

9.
Рефлексия учебной деятельности

ХОД УРОКА

«3нание только тогда знание,

когда оно приобретено усилиями своей
мысли, а не памятью».

Л.Н. Толстой

Этап урока, длительность	Деятельность учителя	Деятельность ученика
1. Мотивация к учебной деятельности	Приветствует учащихся, создает эмоциональный настрой. -Начинаем наш урок! Ты готов к нему, дружок? Все ль на месте, все ль в порядке: Ручка, в клеточку тетрадка? Все ребята подмечайте, Не вертитесь, не зевайте, На вопросы отвечайте, Ничего не забывайте.	Приветствуют учителя, настраиваются на работу
2. Актуализация имеющихся знаний и умений учащихся	— Какую тему мы изучаем на последних нескольких уроках математики?	— обыкновенные дроби
-какие виды обыкновенных дробей вы знаете?	— правильные, неправильные
-что мы умеем делать с обыкновенными дробями? (фиксирует ответы в виде схемы)	— читать, записывать, изображать на числовом луче, сокращать, приводить к новому знаменателю
3. Создание проблемной ситуации, мотивация	—Перед вами ряд дробей:1/2, 1/3, 5/3, 2/8, 9/7, 11/2, 4/4, 2/1, ¾, 8/2 -Придумайте для ваших одноклассников задания, которые можно выполнить с данными дробями.	(называют задание, контролируют правильность ответа на поставленный вопрос, дополняют, исправляют) —назовите правильные (неправильные) дроби -выберите несократимые дроби -назовите дробь, равную 4 -назовите дробь, равную ¼ и т.д.
-расположите данные дроби в порядке возрастания (в порядке убывания)	(последнее задание вызывает у учащихся затруднения)
— Почему вы не можете расположить данные дроби в порядке убывания или в порядке возрастания? дроби?	—Мы еще не умеем сравнивать такие дроби
4. Построение проекта выхода из затруднения	-Как вы считаете, чему будет посвящен наш урок?	— Сравнению дробей
— Я предлагаю следующий план выхода из создавшейся ситуации: мы с вами проведем небольшое исследование. Предлагаю разделиться на 5 групп. Каждая группа получает задание для исследования, по результатам которого нужно будет сделать необходимые выводы. А затем мы все вместе сформулируем общее правило, которое поможет нам сравнить данные дроби и выполнить первоначальную задачу: расположить предложенный ряд дробей в порядке возрастания, а затем в порядке убывания. Принимаете мое предложение? Как же сформулировать нам цель работы на уроке? (фиксирует предложенные варианты на доске)	-да -исследовать дроби -научиться сравнивать дроби -написать правило сравнения дробей -научиться сравнивать различные виды обыкновенных дробей
5. Реализация построенного проекта	Раздает карточки с заданиями для групп учащихся, дает необходимые рекомендации и пояснения.	Задание для исследования 1 группе. Используя числовой луч, сравните дроби 4/7 и 6/7, ¼ и 4/4, 3/14 и 9/14. Сделайте вывод, вставив пропущенные слова на карточке. Из двух дробей с одинаковыми … меньше та, у которой …, и больше та, у которой ….
Задание для исследования 2 группе. Сравните дроби 1/2 и 1/5, 3/5 и 3/10, 7/11 и 7/20. Сделайте вывод, вставив пропущенные слова на карточке. Из двух дробей с одинаковыми … меньше та, у которой …, и больше та, у которой ….
	Задание для исследования 3 группе. Сравните дроби 1/3 и 1, 4/4 и 1, 8/2 и 1 Сделайте вывод, вставив пропущенные слова на карточке. Правильная дробь всегда … единицы. Неправильная дробь всегда … или … единице.
Задание для исследования 4 группе. Сравните дроби ½ и 4/4, 7/6 и 6/7, ¼ и 4/1 Сделайте вывод, вставив пропущенные слова на карточке. Правильная дробь всегда … неправильной.
		Задание для исследования 5 группе. 6/7 и 9/14, 5/10 и 3/5, 11/2 и 2/8 Сделайте вывод, вставив пропущенные слова на карточке. Чтобы сравнить две дроби с разными знаменателями нужно …, а затем сравнить, используя правило сравнения дробей.
	Предлагает каждой группе представить свои выводы по проведенным исследованиям и пояснить свой ответ.	Из двух дробей с одинаковыми знаменателями меньше та, у которой знаменатель меньше, и больше та, у которой знаменатель больше
Из двух дробей с одинаковыми числителями меньше та, у которой знаменатель больше, и больше та, у которой знаменатель меньше
Правильная дробь всегда меньше единицы. Неправильная дробь всегда больше или равна единице.
Правильная дробь всегда меньше неправильной.
	Сформулируйте правило сравнения правильных и неправильных дробей.	Чтобы сравнить две дроби с разными знаменателями нужно привести данные дроби к общему знаменателю, а затем сравнить, используя правило сравнения дробей с одинаковыми знаменателями.
Физкультминутка	Сели, встали, сели, встали И до потолка достали. Влево, вправо, влево, вправо Получается на славу. Друг на друга посмотрели И опять на место сели	Выполняют упражнения разминки вместе с учителем
6. Первичное закрепление нового материала с проговариванием во внешней речи	Вернемся к ряду дробей, предложенному вам в начале урока. Сравните дроби . Расположите данные дроби в порядке возрастания.	½ и 1/3, 5/3 и 2/8, 9/7 и 11/2, 1/3 и 4/4, 2/8 и 2/1, ¾ и 8/2
7.Самостоятельная работа с самопроверкой по образцу	Предлагает учащимся выполнить самостоятельную работу с последующей взаимопроверкой в парах. Сравните дроби.	85/97 и 17/97, 100/106 и 100/108, 11/8 и 1, 4/5 и 1, 9/4 и 17/18, 21/91 и 3/2
8. Включение в систему знаний и повторение	Придумайте свои задания на применение правил сравнения дробей, изученных сегодня.	называют задание, контролируют правильность ответа на поставленный вопрос, дополняют, исправляют
	-итак, что мы сегодня научились еще делать с обыкновенными дробями?	— сравнивать
9. Рефлексия учебной деятельности	— Урок подходит к концу. Давайте вспомним, какую цель мы пытались достичь на сегодняшнем уроке? — Теперь вы сможете сравнить дроби, предложенные в начале урока? -Удалось ли нам достичь поставленной цели? -что больше всего понравилось на уроке, что запомнилось?	-Научиться сравнивать различные виды обыкновенных дробей — Мы уже сравнили их в последнем задании -да Ответы учащихся
10. Домашнее задание	На каждое из изученных на уроке правил придумать и решить по 2 примера. Правила сравнения дробей выучить.	Записывают домашнее задание в дневник
	Спасибо за урок!

ПРИЛОЖЕНИЕ
2 [13]

Конспект урока

по теме:
«Отношение чисел»

1. Предмет
математика

Класс
6
Тема
и номер урока в теме «Сравнение
обыкновенных дробей», 13-ый урок
Базовый
учебник Дорофеев, Г.В., Шарыгин, И.Ф.
Математика: учебник для 6 класса общеобразовательных учреждений / Г.В.
Дорофеев, И.Ф. Шарыгин, С.Б. Суворова, Е.А. Бунимович и др. – М.:
Просвещение, 2014.
Цель
урока: Создать условия для освоения основных понятий: отношения,
члены отношения, масштаб; применения изученных свойств при решении учебных
и практических задач, развития вычислительных навыков, воспитания
информационной культуры
Планируемые результаты:

Предметные:
Научатся: формулировать определения понятий «отношение», «отношение чисел»;
записывать с помощью букв отношение; находить отношение чисел; применять
понятие «масштаб» при решении задач

Метапредметные:

Познавательные: уметь ориентироваться в различных
источниках информации, критически оценивать и интерпретировать информацию,
получаемую из различных источников, использовать средства информационных и
коммуникационных технологий в решении практических задач с соблюдением требований
техники безопасности, норм информационной безопасности; владеть навыками
разрешения проблем, самостоятельного поиска методов решения практических задач.

Коммуникативные: владеть языковыми средствами – умением
ясно, логично и точно излагать свою точку зрения; уметь продуктивно общаться и
взаимодействовать в процессе совместной деятельности, учитывать позиции других
участников деятельности, эффективно разрешать конфликты.

Регулятивные: уметь самостоятельно определять цели и
составлять планы деятельности, самостоятельно осуществлять, контролировать и
корректировать свою деятельность; использовать все возможные ресурсы для
достижения поставленных целей и реализации планов деятельности

Личностные: Формировать основы
саморазвития и самовоспитания в соответствии с общечеловеческими ценностями;
уметь вести диалог с учителем, одноклассниками,

достигать в нем взаимопонимания, находить общие цели и
сотрудничать для их достижения; развивать способность к образованию, в том
числе самообразованию и непрерывному образованию как условию успешной
профессиональной и общественной деятельности

Тип урока: Урок
открытия новых знаний
методы и формы
обучения

Методы: устный контроль и самоконтроль (фронтальный и индивидуальный
опрос), стимулирование интереса к обучению (создание познавательно-игровых
моментов, эмоционально-позитивных ситуаций), организация и осуществление
учебной деятельности (по способу передачи информации – наглядный и словесный,
по степени самостоятельности мышления – репродуктивный и частично-поисковый, по
степени управления учебной работой – под руководством преподавателя и
самостоятельная работа).

Организационная структура урока

Этапы урока

Деятельность учащихся

Деятельность учителя

Универсальные учебные действия

Организационный момент

Приветствие

Проверка готовности
учащихся к уроку. Приветствие учащихся

Мотивация

(самоопределение) к учебной деятельности

Настрой на работу.

Отвечают на вопросы
учителя, аргументируют свою точку зрения. (Фронтальная работа.)

– Известный
белорусский писатель Якуб Колас говорил: «Только те знания становятся нашим
достоянием, которые мы добываем сами».

– Как вы
понимаете эти слова? Согласны вы с ними. Свой ответ аргументируйте.

– Как вы
думаете, что вам предстоит сегодня сделать на уроке?

Личностные:
самоопределение.

Коммуникативные: умение с
достаточной полнотой и точностью выражать свои мысли

Актуализация

и пробное учебное действие

Отвечают на вопросы учителя.

Интеллектуальная
разминка. Подготовка к открытию новых знаний.

Записывают в тетрадях
число, фразу: «Классная работа».

Самостоятельно
выполняют в тетрадях предложенное учителем задание.

Проверяют
правильность выполнения задания по эталону (ответы демонстрируются на слайде
презентации).

Анализируют причины ошибок
и способы их исправления.

Отвечают на вопрос
учителя.

– Надо понять, что мы
не знаем, и найти способ это узнать.

Отгадывают ребус
(работа в парах сидящих за одной партой обучающихся).

Отвечают на вопросы учителя.

– Отношение. Числа. (На
каждой парте у обучающихся находится краткая инструкция по отгадыванию
ребусов – Приложение 1.)

– Отношение чисел.

–Записывать, читать,
складывать, вычитать, умножать, делить.

Учащие предлагают
свои варианты ответов. (Работа с толковыми словарями, в том числе при наличии
Интернета с онлайн-словарями.)

Предлагают свои
варианты (с аргументацией), которые учитель фиксирует на доске

– Что предшествует
открытию новых знаний? Свой ответ поясните.

– Откройте тетради,
запишите число, «Классная работа».

–
Самостоятельно в тетрадях выполните следующее задание (задания
демонстрируются на слайдах презентации): найти частное чисел
(индивидуальная работа, самопроверка по эталону):

1) 54 и 9;

2) 48 и 3;

3) 6 и 9;

4) 24 и 3;

5) 7 и 11;

6) 25 и ;

7) 5 и 15;

0,3 и 0, 06;

9) 2 и 0, 05.

– Поднимите руку, кто
не допустил ошибок.

– Поднимите руку, кто
допустил ошибку в заданиях 1–2. – Как вы думаете, почему вы ошиблись? (Аналогично
проводится анализ ошибок по всем примерам.)

– Чтобы узнать тему
урока, отгадайте ребусы.

–
Какие слова у вас получились? (Отношение, чúсла.)

–
Сформулируйте тему урока, составив ее из этих двух слов.

– Что вы
умеете уже делать с числами?

– Что обычно
подразумевается под словом «отношения»? Где можно узнать толкование этого
слова?

–
Предположите, что в математике могут понимать под отношением чисел? Ответ
аргументируйте

Коммуникативные: планирование
учебного сотрудничества с учителем и сверстниками.

Регулятивные: умение
осуществлять контроль и корректировать свою деятельность.

Познавательные: самостоятельное
выделение и формулирование познавательной цели, поиск и выделение необходимой
информации; умение проводить анализ объектов, построение логической
цепи рассуждений, выдвижение гипотез

Выявление места и причины затруднения

Отвечают на вопросы учителя.

– В отношениях точно
используются числа.

Перечисляют, что
хотели бы узнать, заполняют после обсуждения таблицу.

Заполняют таблицу,
предварительно изобразив ее в своей тетради

– Давайте подведем
первые итоги.

– Что вы точно можете
сказать об отношениях чисел?

– Что вы не
знаете и хотели бы узнать об отношениях чисел?

Знаю	Хочу узнать

Регулятивные: прогнозирование,
выделение и осознание того, что усвоено, что еще подлежит усвоению.

Познавательные: умение
проводить анализ

Построение проекта выхода из затруднения

Отвечают на вопросы учителя.

– Узнать, что такое
отношение чисел.

Составляют план
работы для достижения поставленной цели (учитель предлагает возможные пункты
плана, а учащиеся определяют их последовательность – см. презентацию).

– Информацией в
учебниках, что-то могут подсказать одноклассники.

– В группе, так
как это сокращает время работы и повышает шансы на успешное выполнение
задания.
– Одна голова хорошо, а две – лучше.

– Один говорит –
другие слушают.

– Каждый работает на
общий результат. Быть вежливым. С уважением относиться к другому мнению

– Сформулируйте цель урока.

– Составьте план
действий, направленных на достижение поставленной цели.

– Какими источниками
информации вы планируете воспользоваться?

– Как вы планируете
работать: индивидуально или по группам? Почему?

– Приведите пример пословицы
или поговорки, подтверждающей ваши слова.

– Сформулируйте
правила работы в группе.

Предметные: формирование
навыков построения математических моделей и решения практических задач.

Коммуникативные: планирование
учебного сотрудничества с учителем и сверстниками; умение с достаточной
полнотой и точностью выражать свои мысли.

Регулятивные:
целеполагание, планирование.

Познавательные:
моделирование,

решение проблемы,
построение логических цепей, анализ; умение структурировать знания, рефлексия
способов и условий действий

Реализация

построенного

проекта

Учащиеся работают в
группах, ищут необходимую информацию в учебнике, анализируют ее; заполняют
таблицу, готовятся к представлению полученной информации перед классом.

Принцип деления на
группы учитель выбирает самостоятельно, учитывая индивидуальные особенности
учащихся класса.

Возможный вариант:
учащиеся, сидящие за первым рядом, образуют первую группу, за вторым рядом –
вторую группу, за третьим рядом – третью группу.

Отвечают на вопросы учителя

– Оформите
результаты своей работы в таблице:

Числа	Как записывается отношение чисел a и b	Как называются числа a и b, из которых составлено отношение
a
b

– Какое из
ваших предположений о том, что такое отношение чисел, нашло свое
подтверждение?

Предметные: формирование
навыков построения математических моделей и решения практических задач.

Познавательные:
моделирование,

решение проблемы,
построение логических цепей, анализ; умение структурировать знания, поиск и
выделение
необходимой информации, знаково-символические действия

Динамическая
пауза

Выполняют гимнастику
для глаз

Предлагает выполнить
гимнастику для глаз.

Первичное закрепление с проговариванием во внешней речи

Отвечают на вопросы учителя.

– Нет.

– Надо попробовать
применить знания на практике.

Фронтальная работа по
решению заданий, предложенных учителем (каждое задание решают у доски по
одному человеку, остальные – в своих тетрадях)

– Можно ли
утверждать, что вы достигли поставленной цели?

– Что надо еще
предпринять для достижения цели?

1) Запишите с помощью
знака деления « : » отношение чисел:

а) 5 и 3; б) 4 и 24;
в) 1,8 и 2,7; г)

2) Запишите с помощью
черты дроби отношение чисел:

а) 12 и 49; б) 4 и 7;
в) 6 и 3,4; г)

3) Найдите отношение:

а) 63 и 9; б) 3,2 и
0,08; в) 2,8 и 4,9; г) 8,1 и 0,09;

д) е)

4) Равны ли
отношения:

а) 15 : 3 и 2,5 :
0,5; б) в)

г) 0,8 : 0,04 и

Коммуникативные: планирование
учебного сотрудничества с учителем и сверстниками.

Познавательные: выбор
наиболее эффективных способов решения задач

Самостоятельная работа с самопроверкой по эталону

Отвечают на вопросы учителя.

– Выполнить
самостоятельную работу.

– Каждый сам.

– По эталону.

Самостоятельно
выполняют типовые задания на новый способ действия.

Выполняют
самопроверку по эталону.

Выявляют причины
ошибок и их исправляют

– Как проверить,
достигли ли вы поставленной цели?

– Как вы будете
выполнять задания?

– Как будете
проверять правильность выполнения заданий?

Самостоятельная
работа. (Каждый ученик получает лист с заданием

Задание № 1.

Заполните таблицу (1
балл при полном правильном решении, 0 баллов – в других случаях).

1-й вариант.

Отношение	5 : 12
Предыдущий член		30
Последующий член		0,9	8

2-й вариант.

Отношение	7 : 18
Предыдущий член		10
Последующий член		0,4	9

Задание № 2.

Найдите
отношение (за каждый правильно выполненный пример – 1 балл).

1-й вариант	2-й вариант
1,6 : 6,4	1,7 : 6,8
3,5 : 0,007	4,2 : 0,006

Перевод баллов,
полученных на уроке, в отметку (самостоятельная работа + ответы на уроке):

5 и более «+» – «5»;
4 «+» – «4»; 3 «+» – «3»; менее 3 «+» – надо еще проработать тему (без
выставления в журнал)

Регулятивные: умение
осуще-

ствлять контроль и
корректировать свою деятельность.

Познавательные: умение
проводить анализ

Включение в систему знаний

и повторения

Фиксируют границы
нового знания, выполняют задания, в которых новый способ действий связывается
с ранее изученными.

Отвечают на вопросы
учителя.

Выдвигают гипотезы.

Предлагают свои
варианты

Помогает выявить и
зафиксировать границы применимости новых знаний; организовать выполнение
заданий, в которых новый способ действий связывается с ранее изученными;
организовать тренировку ранее сформированных умений, требующих доработки или
доведения
до уровня автоматизированного навыка;

при необходимости
организовать подготовку к изучению следующих разделов курса.

– Как вы думаете, где
могут пригодиться открытые вами на уроке знания?

– Посмотрите
внимательно на слайд (демонстрируется карта страны). Что вы видите на
экране? Как называется запись в нижнем правом углу карты? Что она показывает?

– Продолжите фразу:
«Масштаб – это…».

– То есть отношение
чисел используется для того, чтобы…

Регулятивные: оценка
(выделение и осознание того, что усвоено, что еще подлежит усвоению).

Познавательные: умение
проводить анализ, подведение под понятие

Рефлексия учебной деятельности

Осуществляют
самооценку собственной учебной деятельности, соотносят цель и результаты,
степень их соответствия.

Намечают перспективу
последующей работы.

Рисуют «Лестницу
достижений», отмечают свое «положение» на ней.

Отвечают на вопросы учителя.

Поясняют свои слова

Организуется
учениками рефлексия и самооценка собственной учебной деятельности на уроке;
намечаются цели дальнейшей деятельности и определяются задания для
самоподготовки (домашнее задание с элементами творческой деятельности).

Отметьте ту
ступеньку, на которой вы находитесь, на ваш взгляд, на момент окончания
урока.

Прием «Лестница
достижений».

1 – учебный материал
понятен, самостоятельную работу выполнил без ошибок.

2 – учебный материал
понятен, в самостоятельной работе допустил 1–2 ошибки.

3 – учебный материал
не очень понятен, в самостоятельной работе допустил более 2 ошибок.

– Что надо
предпринять ребятам, которые сделали отметку на нижней ступени? (На средней
ступени? на верхней ступени?) Поясните свою точку зрения

Коммуникативные: умение с
достаточной полнотой и точностью выражать свои мысли.

Регулятивные: выделение и
осознание того, что усвоено, что еще подлежит усвоению.

Познавательные: умение
структурировать знания.

Личностные:
смыслообразование

Домашнее задание

Записывают домашнее
задание в дневники, задают возникшие вопросы

Предлагает и
комментирует дифференцированное домашнее задание:

«3».

1. Найдите отношение:
1) 45 к 5; 2) 4 к 32;

«4».

2. Найдите отношение:
1) 45 к 5; 2) 4 к 32;

3. Во сколько раз
расстояние на местности больше расстояния на карте, если масштаб карты 1:
50 000?

«5».

1. Найдите отношение:
1) 45 к 5; 2) 4 к 32;

2. Во сколько раз
расстояние на местности больше расстояния на карте, если масштаб карты

1 : 50 000?

3. На листе
миллиметровой бумаги нарисовать план своей комнаты в масштабе 1 : 10.

ПРИЛОЖЕНИЕ
3

Примеры приемов
создания проблемных ситуаций на уроке:

стихотворение
«Треугольник и квадрат»

Жили были два брата:
Треугольник с Квадратом.
Старший – квадратный,
Добродушный, приятный.
Младший – треугольный,
Вечно недовольный.
Стал расспрашивать Квадрат:
«Почему ты злишься, брат?»
Тот кричит ему: «Смотри:
Ты полней меня и шире.
У меня углов лишь три,
У тебя же их четыре».
Но Квадрат ответил: «Брат!
Я же старше, я – квадрат».
И сказал еще нежней:
«Неизвестно, кто нужней!»
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя, сказал: «Приятных
Я тебе желаю снов!
Спать ложился – был квадратным,
А проснешься – без углов!»
Но наутро младший брат
Страшной мести был не рад.
Поглядел он – нет квадрата,
Онемел… Стоял без слов…
Вот так месть! Теперь у брата
Восемь новеньких углов!

Приложение
4 [8]

Практическая
задача по математике
по теме «Четырёхугольники»
(геометрия
8 класс)

Компетенции: учебно-познавательная,
информационная, коммуникативная.

Аспекты компетенций направлены:

–
на умение применять знания по вычислению периметра четырёхугольника в
нестандартной ситуации, полученные на уроках математики в разделе «Измерение
величин» по теме «Четырёхугольники»; творческую деятельность обучающихся при
решении практической задачи;

–
анализ информации;

–
овладение письменной коммуникацией (составление сметы).

Название: «Применение знаний о нахождении
периметра прямоугольника в жизненных ситуациях».

Преамбула: Вы решили заменить пришедшее в
негодность ограждение своего участка. Участок прямоугольной формы ограждён
штакетником.

Задачная формулировка:

1.
Вычислите периметр ограждения, рассчитайте, сколько штакетин необходимо, какая
сумма нужна для покупки штакетника, составьте смету покупки штакетника для
замены ограждения.

2.
Проведите сравнительный анализ и сделайте вывод, какое ограждение, на ваш взгляд, будет наиболее
предпочтительным.

Рекомендованный план работы:

1.
Заменить штакетник на обычный, изготовленный из берёзы.

2.
Заменить штакетник на обычный, изготовленный из сосны.

3.
Заменить штакетник на декоративный, изготовленный из берёзы.

4.
Заменить штакетник на декоративный, изготовленный из сосны.

Источник информации: (информация из интернета)

«Древесина
является одним из самых распространенных материалов. Из дерева строятся многие
дома, мосты и другие сооружения. В каменных и железобетонных сооружениях почти
всегда применяется дерево для настилки полов, изготовления окон и дверей,
разных отделочных работ.

Древесина
– выгодный и дешевый материал. По весу она легче многих других материалов,
прочна, легко и хорошо обрабатывается, окрашивается и соединяется при помощи
клея, гвоздей, болтов и шурупов.

Древесных
пород очень много.

Сосна.
Наиболее доступна, очень распространенная и легко обрабатываемая. Сосновая
древесина не очень твердая, но прочная, легко колется, пилится и строгается
вдоль волокон. Поперек волокон сосновую доску распилить и, особенно, гладко
выстрогать значительно труднее. Цвет сосновой древесины – светло-желтый, с
легким розовым оттенком.

Береза.
Наиболее доступна, очень распространенная и легко обрабатываемая. В тех
случаях, когда требуется тщательно отделать края изделия, особенно не
прямолинейной формы, лучше применять березу. Березовая древесина плотнее и
тверже сосновой, но также легко пилится и строгается. Колоть березу тоже легко,
однако расколоть березовую доску или брусок по прямой линии не всегда
удается. Сырая березовая древесина при высыхании чаще трескается и
сильнее коробится, чем сосновая. Цвет древесины – светло-желтый, с
розоватым оттенком».

3.
План участка:

4.
Рекомендации: расстояние между штакетинами должно быть равно ширине штакетины.

5. В таблице приведены цены
за различные варианты штакетника, предлагаемого местным частным
предпринимателем:

Вид штакетника	Материал	Количество	Цена (р.)	Ширина штакетника (мм)
Обычный	берёза	1 штука	6	50
Обычный	сосна	1 штука	7	50
Декоративный	берёза	1 штука	12	80
Декоративный	сосна	1 штука	14	80

Критерии
оценивания.

Тебе
предлагают поставить баллы за выполненную работу в соответствии со следующими
критериями:

–
0–2 балла – за правильное составление плана;

–
0–1 балл – за разбор теоретического материала;

–
0–1 балл – за расчёт периметра ограждения;

–
0–2 балла – за расчет количества штакетин;

–
0–2 балла – за решение задачи;

–
0–1 балл – за правильный выбор древесины;

–
0–2 балла – за активность в группе.

Шкала перевода
баллов в оценку:

10–11 баллов	отлично
8–9 баллов	хорошо
6 баллов	удовлетворительно
менее 6 баллов	неудовлетворительно

Приложение
5
[8]

Ситуационное задание по математике по теме
«Натуральные числа»
(математика
5 класс)

«Поездка
к бабушке».

Ситуация.
На летних каникулах
семья обычно навещает бабушку. В этом году папа купил машину и перед семьей
возник вопрос: «Ехать, как обычно, на поезде или поехать на своей машине?»

Задачная формулировка. Рассчитать, какая поездка
обойдется для семьи из трех человек дешевле. Можно ехать поездом, а можно – на
своей машине. Семья живет в Москве, а бабушка – в Чебоксарах.

Источник информации:

1.
Стоимость билета на одного человека:

–
плацкарт – 990 рублей;

–
купе – 1570 рублей.

2.
Расстояние от г. Москвы до г. Чебоксары – 700 километров.

3.
Расход бензина – 11 литров на 100 километров пути.

4.
Цена бензина – 32 рубля за один литр.

Источник

Подборка по базе: Темы рефератов.docx, Теория методики обучения биологии.docx, мой реферат.docx, бж реферат 2.docx, Ғимараттар мен үймереттерді тұрғызу технологиясы Бидебаев Ербол., Темы рефератов (1).doc, Задание на дистант слесаря 2 год обучения 21_11_2022.docx, Использование интерактивных методов обучения на уроках географии, Темы рефератов.docx, Плавание реферат.docx

Создание проблемных ситуаций через умышленно допущенные учителем ошибки.

Найдите ошибки: 0+(-1) = 0 16+(-2) = 18 5+2 = 7 -4+(-1) = 3 5+(-2) = -3

Найди ошибку: Отец в подарок сыну сделал счетную машину. К сожалению, она недостаточно точна. Результаты перед вами, быстро всё исправьте сами:

39,4+10,1 = 4954; 97,3 + 9,04 = 10,634; 47,03 + 4,8 = 5183; 729,004 + 10 = 729,014; 3,067 + 2,033 = 51; 31,26 + 0 = 312,6.

Создание проблемных ситуаций на внимание.

Заметить закономерность в рядах чисел, записать в каждую строчку по два следующих числа. 2,3,4,5,6,7,…; 3,7,11,15,19,23,…;10,9,8,7,6,5, … 9,1,7,1,5,1,… ; 5,10,15,20,25,30,…;4,5,8,9,12,13,…;9,12,15,18,21, … 25,25,21,21,17,17,…;8,8,6,6,4,4,…;1,2,4,8,16,32,…

Создание проблемных ситуаций при выполнении упражнеий на сравнение.

Как можно быстрее поставьте вместо “снежинки” один из знаков: “=”, “+”, “-”, “<”, “>”, чтобы решение задачи было верным.

36*5*21 136*54+236 3х4*17=29 81*13=81*13 23+8*31- 9 400*313+8 14*4=10 72=144*72 6*8*4=10 9х8*16: 4 100+13*96*17 96:6*4х4

Создание проблемных ситуаций на уроках, посвященных истории математики.

Знайка, как самый образованный и любознательный, часто рассказывал своим друзьям о чем то новом и интересном. Однажды он рассказал об одном известном математике. Его имя и вы узнаете, если правильно выполните действия и найдете буквы, соответствующие полученным числам. (Учащиеся выполняют вычисления, находят нужную букву. Буквы вписываются в колонку рядом с примером).

-6+2=-4 (Д) 8+(-1)=7 (Е) -10,6+2,6=-8 (К)

-3+(-3)=-6 (А) 2+(-7)=-5 (Р) -1+1=0 (Т)

ДЕКАРТ. Рене Декарт – французский философ, физик, математик. Считал математику идеалом и образцом для всех наук. Ввел понятие координатной прямой. Его знаменитое изречение: «Я мыслю, следовательно, я существую».

Создание проблемных ситуаций через решение задач, связанных с другими предметами.

Хлебное дерево (джек-фрут) – родное для западных островов Тихого океана. Хлебное дерево вырастает примерно до 20-26 метров в высоту, листья его большие и толстые. Но не за рост его уважают. Эти плоды являются основным продуктом питания для жителей тропических островов, где растут хлебные деревья. Плоды едят и жареными, и печёными, и варёными. На вкус эта еда – что-то среднее между картошкой и хлебом. Но не хлебом единым жив человек! Из хлебного дерева также делают лодки, ведь древесина его лёгкая и прочная, к тому же чрезвычайно устойчива к термитам. Артокарпус – научное название хлебного дерева. Продолговатые плоды артокарпуса поражают своими размерами. Найдите значения выражений и узнайте эти размеры.

Масса плодов;

∙45+25,5=36 (кг)

Длина плодов:

72,5-45∙ =90 (м)

Диаметр плодов:

( )∙10=50 (м)

В каждом из примеров найдите сумму, а потом расположите ответы в порядке убывания. Если вы сделаете всё правильно, получите слово, которое является названием самого высокого в мире вулкана.

Л 746+354 А 27+72 Ь 104+46 К 36+64 Ю 540+360 Л 146+44 Й 171+29

Ь 276+724 Ь 140+260 Я 188+112 Я 117+3 Л 169+331

Ответ. Льюльяйльяка

Экскурсантов можно разместить в лодки по 8 и 12 человек в каждой. И в том, и в другом случае свободных мест не останется. Если экскурсантов больше 100, но меньше 130, то всего их: а)120 человек; б)104 человека; в)128 человек; г)116 человек.

Правильный ответ подскажет вам, сколько лет было Тутанхамону, когда он стал фараоном (а-9; б-14; в-21; г-33).

Учитель объяснял новый материал 0,4 урока, урока ушло на решение задач, а в оставшееся время учащиеся писали самостоятельную работу. Если продолжительность урока 45 мин, то самостоятельная работа длилась: а) 12 мин; б) 10 мин; в) 5 мин; г) 7 мин.

Правильный ответ подскажет вам, какой предмет не изучали в школе древние греки

(а – физкультуру; б – чтение; в – музыку; г – математику).
Создание проблемных ситуаций через самостоятельную работу.

На доске записаны координаты точек: (0;0), (-1;1) ,(-3;1), (-2;3), (-3;3),

(-4;6), (0;8), (2;5), (2;11) (6;10), (3;9), (4;5), (3;0), (2;0), (1;-7), (3;-8), (0;-8), (0;0).

Отметить на координатной плоскости каждую точку и соединить с предыдущей отрезком. Результат – определенный рисунок.

Можно предложить обратное задание: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.

Создание проблемных ситуаций через решение задач, связанных со сказочными персонажами.

Ужинали вместе Змей Горыныч и Кощей Бессмертный и решали давний спор: кому свататься к Бабе Яге? Спорили они спорили и решили, что свататься будет тот, кто умнее, и решит задачу другого. Решите эти задачи:

1. Змей Горыныч — Кощею Бессмертному: «Лететь мне от своего царства до Бабы Яги 3 дня и 3 ночи, а расстояние между нами 33 раза по 33 версты. Сколько же мне лететь от своего царства до тебя, если между нами все полные 3993 версты?»

2. Кощей Бессмертный — Змею Горынычу: «Богат я, Змей Горыныч, да нет у меня кареты, чтобы ехать свататься, а мастер просит за карету 144 золотых перстня по 144 унции каждый. Перстни у меня есть, да только мне проще отдать цепями. Сколько же мне нужно отдать цепей, если каждая весит 324 унции?»

3. Собралась Баба Яга на шабаш. Чем удивить подружек? Решила Баба Яга испечь громадный пирог с лягушками. Открыла кулинарную книгу и прочитала, что на приготовление маленького пирожка с лягушками (всего 1,5 кг) требуется 33 лягушки. Стала Баба Яга считать, сколько же лягушек заказать кикиморам, чтобы испечь громадный пирог весом 35 кг, да так до сих пор и считает. Помоги Бабе Яге: посчитай, сколько лягушек потребуется на такой пирог.

4. Не хотела Василиса Прекрасная выходить замуж и задала глупым своим женихам «неразрешимую» задачу: «15 раз по 15 синиц смогут очистить мой лес от гусениц за 15 лет. Сколько лет потребуется 3 раза по 3 синицам, чтобы проделать ту же работу?» А ты сможешь решить эту задачу?

5. Спорят Леший с Кикиморой: — Чьё болото? — и пришли за разрешением спора к Бабе Яге, а Баба Яга задала им задачу — кто правильно ответит, тот и владелец болота: «Ваше болото Водяной выпьет за 77 дней, а змей Горыныч имеет голов в 7 раз больше, чем Водяной, да каждая из них пьет в 33 раза медленней. Сколько дней Змею Горынычу пить ваше болото?» Что им отвечать?

В ходе решения задач вырабатывается быстрота вычислений, внимательность, сообразительность.

Основным в создании проблемной ситуации на уроках математики является обучение математике. Проблемные ситуации, созданные учителем на уроке активизируют деятельность учащихся, делают восприятие более активным, эмоциональным, творческим. Создание проблемных ситуаций на уроках повышает интерес к предмету, влияют на повышение качества знаний, умений и навыков учащихся, развитие умственной деятельности.

Заключение

Все ли обучение должно быть проблемным? Нет не все, если под проблемным обучением иметь в виду только решение учебных проблем и только самостоятельное усвоение всего учебного материала. Все обучение должно быть развивающим, в котором самостоятельное усвоение знаний путем решения учебных проблем, путем открытий сочетается с репродуктивным усвоением знаний, излагаемых учителем или учеником. Ученик не может и не должен повторять весь исторический путь развития человеческого знания. Но принципы этого развития и обобщенные способы действия он должен повторить для того, чтобы усвоить их выработать у себя способы творческой деятельности.

Обучение не может считаться развивающим, если не используются закономерности проблемного обучения (принцип проблемности, проблемная ситуация).

Проблемный тип обучения не решает всех образовательных и воспитательных задач, поэтому он не может заменить собой всей системы обучения, включающей разные типы, способы, организации учебно-воспитательного процесса. Но также система обучения не может быть подлинно развивающей без проблемного обучения.

Всем ли учащимся доступно проблемное обучение? Практически всем. Однако уровень проблемности и степень познавательной самостоятельности будут сильно различаться в зависимости от возрастных и индивидуальных особенностей учащихся, от степени их обученности методам проблемного обучения и так далее.

Рассмотрев основные аспекты реализации проблемного обучения в качестве педагогической технологии на уроках математики, можно сделать следующие выводы:

1. Проблемное обучение – это обучение, при котором педагог ставит перед учениками проблему и организует процесс её решения.

2. Разработкой вопрос о сущности проблемного обучения занимались Ю.К. Бабанский, П.Л. Гальперин, Н.А. Менчинский, А.М. Матюшкина, М.И. Махмутова и другие авторы.

3. Проблемное обучение является одним из наиболее эффективных средств активизации мышления учащихся.

4. Проблемная ситуация и учебная проблема являются основными понятиями проблемного обучения.

5. Существуют принципы основных способов создания проблемных ситуаций, а также правила создания проблемных ситуаций.

6. Учебная проблема – это форма реализации принципа проблемности в обучении.

7. К выдвигаемой проблеме предъявляются требования, которые необходимо учитывать учителю при организации обучения в рамках рассматриваемой педагогической технологии.

8. Учебная проблема не является проблемой для учителя.

9. Существует три вида решения проблемы в зависимости от наличия у решающего определённого опыта в отношении класса проблемных задач.

10. Решение учебной проблемы есть результат активного мыслительного процесса.

11. Проблемными являются первые уроки любой темы.

12. Существует структура организации проблемного обучения в средней школе.

13. Проблемное обучение сочетает в себе индивидуальную и коллективную формы работы учащихся.

14. Существуют следующие методы проблемного обучения: метод монологического изложения, рассуждающий, диалогический, эвристический, исследовательский, метод программных заданий.

15. Существуют следующие виды проблемного обучения: теоретическое исследование, поиск практического решения, художественное отображение действительности и другие.

Список используемой литературы:

1. Бабанский Ю.К. Методы обучения в современной общеобразовательной школе.-М. Просвещение, 1985.

2. Бабанский Ю.К. Проблемное обучение как средство повышение эффективности учения школьников.- Ростов-на-Дону, 1970.

3. Вилькеев Д.В. Познавательная деятельность учащихся при проблемном характере обучения основам наук в школе.- Казань, 1967.

4. Гальперин П.Я. Методы обучения и умственное развитие ребенка. — М.:Изд-во МГУ, 1985.

5. Крутецкий В.А. Психология обучения и воспитания школьников. — М.: Просвещение, 1986.

6. Кудрявцев Т.В. Исследование и опыт проблемного обучения. В кн.: «О проблемном обучении»: Вып. 2.- М.:Высшая школа, 1969.

7. Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы. — М.:3нание, 1991.

8. Лернер И.Я. Вопросы проблемного обучения на Всесоюзных педагогических чтениях.// Советская педагогика.-1968.-№ 7.

9. Лернер И.Я. Система методов обучения. — М.: Знание, 1976.

10. Людмилов Д.С., Дышинский Е.А., Лурье A.M. Некоторые вопросы проблемного обучения математике: Пособие для учителей.- Пермь, 1975.

11. Матюшкин A.M. Проблемные ситуации в мышлении и обучении.- М.: Педагогика, 1972.

12. Махмутов М.И. Организация проблемного обучения в школе. Книга для учителей.- М.: Просвещение, 1977.

13. Махмутов М.И. Проблемное обучение. Основные вопросы теории.- М.: Педагогика, 1975.

14. Мочалова Н.М. Методы проблемного обучения и границы их применения.- Казань, 1978.

15. Оконь В. Основы проблемного обучения.- М.: Просвещение, 1968.

16. Поиски рациональных способов преподавания математики (из опыта учителей Татарии).- М. Просвещение, 1968.

17. Развитие учащихся в процессе обучения: Под ред. Л.В. Занкова.-М., 1963.

Источник

Создание проблемных ситуаций на уроках математики

Создание проблемных ситуаций на уроках математики

Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей

Уровни проблемного обучения :

1 уровень – ученик усваивает приёмы логического мышления

репродуктивным методом, следуя образцу рассуждения учителя

;

2 уровень – учитель создаёт проблемную ситуацию, указывает на проблему и вовлекает их в совместный поиск путей её решения и в процесс самого решения;

3 уровень – учащиеся формулируют аналоговую неполнозначную проблему и анализируют её вместе с учителем, совместно выдвигают предположения и обосновывают гипотезу, а доказывают и проверяют решения самостоятельно, решаются познавательные задачи;

4 уровень – наличие любых типов проблем и полная

самостоятельность в их решении.

Технология проблемного обучения реализуется на основе следующих факторов: оптимальный подбор проблемных ситуаций и средств их создания; отбор ситуаций тесно связан с применением их в повседневной жизни; учет особенностей проблемных ситуаций в различных видах учебной работы и в различных классах; личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка

Технология проблемного обучения реализуется на основе следующих факторов:

оптимальный подбор проблемных ситуаций и средств их создания;

отбор ситуаций тесно связан с применением их в повседневной жизни;

учет особенностей проблемных ситуаций в различных видах учебной работы и в различных классах;

личностный подход и мастерство учителя, способные вызвать активную познавательную деятельность ребенка

Проблемное обучение, в первую очередь, включает в себя создание проблемных ситуаций

Проблемное обучение, в первую очередь, включает в себя создание

проблемных ситуаций

Создание проблемных ситуаций через умышленно допущенные учителем ошибки Решаются задачи с несформулированным вопросом с недостаточными или избыточными исходными данными; с неопределенностью в постановке вопроса; с противоречивыми данными; с заведомо допущенными ошибками; с ограниченным временем решения.

Создание проблемных ситуаций через умышленно допущенные учителем ошибки

Решаются

задачи с несформулированным вопросом
с недостаточными или избыточными исходными данными;
с неопределенностью в постановке вопроса;
с противоречивыми данными;
с заведомо допущенными ошибками;
с ограниченным временем решения.

«Обманные задачи» Больший угол треугольника равен 50°. Найдите остальные углы. Две стороны треугольника перпендикулярны третьей. Определите вид треугольника. Внешний угол при основании равнобедренного треугольника равен 75°. Найдите углы треугольника. Диагональ ромба в два раза больше его стороны. Найдите углы ромба.

«Обманные задачи»

Больший угол треугольника равен 50°. Найдите остальные углы.
Две стороны треугольника перпендикулярны третьей. Определите вид треугольника.
Внешний угол при основании равнобедренного треугольника равен 75°. Найдите углы треугольника.
Диагональ ромба в два раза больше его стороны. Найдите углы ромба.

«Обманные задачи»: 7 кл. Тема «Линейные уравнения с одной переменной». Проверьте решение уравнения: (5х+ 8)  2 – 3 = 19 10х + 16 – 3 = 19 10х = 19 – 16 – 3 10х = 0 х = 0 Естественно при проверке выясняется, что ответ неверный.

«Обманные задачи»:

7 кл. Тема «Линейные уравнения с одной переменной».

Проверьте решение уравнения:

(5х+  2 – 3 = 19

10х + 16 – 3 = 19

10х = 19 – 16 – 3

10х = 0

х = 0

Естественно при проверке выясняется, что ответ неверный.

Создание проблемных ситуаций через выполнение практических заданий

7 класс. Темы: «Построение треугольника по трем элементам», «Неравенство треугольника». Предлагаю ученикам построить с помощью циркуля и линейки треугольник со сторонами:

а) 5см; 6см; 7см; б) 9см; 5см; 6см;

в) 1см; 2см; 3см; г) 3см; 4см; 10см. Вывод: построить треугольник в последних двух случаях не удается.

Возникает проблема : «При каких же условиях можно построить треугольник, т. е. каково условие существования треугольника»? Чертежи, полученные учащимися при решении этой задачи дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон».

Создание проблемных ситуаций через решение задач на сравнение и внимание 8кл. Тема «Осевая и центральная симметрия». а) Какие из следующих букв имеют центр симметрии: А, О, М, Х, К ? б) Какие из следующих букв имеют ось симметрии : А, Б, Г, Е, О, F?

Создание проблемных ситуаций через решение задач на сравнение и внимание

8кл. Тема «Осевая и центральная симметрия».

а) Какие из следующих букв имеют центр симметрии: А, О, М, Х, К ?

б) Какие из следующих букв имеют ось симметрии : А, Б, Г, Е, О, F?

Создание проблемных ситуаций через решение задач на сравнение и внимание Задачи на внимание 5-8 классы У Гарри Поттера есть волшебные очки, в которых он видит все зеленое - белым, а все белое - зеленым. Гарри посмотрел через эти очки на прямоугольник, изображенный справа. Что он увидел?

Создание проблемных ситуаций через решение задач на сравнение и внимание

Задачи на внимание 5-8 классы

У Гарри Поттера есть волшебные очки, в которых он видит все зеленое — белым, а все белое — зеленым.

Гарри посмотрел через эти очки на прямоугольник, изображенный справа.

Что он увидел?

Создание проблемных ситуаций через противоречие нового материала старому, уже известному 7 кл. Тема «Формулы сокращённого умножения» Вычисляем: (2  5)²= 2²  5² = 100 (5 : 6)² = 5² : 6² = 25 : 36 (3 + 4)² = 3² + 4² = 9 + 16 = 25 Попробуйте сосчитать по-другому. ( 3 + 4)² =7² = 49 Проблемная ситуация создана . Почему разные результаты? ( 3 +4)² ≠ 3² + 4²

Создание проблемных ситуаций через противоречие нового материала старому, уже известному

7 кл. Тема «Формулы сокращённого умножения»

Вычисляем:

(2  5)²= 2²  5² = 100

(5 : 6)² = 5² : 6² = 25 : 36

(3 + 4)² = 3² + 4² = 9 + 16 = 25

Попробуйте сосчитать по-другому.

( 3 + 4)² =7² = 49

Проблемная ситуация создана .

Почему разные результаты? ( 3 +4)² ≠ 3² + 4²

Создание проблемных ситуаций через выполнение небольших исследовательских заданий

5кл. Тема «Длина окружности».

Ещё древние греки находили длину окружности по формуле C = *d.

d – диаметр окружности. Вопрос : что же такое ?

1. Опоясать стакан ниткой, распрямить нитку, длина нитки примерно

равна длине окружности стакана. Чтобы получить более точный

результат, нужно это проделать несколько раз.

Занесите данные в следующую таблицу:

2. Измерьте диаметр стакана линейкой. Данные занесите в табл.

3. Найдите значение , как неизвестного множителя.

Исследование проведено. Проблема решена.

С1

С2

С3

С сред.

Создание проблемных ситуаций через использование занимательных задани й

7 кл. Тема: «Формулы сокращённого умножения»

( 2y +1) 2 – 4y 2 =9

y = 2

597 2 = (600 – 3) 2 =600 2 -2 х 600 х 3 + 3 2 = 360000 – 3600 + 9 =356409

Создание проблемных ситуаций через решение задач , связанных с жизнью

8кл. Тема «Площадь прямоугольника».

Родители решили поменять входную дверь и заказали в фирме изготовить металлическую дверь. Им предоставили платёжный документ, в правильности которого папа усомнился, а именно в стоимости покраски двери. Попросил своего сына самому рассчитать стоимость данной работы.

Проблемная ситуация : нужно знать площадь двери (площадь прямоугольника) . Причём норма краски на 1 кв.м и стоимость работы покраски 1кв.м даны в документе.

Задача арабского математика XI в

На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Создание проблемных ситуаций через использование занимательных заданий

. 9 кл. Тема «Сумма n-первых членов арифметической прогрессии»

Изучение вопроса о сумме n–первых членах арифметической прогрессии в 9-ом классе начинаю с рассказа: “Примерно 200 лет тому назад в одной из школ Германии на уроке математики учитель предложил ученикам найти сумму первых 100 натуральных чисел. Все принялись подряд складывать числа, а один ученик почти сразу же дал правильный ответ. Имя этого ученика Карл Фридрих Гаусс. В последствии он стал великим математиком. Как удалось Гауссу так быстро подсчитать эту сумму?”

Проблемная ситуация: как найти быстро сумму первых 100 натуральных чисел?

Решение проблемы (1 + 100)  50 = 5050

Создание проблемных ситуаций через различные способы решения одной задачи

Пример№1.8кл.Тема:«Квадратные уравнения»

Решить уравнение 3х 2 + 2х – 1 = 0 , используя различные способы.

1 способ . По общей формуле . D = b 2 – 4ac; D = 4 + 12 = 16 = 4 2. . Ответ: -1; 1/3. 2способ. По формуле с чётным коэффициентом b . D 1 = ( b/ 2) 2 – ac; D 1 = 1 + 3 = 4 = 2 2. Ответ: -1; 1/3. 3 способ. По теореме Виета

4 способ . Из условия , если а + с = b, то х 1 = — 1; х 2 = — с / а

5 способ . Выделение полного квадрата.

6 способ . Разложение на множители способом группировки 7 способ . Графический.

8 способ . Приведение к виду ( f( x) ) 2 = ( g(x) ) 2 .

Определение степени с рациональным показателем. (= = - = -2 (=( == = 2 Проблема: почему разные ответы.

Определение степени с

рациональным показателем.

(= = — = -2

(=( == = 2

Проблема: почему разные ответы.

Подсказка №1. = 3∙ Решите систему уравнений: Подсказка №2. Умножить первое уравнение на (-2) и сложить со вторым Подсказка №3. Выразить из первого уравнения или и подставить во второе уравнение Подсказка №4 Заменить дроби и другими буквами

Подсказка №1.

= 3∙

Решите систему уравнений:

Подсказка №2.

Умножить первое

уравнение на (-2)

и сложить

со вторым

Подсказка №3.

Выразить из первого

уравнения

или и подставить

во второе уравнение

Подсказка №4

Заменить дроби

и другими

буквами

Найдите ошибки в решении системы уравнений. Ответ:(-1,25; - 3). + ∙ (-2 ) 11y = -33 y = -3

Найдите ошибки в решении системы уравнений.

Ответ:(-1,25; — 3).

∙ (-2 )

11y = -33

y = -3

Найти соответствие между системой уравнений и парой чисел, которая является её решением Нажмите на клавишу изображением ладони При правильно выбранном соответствии пара клавиш окрашивается в одинаковый цвет.

Найти соответствие между системой

уравнений и парой чисел, которая является её решением

Нажмите на клавишу изображением ладони

При правильно выбранном соответствии пара клавиш окрашивается в одинаковый цвет.

БАЙКАЛ Тема: -7 - М 3 - А -10 - Й 1 - К 8 - Л 0,2 - Б 20 - Е 3 0,2 5 + : -10 8 - -2 8 -10 - * -1/2 : -10 -2/3 1 3

БАЙКАЛ

Тема:

-7 — М

3 — А

-10 — Й

1 — К

8 — Л

0,2 — Б

20 — Е

0,2

-10

—

-2

-10

—

-1/2

-10

-2/3

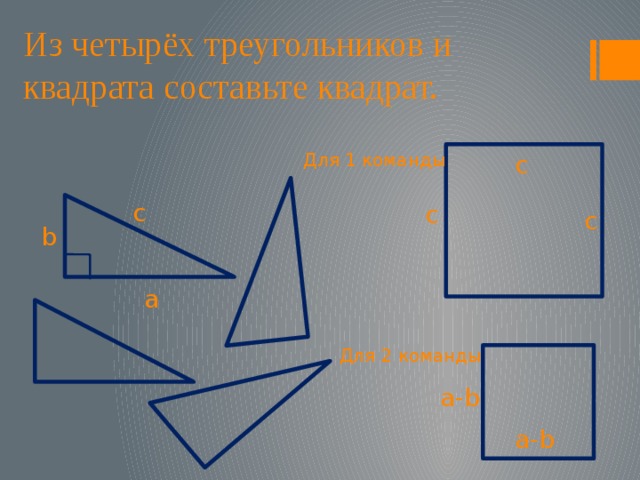
Из четырёх треугольников и квадрата составьте квадрат. Для 1 команды c c c c b a Для 2 команды а-b а-b

Из четырёх треугольников и квадрата составьте квадрат.

Для 1 команды

Для 2 команды

а-b

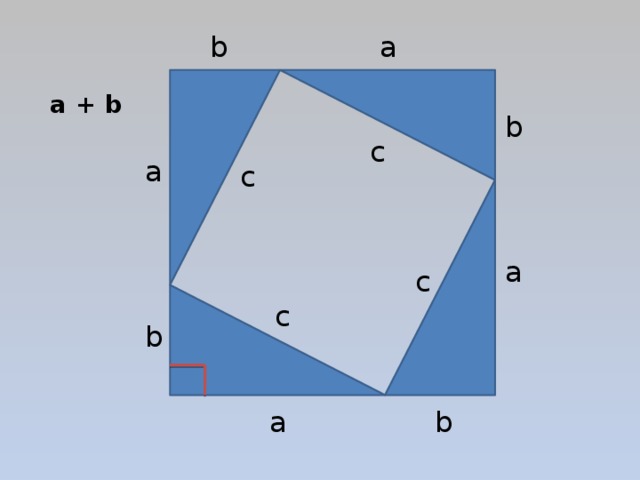
a b a + b b c a c a c c b b a

a + b

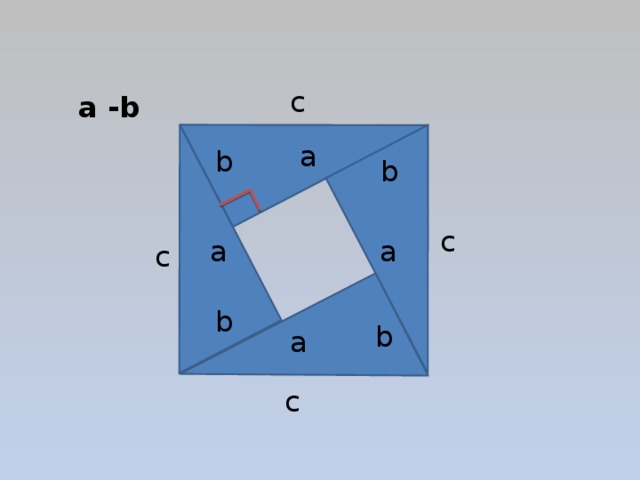
c a -b a b b c a a c b b a c

a -b

Запишите площадь полученной фигуры c 2 = 4  ab + (a -b) 2 c 2 = 2ab + a 2 - 2ab + b 2 (a+b) 2 =4  ab + c 2 a 2 +b 2 +2ab = 2ab + c 2 a 2 +b 2 = c 2 a 2 +b 2 = c 2 Доказательство индийского математика Бхаскары (труд «Венец науки») Доказательство Пифагора

Запишите площадь полученной фигуры

c 2 = 4  ab + (a -b) 2

c 2 = 2ab + a 2 — 2ab + b 2

(a+b) 2 =4  ab + c 2

a 2 +b 2 +2ab = 2ab + c 2

a 2 +b 2 = c 2

Доказательство индийского математика Бхаскары (труд «Венец науки»)

Доказательство Пифагора

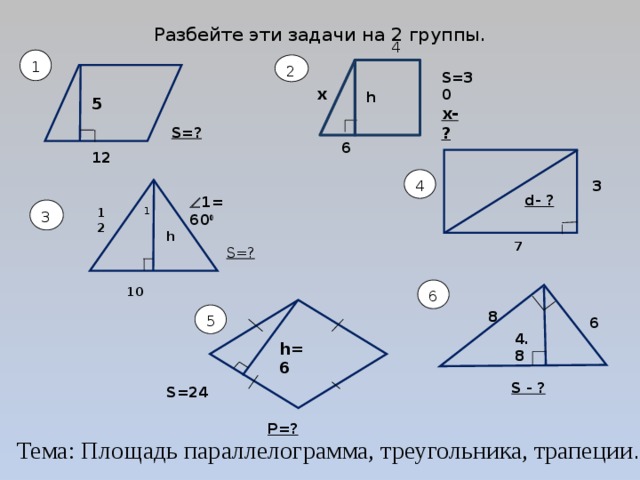
Разбейте эти задачи на 2 группы. 4 1 2 S=30 x h 5 x-? S=? 6 12 4 3 d- ?  1=60 0 3 12 1 h 7 S=? 6 10 8 5 6 4.8 h=6 S - ? S=24 Р=? Тема: Площадь параллелограмма, треугольника, трапеции .

Разбейте эти задачи на 2 группы.

S=30

x-?

S=?

d- ?

 1=60 0

S=?

4.8

h=6

S — ?

S=24

Р=?

Тема: Площадь параллелограмма, треугольника, трапеции .

1 группа(можем решить): 1, 3, 5 2 группа(пока не можем решить): 2, 4, 6 Почему не можем решить задачи из 2-ой группы?

1 группа(можем решить): 1, 3, 5

2 группа(пока не можем решить): 2, 4, 6

Почему не можем решить задачи из 2-ой группы?

Практическая работа . Исследование взаимного расположения графиков линейных функций. Учитель утверждает , что графики функций y = 2x+5 и y = 2x-3 параллельны, а y = 2x+5 и y = - 6x+5 пересекаются в т (0;5). Верно ли это? Проблема : выяснить как зависит взаимное расположение графиков линейных функций от коэффициентов k и b.

Практическая работа . Исследование взаимного расположения графиков линейных функций.

Учитель утверждает , что графики функций

y = 2x+5 и y = 2x-3 параллельны, а

y = 2x+5 и y = — 6x+5 пересекаются в т (0;5).

Верно ли это?

Проблема : выяснить как зависит взаимное расположение графиков линейных функций от коэффициентов k и b.

Сильные стороны проблемного обучения Способствует развитию познавательной активности, осознанности знаний, предупреждает появление формализма, бездумности. Обеспечивает более прочное усвоение знаний; Развивает аналитическое мышление. Ориентирует на комплексное использование знаний. Приучает учащихся, сталкиваясь с противоречиями, разбираться в них, искать решение.

Сильные стороны проблемного обучения

Способствует развитию познавательной активности, осознанности знаний, предупреждает появление формализма, бездумности.
Обеспечивает более прочное усвоение знаний;
Развивает аналитическое мышление.
Ориентирует на комплексное использование знаний.
Приучает учащихся, сталкиваясь с противоречиями, разбираться в них, искать решение.

Слабые стороны проблемного обучения

Значительно больший расход времени на изучение учебного материала;
Слабая эффективность при усвоении принципиально новых разделов учебного материала, где не может быть применен принцип апперцепции (опоры на прежний опыт);
При изучении сложных тем, где крайне необходимо объяснение учителем, а самостоятельный поиск оказывается недоступным для большинства школьников.

Рекомендации учителям по созданию проблемных ситуаций на уроке

Подводить к противоречию с уже известным и предлагать самим находить способ разрешения.
Побуждать делать сравнения, обобщения, выводы.
Создавать ситуации включения, используя задания, связанные с их жизненным опытом.
Использовать задачи с заведомо допущенными ошибками.
Предлагать практические исследовательские задания.
Отыскивать различные способы решения одной и той же задачи.
Излагать различные точки зрения на один и тот же вопрос.
Учить составлять задачи по статистическим данным своего населённого пункта.
Использовать тесты с выбором правильного ответа.

Спасибо за внимание!

Спасибо за внимание!

Источник

1.

Разработала учитель математики
МКОУ Рождественская СОШ
Филиппова Екатерина Леонидовна

2.

Подготовка учителя к уроку – это планирование
урока, продумывание и составление плана и
конспекта урока. Безусловно, план урока
необходим каждому учителю. Но перед
составлением плана урока я всегда задумываюсь.
С одной стороны, план урока – это личный
документ учителя. С другой стороны, план урока –
это мечта учителя, которая завтра будет или
осуществлена, или нет.

3.

Проблемное обучение, в первую очередь,
включает в себя создание проблемных
ситуаций

4. Создание проблемных ситуаций через умышленно допущенные учителем ошибки

Решаются задачи недостаточными или
избыточными исходными данными; с
неопределенностью в постановке вопроса; с
противоречивыми данными; с заведомо
допущенными ошибками; с ограниченным
временем решения.

5. «Обманные задачи»:

1. Постройте прямоугольник со сторонами 2, 3 и 5 см.
2. Больший угол треугольника равен 50°. Найдите
остальные углы.
3. Две стороны треугольника перпендикулярны третьей.
Определите вид треугольника.
4. Внешний угол при основании равнобедренного
треугольника равен 75°. Найдите углы треугольника.
5. Диагональ ромба в два раза больше его стороны.
Найдите углы ромба.

6. «Обманные задачи»:

Пример 7 кл. Тема «Линейные уравнения с одной
переменной».
Решаю быстро уравнение:
(5Х+ х 2 – 3 = 19
10Х + 16 – 3 = 19
10Х = 19 – 16 – 3
10Х = 0
Х=0
Естественно при проверке ответ не сходится

7. Создание проблемных ситуаций через выполнение практических заданий

7 класс. Темы: «Построение треугольника по трем
элементам», «Неравенство треугольника».
Теорему о неравенстве треугольника ввожу при изучении темы
«Построение треугольника по трем элементам», решая задачу на
построение треугольника по трем его сторонам. Предлагаю
ученикам построить с помощью циркуля и линейки треугольник
со сторонами: а) 5см; 6см; 7см; б) 9см; 5см; 6см; в) 1см; 2см; 3см;
г) 3см; 4см; 10см.
Ребята работают самостоятельно и приходят к тому, что построить
треугольник в последних двух примерах не удается.
Возникает проблема: «При каких же условиях существует
треугольник»? Чертежи, полученные учащимися при решении
этой задачи дают возможность легко сделать вывод: «Каждая
сторона треугольника меньше суммы двух других сторон».
Доказываем полученную теорему.

8. Создание проблемных ситуаций через решение задач на сравнение и внимание

Пример. 8кл. Тема «Осевая и центральная
симметрия».
а) Какие из следующих букв имеют центр
симметрии: А, О, М, Х, К ?
б) Какие из следующих букв имеют ось симметрии :
А, Б, Г, Е, О, F?

9. Создание проблемных ситуаций через противоречие нового материала старому, уже известному

Пример№1. 7 кл. Тема «Формулы сокращённого
умножения»
Вычисляем (2 х 5)²= 2² х5² = 100
(3 х 4)²= 3² х 4² = 9 х 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25 Попробуйте сосчитать подругому.
( 3 + 4)² =7² = 49
Проблемная ситуация создана. Почему разные
результаты?
( 3 +4)² ≠ 3² + 4²

10. Создание проблемных ситуаций через выполнение небольших исследовательских заданий

Пример. 5кл. Тема «Длина окружности».
Ещё древние греки находили длину окружности по формуле C = П*d.
d – диаметр окружности. Вопрос : что же такое П?
1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно
равна длине окружности стакана. Чтобы получить более точный
результат, нужно это проделать несколько раз.
Занесите данные в следующую таблицу:
С1
С2
С3
С сред. Д
П
2. Измерьте диаметр стакана линейкой. Данные занесите в табл.
3. Найдите значение П, как неизвестного множителя.
Исследование проведено. Проблема решена.

11. Сильные стороны проблемного обучения

Способствует развитию познавательной активности,
осознанности знаний, предупреждает появление формализма,
бездумности.
Обеспечивает более прочное усвоение знаний;
Развивает аналитическое мышление.
Способствует сделать учебную деятельность для учащихся более
привлекательной, основанной на постоянных трудностях.
Ориентирует на комплексное использование знаний.
Приучает учащихся сталкиваться с противоречиями, разбираться
в них, искать решение.

12. Слабые стороны проблемного обучения

Значительно большие расходы времени на изучение учебного
материала;
Недостаточная эффективность их при решении задач
формирования практических умений и навыков, особенно
трудового характера, где показ и подражание имеют большое
значение
Слабая эффективность их при усвоении принципиально новых
разделов учебного материала, где не может быть применен
принцип апперцепции (опоры на прежний опыт);
При изучении сложных тем, где крайне необходимо объяснение
учителем, а самостоятельный поиск оказывается недоступным для
большинства школьников.

13. Спасибо за внимание!

Источник

1.

2.

3.

4. Создание проблемных ситуаций через умышленно допущенные учителем ошибки

5. «Обманные задачи»:

6. «Обманные задачи»:

7. Создание проблемных ситуаций через выполнение практических заданий

8. Создание проблемных ситуаций через решение задач на сравнение и внимание

9. Создание проблемных ситуаций через противоречие нового материала старому, уже известному

10. Создание проблемных ситуаций через выполнение небольших исследовательских заданий

11. Сильные стороны проблемного обучения

12. Слабые стороны проблемного обучения

13. Спасибо за внимание!

Возможно, вам также будет интересно: