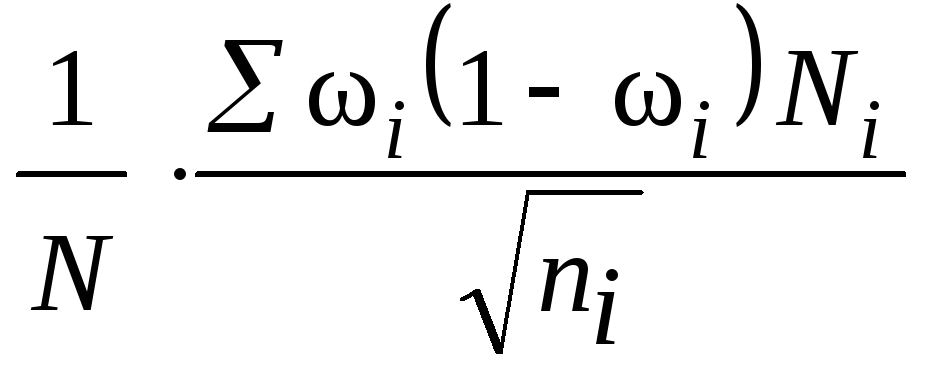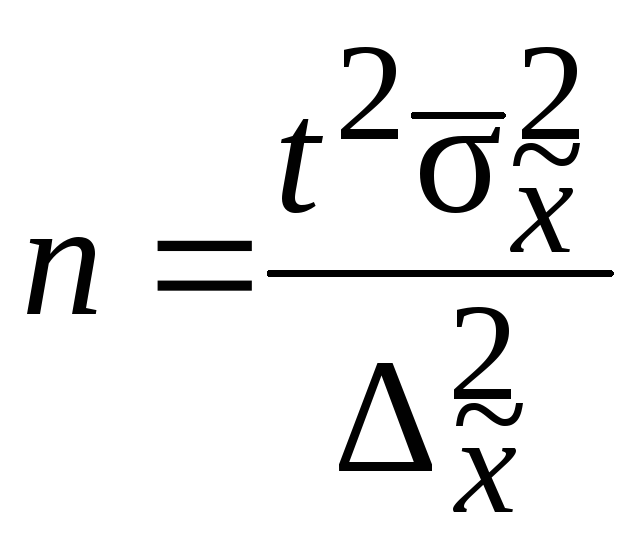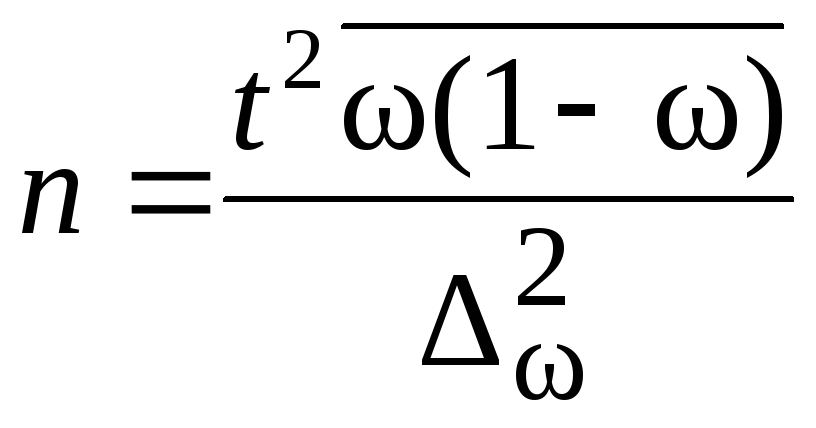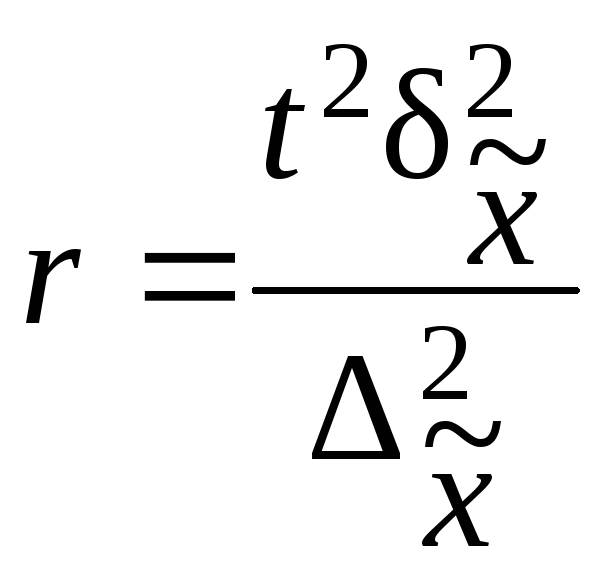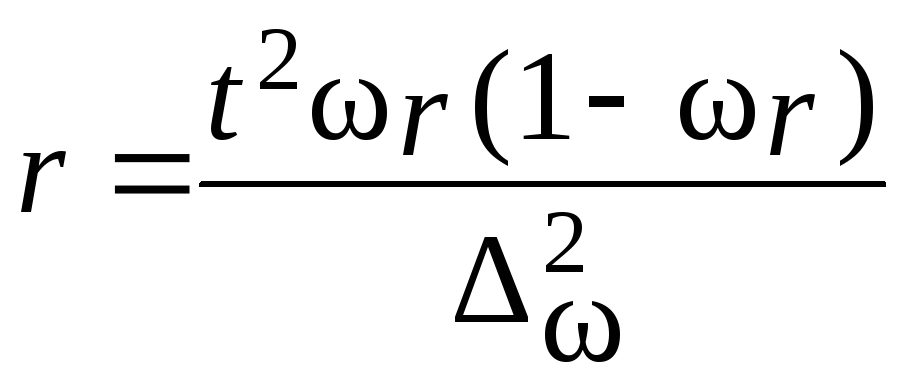Случайные ошибки репрезентативности возникают при - Ремонт и установка крупной бытовой техники

2.4. Точность статистического наблюдения

Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.

Различают две группы ошибок:

ошибки регистрации;
ошибки репрезентативности.

Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.

Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.

Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.

Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.

Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».

Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.

Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.

Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).

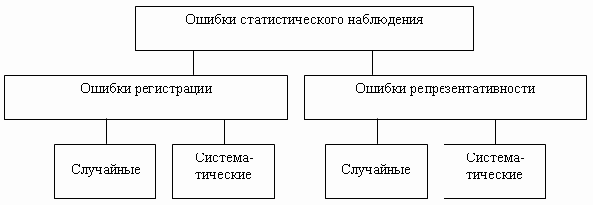
Виды ошибок статистического наблюдения

Рис.
2.1.
Виды ошибок статистического наблюдения

Для повышения точности наблюдения необходимо:

правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
иметь хорошо обученный персонал для проведения обследования;
строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.

Источник

Расхождения
между величиной какого-либо показателя,
найденного посредством статистического
наблюдения, и действительными его
размерами называются ошибками
наблюдения.В зависимости от
причин возникновения различают ошибки
регистрации и ошибки репрезентативности.

Ошибки
регистрациивозникают в результате
неправильного установления фактов или
ошибочной записи в процессе наблюдения
или опроса. Они бывают случайными или
систематическими. Случайные ошибки
регистрации могут быть допущены как
опрашиваемыми в их ответах, так и
регистраторами. Систематические ошибки
могут быть и преднамеренными, и
непреднамеренными. Преднамеренные –
сознательные, тенденциозные искажения
действительного положения дела.
Непреднамеренные вызываются различными
случайными причинами (небрежность,
невнимательность).

Ошибки
репрезентативности(представительности)
возникают в результате неполного
обследования и в случае, если обследуемая
совокупность недостаточно полно
воспроизводит генеральную совокупность.
Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности
– это отклонения, возникающие при
несплошном наблюдении из-за того, что
совокупность отобранных единиц наблюдения
(выборка) неполно воспроизводит всю
совокупность в целом. Систематические
ошибки репрезентативности – это
отклонения, возникающие вследствие
нарушения принципов случайного отбора
единиц. Ошибки репрезентативности
органически присущи выборочному
наблюдению и возникают в силу того, что
выборочная совокупность не полностью
воспроизводит генеральную. Избежать
ошибок репрезентативности нельзя,
однако, пользуясь методами теории
вероятностей, основанными на использовании
предельных теорем закона больших чисел,
эти ошибки можно свести к минимальным
значениям, границы которых устанавливаются
с достаточно большой точностью.

Ошибки
выборки –разность между
характеристиками выборочной и генеральной
совокупности. Для среднего значения
ошибка будет определяться по формуле

(7.1)

где

Величина
называетсяпредельной ошибкойвыборки.

Предельная
ошибка выборки – величина случайная.
Исследованию закономерностей случайных
ошибок выборки посвящены предельные
теоремы закона больших чисел. Наиболее
полно эти закономерности раскрыты в
теоремах П. Л. Чебышева и А. М. Ляпунова.

Теорему П.
Л. Чебышева применительно к
рассматриваемому методу можно
сформулировать следующим образом: при
достаточно большом числе независимых
наблюдений можно с вероятностью, близкой
к единице (т. е. почти с достоверностью),
утверждать, что отклонение выборочной
средней от генеральной будет сколько
угодно малым. В теореме П. Л. Чебышева
доказано, что величина ошибки не должна
превышать.
В свою очередь величина,
выражающая среднее квадратическое
отклонение выборочной средней от
генеральной средней, зависит от
колеблемости признака в генеральной
совокупностии числа отобранных единицn. Эта
зависимость выражается формулой

,
(7.2)

где
зависит также от способа производства
выборки.

Величину
=называютсредней ошибкой выборки. В
этом выражении– генеральная дисперсия,n– объем
выборочной совокупности.

Рассмотрим, как
влияет на величину средней ошибки число
отбираемых единиц n. Логически
нетрудно убедиться, что при отборе
большого числа единиц расхождения между
средними будут меньше, т. е. существует
обратная связь между средней ошибкой
выборки и числом отобранных единиц. При
этом здесь образуется не просто обратная
математическая зависимость, а такая
зависимость, которая показывает, что
квадрат расхождения между средними
обратно пропорционален числу отобранных
единиц.

Увеличение
колеблемости признака влечет за собой
увеличение среднего квадратического
отклонения, а следовательно, и ошибки.
Если предположить, что все единицы будут
иметь одинаковую величину признака, то
среднее квадратическое отклонение
станет равно нулю и ошибка выборки
также исчезнет. Тогда нет необходимости
применять выборку. Однако следует иметь
в виду, что величина колеблемости
признака в генеральной совокупности
неизвестна, поскольку неизвестны размеры
единиц в ней. Можно рассчитать лишь
колеблемость признака в выборочной
совокупности. Соотношение между
дисперсиями генеральной и выборочной
совокупности выражается формулой

Поскольку
величина
при достаточно большихnблизка к
единице, можно приближенно считать, что
выборочная дисперсия равна генеральной
дисперсии, т. е.

Следовательно,
средняя ошибка выборки показывает,
какие возможны отклонения характеристик
выборочной совокупности от соответствующих
характеристик генеральной совокупности.
Однако о величине этой ошибки можно
судить с определенной вероятностью. На
величину вероятности указывает множитель

Теорема А.
М. Ляпунова. А. М. Ляпунов доказал,
что распределение выборочных средних
(следовательно, и их отклонений от
генеральной средней) при достаточно
большом числе независимых наблюдений
приближенно нормально при условии, что
генеральная совокупность обладает
конечной средней и ограниченной
дисперсией.

Математически
теорему Ляпуноваможно записать
так:

(7.3)

где

,
(7.4)

где – математическая постоянная;

–предельная ошибка выборки,которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.

Значения этого
интеграла для различных значений
коэффициента доверия tвычислены и
приводятся в специальных математических
таблицах. В частности, при:

Поскольку tуказывает на вероятность расхождения,
т. е. на вероятность того, на какую
величину генеральная средняя будет
отличаться от выборочной средней, то
это может быть прочитано так: с вероятностью
0,683 можно утверждать, что разность между
выборочной и генеральной средними не
превышает одной величины средней ошибки
выборки. Другими словами, в 68,3 % случаев
ошибка репрезентативности не выйдет
за пределыС вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает(т. е. в 95 % случаев). С вероятностью
0,997, т. е. довольно близкой к единице,
можно ожидать, что разность между
выборочной и генеральной средней не
превзойдет трехкратной средней ошибки
выборки и т. д.

Логически связь
здесь выглядит довольно ясно: чем больше
пределы, в которых допускается
возможная ошибка, тем с большей
вероятностью судят о ее величине.

Зная выборочную
среднюю величину признака
и предельную ошибку выборки,
можно определить границы (пределы),
в которых заключена генеральная
средняя

(7.5)

1.
Собственно-случайная выборка–
этот способ ориентирован на выборку
единиц из генеральной совокупности без
всякого расчленения на части или группы.
При этом для соблюдения основного
принципа выборки – равной возможности
всем единицам генеральной совокупности
быть отобранным – используются схема
случайного извлечения единиц путем
жеребьевки (лотереи) или таблицы случайных
чисел. Возможен повторный и бесповторный
отбор единиц

Средняя ошибка
собственно-случайной выборки
представляет собой среднеквадратическое
отклонение возможных значений выборочной
средней от генеральной средней. Средние
ошибки выборки при собственно-случайном
методе отбора представлены в табл. 7.2.

Таблица 7.2

Средняя ошибка выборки μ	При отборе
повторном	бесповторном
Для средней
Для доли

В таблице
использованы следующие обозначения:

– дисперсия выборочной совокупности;

– численность выборки;

– численность генеральной совокупности;

– выборочная доля единиц, обладающих
изучаемым признаком;

– число единиц, обладающих изучаемым
признаком;

– численность выборки.

Для увеличения
точности вместо множителя
следует
брать множитель
,
но при большой численностиNразличие
между этими выражениями практического
значения не имеет.

Предельная
ошибка собственно-случайной выборки
рассчитывается по формуле

,
(7.6)

где t
– коэффициент доверия зависит от
значения вероятности.

Пример.При
обследовании ста образцов изделий,
отобранных из партии в случайном порядке,
20 оказалось нестандартными. С вероятностью
0,954 определите пределы, в которых
находится доля нестандартной продукции
в партии.

Решение.
Вычислим генеральную долю (Р):
.

Доля нестандартной
продукции:
.

Предельная
ошибка выборочной доли с вероятностью
0,954 рассчитывается по формуле (7.6) с
применением формулы табл. 7.2 для доли:

С вероятностью
0,954 можно утверждать, что доля нестандартной
продукции в партии товара находится в
пределах 12 % ≤ P≤ 28 %.

В практике
проектирования выборочного наблюдения
возникает потребность определения
численности выборки, которая необходима
для обеспечения определенной точности
расчета генеральных средних. Предельная
ошибка выборки и ее вероятность при
этом являются заданными. Из формулы
и формул средних ошибок выборки
устанавливается необходимая численность
выборки. Формулы для определения
численности выборки (n) зависят от
способа отбора. Расчет численности
выборки для собственно-случайной выборки
приведен в табл. 7.3.

Таблица 7.3

Предполагаемый отбор	Формулы
для средней	для доли
Повторный
Бесповторный

2.
Механическая выборка– при этом
методе исходят из учета некоторых
особенностей расположения объектов в
генеральной совокупности, их упорядоченности
(по списку, номеру, алфавиту). Механическая
выборка осуществляется путем отбора
отдельных объектов генеральной
совокупности через определенный интервал
(каждый 10-й или 20-й). Интервал рассчитывается
по отношению,
гдеn– численность выборки,N–
численность генеральной совокупности.
Так, если из совокупности в 500 000 единиц
предполагается получить 2 %-ную выборку,
т. е. отобрать 10 000
единиц, то пропорция отбора составитОтбор
единиц осуществляется в соответствии
с установленной пропорцией через равные
интервалы. Если расположение объектов
в генеральной совокупности носит
случайный характер, то механическая
выборка по содержанию аналогична
случайному отбору. При механическом
отборе применяется только бесповторная
выборка [1, 5–10].

Средняя ошибка
и численность выборки при механическом
отборе подсчитывается по формулам
собственно-случайной выборки (см.
табл. 7.2 и 7.3).

3.
Типическая выборка, при котрой
генеральная совокупность делится по
некоторым существенным признакам на
типические группы; отбор единиц
производится из типических групп. При
этом способе отбора генеральная
совокупность расчленяется на однородные
в некотором отношении группы, которые
имеют свои характеристики, и вопрос
сводится к определению объема выборок
из каждой группы. Может бытьравномерная
выборка– при этом способе из каждой
типической группы отбирается одинаковое
число единицТакой подход оправдан лишь при равенстве
численностей исходных типических групп.
При типическом отборе, непропорциональном
объему групп, общее число отбираемых
единиц делится на число типических
групп, полученная величина дает
численность отбора из каждой типической
группы.

Более совершенной
формой отбора является пропорциональная
выборка. Пропорциональной называется
такая схема формирования выборочной
совокупности, когда численность выборок,
взятых из каждой типической группы в
генеральной совокупности, пропорциональна
численностям, дисперсиям (или комбинированно
и численностям, и дисперсиям). Условно
определяем численность выборки в 100
единиц и отбираем единицы из групп:

– пропорционально
численности их генеральной совокупности
(табл. 7.4). В таблице
обозначено:

N_i– численность типической группы;

d_j– доля (N_i/N);

N– численность
генеральной совокупности;

n_i– численность выборки из типической
группы вычисляется:

, (7.7)

n – численность выборки из генеральной
совокупности.

Таблица
7.4

Группы	N_i	d_j	n_i
1	300	0,3	30
2	500	0,5	50
3	200	0,2	20
	1000	1,0	100

–
пропорционально среднему квадратическому
отклонению(табл. 7.5).

здесь
_i– среднее
квадратическое отклонение типических
групп;

n_i
– численность выборки из типической
группы вычисляется по формуле

(7.8)

Таблица
7.5

N_i	_i		n_i
300	5	0,25	25
500	7	0,35	35
200	8	0,40	40
1000	20	1,0	100

–
комбинированно (табл. 7.6).

Численность
выборки вычисляется по формуле

. (7.9)

Таблица 7.6

	_i	_iN_i
300	5	1500	0,23	23
500	7	2100	0,53	53
200	8	1600	0.24	24
1000	20	6600	1,0	100

При проведении
типической выборки непосредственный
отбор из каждой группы проводится
методом случайного отбора.

Средние ошибки
выборки рассчитываются по формулам
табл. 7.7 в зависимости от способа отбора
из типических групп.

Таблица 7.7

Способ отбора	Повторный	Бесповторный
для средней	для доли	для средней	для доли
Непропорциональный объему групп
Пропорциональный объему групп
Пропорциональный колеблемости в группах (является наивыгоднейшим)

здесь
– средняя из внутригрупповых дисперсий
типических групп;

– доля единиц, обладающих изучаемым
признаком;

– средняя из внутригрупповых дисперсий
для доли;

– среднее квадратическое отклонение
в выборке изi-й типической группы;

– объем выборки из типической группы;

– общий объем выборки;

–
объем типической группы;

– объем генеральной совокупности.

Численность
выборки из каждой типической группы
должна быть пропорциональна среднему
квадратическому отклонению в этой
группе
.Расчет численности
производится по формулам, приведенным
в табл. 7.8.

Таблица 7.8

	Повторный	Бесповторный
Для определения средней
Для определения доли

4. Серийная
выборка– удобена в тех случаях,
когда единицы совокупности объединены
в небольшие группы или серии. При серийной
выборке генеральную совокупность делят
на одинаковые по объему группы – серии.
В выборочную совокупность отбираются
серии. Сущность серийной выборки
заключается в случайном или механическом
отборе серий, внутри которых производится
сплошное обследование единиц. Средняя
ошибка серийной выборки с равновеликими
сериями зависит от величины только
межгрупповой дисперсии. Средние ошибки
сведены в табл. 7.9.

Таблица 7.9

Способ отбора серии	Формулы
для средней	для доли
Повторный
Бесповторный

Здесь
R– число серий в генеральной
совокупности;

r – число
отобранных серий;

– межсерийная (межгрупповая) дисперсия
средних;

– межсерийная (межгрупповая) дисперсия
доли.

При серийном
отборе необходимую численность отбираемых
серий определяют так же, как и при
собственно-случайном методе отбора.

Расчет численности
серийной выборки производится по
формулам, приведенным в табл. 7.10.

Таблица 7.10

	Повторный	Бесповторный
Для определения среднего признака
Для определения доли

Пример.В
механическом цехе завода в десяти
бригадах работает 100 рабочих. В целях
изучения квалификации рабочих была
произведена 20 %-ная серийная бесповторная
выборка, в которую вошли две бригады.
Получено следующее распределение
обследованных рабочих по разрядам:

Рабочие

Разряды

рабочих
в бригаде 1

Разряды

рабочих
в бригаде 2

Рабочие

Разряды
рабочих
в бригаде 1

Разряды
рабочих
в бригаде 2

Необходимо
определить с вероятностью 0,997 пределы,
в которых находится средний разряд
рабочих механического цеха.

Решение.
Определим выборочные средние по
бригадам и общую среднюю как среднюю
взвешенную из групповых средних:

Определим
межсерийную дисперсию по формулам
(5.25):

Рассчитаем
среднюю ошибку выборки по формуле табл.
7.9:

Вычислим
предельную ошибку выборки с вероятностью
0,997:

С вероятностью
0,997 можно утверждать, что средний разряд
рабочих механического цеха находится
в пределах

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

2.4. Точность статистического наблюдения

Различают две группы ошибок:

ошибки регистрации;
ошибки репрезентативности.

Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.

Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).

Виды ошибок статистического наблюдения

Рис.
2.1.
Виды ошибок статистического наблюдения

Для повышения точности наблюдения необходимо:

правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
иметь хорошо обученный персонал для проведения обследования;
строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.

Ошибка выборки

2.1. Понятие и виды ошибок выборки

Поскольку изучаемая статистическая
совокупность состоит из единиц с
варьирующими признаками, то состав
выборочной совокупности может в той
или иной мере отличаться от состава
генеральной совокупности.

Расхождение
между характеристиками выборки и
генеральной совокупности составляет
ошибку
выборки.

Виды ошибок выборки

Ошибки

выборки

Систематические

Случайные

Ошибки

регистрации

Обусловлены
причинами, действующими в одном
направлении (например, округление
цифр).

Проявляются
в различных направлениях и уравновешивают
друг друга (невнимательность).

Ошибки

репрезентативности

Неправильный,
тенденциозный отбор единиц, без
соблюдения принципа случайности
(выбираются преднамеренно худшие или
лучшие единицы).

Несмотря
на принцип случайности отбора единиц,
все же имеются расхождения между
характеристиками выборки и генеральной
совокупности (но эти ошибки объективны
и не связаны с волей наблюдателя).

Основная
задача выборочного метода – изучение
случайных ошибок репрезентативности.

2.2. Средняя ошибка выборки

Случайная ошибка
репрезентативности зависит от следующих
фактов (при этом считается, что ошибок
регистрации нет):

Чем
больше численность выборки при прочих
равных условиях, тем меньше величина
ошибки выборки, т.е. ошибка выборки
обратно пропорциональна ее численности.
Чем
меньше варьирование признака, тем
меньше ошибка выборки. Если признак
совсем не варьирует, а, следовательно,
величина дисперсии равна нулю, то ошибки
выборки не будет, т.к. любая единица
совокупности будет совершенно точно
характеризовать всю совокупность по
этому признаку. Таким образом, ошибка
выборки прямо пропорциональна величине
дисперсии.

В
математической статистике доказывается,
что величина средней ошибки случайной
повторной выборки может быть определена
по формуле

(6.1)

Однако
следует иметь в виду, что величина
дисперсии в генеральной совокупности

²
нам не известна, т.к. наблюдение выборочное.
Мы можем рассчитать лишь дисперсию в
выборочной совокупности S².
Соотношение между дисперсиями генеральной
и выборочной совокупности выражается
формулой:

(6.2)

Если
n
велико, следовательно

Таким
образом, можно приблизительно считать,
что выборочная дисперсия равна генеральной
дисперсии.


²=
S²

И формула средней ошибки повторной
выборки (6.1.) примет вид:

(6.3)

Но
здесь мы рассмотрели только ошибку
выборки для средней величины интересующего
признака. Существует также показатель
доли единиц с интересующим признаком.
Расчет ошибки этого показателя имеет
свои особенности.

Дисперсия
для показателя доли признака определяется
по формуле:

S²=(1-)
(6.4)

Тогда средняя ошибка повтора выборки
для показателя доли признака будет
равна:

(6.5)

Доказательство
формул (6.3) и (6.5) исходит из схемы повторной
выборки. Обычно же выборку организуют
бесповторным способом. Т.к. при бесповторном
отборе численность генеральной
совокупности N
в коде выборки сокращается, то в формулы
ошибки выборки включают дополнительный
множитель
,
и формулы
принимают вид:

(6.6)

(6.7)

Пример
1. Определим, на сколько отличаются
выборочные и генеральные показатели
по данным 10%-ной бесповторной выборки
успеваемости студентов.

Оценка, х_i	Число студентов в выборке, f_i
2	9
3	27
4	54
5	10
Итого	100

Расчет ошибки бесповторной выборки для
средней величины:

n
= 100 N
= 1000

Найдем выборочную
дисперсию по формуле:

Здесь
не известна величина
,
которую можно найти как обычную среднюю
взвешенную величину:

Таким
образом,

Т.е.
можно сказать, что средний балл всех
студентов ()
равен 3,650,07

Теперь
рассчитаем долю студентов в генеральной
совокупности, обучающихся на «4» и «5».

Найдем по выборке
долю студентов, получивших оценки «4»
и «5».

(или
64%)

Расчет
ошибки бесповторной выборки для доли
производится по формуле:

(или
4,5%)

Таким образом, доля студентов, обучающихся
на «4» и «5» по генеральной совокупности
(P) составляет
0,640,045 (или 64%4,5%).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Во-первых, как это ни парадоксально, это повышение точности данных уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации. Правда, за счет неполноты охвата единиц возникает ошибка репрезентативности, т. е. представительности выборочных данных. Но даже взятые вместе ошибка наблюдения для выборки плюс ошибка репрезентативности обеспечивают большую точность выборочных данных по сравнению с массовым сплошным наблюдением.
[c.156]

Ошибка выборки или, иначе говоря, ошибка репрезентативности — это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна ег = х — ц, выборочной относительной величины гг=р-п, дисперсии едЛ = s1 — а2, коэффициента корреляции ЕГ = г — р.
[c.165]

Если представить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, то показатели отдельных выборок образовали бы ряд возможных значений выборочных средних величин х,, х-,, х3,. … относительных величин / ,, р2, ръ. … дисперсий s, s 2, s . .., и т. д. Каждая выборка имеет свою ошибку репрезентативности. Следовательно, можно построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя для средней, относительной величины и т.д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности. [c.165]

Фактическая ошибка репрезентативности
[c.177]

Фактическая ошибка репрезентативности составляет [c.177]

После проведения выборки рассчитывают возможные ошибки выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.
[c.185]

Так как средняя величина имеет ошибку репрезентативности Ах, то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах
[c.188]

Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.
[c.193]

Расхождение между расчетным и действительным значением изучаемых величин называется ошибкой наблюдения. В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности.
[c.21]

В отличие от ошибок регистрации ошибки репрезентативности характерны только для несплошного наблюдения. Они возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит генеральную совокупность в целом.
[c.22]

Отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности называется ошибкой репрезентативности.
[c.22]

Ошибки репрезентативности также бывают случайными и систематическими. Случайные ошибки репрезентативности возникают, если отобранная совокупность неполно воспроизводит совокупность в целом. Величина этих ошибок может быть оценена.
[c.22]

Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению. Для устранения ошибок наблюдения необходимо осуществить контроль полученной информации.
[c.22]

Поскольку / указывает на вероятность расхождения х-х , т.е. на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ц. С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает 2ц, (т.е. в 95% случаев). С вероятностью 0,997, т.е. довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д. Логически связь здесь выглядит довольно ясно чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине.
[c.132]

Среднее значение удельных приведенных затрат для внутризаводских сетей промышленной канализации на 1 м3 часовой суммарной пропускной способности равно 99,36 руб/м3/ч. Вследствие небольшого объема представленной выборки определили, можно ли пользоваться найденным средним значением, используя для определения ошибки репрезентативности малой выборки критерий t — Стьюдента. . [c.39]

Д, , — ошибка репрезентативности выборки, зависящая от уровня доверительной вероятности [c.147]

Степень варьирования оценивается дисперсией G 2, а ошибка репрезентативности
[c.147]

Разность между результатами выборочного и сплошного наблюдения называется ошибками репрезентативности. На основе применения математики можно заранее рассчитать репрезентативность выборки информации, ее соответствие генеральной совокупности.
[c.481]

Предельная ошибка выборки А= Л ц. Доверительное число t показывает, что расхождение не превышает кратную ему ошибку выборки. С вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной не превысит двух величин средней ошибки выборки, т.е. в 954 случаях ошибка репрезентативности не выйдет за 2ц.
[c.222]

Ошибки наблюдения подразделяются на два вида ошибки регистрации и ошибки репрезентативности.
[c.36]

Ошибки репрезентативности возникают при несплошном обследовании в силу того, что состав отобранной для него части единиц совокупно-
[c.36]

Ошибки репрезентативности. Основные проблемы выборочного наблюдения сводятся к тому, что при его применении могут возникать определенные ошибки. Следовательно, аудиторы вынуждены учитывать риски, свойственные выборочному наблюдению, а также знать, как необходимо минимизировать эти риски. Аудиторы называют это риском ошибочного принятия (непринятия) результатов выборки. При этом в аудиторской практике различают риски первого и второго рода для тестов системы контроля и проверки верности оборотов и сальдо по счетам [там же].
[c.49]

Главные ошибки, возникающие при выборочном наблюдении, — это ошибки репрезентативности. Аудитор обязан обеспечить представительную (репрезентативную) выборку для данной совокупности. Проявляя должную тщательность в работе, он стремится точно установить и зарегистрировать в своей выборке факты хозяйственной жизни экономического субъекта, остатки по счетам, статьи баланса и т.д., но тем не менее по окончании всех
[c.49]

Случайные ошибки репрезентативности. Риск (опасность) возникновения этих ошибок проистекает из собственно случайных обстоятельств (типа арифметических ошибок при отсутствии контроля, описок и т.д.). Но мы сознательно оставляем в стороне и не анализируем здесь тривиальные ошибки наблюдения, которые выражаются, скажем, в описках и которые может допустить любой ассистент аудитора, осуществляющий выборку.
[c.50]

Систематические ошибки репрезентативности. Если же аудитор или его ассистент нарушают принцип случайности при отборе, то они рискуют получить систематические ошибки репрезентативности. Например, из всей совокупности дебиторской задолженности аудитор отобрал только просроченную (такой было 10%) и на основании других свидетельств установил, что половина отобранных им остатков по счетам — это задолженность безнадежная. Если на основе такой выборки аудитор будет считать, что безнадежная задолженность составляет 50% всех дебиторов проверяемого экономического субъекта, то скорее всего он глубоко ошибается (она вполне может быть на уровне, близком к 5%), поскольку уровень вероятности появления безнадежной задолженности намного выше именно в просроченной задолженности. Другими словами, аудитор рискует получить подобные погрешности в тех случаях, когда выборочная совокупность недостаточно точно воспроизводит те особенности и пропорции, которые имеются в проверяемой совокупности.
[c.51]

Систематические ошибки репрезентативности — это неточности, которые аудитор может получить в процессе статистического выборочного наблюдения по вполне определенным причинам. Такие ошибки могут возникнуть как следствие преднамеренного или непреднамеренного искажения информации. Систематические ошибки репрезентативности тоже могут привести к искажению полученных результатов (как в сторону увеличения, так и в сторону уменьшения), по которым аудитор будет судить о всей проверяемой совокупности. Таким образом, в основе систематических ошибок репрезентативности лежит именно выборка, именно сам несплошной характер наблюдения.
[c.51]

Ошибка репрезентативности — разница между результатами выборочного и сплошного наблюдения.
[c.546]

Выборочному обследованию свойственна некоторая погрешность в сравнении со сплошным, которая органически присуща вообще любому выборочному наблюдению. Указанная погрешность или ошибка носит название ошибки репрезентативности.
[c.101]

Выборочной средней и выборочной доле свойственны, как указано выше, ошибки репрезентативности. Теория выборочного метода дает возможность определить средние этих ошибок.
[c.102]

Сравнивая выборочную среднюю с генеральной средней, видим расхождение — 0,8 млн. руб. (11,6—10,8 = = 0,8). Это так называемая ошибка репрезентативности случайного бесповторного отбора.
[c.106]

В среднем объем строительно-монтажных работ по этим трестам составил 10,6 млн. руб. Ошибка репрезентативности — 1,0 млн. руб.
[c.107]

В среднем по 16 отобранным трестам объем строительно-монтажных работ составил 10,5 млн. руб. Ошибка репрезентативности 1,1 млн. руб.
[c.108]

Выше разобраны пять основных способов отбора выборочной совокупности. Каждый из них имеет свою ошибку репрезентативности. Наименьшие ошибки репрезентативности получены при механическом отборе и при случайной выборке и наибольшая — при серийном отборе. В других случаях результаты могут получиться иные. В учебниках по статистике указывается, что теоретически наименьшая ошибка должна наблюдаться при типическом, затем при механическом отборах и случайной выборке. Наибольшая ошибка — при серийном отборе.
[c.108]

Практически при пользовании выборочным методом остаются неизвестными ошибки репрезентативности, так как неизвестна бывает генеральная средняя. В связи с этим необходимо теоретически определить возможную величину этой ошибки.
[c.108]

Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
[c.22]

Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки — принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между
[c.22]

Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности. Ошибки репрезентативности [c.23]

При определении ошибки репрезентативности и объема выборки
[c.16]

Как видно из приведенных расчетов, метод высшей и низшей точек довольно прост в применении. Его цель состоит в том, чтобы спрогнозировать поведение издержек при изменении деловой активности предприятия. Как и в любом прогнозе, здесь существует некоторая вероятность ошибки. Это связано с тем, что значение двух крайних показателей не всегда имеет репрезентативный характер. Поэтому из расчета следует исключать случайные, нехарактерные данные.
[c.64]

Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку.
[c.177]

Ошибки репрезентативности, т.е. расхождения между данными выборочного наблюдения и данными всей совокупности, могут быть получены только при несплошном наблюдении, они про-изводны от самой сути выборочного наблюдения. При этом существуют и, соответственно, аудиторы должны различать две разные группы ошибок репрезентативности случайные и систематические.
[c.50]

В среднем объем по этим 16 трестам к = 12,2 млн. руб. Отклонение от генеральной средней — 0,6 млн. руб. (11,6 — 12,2 — — 0,6). Ошибка репрезентативности случайного повторного итоора получилась в данном случае несколько меньше, чем в бесповторпом.
[c.106]

Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызвано недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400 квартир, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная — в большей пропорции, чем в генеральной совокупности. Пенсионеров, например, можно чаще застать дома, чем студентов-вечерников. При увеличении выборки эта ошибка не устраняется если мы проведем опрос в 800 квартирах или даже во всех квартирах города (сплошной опрос), то полученные данные будут репрезентативны для населения, находящегося дома в момент прихода интервьюера, а не для всех жителей города.
[c.164]

Источник

Ошибка — репрезентативность

Cтраница 1

Ошибки репрезентативности делятся на случайные и систематические. Случайные ошибки возникают вследствие того, что выборочная совокупность недостаточно точно воспроизводит всю совокупность вследствие несплошного характера наблюдения. Случайные ошибки могут быть доведены до незначительных размеров, как это показано далее, а главное, размеры и пределы их можно определить с достаточной точностью на основании закона больших чисел. На этом законе базируется теория выборочного метода.
[1]

Ошибки репрезентативности, т.е. расхождения между данными выборочного наблюдения и данными всей совокупности, могут быть получены только при несплошном наблюдении, они про-изводны от самой сути выборочного наблюдения. При этом существуют и, соответственно, аудиторы должны различать две разные группы ошибок репрезентативности: случайные и систематические.
[2]

Ошибка Д является ошибкой репрезентативности ( представительства) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть ее ( выборка), отобранная случайно. Эту ошибку часто называют случайной ошибкой репрезентативности. Ее не следует путать с систематической ошибкой репрезентативности, появляющейся в результате нарушения принципа случайности при отборе элементов в выборку.
[4]

При прочих равных условиях ошибка репрезентативности возрастает по мере увеличения вариабельности объектов изучаемой совокупности и уменьшается при увеличении объема выборки.
[5]

Разность между результатами выборочного и сплошного наблюдения называется ошибками репрезентативности.
[7]

После проведения выборки рассчитывают возможные ошибки выборочных показателей ( ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.
[8]

Очень часто малоопытный социолог не улавливает разницы между проблемой ошибки репрезентативности выборки и ошибки вывода из данного конкретного распределения в рамках выборочной совокупности.
[9]

Если разность между ошибками регистрации этих видов обследования превысит ошибку репрезентативности, то общая ошибка при несплошном наблюдении может оказаться меньше, чем ошибка регистрации сплошного наблюдения. Особенно вероятен такой результат при выборочном наблюдении.
[10]

Ошибки наблюдения подразделяются на два вида: ошибки регистрации и ошибки репрезентативности.
[11]

Ошибки статистического наблюдения могут быть разбиты на две группы: ошибки репрезентативности и ошибки регистрации.
[12]

Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.
[13]

Поэтому при несплошном обследовании общая ошибка наблюдения является суммой ошибки регистрации и ошибки репрезентативности. Однако это отнюдь не означает, что при любом несплошном наблюдении ошибка будет больше, чем при сплошном.
[14]

Отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности называется ошибкой репрезентативности.
[15]

Страницы:

Источник

2.4. Точность статистического наблюдения

2.4. Точность статистического наблюдения

Ошибка выборки

2.1. Понятие и виды ошибок выборки

Виды ошибок выборки

2.2. Средняя ошибка выборки

Ошибка — репрезентативность

Возможно, вам также будет интересно: