Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 20 мм - Ремонт и установка крупной бытовой техники

Условие

4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.

Отв. 0,96.

математика ВУЗ
10140

Решение

★

Пусть случайная величина Х — ошибка измерения.

Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994

Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006

Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04

Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96

Написать комментарий

Нормальным
называют распределение вероятностей
непрерывной случайной величины X,
плотность которого имеет вид

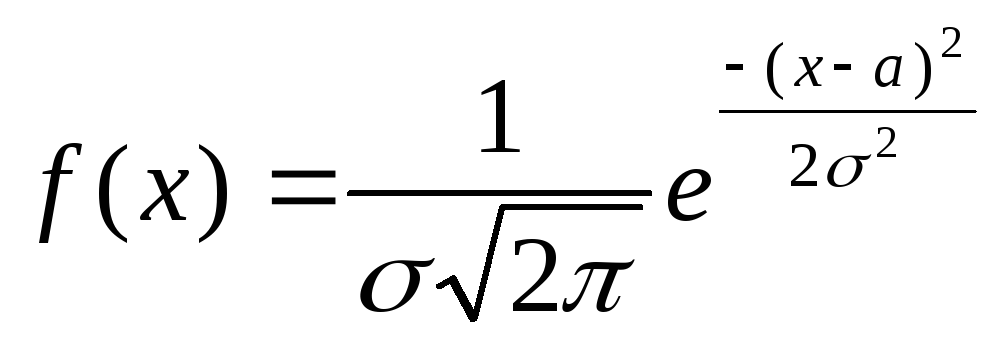где
a-математическое
ожидание,— среднее квадратичное отклонение X.
Вероятность того, что Х примет значение,
принадлежащее интервалу (α,β):

где
— функция Лапласа.

Пример
99.Математическое ожидание и среднее
квадратическое отклонение нормально
распределенной случайной величины Х
примет значение: а) в интервале (-1,2); б)
меньше -1; в) больше 2; г) отличающееся от
своего среднего значения по абсолютной
величине не больше, чем на 1.

Решение.По условию задачи a=0, σ=2, тогда:

а)

б)

в)

г)

Здесь
значения функции Φ(x) были найдены по
таблице и учитывалось, что Φ(-x) = -Φ(x), а
.

100.
Плотность распределения ошибки выходного
параметра РЭА имеет вид

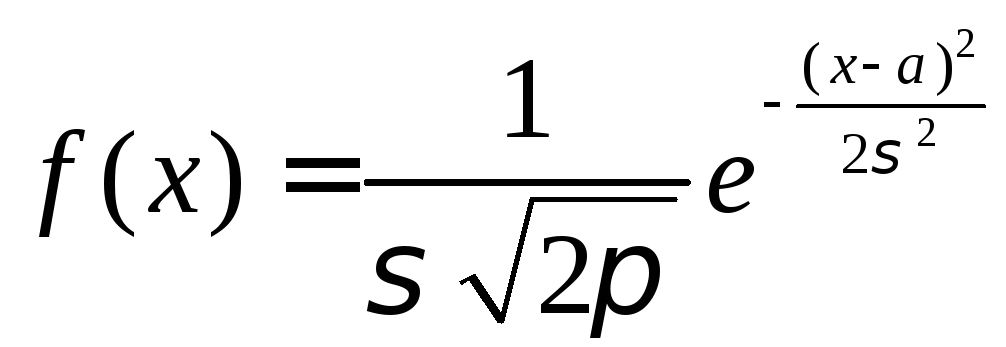Сборочные
операции изменяют числовые характеристики
распределения, не изменяя закона. Что
больше увеличивает вероятность появления
брака: систематическое смещение значения
ошибки выходного параметра на а
единиц или увеличение
дисперсии ошибки на эти же а
единиц?

101.
Математическое ожидание и дисперсия
случайного напряжения с нормальным
распределением равны 10 В и 25 В²
соответственно. Какова вероятность
того, что измеренное значение напряжения

а) будет больше
0?

б) будет находиться
в интервале от 0 до математического
ожидания?

в) будет в два раза
больше математического ожидания?

102.
Широко распространенный метод обнаружения
сигнала в присутствии шума заключается
в установлении определенного порогового
уровня, с которым производится
сравнение результатов измерения
напряжения, включающего полезный сигнал
и шум. Если установленный порог
превышается, то считают, что полезный
сигнал присутствует. Естественно, иногда
и при отсутствии сигнала шум превосходит
этот порог, и такая ситуация называется
ложной тревогой.
Желательно, чтобы
вероятность ложной тревоги была ничтожно
мала. В то же время необходимо, чтобы
результат любого измерения, проведенного
при наличии сигнала, смешанного с шумом,
с большой вероятностью превосходил
установленный порог. Она называется
вероятностью правильного
обнаружения и должна
как можно меньше отличаться от 1.
Пусть шум характеризуется
нормальным распределением с нулевым
математическим ожиданием и дисперсией
1В²,
а установленный порог равен 5 В.

а) Определите
вероятность ложной тревоги.

б) Определите
вероятность правильного обнаружения
сигнала величиной 8 В в присутствии шума
с заданными выше параметрами.

103.
Математическое ожидание и среднее
вадратическое отклонение нормально
распределенной случайной величины X
соответственно равны 20 и 5. Найти
вероятность того, что в результате
испытания X примет значение, заключенное
в интервале (15, 25).

104.
Производится взвешивание некоторого
вещества без систематических ошибок.
Случайные ошибки взвешивания подчинены
нормальному закону со средним
квадратическим отклонением σ = 20 г. Найти
вероятность того, что взвешивание будет
произведено с ошибкой, не превосходящей
по абсолютной величине 10 г.

105. Случайные ошибки
измерения подчинены нормальному закону
со средним квадратическим отклонением
σ = 20 мм и математическим ожиданием а =
0. Найти вероятность того, что из трех
независимых измерений ошибка хотя бы
одного не превзойдет по абсолютной
величине 4 мм.

106.
Вывести «правило трех сигм»: вероятность
того, что абсолютная величина отклонения
нормально распределенной случайной
величины будет меньше утроенного
среднего квадратического отклонения,
равна 0,9973. 107. Станок-автомат изготовляет
валики, причем контролируется их диаметр
X. Считая, что X—нормально распределенная
случайная величина с математическим
ожиданием а=10мм и средним квадратическим
отклонением σ = 0,1 мм, найти интервал,
симметричный относительно математического
ожидания, в котором с вероятностью
0,9973 будут заключены диаметры изготовленных
валиков.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Преподаватель который помогает студентам и школьникам в учёбе.

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16373
		Прошла проверку преподавателем МГУ
		225 руб.

Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением 𝜎 = 20 мм и математическим

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Закажите у меня новую работу, просто написав мне в чат!

Описание заказа и 38% решения ( + фото):

Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением 𝜎 = 20 мм и математическим ожиданием 𝑎 = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм.

Решение

Вероятность того, что модуль отклонения случайной величины Х от своего математического ожидания 𝑎 меньше любого положительного 𝜀, равна где Ф(𝑥) – функция Лапласа. По условию тогда, вероятность того, что при одном независимом измерений ошибка измерения не превзойдет по абсолютной величине 4 мм, равна: Воспользуемся формулой Бернулли. Если производится 𝑛 независимых испытаний, при каждом из которых вероятность осуществления события 𝐴 постоянна и равна 𝑝, а вероятность противоположного события равна , то вероятность того, что при этом событие 𝐴 осуществляется ровно 𝑚 раз, вычисляется по формуле где 𝐶𝑛 𝑚 — число сочетаний из 𝑛 элементов по 𝑚. Для данного случая Вероятность события 𝐴 – из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм, равна: Ответ:

Похожие готовые решения по теории вероятности:

Пачки чая упаковываются автоматически. Масса одной пачки чая распределена по нормальному закону со средним
Диаметр детали – случайная величина, подчиненная нормальному закону с 𝑎 = 5 см и 𝜎 = 0,9 см. Найти вероятность
Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того
Ошибка измерения подчинена нормальному закону с математическим ожиданием, равным 1, и дисперсией, равной 4. Определить вероятность
Определить вероятность того, что случайная ошибка измерения ∆ не превзойдет по абсолютной величине удвоенное значение
Диаметр выпускаемых деталей имеет нормальное распределение со стандартным значением М(Х) и средним квадратическим
Деталь, изготовленная автоматом, считается бракованной, если отклонение ее контролируемого размера Х от номинала превышает
Ошибка взвешивания – случайная величина, распределенная по нормальному закону с математическим ожиданием, равным нулю

Дана выборка 1 1 3 5 4 3 2 1 1 6 3 4 4 5 0 7 5 3 0 4 Составить статистический ряд частот, статистический ряд
Дана выборка 1 3 3 1 4 1 2 3 1 5 3 4 4 5 2 6 2 3 3 4 Составить статистический ряд частот, статистический ряд
Дана выборка 2 3 3 5 4 2 2 1 4 6 1 4 4 5 2 7 5 5 7 2 Составить статистический ряд частот, статистический ряд
Дана выборка -2 3 3 5 4 -1 2 -1 1 0 3 4 4 0 2 7 5 3 3 0 Составить статистический ряд частот, статистический ряд

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,607
гуманитарные
33,643
юридические
17,916
школьный раздел
611,340
разное
16,895

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

2. Пусть [math]X[/math]— ошибка измерения, [math]sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = Pleft( {left| X right| < 2} right) = Pleft( {left| {frac{X}{sigma }} right| < frac{2}{sigma }} right) = Phi left( {0.2} right) — Phi left( { — 0.2} right) = 2 cdot Phi left( {0.2} right) — 1 = 2 cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]Phi left( x right)[/math] отличается от функции, которую использовал Alexdemath

3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]Pleft( {X < 15} right) = intlimits_0^{15} {lambda cdot e^{ — lambda x} dx} = 1 — e^{ — 15lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]pleft( t right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]Pleft( {X < 15} right) = 1 — Pleft( {X > 15} right) = 1 — intlimits_{15}^infty {pleft( t right)dt} = 1 — intlimits_{15}^infty {frac{t}{t}pleft( t right)dt} geqslant 1 — frac{1}{{15}}intlimits_0^infty t pleft( t right)dt = 1 — frac{8}{{15}} = frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.

Источник

Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением σ=20 мм и математическим ожиданием m=7. Найти вероятность того, что ошибка при измерении не превзойдет по абсолютной величине 4 мм.

Мне нужно воспользоваться формулой P(|X − m| < δ) = 2Ф(δ/σ)? Хотя я не понимаю, причем здесь |X − m|, ведь ничего не сказано про отклонение случайной величины от мат. ожидания. Или же нужно найти вероятность P(|X| < 4)?

Источник

СВ Х подчинена
нормальному
закону
распределения,
если ее
плотность распределения вероятностей
имеет вид:

,
(5.14)

где
a ‑ математическое
ожидание,
‑среднее
квадратичное отклонение
Х.

Интегральная
функция нормального распределения
имеет вид

;
(5.15)

где

— функция
Лапласа, или интеграл вероятностей.

Основные
свойства
функции Лапласа:

(0)
= 0;

2)
(нечетная функция);

3) ()=0,5

Таблица значений
функции (х)
для
приведена в приложении, поскольку она
является нечетной, то для отрицательных
значенийх
пользуются теми же таблицами, что и для
положительных.

Вероятность
попадания Х в заданный интервал значений
:

,
(5.16)

Вероятность того,
что абсолютная величина отклонения
нормальной СВХ
от ее математического ожидания меньше
положительного числа ,
определяется выражением:

.
(5.17)

В частности, при
а=0,
P(Х
<)
=2().

Если
в равенстве 5.17.
взять,
получимтак
называемое
«правило
трёх сигм»,
которое является одним из необходимых
условий
того, что СВ имеет нормальный закон
распределения. В самом деле,

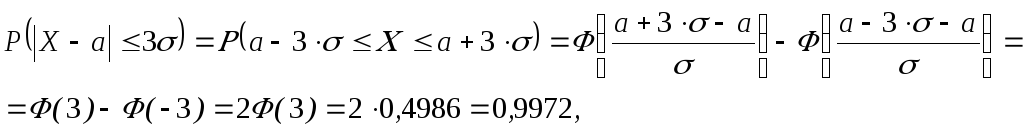
т.е.
отклонение нормальной
СВ от своего математического ожидания
а
на
величину,
равную

является событием практически достоверным.

Асимметрия,
эксцесс, мода и медиана

нормального
распределения соответственно равны:

а_s=0,
е_k=0,
M_o=a,
M_e=a,
где
a=M[X].

График плотности
вероятности нормального распределения
(рис.5.5) называют нормальной
кривой
(кривой Гаусса).

Пример 5.6.
Ошибка измерения длины платформы станции
метро подчинена нормальному закону.
Математическое ожидание этой ошибки
равно 5см, а среднее квадратичное
отклонение равно 10см. Найти вероятность
того, что измеряемое значение длины
платформы будет отклоняться от истинного
не более чем на 20см.

Решение задачи
сводится к определению вероятности
попадания СВ Х
(ошибка
измерения) с математическим ожиданием
а=5см
и средним квадратичным отклонением
=10см
в интервал значений (‑20, 20).
По формуле
вычисления вероятности попадания Х
в заданный интервал имеем:

P(‑20<Х<20)
=
=.

Пример 5.7.
Доказать, что параметр а
нормальной плотности распределения СВ
Х является математическим ожиданием
Х.

Доказательство.
По определению:
.
Для нормального распределения получим:

=
=
==+=a

(так
как
=0,
а интеграл Пуассона:).

Задачи

Биномиальный
закон.

Вероятность
выигрыша по облигации займа за все
время его действия равна 0,1. Составить
закон распределения числа выигравших
облигаций среди приобретенных 19. Найти
математическое ожидание, дисперсию,
среднее квадратическое отклонение.

Ответ:

Партия из 10 изделий
проверяется на стандартность. Вероятность
того, что изделие стандартно, равна
0.8. Определить математическое ожидание
и дисперсию СВ Х = {число стандартных
изделий в партии}.

Ответ:

В большой партии
20% нестандартных деталей. Из них наудачу
отобраны 5 деталей. а) написать биномиальный
закон распределения дискретной СВ Х —
числа нестандартных деталей среди пяти
отобранных; б) построить многоугольник
распределения; в) найти математическое
ожидание и среднее квадратичное
отклонение.

Ответ:	Х	0	1	2	3	4	5
p	0.328	0.41	0.205	0.051	0.0064	0.00032

M(X)
= 1;

Написать биномиальный
закон распределения дискретной СВ Х
‑ числа появлений “герба” при двух
бросках монеты. Построить функцию
распределения.

Ответ:	Х	0	1	2
p	0,25	0,5	0,25

Гипергеометрическое
распределение

В партии из 10
деталей имеется 8 стандартных. Наугад
отобраны 2 детали. Составить закон
распределения числа стандартных деталей
среди отобранных. Определить вероятность
того, что число стандартных деталей
среди отобранных будет меньше двух.

Ответ:	Х	0	1	2
p

; Р(Х<2)
=
.

В партии из 6
деталей имеется 4 стандартных. Наудачу
отобраны 3 детали. Составить закон
распределения СВ Х ‑ числа стандартных
деталей среди отобранных. Построить
функцию распределения. Найти M[X],
D[X], _x.

Ответ:

0.2

0.6

0.2

M(X)
=
2;

Партия из 20 деталей
содержит 16 стандартных. Наугад отобраны
4 детали. Составить закон распределения
СВ Х = {число стандартных деталей среди
четырёх отобранных}. Определить
вероятность того, что среди отобранных
деталей число стандартных будет не
меньше двух.

Ответ:	Х	0	1	2	3	4
p	0.0002	0.013	0.149	0.462	0.376

Р(2<Х<4)
= 0.987.

В партии из 10
деталей содержится 4 нестандартных.
Наугад отобраны 2 детали. Найти дисперсию
и среднее квадратичное отклонение СВ
Х={число
стандартных деталей среди отобранных}.

Ответ:

В партии из 10
деталей содержится 4 нестандартных.
Наугад отобраны 3 детали. Записать закон
распределения СВ Х={число
стандартных деталей среди отобранных}.
Определить вероятность того, что число
нестандартных деталей среди отобранных
будет не меньше двух.

Ответ:	Х	0	1	2	3
p

p=1/3.

Н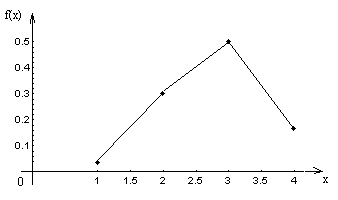а
складе магазина имеется 10 телевизоров,
среди которых 3 бракованных, что визуально
не определяется. Наугад берутся 4
телевизора и подключаются к сети. Найти
и построить (в виде многоугольника
распределения) ряд распределе-ния числа
телевизоров Х, которые будут работать.
Найти математическое ожидание, дис-персию
и среднее квадратичное отклонение СВХ.

Ответ:
M(X)
= 2.8;

Распределение
Пуассона

СВ Х представляет
число бракованных деталей из возвратной
выборки в 50 штук. Вероятность брака
одной детали p=0,06.
Найти математическое ожидание, дисперсию
и средне квадратичное отклонение числа
бракованных деталей в выборке.

Ответ:

Устройство состоит
из 1000 элементов, работающих независимо
один от другого. Вероятность отказа
любого элемента в течение времени Т
равна 0,002. Найти вероятность того, что
за время Т откажут : а) ровно три; б) менее
трех; в) более трех; г) хотя бы одно.

Ответ:

Найти среднее
число 
— бракованных изделий в партии изделий,
если вероятность того, что в этой партии
содержится хотя бы одно бракованное
изделие, равна 0,95. Предполагается, что
число бракованных изделий распределено
по закону Пуассона.

Ответ:

Равномерное
распределение

Предполагая, что
индекс цен на продовольственные товары
равномерно распределен в пределах от
110 до 150%, найти вероятность того, что он
не превысит 135%, а также вычислить
характеристики его разброса.

Ответ:

Коммерческая
маржа Х посреднической фирмы равномерно
распределена с параметрами
=20
тыс. гривень
в месяц и
=3,464
тыс. гривень
в месяц. Найти вероятность того, что в
следующем месяце она превысит 25 тыс.
гривень.

Ответ:

Минутная стрелка
электрических часов передвигается
скачками поминутно. Вы бросили взгляд
на часы. Они показывают
минут. Тогда для вас истинное время в
данный момент будет случайной величиной.
Найти её функцию распределения, считая,
что время течёт равномерно.

Ответ:
.

Автобусы некоторого
маршрута идут строго по расписанию.
Интервал движения 5 мин. Найти вероятность
того, что пассажир, подошедший к
остановке, будет ожидать очередной
автобус менее 3 мин.

Ответ:
0,6.

Показательное
распределение

Регулярным
контролем состояния овощей, завезенных
на склад, определяется срок их годности.
В среднем он равен 125 дням. Описать этот
срок с помощью показательного закона
распределения и найти вероятность
того, что он превысит средний.

Ответ:

Плотность
показательного распределения имеет
вид:
;
. Найтипостоянную
С

Ответ:

Дана плотность
вероятности СВ:
.
Найти коэффициента
и вероятность того, что
.

Ответ:
а = 2; Р()=
0,75.

Время, необходимое
для устранения неисправностей в
телевизоре, есть СВ Т. Найти математическое
ожидание, дисперсию и среднее квадратичное
отклонение времени обслуживания, если
.

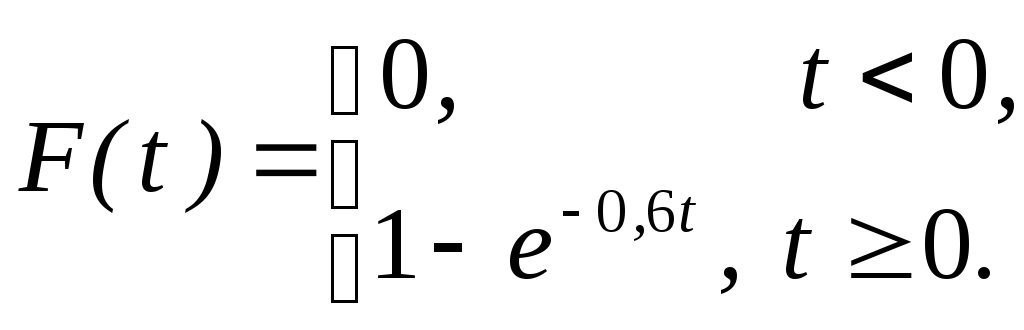Ответ:

Найти математическое
ожидание, дисперсию, асимметрию и
эксцесс СВ Х,
подчиненной показательному распределению:

Ответ:

СВ Х
распределена по показательному закону,
заданному функцией распределения:
.
Найти вероятность того, что в результате
испытания Х попадет в интервал (2, 5).

Ответ:
0,251.

СВ Х
— продолжительность жизни мужчин в
некотором регионе – задана функцией
распределения
.
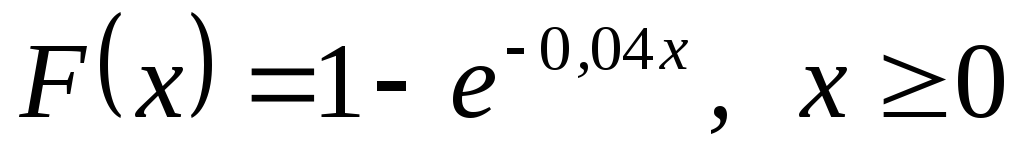Найти вероятность того, что случайно
выбранный мужчина доживет до 60 лет.

Ответ:
0,091.

Нормальное
распределение СВ.

Текущая цена акции
моделируется нормальным законом
распределения с математ. ожиданием 15
ден. ед. и средним квадратическим
отклонением 0,2 ден. ед. Найти: 1 вероятность
того, что цена акции: а) не выше 15,3 ден.
ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3
ден. ед. 2. С помощью правила
найти границы, в которых будет находиться
текущая цена акции.

Ответ:
1. а) 0,4332;
б) 0,0228;
в) 0,6246;
2.
.

Цена акции
распределена нормально. В течение
последнего года 20% рабочих дней она
была ниже 88 ден. ед., а 75% — выше 90 ден. ед.
Найти: а) математическое ожидание и
среднее квадратическое отклонение
цены ценной бумаги; б) вероятность того,
что в день покупки цена будет заключена
в пределах от 83 до 96 ден. ед.; в) с
надежностью 0,95 определить максимальное
отклонение цены от среднего (прогнозного)
значения по абсолютной величине.

Ответ: а)
М(х) = 98;
σ = 12;
б) 0,33;
в)
.

По многолетним
наблюдениям за балансовой прибылью
фирмы установлено, что эта прибыль
меняется в пределах от 10000 до 40000грив.
в месяц. Считая, что она распределена
нормально, определить параметры этого
распределения и найти вероятность
того, что балансовая прибыль в следующем
месяце составит 24000-28000 гривен. Указание.
Из неравенства
,
предварительно найти

Ответ:

Система, «следящая»
за процессом ценообразования, содержит
систематические и случайные ошибки.
Систематическая ошибка равна 0,5 цента
в сторону занижения. Случайные ошибки
подчиняются нормальному закону
распределения со средним квадратичным
отклонением =1цент.
Найти а) вероятность фиксации цены по
абсолютной величине 1,5 цента; б)
вероятность того, что фиксированная
цена не превзойдет истинной.

Ответ:
.

Производится
взвешивание некоторого вещества без
систематических ошибок. Случайные
ошибки взвешивания подчинены нормальному
закону со средним квадратичным
отклонением =20г.
Найти вероятность того, что взвешивание
будет произведено с ошибкой, не
превосходящей по абсолютной величине
10г.

Ответ:

Фирма изготавливает
железобетонные изделия, используя в
качестве основного сырья цемент. В
связи с неопределенностью спроса на
эти изделия потребность в цементе
меняется из месяца в месяц, причем в
среднем она составляет 2500 т/мес., а ее
разброс характеризуется среднеквадратичным
отклонением 600 т/мес. Считая распределение
потребности в цементе нормальным,
определить вероятность того, что в
следующем месяце она не выйдет за
пределы 2200-2700 т.

Ответ:

Деталь, изготовленная
автоматом, считается годной, если
отклонение ее контролируемого размера
от проектного не превышает 10 мм. Случайные
отклонения контролируемого размера
от проектного подчинены нормальному
закону со средним квадратичным
отклонением =5мм.
и математическим ожиданием а=0.
Сколько процентов годных деталей
изготавливает автомат?

Ответ:

,
т.е. автомат изготовил примерно 95%.

Нормально
распределенная СВ Х
задана плотностью вероятности
.
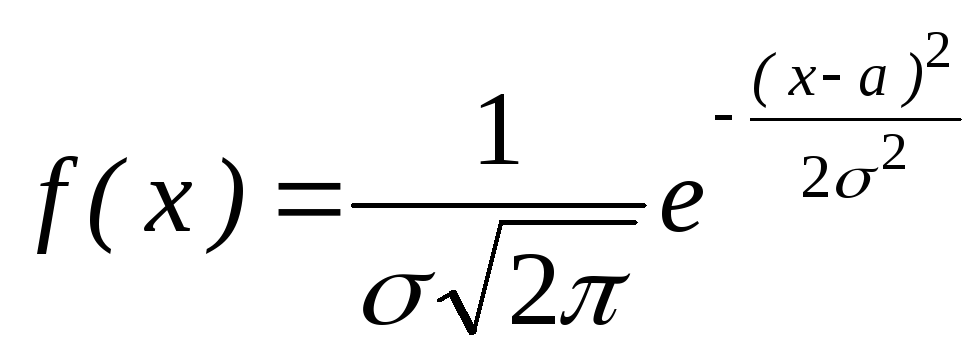Найти моду и медиану.

Ответ:

СВ Х
распределена нормально с математическим
ожиданием а=10 и средним квадратичным
отклонением =5.
Найти интервал, симметричный относительно
математического ожидания, в который с
вероятностью 0,9973 попадет величина Х в
результате испытания.

Ответ: