Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 1мм

Условие

Решение

Написать комментарий

Корреляционный анализ.

Проверка
гипотезы о значимости выборочного

коэффициента
корреляции.

Рассмотрим
выборку объема п,
извлеченную из нормально распределенной
двумерной генеральной совокупности
(X,
Y).
Вычислим выборочный коэффициент
корреляции r_B.
Пусть он оказался не равным нулю. Это
еще не означает, что и коэффициент
корреляции генеральной совокупности
не равен нулю. Поэтому при заданном
уровне значимости α возникает необходимость
проверки нулевой гипотезы Н₀:
r_г
= 0 о равенстве нулю гене-рального
коэффициента корреляции при конкурирующей
гипотезе Н₁:
r_г
≠ 0. Таким образом, при принятии нулевой
гипотезы Х
и Y
некоррелированы, то есть не связаны
линейной зависимостью, а при отклонении
Н₀
они коррелированы.

В
качестве критерия примем случайную
величину

,

которая
при справедливости нулевой гипотезы
имеет распределение Стьюдента (см.
лекцию 12) с k
= n
– 2 степенями свободы. Из вида конкурирующей
гипотезы следует, что критическая
область двусторонняя с границами ± t_кр,
где значение t_кр(α,
k)
находится из таблиц для двусторонней
критической области.

Вычислив
наблюдаемое значение критерия

и
сравнив его с t_кр,
делаем вывод:

—
если |T_набл|
< t_кр
– нулевая гипотеза принимается
(корреляции нет);

—
если |T_набл|
> t_кр
– нулевая гипотеза отвергается
(корреляция есть).

Ранговая
корреляция.

Пусть
объекты генеральной совокупности
обладают двумя качественными признаками
(то есть признаками, которые невозможно
измерить точно, но которые позволяют
сравнивать объекты между собой и
располагать их в порядке убывания или
возрастания качества). Договоримся для
определенности располагать объекты в
порядке ухудшения качества.

Пусть
выборка объема п
содержит независимые объекты, обладающие
двумя качествен-ными признаками: А
и В.
Требуется выяснить степень их связи
между собой, то есть установить наличие
или отсутствие ранговой
корреляции.

Расположим
объекты выборки в порядке ухудшения
качества по признаку А,
предполагая, что все они имеют различное
качество по обоим признакам. Назовем
место, занимаемое в этом ряду некоторым
объектом, его рангом
х_i:
х₁
= 1, х₂
= 2,…, х_п
= п.

Теперь
расположим объекты в порядке ухудшения
качества по признаку В,
присвоив
им ранги у_i
,
где номер i
равен порядковому номеру объекта по
признаку А,
а само значение ранга равно порядковому
номеру объекта по признаку В.
Таким образом, получены две последовательности
рангов:

по
признаку А
… х₁,
х₂,…,
х_п

по
признаку В
… у₁,
у₂,…,
у_п
.

При
этом, если, например, у₃
= 6, то это означает, что данный объект
занимает в ряду по признаку А
третье место, а в ряду по признаку В
– шестое.

Сравним
полученные последовательности рангов.

1. Если
   x_i
   = y_i
   при всех значениях i,
   то ухудшение качества по признаку А
   влечет за собой ухудшение качества по
   признаку В,
   то есть имеется «полная ранговая
   зависимость».

2. Если
   ранги противоположны, то есть х₁
   = 1, у₁
   = п;
   х₂
   = 2, у₂
   = п
   – 1;…, х_п
   = п, у_п
   = 1,
   то признаки тоже связаны: ухудшение
   качества по одному из них приводит к
   улучшению качества по другому
   («противоположная зависимость»).

3. На
   практике чаще всего встречается
   промежуточный случай, когда ряд у_i
   не монотонен. Для оценки связи между
   признаками будем считать ранги х₁,
   х₂,…,
   х_п
   возможными значениями случайной
   величины Х,
   а у₁,
   у₂,…,
   у_п
   – возможными значениями случайной
   величины Y.
   Теперь можно исследовать связь между
   Х
   и Y,
   вычислив для них выборочный коэффициент
   корреляции

,

где
(условные
варианты). Поскольку каждому рангуx_i
соответствует
только одно значение
y_i,
то частота любой пары условных вариант
с одинаковыми индексами равна 1, а с
разными индексами – нулю. Кроме того,
из выбора условных вариант следует, что
,
поэтому формула приобретает более
простой вид:

.

Итак,
требуется найти
и.

Можно
показать, что
.
Учитывая, что,
можно выразитьчерез
разности рангов.
После преобразований получим:,,
откуда.
Подставив эти результаты в (21.3), получимвыборочный
коэффициент ранговой корреляции
Спирмена:

.

Свойства
выборочного коэффициента корреляции
Спирмена.

1. Если
   между А
   и В
   имеется «полная прямая зависимость»,
   то есть ранги совпадают при всех i,
   то ρ_В
   = 1. Действительно, при этом d_i
   = 0, и из формулы (21.4) следует справедливость
   свойства 1.

2. Если
   между А
   и В
   имеется «противоположная зависимость»,
   то ρ_В
   = — 1. В этом случае, преобразуя d_i
   = (2i
   – 1) – n,
   найдем, что
   ,
   тогда из

3. В
   остальных случаях -1 < ρ_B
   <
   1, причем зависимость между А
   и В
   тем меньше, чем ближе |
   ρ_B
   | к нулю.

Итак,
требуется при заданном уровне значимости
α проверить нулевую гипотезу о равенстве
нулю генерального коэффициента ранговой
корреляции Спирмена ρ_г
при конку-рирующей гипотезе Н₁:
ρ_г
≠
0. Для этого найдем критическую точку:

,

где
п
– объем выборки, ρ_В
– выборочный коэффициент ранговой
корреляции Спирмена, t_кр
(α,
k)
– критическая точка двусторонней
критической области, найденная по
таблице критических точек распределения
Стьюдента, число степеней свободы k
= n
–
2.

Тогда,
если | ρ_B
| < T_кр,
то нулевая гипотеза принимается, то
есть ранговая корреляционная связь
между признаками незначима.

Если
| ρ_B
| > T_кр,
то нулевая гипотеза отвергается, и между
признаками существует значимая ранговая
корреляционная связь.

Можно
использовать и другой коэффициент –
коэффициент ранговой корреляции
Кендалла. Рассмотрим ряд рангов у₁,
у₂,…,
у_п,
введенный так же, как и ранее, и зададим
величины R_i
следующим образом: пусть правее у₁
имеется R₁
рангов, больших у₁;
правее у₂
– R₂
рангов, больших у₂
и т.д. Тогда, если обозначить R
=R₁
+ R₂
+…+ R_n—1,
то выборочный
коэффициент ранговой корреляции Кендалла
определяется формулой

где
п
– объем выборки.

Замечание.
Легко
убедиться, что коэффициент Кендалла
обладает теми же свойствами, что и
коэффициент Спирмена.

Для
проверки нулевой гипотезы Н₀:
τ_г
= 0 (генеральный коэффициент ранговой
корреляции Кендалла равен нулю) при
альтернативной гипотезе Н₁:
τ_г
≠ 0 необходимо найти критическую точку:

,

где
п
– объем выборки, а z_кр
– критическая точка двусторонней
критической области, определяемая из
условия
по таблицам для функции Лапласа.

Если
| τ_B
| < T_кр
,
то нулевая гипотеза принимается (ранговая
корреляционная связь между признаками
незначима).

Если
| τ_B
| > T_кр
,
то нулевая гипотеза отвергается (между
признаками существует значимая ранговая
корреляционная связь).

Моделирование
случайных величин методом Монте-Карло
(статистических испытаний).

Задачу,
для решения которой применяется метод
Монте-Карло, можно сформулировать так:
требуется найти значение а
изучаемой случайной величины. Для его
определения выбирается случайная
величина Х,
математическое ожидание которой равно
а,
и для выборки из п
значений Х,
полученных в п
испытаниях, вычисляется выборочное
среднее:

,

которое
принимается в качестве оценки искомого
числа а:

Этот
метод требует проведения большого числа
испытаний, поэтому его иначе называют
методом
статистических испытаний.
Теория метода Монте-Карло исследует,
как наиболее целесообразно выбрать
случайную величину Х,
как найти ее возможные значения, как
уменьшить дисперсию используемых
случайных величин, чтобы погрешность
при замене а
на а*
была возможно меньшей.

Поиск
возможных значений Х
называют разыгрыванием
случайной
величины.
Рассмотрим некоторые способы разыгрывания
случайных величин и выясним, как оценить
допускаемую при этом ошибку.

Оценка
погрешности метода Монте-Карло.

Если
поставить задачу определения верхней
границы допускаемой ошибки с заданной
доверительной вероятностью ,
то есть поиска числа ,
для которого

,

то
получим известную задачу определения
доверительного интервала для
математичес-кого ожидания генеральной
совокупности (см. лекцию 18). Воспользуемся
результатами решения этой задачи для
следующих случаев:

1. случайная
   величины Х
   распределена нормально и известно ее
   среднее квадратическое отклонение.
   Тогда из формулы (18.1) получаем:
   ,
   гдеп
   – число испытаний, 
   — известное среднее квадратическое
   отклонение, а t
   – аргумент функции Лапласа, при котором
   Ф(t)
   = /2.

2. Случайная
   величина Х
   распределена нормально с неизвестным
   .
   Воспользуемся формулой (18.3), из которой
   следует, что
   ,
   гдеs
   – исправленное выборочное среднее
   квадратическое отклонение, а
   определяется
   по соответствующей таблице.

3. Если
   случайная величина распределена по
   иному закону, то при достаточно большом
   количестве испытаний (n
   > 30) можно использовать для оценки 
   предыдущие формулы, так как при п
   распределение Стьюдента стремится к
   нормальному, и границы интервалов,
   полученные по формулам, различаются
   незначительно.

Разыгрывание
случайных величин.

Определение.
Случайными
числами
называют возможные значения r
непрерывной случайной величины R,
распределенной равномерно в интервале
(0; 1).

1. Разыгрывание
   дискретной случайной величины.

Пусть
требуется разыграть дискретную случайную
величину Х,
то есть получить последовательность
ее возможных значений, зная закон
распределения Х:

Х
х₁
х₂
… х_п

р
р₁
р₂
… р_п
.

Рассмотрим
равномерно распределенную в (0, 1) случайную
величину R
и разобьем интервал (0, 1) точками с
координатами
р_1,

р₁
+ р₂,
…, р₁
+ р₂
+… +р_п-1
на
п
частичных интервалов
,
длины которых равны вероятностям с теми
же индексами.

Теорема.
Если
каждому случайному числу
,
которое попало в интервал,
ставить в соответствие возможное
значение,
то разыгрываемая величина будет иметь
заданный закон распределения:

Х
х₁
х₂
… х_п

р
р₁
р₂
… р_п
.

Доказательство.

Возможные
значения полученной случайной величины
совпадают с множеством
х₁
, х₂
,… х_п,
так как число интервалов равно п,
а при попадании r_j

в интервал
случайная величина может принимать
только одно из значенийх₁
, х₂
,… х_п.

Так
как R
распределена равномерно, то вероятность
ее попадания в каждый интервал равна
его длине, откуда следует, что каждому
значению
соответствует вероятностьp_i.
Таким образом, разыгрыываемая случайная
величина имеет заданный закон
распределения.

Пример.
Разыграть 10 значений дискретной случайной
величины Х,
закон распределения которой имеет вид:
Х
2 3 6 8

р
0,1 0,3 0,5 0,1

Решение.
Разобьем интервал (0, 1) на частичные
интервалы: ₁—
(0; 0,1), ₂
– (0,1; 0,4), ₃
— (0,4; 0,9), ₄
– (0,9; 1). Выпишем из таблицы случайных
чисел 10 чисел: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01;
0,35; 0,86; 0,34. Первое и седьмое числа лежат
на интервале ₁,
следовательно, в этих случаях разыгрываемая
случайная величина приняла значение
х₁
= 2; третье, четвертое, восьмое и десятое
числа попали в интервал ₂,
что соответствует х₂
= 3; второе, пятое, шестое и девятое числа
оказались в интервале ₃
– при этом Х
= х₃
=
6; на последний интервал не попало ни
одного числа. Итак, разыгранные возможные
значения Х
таковы: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

Разыгрывание
противоположных событий.

Пусть
требуется разыграть испытания, в каждом
из которых событие А
появляется с известной вероятностью
р.
Рассмотрим дискретную случайную величину
Х,
принимающую значения 1 (в случае, если
событие А
произошло) с вероятностью р
и 0 (если А
не произошло) с вероятностью q
= 1 – p.
Затем разыграем эту случайную величину
так, как было предложено в предыдущем
пункте.

Пример.
Разыграть 10 испытаний, в каждом из
которых событие А
появляется с вероятностью 0,3.

Решение.
Для случайной величины Х
с законом распределения
Х
1 0

р
0,3 0,7

получим
интервалы ₁
– (0; 0,3) и ₂
– (0,3; 1). Используем ту же выборку случайных
чисел, что и в предыдущем примере, для
которой в интервал ₁
попадают числа №№1,3 и 7, а остальные –
в интервал ₂.
Следовательно, можно считать, что событие
А
произошло в первом, третьем и седьмом
испытаниях, а в остальных – не произошло.

Разыгрывание
полной группы событий.

Если
события А₁,
А₂,
…, А_п,
вероятности которых равны р₁
, р₂
,… р_п,
образуют полную группу, то для из
разыгрывания (то есть моделирования
последовательности их появлений в серии
испытаний) можно разыграть дискретную
случайную величину Х
с
законом распределения Х
1 2 … п,
сделав
это так же, как в пункте 1. При этом
считаем, что

р
р₁
р₂
… р_п

если
Х
принимает значение х_i
= i,
то в данном испытании произошло событие
А_i.

1. Разыгрывание
   непрерывной случайной величины.

а)
Метод обратных функций.

Пусть
требуется разыграть непрерывную
случайную величину Х,
то есть получить последовательность
ее возможных значений x_i
(i
= 1, 2, …, n),
зная функцию распределения F(x).

Теорема.
Если
r_i
–
случайное число, то возможное значение
x_i
разыгрываемой непрерывной случайной
величины Х
с заданной функцией распределения F(x),
соответствующее r_i
,
является корнем уравнения

F(x_i)
= r_i.

Доказательство.

Так
как F(x)
монотонно возрастает в интервале от 0
до 1, то найдется (причем единственное)
значение аргумента x_i
, при котором функция распределения
примет значение r_i
.
Значит, уравнение F(x_i)
= r_i.
имеет единственное решение: х_i
=
F^-1(r_i
),
где F^-1—
функция, обратная к F.
Докажем, что корень уравнения F(x_i)
= r_i.
является возможным значением
рассматриваемой случайной величины Х.
Предположим
вначале, что x_i
–
возможное значение некоторой случайной
величины ,
и докажем, что вероятность попадания 
в интервал (с,
d)
равна F(d)
– F(c).
Действительно,
в силу монотонностиF(x)
и того, что F(x_i)
= r_i.
Тогда

,
следовательно,
Значит, вероятность попадания
в интервал (c,
d)
равна приращению функции распределения
F(x)
на этом интервале, следовательно, 
= Х.

Пример.
Разыграть 3 возможных значения непрерывной
случайной величины Х,
распределенной равномерно в интервале
(5; 8).

Решение.

F(x)
=
,
то есть требуется решить уравнение

Выберем 3 случайных числа: 0,23; 0,09 и 0,56 и
подставим их в это уравнение. Получим
соответствующие возможные значения Х:

б)
Метод суперпозиции.

Если
функция распределения разыгрываемой
случайной величины может быть представлена
в виде линейной комбинации двух функций
распределения:

,

то
,
так как прих
F(x)

1.

Введем
вспомогательную дискретную случайную
величину Z
с законом распределения

Z
1 2 . Выберем 2 независимых случайных
числа r₁
и r₂
и разыграем возможное

p
C₁
C₂

значение
Z
по числу r₁
(см. пункт 1). Если Z
= 1, то ищем искомое возможное значение
Х
из
уравнения
,
а еслиZ
= 2, то решаем уравнение
.

Можно
доказать, что при этом функция распределения
разыгрываемой случайной величины равна
заданной функции распределения.

в)
Приближенное разыгрывание нормальной
случайной величины.

Так
как для R,
равномерно распределенной в (0, 1),
,
то для суммып
независимых, равномерно распределенных
в интервале (0,1) случайных величин
.
Тогда в силу центральной предельной
теоремы нормированная случайная величинаприп


будет иметь распределение, близкое к
нормальному, с параметрами а
= 0 и 
=1. В частности, достаточно хорошее
приближение получается при п
= 12:

Итак,
чтобы разыграть возможное значение
нормированной нормальной случайной
величины х,
надо сложить 12 независимых случайных
чисел и из суммы вычесть 6.

Контрольные
вопросы:

1. Задачи
   математической статистики

2. Выборки.

3. Способы
   отбора.

4. Статистическое
   распределение выборки.

5. Эмпирическая
   функция распределения.

6. Полигон
   и гистограмма.

7. Виды
   статистических оценок.

8. Эмпирические
   моменты.

9. Асимметрия
   и эксцесс эмпирического распределения.

10. Доверительный
    интервал.

11. Виды
    статистических гипотез.

12. Общая
    схема проверки статистических гипотез.

13. Типы
    статистических критериев проверки
    гипотез.

14. Предмет
    метода Монте – Карло.

15. Оценка
    погрешности методом Монте – Карло.

16. Случайные
    ошибки измерения подчинены нормальному
    закону со средним квадратическим
    отклонением σ =1мм и математическим
    ожиданием a = 0. Найти вероятность того,
    что из двух независимых наблюдений
    ошибка хотя бы одного из них не превзойдет
    по абсолютной величине 1,28 мм.

a)
0,04; б) 0,96
;
в) 0,54.

Найти
числовые характеристики случайной
величины Y
и вероятность попадания этой величины
на
).

Решение.
Вычисления проводим по формулам (2.2.1),
(2.2.5) и свойству 4 плотности распределения:

18

20
Измерение дальности до объекта
сопровождается систематическими и
случайными ошибками. Систематическая
ошибка равна 50 м в сторону занижения
дальности. Случайные ошибки подчиняются
нормальному закону со средним
квадратическим отклонением, равным
100 м. Найти вероятность того, что
измеренная дальность не превзойдет
истинной

21
. Коробки
с шоколадом упаковываются автоматически:
их средняя масса равна 1.06 кг. Найти
среднее квадратическое отклонение,
если известно, что 5% коробок имеют
массу, меньшую 1 кг. Предполагается, что
масса коробок распределена по нормальному
закону.

22
. Размер
деталей подчинен закону нормального
распределения с математическим ожиданием
15 мм и дисперсией 0.25 мм².
Определить ожидаемый процент брака,
если допустимые размеры деталей
находятся в пределах от 14 до17 мм.

23
. Найти
среднее время безотказной работы
устройства, если известно, что для
данного устройства вероятность работы
без сбоев в течение 100 часов равна 0.2.
(Предполагается, что время безотказной
работы распределено по экспоненциальному
закону.)

24
. Считается,
что изделие – высшего качества, если
отклонение его размеров от номинальных
не превосходит по абсолютной величине
3.6 мм. Случайные отклонения размера
изделия от номинального подчиняются
нормальному закону со средним квадратичным
отклонением, равным 3 мм. Систематические
отклонения отсутствуют. Определить
среднее число изделий высшего качества
среди 100 изготовленных.

25
Время безотказной работы механизма
подчинено показательному закону с
плотностью распределения вероятностей
приt>0
(t
– время в часах). Найти вероятность
того, что механизм проработает безотказно
100 часов.

26
. Считается,
что отклонение длины изготавливаемых
деталей от стандартной является
случайной величиной, распределенной
по нормальному закону. Систематические
отклонения размера детали от номинала
отсутствуют. Зная, что длина стандартной
детали 40 см, а среднее квадратичное
отклонение равно 0.4 см, определить,
какую точность длины изделия можно
гарантировать с вероятностью 0.8.

71

14
. Все значения равномерно распределенной
случайной величины X принадлежат отрезку
[3; 9]. Найти вероятность попадания
значения случайной величины X а) в
отрезок [1; 5]; б) в отрезок [4; 10 ]
.

15
. Автоматический
станок производит однотипные изделия,
номинальный размер которыхравен 3 см.
Фактический размер изделий имеет
разброс, подчиненный нормальному закону
с [X]
= 0.05 см. Систематические отклонения
размера отсутствуют. При контроле
отбраковываются все изделия, размер
которых отличается от номинального
больше, чем на 0.12 см. Определить, какой
процент изделий в среднем будет
отбраковываться.

16.
Завод
изготовляет шарики для подшипников,
номинальный диаметр которых равен 10
мм, а фактический диаметр случаен и
распределен по нормальному закону с
математическим ожиданием, равным 10 мм
и средним квадратическим отклонением
0.4 мм. При контроле бракуются все шарики,
не проходящие через круглое отверстие
диаметром 10.7 мм, и все, проходящие через
круглое отверстие диаметром 9.3 мм. Какой
процент шариков в среднем будет
отбраковываться?

17
. Случайная
величина Х – ошибка измерительного
прибора распределена по нормальному
закону с дисперсией, равной 16 мкм и
математическим ожиданием, равным нулю.
Найти вероятность того, что величина
ошибки при одном измерении не превзойдет
по абсолютной величине 6 мкм.

18.
Измерительный
прибор имеет систематическую ошибку,
равную 5 м и среднее квадратическое
отклонение случайной ошибки – 75 м.
(Предполагается, что возникающие ошибки
распределены по нормальному закону.)
Какова вероятность того, что ошибка
измерения не превзойдет по абсолютной
величине 5 м?

19.
Измерение
дальности до объекта сопровождается
систематическими и случайными ошибками.
Систематическая ошибка равна 50 м в
сторону занижения дальности. Случайные
ошибки подчиняются нормальному закону
со средним квадратическим отклонением,
равным 100 м. Найти вероятность измерения
дальности с ошибкой, не превосходящей
по абсолютной величине 150 м

70

2. 3 ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

2.3.1 БИНОМИАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ

Говорят,
что дискретная случайная величина Х
имеет биномиальное распределение,
если возможные значенич этой случайной
величины есть 0, 1, …,n,
а вероятности, с которыми Х принимает
указанные возможные значения определяются
по формуле Бернулли

Математическое
ожидание Х
есть М(Х) =
n
p
, а дисперсия — D(X)
= n
p
q

2.3.2 РАСПРЕДЕЛЕНИЕ
ПУАССОНА

Говорят,
что случайная величина Х имеет
распределение Пуассона, если ее возможные
значения есть 0,
1, …,n,
…, а соответствующие им вероятности
определяются по формуле

,
где

Для
этой случайной величины
Д(Х)
=

19

2. 3. 3 РАВНОМЕРНОЕ
РАСПРЕДЕЛЕНИЕ

Говорят,
что случайная величина Х имеет
равномерное распределение на отрезке
[a,b],
если плотность распределения вероятностей
постоянна на этом отрезке. С учетом
свойств плотности распределения
получаем, что

Функция
распределения вероятностей величины
Х имеет вид

Для
этой случайной величины

,

2. 3. 4 ПОКАЗАТЕЛЬНОЕ
( ЭКСПОНЕНЦИАЛЬНОЕ ) РАСПРЕДЕЛЕНИЕ

Говорят,
что случайная величина Х
имеет показательное ( экспоненциальное
) распределение, если плотность
распределения вероятностей Х
есть

20

8
. Взвешивание на весах производится
без систематических ошибок. Случайные
ошибки имеют с дисперсию, равную 100 г².
Полагая, что ошибки распределены по
нормальному закону, определить
вероятность того, что ошибка при
взвешивании предмета по абсолютной
величине не превысит 50 г

9
Производится измерение вала без
систематических ошибок. Случайные
ошибки измерения подчинены нормальному
закону распределения со средним
квадратическим отклонением, равным 1
мм. Найти вероятность того, что измерение
будет произведено с ошибкой, не
превосходящей по абсолютной величине
1.5 мм.

10
. Автоматический
станок производит однотипные изделия,
номинальный размер которых равен 3 см.
Фактический размер изделий имеет
разброс, подчиненный нормальному закону
с [X]
= 0.05 см. Систематические отклонения
размера отсутствуют. При контроле
отбраковываются все изделия, размер
которых отличается от номинального
больше, чем на 0.12 см. Определить, какой
процент изделий в среднем будет
отбраковываться.

11.
Случайная величина Х распределена
нормально с математическим ожиданием
а = 25 и дисперсией D(X) = 100. Напишите
выражение для плотности вероятности
f(x) и функции распределения F(x). Чему
равна вероятность события 15 
X 
35 ?

12
. Производится измерение вала без
систематических ошибок. Случайные
ошибки измерения подчинены нормальному
закону распределения со средним
квадратическим отклонением, равным
1 мм. Найти вероятность того, что
измерение будет произведено с ошибкой,
не превосходящей по абсолютной величине
1 мм.

13.
Случайная величина X,
сосредоточенная на интервале [2;6], задана
функцией распределения
F{x) =1/16(x²–4x+4).
Найти вероятность того, что случайная
величина Х
примет
значения: а) меньше 4; б) меньше 6;
в) не меньше 3; г) не меньше 6.

69

Задание 6

1.
Все значения равномерно распределенной
случайной величины Х принадлежат
отрезку [2, 8]. Найти вероятность попадания
случайной величины Х в отрезок [3, 5].

2.
Найти среднее время безотказной работы
устройства, если известно, что для
данного устройства вероятность работы
без сбоев в течение 100 часов равна 0,2.
(Предполагается, что время безотказной
работы распределено по экспоненциальному
закону)

3
Время безотказной работы механизма
подчинено показательному закону с
плотностью распределения вероятностей
приt > 0
(t –
время в часах). Найти вероятность того,
что механизм проработает безотказно
не менее 100 часов.

4.
Время простоя оборудования в ожидании
ремонта распределено по показательному
(экспоненциальному) закону с математическим
ожиданием, равным 2 часа. Найти вероятность
простоя более трех часов.

5
. Предполагая, что время, необходимое
для ремонта поступившего вагона,
распределено по показательному
(экспоненциальному) закону с параметром
 = 0,125 [час^-1],
найти вероятность того, что для ремонта
одного вагона понадобится не более
шести часов.

6.
В результате проверки точности работы
прибора установлено, что 60% ошибок не
вышло за пределы 20
мм, а остальные ошибки вышли за эти
пределы. Определите среднее квадратическое
отклонение ошибок прибора, если известно,
что систематических ошибок прибор не
дает, а случайные ошибки распределены
по нормальному закону

7.
Случайная величина Х распределена
нормально с математическим ожиданием
а = 25 и дисперсией D(X) = 100. Напишите
выражение для плотности вероятности
f(x) и функции распределения F(x). Чему
равна вероятность события 15 
X 
35 ?

68

Функция
распределения вероятностей величины
Х
имеет вид

Для
этой случайной величины
,

2. 3. 5 НОРМАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ

Говорят,
что случайная величина Х
имеет показательное ( экспоненциальное
) распределение, если плотность
распределения вероятностей Х
есть

Функция
распределения вероятностей величины
Х
имеет вид

Для
этой случайной величины
,

Вероятность
попадания величины Х
в промежуток
определяется
по формуле

где

— функция Лапласа, значения которой
находятся по таблицам

21

3 . МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА

3.1.
ВЫБОРОЧНЫЙ МЕТОД. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ
РАСПРЕДЕЛЕНИЯ

СТАТИСТИЧЕСКОЕ
ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
МЕТОДОМ МОМЕНТОВ

Предположим,
что для изучения некоторого количественного
признака 
из генеральной совокупности извлечена
выборка объема n

(3.1.1)

Эмпирической
(или
выборочной) функцией распределения
называется функция действительного
переменного

,
(3.1.2)

где

– число
элементов выборки, меньших х.

Если
признак 
имеет непрерывное распределение, то
по выборке (3.1.1) строят
интервальный вариационный ряд,
разбивая интервал, содержащий все
элементы выборки (3.1.1) на ряд частичных
интервалов шириной h
и,
подсчитывая–
частоту элементов выборки, попавшихi-й
интервал

Интервалы

Частоты

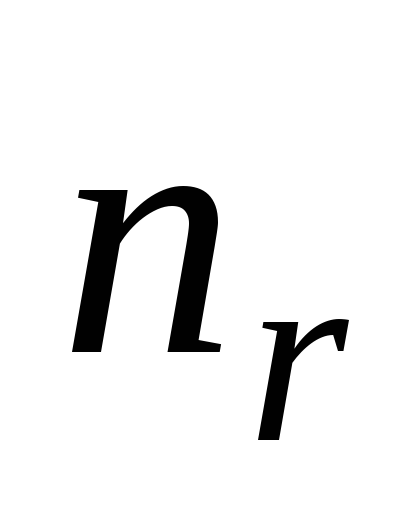
где

22

25.
Каждый поступающий в институт должен
сдать 3 экза­мена. Вероятность успешной
сдачи первого экзамена 0,9, второго —-
0,8, третьего — 0,7. Следующий экзамен
поступающий сдает только в случае
успешной сдачи предыдущего. Составить
закон распределения числа экзаменов,
сдававшихся поступающим в институт.
Найти математическое ожидание и
дисперсию этой случайной вели­чины.

26
. По данным длительной проверки качества
запчастей определенного вида брак
составляет 3 %. Изготовлено 1000
запчастей. Определить математическое
ожидание и среднее квадратическое
отклонение числа годных запчастей.

27.
Найти вероятность того, что в течение
смены произойдет не более двух отказов
оборудования, при условии, что среднее
число отказов в течение смены равно
1,6. (Предполагается, что число отказов
имеет распределение Пуассона.)

28
Вероятность сдачи первого экзамена
для данного студента равна 0.7 , второго
экзамена – 0.8 , третьего – 0.7 . С.в. x
– число сданных экзаменов. Найти ряд
распределения и математическое ожидание
с.в. x.
Вычислить значение функции распределения
с.в. x
в точках 0; 1; 2.5; 10.

29
Вероятность выпуска прибора,
удовлетворяющего требованиям качества,
равна 0.9 . В контрольной партии четыре
прибора. С.в. x
– число приборов, удовлетворяющих
требованиям качества. Найти ряд
распределения и математическое ожидание
с.в. x.
Вычислить значение функции распределения
с.в. x
в точках 0; 1; 2.5; 10.

30 Функция
распределения случайной величины
имеет вид:

0 ,
x
< 1 ;

F(x)=
0.5*(x²-x) ,
1 <= x<=
2 ;

1 , x > 2 .

Найти
функцию плотности распределения с.в.
x
и построить ее график. Найти медиану
с.в. x
. Вычислить значение функции распределения
с.в. x
в точках 0; 1; 2.5; 10. Найти вероятность
попадания значения с.в. x
в интервал (1.2, 1.5).

67

20.
Случайная величина X,
сосредоточенная на интервале [2;6], задана
функцией распределения
F{x) =1/16(x²–4x+4).
Найти вероятность того, что случайная
величина Х
примет
значения: а) меньше 4; б) меньше 6;
в) не меньше 3; г) не меньше 6.

21
Торговый агент имеет 5 телефонных
номеров потенциальных покупателей и
звонит им до тех пор, пока не получит
заказ на покупку товара. Вероятность
того, что потенциальный покупатель
сделает заказ, равна 0,4. Составить закон
распределения числа телефонных
разговоров, которые предстоит провести
агенту. Найти математическое ожидание
и дисперсию этой случайной величины

22
. Стрелок ведет стрельбу по цели с
вероятностью попа­дания при каждом
выстреле 0,2. За каждое попадание он
получает 5 очков, а в случае промаха
очков ему не начисляют. Составить закон
распределения числа очков, полученных
стрелком за 3 выстрела. Найти математическое
ожидание, дисперсию и среднее
квадратическое отклонение этой случайной
величины.

23
. Охотник, имеющий 4 патрона, стреляет
по дичи до первого попадания или до
израсходования всех патронов. Вероятность
попадания при первом выстреле равна
0,6, при каждом последующем ~ уменьшается
на 0,1. Необходимо: а) составить закон
распределения числа патронов,
израсходованных охотником; б) найти
математическое ожидание и дисперсию
этой случайной величины.

24.
Экзаменатор задает студенту вопросы,
пока тот правильно отвечает. Как только
число правильных ответов достигнет
четырех либо студент ответит неправильно,
экзаменатор прекращает задавать
вопросы. Вероятность правильного ответа
на один вопрос равна 2/3. Составить закон
распределения числа заданных студенту
вопросов. Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение этой случайной величины.

66

Гистограммой
вариационного
ряда (3.1.3) называется ступенчатая
фигура, состоящая из прямоугольников,
построенных в прямоугольной системе
координат так, что их основаниями служат
интервалы
отложенные на оси абсцисс, а высоты
равнысоответственноi—му
основанию
(см. рис.1).

Рис.
1

Кривая
l
, проходящая через середины ступеней
гистограммы дает приближенное
представление о кривой распределения
признака X
и называется эмпирической кривой
распределения. Площадь гистограммы
равна единице. Часто из некоторых
предпосылок бывает известен тип закона
распределения признака X,
но неизвестны параметры этого
распределения. Например, известно, что
плотность распределения признака X
задана функцией
,
где– неизвестные параметры. Ставится
задача нахождения статистических
оценок
параметровпо выборке (3.1.1) наблюдений надX
. Таким образом, оценки – функции от
выборочных значений.

Одним
из методов построения таких оценок
является метод
моментов,
который основывается на близости
теоретических и эмпирических моментов.
Он состоит в следующем:

23

По
формуле (2 2 9) по плотности распределения
находимk
первых начальных теоретических моментов
признака X

(3.1.4)

затем
по выборке (3.1.1) вычисляем соответственные
выборочные моменты

(3.1.5)

Приравнивая
каждый теоретический момент
соответствующему выборочному, получаем
систему из k
уравнений

,

(3.1.6)

с
неизвестными
.

Решение
системы (3.1.6), зависящее от элементов
выборки (3.1.1), принимают в качестве
статистических оценок параметров.

Величина
(3.1.7)

называется
выборочной
средней и
служит статистической оценкой для МХ.

Величина

(3.1.8)

называется
несмещенной выборочной дисперсией и
служит статистической оценкой для DX.

и
– точечные оценки параметровMX
и DX.

В
математической статистике используются
еще и интервальные оценки. Доверительным
называют интервал, концы которого
зависят от выборочных значений и которые
с заданной доверительной
вероятностью
покрывает оцениваемый параметр.

24

14.
Два стрелка стреляют по одной мишени,
делая независимо друг от друга по два
выстрела. Вероятность попадания в
мишень для первого стрелка — 0,5, для
второго — 0,6. Найдите закон распределения
случайной величины Х, равной общему
числу попаданий в мишень. Найти
математическое ожидание М(Х), дисперсию
D(X), среднее квадратическое отклонение
(Х)

15
Рабочий обслуживает 3 независимо
работающих станка. Вероятность того,
что в течение часа станок не потребует
внимания рабочего, равна для первого
станка- 0,7, для второго — 0,8, для третьего
— 0,9. Найдите закон распределения
случайной величины Х, равной числу
станков, которые не потребуют внимания
рабочего. Найти математическое ожидание
М(Х), дисперсию D(X), среднее квадратическое
отклонение (Х).

16
Случайная величина X,
сосредоточенная на интервале [2;6],
задана функцией распределения

F{x) =1/16(x²–4x+4).
Найти вероятность того, что случайная
величина Х
примет
значения: а) меньше 4; б) меньше 6;
в) не меньше 3; г) не меньше 6.

17.
Случайная величина X,
сосредоточенная на интервале [-1,3],
задана функцией распределения
F(x)=0,25x+0,25
Найти вероятность попадания случайной
величины Х
в интервал [0; 2]. Построить график функции
F(x).

18
. Случайная
величина X,
сосредоточенная на интервале [2;6], задана
функцией распределения
F{x) =1/16(x²–4x+4).
Найти вероятность того, что случайная
величина Х
примет
значения: а) меньше 4; б) меньше 6;
в) не меньше 3; г) не меньше 6.

19.
Вероятность попадания стрелком при
каждом выстреле равна 0,4. Имея в запасе
6 патронов, он ведет стрельбу до первого
попадания в мишень или до израсходования
всех патронов. Найдите закон распределения
случайной величины Х, равной числу
израсходованных патронов. Найти
математическое ожидание М(Х), дисперсию
D(X), среднее квадратическое отклонение
(Х).

65

9
C вероятностью попадания при одном
выстреле 0,8 охотник стреляет по дичи
до первого попадания, но успевает
сделать не более 3 выстрелов. Дискретная
случайная величина Х — число промахов.
а) Найдите закон распределения
Х. б) Найдите вероятности событий: Х <
2; Х 
2; 1 < Х 
3. в) Найти математическое ожидание
М(Х), дисперсию D(X), среднее квадратическое
отклонение 
(Х)

10.
2 стрелка делают по одному выстрелу в
мишень. Вероятность попадания для
первого стрелка при одном выстреле —
0,6, для второго — 0,7. Дискретная случайная
величина Х — число попаданий в мишень.
а) Найдите закон распределения Х. б)
Найдите вероятность события Х 
1.в) Найти математическое ожидание
М(Х), дисперсию D(X), среднее квадратическое
отклонение (Х)

11.
В коробке имеется 8 карандашей, из
которых 3 красных. Из этой коробки
наудачу извлекаются 3 карандаша. а)
Найдите закон распределения случайной
величины Х, равной числу красных
карандашей в выборке. б) Найдите
вероятность события 0 < Х 
2. в) Найти математическое ожидание
М(Х), дисперсию D(X), среднее квадратическое
отклонение (Х)

12.
Автомат штампует детали. Контролируется
длина детали Х, которая распределена
нормально с математическим ожиданием
(проектная длина), равным 50 мм. Фактическая
длина изготовленных деталей не менее
48 мм и не более 52 мм. Найти вероятность
того, что длина наудачу взятой детали:
а) больше 49 мм; б) меньше 51 мм. (Указание:
из равенства Р(48 <X< 52) = 1 предварительно
найти 
).

13.
В партии из 10 деталей имеется 5 стандартных.
Из этой партии наудачу взято 3 детали.
Найдите закон распределения случайной
величины, равной числу стандартных
деталей в выборке. Найти математическое
ожидание М(Х), дисперсию D(X), среднее
квадратическое отклонение (Х)

64

Предположим,
что выборка (3.1.1) взята из нормально
распределенной генеральной совокупности
признака Х
с неизвестными параметрами a
= МХ и
.

Связь
между доверительным интервалом,
покрывающим параметр а,
с доверительной вероятностью
задается при этих условиях формулой

,
(3.1.9)

где
t—
критическая точка распределения
Стьюдента с n-1
степенью свободы, соответствующая
уровню значимости
.
Для построения доверительного интервала,
покрывающего параметрс доверительной вероятностью,
используется другая формула

(3.1.10)

где
числа
инаходятся из уравнений

(3.1.11)

(3.1.12)

по
таблицам
—
распределения с (n-1)
степенью свободы, то есть
и—
критические точки— распределения с (n
– 1) соответствующие уровням значимости
и.

25

Пример.
Приведенные ниже данные о ценах на 100
видов товаров ( в у. е.) записаны в
случайном порядке

Используя
эти данные, необходимо:

1)
получить выборку, выбрав 20 значений,

2)
записать
эмпирическую функцию распределения;

3)
построить интервальный вариационный
ряд с шириной интервала 20 у.е;

4)
построить гистограмму и эмпирическую
кривую распределения;

5)
предполагая, что генеральная совокупность
имеет нормальное распределение с
плотностью распределения
найти методом моментов оценкиа
и

Решение

1. Произведем
   выборку. Получаем 125, 170, 151, 195, 173, 117,
   190, 133, 102, 151, 94, 94, 114, 153, 109, 148, 101, 139, 110, 144.

2. Для
   построения
   запишем элементы выборки в порядке
   возрастания: 94, 94, 101, 102, 109, 110, 114, 117, 125,
   133, 139, 144, 148, 151, 151, 153, 170, 173, 190, 196.

26

3
Вероятность того, что в библиотеке
необходимая студенту книга свободна,
равна 0,3 Составить закон распределения
числа библиотек, которые посетит
студент, если в городе пять библиотек
.Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение полученной случайной
величины

4
Вероятность того, что вошедший в
магазин покупатель сделает покупку,
равна 0,4. Предполагая, что покупатель
делает не более одной покупки, составить
закон распределения числа покупок,
сделанных в магазине, если вошло 5
человек Вычислить математическое
ожидание, дисперсию и среднее
квадратическое отклонение, полученной
случайной величины

5
Имеются 4 ключа из которых только один
подходит к замку. Составить закон
распределения числа попыток открывания
замка, если испробованный ключ в
после­дующих попытках не участвует.
Найти математическое ожидание, дисперсию
и среднее квадратическое откло­нение
этой случайной величины.

6
В магазине имеются 20 телевизоров, из
них 7 имеют дефекты. Необходимо:
а) составить закон распределе­ния
числа телевизоров с дефектами среди
выбранных наудачу пяти; б) найти
математическое ожидание и дисперсию
этой случайной величины: в) определить
вероятность того, что среди выбранных
нет телевизо­ров с дефектами

7. Распределение
дискретной случайной величины Х
за­дано формулой p{X=k}
=Ck²,
где k=1,
2, 3, 4, 5. Найти: а) константу С;
б) вероятность события |Х-2|  1
.

8.
Дискретная случайная величина Х- число
мальчиков в семьях с 4 детьми.
Предполагая равновероятными рождения
мальчика и девочки: а) найдите закон
распределения Х; б)найдите вероятности
событий: А — в семье не менее 2, но не
более 3 мальчиков; В — не более 3 мальчиков;
С — более одного мальчика. Найти среднее
квадратическое отклонение случайной
величины Х

63

28.
Промышленная телевизионная установка
содержит 1700 транзисторов. Вероятность
выхода из строя в течение гарантийного
срока каждого из транзисторов равна
0,002. Найти вероятность выхода из строя
в течение гарантийного срока: а) хотя
бы одного транзистора; б) не менее трех
транзисторов.

29. Из промежутка
[0;1] наугад выбраны два числа. Какова
вероятность того, что их сумма меньше
либо равна 1, а их разность больше 0?

30
Поток заявок, поступающих на телефонную
станцию, представляет собой простейший
поток событий. Известно, что в течение
некоторого промежутка времени среднее
число вызовов, поступающих за один час
равно 240. Для этого промежутка времени
найти вероятность того, что за одну
минуту поступит не менее трех вызовов.

Задание 5

1
Товаровед проверяет изделия на
стандартность, но проверяет не более
пяти изделий. Составить закон распределения
числа проверенных изделий, если
вероятность того, что изделие будет
признано стандартным, равна 0,6 Найти
математическое ожидание, дисперсию и
среднее квадратическое отклонение
полученной случайной величины

2
В лотерее на 1000 билетов разыгрываются
три вещи, стоимости которых 50, 30 и 20
рублей. Составить закон распределения
суммы выигрыша для лица, имеющего два
билета Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение полученной случайной
величины

62

3).
Составляем вариационный ряд с шириной
интервала h
= 20 (у .е )

27

4).
Строим гистограмму и эмпирическую
(выборочную) кривую распределения (рис
.2), откладывая на оси абсцисс интервалы,
а по оси координат

Рис.2

5).
При изучении нормального закона
доказывается, что в плотности
параметресть математическое ожидание, а параметр— дисперсия:

.

Приравнивая
теоретические моменты
ивыборочными,
получаем:

(3.1.13)

28

21
.Учебник издан тиражом 10000 экземпляров.
Вероят­ность того, что экземпляр
учебника сброшюрован не­правильно,
равна 0,0001. Найти вероятность того, что:
а) тираж содержит 5 бракованных книг;
б) по крайней мере 9998 книг сброшюрованы
правильно.

22.
Известно, что в среднем 60% всего числа
изготовляе­мых заводом телефонных
аппаратов является продукци­ей
первого сорта. Чему равна вероятность
того, что в из­готовленной партии
окажется: а) 6 аппаратов первого
сор­та, если партия содержит 10
аппаратов; б) 120 аппаратов первого
сорта, если партия содержит 200 аппаратов?

23
.Аудиторную работу по теории вероятностей
с первого раза успешно выполняют 50%
студентов. Найти веро­ятность того,
что из 400 студентов работу успешно
вы­полнят: a) 120 студентов, б) не
менее 180 студентов.

24. Сколько
нужно взять деталей, чтобы наивероятнейшее
число годных деталей было равно 50, если
вероятность того, что наудачу взятая
деталь будет бракованной равна 0,1?

25
. Вероятность того, что пассажир опоздает
к отправлению поезда, равна 0,01. Найти
наиболее вероятное число опоздавших
из 800 пассажиров и вероятность та­кого
числа опоздавших.

26.
Монета бросается до тех пор, пока герб
не выпадет 5 раз. Определить вероятность
того, что при этом решка выпадет 6 раз

27.
На контроль поступила партия деталей
из цеха. Известно, что в среднем 5 %
всех деталей не удовлетворяют стандарту.
Сколько нужно испытать деталей, чтобы
с вероятностью не менее чем 0,95 обнаружить
хотя бы одну нестандартную деталь?

61

14
Вероятность некоторого события равна
р в каждом
из
n
испытаний. Найти вероятность того, что
частота наступления события при n=1500
отклонится от р==0,4 в ту или другую
сторону меньше, чем на 0,02

15
. Сколько нужно произвести опытов, чтобы
с вероятностью 0,9 утверждать, что частота
интересующего нас события будет
отличаться от вероятности появления
этого события, равной 0.7 не более чем
на 0.01

16
. Вероятность появления некоторого
события в одном опыте равна 0,6. Какова
вероятность тоге, что это событие
появится в большинстве из 60 опытов?

17
Имеются 100 станков одинаковой мощности,
работающих независимо друг от друга в
одном режиме, при котором
их
привод оказывается включенным в течении
0,8 всего рабочего времени. Какова
вероятность того, что в произвольно
взятый момент времени окажутся
включенными от 70 до 86 станков?

18
Два равносильных противника играют
в шахматы. Что более вероятно: а) выиграть
2 партии из 4 или 3 партии из 6?; б) не
менее 2 партий из б или не менее 3 партий
из б? (Ничьи в расчет не принимаются).

19
В банк отправлено 4000 пакетов денежных
знаков. Ве­роятность того, что пакет
содержит недостаточное или избыточное
число денежных знаков, равна 0,0001. Най­ти
вероятность того, что при проверке
будет обнаруже­но: а) три ошибочно
укомплектованных пакета; б) не более
трех пакетов.

20.
Строительная фирма, занимающаяся
установкой лет­них коттеджей,
раскладывает рекламные листки по
почтовым ящикам. Прежний опыт работы
компании показывает, что примерно в
одном случае из двух ты­сяч следует
заказ. Найти вероятность того, что при
размещении 100 тыс. листков число заказов
будет: а) равно 48; б) находиться в
границах от 45 до 55

60

(3
.1. 14)

Используя
обозначение
(3.1.7),
имеем

(3.1.
15)

Преобразовывая
(3.1.10),
находим

.

Итак,

. (3. 1. 16)

Полученная
нами методом моментов оценка (3.1.16)
называется смещенной выборочной
дисперсией.

По выборке вычислим
оценки (3.1.15) и (3.1.16):

29

6)
По формуле (3.1..9):

.

По
условию задачи
.

В
5) мы вычислили
.
Для вычисления несмещенной выборочной
дисперсии,
сравним формулы (3. 1. 3) и (3. 1. 16). Видим,
что

.

Подставляя
в эту формулу, имеем

.

Отсюда
.

По
таблицам распределения Стьюдента с
n-1=19
степенью свободы находим t
при доверительной вероятности 0,95.

.

Выписываем
из (3. 1. 9) доверительный интервал:

покрывающий
параметр
с вероятностью 0,95.

По формуле (3.1.10)

и
находим по таблице распределениясn-1=19
степенью свободы, используя формулы
(3.1. 11) и (3 1 12) с
.

30

6
. Определите вероятность того, что номер
первой встретившейся автомашины не
содержит : а) цифры пять; б) двух и более
пятерок; в) ровно двух пятерок Известно,
что все номера четырехзначные,
неповторяющееся и равновозможные(считается
возможным номер 0000).

7
. При передаче сообщения вероятность
искажения одного знака равна 1/10. Каковы
вероятность того, что сообщение из 10
знаков: а не будет искажено; б) содержит
ровно 3 искажения; в) содержит не более
трех искажений

8
Если в среднем левши составляют I,
каковы шансы на то, что среди 200 человек
а) окажется ровно четверо левшей; б)
найдется четверо левшей

9
Вероятность выпуска сверла повышенной
хрупкости (брак) равна 0.02. Сверла
укладываются в коробки по 100 штук. Найти
вероятность того, что а) в коробке не
окажется бракованных сверл; б) число
бракованных сверл окажется не более
3; в) сколько нужно класть в коробку
сверл, чтобы с вероятностью не меньшей
0,9, в ней было не менее 100 исправных

10
Аппаратура содержит 2000 одинаково
сделанных элементов, вероятность отказа
каждого из которых равна 0,0005. Какова
вероятность того, что откажет аппаратура,
если он наступает при отказе хотя бы
одного из элементов?

11.
Найти вероятность того, что среди 200
изделий окажется
более трех
бракованных, если в среднем бракованные
изделия составляют I .%.

12
. В первые классы должно быть принято
200 детей. Определить вероятность того,
что среди них окажется 100 девочек, если
вероятность рождения мальчика равна
0,515.

13
.Вероятность появления успеха в каждом
испытании равна 0,25. Какова вероятность,
что при 300 испытаниях успех наступит:
а) ровно 75 раз, б) ровно 85 раз?

59