-
-
January 27 2009, 16:59
- Наука
- Cancel
Нормальное распределение
Научно-аналитический центр Интеграл
Ошибка взвешивания – случайная величина, распределенная по нормальному закону с математическим ожиданием a = 0 и среднеквадратическим отклонением σ = 2 грамма. Найти вероятность того,что взвешивание проведено с ошибкой, не превышающей по модулю ε = 4 грамма.
Вероятность того, что абсолютная величина отклонения нормально распределённой случайной величины не превысит положительного числа ε, определяется по формуле:
P = P(|X – a| ≤ ε) = 2∙Φ(ε/σ),
где Φ(t) – функция Лапласа.
Подставим численные значения
P = 2∙Φ(4/2) = 2∙Φ(2)
По таблице значений функции Лапласа находим: Φ(2) = 0,4772
Тогда P = 2∙0,4772 = 0,9544
Условие
![]()
4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.
Отв. 0,96.
математика ВУЗ
10140
Решение
![]()
★
Пусть случайная величина Х — ошибка измерения.
Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994
Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006
Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04
Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96
Написать комментарий
Нормальным
называют распределение вероятностей
непрерывной случайной величины X,
плотность которого имеет вид
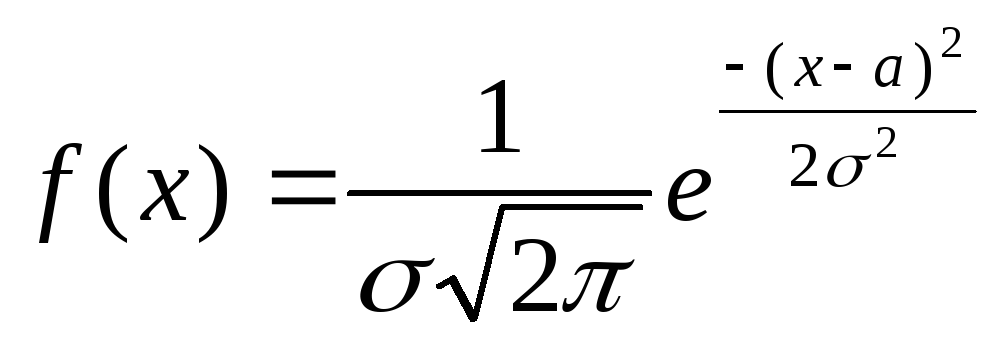 ,
,
где
a-математическое
ожидание,![]() — среднее квадратичное отклонение X.
— среднее квадратичное отклонение X.
Вероятность того, что Х примет значение,
принадлежащее интервалу (α,β):
![]() ,
,
где
![]() — функция Лапласа.
— функция Лапласа.
Пример
99.Математическое ожидание и среднее
квадратическое отклонение нормально
распределенной случайной величины Х
примет значение: а) в интервале (-1,2); б)
меньше -1; в) больше 2; г) отличающееся от
своего среднего значения по абсолютной
величине не больше, чем на 1.
Решение.По условию задачи a=0, σ=2, тогда:
а)

б)
![]()
в)
![]()
г)
![]()
Здесь
значения функции Φ(x) были найдены по
таблице и учитывалось, что Φ(-x) = -Φ(x), а
![]() .
.
100.
Плотность распределения ошибки выходного
параметра РЭА имеет вид
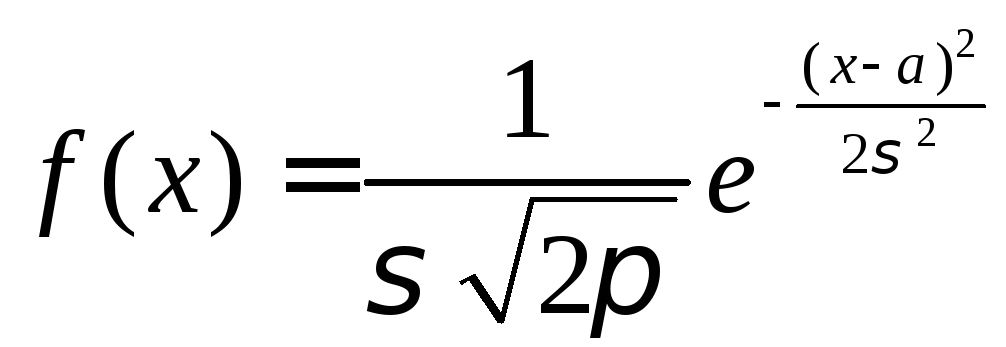 .
.
Сборочные
операции изменяют числовые характеристики
распределения, не изменяя закона. Что
больше увеличивает вероятность появления
брака: систематическое смещение значения
ошибки выходного параметра на а
единиц или увеличение
дисперсии ошибки на эти же а
единиц?
101.
Математическое ожидание и дисперсия
случайного напряжения с нормальным
распределением равны 10 В и 25 В2
соответственно. Какова вероятность
того, что измеренное значение напряжения
а) будет больше
0?
б) будет находиться
в интервале от 0 до математического
ожидания?
в) будет в два раза
больше математического ожидания?
102.
Широко распространенный метод обнаружения
сигнала в присутствии шума заключается
в установлении определенного порогового
уровня, с которым производится
сравнение результатов измерения
напряжения, включающего полезный сигнал
и шум. Если установленный порог
превышается, то считают, что полезный
сигнал присутствует. Естественно, иногда
и при отсутствии сигнала шум превосходит
этот порог, и такая ситуация называется
ложной тревогой.
Желательно, чтобы
вероятность ложной тревоги была ничтожно
мала. В то же время необходимо, чтобы
результат любого измерения, проведенного
при наличии сигнала, смешанного с шумом,
с большой вероятностью превосходил
установленный порог. Она называется
вероятностью правильного
обнаружения и должна
как можно меньше отличаться от 1.
Пусть шум характеризуется
нормальным распределением с нулевым
математическим ожиданием и дисперсией
1В2,
а установленный порог равен 5 В.
а) Определите
вероятность ложной тревоги.
б) Определите
вероятность правильного обнаружения
сигнала величиной 8 В в присутствии шума
с заданными выше параметрами.
103.
Математическое ожидание и среднее
вадратическое отклонение нормально
распределенной случайной величины X
соответственно равны 20 и 5. Найти
вероятность того, что в результате
испытания X примет значение, заключенное
в интервале (15, 25).
104.
Производится взвешивание некоторого
вещества без систематических ошибок.
Случайные ошибки взвешивания подчинены
нормальному закону со средним
квадратическим отклонением σ = 20 г. Найти
вероятность того, что взвешивание будет
произведено с ошибкой, не превосходящей
по абсолютной величине 10 г.
105. Случайные ошибки
измерения подчинены нормальному закону
со средним квадратическим отклонением
σ = 20 мм и математическим ожиданием а =
0. Найти вероятность того, что из трех
независимых измерений ошибка хотя бы
одного не превзойдет по абсолютной
величине 4 мм.
106.
Вывести «правило трех сигм»: вероятность
того, что абсолютная величина отклонения
нормально распределенной случайной
величины будет меньше утроенного
среднего квадратического отклонения,
равна 0,9973. 107. Станок-автомат изготовляет
валики, причем контролируется их диаметр
X. Считая, что X—нормально распределенная
случайная величина с математическим
ожиданием а=10мм и средним квадратическим
отклонением σ = 0,1 мм, найти интервал,
симметричный относительно математического
ожидания, в котором с вероятностью
0,9973 будут заключены диаметры изготовленных
валиков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
 |
 |
Теория вероятностей |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №16373 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
225 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением 𝜎 = 20 мм и математическим ожиданием 𝑎 = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм.
Решение
Вероятность того, что модуль отклонения случайной величины Х от своего математического ожидания 𝑎 меньше любого положительного 𝜀, равна где Ф(𝑥) – функция Лапласа. По условию тогда, вероятность того, что при одном независимом измерений ошибка измерения не превзойдет по абсолютной величине 4 мм, равна: Воспользуемся формулой Бернулли. Если производится 𝑛 независимых испытаний, при каждом из которых вероятность осуществления события 𝐴 постоянна и равна 𝑝, а вероятность противоположного события равна , то вероятность того, что при этом событие 𝐴 осуществляется ровно 𝑚 раз, вычисляется по формуле где 𝐶𝑛 𝑚 — число сочетаний из 𝑛 элементов по 𝑚. Для данного случая Вероятность события 𝐴 – из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм, равна: Ответ:

Похожие готовые решения по теории вероятности:
- Пачки чая упаковываются автоматически. Масса одной пачки чая распределена по нормальному закону со средним
- Диаметр детали – случайная величина, подчиненная нормальному закону с 𝑎 = 5 см и 𝜎 = 0,9 см. Найти вероятность
- Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того
- Ошибка измерения подчинена нормальному закону с математическим ожиданием, равным 1, и дисперсией, равной 4. Определить вероятность
- Определить вероятность того, что случайная ошибка измерения ∆ не превзойдет по абсолютной величине удвоенное значение
- Диаметр выпускаемых деталей имеет нормальное распределение со стандартным значением М(Х) и средним квадратическим
- Деталь, изготовленная автоматом, считается бракованной, если отклонение ее контролируемого размера Х от номинала превышает
- Ошибка взвешивания – случайная величина, распределенная по нормальному закону с математическим ожиданием, равным нулю
- Дана выборка 1 1 3 5 4 3 2 1 1 6 3 4 4 5 0 7 5 3 0 4 Составить статистический ряд частот, статистический ряд
- Дана выборка 1 3 3 1 4 1 2 3 1 5 3 4 4 5 2 6 2 3 3 4 Составить статистический ряд частот, статистический ряд
- Дана выборка 2 3 3 5 4 2 2 1 4 6 1 4 4 5 2 7 5 5 7 2 Составить статистический ряд частот, статистический ряд
- Дана выборка -2 3 3 5 4 -1 2 -1 1 0 3 4 4 0 2 7 5 3 3 0 Составить статистический ряд частот, статистический ряд
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.
поделиться знаниями или
запомнить страничку
- Все категории
- экономические
43,607 - гуманитарные
33,643 - юридические
17,916 - школьный раздел
611,340 - разное
16,895
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
2. Пусть [math]X[/math]— ошибка измерения, [math]sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = Pleft( {left| X right| < 2} right) = Pleft( {left| {frac{X}{sigma }} right| < frac{2}{sigma }} right) = Phi left( {0.2} right) — Phi left( { — 0.2} right) = 2 cdot Phi left( {0.2} right) — 1 = 2 cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]Phi left( x right)[/math] отличается от функции, которую использовал Alexdemath
3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]Pleft( {X < 15} right) = intlimits_0^{15} {lambda cdot e^{ — lambda x} dx} = 1 — e^{ — 15lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]pleft( t right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]Pleft( {X < 15} right) = 1 — Pleft( {X > 15} right) = 1 — intlimits_{15}^infty {pleft( t right)dt} = 1 — intlimits_{15}^infty {frac{t}{t}pleft( t right)dt} geqslant 1 — frac{1}{{15}}intlimits_0^infty t pleft( t right)dt = 1 — frac{8}{{15}} = frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.
Ошибка взвешивания – случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 0, и среднеквадратическим отклонением равным 9 грамм. Найти вероятность того, что взвешивание проведено с ошибкой, не превышающей по модулю 18 грамм.
Для нормального распределения вероятность того, что абсолютная величина отклонения Х – а будет меньше чем : .
У нас а = 0, σ = 9, = 18.
Ответ:

- Ошибка измерения X имеет нормальный закон распределения N(-1;2).
1) Найдите вероятность того, что при измерении - Ошибки измерения распределены нормально, причем математическое ожидание равно нулю, а среднее квадратичное отклонение равно
- Ошнурова Анастасия Сергеевна: n=8 – количество букв в фамилии, m=9 – количество букв в
- Ощущаются ли участниками достоверные сдвиги в уровне владения этим навыком после тренинга?
Образец решения - Ощущаются ли участниками достоверные сдвиги в уровне владения этим навыком после тренинга?
Образец решения. 2 - Ощущаются ли участниками достоверные сдвиги в уровне владения этим навыком после тренинга?
Образец решения задачи - П. 10 ноября 2018 года выдал доверенность С. на продажу принадлежащего ему автомобиля ВАЗ
- Оценочная стоимость активов предприятия составляет 22000 долл. Для его ликвидации потребуется 2 года. Затраты
- Оценщику следует оценить поправку на наличие камина. В таблицу 1 занесена необходимая информация о
- Оценщик устанавливает наиболее эффективное использование земельного участка. Объект недвижимости приносит владельцу доход в размере
- Оценщик устанавливает наиболее эффективное использование свободного участка земли. При первом из возможных вариантов использования
- Очень длинный проводник, по которому идет ток силой I=5A, изогнут, как показано на рисунке.
- Очень тонкий провод диаметром 5 мкм помещен между двумя плоскопараллельными стеклянными пластинами. Свет с
- Очень тонкий провод диаметром 5 мкм помещен между двумя плоскопараллельными стеклянными пластинами. Свет с. 2
Тема. Законы распределения случайных величин
1. Нормальное распределение
Пример 1.Вес вылавливаемых в пруду
рыб подчиняется нормальному закону с
математическим ожиданием, равным 375 г,
и средним квадратическим отклонением
25 г. Определить вероятность того, что
вес одной пойманной рыбы будет заключен
в пределах от 300 до 400г.
Решение.
Дано: М(Х)=а=375 г.,
![]() г.,
г.,
с=300г.,d=400г.
Найдем искомую вероятность.
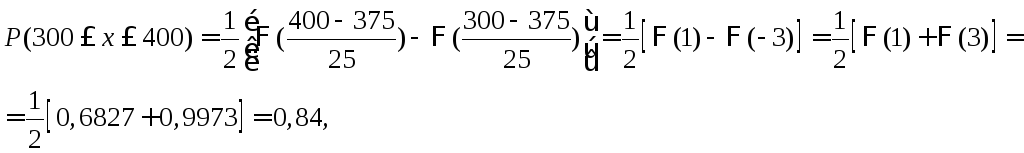
где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.
Пример 2. Ошибка измерения прибора
подчиняется нормальному распределению.
С вероятностью 0,92 ошибка измерения не
превосходит 4. Найти среднее квадратическое
отклонение ошибки прибора. Систематическая
ошибка отсутствует.
Решение.
Дано:
![]() ,
,![]()
Воспользовавшись второй теоремой о
нормальной случайной величине, найдем
величину
![]() .
.
Из таблицы Лапласа, зная
![]() , найдемt=1,75.
, найдемt=1,75.
Тогда
![]() или
или![]()
Ответ:
![]() .
.
2. Равномерное распределение
Пример 3. Цена деления шкалы
прибора 0,5 вольт. При измерениях показания
округляются до ближайшего целого
деления. Найти вероятность того, что
при считывании показаний будет сделана
ошибка, не превышающая 0,01 вольт.
Решение.
Дано: Случайная величина Х — истинное
показание прибора имен равномерное
распределение с параметрами а=0 ,в=0,5. Тогда![]() .
.
Искомая вероятность – это вероятность
показания х либо на![]() ,
,
либо на![]() .
.
![]()
Задания для самостоятельной работы
1) Размер детали подчиняется
нормальному закону распределения со
средней арифметической 15 мм и дисперсией
0,25. Определить ожидаемый процент брака,
если допустимые размеры находятся в
пределах от 14 мм до 17 мм. Найти выражение
интегральной и дифференциальной функции.
2) Изготовленные цехом детали по
размерам диаметра распределяются по
нормальному закону с математическим
ожиданием, равным 4,5 см, и средним
квадратическим отклонением 0,5 см.
Определить вероятность того, что размер
диаметра наудачу взятой детали отклонится
от математического ожидания не более,
чем на 1 см.
3) Математическое ожидание нормально
распределенной случайной величины
равно 15, среднее квадратическое отклонение
равно 5. Определить вероятность того,
что абсолютная величина отклонения
Х-М(Х) будет меньше 10.
4) Ошибка измерения – нормально
распределенная случайная величина с
дисперсией, равной 100. Систематическая
ошибка отсутствует. Найти вероятность
того, что ошибка измерения окажется в
интервале (3;6).
5) Ошибка взвешивания – случайная
нормально распределенная величина с
дисперсией 400. Весы заранее настроены
на обвес 50 г. Найти вероятность того,
что ошибка взвешивания находится в
пределах от 30 до 70 г.
6) Автобус некоторого маршрута идет
с интервалом в десять минут. Пассажир
в какой-то момент подходит к остановке.
Время, в течении которого пассажир
ожидает автобус, представляет случайную
величину, имеющую равномерное
распределение. Определить дифференциальную
функцию распределения этой случайной
величины, ее математическое ожидание
и дисперсию.
7) По данным задачи 6 определить
вероятность того, что пассажир подошедший
к остановке, будет ждать автобус менее
4 минут.
 Цена деления шкалы измерительного
Цена деления шкалы измерительного
прибора равна 0,2. Показания прибора
округляют до ближайшего целого деления.
Найти вероятность того, что при отсчете
будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05.
9) Минутная стрелка электрических
часов перемещается скачком в конце
каждой минуты. Найти вероятность того,
что в данное мгновение часы покажут
время, которое отличается от истинного
не более чем на 20 сек.
Форма контроля:
Проверка
решений задач и заданий
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закажите у меня новую работу, просто написав мне в чат!
Пачки чая упаковываются автоматически. Масса одной пачки чая распределена по нормальному закону со средним значением веса 200 граммов и средним квадратическим отклонением 5 граммов. Определите вероятность того, что вес случайно выбранной пачки чая отличается от среднего веса по абсолютной величине не более чем на 5 граммов.
Вероятность того, что модуль отклонения случайной величины 𝑋 от своего математического ожидания 𝑎 меньше любого положительного 𝜀, равна где Ф(𝑥) – функция Лапласа, 𝜎 – среднее квадратическое отклонение. При заданных условиях: Ответ:






