Нормальным
называется распределение непрерывной
случайной величины, дифференциальная
функция (плотность распределения)
которой имеет вид
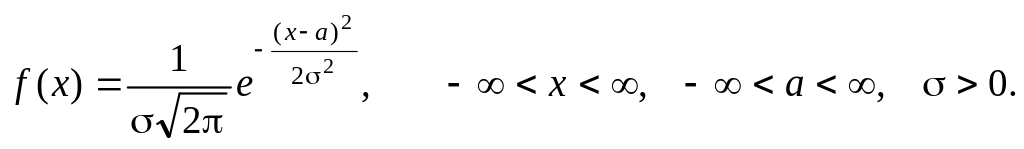
(5.17)
Параметр а
является математическим ожиданием
случайной величины, параметр
– ее средним квадратическим отклонением.
Нормальное распределение с указанными
параметрами обозначается
![]()
Интегральная
функция нормального распределение
нормированной случайной величины N(0,
1) имеет вид
![]()
(5.18)
Вероятность
попадания случайной величины
![]()
в интервал
![]()
равна
приращению интегральной функции Лапласа:
![]()
где
![]()
а
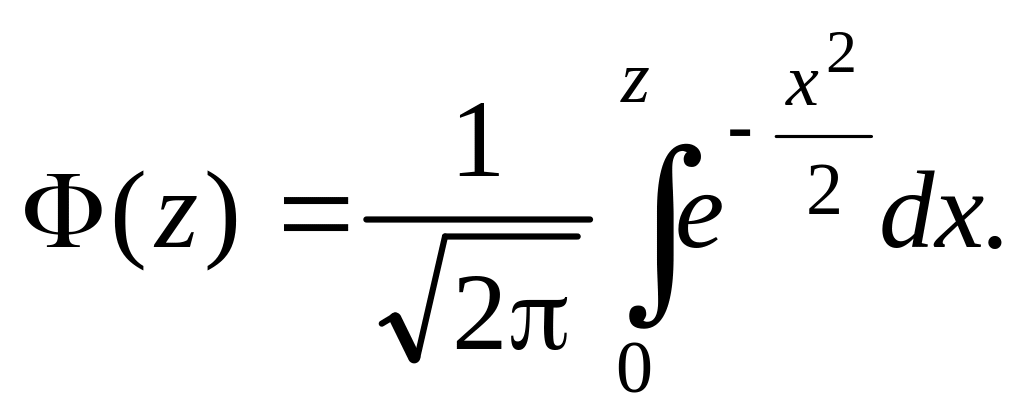
Отсюда
![]()
Вероятность
заданного отклонения случайной величины
от ее математического ожидания вычисляется
как удвоенная функция Лапласа:
![]()
.
Для нормального
распределения асимметрия и эксцесс
равны нулю, а мода и медиана совпадают
с математическим ожиданием, т.е. равны
а.
-
Измерение
дальности до объекта сопровождается
случайной ошибкой, подчиненной
нормальному закону со средним
квадратическим отклонением
= 100 м. Найти: а) вероятность того, что
измеренная дальность не превзойдет
истинной более чем на 150 м ; б) вероятность
измерения дальности с ошибкой, не
превосходящей по абсолютной величине
150 м.
Пусть случайная
величина Х – случайная ошибка
измерения дальности. По условию она
распределена по закону N(0,
100).
а) Событие А =
измеренная дальность
не превзойдет истинной
означает, что ошибка измерения Х
150. Тогда искомая вероятность
![]()
Из таблицы значений
функции
![]()
(табл.
2 Приложений) находим:
![]()
Значит,
![]()
б) Вероятность
заданного отклонения
![]()
где
![]()
Отсюда
![]()
-
Случайная
величина Х
распределена
по закону N(10;
2). Найти вероятность того, что в
результате испытания она примет
значение из интервала (12, 14). -
Деталь,
изготовленная автоматом, считается
годной, если отклонение ее размера Х
от номинала
не превышает 10 мк. Точность изготовления
детали характеризуется средним
квадратическим отклонением .
Считая, что
= 5 мк и Х
подчиняется закону N(a,
),
определить процент выпускаемых годных
изделий. -
Химический
завод выпускает серную кислоту
номинальной плотности 1,84 г/см3.
Известно, что плотность 99,9% всех
реактивов лежит в интервале (1,82; 1,86).
Найти вероятность того, что партия
кислоты удовлетворяет стандарту, если
для этого достаточно, чтобы ее плотность
не отклонялась от номинала более чем
на 0,01 г/см3. -
Случайное
отклонение размера детали от номинала
имеет параметры а
= 0 и
= 5 мк. Сколько необходимо изготовить
деталей, чтобы с вероятностью не менее
0,9 среди них была хотя бы одна годная,
если для этого отклонение размера от
номинала должно быть не более 2 мк? -
Случайная
величина Х
– годовая
процентная ставка потребительского
кредита – подчинена закону нормальному
распределения с параметрами а
= 12,0% и
= 1,75%. Найти вероятность того, что в
текущем году процентная ставка не
превысит 15,5%. -
Размер
отчислений предприятия в социальные
и культурные фонды зависит от текущей
прибыли и является величиной случайной,
подчиненной закону N(27,
6). Найти доверительный интервал для
случайной величины отчислений при
заданной вероятности
= 0,95. -
Размер
потребительского кредита есть величина
случайная, подчиненная нормальному
распределению с параметрами а
= = 45 тыс.руб. и
= 12 тыс.руб. Найти вероятность того, что
очередной кредит будет выдан на сумму
не менее чем в 30 тыс.руб. -
Улов
тихоокеанской камбалы (в тоннах)
является величиной случайной, подчиненной
закону N(2,4;
0,6). Найти доверительный интервал, в
котором с вероятностью 0,9 окажется
очередное значение улова. -
Нагрузка,
испытываемая ваерным канатом при
донном тралении, является величиной
случайной, подчиненной нормальному
распределению с параметрами а
= 4,8 тс и
= 1,75 тс. При заданной вероятности 0,98
найти разрывную прочность каната, если
запас прочности должен быть не менее
трех.
61
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основы математической статистики
-
Выборочный
метод.
-
В городе А для
определения сроков гарантийного
обслуживания проведено исследование
величины среднего пробега автомобилей
(X), находящихся в
эксплуатации в течение двух лет с
момента продажи автомобиля магазином.
Получен следующий результат (тыс. км):
3,0; 14,4; 25; 18,6; 12,1; 10,6; 18; 17,3; 29,1; 20; 18,3; 21,5;
26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3;
4,2; 29,6; 25; 20; 14,4; 11,2. Требуется: а) составить
ряд распределения частот (вариационный
ряд); б) составить ряд распределения
относительных частот. -
По наблюденным
данным предыдущей задачи построить
многоугольник распределения (полигон
частот либо относительных частот). -
Выборка
задана интервальным вариационным
рядом:
|
i |
xi |
ni |
|
1 |
11-14 |
16 |
|
2 |
14-17 |
24 |
|
3 |
17-20 |
30 |
|
4 |
20-23 |
7 |
|
5 |
23-26 |
8 |
Построить гистограммы
выборочной оценки плотности вероятности
(гистограмму частот и гистограмму
относительных частот).
-
Найти числовые
характеристики выборки, по данным
задачи (1), такие как: размах, моду,
медиану, выборочное среднее, выборочную
дисперсию, выборочное ср. кв. отклонение. -
Найти
асимметрию и эксцесс по заданному
распределению выборки:
-

-2
0
1
2

5
15
30
10
-
Оценка
параметров распределения.
-
Найти
несмещенную оценку математического
ожидания и дисперсии с.в. Х.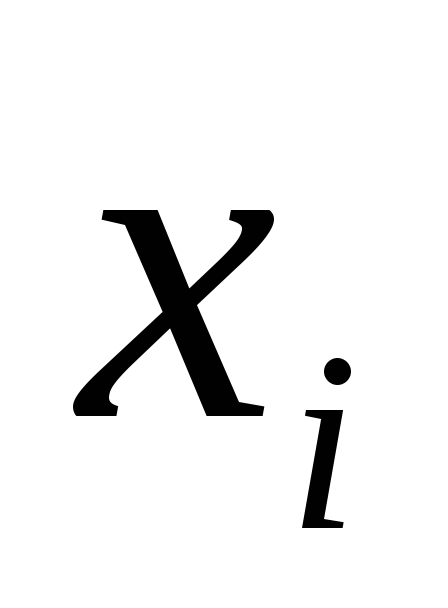
—
10-5
—
14

25
44
16
15
-
Случайная величина
X (время работы элемента)
имеет показательное распределение.
Ниже приведено эмпирическое распределение
среднего
времени работып=200 элементов
(в первой строке приведено среднее
время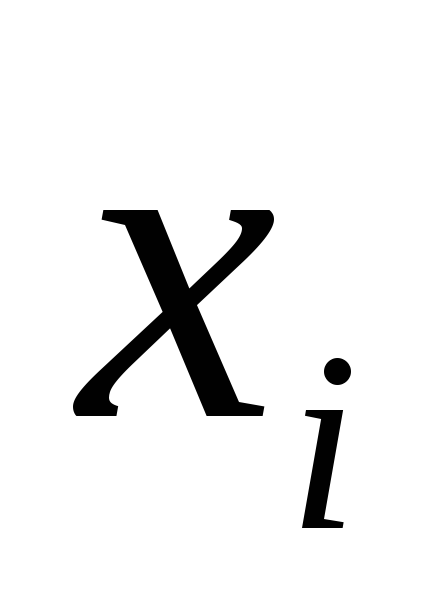 работы элемента в часах; во второй
работы элемента в часах; во второй
строке указана частота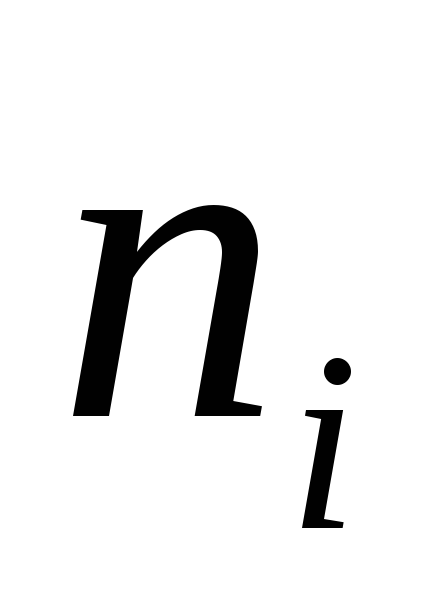 — количество элементов, проработавших
— количество элементов, проработавших
в среднем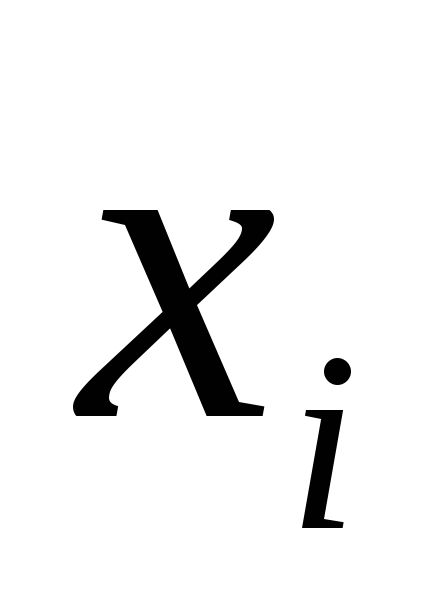 часов):
часов):
|
|
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
|
|
133 |
45 |
15 |
4 |
2 |
1 |
Найти методом
моментов точечную оценку неизвестного
параметра
![]() показательного распределения.
показательного распределения.
-
Случайная величина
X (ошибка измерения дальности
радиодальномером) подчинена равномерному
закону распределения с неизвестными
параметрами и
и .Ниже приведено эмпирическое распределение
.Ниже приведено эмпирическое распределение
средней ошибки = 200 измерений дальности (в первой строке
= 200 измерений дальности (в первой строке
указана средняя ошибка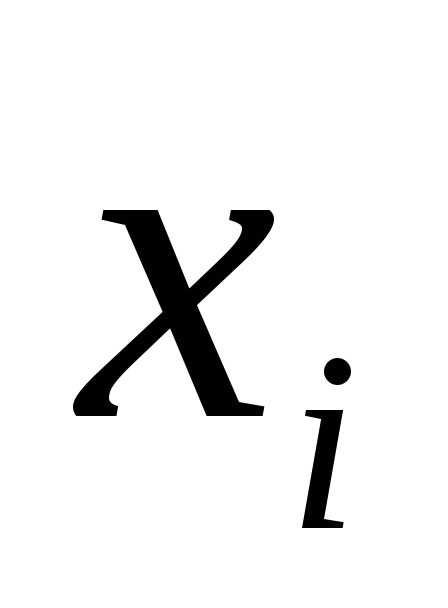 ;
;
во второй строке указана частота — количество измерений, имеющих среднюю
— количество измерений, имеющих среднюю
ошибку ):
):
![]() :
:
3 5 7 9 11 13 15 17 19 21
![]() :
:
21 16 15 26 22 14 21 22 18 25
Найти методом
моментов точечные оценки неизвестных
параметров
![]() и
и![]() равномерного распределения.
равномерного распределения.
-
Случайная величина
X (число семян сорняков в
пробе зерна) распределена по закону
Пуассона. Ниже
приведено распределение семян
сорняков вп= 1000 пробах
зерна (в первой строке указано
количество сорняков
сорняков
в одной пробе; во второй строке
указано — число проб, содержащих
— число проб, содержащих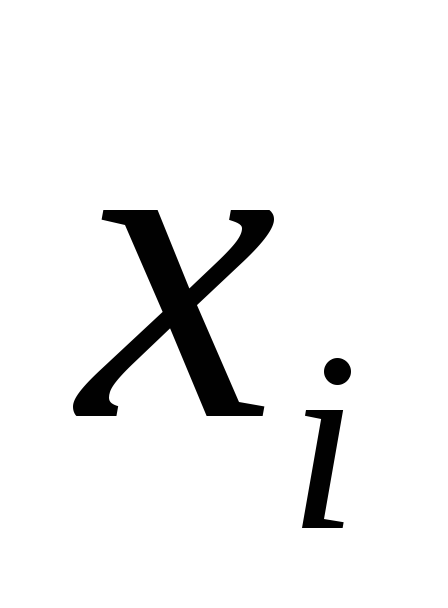
семян сорняков):
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
405 |
366 |
175 |
40 |
8 |
4 |
2 |
Найти методом
моментов точечную оценку неизвестного
параметра распределения Пуассона
![]() .
.
-
Случайная величина
X (отклонение контролируемого
размера изделия от номинала)
подчинена нормальному
закону распределения с неизвестными
параметрами и
и .
.
Ниже приведено эмпирическое
распределение отклонения
от номинала 200-т изделий (в первой
строке
указано отклонение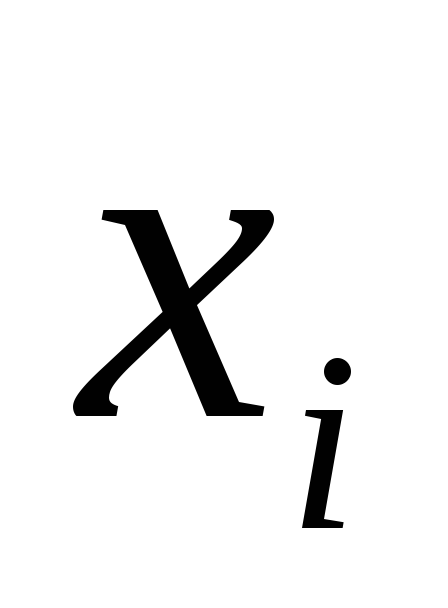 —
—
(мм); во второй строке приведена
частота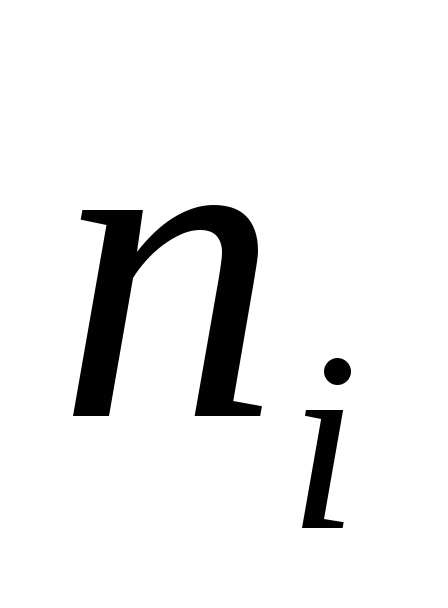 — количество изделий, имеющих отклонение
— количество изделий, имеющих отклонение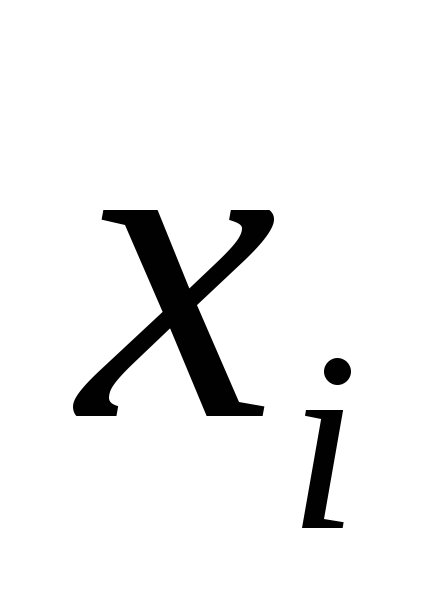 ):
):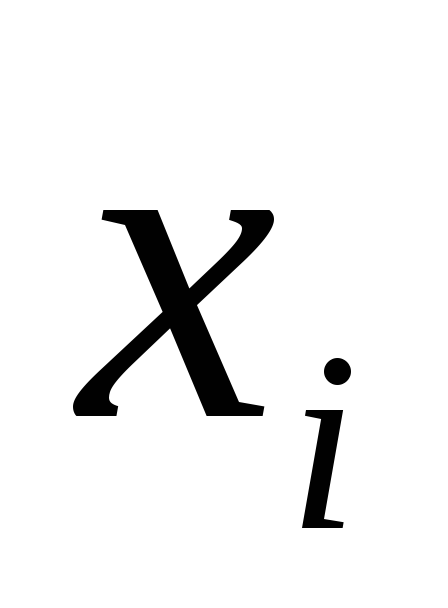 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9
0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9
2,2 2,3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
. . ,Хп точечную оценку параметра р биномиального распределениягде Х( — число появлений события в /-м опыте (/ = 1, 2,. . . , /г), т — количество испытаний в одном опыте.У к а з а н и е . Приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка.475. Случайная величина X (число появлений события А ъ т независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределениечисла появлений события в 10 опытах по 5 испытанийв каждом (в первой строке указано число Xi появленийсобытия А в одном опыте; во второй строке указаначастота л,- — количество опытов, в которых наблюдалосьXi появлений события Л):X,.л,.О512213141Найти методом моментов точечную оценку параметра рбиномиального распределения.У к а з а н и е .
Использовать решение задачи 474.476. Найти методом моментов по выборке х^, Xg, . . . ,Хп точечную оценку неизвестного параметра X показательного распределения, плотность которого f{x) = Xe-‘^^(х>0).477. Случайная величина X (время работы элемента)имеет показательное распределение f{x) = Xe-^ (х^О).Ниже приведено эмпирическое распределение среднеговремени работы п = 2 0 0 элементов (в первой строке при165ведено среднее время х^ работы элемента в часах; во второй строке указана частота щ—количество элементов»проработавших в среднем Х/ часов):Xi 2,5 7,5 12,5 17,5 22,5 27,5л^ 133 45 15421Найти методом моментов точечную оценку неизвестного параметра показательного распределения.У к а з а н и е .
Использовать решение задачи 476.478. Найти методом моментов точечную оценку параметра р (вероятности) геометрического распределенияP(X = Xi) = {}—pY»’^-pf где X/—число испытаний, произведенных до появления события; р—вероятность появления события в одном испытании.У к а з а н и е . Принять во внимание, что М(X) = 1/р (см. задачу 222).479. Найти методом моментов оценку параметра ргеометрического распределения Р{Х = х^) = {1—ру^’^-р^если в четырех опытах событие появилось соответственнопосле двух, четырех, шести и восьми испытаний.480. Найти методом моментов по выборке х^, х,, …»Хп точечные оценки неизвестных параметров а и р гамма-распределения, плотность которого/(^) = ра^хга+1)^^^»^^ ( а > — 1 . Р > 0 , х > 0 ) .Р е ш е н и е .
Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретическиймомент первого порядка Vi начальному эмпирическому моменту первого порядка Ml и центральный теоретический момент второго порядка fis центральному эмпирическому моменту второго порядка т^;Учитывая, что Vi = Ai(X), Мг^х^^ ^ia=Z>(X), m^^D^, имеемГЛ1(Х)=7,.*.Математическое ожидание и дисперсия гамма-распределения соответственно равны Л1 (Х) = (а+1)Р» D(X)=(aH-l)p* (см.
задачу 302), поэтому (^) можно записать в виде/(а+1)р=7„Ua+1)P*=I>B.Решив эту систему, окончателыю^ получим искомые JFOчeчныeоценки ненэтестяых параметров: а*=(х^)^/0,^—1, ^*=0^/х^’16в481. Случайная величина X (уровень воды в реке посравнению с номиналом) подчинена гамма-распределению,плотность которого определяется параметрами а и Э(а>—1, р>0):Ниже приведено распределение среднего уровня воды поданным /г = 45 паводков (в первой строке указан средний уровень воды х^ (см); во второй строке приведеначастота п^- — количество паводков со средним уровнемводы JC,):Xi 37,5 62,5 87,5 112,5 137,5 162,5 187,5 250 350п ^ 1 3 6 7754 8 4Найти методом моментов точечные оценки неизвестныхпараметров а и р рассматриваемого гамма-распределения.Р е ш е н и е . Используем точечные оценки параметров гаммараспределения (см.
задачу 480):OC*=(7B)VZ)B-1,Р*=^ВМВ.ППо заданному распределению легко найдем выборочную среднююи выборочную дисперсию: х^=1&6, DB = 6782.Подставив эти числа в формулы (*), окончательно получимискомые точечные оценки неизвестных параметров рассматриваемогогамма-распределения: а* =3,06, р* =40,86.482. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению.Испытания пяти элементов дали следующие наработки(время работы элемента в часах до отказа): 50, 75, 125, 250,300. Найти методом моментов точечные оценки неизвестных параметров а и р , которыми определяется гаммараспределение.У к а з а н и е .
Использовать решение задачи 480. Учесть, чтообъем выборки п = 5 мал, поэтому в формулах для вычисления параметров а и р вместо выборочной дисперсии подставить исправленную дисперсию s^ = ‘Lni(Xi—х^)^/(п — 1).483. Найти методом моментов по выборке лг^, Xg, .
. . ,Хп точечные оценки неизвестных параметров а и о нормального распределения, плотность которого/(л:) = —i=e-<^-«>V(2a«).У к а з а н и е . Приравнять начальный теоретический моментпервого порядка и центральный теоретический момент второго порядка соответствующим эмпирическим моментам.167484. Случайная величина X (отклонение контролируемого размера изделия от номинала; подчинена нормальному закону распределения с неизвестными параметрамиа и о.
Ниже приведено эмпирическое распределение отклонения от номинала п = 200 изделий (в первой строкеуказано отклонение х^- (мм); во второй строке приведеначастота п,- — количество изделий, имеющих отклонение Xf):Xi 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3п^ 6926 25 30 26 21 24 2085Найти методом моментов точечные оценки неизвестныхпараметров а и о нормального распределения.У к а з а н и е .
Использовать задачу 483.485. Найти методом моментов по выборке х^, дг^, …»х„ точечные оценки параметров а и b равномерного распределения, плотность которого / (х) = 1/(6—а) (6 > а).У к а з а н и е . Использовать решения задач 313, 315.486. Случайная величина X (ошибка измерения дальности радиодальномером) подчинена равномерному закону распределения с неизвестными параметрами а и Ь.Ниже приведено эмпирическое распределение среднейошибки л = 200 измерений дальности (в первой строкеуказана средняя ошибка л:,-; во второй строке указаначастота п^—количество измерений, имеющих среднююошибку АГ/):л:,.
3 5 7 9 11 13 15 17 19 21п^ 21 16 15 26 22 14 21 22 18 25Найти методом моментов точечные оценки неизвестныхпараметров а и Ь равномерного распределения.У к а з а н и е . Использовать задачу 485.487. Найти методом моментов по выборке х^, х^, . . . ,л:„ точечные оценки неизвестных параметров Х^ и Яд«двойного распределения» Пуассона1*Х= Xf) = -оГ •Х^’е~^«;1h «о* •Х^’е~^«i— »где х^ — число появлений события в п^ испытаниях Х^ иЯа—положительные числа, причем X2>^i.Р е ш е н и е . Если случайная величина Z распределена по законуПуассона с параметром X, то ее начальные теоретические моменты168первого и второго порядка соответственно равны (см.
задачи 207,227):Vi = Af(Z)==^,Найдем начальные теоретические моменты первого и второгопорядка рассматриваемой случайной величины X, учитывая соотношения (*):Vi = M (X) = A,,/2 + X2/2=(Xi + X2)/2,V2=Af(X2) = (l/2)(^i + A?)+(l/2)(X2 + ^ l ) = V i + ( > . ? + X i ) / 2 .Отсюда/Xi + X2 = 2vbXf + X| = 2v2 —2vi.Решив эту систему относительно неизвестных параметров, принявво внимание, что Лг > Ki, получим:^i = vi —Kv2-—Vi —V?, X2 = V i + K Va —Vi —V?.488. Случайная величина X распределена по «двойному» закону Пуассона:1 Xfe-^*1 Ц^e-^*Р (2С = X:) == «7Г •iЬ 7Г «i•Ниже приведено эмпирическое распределение числапоявлений события в л = 327 испытаниях (в первойстроке указано число х,- появлений события; во второйстроке приведена частота n^• — количество испытаний,в которых появилось Х/ событий):X,.
О 1 2 3 4 5 6 7 8 9 10п^ 28 47 81 67 53 24 13 8 3 2 1Найти методом моментов точечные оценки неизвестных параметров Х^ и К^ «двойного распределения» Пуассона.У к а з а н и е . Использовать решение задачи 487. Вычислить повыборке начальные эмпирические моменты первого и второго порядков:Ml = ( 2 niXi)/n, Af 2 = ( 2 ^i^b/^§ 3. Метод наибольшего правдоподобияМетод наибольшего правдоподобия точечной оценки неизвестныхпараметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров.А. Дискретные случайные величины.
Пусть X—дискретная случайная величина, которая в результате «опытов приняла возможные значения Xi, х^, . . . , л:„. Допустим, что вид закона распределения величины X задан, но неизвестен параметр в , которым оп169ределяетсяэтотзакон;требуетсянайтиего точечную оценкуОбозначим вероятность того, что в результате испытания величина X примет значение Xi через p(Xi 0 ) .Функцией правдоподобия дискретной ‘случайной величины Xназывают функцию аргумента 0 :ЦхиХ2, …,Хп 0) = p(-ti; е)’Р(Х2 в)…р(Хп).Оценкой наибольшего правдоподобия параметра 0 называюттакое его значение 0*, при котором функция правдоподобия достигает максимума.Функции L и In L достигают максимума при одном и том жезначении 0 , поэтому вместо отыскания максимума функции L ищут,что удобнее, максимум функции In L.Логарифмической функцией правдоподобия называют функцию InL.Точку максимума функции InL аргумента 0 можно искать, например, так:1 и чd InL1.
481. Случайная величина X (уровень воды в реке по сравнению с номиналом) подчинена гамма-распределению, плотность которого определяется параметрами а и Э (а>—1, р>0): Ниже приведено распределение среднего уровня воды по данным /г = 45 паводков (в первой строке указан средний уровень воды х^ (см); во второй строке приведена частота п^- — количество паводков со средним уровнем воды JC,): Xi 37,5 62,5 87,5 112,5 137,5 162,5 187,5 250 350 п ^ 1 3 6 7 7 5 4 8 4 Найти методом моментов точечные оценки неизвестных параметров аир рассматриваемого гамма-распределения. Решение. Используем точечные оценки параметров гаммараспределения (см. задачу 480): OC*=(7B)VZ)B-1, Р*=^ВМВ. П По заданному распределению легко найдем выборочную среднюю и выборочную дисперсию: х^=1&6, DB = 6782. Подставив эти числа в формулы (*), окончательно получим искомые точечные оценки неизвестных параметров рассматриваемого гамма-распределения: а* =3,06, р* =40,86. 482. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению. Испытания пяти элементов дали следующие наработки (время работы элемента в часах до отказа): 50, 75, 125, 250, 300. Найти методом моментов точечные оценки неизвестных параметров аир, которыми определяется гаммараспределение. Указание. Использовать решение задачи 480. Учесть, что объем выборки п = 5 мал, поэтому в формулах для вычисления параметров аир вместо выборочной дисперсии подставить исправленную дисперсию s^ = ‘Lni(Xi—х^)^/(п — 1). 483. Найти методом моментов по выборке лг^, Xg, …, Хп точечные оценки неизвестных параметров а и о нормального распределения, плотность которого /(л:) = —i=e-V(2a«). Указание. Приравнять начальный теоретический момент первого порядка и центральный теоретический момент второго порядка соответствующим эмпирическим моментам. 167
484. Случайная величина X (отклонение контролируемого размера изделия от номинала; подчинена нормальному закону распределения с неизвестными параметрами а и о. Ниже приведено эмпирическое распределение отклонения от номинала п = 200 изделий (в первой строке указано отклонение х^- (мм); во второй строке приведена частота п,- — количество изделий, имеющих отклонение Xf): Xi 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3 п^ 6 9 26 25 30 26 21 24 20 8 5 Найти методом моментов точечные оценки неизвестных параметров а и о нормального распределения. Указание. Использовать задачу 483. 485. Найти методом моментов по выборке х^, дг^, …» х„ точечные оценки параметров а и b равномерного распределения, плотность которого / (х) = 1/(6—а) (6 > а). Указание. Использовать решения задач 313, 315. 486. Случайная величина X (ошибка измерения дальности радиодальномером) подчинена равномерному закону распределения с неизвестными параметрами а и Ь. Ниже приведено эмпирическое распределение средней ошибки л = 200 измерений дальности (в первой строке указана средняя ошибка л:,-; во второй строке указана частота п^—количество измерений, имеющих среднюю ошибку АГ/): л:,. 3 5 7 9 11 13 15 17 19 21 п^ 21 16 15 26 22 14 21 22 18 25 Найти методом моментов точечные оценки неизвестных параметров а и Ь равномерного распределения. Указание. Использовать задачу 485. 487. Найти методом моментов по выборке х^, х^, …, л:„ точечные оценки неизвестных параметров Х^ и Яд «двойного распределения» Пуассона 1 Х^’е~^« 1 Х^’е~^« * Х = Xf) = -оГ • ; h «о* • i— » где х^ — число появлений события в п^ испытаниях Х^ и Яа—положительные числа, причем X2>^i. Решение. Если случайная величина Z распределена по закону Пуассона с параметром X, то ее начальные теоретические моменты 168
- Page 2 and 3:
В.Е. ГМУРМАН Руково
- Page 4 and 5:
Глава первая. < ОГЛА
- Page 6 and 7:
§ 2. Метод моментов 1
- Page 8 and 9:
§ 2. Характеристики
- Page 10 and 11:
Решение, а) Извлече
- Page 12 and 13:
14. В ящике 100 детале
- Page 14 and 15:
26. На отрезке L длин
- Page 16 and 17:
Искомая вероятност
- Page 18 and 19:
2. Пусть точка С рас
- Page 20 and 21:
Теорема сложення в
- Page 22 and 23:
несовместны, поэто
- Page 24 and 25:
вероятности следую
- Page 26 and 27:
72* Найти вероятност
- Page 28 and 29:
Сумма вероятностей
- Page 30 and 31:
Если p = (l + К 1—4*/3)/2,
- Page 32 and 33:
§ 3. Формула полной
- Page 34 and 35:
где Р (Л) = Р (В,) Рв, {А
- Page 36 and 37:
которая также оказ
- Page 38 and 39:
По формуле полной в
- Page 40 and 41:
115. В семье пять дет
- Page 42 and 43:
122. Вероятность рож
- Page 44 and 45:
произвести опытов,
- Page 46 and 47:
Отсюда По таблице п
- Page 48 and 49:
испытание, равна 0,9.
- Page 50 and 51:
Решение. По условию
- Page 52 and 53:
Окггавим производя
- Page 54 and 55:
Если число испытан
- Page 56 and 57:
среди отобранных),
- Page 58 and 59:
Второе орудие изра
- Page 60 and 61:
181. а) Устройство со
- Page 62 and 63:
можно. Другими слов
- Page 64 and 65:
§ 3. Числовые характ
- Page 66 and 67:
Pi^ p2> Pa» соответству
- Page 68 and 69:
Очевидно, все велич
- Page 70 and 71:
получим ….»М(?.)»‘1;+-+(
- Page 72 and 73:
209. Случайные велич
- Page 74 and 75:
21в. Найти дисперсию
- Page 76 and 77:
«первой» кости. Сде
- Page 78 and 79:
Преобразуем левую
- Page 80 and 81:
Принимая во вниман
- Page 82 and 83:
Найти центральные
- Page 84 and 85:
237. Доказать нераве
- Page 86 and 87:
§ 2. Теорема Чебышев
- Page 88 and 89:
Временно предполож
- Page 90 and 91:
254. Случайная велич
- Page 92 and 93:
261 • Дискретная слу
- Page 94 and 95:
Если х
- Page 96 and 97:
где f(x)—плотность р
- Page 98 and 99:
Центральные момент
- Page 100 and 101:
284. Случайная велич
- Page 102 and 103:
293. Случайная велич
- Page 104 and 105:
300. Случайная велич
- Page 106 and 107:
Решение. Преобразу
- Page 108 and 109:
310. Автобусы некото
- Page 110 and 111:
Найдем М(Х*) по форм
- Page 112 and 113:
величины X соответс
- Page 114 and 115:
X—а нормально расп
- Page 116 and 117:
Решение. Подставив
- Page 118 and 119: Учитывая, что /(х)=0 п
- Page 120 and 121: § 7. Функция надежно
- Page 122 and 123: надежности: вероят
- Page 124 and 125: Найти закон распре
- Page 126 and 127: распределения g{y) п
- Page 128 and 129: Подставляя (**) и (***)
- Page 130 and 131: Учитывая, что интег
- Page 132 and 133: где Л1(К) = (л2—в)/4 (см
- Page 134 and 135: 0(г), а затем продифф
- Page 136 and 137: Выполнив элементар
- Page 138 and 139: График плотности р
- Page 140 and 141: угольник со сторон
- Page 142 and 143: Итак, искомая двуме
- Page 144 and 145: зывают совокупност
- Page 146 and 147: все возможные знач
- Page 148 and 149: можных значений си
- Page 150 and 151: 433. Задана плотност
- Page 152 and 153: Часть третья ЭЛЕМЕ
- Page 154 and 155: Полигоном относите
- Page 156 and 157: а) Номер интервала
- Page 158 and 159: б) Номер интервала i
- Page 160 and 161: Решение. Несмещенн
- Page 162 and 163: 460. Найти выборочну
- Page 164 and 165: Найдем исправленну
- Page 166 and 167: ассона. Ниже привед
- Page 170 and 171: первого и второго п
- Page 172 and 173: появления события
- Page 174 and 175: Найдем логарифмиче
- Page 176 and 177: ратическом отклоне
- Page 178 and 179: Решение. Воспользу
- Page 180 and 181: покрывающий генера
- Page 182 and 183: Глава одиннадцатая
- Page 184 and 185: Б. Неравноотстоящи
- Page 186 and 187: столбце над и под у
- Page 188 and 189: Итак, для отыскания
- Page 190 and 191: ми, получим число 64
- Page 192 and 193: Выборочное уравнен
- Page 194 and 195: со а X ^ Si 1 ^ II ^ 1 ^ 1 о 7
- Page 196 and 197: 536. Найти выборочны
- Page 198 and 199: где п—объем выборк
- Page 200 and 201: б) у 7 13 40 80 200 Пх 0 19 2 2
- Page 202 and 203: § 3. Ранговая коррел
- Page 204 and 205: При проверке спосо
- Page 206 and 207: 548. Знания 10 студент
- Page 208 and 209: Для отыскания крит
- Page 210 and 211: генеральных диспер
- Page 212 and 213: Замечание. Если чис
- Page 214 and 215: затрачиваемого им
- Page 216 and 217: при уровне значимо
- Page 218 and 219:
572. Из двух партий и
- Page 220 and 221:
Мощность критерия
- Page 222 and 223:
Таким образом, ^=^’кр
- Page 224 and 225:
где 6 = r=r,A,= -i—7п= . Ис
- Page 226 and 227:
Если I Т’набд I ^двус
- Page 228 and 229:
значение критерия:
- Page 230 and 231:
§ 8. Сравнение наблю
- Page 232 and 233:
590. Завод рассылает
- Page 234 and 235:
1 , Номер выборки 1 I 2
- Page 236 and 237:
ные дисперсии si, S2, .
- Page 238 and 239:
изделий. С этой цел
- Page 240 and 241:
608. Для оценки качес
- Page 242 and 243:
гипотезу о равенст
- Page 244 and 245:
Y 65 70 75 80 85 90 95 Пх 12 —
- Page 246 and 247:
Решение. Найдем кри
- Page 248 and 249:
Найдем критическую
- Page 250 and 251:
строке приведены п
- Page 252 and 253:
§ 16. Проверка гипот
- Page 254 and 255:
1 1 о 3 4 5 G 7 8 9 2 «^i 1 15 26
- Page 256 and 257:
правило 2. Для того
- Page 258 and 259:
i 1 2 3 4 5 6 7 2 1 Границы
- Page 260 and 261:
в) Номер интер* вала
- Page 262 and 263:
Замечание 2. Если по
- Page 264 and 265:
б) Найдем графическ
- Page 266 and 267:
1 Номер варианты i 2
- Page 268 and 269:
среднего квадратич
- Page 270 and 271:
‘/•»‘/+1 0-5 б—10 10-15 133 45
- Page 272 and 273:
валы в часах, во вто
- Page 274 and 275:
требуется при уров
- Page 276 and 277:
во второй строке—ч
- Page 278 and 279:
Решение. 1. Найдем о
- Page 280 and 281:
Требуется при уров
- Page 282 and 283:
Из расчетной табли
- Page 284 and 285:
Глава четырнадр^ат
- Page 286 and 287:
668. Произведено по ч
- Page 288 and 289:
Номер испытания i 1 2
- Page 290 and 291:
выборки извлечены
- Page 292 and 293:
Сравним факторную
- Page 294 and 295:
новых средних. Пред
- Page 296 and 297:
Решение. Разобьем и
- Page 298 and 299:
Используя правило
- Page 300 and 301:
Указание. Для опред
- Page 302 and 303:
Выберем независимы
- Page 304 and 305:
Аналогично найдем
- Page 306 and 307:
Пусть задан закон р
- Page 308 and 309:
Разыграем X по прав
- Page 310 and 311:
б) Найдем надежност
- Page 312 and 313:
Абсолютная погрешн
- Page 314 and 315:
Номерзаявки i 1 2 3 4 5
- Page 316 and 317:
7*23 = 31,35 > 30, поэтому
- Page 318 and 319:
Номер испытания / 1 2
- Page 320 and 321:
можные значения X, к
- Page 322 and 323:
Из табл. 63 находим Е
- Page 324 and 325:
Результаты испытан
- Page 326 and 327:
Сравнительно больш
- Page 328 and 329:
Е е** si 1,42 Искомая оц
- Page 330 and 331:
751 • Найти оценку /J
- Page 332 and 333:
Часть пятая СЛУЧАЙ
- Page 334 and 335:
Нормированной корр
- Page 336 and 337:
Таким образом, У^ (0 =
- Page 338 and 339:
77в. Найти: а) матема
- Page 340 and 341:
взаимную корреляци
- Page 342 and 343:
796. Доказать, что ма
- Page 344 and 345:
функция которой из
- Page 346 and 347:
817. Задана корреляц
- Page 348 and 349:
Решение. Используе
- Page 350 and 351:
1. Корреляционная ф
- Page 352 and 353:
Введем в рассмотре
- Page 354 and 355:
Указание. Использо
- Page 356 and 357:
функции X{t). Найти: а
- Page 358 and 359:
ляционная функция
- Page 360 and 361:
865. Доказать, что вз
- Page 362 and 363:
874*. Известна коррел
- Page 364 and 365:
881. Задана спектрал
- Page 366 and 367:
891*. Найти спектраль
- Page 368 and 369:
895*. Может ли функци
- Page 370 and 371:
^JC(T)= 5j^(ft>)e’^**da), пол
- Page 372 and 373:
где X{t)—входная ста
- Page 374 and 375:
913. На вход wiHHeuHOH ста
- Page 376 and 377:
-l/U. 88. a) Р=-1/Б.1/4.1/3=.1/60
- Page 378 and 379:
=-25/18. 208. M(X)-=3xe/2; D (X) =-
- Page 380 and 381:
= (1/2) [snx + siny-^sinix—y)l 4
- Page 382 and 383:
Глава тринадцатая 5
- Page 384 and 385:
ности методов А н В.
- Page 386 and 387:
A%f Л4. 686. i49, А%, At* A^ А
- Page 388 and 389:
0) *. (0)»3. 859. Р (У5 О. ** *
- Page 390 and 391:
Продолжение прилож
- Page 392 and 393:
ц ^ »$ S S tS SI tf6^^fs^^fs 2 at
- Page 394 and 395:
ПРИЛОЖЕНИЕ S Критич
- Page 396 and 397:
ПРИЛОЖЕНИЕ 7 Критич
- Page 398 and 399:
ОООО|Й.ОСЛЬ9О^00^ФСЛ||
- Page 400 and 401:
Продолжение прилож
- Page 402 and 403:
lOOPf % 60 61 62 63 64 65 66 67 68
- Page 404 and 405:
Продояженш прилож,
- Page 406 and 407:
Учебное издание Гм
Решение типовых задач. Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками
Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением  =100 м. Найти:
=100 м. Найти:
1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,
2) вероятность того, что измеренная дальность не превзойдет истинной.
Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая  — 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
— 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
 .
.
1) Согласно общей формуле имеем
 .
.
Интеграл вероятности является функцией нечетной, поэтому
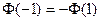
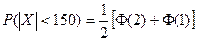 .
.
 ;
;
 .
.
2) Вероятность того, что измеренная дальность не превзойдет истинной,
 .
.
Так как 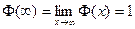 , а из таблицы находим
, а из таблицы находим  , то
, то
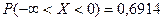 .
.
Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.
Из условия задачи следует, что
 .
.
Неизвестное значение срединной ошибки находим как решение уравнения
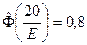 .
.
С помощью таблицы получим
 ,
,
 м.
м.
Дата добавления: 2014-12-23 ; просмотров: 177 ; Нарушение авторских прав
Источник
Занятие 12. Закон нормального распределения.
Краткая теоретическая часть
Плотность вероятности нормально распределенной случайной величины имеет вид

 ,
,
где  — среднее квадратическое отклонение,
— среднее квадратическое отклонение,  — срединное отклонение (иногда называемое и «вероятным отклонением»),
— срединное отклонение (иногда называемое и «вероятным отклонением»), 
Вероятность попадания нормально распределенной случайной величины X в интервал  вычисляется по одной из следующих формул:
вычисляется по одной из следующих формул:
1)  ,
,
где  — функция Лапласа (интеграл вероятности);
— функция Лапласа (интеграл вероятности);
2)  ,
,
где  — приведенная функция Лапласа.
— приведенная функция Лапласа.
Значения функций  и
и  даны в специальных таблицах.
даны в специальных таблицах.
Во всех задачах данного параграфа ошибки измерения считаются нормальными величинами.
1. Нормальное распределение играет достаточно важную роль в теории вероятностей и среди законов занимает особое положение. Укажите причины, по которым, на Ваш взгляд, это происходит:
а) Это наиболее часто употребляемый во многих приложениях закон распределения
б) Нормальный закон распределения применим как для дискретных, так и для непрерывных случайных величин
в) Нормальный закон распределения является предельным законом, к которому сходятся другие при весьма типичных часто встречающихся условиях
г) Нормальный закон распределения таков, что позволяет характеризовать сравнительную крутость других законов относительно него
2. Плотность вероятности нормально распределенной случайной величины имеет вид:
а) 
б) 
в)  или
или 
г) 
д) 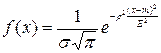
е)  или
или 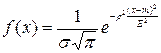
3. Параметры  и
и  закона нормального распределения совпадают с математическим ожиданием и среднеквадратическим отклонением нормально распределенной случайной величины соответственно. Следовательно, они определенным образом характеризуют случайную величину. А как? Выберите наиболее точный, на Ваш взгляд, вариант ответа.
закона нормального распределения совпадают с математическим ожиданием и среднеквадратическим отклонением нормально распределенной случайной величины соответственно. Следовательно, они определенным образом характеризуют случайную величину. А как? Выберите наиболее точный, на Ваш взгляд, вариант ответа.
а) Характеризуют форму кривой распределения и положение распределения случайной величины на оси абсцисс соответственно
б) Характеризуют положение распределения случайной величины на оси абсцисс и форму кривой распределения соответственно
в) Определяют центр рассеянья и центр симметрии случайной величины соответственно
г) Определяют центр симметрии и центр рассеянья случайной величины соответственно
4. Какой особенностью обладают моменты нормального распределения?
а) Все четные центральные моменты равны нулю.
б) Все нечетные центральные моменты равны нулю.
в) Все центральные моменты равны нулю
5. Одной из формул, по которым можно вычислить вероятность попадания нормально распределенной случайной величины  в заданный интервал
в заданный интервал  является (здесь
является (здесь  — функция Лапласа (интеграл вероятности)):
— функция Лапласа (интеграл вероятности)):
а) 
б) 
в) 
г) 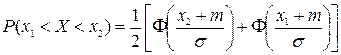
6. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством:
в) равны параметру Пуассона
Решение типовых задач
Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением  =100 м. Найти:
=100 м. Найти:
1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,
2) вероятность того, что измеренная дальность не превзойдет истинной.
Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая  — 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
— 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
 .
.
1) Согласно общей формуле имеем
 .
.
Интеграл вероятности является функцией нечетной, поэтому

 .
.
 ;
;
 .
.
2) Вероятность того, что измеренная дальность не превзойдет истинной,
 .
.
Так как  , а из таблицы находим
, а из таблицы находим  , то
, то
 .
.
Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.
Из условия задачи следует, что
 .
.
Неизвестное значение срединной ошибки находим как решение уравнения
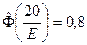 .
.
С помощью таблицы получим
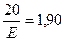 ,
,
 м.
м.
12.4. Задачи для самостоятельной работы
12.1. Измерительный прибор имеет систематическую ошибку 5 м и среднюю квадратическую ошибку 75 м, Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м?
(Ответ: 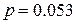 )
)
12.2. Систематическая ошибка удержания высоты самолетом +20 м, а случайная ошибка имеет среднее квадратическое отклонение 75 м. Для полета самолета отведен коридор высотой 100 м. Какова вероятность, что самолет будет лететь ниже, внутри и выше коридора, если самолету задана высота, соответствующая середине коридора?
12.3. Срединная ошибка измерения дальности радиолокатором равна 25 м, а систематическая ошибка отсутствует. Определить:
а) дисперсию ошибок измерения дальности;
б) вероятность получения ошибки измерения дальности, по абсолютной величине не превосходящей 20 м.
12.4. Случайное отклонение размера детали от номинала при изготовлении ее на данном станке имеет нулевое математическое ожидание и среднее квадратическое отклонение, равное 5 мк. Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная, если для годной детали допустимо отклонение размера от номинала не более, чем на 2 мк?
(Ответ:  )
)
12.5. Даны две случайные величины X и Y, имеющие одинаковые дисперсии, но первая распределена нормально,а вторая равномерно. Определить соотношение между их срединными отклонениями.
(Ответ:  )
)
12.6. Нормально распределенная случайная величина X имеет математическое ожидание  м и срединное отклонение 10 м. Вычислить таблицу функции распределения для значений аргумента через каждые 10 м и построить график.
м и срединное отклонение 10 м. Вычислить таблицу функции распределения для значений аргумента через каждые 10 м и построить график.
12.7. Систематическая ошибка высотомера равна +20 м, а случайные ошибки распределены по нормальному закону. Какую среднюю квадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,9 ошибка измерения высоты по абсолютной величине была меньше 100 м?
(Ответ:  . Получающееся трансцендентное уравнение проще решить графически)
. Получающееся трансцендентное уравнение проще решить графически)
12.8. Найти связь между средним арифметическим отклонением

нормально распределенной случайной величины и ее средним квадратическим отклонением.
(Ответ:  )
)
12.9. Определить для нормально распределенной случайной величины X, имеющей М [X] = 0,
1) 
2)  (при
(при 
(Ответ: 1) 0,1587; 0,0228; 0,00135; 2) 0,3173; 0,0455; 0,0027)
12.10. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить вероятность повреждения ружья, если максимально допустимый вес порохового заряда 2,5 г.
(Ответ:  )
)
12.11. Производятся два независимых измерения прибором, имеющим среднюю квадратическую ошибку 30м и систематическую ошибку +10м. Какова вероятность того, что обе ошибки измерений, имея разные знаки, по абсолютной величине превзойдут 10 м?
(Ответ:  )
)
12.12. На плоскости проведены две параллельные прямые, расстояние между ними L. На эту же плоскость бросается круг радиуса R. Центр рассеивания расположен на расстоянии b от одной из линий во внешнюю сторону. Срединное отклонение центра круга в направлении, перпендикулярном линии, равно Е.
Определить при одном бросании:
а) вероятность накрытия кругом хотя бы одной прямой;
б) вероятность накрытия обеих прямых, если L= 10м, R = 8м, b=5м, E=10м.
12.13. Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону со средним квадратическим отклонением, равным 3 мм, а систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготовляются четыре изделия.
(Ответ:  изделия)
изделия)
12.14. Какой ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска подчиняются закону нормального распределения с параметрами  = 0 и
= 0 и  = 5 мк
= 5 мк
12.15. Какое наибольшее расстояние допустимо между двумя рыболовецкими судами, идущими параллельными курсами, чтобы вероятность обнаружения косяка рыбы, находящегося посередине между ними, была не менее 0,5, если дальность обнаружения косяка для каждого из судов является независимой нормально распределенной случайной величиной с  км и средним квадратическим отклонением
км и средним квадратическим отклонением  =1,1 км?
=1,1 км?
12.16. При большом числе измерений установлено, что 75% ошибок
б) не превосходят по абсолютной величине 1,25 мм.
Заменяя частоты появления ошибок их вероятностями, определить в обоих случаях среднее квадратическое отклонение ошибок измерения, считая их нормально распределенными с нулевым математическим ожиданием.
12.17. Случайное отклонение X размера детали от номинала распределено по нормальному закону с математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными деталями являются те, для которых а b.
. Годными деталями являются те, для которых а b.
а) функцию распределения случайных отклонений размеров деталей, подлежащих переделке;
б) функцию распределения случайных отклонений размеров годных деталей.
(Ответ: а)  ) для
) для  ; б)
; б)  для
для 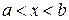 )
)
12.18. Нормально распределенная случайная величина X имеет нулевое математическое ожидание. Определить среднее квадратическое отклонение  , при котором вероятность
, при котором вероятность  была бы наибольшей (
была бы наибольшей (  ).
).
(Ответ:  )
)
1. Б.В. Гнеденко. Курс теории вероятностей, Изд. «Наука», 1969.
2. Е.С. Вентцель. Теория вероятностей, Изд. «Наука», 1969.
3. И.В. Дунин – Барковский, Н.В. Смирнов, Теория вероятностей и математическая статистика, ГТТИ, 1965.
4. И.Н. Коваленко, А.А. Филиппова, Теория вероятностей и математическая статистика, «Высшая школа», 1973.
5. Ю.В. Кожевников, Теория вероятностей и математическая статистика, Изд. «Машиностроение», 2002.
6. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под редакцией А.А Свешникова, «Наука», 1970.
7. Л.Д. Мешалкин, Сборник задач по теории вероятностей, Изд. «МГУ». М., 1963.
8. Г.В. Емильянов , В.П. Скитович, Задачи по теории вероятностей и математической статистике, Изд. «ЛГУ». Ленинград, 1967.
9. В.В. Скворцов, Теория вероятностей, Изд. «Мир». М., 1993.
10. Руководство для инженеров по решнию задач теории вероятностей. Под редакцией А.А Свешникова, «Судпромгиз». Ленинград, 1962.
Источник
Систематической погрешности нет. Ошибка измерения определяется только случайной погрешностью.
Нормальный закон распределения со средним квадратичным отклонением σ означает, что функция плотности вероятности имеет вид: (1)
График функции (1) имеет вид «колокола» симметричного относительно прямой х=0. (В более общем виде тут еще задействовано матожидание (или «среднее значение» х) m (и колокол тогда смещатся), но тогда в смысле ошибок можно было бы говорить о наличии систематической погрешности, а она у нас равна 0. Вот мы и считаем что функция распределения вероятности симметрична относительно 0 ).
С учетом того, что среднее квадратичное отклонение σ=25 функция (1) примет вид: (2)
Функция плотности вероятности f(x) является 1-й производной функции распределения случайной величины x F(x). Т.е: (3)
Что означают такие функции? Что можно найти с их помощью?
Например вероятность того, что случайная величина х попадет в диапазон (интервал) (a1; a2) определяется отношением: (4)
При этом функция распределения F(x) задает вероятность попадания случайной величины в интервал (-∞, x).
Итак У нас известна функция распределения вероятности (2) известен задан диапазон в который должна попасть случайная величина (наша погрешность), (-25, 25 ). Чтобы найти вероятность того, что ошибка не вылезет за пределы заданного интервала, все что нам нужно сделать, это взять интеграл вида (4), подставив туда вместо f(x) её выражение (2) и вместо пределов интегрирования поставить границы интервала -25 и 25. Т.е. (5)
И все бы хорошо, НО интеграл вида (5) «неберушка», т.е. его нельзя выразить в элементарных функциях. Исключение составляют интегралы с бесконечными, или «полубесконечными» пределами интегрирования (интеграл Пуассона например). Что нам делать? Как быть? Инегралы такого рода можно посчитать различными способами численно (приближенно) с любой наперед заданной точностью. Мы этого правда делать не будем. Это уже все проделано до нас и составлено уйма таблиц. Их можно найти и в книжном(бумажном) и в электроном вариантах. Однако есть один момент.Затабулировано целое семейство похожих функций, имеющих к тому же похожие названия, например мне по запросу навскидку попались попадались такие:
1) Функция Лапласа (в другом месте Интеграл вероятности) или даже так:
Функция стандартного нормального распределения (6)
2) Еще один интеграл вероятности: (7)
3) где то вылезла таблица функции (8).
Что с этим делать? Смириться и внимательно смотреть, какая именно функция дана в таблице. При этом исходный интеграл (5) можно свести к табличному интегралу путем замены переменных и вынесения множителя.
Например так:
Подынтегральная функция (четная) ⇒ можно записать: (9)
далее вводим новую переменную тогда
при этом если x=0, то u=0,
x=25, u=σx=σ*25=A
интеграл (9) приобретает вид: (10)
Получили интеграл вида (6) умноженный на 2σ,
ВНИМАНИЕ! ПРЕДЕЛЫ ИНТЕГРИРОВАНИЯ ИЗМЕНИЛИСЬ!
Тот, кто «дружит» с электронными таблицами может поискать в них похожие функции. Это будет удобно, если необходимо выполнить «серию» расчетов, мне например (после некоторых мытарств) удалось в своем Сalc( у меня Libre Office 4.2 ) найти функцию
NORMDIST(X; m; σ; C), которая в зависимости от параметра C выдает
значение либо функции распределения случайной величины (с=1), либо значение плотности вероятности (c=0) в точке X.
Тут
m матожидание случайной величины, у нас оно =0 как мы уже говорили выше.
σ среднеквадратичное отклонение =25.
Таким образом вычиление интеграла (5) обошлось сравнительно «малой кровью»
когда в таблице вычислили выражение:
NORMDIST(25; 0; 25; 1) — NORMDIST(-25; 0; 25; 1)
Итого
Ответ P(-25;25)≈0,6827
Определить коэффициент «a» и построить график плотности. Найти функцию распределения F(x).
7.26. Случайная величина X подчинена закону распределения с плотностью
Найти коэффициент a. Построить график плотности. Найти вероятность попадания случайной величины X в интервал (1; 2).
7.27. Случайная величина X задана функцией распределения

Вычислить вероятность попадания случайной величины X в интервал (1; 2,5). Найти плотность распределения f(x), математическое ожидание M[X], дисперсию D[X].
7.28. Дана функция 
При каком значении функция f(x) может быть принята за плотность распределения вероятности случайной величины X? Определить это значение , найти математическое ожидание и среднее квадратическое отклонение случайной величины X .
7.29. Плотность распределения случайной величины 
Найти начальные и центральные моменты первых четырех порядков, коэффициент асимметрии и эксцесс.
7.30. Функция распределения случайной величины X имеет вид:

Определить: 1)при каких значениях A и B функция распределения является непрерывной; 2) плотность распределения вероятностей f(x); 3) P(-a/2 < X< a/2).
Задача № 8.
8.1. Случайная величина Х — число попаданий мячом в корзину при трех бросках. Вероятность попадания при каждом броске равна P. Найти матема-тическое ожидание и дисперсию этой случайной величины.
8.2. Функция распределения случайной величины Х задана графиком
 F(x)
F(x)
1
x
0 a b
Найти математическое ожидание и дисперсию случайной величины Х.
8.3. Система состоит из 4-х дублирующих блоков, надежность каждого из которых равна P. Число блоков, отказавших за фиксированное время работы системы, есть случайная величина X. Найти ее математическое ожидание и дисперсию.
8.4. Вероятность отказа определенного транзистора после оговоренного числа лет работы равна «р», а вероятность того, что он будет работать исправно после этого времени, равна  . Проведена проверка n транзисторов. Построить ряд распределения числа неисправных транзисторов в партии для значений 0, 1, 2, 3, 4, 5, 6, если n = 100, p = 0,02. Вычислить математическое ожидание.
. Проведена проверка n транзисторов. Построить ряд распределения числа неисправных транзисторов в партии для значений 0, 1, 2, 3, 4, 5, 6, если n = 100, p = 0,02. Вычислить математическое ожидание.
8.5. Найти математическое ожидание случайной величины, заданной функцией распределения

8.6. Случайная величина Х, возможные значения которой неотрицательны, задана функцией распределения F(x) =  . Найти математическое ожидание этой случайной величины.
. Найти математическое ожидание этой случайной величины.
8.7. Случайная величина X подчинена показательному закону с параметром  :
:

Построить кривую распределения. Найти функцию распределения. Найти вероятность того, что случайная величина X примет меньшее значение, чем ее математическое ожидание.
8.8. Подлежат исследованию 1200 проб руды. Пусть вероятность про-мышленного содержания металла в каждой пробе равна 0,9. Найти математическое ожидание и дисперсию числа проб с промышленным содержанием металла.
8.9. Функция распределения непрерывной случайной величины Х — времени безотказной работы некоторого устройства равна  . Найти вероятность безотказной работы устройства за время
. Найти вероятность безотказной работы устройства за время 
8.10. Математическое ожидание числа отказов радиоаппаратуры за 10000 ч. работы равно 10. Определить вероятность отказа радиоаппаратуры за 100 ч. работы. Предполагается, что отказы независимы и вероятность каждого отказа от опыта к опыту не изменяется.
8.11. Игральная кость бросается три раза. Записать закон распределения числа появлений шестерки.
8.12. Монета бросается три раза. Записать в виде таблицы закон распреде-ления случайной величины Х — числа выпадений герба.
8.13. Вероятность попадания в мишень при одном выстреле равна 0,07. Построить ряд распределения случайной величины Х — числа попаданий в мишень при двух выстрелах. Найти функцию распределения и построить ее график.
8.14. Плотность распределения вероятностей случайной величины Х имеет вид:

Найти функцию распределения случайной величины Х и построить ее график.
Вычислить  и
и  . Найти вероятность того, что случайная величина примет значение, заключенное между 2,5 и 3,5.
. Найти вероятность того, что случайная величина примет значение, заключенное между 2,5 и 3,5.
8.15. Случайная величина Х имеет равномерное распределение на интерва-
ле (2; 3). Найти плотность распределения, математическое ожидание и дисперсию случайной величины Х.
8.16. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром «а». Если неисправностей не обнаружено, техническое обслуживание машины продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 ч. Определить закон распределения среднего времени обслуживания и ремонта машины и его математическое ожидание  .
.
8.17. Случайная величина Х распределена равномерно с  . Найти плотность распределения случайной величины Х.
. Найти плотность распределения случайной величины Х.
8.18. На колышек одно за другим набрасывается 4 кольца, причем вероятность попадания для каждого броска одна и та же и равна 0,8. Найти закон распределения, математическое ожидание и дисперсию числа колец, попавших на колышек, если броски независимы.
8.19. Вероятность того, что изделие не выдержит испытание, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытание.
8.20. Плотность распределения случайной величины Х имеет вид:
 f(x)
f(x)
A
0 1 3 x
1) Найти A и написать выражение плотности. 2) Найти и построить график функции распределения F(x). 3) Вычислить математическое ожидание и дисперсию.
8.21. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти среднее число отказавших деталей, если испытанию будут подвергнуты 10 деталей.
8.22. Время безотказной работы элемента распределено по показательному закону  при t
при t 0 (t — время в часах). Найти вероятность того, что элемент проработает безотказно 100 ч.
0 (t — время в часах). Найти вероятность того, что элемент проработает безотказно 100 ч.
8.23. Известно, что в партии из 20 телефонных аппаратов имеется 5 неисправных. Из партии выбрано 4 аппарата. Найти закон распределения, математическое ожидание и дисперсию числа неисправных аппаратов среди отобранных.
8.24. По известному «правилу трех сигм» вероятность отклонения случайной величины от своего математического ожидания более чем на три корня из дисперсии мала. Найти  если Х имеет: а) нормальное распре-
если Х имеет: а) нормальное распре-
деление; б) показательное распределение.
8.25. По известному «правилу трех сигм» вероятность отклонения случайной величины от своего математического ожидания более чем на три корня из дисперсии мала. Найти  если Х имеет: а) нормальное распреде-ление, б) равномерное на отрезке
если Х имеет: а) нормальное распреде-ление, б) равномерное на отрезке 
8.26. По известному «правилу трех сигм» вероятность отклонения случайной величины от своего математического ожидания более, чем на три корня из дисперсии мала. Найти  если Х распределена: а) нормально;
если Х распределена: а) нормально;
б) по закону Пуассона с  .
.
8.27. Для случайной величины Х, распределенной по закону Пуассона, вычислить  , математическое ожидание и дисперсию, если параметр а = 0,3; k = 2.
, математическое ожидание и дисперсию, если параметр а = 0,3; k = 2.
8.28. Все значения равномерно распределенной случайной величины лежат на отрезке  . Найти вероятность попадания значений случайной величины в промежуток
. Найти вероятность попадания значений случайной величины в промежуток  .
.
8.29. Трамваи данного маршрута городского трамвая идут с интервалом 5 мин. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего поезда, но не позднее, чем за две минуты до отхода следующего поезда?
8.30. Определить постоянную вероятность попадания в цель при каждом выстреле и число произведенных выстрелов, если среднее число попаданий рав-
но 72, а среднее квадратическое отклонение случайной величины, характеризу-ющей число попаданий, равно 6.
Задача № 9.
9.1. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением  = 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
= 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
9.2. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением = 100 м. Найти: 1) вероятность измерения даль-ности с ошибкой, не превосходящей по абсолютной величине 150 м; 2) вероятность того, что измеренная дальность не превзойдет истинной.
9.3. Определить среднее квадратическое отклонение случайной ошибки прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы  20 м.
20 м.
9.4. Случайная величина X подчинена нормальному закону распределения с параметрами а = -1, = 2. Определить вероятность неравенства -2 < X < 1. Построить график плотности распределения.
9.5. На автомате изготавливаются заклепки. Диаметр их головок пред-ставляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение, равное 2 мм, и дисперсию, равную 0,01. Какие размеры диаметра головок заклепки можно гарантировать с вероятностью 0,95?
9.6. Случайная величина X распределена по нормальному закону с парамет-рами a = 30, = 10. В какой интервал с вероятностью практической достоверности 0,997 попадут значения случайной величины X?
9.7. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная X величина распределена нормально со средним квадратическим отклонением = 0,4 мм, найти, сколько будет готовых шариков среди 100 изготовленных.
9.8. Случайная величина Х подчинена нормальному закону распределения с плотностью  Определить вероятность того, что случайная величина Х примет значение, не меньшее 0 и не больше 12.
Определить вероятность того, что случайная величина Х примет значение, не меньшее 0 и не больше 12.
9.9.Случайная величина Х подчинена нормальному закону распределения с параметрами  Написать выражение для плотности распределения и функции распределения этой случайной величины. Построить график функции распределения.
Написать выражение для плотности распределения и функции распределения этой случайной величины. Построить график функции распределения.
9.10. Длина изготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами  см,
см,  см. Найти вероятность брака, если допустимые размеры детали должны быть 15 0,3 см. Какую точность изготовляемой автоматом детали можно гаран-тировать с вероятностью 0,97?
см. Найти вероятность брака, если допустимые размеры детали должны быть 15 0,3 см. Какую точность изготовляемой автоматом детали можно гаран-тировать с вероятностью 0,97?
9.11. При взвешивании тела установлен средний вес 2,36 г и среднее квадратическое отклонение веса 0,025 г. Вес – случайная величина Х, распреде-ленная нормально. Найти: а) какой процент значений находится между 2,3 г и 2,4 г; б) какую точность взвешивания можно гарантировать с вероятностью 0,97?
9.12. Размер диаметра втулок, изготовляемых цехом, можно считать нормаль-но распределенной случайной величиной с математическим ожиданием 2,5 см и дисперсией 0,0001 см2, в каких границах можно практически гарантировать размер диаметра втулки, если за вероятность практической достоверности принимается 0,997?
9.13. На стенке изготовляются детали заданной длины. Установлено, что
60 % деталей отклоняются от заданной длины не более чем на 2 мм (в обе стороны). Какой процент деталей будет отклоняться от заданной длины не более чем на 5 мм, если предполагается, что величина отклонения есть случайная величина, распределенная по нормальному закону?
9.14. Бомбардировщики сбросили бомбы на мост длиной 60 м и шириной 12 м. Рассеивание попаданий происходит по нормальному закону с дисперсией, равной 225 м2 по длине и 36 м2 по ширине, средняя точка попаданий — центр моста. Рассеивания по длине и ширине независимы. Найти вероятность попадания в мост при сбрасывании одной бомбы.
9.15. Стрельба ведется от точки Х вдоль прямой ОХ. Средняя дальность полета «а». Предполагается, что дальность полета распределена по нормальному закону со средним квадратическим отклонением 80 м. Найти, какой процент выпускаемых снарядов дает перелет от 120 м до 160 м.
9.16. Случайная величина X подчинена нормальному закону с параметрами а, . Вычислить с точностью до 0,01 вероятность попадания значений случайной величины X в интервал (а; а+) (без использования таблиц функции Лапласа).
9.17. Считается, что отклонение длины изготовляемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина равна 40 см и среднее квадратическое отклонение равно 0,4 см, то какую точность длины изделия можно гарантировать с вероятностью 0,8?
9.18. Пусть вес пойманной рыбы подчиняется нормальному закону. Параметры его следующие: cреднее квадратическое отклонение  математическое ожидание а = 375 г. Найти вероятность того, что вес пойманной рыбы будет заклю-чен в границах от 300 г до 425 г.
математическое ожидание а = 375 г. Найти вероятность того, что вес пойманной рыбы будет заклю-чен в границах от 300 г до 425 г.
9.19.Пусть диаметр изготовляемой детали является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее а = 4,5 см, а среднее квадратическое отклонение = 0,05 см. Найти вероятность того, что размер диаметра взятой наудачу детали отличается от математического ожидания не более чем на 1 мм.
9.20. Среднее квадратическое отклонение случайной величины, распределенной по нормальному закону, равно 2 см, а математическое ожидание равно 16 см. Най-ти границы, в которых с вероятностью 0,95 следует ожидать значение случайной величины.
9.21. Найти дисперсию случайной величины, распределенной по нормальному закону, если известно, что отклонения от математического ожидания, не превосходящие 0,1 см, имеют место с вероятностью 0,7887.
9.22. Станок-автомат изготавливает валики, причем одновременно контролирует их диаметр Х. Считая, что Х — нормально распределенная случайная величина с математическим ожиданием 10 мм и средним квадратическим отклонением
= 0,1 мм, найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.
9.23. Плотность распределения вероятностей случайной величины Х имеет вид  Найти: 1) ; 2) математическое ожидание, дисперсию
Найти: 1) ; 2) математическое ожидание, дисперсию  ; 3) вероятность выполнения неравенства
; 3) вероятность выполнения неравенства  .
.
9.24. Случайная величина X имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1. Какое из двух событий  или
или  имеет большую вероятность?
имеет большую вероятность?
9.25. Случайная величина X имеет нормальное распределение с параметрами  .Что больше:
.Что больше:  или
или 
9.26. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с  мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей 15 мм; не превосходящей 20 мм.
мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей 15 мм; не превосходящей 20 мм.
9.27. Автомат изготовляет подшипники, которые считаются годными, если отклонение Х от проектного размера по модулю не превосходит 0,77 мм. Каково наиболее вероятное число годных подшипников из 100, если Х — случайная вели-чина, распределенная нормально с = 0,4мм?
9.28. Диаметр деталей, изготовленных цехом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001 cм2,а математическое ожидание 2,5 см. В каких границах можно практически гарантировать диаметр детали (за достоверное принимается событие, вероятность которого 0,9973)?
9.29. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее пусть равно 164 см, а среднее квадратическое отклонение 5,5 см. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см.
9.30. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с параметрами: математическое ожидание равно 16 км, а среднее квадратическое отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами а) не меньше 15,8 км; б) не более 16,25 км.
Задача № 10.
10.1. По некоторой цели производятся два выстрела. Вероятность попадания при одном выстреле равна P. Рассматриваются две случайные величины: Х — число попаданий в цель, Y — число промахов. Составить таблицу распределения и определить числовые характеристики системы.


 10.2. Случайная точка на плоскости распределена по закону, заданному таблицей:
10.2. Случайная точка на плоскости распределена по закону, заданному таблицей:
 Y X 0 1
Y X 0 1
-1 0,1 0,15
0 0,15 0,25
1 0,2 0,15
Найти числовые характеристики системы (X,Y).
 10.3. Матрица распределения системы двух дискретных случайных величин(X,Y) задана таблицей: X Y 0 2 5
10.3. Матрица распределения системы двух дискретных случайных величин(X,Y) задана таблицей: X Y 0 2 5
1 0,1 0 0,2
2 0 0,3 0
4 0,1 0,3 0
Найти числовые характеристики системы (Х,Y).
10.4. Изготовляемые в цехе втулки сортируются по отклонению их внутреннего диаметра от номинального размера на 4 группы со значениями 0,01; 0,02; 0,03 и 0,04 мм и по овальности на четыре группы 0,002; 0,004; 0,006;
0 ,008 мм. Совместное распределение диаметра (X) и овальности (Y) втулок задано таблицей (Табл.10.3):
,008 мм. Совместное распределение диаметра (X) и овальности (Y) втулок задано таблицей (Табл.10.3):
Y Х 0,01 0,02 0,03 0,04
0,002 0,01 0,02 0,03 0,04
0,004 0,03 0,24 0,15 0,06
0,004 0,04 0,10 0,08 0,08
0,008 0,02 0,04 0,04 0,02
Найти числовые характеристики системы случайных величин  .
.
10.5. Дана таблица, определяющая закон распределения системы двух cлучайных величин (X,Y):



 Y
Y
X 20 40 60
 10 3 0
10 3 0
20 2 4 2
30 2 5
Найти :  .
.


 10.6. Система (X,Y) задана следующей двумерной таблицей распределения вероятностей:
10.6. Система (X,Y) задана следующей двумерной таблицей распределения вероятностей:
X 0 1 2 3 4 5 6
Y
0 0,202 0,174 0,113 0,062 0,049 0,023 0,004
1 0 0,099 0,064 0,040 0,031 0,020 0,006
2 0 0 0,031 0,025 0,018 0,013 0,008
3 0 0 0 0,001 0,002 0,004 0,011
Найти вероятность  и корреляционную матрицу.
и корреляционную матрицу.
10.7. Однотипные детали в зависимости от точности изготовления различаются по форме на круглые и овальные, а по весу — на легкие и тяжелые. Вероятности того, что взятая наудачу деталь окажется круглой и легкой, овальной и легкой, круглой и тяжелой, овальной и тяжелой, соответственно равны  . Взята одна деталь. Найти математические ожидания и дисперсии числа круглых деталей X и числа легких деталей Y, а также корреляционный момент kxy между числом круглых и числом легких деталей, если = 0,40, = 0,05,
. Взята одна деталь. Найти математические ожидания и дисперсии числа круглых деталей X и числа легких деталей Y, а также корреляционный момент kxy между числом круглых и числом легких деталей, если = 0,40, = 0,05,  = 0,10.
= 0,10.
-
-
Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна P. Случайные величины: X — число выстрелов до первого попадания (включительно), Y — число промахов. Необходимо: а) описать закон распределения случайного вектора (X,Y) и законы распределения каждой компоненты; б) вычислить вероятность P(X = Y);
-
в) вычислить коэффициент корреляции rxy.; г) определить зависимы или неза-висимы компоненты X, Y.
10.9. Бросаются две одинаковые игральные кости. Случайные величины:
X — индикатор четности суммы выпавших очков (т.е. X = 1, если эта сумма четная, и X = 0 в противном случае), Y — индикатор четности произведения выпавших очков (т.е. Y = 1, если это произведение четно и Y = 0 в противном случае).
а) Описать закон распределения случайного вектора (X, Y).
б) Вычислить функцию распределения F(X, Y).
в) Вычислить корреляционный момент.
-
-
Число X выбирается случайным образом из множества целых чисел
-
 . Затем из того же множества выбирается наудачу число Y, больше первого или равное ему.
. Затем из того же множества выбирается наудачу число Y, больше первого или равное ему.
а) Описать закон распределения случайного вектора (X,Y).
б) Определить, зависимы или независимы случайные компоненты X и Y.
в) Построить условный закон распределения компоненты X при условии, что Y приняло значение, равное 2.
г) Вычислить основные характеристики 
10.11. Случайный вектор (X,Y) имеет следующее распределение вероятностей:




Y X 0 1
-1 0,1 0,2
0 0,2 0,2
1 0,1 0,2
Найти математическое ожидание и дисперсию величины 
10.12. В продукции завода брак вследствие дефекта A составляет 3 %, а вследствие дефекта B — 4,5 %. Годная продукция составляет 95 %. Найти коэффициент корреляции дефектов A и B. Указание. Ввести в рассмотрение случайную величину X = 1, если данное изделие обладает дефектом A и X = 0 в противном случае. Аналогично Y = 1; 0 в зависимости от того, обладает или нет это изделие дефектом B.
10.13. Два стрелка, независимо друг от друга, делают по два одиночных (независимых) выстрела каждый по своей мишени. Случайная величина X — число попаданий первого стрелка, Y — число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P1 = 0,7; для второго P2 = 0,4. Построить матрицу распределения вероятностей системы случайных величин (X,Y).
10.14. Два стрелка независимо друг от друга делают по одному выстрелу каждый по своей мишени. Случайная величина X — число попаданий первого стрелка. Y — число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P1 = 0,7, для второго P2 = 0,4. Построить матрицу распределения вероятностей системы случайных величин (u,v), где 
 .
.

 10.15. Система случайных величин (Х,Y) имеет следующее распределение вероятностей:
10.15. Система случайных величин (Х,Y) имеет следующее распределение вероятностей:
Y X 0 1
-1 0,1 0,2
0 0,2 0,3
1 0 0,2
Найти математическое ожидание и дисперсию случайной величины  .
.
10.16. Имеется система случайных величин (X,Y), где
 и коэффициент корреляции
и коэффициент корреляции  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины 
10.17. Случайные величины X и Y связаны соотношением  , где
, где  — неслучайные величины
— неслучайные величины  . Найти: а) Коэффициент корре-ляции
. Найти: а) Коэффициент корре-ляции  ; б) Отношение среднеквадратических отклонений
; б) Отношение среднеквадратических отклонений  .
.
10.18. Дважды бросается игральная кость. Случайные величины: X — число появлений шестерки, Y — число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X, Y). Установить зависимы или независимы компоненты Х и Y.
10.19.Дважды бросается игральная кость. Случайные величины: X — число появлений единицы, Y — число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X,Y). Вычислить основные характеристики случайного вектора:  .
.
10.20. Дважды бросается игральная кость. Случайные величины: X — число появлений шестерки, Y — число появлений четной цифры. Описать закон распределения случайного вектора (X, Y). Описать условный закон распределения случайной величины X при условии Y = 2 и при этом условии вычислить условное математическое ожидание  .
.
10.21. Совместное распределение (X,Y) задано формулами:


Найти одномерные распределения X,Y и распределения  .
.
10.22. Совместное распределение задано формулами:


 ,
,

Найти совместное распределение случайных величин: 
10.23. Совместное распределение (X,Y) задано формулами

Найти 
10.24. Совместное распределение случайных величин определяется формулами

Найти Являются ли X,Y независимыми величинами?
10.25. Случайные величины  независимы;
независимы;  Найти:
Найти:
а) коэффициент корреляции величин Х1+Х2, Х3+Х4+Х5; б) коэффициент корреляции величин Х1+Х2+Х3, X3+X4+X5 .
10.26.Дана таблица, определяющая закон распределения системы двух случайных величин (Х,Y):


X Y 2 4 6
1 3 0
2 4 2 2
3 5 2
Найти: а)., б).  в).
в).  г) .
г) .

 10.27. Система случайных величин (Х,Y) распределена по закону, выраженному таблицей:
10.27. Система случайных величин (Х,Y) распределена по закону, выраженному таблицей:
 Y X 0 1
Y X 0 1
-1 0,1 0,15
0 0,15 0,25
1 0,2 0,15
Описать условный закон распределения случайной величины Х, при условии Y = 0, при этом же условии вычислить условное математическое ожидание 
 .
.
 10.28. В таблице приведены данные о возможных сочетаниях отклонений длины валика (Х) и диаметра (Y) от номинальных размеров и соответствующие вероятности:
10.28. В таблице приведены данные о возможных сочетаниях отклонений длины валика (Х) и диаметра (Y) от номинальных размеров и соответствующие вероятности:
-
-
-
-
X Y
-1
0
1
-2
0,15
0,35
0,05
3
0,10
0,25
0,10
-
-
-
Найти закон распределения случайной величины Z = X + Y и проверить справед-ливость формулы 


 10.29. Случайные величины независимы. По заданным законам распреде-ления случайных величин найти закон распределения системы случайных величин
10.29. Случайные величины независимы. По заданным законам распреде-ления случайных величин найти закон распределения системы случайных величин
 X 1 2 3 Y 4 6 8 10
X 1 2 3 Y 4 6 8 10
P 0,3 0,5 0,2 P 0,1 0,4 0,3 0,2
10.30. Дважды бросается игральная кость. Случайные величины: Х — число появлений шестерки, Y — число появлений нечетной цифры. Вычислить вероятности  .
.
Задача № 11.
11.1. Система случайных величин имеет равномерное распределение внутри квадрата со стороной a. Диагонали квадрата совпадают с осями координат. Определить: а) плотность совместного распределения вероятностей системы (X,Y);
б) плотность распределения вероятностей каждой из случайных величин, входящих в систему.
11.2. Система трех случайных величин (X, Y, Z) распределена равномерно внутри цилиндра, ось которого совпадает с осью OZ и точкой O делится пополам. Радиус цилиндра равен R, а высота 2h. Определить: а) плотность совместного распределения вероятностей системы (X, Y, Z); б) плотность распределения каждой из случайных величин, входящих в систему.
11.3. Система случайных величин (X, Y) подчинена закону распределения с плотностью распределения вероятностей 
 , если
, если  и
и  если
если  . Найти: 1) a; 2)
. Найти: 1) a; 2) ; 3)дисперсии
; 3)дисперсии  ;
;
4) коэффициент корреляции .
11.4. Система двух случайных величин (X,Y) подчинена нормальному закону распределения. Рассеивание круговое. Найти вероятность попадания случайной точки (X, Y) в круг, центр которого cовпадает с центром рассеивания, а радиус равен двум вероятным отклонениям (Вероятное отклонение  где
где
 = 0,476936).
= 0,476936).
11.5. Плотность совместного распределения вероятностей системы случайных величин X,Y имеет вид:  , где
, где  Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
11.6. Плотность совместного распределения системы случайных величин X, Y:
 . Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
. Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
11.7. Система двух случайных величин (X, Y) подчинена закону распределения с плотностью совместного распределения:  . Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
. Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
11.8. Система случайных величин (X,Y) имеет плотность совместного распределения
 , где
, где  . Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
. Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
11.9. Производится единичное бомбометание по прямоугольной наземной цели. Ширина цели равна 20 м, а длина 100 м. Прицеливание по центру цели. Оси рассеивания совпадают с направлением полета и с перпендикуляром к этому направлению. Вероятное отклонение в направлении полета равно 60 м, в направлении, перпендикулярном полету – 40 м. Систематические ошибки отсут-ствуют. Вероятность попадания в цель при сбрасывании одной бомбы. Указание: Вероятное отклонение 
11.10. Плотность совместного распределения системы случайных величин X, Y равна  . Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
. Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
11.11. Дана плотность совместного распределения случайных величин X, Y:
 Определить вероятность попадания в прямоугольник:
Определить вероятность попадания в прямоугольник:
 y
y
 (2;1,5)
(2;1,5)
0
(0;-1) (2;-1) х
11.12. Система случайных величин (X, Y) распределена с постоянной плот-ностью внутри квадрата. Найти плотности распределения случайных величин X, Y входящих в систему:
 y
y
 1
1
-1 1 x
-1
11.13. Система случайных величин (X, Y) подчинена закону распределения с плотностью:

Область D — квадрат, ограниченный линиями x = 0; x = 3; y = 0; y = 3.
Найти: а) Коэффициент a; б) вероятность попадания случайной точки (x, y) в квадрат, ограниченный прямыми x = 1, x = 2, y = 1, y = 2; в) 
11.14. Определить плотность распределения вероятностей, математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если  ,
, 
11.15. Плотность совместного распределения случайных величин (X,Y):  Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
кие ожидания каждой из случайных величин.
11.16. Плотность совместного распределения системы случайных величин X, Y равна  . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
. Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
11.17. Координаты случайной точки (X,Y) раcпределены равномерно внутри прямоугольника, ограниченного прямыми x = 0, x = a, y = 0, y = b. Определить вероятность попадания случайной точки в круг радиуса R = a ,если a > b, а центр круга совпадает с началом координат.
11.18. Координаты (X, Y) случайной точки распределены равномерно внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c, y = d (в > a, d > c). Найти плотность распределения вероятностей и функцию распределения системы случайных величин X, Y. Выяснить, являются ли X, Y независимыми величинами.
11.19. Плотность совместного распределения случайных величин X, Y равна:
 в области D и f(x,y)=0 вне этой области. Область D — треугольник, ограниченный прямыми
в области D и f(x,y)=0 вне этой области. Область D — треугольник, ограниченный прямыми  Найти а)
Найти а)  ; б) коэффициент корреляции, дисперсии
; б) коэффициент корреляции, дисперсии 
11.20. Плотность совместного распределения системы случайные величины
(X, Y), заданной внутри круга радиуса R, равна  . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
. Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
11.21. Плотность совместного распределения системы случайных величин
(X, Y): в области D и
в области D и  вне этой области. Область D определяется неравенствами
вне этой области. Область D определяется неравенствами  Определить: a) постоянную a;
Определить: a) постоянную a;
б)  ; в) определить коэффициент корреляции r xy.
; в) определить коэффициент корреляции r xy.
11.22. Дана плотность совместного распределения системы случайных величин 
 . Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
. Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
11.23. Плотность распределения вероятностей двумерного случайного вектора (X, Y) имеет следующий вид:  .
.
Вычислить: а) значение постоянной c; б) вероятность  ); в) центр рассеивания.
); в) центр рассеивания.
11.24. Случайные величины X и Y независимы и распределены каждая по показательному закону с параметрами соответственно 1 и 2. Найти вероятность 
11.25. Функция совместного распределения двух случайных величин X и Y имеет следующий вид:

Найти одномерные законы распределения компонент и решить вопрос об их зависимости или независимости.
11.26. Случайные величины X и Y независимы и распределены следующим образом: X — по закону N(1; 2), Y — по равномерному закону на отрезке [0; 2].
Найти вероятность следующих событий:  , где область
, где область
D = {(x,y) / (0 x 2, 0 y 1); B = {X > Y}.
11.27. Случайная точка на плотности (X,Y) распределена по круговому нормальному закону (rxy = 0, x = y = = 1,) с центром рассеивания в начале координат. Вычислить вероятности следующих событий: A = {Y > X},
B = {Y> X}, C = {Y < 3X}, D = {X < 1}, E = {X < 1, Y < 2}.
11.28. Заданы следующие характеристики двумерного нормального вектора:
mx = -2; my = 3 и ковариационная матрица  . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y.
. Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y.
11.29. Определить вероятность попадания точки с координатами (X, Y) в область, определяемую неравенствами (1 X 2, 1 Y 2), если функция распреде-ления 
11.30. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения вероятностей 
