Если учащийся научится самостоятельно изучать материал, пользуясь учебником или какими- то специально подобранными заданиями, то будет успешно решена задача сознательного овладения знаниями. Знания, которые усвоил учащийся сам, значительно прочнее тех, которые он получил после объяснения учителя.
Поэтому после написания контрольной работы даю возможность учащимся самим ликвидировать пробелы, творчески применять их в решении различных задач.
Контрольная работа
Многоугольники
Вариант 1
1. Укажите неверное утверждение. У любого ромба:
а) диагонали лежат на биссектрисах его углов;
б) противоположные углы равны;
в) все углы равны;
г) диагонали пересекаются под прямым углом.
2. АВСD – прямоугольник, АС=12см, CD=8 см. Найдите периметр треугольника АОВ, где О – точка пересечения диагоналей.
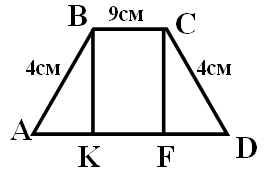
3. Длины боковых сторон трапеции равны 4см и 4см, а длины оснований – 9см и 13см. Найдите углы трапеции.
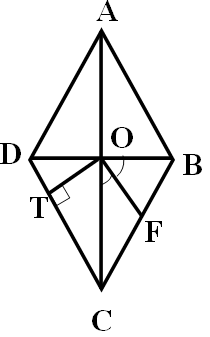
4. Диагонали ромба ABCD пересекаются в точке О. Отрезок OF – биссектриса ВОС, а отрезок ОТ – перпендикуляр, проведенный к стороне DC. Вычислите градусную меру , если BD=AD.
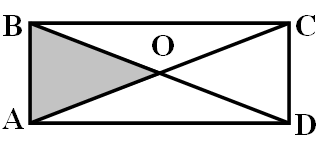
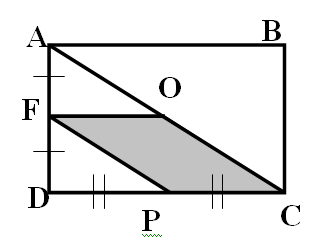
5. В прямоугольнике ABCD диагонали пересекаются в точке О, а P и F – середины сторон DCи AD соответственно. Доказать, что FOCP – параллелограмм
Вариант 2
1. Укажите неверное утверждение. У любого параллелограмма:
а) противоположные стороны равны;
б) диагонали равны;
в) противоположные углы равны;
г) диагонали, пересекаясь, делятся пополам.
2. АВСD – параллелограмм, АС=10см, ВD=6 см, AD=5см. Найдите периметр треугольника АОD, где О – точка пересечения диагоналей.
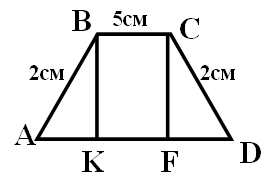
3. Найдите углы равнобедренной трапеции, если длина боковой стороны равна 2см, а длины оснований – 5см и 7см.
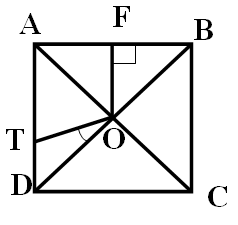
4. Диагонали квадрата ABCD пересекаются в точке О. Точко Т лежит на стороне AD так, что DОТ=30°. Отрезок OF – перпендикуляр, проведенный к стороне AB. Вычислите градусную меру FOT.
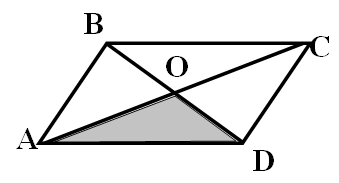
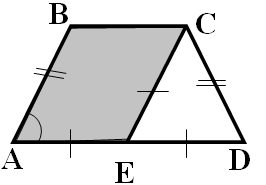
5. В равнобедренной трапеции ABCD точка Е – середина большого основания AD, ED=EC, BAD=60°. Доказать, что АВСЕ – ромб.
Работа над ошибками в контрольной работе по теме «Многоугольники»
|
Знать, уметь: |
|||
|
Свойства и признаки параллелограмма, прямоугольника, ромба, квадрата и трапеции. Уметь применять свойства и признаки при решении вычислительных задач и задач на доказательство |
|||
|
2 |
Знать и уметь применять свойства диагоналей прямоугольника и параллелограмма |
Вариант 1
1. АB=CD=__см (т.к____) 2. AC=BD=__см (т.к____) 3. АО=CO=__ см и ВО=OD=__см (т.к____) 4. АОВ. Р=АВ+АО+ВО=__+__+__=20(см) Ответ:________ |
Вариант 2 1. BC=AD=__см (т.к____) 2.AО=СО=__см, DО=ВО=__см (т.к______) 3. АОD. Р=АD+АО+DО=__+__+__=13(см) Ответ:________ |
|
3 |
Знать свойства равнобедренной трапеции и применять при решении задач |
Вариант 1 1. ABCD равнобедренная трапеция ( т.к____) 2. BK,CF–высоты. KBCF – прямоугольник, Значит __=__=___см(т.к________) 3. ABK и CDF прямоугольные. ABK = CDF по гипотенузе и острому углу: __=__ =__см (как ___); как_______);
Следовательно __=___= (13 – 9):2=___см. 4. В ABK катет __ равен ½ гипотенузы, значит 30°, а 60°.
Значит 30°, а 60°(т.к _____)
5. 180° — 60° (т.к___________), значит
Ответ:
|
Вариант 2 1. ABCD равнобедренная трапеция ( т.к____) 2. BK,CF–высоты. KBCF – прямоугольник, Значит __=__=___см(т.к________) 3. ABK и CDF прямоугольные. ABK = CDF по гипотенузе и острому углу: __=__ =__см (как ___); как_______);
Следовательно __=___= (7 – 5):2=___см. 4. В ABK катет __ равен ½ гипотенузы, значит 30°, а 60°.
Значит 30°, а 60°(т.к _____)
5. 180° — 60° (т.к___________), значит
Ответ:
|
|
4 |
Знать и уметь применять свойства ромба и квадрата |
Вариант 1 1. BD=AD= (по ____); AD=AB (____). Значит АDВ – равносторонний и все углы по ___°. 2. BCD=BAD=60°(т.к___) 3. CA – диагональ, значит ACD=30° 4. OTC- прямоуг. OCT=30°, значитTOC=__° 5. BOC. COB =90°(т.к__) OF – биссектриса, значит COF=___°, 6. = + =__°+__°=__° |
Вариант 2 1. АOВ – равнобедренный BО=AО (т.к. ____); 2. OF–высота (по условию), значит ОF – ____ и FOA=____° 3. АOD – прямоугольн ° (т.к. ____); 4. DOT==30°, (по условию), значит OT=___° 5. Т = А +АOT =__°+__°=__° |
|
5 |
Уметь использовать признаки и свойства фигур при решении задач на доказательство |
Вариант 1 АDС. 1.FP – средняя линия (обосновать почему и доказать, что _║_ ). 2. FО – средняя линия (обосновать почему и доказать, что _║_ ). 3 . FOCP – параллелограмм( т.к____________). |
Вариант 2
1.ЕDС–равносторон. (обосновать почему) 2. ABCE– параллелограмм (доказать), 3. ABCE –ромб(т.к____________). |
Если учащийся научится самостоятельно изучать материал, пользуясь учебником или какими- то специально подобранными заданиями, то будет успешно решена задача сознательного овладения знаниями. Знания, которые усвоил учащийся сам, значительно прочнее тех, которые он получил после объяснения учителя.
Поэтому после написания контрольной работы даю возможность учащимся самим ликвидировать пробелы, творчески применять их в решении различных задач.
Контрольная работа
Многоугольники
Вариант 1
1. Укажите неверное утверждение. У любого ромба:
а) диагонали лежат на биссектрисах его углов;
б) противоположные углы равны;
в) все углы равны;
г) диагонали пересекаются под прямым углом.
2. АВСD – прямоугольник, АС=12см, CD=8 см. Найдите периметр треугольника АОВ, где О – точка пересечения диагоналей.
3. Длины боковых сторон трапеции равны 4см и 4см, а длины оснований – 9см и 13см. Найдите углы трапеции.
4. Диагонали ромба ABCD пересекаются в точке О. Отрезок OF – биссектриса ВОС, а отрезок ОТ – перпендикуляр, проведенный к стороне DC. Вычислите градусную меру , если BD=AD.
5. В прямоугольнике ABCD диагонали пересекаются в точке О, а P и F – середины сторон DCи AD соответственно. Доказать, что FOCP – параллелограмм
Вариант 2
1. Укажите неверное утверждение. У любого параллелограмма:
а) противоположные стороны равны;
б) диагонали равны;
в) противоположные углы равны;
г) диагонали, пересекаясь, делятся пополам.
2. АВСD – параллелограмм, АС=10см, ВD=6 см, AD=5см. Найдите периметр треугольника АОD, где О – точка пересечения диагоналей.
3. Найдите углы равнобедренной трапеции, если длина боковой стороны равна 2см, а длины оснований – 5см и 7см.
4. Диагонали квадрата ABCD пересекаются в точке О. Точко Т лежит на стороне AD так, что DОТ=30°. Отрезок OF – перпендикуляр, проведенный к стороне AB. Вычислите градусную меру FOT.
5. В равнобедренной трапеции ABCD точка Е – середина большого основания AD, ED=EC, BAD=60°. Доказать, что АВСЕ – ромб.
Работа над ошибками в контрольной работе по теме «Многоугольники»
|
Знать, уметь: |
|||
|
Свойства и признаки параллелограмма, прямоугольника, ромба, квадрата и трапеции. Уметь применять свойства и признаки при решении вычислительных задач и задач на доказательство |
|||
|
2 |
Знать и уметь применять свойства диагоналей прямоугольника и параллелограмма |
Вариант 1
1. АB=CD=__см (т.к____) 2. AC=BD=__см (т.к____) 3. АО=CO=__ см и ВО=OD=__см (т.к____) 4. АОВ. Р=АВ+АО+ВО=__+__+__=20(см) Ответ:________ |
Вариант 2 1. BC=AD=__см (т.к____) 2.AО=СО=__см, DО=ВО=__см (т.к______) 3. АОD. Р=АD+АО+DО=__+__+__=13(см) Ответ:________ |
|
3 |
Знать свойства равнобедренной трапеции и применять при решении задач |
Вариант 1 1. ABCD равнобедренная трапеция ( т.к____) 2. BK,CF–высоты. KBCF – прямоугольник, Значит __=__=___см(т.к________) 3. ABK и CDF прямоугольные. ABK = CDF по гипотенузе и острому углу: __=__ =__см (как ___); как_______);
Следовательно __=___= (13 – 9):2=___см. 4. В ABK катет __ равен ½ гипотенузы, значит 30°, а 60°.
Значит 30°, а 60°(т.к _____)
5. 180° — 60° (т.к___________), значит
Ответ: |
Вариант 2 1. ABCD равнобедренная трапеция ( т.к____) 2. BK,CF–высоты. KBCF – прямоугольник, Значит __=__=___см(т.к________) 3. ABK и CDF прямоугольные. ABK = CDF по гипотенузе и острому углу: __=__ =__см (как ___); как_______);
Следовательно __=___= (7 – 5):2=___см. 4. В ABK катет __ равен ½ гипотенузы, значит 30°, а 60°.
Значит 30°, а 60°(т.к _____)
5. 180° — 60° (т.к___________), значит
Ответ: |
|
4 |
Знать и уметь применять свойства ромба и квадрата |
Вариант 1 1. BD=AD= (по ____); AD=AB (____). Значит АDВ – равносторонний и все углы по ___°. 2. BCD=BAD=60°(т.к___) 3. CA – диагональ, значит ACD=30° 4. OTC- прямоуг. OCT=30°, значитTOC=__° 5. BOC. COB =90°(т.к__) OF – биссектриса, значит COF=___°, 6. = + =__°+__°=__° |
Вариант 2 1. АOВ – равнобедренный BО=AО (т.к. ____); 2. OF–высота (по условию), значит ОF – ____ и FOA=____° 3. АOD – прямоугольн ° (т.к. ____); 4. DOT==30°, (по условию), значит OT=___° 5. Т = А +АOT =__°+__°=__° |
|
5 |
Уметь использовать признаки и свойства фигур при решении задач на доказательство |
Вариант 1 АDС. 1.FP – средняя линия (обосновать почему и доказать, что _║_ ). 2. FО – средняя линия (обосновать почему и доказать, что _║_ ). 3 . FOCP – параллелограмм( т.к____________). |
Вариант 2
1.ЕDС–равносторон. (обосновать почему) 2. ABCE– параллелограмм (доказать), 3. ABCE –ромб(т.к____________). |
Технологическая карта урока геометрии в 8 «К» классе Повторение изученного по теме «Четырёхугольники»
ФИО
Обмочиева Галина Леонтьевна
Место работы
МАОУ СОШ № 93
Должность
Учитель математики
Предмет
Алгебра
Класс
8 «К»
Дата
03.10.2017
Базовый учебник
Геометрия. 7-9 : учеб.для общеобразоват. учреждений /Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.М.: Просвещение, 2013.
Название урока
Повторение изученного по теме «Четырёхугольники»
Тип урока
рефлексия
Форма проведения урока
Традиционная
Образовательная среда урока
Компьютер, проектор, учебники по геометрии, раздаточный материал,мел, доска, электронная презентация, выполненная в программе Power Point
Формы работы учащихся
Индивидуальная, парная, групповая
Цель урока: Систематизация знаний по теме “Четырехугольники”.
Задачи:
обучающие:
• привести в систему теоретические знания по теме “Четырехугольники”;
• закрепление навыков решения задач по данной теме;
• определить сферы практического использования знаний.
развивающие:
• развивать мыслительные операции (проведение аналогии, анализ, синтез);
• развивать пространственное мышление;
• развивать логическое мышление.
воспитывающие:
• развивать чувство коллективизма, умение выслушивать ответы товарищей;
• прививать интерес к предмету.
Этапы урока
Деятельность учителя
Деятельность ученика
Формируемые УУД
Организационный (1 мин)
— Наш сегодняшний урок мы начинаем с высказывания великого русского писателя Льва Николаевича Толстого. Как вы понимаете эти слова? (Можно знать многое, но все эти знания могут не иметь никакой ценности для человека и человечества в целом. Можно знать, познавать важное, основное, нужное для развития самого человека и человечества в целом.)
Слушают учителя, настраиваются на работу, проверяют готовность к уроку.
Умение слушать и вступать в диалог.
Умение выделять нравственный аспект поведения.
Актуализация знаний (2 мин)
— А как вы думаете, что действительно важно и нужно знать? (Важно то, что ведёт человека и человечество к развитию, к новым знаниям, к прогрессу.)
— А где можно черпать, находить эти важные знания? (Эти знания можно черпать в науках).
-Я с вами согласна, спасибо.
— Какие важные, нужные знания понадобятся нам сегодня на уроке? (Сегодня на уроке нам понадобится теоретический материал по теме «Четырёхугольники».)
Отвечают на вопросы, повторяют материал предыдущих уроков.
Познавательные – применение предметных знаний; выполнение учебных заданий.
Регулятивные – выделение и осознание того, что уже пройдено; умение распознавать на слух вопросы и отвечать на них.
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог.
Личностные – самооценка, взаимооценка.
Актуализация знаний.
Постановка цели и задачи урока.
Мотивация учащихся.
( 2 мин )
— Как можно проверить, владеете ли вы материалом по изученной теме?
(Проверить свои знания в ходе самостоятельной работы).
— Из чего будет складываться ваша успешность работы сегодня на уроке? (Из знания теории и умения её применять в решении задач).
-Итак, нам сегодня предстоит пройти два этапа ( 1 этап. – знаю, 2 этап –учусь применять)
-Ну а ещё мне хочется пожелать вам удачи!
Отвечают на вопросы, повторяют материал предыдущих уроков.
Комментируют полученный результат. Выявляют проблему, формируют тему урока, ставят цель.
Записывают тему урока.
Познавательные извлечение из текстов математической информации; постановка и формулирование проблеммы; самостоятельное формулирование познавательной цели..
Регулятивные – умение анализировать, целеполагание, прогнозирование.
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог, участвовать в коллективном обсуждении проблем.
Личностные – самооценка.
Актуализация знаний и фиксация затруднений в индивидуальной деятельности (10 мин)
Возьмите карточку с самостоятельной работой №1.
Вам предстоит определить, какие из предложенных вам 10 высказываний являются верными, а какие – нет. Для выполнения этого задания у вас есть 2 минуты.
Самостоятельная работа № 1.
1.Четырёхугольник, у которого только две стороны параллельны, а две другие стороны не параллельны, называется трапецией.
2.Трапеция, у которой один из углов равен 90 градусов, называется равнобедренной.
3.Любой ромб является параллелограммом.
4.У прямоугольника все углы — прямые
5.У трапеции стороны попарно параллельны
6.Диагонали квадрата взаимно перпендикулярны
7.У ромба все стороны равны
8.Сумма углов выпуклого четырехугольника равна 540 градусов.
9.Диагонали прямоугольника равны.
10.Периметр – это произведение сторон.
Один из учащихся поясняет выбранные им ответы, аргументирует свой выбор, другие имеют право исправить его.
— А теперь проверим вашу работу. Поменяйтесь работой с соседом по парте. Он оценит правильность ваших ответов. (Правильные ответы появляются на слайде, учащиеся сверяются с ними.)
-Кто допустил ошибки при выполнении работы? (Учащиеся поднимают руки)
— У кого при выполнении работы не возникло затруднений? (Учащиеся поднимают руки)
Отметьте успешность вашей работы в таблице фиксации результатов.
Переходим к выполнению самостоятельной работы №2. Положите перед собой карточку с заданием. Для выполнения этого задания вам даётся 3 минуты.Самостоятельная работа №2.
Заполни таблицу, отметив знаки “+” – да,“ –” – нет.
Таблица “Свойства четырехугольников”.
|
Парал- лограмм |
Прямо- угольник |
Ромб |
Квадрат |
|
|
1. Противоположные стороны параллельны и равны. |
||||
|
2. Все стороны равны |
||||
|
3. Противоположные углы равны, сумма соседних углов равна 1800. |
||||
|
4. Все углы прямые. |
||||
|
5. Диагонали пересекаются и точкой пересечения делятся пополам. |
||||
|
6. Диагонали равны. |
||||
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами углов. |
Индивидуальная работа и работа по проверке результатов в паре. Ведение таблицы фиксации результатов.
— Выполняют самопроверку по ключу.
— Осуществляют самооценку за самостоятельную работу 2..
«5» — 25-28 правильных ответов,
0-3 ошибки.
«4» — 20-24 правильных ответов,
4-8 ошибок.
«3» — 15-19 правильных ответов,
9-13 ошибок.
«2» — Менее 15,
более 13 ошибок.
Познавательные – уметь решать примеры по выбранному правилу; применение предметных знаний, выбор способов решения задач.
Регулятивные – умение проговаривать последовательность действий на уроке, анализировать и оценивать результат работы.
Коммуникативные – умение слушать, обращаться с вопросом к учителю и сверстнику.
Личностные – самооценка.
Коммуникативные – умение работать в парах.
Локализация затруднений. (10 мин)
— Какими знаниями вы пользовались при выполнении самостоятельных работ №1 и №2?( Мы использовали теорию по теме «Четырёхугольники».)
— Кто испытывал затруднения при выполнении задания самостоятельной работы №2? ( Учащиеся поднимают руки)
— В чём может быть причина вашего затруднения?( В недостаточном знании теории по теме «Четырёхугольники».)
— Какие могут быть пути выхода из затруднения?(Необходимо выучить теоретический материал по теме «Четырёхугольники».)
— Следующая самостоятельная работа № 3 имеет название « От теории к практике».
Вам предстоит решить три задачи по готовым чертежам и записать в тетради их решение.
Возьмите карточку с самостоятельной работой № 3. Перед вами три задачи по готовым чертежам. На выполнение работы я даю вам 10 минут.
Самостоятельная работа № 3.
Найдите углы трапеции МSRK
Найдите периметр параллелограмма АВСD
Найдите периметр параллелограмма MFEL
Работают в группах по 4 человека. Проверяем решения. ( По одному из группы учащиеся выходят к доске, объясняя решение задач.)
Выполняют самопроверку по ключу.
Осуществляют самооценку за самостоятельную работу 3.
Познавательные – выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов.
Регулятивные – Оценка – осознание уровня и качества усвоения.
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог.
Личностные – ценностно-смысловая ориентация.
Коммуникативные – умение работать в группах.
Коррекция выявленных затруднений (10 мин)
— Если вы не допустили ошибок, то какую поставите перед собой цель? ( Я не допустил ошибок, значит я знаю теорию, могу переходить к выполнению более сложных заданий) Учащиеся, справившиеся с самостоятельной работой № 3 без ошибок переходят к выполнению задач самостоятельной работы № 5.
Самостоятельная работа № 5.
№1. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.
№2.Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.
— А какую цель поставят перед собой те, кто допустил ошибки в ходе решения задач самостоятельной работы № 3?( Я допустил ошибки, значит , мне нужно потренироваться и преодолеть затруднения.)
— Возьмите карточку с самостоятельной работой №4.
Самостоятельная работа №4.
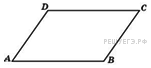
Найдите периметр параллелограммаKMNR. Найдите углы трапеции TPLO.
Найдите периметр параллелограмма MSLK.
Учащиеся обеих групп по истечении времени, отведённого на самостоятельную работу ( 10 минут), проверяют ответы , сверяясь с ключом на слайде, оценивают свою работу.
Работают в группах по 4 человека. Проверяем решения. ( По одному из группы учащиеся выходят к доске, объясняя решение задач.)
Выполняют самопроверку по ключу.
Осуществляют самооценку за самостоятельную работу 3.
Самостоятельная работа № 4.
|
Номер задачи |
Ответ |
|
№ 5 |
22 |
|
№ 9 |
90°; 90°; 55°; 125° |
|
№ 14 |
32 |
|
Количество правильно решённых задач |
Оценка |
|
3 |
«5» |
|
2 |
«4» |
|
1 |
«3» |
|
0 |
«2» |
Самостоятельная работа № 5.
|
Номер задачи |
Ответ |
|
№ 1. |
10 |
|
№ 2. |
20 |
|
Количество правильно решённых задач |
Оценка |
|
2 |
5 |
|
1 |
4 |
Результаты выполнения ваших самостоятельных работ заносятся в таблицу фиксации результатов.
Познавательные – извлекают необходимую информацию, структурируют информацию в виде записи выводов и определений.
Регулятивные – выполнение поставленной задачи
Личностные – развитие познавательных интересов, учебных мотивов
Коммуникативные – умение работать в группах.
Рефлексия деятельности на уроке. (5 мин)
— Какой была цель нашего урока? ( Выявить свои затруднения, поработать над их устранением.)
-Мне бы хотелось узнать, кто из вас достиг этой цели. Для этого в таблице фиксации результатов проанализируйте свою деятельность на уроке.
— Я тоже смогу оценить вашу работу на уроке с помощью вашей таблицы фиксации результатов.
— Как вы думаете как тема « Четырёхугольники» может быть связана с дальнейшим материалом курса геометрии? (Теория и навык решения задач по теме «Четырёхугольники» будет нужна при решении задач по другим темам, в том числе при изучении следующей темы «Площади», при решении задач ОГЭ и ЕГЭ.)
— Всё верно, но оказывается, что известные нам четырёхугольники имеют отношение не только к геометрии, но и к географии, и к истории, и к физкультуре, и даже к астрономии.
Домашнее задание.
Вам предстоит поработать с заданиями карточки« Домашняя работа» ( в зависимости от затруднений, испытываемых на уроке ).
— Спасибо за урок!
Рефлексия деятельности на уроке.
На уроке я узнала (узнал)__
На уроке я научилась (научился) __
Я справился со своими затруднениями (если они были) _
Я ничего нового не открыла (не открыл ) для себя и ничему не научилась (не научился ) __
Познавательные – рефлексия.
Регулятивные – оценка своей деятельности и деятельности других людей..
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли.
Личностные – самооценка на основании критерия успешности.
Урок математики в 8 классе
Тема: Повторение изученного по теме «Четырёхугольники»
Тип урока: рефлексия
Цель урока: Систематизация знаний по теме “Четырехугольники”.
Задачи:
обучающие:
-
привести в систему теоретические знания по теме “Четырехугольники”;
-
закрепление навыков решения задач по данной теме;
-
определить сферы практического использования знаний.
развивающие:
-
развивать мыслительные операции (проведение аналогии, анализ, синтез);
-
развивать пространственное мышление;
-
развивать логическое мышление.
воспитывающие:
-
развивать чувство коллективизма, умение выслушивать ответы товарищей;
-
прививать интерес к предмету.
Оборудование урока:
-
видеопроектор
-
компьютер
-
доска
-
презентация к уроку
-
карточки с задачами
-
листы с готовыми чертежами;
-
карточки с кроссвордами;
Ход урока.
-
Мотивация к коррекционной деятельности.
На слайде высказывание:
Важно не количество знаний, а качество их. Можно знать очень многое, не зная самого нужного.
Л.Н. Толстой
— Наш сегодняшний урок мы начинаем с высказывания великого русского писателя Льва Николаевича Толстого. Как вы понимаете эти слова? (Можно знать многое, но все эти знания могут не иметь никакой ценности для человека и человечества в целом. Можно знать, познавать важное, основное, нужное для развития самого человека и человечества в целом.)
— А как вы думаете, что действительно важно и нужно знать? (Важно то, что ведёт человека и человечество к развитию, к новым знаниям, к прогрессу.)
— А где можно черпать, находить эти важные знания? (Эти знания можно черпать в науках).
-Я с вами согласна, спасибо.
— Какие важные, нужные знания понадобятся нам сегодня на уроке? (Сегодня на уроке нам понадобится теоретический материал по теме «Четырёхугольники».)
— Как можно проверить, владеете ли вы материалом по изученной теме?
(Проверить свои знания в ходе самостоятельной работы).
— Из чего будет складываться ваша успешность работы сегодня на уроке? (Из знания теории и умения её применять в решении задач).
-Итак, нам сегодня предстоит пройти два этапа ( 1 этап. – знаю, 2 этап –учусь применять)
-Ну а ещё мне хочется пожелать вам удачи!
2. Актуализация знаний и фиксация затруднений в индивидуальной деятельности.
Возьмите карточку с самостоятельной работой №1.
Вам предстоит определить, какие из предложенных вам 10 высказываний являются верными, а какие – нет. Для выполнения этого задания у вас есть 2 минуты.
Самостоятельная работа № 1.
-
Четырёхугольник, у которого только две стороны параллельны, а две другие стороны не параллельны, называется трапецией.
-
Трапеция, у которой один из углов равен 90 градусов, называется равнобедренной.
-
Любой ромб является параллелограммом.
-
У прямоугольника все углы — прямые
-
У трапеции стороны попарно параллельны
-
Диагонали квадрата взаимно перпендикулярны
-
У ромба все стороны равны
-
Сумма углов выпуклого четырехугольника равна 540 градусов.
-
Диагонали прямоугольника равны.
-
Периметр – это произведение сторон.
Один из учащихся поясняет выбранные им ответы, аргументирует свой выбор, другие имеют право исправить его.
— А теперь проверим вашу работу. Поменяйтесь работой с соседом по парте. Он оценит правильность ваших ответов. (Правильные ответы появляются на слайде, учащиеся сверяются с ними.)
-Кто допустил ошибки при выполнении работы? (Учащиеся поднимают руки)
— У кого при выполнении работы не возникло затруднений? (Учащиеся поднимают руки)
Отметьте успешность вашей работы в таблице фиксации результатов.
Переходим к выполнению самостоятельной работы №2. Положите перед собой карточку с заданием. Для выполнения этого задания вам даётся 3 минуты.Самостоятельная работа №2.
Заполни таблицу, отметив знаки “+” – да,“ –” – нет.
Таблица “Свойства четырехугольников”.
|
Параллелограмм |
Прямоугольник |
Ромб |
Квадрат |
|
|
1. Противоположные стороны параллельны и равны. |
||||
|
2. Все стороны равны |
||||
|
3. Противоположные углы равны, сумма соседних углов равна 1800. |
||||
|
4. Все углы прямые. |
||||
|
5. Диагонали пересекаются и точкой пересечения делятся пополам. |
||||
|
6. Диагонали равны. |
||||
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами углов. |
— Выполните самопроверку по ключу:
|
Параллелограмм |
Прямоугольник |
Ромб |
Квадрат |
|
|
1. Противоположные стороны параллельны и равны. |
+ |
+ |
+ |
+ |
|
2. Все стороны равны |
— |
— |
+ |
+ |
|
3. Противоположные углы равны, сумма соседних углов равна 1800. |
+ |
+ |
+ |
+ |
|
4. Все углы прямые. |
— |
+ |
— |
+ |
|
5. Диагонали пересекаются и точкой пересечения делятся пополам. |
+ |
+ |
+ |
+ |
|
6. Диагонали равны. |
— |
+ |
— |
+ |
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами углов. |
— |
— |
+ |
+ |
— Оцените правильность выполнения вашей самостоятельной работы:
«5» — 25-28 правильных ответов,
0-3 ошибки.
«4» — 20-24 правильных ответов,
4-8 ошибок.
«3» — 15-19 правильных ответов,
9-13 ошибок.
«2» — Менее 15,
более 13 ошибок.
—Поставьте себе оценку за самостоятельную работу №2.
Отметьте успешность вашей работы в таблице фиксации результатов.
3.Локализация затруднений.
— Какими знаниями вы пользовались при выполнении самостоятельных работ №1 и №2?( Мы использовали теорию по теме «Четырёхугольники».)
— Кто испытывал затруднения при выполнении задания самостоятельной работы №2? ( Учащиеся поднимают руки)
— В чём может быть причина вашего затруднения?( В недостаточном знании теории по теме «Четырёхугольники».)
— Какие могут быть пути выхода из затруднения?(Необходимо выучить теоретический материал по теме «Четырёхугольники».)
— Следующая самостоятельная работа № 3 имеет название « От теории к практике».
Вам предстоит решить три задачи по готовым чертежам и записать в тетради их решение.
Возьмите карточку с самостоятельной работой № 3. Перед вами три задачи по готовым чертежам. На выполнение работы я даю вам 10 минут.
Самостоятельная работа № 3.
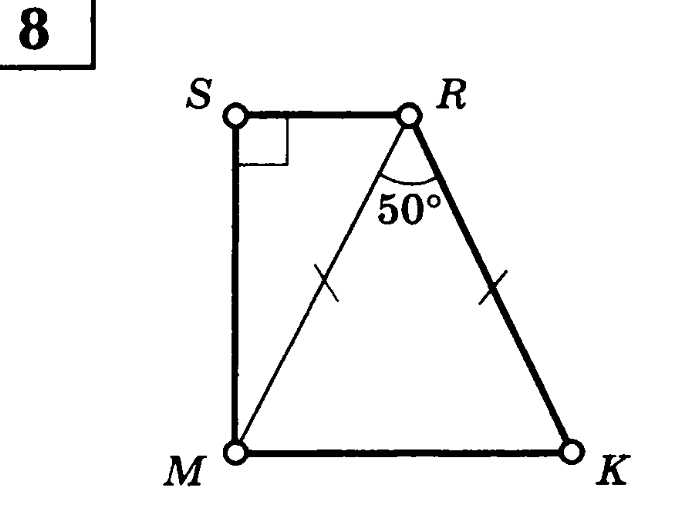
Найдите углы трапеции МSRK
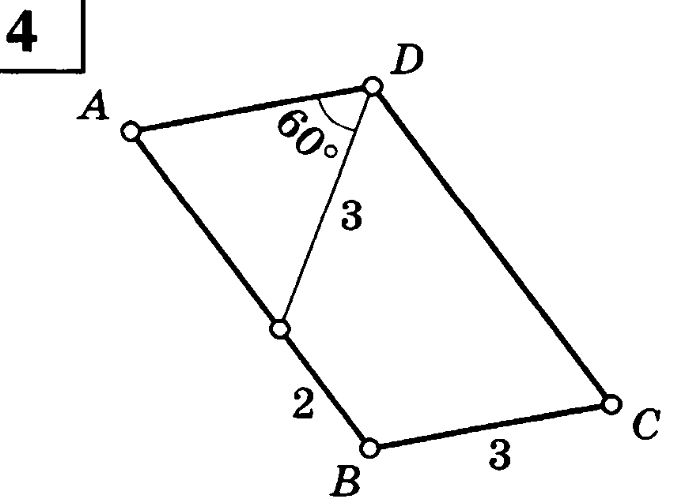
Найдите периметр параллелограмма АВСD
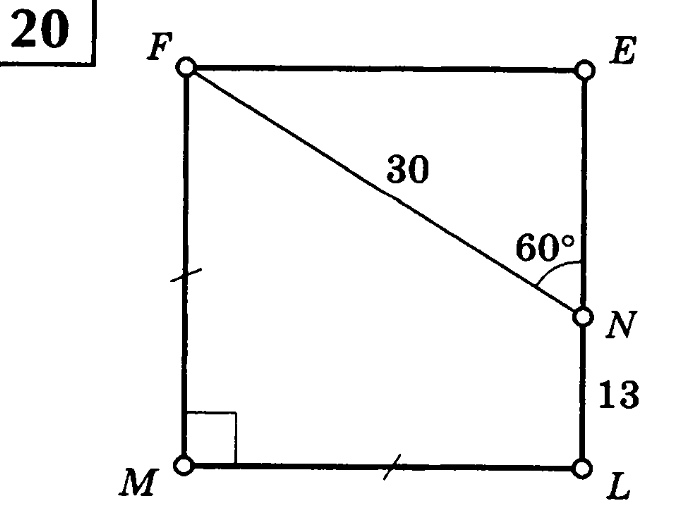
Найдите периметр параллелограмма MFEL
Проверим ваши решения. ( Учащиеся выходят к доске, объясняя решение задач.)
|
Номер задачи |
Ответ |
|
№ 4 |
16 |
|
№ 8 |
90°; 90°; 65°;115° |
|
№ 20 |
112 |
А теперь оцените правильность выполнения вами каждой задачи.
|
Количество правильно решённых задач |
Оценка |
|
3 |
«5» |
|
2 |
«4» |
|
1 |
«3» |
|
0 |
«2» |
— Занесите результаты вашей работы в таблице фиксации результатов.
4. Коррекция выявленных затруднений.
— Если вы не допустили ошибок, то какую поставите перед собой цель? ( Я не допустил ошибок, значит я знаю теорию, могу переходить к выполнению более сложных заданий) Учащиеся, справившиеся с самостоятельной работой № 3 без ошибок переходят к выполнению задач самостоятельной работы № 5.
Самостоятельная работа № 5.
№1. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.
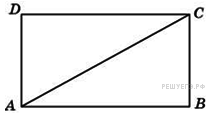
№2.Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.
— А какую цель поставят перед собой те, кто допустил ошибки в ходе решения задач самостоятельной работы № 3?( Я допустил ошибки, значит , мне нужно потренироваться и преодолеть затруднения.)
— Возьмите карточку с самостоятельной работой №4.
Самостоятельная работа №4.
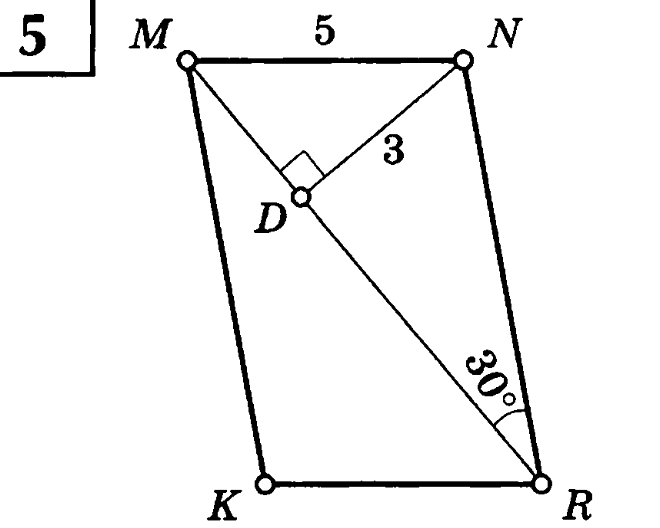
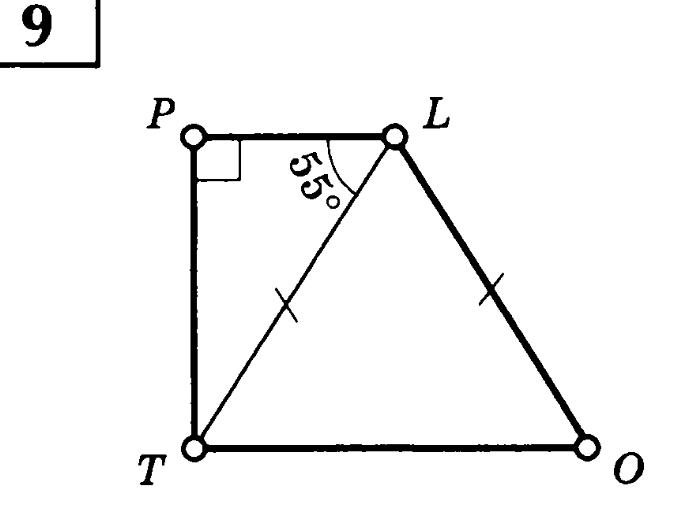
Найдите периметр параллелограммаKMNR. Найдите углы трапеции TPLO.
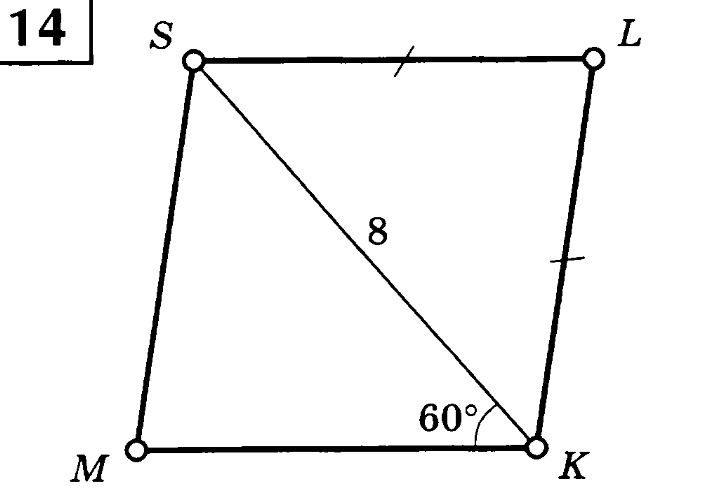
Найдите периметр параллелограмма MSLK.
Учащиеся обеих групп по истечении времени, отведённого на самостоятельную работу ( 10 минут), проверяют ответы , сверяясь с ключом на слайде, оценивают свою работу.
Самостоятельная работа № 4.
|
Номер задачи |
Ответ |
|
№ 5 |
22 |
|
№ 9 |
90°; 90°; 55°; 125° |
|
№ 14 |
32 |
|
Количество правильно решённых задач |
Оценка |
|
3 |
«5» |
|
2 |
«4» |
|
1 |
«3» |
|
0 |
«2» |
Самостоятельная работа № 5.
|
Номер задачи |
Ответ |
|
№ 1. |
10 |
|
№ 2. |
20 |
|
Количество правильно решённых задач |
Оценка |
|
2 |
5 |
|
1 |
4 |
Занесите результаты выполнения ваших самостоятельных работ в таблицу фиксации результатов.
5. Обобщение затруднений во внешней речи.
— Итак, почему при выполнении самостоятельной работы вам пришлось разделиться на две группы? ( У некоторых из нас были затруднения. )
— Какие затруднения вы испытывали?(Учащиеся проговаривают свои затруднения.)
— Что вам помогает их преодолевать?( Работа над ошибками.)
— При выполнении заданий дома вы сможете проверить, справились ли вы со своими затруднениями.
6. Рефлексия деятельности на уроке.
— Какой была цель нашего урока? ( Выявить свои затруднения, поработать над их устранением.)
-Мне бы хотелось узнать, кто из вас достиг этой цели. Для этого в таблице фиксации результатов проанализируйте свою деятельность на уроке.
Рефлексия деятельности на уроке.
На уроке я узнала (узнал)__________________________________________________________________________________________________________________________________________________________
На уроке я научилась (научился) ________________________________________________________________________________
Я справился со своими затруднениями (если они были) ________________________________
Я ничего нового не открыла (не открыл ) для себя и ничему не научилась (не научился ) ________________________________________________________________________________
— Я тоже смогу оценить вашу работу на уроке с помощью вашей таблицы фиксации результатов.
— Как вы думаете как тема « Четырёхугольники» может быть связана с дальнейшим материалом курса геометрии? (Теория и навык решения задач по теме «Четырёхугольники» будет нужна при решении задач по другим темам, в том числе при изучении следующей темы «Площади», при решении задач ГИА и ЕГЭ.)
— Всё верно, но оказывается, что известные нам четырёхугольники имеют отношение не только к геометрии, но и к географии, и к истории, и к физкультуре, и даже к астрономии.
Учитель показывает слайды № 15, № 16, № 17.
7. Домашнее задание.
— По мере выполнения заданий сегодня на уроке, на доске мы получили слово ДЕЛЬТОИД (Учитель открывал по букве на каждое выполняемое на уроке задание, получилось слово ДЕЛЬТОИД) Ваше домашнее задание — узнать что такое ДЕЛЬТОИД и какое отношение он имеет к теме нашего сегодняшнего урока.
-А так же дома вам предстоит поработать с заданиями карточки« Домашняя работа» ( в зависимости от затруднений, испытываемых на уроке ).
— Спасибо за урок!
Приложение .
Самостоятельная работа № 1.
1.Четырёхугольник, у которого только две стороны параллельны, а две другие стороны не параллельны, называется трапецией.
2. Трапеция, у которой один из углов равен 90 градусов, называется равнобедренной.
3. Любой ромб является параллелограммом.
4. У прямоугольника все углы — прямые
5. У трапеции стороны попарно параллельны
6. Диагонали квадрата взаимно перпендикулярны
7. У ромба все стороны равны
8. Сумма углов выпуклого четырехугольника равна 540 градусов.
9. Диагонали прямоугольника равны.
-
Периметр – это произведение сторон.
Самостоятельная работа №2.
Заполни таблицу, отметив знаки “+” – да,“ –” – нет.
Таблица “Свойства четырехугольников”.
|
Параллелограмм |
Прямоугольник |
Ромб |
Квадрат |
|
|
1. Противоположные стороны параллельны и равны. |
||||
|
2. Все стороны равны |
||||
|
3. Противоположные углы равны, сумма соседних углов равна 1800. |
||||
|
4. Все углы прямые. |
||||
|
5. Диагонали пересекаются и точкой пересечения делятся пополам. |
||||
|
6. Диагонали равны. |
||||
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами углов. |
Самостоятельная работа № 3.
Найдите углы трапеции МSRK
Найдите периметр параллелограмма АВСD
Найдите периметр параллелограмма MFEL
Самостоятельная работа №4.
Найдите периметр параллелограммаKMNR. Найдите углы трапеции TPLO.
Найдите периметр параллелограмма MSLK.
Самостоятельная работа № 5.
№1. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.
№2.Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.
Таблица фиксации результатов.
Фамилия Имя________________________________________________________________
|
Номер самостоятельной работы |
Количество правильных ответов /правильно решённых задач |
Оценка |
|
Самостоятельная работа № 1. |
||
|
Самостоятельная работа № 2. |
||
|
Самостоятельная работа № 3. |
||
|
Самостоятельная работа № 4. |
||
|
Самостоятельная работа № 5. |
Рефлексия деятельности на уроке.
На уроке я узнала (узнал)__________________________________________________________________________
На уроке я научилась ( научился) ________________________________________________________________________________
Я справился со своими затруднениями ( если они были) ________________________________
Я ничего нового не открыла ( не открыл ) для себя и ничему не научилась ( не научился ) ________________________________________________________________________________
Таблица фиксации результатов.
Фамилия Имя________________________________________________________________
|
Номер самостоятельной работы |
Количество правильных ответов /правильно решённых задач |
Оценка |
|
Самостоятельная работа № 1. |
||
|
Самостоятельная работа № 2. |
||
|
Самостоятельная работа № 3. |
||
|
Самостоятельная работа № 4. |
||
|
Самостоятельная работа № 5. |
Рефлексия деятельности на уроке.
На уроке я узнала (узнал)__________________________________________________________________________
На уроке я научилась ( научился) ________________________________________________________________________________
Я справился со своими затруднениями ( если они были) ________________________________
Я ничего нового не открыла ( не открыл ) для себя и ничему не научилась ( не научился ) ________________________________________________________________________________
Домашняя работа
Задача 1. Диагонали прямоугольника АВСD пересекаются в точке О,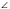 
АВО = 36°. Найдите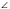АОD.
Задача 2. Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.
Задача 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.
Задача 4. В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.
Задача 5. Найдите периметр ромба ABCD, если 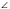В равен 120°, аBD=8 см.
Разгадай кроссворд:По горизонтали:
|
5 |
6 |
||||||||||||||
|
7 |
|||||||||||||||
|
1 |
|||||||||||||||
|
2 |
|||||||||||||||
|
8 |
|||||||||||||||
|
3 |
|||||||||||||||
|
4 |
|||||||||||||||
1. Четырехугольник, у которого противоположные стороны параллельны
2. Четырехугольник, у которого только две стороны параллельны
3. Параллелограмм, у которого все углы прямые
4. Точки из которых выходят стороны четырехугольника
По вертикали:
1. Сумма длин всех сторон
5. Отрезок, соединяющий противолежащие вершины
6. Прямоугольник, у которого все стороны равны
7. Параллелограмм , у которого все стороны равны
8. Отрезок, соединяющий соседние вершины
Д Е Л Ь
Т О И Д
Год: 2019
Издательство: O’zbekiston
Авторы: Рахимкариев А.А., Тохтаходжаева М.А.
Повторение курса 7-ого класса
1
2
3
5
6
7
8
9
10
11
13
14
15
16
17
18
19
§ 1. Основные четырехугольники и их свойства
Тема 1.Сумма внутренних и внешних углов выпуклого многоугольника
1
2
3
4
5
6
7
8
9
10
Тема 2. Параллелограмм и его свойства
1
2
3
5
6
7
Тема 3. Признаки параллелограмма
1
2
3
5
6
7
8
9
Тема 4. Прямоугольник и его свойства
1
2
3
4
5
6
7
Темы 5-6 Свойства ромба и квадрата
1
2
3
5
6
8
9
10
11
12
13
Темы 7-8. Трапеция и ее свойства
1
2
3
4
5
6
7
8
9
10
11
12
§ 2. Теорема Фалеса и ее применение
Тема 9. Теорема Фалеса
1
2
3
4
5
6
7
8
Темы 10-11. Свойство средней линии треугольника. Свойство средней линии трапеции
1
2
3
4
5
6
7
8
9
10
11
12
Темы 13- 14. Контрольная работа 1. Работа над ошибками
1
2
3
4
Тест 1
1
2
3
4
5
6
7
8
9
§ 3. Тригонометрические функции острого угла
Тема 15. Синус. косинус, тангенс и котангенс острого угла
1
2
3
4
5
6
7
Тема 16. Синус. косинус, тангенс и котангенс острого угла (продолжение)
1
2
3
4
5
6
7
8
§ 4. Теорема Пифагора и его применение
Тема 17. Теорема Пифагора и ее разные доказательства
1
2
3
4
5
6
Тема 18. Теорема, обратная теореме Пифагора
1
2
3
4
5
6
Тема 19. Применение теоремы Пифагора
1
2
3
4
5
6
7
8
§ 5. Тригонометрические тождества
Темы 20-21. Основное тригонометрическиое тождество и его следствие
1
2
3
4
5
6
7
9
10
11
12
13
14
Тема 22. Формулы для тригонометрических функций дополнительных углов
1
2
3
4
5
6
7
8
Тема 23. Вычисление значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
1
2
3
4
5
6
7
8
§ 6. Решение прямоугольных треугольников
Тема 24. Таблица значений тригонометрических функций
1
2
3
4
5
6
7
8
Тема 25. Решение прямоугольных треугольников
1
2
3
4
5
7
Тема 26. Решение прямоугольных треугольников (продолжение)
1
2
3
4
5
6
7
Тема 27. Построение прямоугольных треугольников
1
2
3
4
5
6
7
Темы 29-30. Контрольная работа 2. Работа над ошибками
1
2
3
4
Тест 2
1
2
3
4
5
6
7
8
9
10
§ 7. Система координат на плоскости
Тема 31. Координаты точки на плоскости. Координаты середины отрезка
1
2
3
4
5
6
7
8
Темы 32-33. Расстояние между точками. Уравнение окружности
1
2
3
4
5
6
7
8
9
10
11
Тема 34. Уравнение прямой. Метод координат при решении геометрических задач
1
2
3
5
6
7
8
9
Тема 35. Понятие вектора. Длина и направление вектора
1
2
3
4
5
6
7
Темы 36-37. Сложение и вычитание векторов
1
2
3
4
5
6
7
8
9
10
11
Темы 38-39. Умножение вектора на число. Координаты вектора
1
2
3
4
5
6
7
8
9
10
11
12
13
Тема 40. Действия над векторами, заданными своими координатами
1
2
3
4
5
6
7
8
9
Тема 41. Физические и геометрические интерпретации векторов. Решение геометрических задач методом координат
1
2
3
5
6
7
8
Темы 43-44. Контрольная работа 3. Работа над ошибками
1
2
3
4
Тест 3
1
2
3
4
5
6
§ 9. Площадь многоугольника
Тема 45. Понятие о площади
1
2
3
4
5
6
7
8
9
10
11
12
13
Темы 46-47. Площадь прямоугольника и параллелограмма
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Тема 48. Площадь треугольника
1
2
3
4
5
6
7
8
9
10
11
Темы 49-50. Площадь ромба и трапеции
1
2
3
4
5
7
8
9
10
11
12
13
14
15
Тема 51. Площадь многоугольника
1
2
3
4
5
6
Темы 53-54. Контрольная работа 4. Работа над ошибками
1
2
3
Тест 4
1
2
3
4
5
6
7
8
9
10
§ 10. Углы в окружности
Тема 55. Взаимное расположение прямой и окружности. Касательная к окружности и ее свойства
2
3
4
5
6
7
8
Тема 56. Взаимное расположение двух окружностей. Центральный угол и угловая величина дуги окружности
2
3
4
5
6
7
8
9
10
Тема 57. Угол, вписанный в окружность
3
4
5
6
7
8
Тема 58. Измерение углов, образованных секущими окружности
2
3
4
5
6
7
8
9
Тема 59. Свойства хорд и диаметров окружности
2
3
4
5
6
7
8
9
10
11
Тема 60. Практические задания и их применение Замечательные точки в треугольнике
2
4
5
6
7
Темы 61-62. Контрольная работа 5. Работа над ошибками
1
2
3
4
Тест 5
1
2
3
4
5
6
Упражнения для повторения материала, пройденного в 8-м классе
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Тест 6
1
2
3
4
5
6
7
8
9
Добро пожаловать на сайт uzgdz.com, ты сделал верный выбор!
Насыщенная программа обучения включает в себя множество дисциплин.
Каждый новый урок несёт поток терминов, теорем, примеров. Уроки в классе,
домашняя подготовка, дополнительные занятия, факультативы забирают много
сил и времени у современного школьника. Порой, информация данная учителем,
сложно воспринимается и не усваивается за сорок минут. Придя домой, ученик не
может грамотно выполнить «домашку», чувствует себя глупо, снижается интерес к учёбе.
В такие моменты пригодится специализированная литература, которую наша команда заботливо
оставила для тебя.
Тут собраны все решения и правильные ответы по самым сложным наукам: математика, алгебра
и геометрия, физика и химия.
Мы отмечаем полезные функции решебников:
- самопроверка, анализ своей работы на предмет ошибок, выявление пробелов в знаниях на начальной стадии
- подмога в выполнении сложный задач
- возможность родителей курировать образовательный процесс ребёнка, а также дать объяснение той или иной терминологии
- повышение самооценки и уверенности в себе, адаптация к школьному курсу, проявление конкурентной заинтересованности.
Знание-сила, будь в этом уверен!
ГДЗ(TUV) Готовые домашние задания (Tayyor uyga vazifa, Yechim) — это не про бездумное списывание, это, в первую очередь,
инструмент для увеличения успеваемости в школе, получения максимальной пользы
и удовольствия из учебной деятельности. Пособие так же отлично подойдет для мам и пап,
преподавателей и репетиторов.
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Основные дидактические цели урока: совершенствовать навыки решения задач на применение признаков подобия треугольников; подготовка учащихся к предстоящей контрольной работе.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Анализ ошибок, допущенных в самостоятельной работе
- Провести общий анализ контрольной работы.
- Работа над ошибками. (На интерактивной доске записаны готовые ответы и указания к задачам контрольной работы. Учитель делит класс на группы в зависимости от того, какой уровень и вариант самостоятельной работы они выполняли. В одной группе должны быть учащиеся, выполнявшие один и тот же уровень и вариант. Учитель контролирует работу групп и по мере необходимости оказывает помощь.)
Ответы и указания к задачам самостоятельной работы:
I уровень сложности
II уровень сложности
lll уровень сложности
III. Решение задач
Решить задачи № 1—5. (Учитель делит класс на группы и по мере необходимости оказывает индивидуальную помощь.)
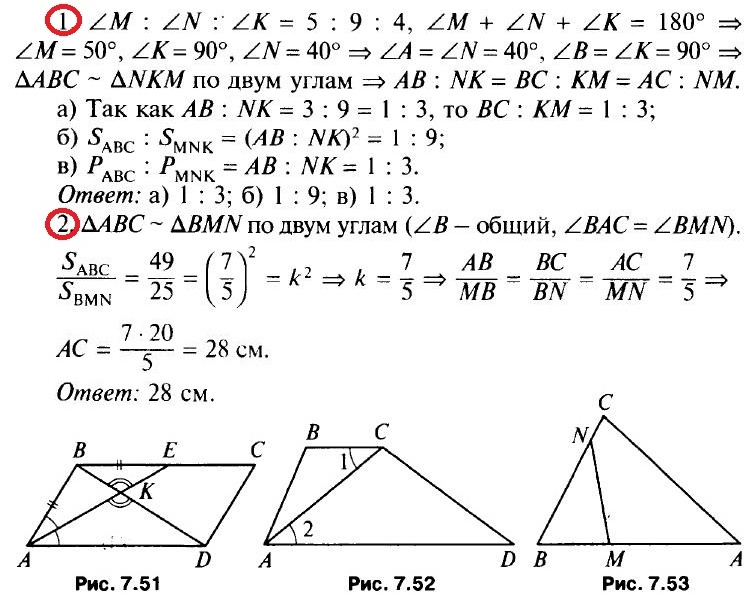
- В прямоугольном треугольнике ABC ∠A = 40°, ∠B = 90°, а в треугольнике MNK углы М, N, К относятся как 5 : 9 : 4. АВ = 3 см, KN — 9 см. Найдите: а) ВС : КМ; б) SABC : SMNK; в) PABC : PMNK.
- Дано: MN||АС, SABC : SBMN = 49 : 25, MN = 20 см (рис. 7.50). Найти: АС.
- В параллелограмме ABCD АЕ — биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4 : 9. АЕ пересекает диагональ BD в точке К. Найдите отношение ВК : KD.
- В трапеции ABCD основания ВС и AD равны 2 и 8 см, а диагональ АС равна 4 см. В каком отношении делит диагональ АС площадь трапеции?
- Прямая MN пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно так, что ВС = 2ВМ, АВ = 2BN, ВМ : BN = 3 : 5. Найдите: а) РАВС : PNBM; б) SABC : SNBM; в) MN : АС.
Краткое решение задач (ответы):
IV. Рефлексия учебной деятельности
- Какие треугольники называются подобными?
- Сформулируйте признаки подобия треугольников.
- Чему равно отношение периметров, площадей подобных треугольников?
- Сформулируйте свойство биссектрисы угла.
Домашнее задание
Решить задачи № 1—3 и дополнительно (по желанию учащихся) задачи № 4—5.
- Диагонали четырехугольника ABCD АС и BD пересекаются в точке О так, что ОС = 5 см, ОВ = 6 см, ОА = 15 см, OD = 18 см. Докажите, что в четырехугольнике ABCD ВС||AD и найдите отношение треугольников AOD и ВОС.
- Перпендикулярно высоте BD треугольника АВС проведена прямая, пересекающая стороны АВ и ВС в точках М и Р соответственно. Найдите АВ и отношение площадей треугольников МРВ и АВС, если известно, что ВМ = 7 см, ВР = 9 см, PC = 18 см.
- Прямая EF пересекает стороны АВ и ВС треугольника АВС в точках Е и F соответственно так, что ∠A + ∠EFC = 180°, а площадь четырехугольника AEFC относится к площади треугольника EBF как 16 : 9. Докажите, что треугольник BFE подобен треугольнику ВАС и найдите коэффициент подобия данных треугольников.
- Диагональ BD четырехугольника ABCD является биссектрисой его угла, ВС • ВА = ВD2. Докажите, что ∠BAD = ∠BDC. В каком отношении площадь четырехугольника делится его диагональю BD, если известно, что DC : AD = 3 : 2?
- На стороне АС треугольника АВС отмечена точка К так, что ΔАВК ~ ΔАВС. Найдите АК, КС, ВК, если известно, что АВ : ВС : АС = 3 : 7 : 9, а периметр треугольника АВС равен 57 см.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников.
Вернуться к Списку уроков Тематического планирования.
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Основные дидактические цели урока: совершенствовать навыки решения задач на применение признаков подобия треугольников; подготовка учащихся к предстоящей контрольной работе.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Анализ ошибок, допущенных в самостоятельной работе
- Провести общий анализ контрольной работы.
- Работа над ошибками. (На интерактивной доске записаны готовые ответы и указания к задачам контрольной работы. Учитель делит класс на группы в зависимости от того, какой уровень и вариант самостоятельной работы они выполняли. В одной группе должны быть учащиеся, выполнявшие один и тот же уровень и вариант. Учитель контролирует работу групп и по мере необходимости оказывает помощь.)
Ответы и указания к задачам самостоятельной работы:
I уровень сложности
II уровень сложности
lll уровень сложности
III. Решение задач
Решить задачи № 1—5. (Учитель делит класс на группы и по мере необходимости оказывает индивидуальную помощь.)
- В прямоугольном треугольнике ABC ∠A = 40°, ∠B = 90°, а в треугольнике MNK углы М, N, К относятся как 5 : 9 : 4. АВ = 3 см, KN — 9 см. Найдите: а) ВС : КМ; б) SABC : SMNK; в) PABC : PMNK.
- Дано: MN||АС, SABC : SBMN = 49 : 25, MN = 20 см (рис. 7.50). Найти: АС.
- В параллелограмме ABCD АЕ — биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4 : 9. АЕ пересекает диагональ BD в точке К. Найдите отношение ВК : KD.
- В трапеции ABCD основания ВС и AD равны 2 и 8 см, а диагональ АС равна 4 см. В каком отношении делит диагональ АС площадь трапеции?
- Прямая MN пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно так, что ВС = 2ВМ, АВ = 2BN, ВМ : BN = 3 : 5. Найдите: а) РАВС : PNBM; б) SABC : SNBM; в) MN : АС.
Краткое решение задач (ответы):
IV. Рефлексия учебной деятельности
- Какие треугольники называются подобными?
- Сформулируйте признаки подобия треугольников.
- Чему равно отношение периметров, площадей подобных треугольников?
- Сформулируйте свойство биссектрисы угла.
Домашнее задание
Решить задачи № 1—3 и дополнительно (по желанию учащихся) задачи № 4—5.
- Диагонали четырехугольника ABCD АС и BD пересекаются в точке О так, что ОС = 5 см, ОВ = 6 см, ОА = 15 см, OD = 18 см. Докажите, что в четырехугольнике ABCD ВС||AD и найдите отношение треугольников AOD и ВОС.
- Перпендикулярно высоте BD треугольника АВС проведена прямая, пересекающая стороны АВ и ВС в точках М и Р соответственно. Найдите АВ и отношение площадей треугольников МРВ и АВС, если известно, что ВМ = 7 см, ВР = 9 см, PC = 18 см.
- Прямая EF пересекает стороны АВ и ВС треугольника АВС в точках Е и F соответственно так, что ∠A + ∠EFC = 180°, а площадь четырехугольника AEFC относится к площади треугольника EBF как 16 : 9. Докажите, что треугольник BFE подобен треугольнику ВАС и найдите коэффициент подобия данных треугольников.
- Диагональ BD четырехугольника ABCD является биссектрисой его угла, ВС • ВА = ВD2. Докажите, что ∠BAD = ∠BDC. В каком отношении площадь четырехугольника делится его диагональю BD, если известно, что DC : AD = 3 : 2?
- На стороне АС треугольника АВС отмечена точка К так, что ΔАВК ~ ΔАВС. Найдите АК, КС, ВК, если известно, что АВ : ВС : АС = 3 : 7 : 9, а периметр треугольника АВС равен 57 см.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников.
Вернуться к Списку уроков Тематического планирования.
Цели и задачи урока «Работа над ошибками»:
- Разобрать, проработать погрешности, допущенные в контрольной работе.
- Сформировать умение работать в роли проверяемого и проверяющего.
- Формировать умение систематизировать и обобщать, закреплять и проводить
анализ по данной теме. - Научить правильно относиться к ошибке, умело и грамотно ее использовать.
Выделим основные компоненты урока:
- Консультация;
- Коррекция знаний и умений;
- Диагностика результатов;
- Оценочная деятельность.
В начале урока(15минут) учащиеся делятся на две группы:
- первая — учащиеся, получившие за контрольную работу «4» и «5»;
- вторая –«3» и «2».
Первая группа работает в парах, в тройках: отличник плюс хорошист,
отличник плюс два хорошиста. Вначале в этих группах идет работа над ошибками,
допущенными хорошистами, затем они вспоминают все правила, которые применяются
при выполнении всех заданий. Заключительный этап их совместной работы —
составление аналогичных заданий, предлагаемых в контрольной работе, которые
потом будут использованы хорошистами, когда они будут работать в роли
консультантов.
Параллельно идет работа учителя со второй группой учащихся. Учитель
подробно останавливается на часто встречающихся ошибках данной темы, допущенных
этой группой учащихся. Идет беседа между учителем и учеником, ответы на вопрос
«А почему?», причем не только со стороны учителя, но и со стороны учащихся
(задача учителя научить задавать вопросы). Прорешивается каждое задание, но не
из контрольной работы, а аналогичное ему, в конце которого учитель обязательно
делает вывод.
В основной части урока (20 минут), идет перераспределение
обязанностей: «хорошисты» становятся консультантами для «троечников» и
«двоечников», у которых идет работа в парах и тройках. Сколько бывает радости у
заядлого «троечника», когда он попадает в разряд консультантов.
Основная цель их совместной работы — провести работу над допущенными
ошибками в контрольной работе: консультируемый решает, проговаривает правила,
применяемые при решении заданий, задает вопросы по непонятым темам; консультант
анализирует, отвечает на вопросы, предлагает аналогичные задания, проверяет их,
оценивает работу над ошибками.
Работа консультанта оценивается учителем в зависимости от понимания материала
их консультируемого (индивидуальные способности консультируемого учитель
учитывает).
«Отличники» получают творческое задание, чаще всего им предстоит поработать
над составлением заданий «со звездочкой» по данной теме. Некоторое время ученики
работают самостоятельно, затем объединяются в группу и под руководством учителя,
а чаще сами, объединяют свои наработки, идеи и получают интересные, а порой
очень оригинальные задания. Эти задания могут быть использованы учителем для
работы с учащимися — участниками олимпиад, для индивидуальной работы на уроке, в
контрольных работах в параллельных классах (как дополнительные задания).
В конце урока подводится итог, в журнале появляется очередной столбик оценок,
причем, на ряд выше предыдущих и обязательно, всем классом, прорешиваем самую
интересную задачу урока, составленную творческой группой.
Итогом урока является тщательно проработанная и усвоенная тема.
Т.о. урок работы над ошибками позволяет индивидуально и дифференцированно
подойти к процессу обучения. У учащихся формируется умение делать самоанализ,
умение работать в группах, умение применять полученные знания на практике.
Проект
самоанализа урока по геометрии в 7Б классе
Ф.И.О. учителя: Баймачева С.Г., первая
категория, МБОУ «СОШ № 26 с углубленным изучением отдельных предметов», г.
Ижевск.
Предмет: геометрия Класс:
7Б Учебник: Геометрия 7-9 класс. Атанасян Л.С., Бутузов В.Ф.,
Кадомцев С.Б., Позняк Э.Г., И.И. Юдина. Москва «Просвещение» 2014г
Тема урока: Работа над ошибками. Анализ
контрольной работы №1 по теме «Начальные геометрические сведения». Тип урока: обобщение
пройденного материала.
Оборудование: карточки с заданиями,
чертежные инструменты.
|
Этапы |
Вид |
Учебные |
Планируемый |
Возможные |
Коррекционная |
|
1 Организационный 2 |
Личностные Регулятивные |
-самоорганизация. -способность регулировать свои действия, |
Организовать самоопределение учащихся к деятельности Учащиеся научены готовиться к уроку на |
Не все приготовили чертежные инструменты |
Напомнить на перемене о подготовке к |
|
2 Опрос 5 |
Личностные Познавательные |
-осознание своих возможностей в учении -осознанное построение речевого |
Систематизировать имеющиеся у учащихся Планируемые результаты были реализованы |
Не ответили на вопросы |
Проверка знаний через устный опрос по |
|
3 Повторение 10 |
Регулятивные Познавательные Личностные |
•самостоятельно ставят цели по –самостоятельно выделяют и формулируют – понимают и могут воспроизвести для |
Учить определять тему урока и ставить Цели данного этапа были достигнуты. Дети |
Может потребоваться много времени, чтобы |
Учитель постоянно обращает внимание на |
|
Закрепление |
Предметные Регулятивные Познавательные |
• понимают и определяют понятия: «луч», «прямая», «смежные и вертикальные –извлекают необходимую информацию из |
Уметь работать с полученной информацией. Учащиеся извлекают необходимую |
Не все учащиеся смогут справиться с этой |
Проговаривание полученной информации |
|
4 20 Просмотр |
Предметные Регулятивные Познавательные Коммуникативные Личностные |
• оценивает действия и способы -осуществляют самоконтроль и осознанно используют в речи новые эффективно сотрудничают с учителем и со |
Уметь применять полученные знания на Успешно справляются с практической Цели данного этапа урока были |
Некоторые учащиеся допускают ошибки при |
Ненавязчиво учитель возвращает их к |
|
5 Итог 6 Рефлексивно-оценочный |
Регулятивные Познавательные УУД: Коммуникативные УУД: |
Проводим -самоанализ деятельности и уровня •умение позитивно оценить учебный |
Учащиеся активно участвуют в ответах по |
Не все проявляют инициативу высказать |
Учитель лично обращается к неактивным |
|
Домашнее 2 |
Личностные |
— |
Дается |
Презентация к уроку по теме «Работа над ошибками контрольной работы»
Оценка 4.9
Работа над ошибками контрольной работы по геометрии № 3 по теме «Параллельность прямых». Презентация содержит теоретический материал, задачи, которые были представлены в контрольной работе и в которых были допущены ошибки. Так же в презентации есть задачи для самостоятельной работы учащихсяРабота над ошибками контрольной работы по геометрии № 3 по теме «Параллельность прямых». Презентация содержит теоретический материал, задачи, которые были представлены в контрольной работе и в которых были допущены ошибки. Так же в презентации есть задачи для самостоятельной работы учащихся
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Слайд 1
Методический совет «Как работать над ошибками ,допущенными в ВПР» Докладчик: Овсиенко Г.В.
Слайд 2
1. Логическая структура курса. 2.Логическая структура темы. 3.Логическая структура урока. 4 Система задач.
Слайд 3
Ключевые задачи Одношаговые ( простые задачи) Многошаговые (составные, сложные задачи) Задачи повышенного уровня Задачи высокого уровня Нестандартные задачи Олимпиадные задачи
Слайд 4
Особенности итогового повторения. 1.Цели итогового повторения. 2.Структура организации материала. 3.Уровни обобщения. 4.Уровни углубления. 5.Особенности оценивания.
Слайд 5
1.Цели итогового повторения: 1)Систематизировать изученный материал, определив его значение и место в изученном курсе, указав его связь с узловыми темами и возможные логические структуры изучения следующих курсов или тем; 2)Выделить узловые темы и указать ключевые задачи ( упражнения) /умение решать которые является обязательным (базовым)/; 3)Выявить «слабые» места и поработав над ними ,таким образом , подготовить к изучению следующего курса.
Слайд 6
2.Структура организации материала. 1)Подобрать серию задач ( или упражнений), самостоятельное последовательное выполнение которых , неизбежно приведет к обобщённой задаче (или упражнению); 2)Серия задач (упражнений ) обязательно должна завершаться задачей (или задачами) повышенной трудности, для выполнения которой необходимо выйти на более высокий уровень решения задач « в принципе», т.е. необходимости указать как решать задачу, не проводя вычислений или доказательств;
Слайд 7
3)Схематизировать изученный курс для иллюстрации его структуры, что позволит увидеть все связи и переходы; 4)Указать фундаментальные определения, формулы, теоремы и задачи, без освоения которых невозможно успешное изучение следующих курсов или тем.
Слайд 8
3.Уровни обобщения. 1)Задачи, подобранные в серию должны быть составными , т.е. состоять из нескольких базовых, и быть более высокого уровня, чем те, что предлагались во время изучения темы, и охватывать весь курс целиком; 2) Уровень сложности должен нарастать линейно так, чтобы ученик мог выполнить все задачи, до критической, т.е.такой ,в которой происходит переход на следующий ,более высокий уровень;
Слайд 9
3 )Уровень задач ориентирован на самого сильного ученика класса ( которого, возможно, нет в данном классе ) и охватывать весь курс; 4 )Последняя задача или несколько последних должны содержать данные ,записанные в обобщенном виде, т.е. без цифр.
Слайд 10
4.Уровни углубления. 1) В зависимости от подготовленности класса, углубляться насколько возможно, не расширяя и увеличивая число теорем, формул, но на имеющейся базе знаний находить и устанавливать такие связи , которые позволяют решать без наличия инструментария сверхсложные задачи; К примеру: находить максимальное значение функции на отрезке без привлечения дифференциального исчисления, или , строить графики элементарных функций, используя метод сложение графиков и т.п.
Слайд 11
2) «Забегать» далеко вперёд ( в следующие курсы и темы) и возвращаться назад, тем самым «сшивая» весь курс; Например , решая задачу нахождении площади треугольника через площадь прямоугольника ( в 5 классе, тогда как тема эта будет изучаться только в 7 классе на уроках геометрии), что вполне доступно с учетом свойства площади состоять из площадей фигур, составляющих данную . ( свойство аддитивности площади).
Слайд 12
3) Градация уровней углубления может быть такою: а) простое углубление ( решение задач, требующих гибкого мышления) или перенос, т.е. решение совершенно новых, иных задач известными методами; б) творческое углубление ( создание своего алгоритма решении задачи, но не метода); в) теоретическое углубление ,исследование всевозможных вариантов( выдвижение гипотезы и её доказательство или опровержение).
Слайд 13
5. Особенности оценивания. 1) Учитель должен подчеркивать, что при такой организации изучения материала важно не то , сколько решено задач, а как. Положительно оценивать даже незначительный успех или удачно высказанное предложение по способу решения задачи, по созданию математической модели, по постановке задачи; 2) Подчеркивать приоритет знаний , а не их оценки, точнее, отметки, которая может быть субъективной;
Слайд 14
3) Использовать в качестве поощрения предложение решить еще более сложную задачу, над решением которой можно думать не один урок или день; 4) Подчеркивать красоту решений и доказательств, неисчерпаемую тягу к знаниям и красоту изучаемой науки , точнее, её основ.