Приборная ошибка машины атвуда

10

Томский Межвузовский
Центр Дистанционного Образования (ТМЦ
ДО)

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И
РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра ИИТ

ОТЧЕТ

Лабораторная
работа по курсу «Общая физика»

Дисциплина
«Физика-1»

ИЗУЧЕНИЕ
ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

НА МАШИНЕ АТВУДА

1. ЦЕЛЬ РАБОТЫ

Целью работы
является изучение закона прямолинейного
ускоренного движения тел под действием
сил земного тяготения с помощью машины
Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ
И МЕТОДИКИ ЭКСПЕРИМЕНТА

С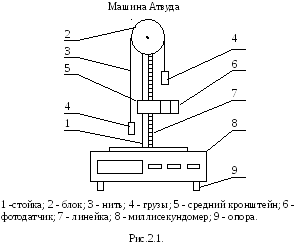
хема
экспериментальной установки на основе
машины Атвуда приведена на рисунке 2.1.

На вертикальной
стойке 1 крепится легкий блок 2, через
который перекинута нить 3 с грузами 4
одинаковой массы. В верхней части стойки
расположен электромагнит, который может
удерживать блок, не давая ему вращаться.
На среднем кронштейне 5 закреплен
фотодатчик 6. На корпусе среднего
кронштейна имеется риска, совпадающая
с оптической осью фотодатчика. Средний
кронштейн имеет возможность свободного
перемещения и фиксации на вертикальной
стойке. На вертикальной стойке укреплена
миллиметровая линейка 7, по которой
определяют начальное и конечное положения
грузов. Начальное положение определяют
по нижнему срезу груза, а конечное — по
риске на корпусе среднего кронштейна.

Миллисекундомер
8 представляет собой прибор с цифровой
индикацией времени. Регулировочные
опоры 9 используют для регулировки
положения экспериментальной установки
на лабораторном столе.

Принцип работы
машины Атвуда заключается в том, что
когда на концах нити висят грузы
одинаковой массы, то система находится
в положении безразличного равновесия.
Если на правый груз положить перегрузок,
то система грузов выйдет из состояния
равновесия и начнет двигаться.

Формула вычисления
случайной погрешности:

(3.1)

где
–
коэффициент Стьюдента,
–
результат среднеквадратичного отклонения.

Выражение
среднеквадратичного отклонения (относит.
погрешность):

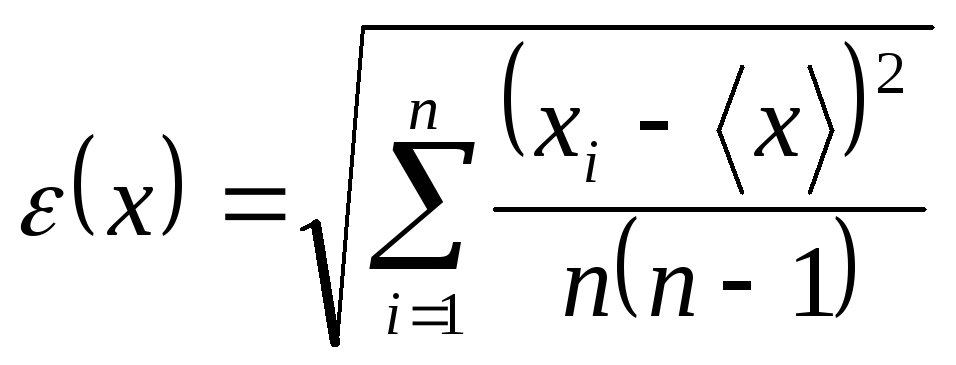
(3.2)

Формула вычисления
среднего результата измерения:

(3.3)

Общая погрешность
измерения:

(3.4)

где

– приборная погрешность,

– случайная погрешность.

Угловой коэффициент
экспериментальной прямой:

 =
(3.5)

Величина ускорения,
определяемого из линеаризованного
графика:

a
= 2²

(3.6)

4. Результаты работы и их анализ.

Измеренные значения
и результаты их обработки приведены в
таблице (4.1).

Рисунки (4.3), (4.4),
(4.5) отражают зависимости пути от времени.

В таблице (4.2)
представлены результаты расчетов
доверительных интервалов.

Таблица (4.1)

Результаты прямых и косвенных измерений

Для расчета значений
и

необходимо из полученных результатов
измерения времени рассчитать
среднеарифметическое значение.
Воспользуемся формулой (3.3), подставив
вместо

параметр

и
,
получаем:

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
.

Произведем расчет
среднеквадратичного отклонения,
воспользовавшись выражением (3.2).

Для

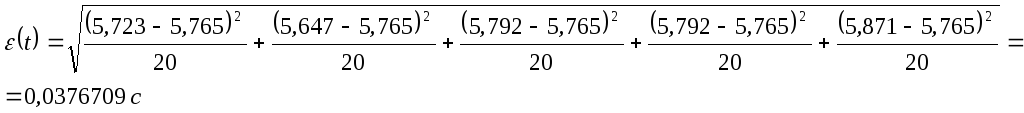
Для

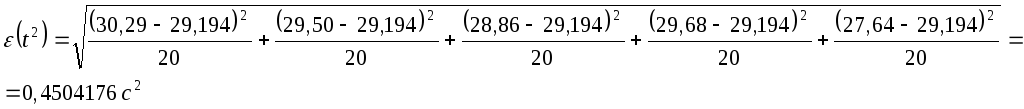
Для

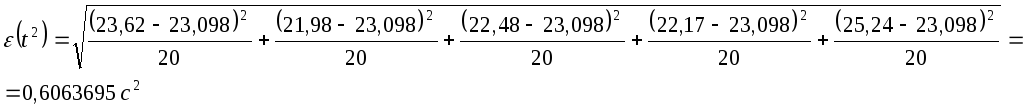
Для

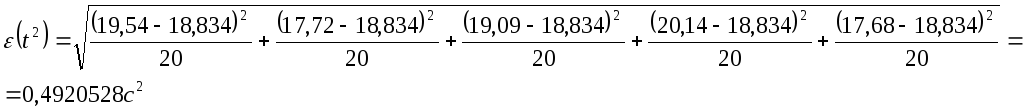
Для

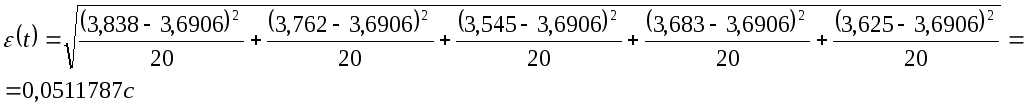
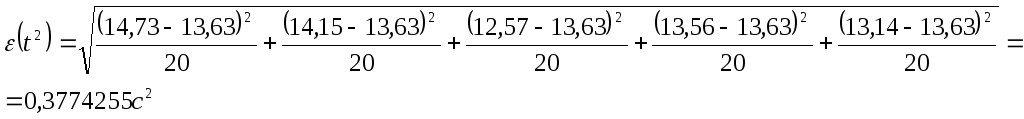
Зная
среднеквадратичное отклонение мы можем
произвести расчет случайной погрешности
для

и
,
следовательно, для этого воспользуемся
выражением (3.1), где

– коэффициент Стьюдента, а вместо

подставляются значения

и
.
При доверительной
вероятности

и числе измерений

коэффициент Стьюдента
.
Получим:

Для

Для

Для

Для

Для

Приборная
погрешность миллисекундомера

установленного на машине Атвуда
изначально нам не указана. Итак, нам
известно, что если прибор цифровой, то
равна
1 в младшем разряде прибора. Делаем
вывод, приборная погрешность
миллисекундомера составляет 0,001 с.

Выяснив
приборную и случайные погрешности мы
можем вычислить общую погрешность по
формуле (3.4). Получаем:

Для

Для

Для

Для

Для

Доверительный
интервал равен
,
где вместо параметра

подставим

и
.
Получается, что для расчета интервала
необходимо общую погрешность каждого
параметра для каждой точки умножить на
2. Чтобы ознакомится с полученными
результатами взгляните на таблицу
(4.2).

Таблица
(4.2)

Таблица доверительных
интервалов

Исходя из
полученных данных построим график
зависимости
:

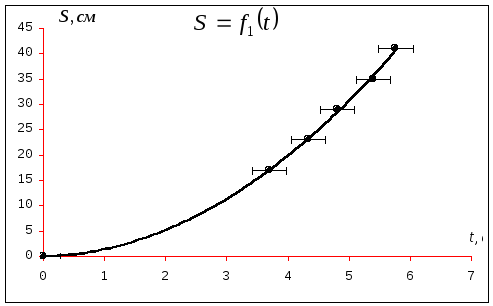
Рис.
4.3 Зависимость пути S
от времени t

Построим график
зависимости
:

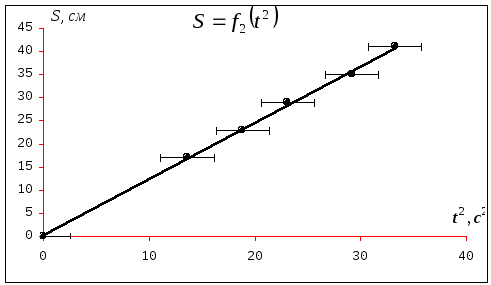
Рис.
4.4 Зависимость пути S
от t²

Построим график
зависимости
:

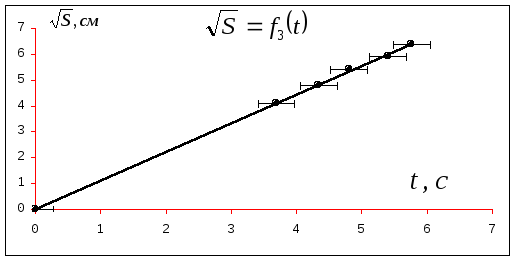
≈1,75

≈4,5

Рис.
4.5 Зависимость
от
t

Исходя из
формул (3.5) и (3.6) вычислим величину
ускорения:

Я взял интервал
по
от
0,2 метров до 0,5 метров, тогда интервалу

соответствует интервал по t
от ≈1,75 до 4,5 секунд. Здесь опять же нужно
учитывать масштаб по t.
И, в принципе, доверительные интервалы
времени можно не указывать.

Цель работы

  Экспериментальная
проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение
ускорения свободного падения  лабораторной установке – машине Атвуда.

Экспериментальная установка

  
Машина Атвуда  (рис.1) состоит из легкого блока 2, через который
переброшена нить с двумя наборными грузами на концах (массы обоих грузов
одинаковы и равны m). Грузы могут двигаться вдоль вертикальной
рейки со шкалой 1. Если на правый груз положить небольшой перегрузок Dm,
грузы начнут двигаться с некоторым ускорением. Для приема падающего груза
служит полочка 3.

   Время
движения грузов измеряется с помощью ручного или стационарного секундомера.   

   Силы трения в машине Атвуда
сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса
одного из грузов (в нашей установке – правого)  делается немного больше массы
другого.  Эта операция производится при помощи кусочков пластилина и
выполняется с таким расчетом, чтобы  а) грузы могли находиться в статическом
положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся
система приходила в равномерное движение. Масса используемого пластилина столь
мала, что в последующих  расчетах  в массу грузов не включается. Перегрузки Dm, с
помощью которых системе задается движение, укладывают также на правый груз
системы.

   Для выполнения работы машина Атвуда должна быть
установлена строго вертикально, что легко проверить по параллельности шкалы и
нити.

Теоретическая часть

   Второй закон Ньютона в проекциях на вертикальную
ось для каждого из тел системы (рис.2) в предположении невесомости блока,
отсутствия силы  трения и нерастяжимости  нити дает:

(1)

Где g —
ускорение свободного падения,

a —
ускорение грузов,

 T₁
и T₂ — сила натяжения нити.

Выразим из данной системы ускорение a.

      (2)

Проверим равноускоренный характер движения грузов,
экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и
время движения t.

Так как
начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

    (3)                                        

  Третье соотношение часто называют законом перемещений:
«Перемещение при равноускоренном движении прямо пропорционально
квадрату времени движения».

   Соотношение (3) может быть проверено
экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность
экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение,
с которым движется тело, прямо пропорционально равнодействующей действующих на
него сил и обратно пропорционально массе этого тела».

Подставляя a_i в
(2) получаем следующую формулу:

(4)

Для получения более точного значения g, необходимо учесть момент инерции
блока — J_б,  (T₁  T₂). Рассмотрим получения вышеописанных формул с учётом новой  величины.
Вычислим g из закона динамики для вращательного
движения тела (в данном случае блока).

 (5)

—
сумма проекций на ось Z всех сил, действующих на
вращающиеся тело; α- угловое ускорение блока; J – его момент инерции

             
(6)

Где r — радиус блока, J_б
— момент инерции блока.

Выразим из уравнения (1) разность сил натяжения  (T₁ – T₂ ) и подставив ее в уравнение (6) получим:

  (7)

Выразим ускорение грузов a:

(8)

Учитывая, что значение момента инерции блока

(9),

 k- коэффициент распределения массы блока
относительно оси вращения (k < 1), окончательно получаем выражение для
определения ускорения свободного падения:  

11)

       Экспериментальная
часть

Задание 1. Проверка второго закона Ньютона.

   Поскольку
ускорение движения является функцией двух переменных – силы и массы, то
изучение второго закона Ньютона выполняется путем раздельного исследования двух
зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе
системы и 2) зависимости ускорения от массы системы при постоянной действующей
силе.

Исследование зависимости ускорения  от  силы при
постоянной массе

Измерения и обработка результатов

1. Тщательно
балансируют грузы, выбрав их массы в пределах 150 — 200
г каждый.

2. Затем
на правый груз последовательно накладывают перегрузки. В результате в системе
появляется движущая сила равная Dmg,  где Dm — суммарная масса перегрузков. При
этом, конечно, общая масса системы незначительно увеличивается, но  этим изменением
массы по сравнению с массой грузов можно пренебречь, считая массу системы
постоянной.

3.
Измеряют время равноускоренного движения системы на пути, например, 1
метр. Все данные заносят в таблицу 1.3 отчета.

4.
Пользуясь законом путей (1.6), вычисляют ускорение а.

5.
Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.

6.
Строят график зависимости ускорения движения от действующей силы. Точку (F=0, a=0) на графике не откладывают. Если
экспериментальные точки ложатся на прямую с небольшим разбросом и прямая
проходит через начало координат, то можно сделать вывод о том, что ускорение
действительно прямо пропорционально силе.

7.
По угловому коэффициенту полученной прямой определяют массу системы и сравнивают
ее реальной массой.

Исследование зависимости ускорения  от  массы при
постоянной силе

Измерения и обработка результатов

1. Все опыты
проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе.
Ускорение системы измеряется также как и в предыдущем задании.

2.
Для изменения массы системы одновременно на правый и левый груз кладут дополнительные
одинаковые грузы. Все данные записывают в таблицу отчета.

3.
График обратно пропорциональной зависимости ускорения от массы представляет
собой гиперболу, которую невозможно идентифицировать. Для проверки предположения
об обратно пропорциональной зависимости между ускорением и массой  необходимо построить график зависимости 
ускорения от обратного значения массы системы: a = f(М^-1). Подтверждением
предположения является прямолинейность этого графика.

4. По угловому коэффициенту полученной прямой
определяют значение приложенной силы и сравнивают ее с реально действующей в
системе

Задание 2. Определение ускорения движения грузов

   В полученном  уравнении прямой  коэффициент k равен половине
ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов (a
=2k)  в данном опыте и определить погрешность его
измерения. Произведите необходимые вычисления и занесите результаты в отчет.

Задание 3. Определение ускорения свободного падения

   (Выполняется по результатам измерений
и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и
перегрузка, а также ускорение движения системы, из формулы (3) найдите
ускорение свободного падения. Результаты занесите в отчет. В выводе сравните
полученный результат с табличной величиной.

Для нахождения погрешности измерения величины
ускорения свободного падения Δg
используем формулу:

12)

где   ;  ;  ;  ;

 – частные производные функции

Проанализируйте  результаты своих наблюдений и
сформулируйте вывод.

Контрольные
вопросы

1.
Какое
движение называется поступательным?

2.
Дайте
определение инерциальной системы отсчета. Приведите примеры ИСО.

3.
 Сформулируйте
первый закон Ньютона. Приведите примеры его проявления.

4.
Дайте
определение инертной массы тела. Гравитационной?  От чего и как зависит  масса
тела?

5.
 Сформулируйте
второй закон Ньютона. Приведите варианты его математической формы.

6.
Покажите
все силы,  действующие на один из грузов в машине Атвуда, и составьте для него
уравнение динамики.

7.
Запишите
систему уравнений  динамики  для машины Атвуда с учетом момента инерции блока.
Силы трения в блоке?

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Что такое машина Атвуда?

Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно:Пространственная экономика: описание специальностей и структура

Вам будет интересно:Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение

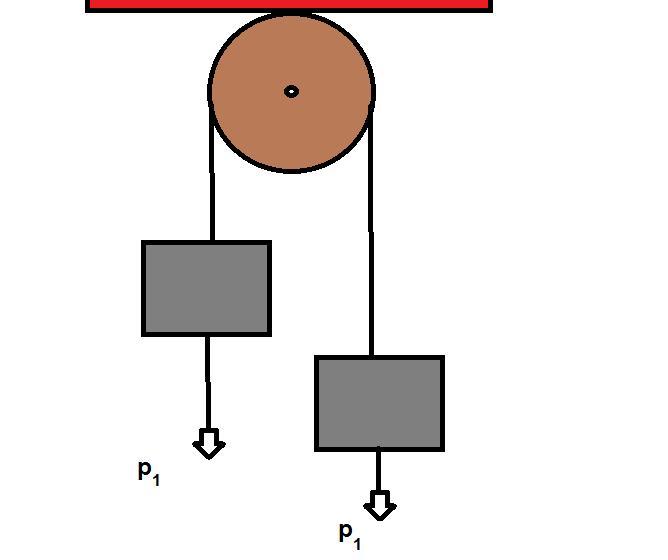
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

F = m*a.

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

F1 – T = m1*a.

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

T – F2 = m2*a.

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

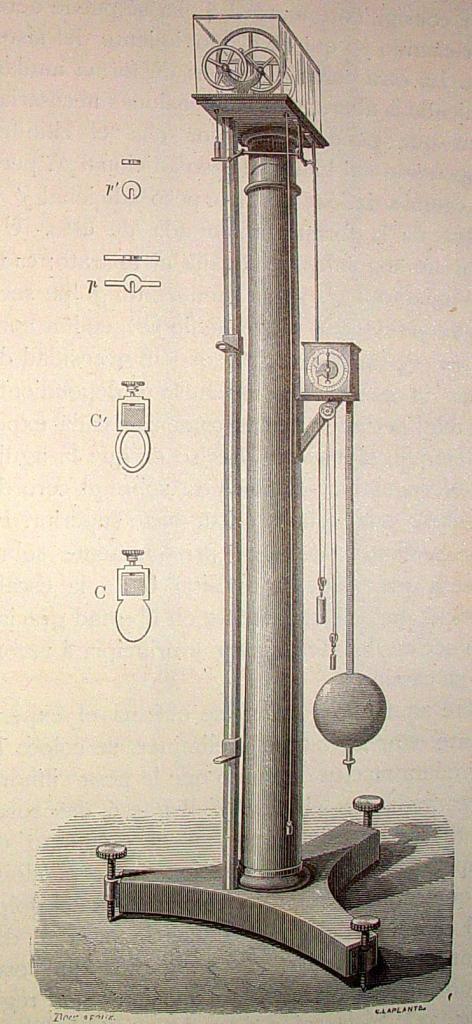
Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

F1 – T = m1*a;

T – F2 = m2*a.

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

a = na*g.

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

h = a*t2/2.

Откуда ускорение определяется однозначно:

a = 2*h/t2.

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

acp = ∑i=1mai/m.

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

acp = na*g.

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

g = a/na.

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

g = 2*h/(t2*na).

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

F1 = 2*h*m1/(t2*na).

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

F1 – T = m1*a;

T – F2 = m2*a.

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

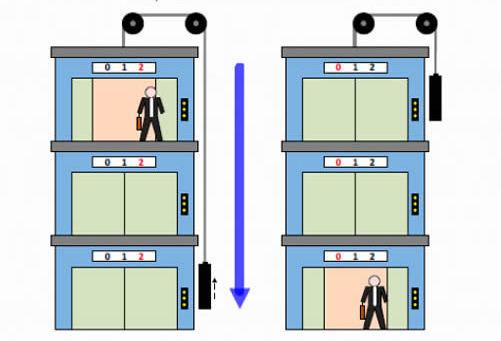
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.

2009

НАУЧНЫЙ ВЕСТНИК МГТУ ГА серия Студенческая наука

№ 150

УДК 378.147

ТЕОРЕТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ В УЧЕБНЫХ ЭКСПЕРИМЕНТАХ С «МАШИНОЙ АТВУДА»

А.А. ЦАРЁВ

Статья представлена доктором технических наук, профессором Кузнецовым В.Л.

Статья подготовлена под руководством кандидата физико-математических наук, доцента Курочкина В.А.

На основе анализа посторонних эффектов построена иерархия теоретических моделей «Машины Атвуда», применяемой в физическом практикуме при изучении кинематики и динамики материальной точки. Получены теоретические соотношения для расчёта систематических погрешностей величины ускорения свободного падения. Приведены экспериментальные данные, подтверждающие достоверность теоретических результатов.

Введение

Предметом рассмотрения в данной статье является устройство для опытного определения величины ускорения свободного падения g, изобретённое английским физиком Дж. Атвудом (1746-1807) — так называемая «Машина Атвуда» (МА). В настоящее время МА широко используется в учебных лабораториях вузов при изучении динамики материальной точки [1].

МА (рис. 1) представляет собой систему из двух одинаковых по массе т грузов 1 и 2 на нити, перекинутой через лёгкий блок 3. Для приведения системы в движение и измерения мгновенной скорости грузов Атвуд предложил использовать перегрузок 4 малой массы Ат. По достижении скорости уо на участке перегрузок удаляется платформой 5. После этого на участке Бр грузы должны двигаться по инерции равномерно и поэтому искомую скорость уо можно рассчитывать как отношение Бр к измеряемому промежутку времени ^.

Опытная величина g находится на основе функциональных соотношений между измеряемыми параметрами МА (Ат, т, £р, £у, ^). Чтобы получить эти соотношения из законов Ньютона, необходимо предварительно построить теоретическую модель (ТМ) МА [4].

В лабораторных работах с МА, проводимых на кафедре физики МГТУ ГА, до последнего времени применялась упрощённая ТМ [2], выбор которой, на наш взгляд, недостаточно обоснован. К тому же, систематическая погрешность величины g, связанная с несовершенством ТМ, составляла 20-25 %.

В настоящей работе поставлена следующая задача: на основе анализа посторонних эффектов и методики математического моделирования [3] уточнить границы применимости упрощённой ТМ и построить систему усовершенствованных ТМ МА, позволяющую снизить систематические погрешности опытной величины g до уровня 3-5 %.

Рис. 1. Схема МА

Построение иерархии теоретической модели «Машины Атвуда» и оценка

систематических погрешностей моделирования

Построение ТМ начинается со всестороннего анализа физического явления в экспериментальном устройстве и оценки влияния посторонних эффектов на точность измерений. Этот анализ позволяет выявить систему постепенно усложняющихся ТМ — так называемую «иерархию содержательных моделей» [3].

Формирование такой системы должно сопровождаться их сравнительной оценкой в основном по двум критериям — адекватности и простоты. Адекватность ТМ означает степень её соответствия основным свойствам исследуемого физического явления; простота — отсутствие излишних подробностей, относительно слабовлияющих на результаты измерений. Как отмечается в работе [3], «две опасности подстерегают при построении математических моделей: первая -увязнуть в подробностях и вторая — слишком огрубить явление».

Общими для всей иерархической системы ТМ являются следующие идеализирующие предположения:

1) грузы 1 и 2, а также перегрузок 3 являются абсолютно твёрдыми телами, которые движутся поступательно и потому подчиняются законам динамики материальной точки;

2) силы тяжести, действующие на грузы в МА, можно считать приближённо постоянными, а само движение — равноускоренным.

Основными посторонними эффектами, влияющими на выбор ТМ, можно считать следующие:

1) влияние массы перегрузков на величину полной инертной массы системы на участке £у;

2) влияние силы трения Гтр на ускорение грузов на участке £у;

3) влияние силы трения ^ на равномерность движения грузов на участке £р;

4) влияние блока, как вращающегося твёрдого тела конечной массы тд, на параметры движения грузов.

Величина силы трения рассматривается здесь как некоторый эффективный параметр, включающий взаимодействие нити с поверхностью блока, трение в других вращающихся элементах конструкции, а также сопротивление воздуха движущимся грузам.

При построении самой грубой упрощённой модели (назовём её ТМ1), пренебрежём всеми указанными выше эффектами 1-4, то есть будем считать, что 2т+Ат»2т; Етр »0; тд »0. В этом случае из уравнений движения получаем:

В результате на основе (1) и (2) находим опытное значение ускорения g1 , соответствующее модели ТМ1:

Переходя от ТМ1 к модели следующего уровня, то есть к ТМ2 , учтём массу перегрузка Ат в общей инертной массе системы. В этом случае:

а =——

2т

Аmg

(1)

Ускорение а можно определить косвенно по измеряемым кинематическим параметрам:

а =

(2)

2та

(3)

& =^Т“ Ат

а =————— ;

2т + Ат

Аmg

при этом опытное значение g2 , соответствующее ТМ2, оказывается равным:

(2т + Ат)а

g2 = ——————т-— = g^ + а . (5)

Ат

В формуле (5) ускорение а представляет собой систематическую погрешность, возникающую при отказе от учёта Ат в общей инертной массе системы.

Восходя далее по иерархии ТМ к ТМ3 , учтём силу трения Гтр на участке Су. Так как сила трения направлена противоположно силе тяжести перегрузка, то вместо (4) получаем:

А^ — Гтр

а =————. (6)

2т + Ат

Тогда опытное значение gз , соответствующее ТМ3 , становится равным:

Г Г

gз = gl + а + 7^ = g 2 + т^. (7)

Ат Ат

Здесь появляется дополнительная систематическая погрешность /Ат , роль которой воз-

растает с понижением массы перегрузка.

Перейдём теперь к ТМ4 и учтём влияние силы трения на участке Ср. Здесь, вопреки идее Атвуда, грузы движутся не равномерно, а равнозамедленно, с ускорением, по величине равным Гф/2т. Как показывает анализ уравнений движения, этот эффект приводит к систематической погрешности косвенного измерения ускорения а на участке Су. Эта погрешность приближённо равна:

г С

Аа = . (8)

4т Су

Подставляя (8) в равенство (6), можно получить следующее приближённое выражение для опытного значения g4, соответствующего ТМ4:

. ^ 2т. 2тАа $р . ГТр

g4 = g3 +Аа(1 +—) » g3 +——= g3 +—- (——) = g1 + а + —- (1 + ——) . (9)

54 53 4 Ат 53 Ат 53 Ат 2Бу 1 Ат 2Бу

Заметим, что в соответствии с (9) влияние силы трения на участке Ср можно свести к эффективному возрастанию силы Гтр на участке Су на величину:

С

АГ = Г (—Ч. (10)

тр тр ^2$

Отсюда следует, что путём уменьшения отношения расстояний Ср/Су можно существенно повысить адекватность модели ТМ3 и соответственно точность опытного определения g3.

Анализ последнего из указанных выше посторонних эффектов — влияния инертной массы вращающегося диска тд — выходит за рамки настоящей статьи. Предварительные оценки показывают, что относительная систематическая погрешность величины g4 вследствие этого эффекта составляет порядка 0,5тд/2т, что не превышает 2-3% для всего принятого в учебном эксперименте диапазона масс перегрузков.

Количественные оценки систематических погрешностей и экспериментальные результаты

В построенном иерархическом ряду ТМ1-ТМ3 каждая последующая ТМ может служить средством оценки адекватности предыдущей, менее совершенной модели.

Количественное сравнение систематических погрешностей различных ТМ по формулам (5)-(9) требует предварительной опытной оценки величины силы трения.

Для этого проводились измерения промежутков времени движения груза 2 при двух значениях расстояний Бр =0,25 м и £р2=0,05 м и одинаковых расстояниях £у1=£у2 =0,2 м. При этом предполагалось, что на участке £р1 груз 2 движется равнозамедленно с величиной ускорения ¥тр/2т, а на участке £р2 — приближённо равномерно; начальные скорости для обоих участков Бр принимались одинаковыми. По результатам этих измерений было получено: ^тр = 0,0086 ± 0,0017 Н.

Таблица 1

Величины ускорений свободного падения g1 — g3, соответствующих моделям ТМ1 — ТМ3

Ат, кг а, м/с2 2 /с ¿в 2 /с ,2 вз, м/с2

0,003 0,147 6,08 6,23 9,10

0,005 0,313 7,34 7,64 9,36

0,010 0,667 8,06 8,71 9,57

0,020 1,30 7,94 9,22 9,65

0,030 1,85 7,56 9,39 9,68

0,040 2,34 7,19 9,51 9,73

= 7,36 м/с2; ^2> = 8,45 м/с2 ; ^э> = 9,52 м/с2

В табл. 1 представлены результаты расчётов величин g1-g3, соответствующих моделям ТМ1-ТМ3. Эталоном для сопоставления результатов служила модель ТМ4, систематические погрешности которой предполагались пренебрежимо малыми, то есть принималось, что g»9,8 м/с2. Значения параметров лабораторного стенда выбирались следующими: т=0,062 кг; Бр = 0,15 м; £у=0,30 м; Дт=0,003-0,04 кг. Ускорения а, для различных масс Ат, рассчитывались

сначала по формуле (6) при опытном значении ^ =0,0086 Н и величине g=9,8 м/с2, а затем

корректировались с учётом систематической погрешности Да (формула (8)).

На основе табл. 1 можно сделать следующие выводы:

1. учёт массы перегрузков Дт в общей инертной массе системы, а также влияния силы трения на участке Бу в модели ТМ3 приводит к требуемому снижению систематической погрешности g3 по отношению к табличному значению ускорения свободного падения;

2. по мере возрастания Дт в зависимости а (Дт) наблюдается экстремум в окрестности Дт » 0,01 кг.

Наличие указанного экстремума можно объяснить, сравнивая графики зависимостей а(Дт) для моделей ТМ1 и ТМ3 (формулы (1) и (6)). Для ТМ3 график а(Дт) имеет выпуклую форму с двумя характерными пределами: а ®g

при Дт и а ® 0 при Дт ®Fтр/g (рис. 2). График

а(Дт) для ТМ1 представляет собой прямую, исходящую из начала координат. Очевидно, что наибольший наклон прямой а(Дт) и, следовательно, наименьшая систематическая погрешность g1 соответствует точке Дт=Дт0, где касательная к графику а(Дт) (то есть, производная а по Дт) будет проходить через начало координат. Решение этой математической задачи даёт приближённый результат:

Рис. 2. Зависимости а(Дт)

Ат„

V

2т^

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

g

При Р = 0,0086 Н, g=9,8 м/с2 и т=0,062 кг получаем Дт0»0,01 кг, что согласуется с

тр

табл. 1. Отсюда, в частности, следует, что измерения на основе модели ТМ1 целесообразно проводить при величинах Дт, лежащих в окрестности полученного значения Дт0.

Перейдём теперь к результатам экспериментов по проверке формул (8), (9), (10) для систематических погрешностей величины g. Идея этих экспериментов состояла в сравнении результатов, полученных в двух сериях измерений.

Серия 1 проводилась в традиционном для МА режиме со снятием перегрузков на границе участков Лу и Лр. Серия 2 осуществлялась в специальном режиме — без снятия перегрузков. В последнем случае перегрузки в виде небольших гирек — навесок, закрепляемых на грузе 2, свободно проходили через отверстие в платформе 5, и ускорение всей системы оставалось неизменным на всём пути Бу+Бр. Такой режим движения позволял исключить эффект дополнительного влияния силы трения на равномерность движения системы после снятия перегрузков.

Величины а2 в серии 2 рассчитывались по измеряемым промежуткам времени ^ на участке Лр по формуле равноускоренного движения:

= У 2(3у + Л р) д/Ч

а2 =* ;2 » (11)

1р 1р

Результаты измерений для обеих серий представлены в табл.2.

Сопоставление результатов серий 1 и 2 проводилось графическим способом при специальном выборе переменных — г и 1/Дт на основе формулы (6):

а(2т + Ат) = 1

Ат Ат

При таком выборе предел экстраполяции г ® а ®g при 1/Дт ® 0 соответствует физическому пределу а ® g при Дт ® ¥, а коэффициент наклона графика г(1/Дт) — величине Р-гр (отметим, что целесообразность введения переменной 1/Дт в экспериментах с МА отмечалась в работе [1]).

Таблица 2

Ускорения грузов при измерениях со снятием (Дт1) и без снятия (Дт2) перегрузков

Аш1, кг ГЧ О е Аш2, кг а2, м/с2

0,00315 0,151 0,0017 0,0552

0,0079 0,511 0,0020 0,0912

0,0106 0,669 0,0030 0,155

0,0111 0,721 0,0050 0,302

0,0138 0,869 0,010 0,657

0,0185 1,15 0,020 1,27

— — 0,030 1,81

Анализ полученных результатов основывался на следующих предположениях. Если величины а1 в табл. 2 скорректировать введением поправки Да (формула (8)), то график г1(1/Дт) должен практически совпадать с графиком г2(1/Дт) при близких значениях g и р,. При отсутствии такой поправки график г1(1/Дт) должен располагаться ниже графика г2(1/Дт); при этом пределы экстраполяции, то есть величины g по-прежнему должны быть близки друг к другу, в то время как наклон графика г1(1/Дт) (то есть величина Рф) должен возрасти на АР^, (формула (10)).

Экспериментальные графики, приведённые на рис. 3, подтверждают эти предположения. Здесь прямая 1 (зачернённые точки) соответствует зависимости г1(1/Дт) без корректировки величин а1; прямая 2 (незачернённые точки) — зависимости г2(1/Дт); точки в виде незачернённых

Рис. 3. Зависимости z(1/Дm)

квадратов зависимости г1(1/Дда) с коррекцией а1 на величину Да по формуле (8) (обозначим эту зависимость как г*(1/Дт)).

По данным расчётов методом наименьших квадратов получены следующие результаты: для верхней прямой £2=9,60 ± 1,8%; ^2=0,0088 ± 6,3%; для прямой 1

£1=9,62 ± 1,5%; Ртр1=0,011 ± 8,0%. Для прямой, проведённой близко к точкам-квадратам, получено ^=0,0085 ± 11%; £*=9,6 ± 1,4%. Здесь величины £1, £2 и

£ в пределах среднеквадратических погрешностей близки друг к другу; тоже можно сказать и относительно величин сил трения, при этом разность Ргр1 и Ктр2 прибли жённо согласуется с величиной ДРтр, рассчитанной по формуле (10):

АК„ = К

тр

тр

А

2£„

0,0086 • 0,15 2 • 0,3

0,0022 Н.

Полученные выше результаты показывают, что модель ТМ3 позволяет достичь необходимого уровня систематических погрешностей величины £ в экспериментах на МА.

Выводы

1. На основе метода математического моделирования построена система — иерархия теоретических моделей, в которых учитываются основные посторонние эффекты при опытном определении ускорения свободного падения £ на учебной установке Машины Атвуда. Получены теоретические соотношения для оценки систематических погрешностей величины £, соответствующих моделям различного уровня.

2. Проведён теоретический анализ влияния силы трения на точность косвенного измерения ускорения грузов методом Атвуда; осуществлён специальный эксперимент без снятия пере-грузков, подтверждающий результаты этого анализа.

3. Теоретически и экспериментально обоснован выбор модели ТМ3, позволяющей снизить систематические погрешности опытного значения ускорения свободного падения до уровня 35%.

4. Полученные результаты могут быть использованы при проведении лабораторных работ по разделу «Механика» с учётом специфики инженерных специальностей, а также при организации научной работы студентов в физическом практикуме.

ЛИТЕРАТУРА

1. Руководство к лабораторным занятиям по физике / под ред. Л. Л. Гольдина, изд. 2-е, перераб. — М.: Наука,

1973.

2. Власов М.Ю., Камзолов С.К., Курочкин В.А., Лысенко С.А., Тихомиров Ю.В. Методические указания к выполнению лабораторных работ по курсу физики. — М.: МГТУ ГА, 1993. Ч. 1.

3. Кузнецов В.Л. Математическое моделирование: учеб. пособие. — М.: МГТУ ГА. 2003. Ч. 1.

4. Курочкин В. А. Теоретическое моделирование как ориентировочная основа экспериментальных действий в физическом лабораторном практикуме / тезисы докладов научно-методической школы-семинара по проблеме «Физика в системе инженерного и педагогического образования стран ЕврАзЭС» — М.: ВВИА им. проф. Н.Е. Жуковского, 2008.

THEORETICAL MODELING AND SYSTEMATIC ERRORS IN LEARNING EXPERIMENTS WITH

«ATVUD’S MACHINE»

Tsarev A.A.

The hierarchy of the theoretical models of the Atvud’s machine is constructed , taking into account of the outside effects. The theoretical correlations of systematic errors of acceleration of the gravity are obtained. The verifying experimental results are gived.

Сведения об авторе

Царёв Александр Андреевич, 1989 г.р., студент механического факультета МГТУ ГА, область научных интересов — математическое моделирование систем, обеспечивающих безопасность полётов ВС.

10

Томский Межвузовский
Центр Дистанционного Образования (ТМЦ
ДО)

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И
РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра ИИТ

ОТЧЕТ

Лабораторная
работа по курсу «Общая физика»

Дисциплина
«Физика-1»

ИЗУЧЕНИЕ
ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

НА МАШИНЕ АТВУДА

1. ЦЕЛЬ РАБОТЫ

Целью работы
является изучение закона прямолинейного
ускоренного движения тел под действием
сил земного тяготения с помощью машины
Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ
И МЕТОДИКИ ЭКСПЕРИМЕНТА

С
хема
экспериментальной установки на основе
машины Атвуда приведена на рисунке 2.1.

На вертикальной
стойке 1 крепится легкий блок 2, через
который перекинута нить 3 с грузами 4
одинаковой массы. В верхней части стойки
расположен электромагнит, который может
удерживать блок, не давая ему вращаться.
На среднем кронштейне 5 закреплен
фотодатчик 6. На корпусе среднего
кронштейна имеется риска, совпадающая
с оптической осью фотодатчика. Средний
кронштейн имеет возможность свободного
перемещения и фиксации на вертикальной
стойке. На вертикальной стойке укреплена
миллиметровая линейка 7, по которой
определяют начальное и конечное положения
грузов. Начальное положение определяют
по нижнему срезу груза, а конечное — по
риске на корпусе среднего кронштейна.

Миллисекундомер
8 представляет собой прибор с цифровой
индикацией времени. Регулировочные
опоры 9 используют для регулировки
положения экспериментальной установки
на лабораторном столе.

Принцип работы
машины Атвуда заключается в том, что
когда на концах нити висят грузы
одинаковой массы, то система находится
в положении безразличного равновесия.
Если на правый груз положить перегрузок,
то система грузов выйдет из состояния
равновесия и начнет двигаться.

Формула вычисления
случайной погрешности:

(3.1)

где
–
коэффициент Стьюдента,
–
результат среднеквадратичного отклонения.

Выражение
среднеквадратичного отклонения (относит.
погрешность):

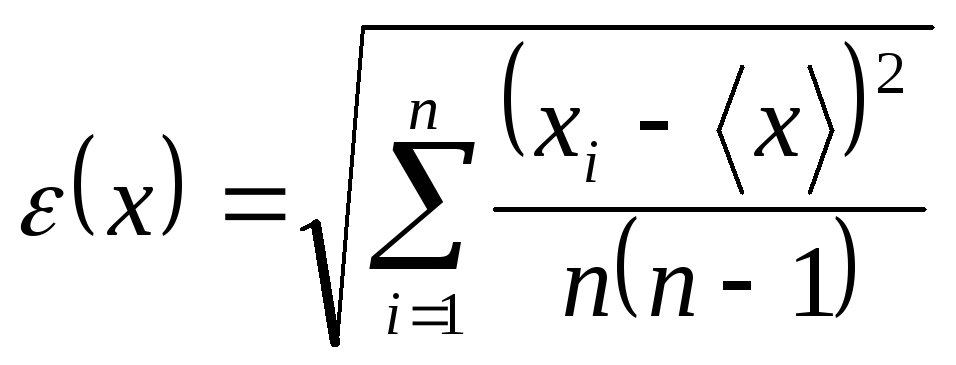
(3.2)

Формула вычисления
среднего результата измерения:

(3.3)

Общая погрешность
измерения:

(3.4)

где

– приборная погрешность,

– случайная погрешность.

Угловой коэффициент
экспериментальной прямой:

 =
(3.5)

Величина ускорения,
определяемого из линеаризованного
графика:

a
= 2²

(3.6)

4. Результаты работы и их анализ.

Измеренные значения
и результаты их обработки приведены в
таблице (4.1).

Рисунки (4.3), (4.4),
(4.5) отражают зависимости пути от времени.

В таблице (4.2)
представлены результаты расчетов
доверительных интервалов.

Таблица (4.1)

Результаты прямых и косвенных измерений

Для расчета значений
и

необходимо из полученных результатов
измерения времени рассчитать
среднеарифметическое значение.
Воспользуемся формулой (3.3), подставив
вместо

параметр

и
,
получаем:

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
;

для
.

Произведем расчет
среднеквадратичного отклонения,
воспользовавшись выражением (3.2).

Для

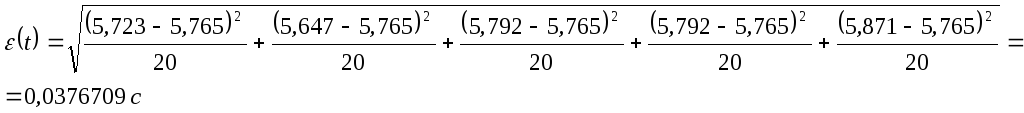
Для

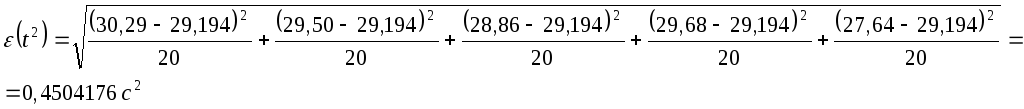
Для

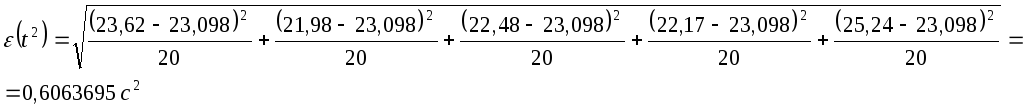
Для

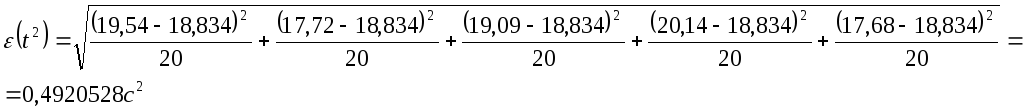
Для

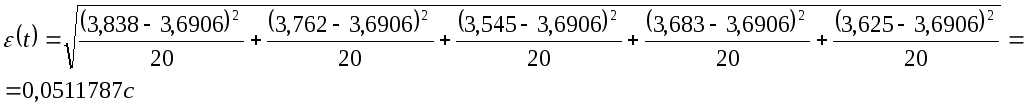
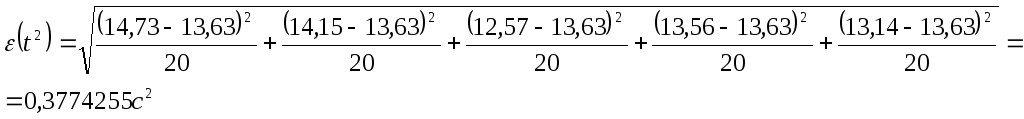
Зная
среднеквадратичное отклонение мы можем
произвести расчет случайной погрешности
для

и
,
следовательно, для этого воспользуемся
выражением (3.1), где

– коэффициент Стьюдента, а вместо

подставляются значения

и
.
При доверительной
вероятности

и числе измерений

коэффициент Стьюдента
.
Получим:

Для

Для

Для

Для

Для

Приборная
погрешность миллисекундомера

установленного на машине Атвуда
изначально нам не указана. Итак, нам
известно, что если прибор цифровой, то
равна
1 в младшем разряде прибора. Делаем
вывод, приборная погрешность
миллисекундомера составляет 0,001 с.

Выяснив
приборную и случайные погрешности мы
можем вычислить общую погрешность по
формуле (3.4). Получаем:

Для

Для

Для

Для

Для

Доверительный
интервал равен
,
где вместо параметра

подставим

и
.
Получается, что для расчета интервала
необходимо общую погрешность каждого
параметра для каждой точки умножить на
2. Чтобы ознакомится с полученными
результатами взгляните на таблицу
(4.2).

Таблица
(4.2)

Таблица доверительных
интервалов

Исходя из
полученных данных построим график
зависимости
:

Рис.
4.3 Зависимость пути S
от времени t

Построим график
зависимости
:

Рис.
4.4 Зависимость пути S
от t²

Построим график
зависимости
:

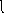
≈1,75

≈4,5

Рис.
4.5 Зависимость
от
t

Исходя из
формул (3.5) и (3.6) вычислим величину
ускорения:

Я взял интервал
по
от
0,2 метров до 0,5 метров, тогда интервалу

соответствует интервал по t
от ≈1,75 до 4,5 секунд. Здесь опять же нужно
учитывать масштаб по t.
И, в принципе, доверительные интервалы
времени можно не указывать.

Цель работы

  Экспериментальная
проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение
ускорения свободного падения  лабораторной установке – машине Атвуда.

Экспериментальная установка

  
Машина Атвуда  (рис.1) состоит из легкого блока 2, через который
переброшена нить с двумя наборными грузами на концах (массы обоих грузов
одинаковы и равны m). Грузы могут двигаться вдоль вертикальной
рейки со шкалой 1. Если на правый груз положить небольшой перегрузок Dm,
грузы начнут двигаться с некоторым ускорением. Для приема падающего груза
служит полочка 3.

   Время
движения грузов измеряется с помощью ручного или стационарного секундомера.   

   Силы трения в машине Атвуда
сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса
одного из грузов (в нашей установке – правого)  делается немного больше массы
другого.  Эта операция производится при помощи кусочков пластилина и
выполняется с таким расчетом, чтобы  а) грузы могли находиться в статическом
положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся
система приходила в равномерное движение. Масса используемого пластилина столь
мала, что в последующих  расчетах  в массу грузов не включается. Перегрузки Dm, с
помощью которых системе задается движение, укладывают также на правый груз
системы.

   Для выполнения работы машина Атвуда должна быть
установлена строго вертикально, что легко проверить по параллельности шкалы и
нити.

Теоретическая часть

   Второй закон Ньютона в проекциях на вертикальную
ось для каждого из тел системы (рис.2) в предположении невесомости блока,
отсутствия силы  трения и нерастяжимости  нити дает:

(1)

Где g —
ускорение свободного падения,

a —
ускорение грузов,

 T₁
и T₂ — сила натяжения нити.

Выразим из данной системы ускорение a.

      (2)

Проверим равноускоренный характер движения грузов,
экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и
время движения t.

Так как
начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

    (3)                                        

  Третье соотношение часто называют законом перемещений:
«Перемещение при равноускоренном движении прямо пропорционально
квадрату времени движения».

   Соотношение (3) может быть проверено
экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность
экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение,
с которым движется тело, прямо пропорционально равнодействующей действующих на
него сил и обратно пропорционально массе этого тела».

Подставляя a_i в
(2) получаем следующую формулу:

(4)

Для получения более точного значения g, необходимо учесть момент инерции
блока — J_б,  (T₁  T₂). Рассмотрим получения вышеописанных формул с учётом новой  величины.
Вычислим g из закона динамики для вращательного
движения тела (в данном случае блока).

 (5)

—
сумма проекций на ось Z всех сил, действующих на
вращающиеся тело; α- угловое ускорение блока; J – его момент инерции

             
(6)

Где r — радиус блока, J_б
— момент инерции блока.

Выразим из уравнения (1) разность сил натяжения  (T₁ – T₂ ) и подставив ее в уравнение (6) получим:

  (7)

Выразим ускорение грузов a:

(8)

Учитывая, что значение момента инерции блока

(9),

 k- коэффициент распределения массы блока
относительно оси вращения (k < 1), окончательно получаем выражение для
определения ускорения свободного падения:  

11)

       Экспериментальная
часть

Задание 1. Проверка второго закона Ньютона.

   Поскольку
ускорение движения является функцией двух переменных – силы и массы, то
изучение второго закона Ньютона выполняется путем раздельного исследования двух
зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе
системы и 2) зависимости ускорения от массы системы при постоянной действующей
силе.

Исследование зависимости ускорения  от  силы при
постоянной массе

Измерения и обработка результатов

1. Тщательно
балансируют грузы, выбрав их массы в пределах 150 — 200
г каждый.

2. Затем
на правый груз последовательно накладывают перегрузки. В результате в системе
появляется движущая сила равная Dmg,  где Dm — суммарная масса перегрузков. При
этом, конечно, общая масса системы незначительно увеличивается, но  этим изменением
массы по сравнению с массой грузов можно пренебречь, считая массу системы
постоянной.

3.
Измеряют время равноускоренного движения системы на пути, например, 1
метр. Все данные заносят в таблицу 1.3 отчета.

4.
Пользуясь законом путей (1.6), вычисляют ускорение а.

5.
Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.

6.
Строят график зависимости ускорения движения от действующей силы. Точку (F=0, a=0) на графике не откладывают. Если
экспериментальные точки ложатся на прямую с небольшим разбросом и прямая
проходит через начало координат, то можно сделать вывод о том, что ускорение
действительно прямо пропорционально силе.

7.
По угловому коэффициенту полученной прямой определяют массу системы и сравнивают
ее реальной массой.

Исследование зависимости ускорения  от  массы при
постоянной силе

Измерения и обработка результатов

1. Все опыты
проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе.
Ускорение системы измеряется также как и в предыдущем задании.

2.
Для изменения массы системы одновременно на правый и левый груз кладут дополнительные
одинаковые грузы. Все данные записывают в таблицу отчета.

3.
График обратно пропорциональной зависимости ускорения от массы представляет
собой гиперболу, которую невозможно идентифицировать. Для проверки предположения
об обратно пропорциональной зависимости между ускорением и массой  необходимо построить график зависимости 
ускорения от обратного значения массы системы: a = f(М^-1). Подтверждением
предположения является прямолинейность этого графика.

4. По угловому коэффициенту полученной прямой
определяют значение приложенной силы и сравнивают ее с реально действующей в
системе

Задание 2. Определение ускорения движения грузов

   В полученном  уравнении прямой  коэффициент k равен половине
ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов (a
=2k)  в данном опыте и определить погрешность его
измерения. Произведите необходимые вычисления и занесите результаты в отчет.

Задание 3. Определение ускорения свободного падения

   (Выполняется по результатам измерений
и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и
перегрузка, а также ускорение движения системы, из формулы (3) найдите
ускорение свободного падения. Результаты занесите в отчет. В выводе сравните
полученный результат с табличной величиной.

Для нахождения погрешности измерения величины
ускорения свободного падения Δg
используем формулу:

12)

где   ;  ;  ;  ;

 – частные производные функции

Проанализируйте  результаты своих наблюдений и
сформулируйте вывод.

Контрольные
вопросы

1.
Какое
движение называется поступательным?

2.
Дайте
определение инерциальной системы отсчета. Приведите примеры ИСО.

3.
 Сформулируйте
первый закон Ньютона. Приведите примеры его проявления.

4.
Дайте
определение инертной массы тела. Гравитационной?  От чего и как зависит  масса
тела?

5.
 Сформулируйте
второй закон Ньютона. Приведите варианты его математической формы.

6.
Покажите
все силы,  действующие на один из грузов в машине Атвуда, и составьте для него
уравнение динамики.

7.
Запишите
систему уравнений  динамики  для машины Атвуда с учетом момента инерции блока.
Силы трения в блоке?