Построить оптимальный код хемминга объемом 5 исправляющий 1 ошибку

Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.

Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.

Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.

Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.

1.
По заданному количеству информационных
символов — k,
либо информационных комбинаций N
= 2^k
, используя соотношения:

n
= k+m, 2ⁿ
(n+1)2^k
и
2^m
n+1 (14)

m
= [log₂
{(k+1)+
[log₂(k+1)]}]

вычисляют
основные параметры кода n
и m.

2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2ⁱ,
где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.

3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае — 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2^k
–1
перечисленных в возрастающем порядке.
Для
m = 3
проверочная матрица имеет вид

.
(15 )

Количество
разрядов m
— определяет количество проверок.

В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b₁,
b₃,
b₅
и т. д.

Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b₂,
b₃,
b₆
и т. д.

В
третью проверку — коэффициенты которые
содержат 1 в третьем разряде и т. д.

Таблица
1

Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.

Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.

Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.

Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.

Решение:

1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:

m
= [log₂
{(k+1)+
[log₂(k+1)]}]=[log₂
{(4+1)+
[log₂(4+1)]}]=3,

при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.

2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2ⁱ
.

Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:

b₁
b₂
b₃
b₄
b₅
b₆
b₇

к₁
к₂
0
к₃
1
0 1

3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).

Первая
проверка:

k₁

b₃
b₅
b₇
= k₁011
будет четной при k₁
=
0.

Вторая
проверка:

k₂

b₃
b₆
b₇
= k₂001
будет четной при k₂
=
1.

Третья
проверка:

k₃

b₅
b₆
b₇
= k₃101
будет четной при k₃
=
0.

1
2 3 4 5 6 7

Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1

Допустим
принято: 0 1 1 0 1 0 1

Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.

1)
k₁

b₃
b₅
b₇
= 0111 = 1.

2)
k₂

b₃
b₆
b₇
= 1101 = 1.

1. k₃
   
   b₅
   b₆
   b₇
   = 0101 = 0.

Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.

Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.

Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.

1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.

m
= [log₂
{(k+1)+
[log₂(k+1)]}]=[log₂
{(9+1)+
[log₂(9+1)]}]=4,

при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.

2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2ⁱ
.

Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.

При
этом кодовая комбинация имеет вид:

b₁
b₂
b₃
b₄
b₅
b₆
b₇
b₈
b₉
b₁₀
b₁₁
b₁₂

к₁
к₂
1
к₃
1
0 1 к₄
1
0 1 1

3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.

Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью — m.

0001
b₁
Количество разрядов m — определяет
количество прове-

0010
b₂
верок.

0011
b₃
1) к₁
b₃
b₅
b₇
b₉
а₁₁
=
к₁11111
=>

0100
b₄
четная
при к₁=1

0101
b₅
2)
к₂
b₃
b₆
b₇
b₁₀
b₁₁=
к₂10101
=>

0110
b₆
четная при к₂=1

0111
b₇
3)
к₃
b₅
b₆
b₇
b₁₂
=
к₃1011=>

1000
b₈
четная
при к₃=1

1001
b₉
4) к₄
b₉
b₁₀
b₁₁
b₁₂
=
к₁1011
=>

1010
b₁₀
четная
при к₄=1

1011
b₁₁

1100
b₁₂

Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12

1
1 1 1 1 0 1 1 1 0 1 1

Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1

Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.

1)
к₁
b₃
b₅
b₇
b₉
b₁₁
=
110111 =1

2)
к₂
b₃
b₆
b₇
b₁₀
b₁₁
=
110101 =0

3)
к₃
b₅
b₆
b₇
b₁₂
=
10011 =1

4)
к₄
b₉
b₁₀
b₁₁
b₁₂
=
11011 =0

Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.

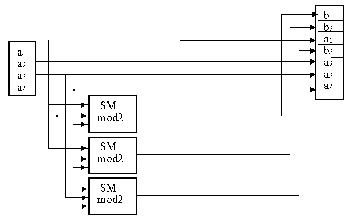
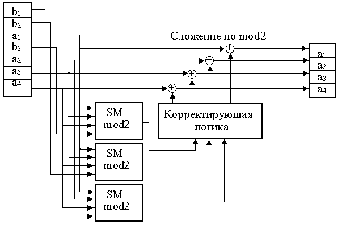
Рис.
1. Схема кодера —а
и декодера –б
для простого (7, 4) кода Хэмминга

Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.

Наибольшее
применение в ЗУ нашли коды Хэмминга с
d_min=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.

Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:

• автоматическое
  исправление ошибки без уведомления
  системы;

—
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;

—
не исправление ошибки, а только уведомление
системы об ошибках;

Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.

Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.

В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB — информационное
слово, CB — контрольное слово).

При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.

(22,16)

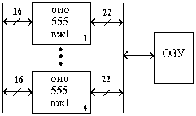
4
схе(72,64)

Рис.2.
Схема контроля

При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.

Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.

Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.

Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.

Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.

Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1

Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.

Код, исправляющий
одиночную и обнаруживающий двойную
ошибки

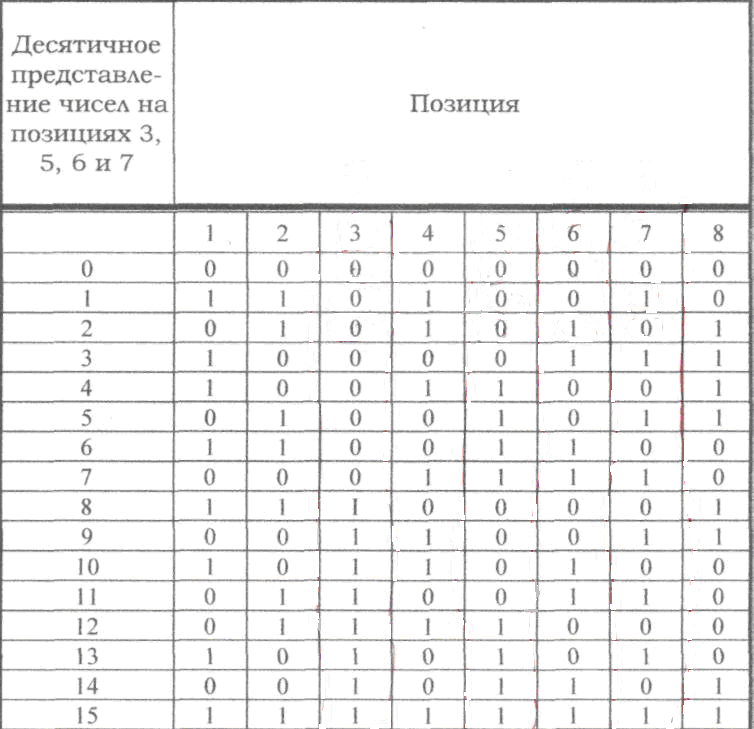
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.

Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.

Лекция 8

8.1 Двоичные циклические коды

Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.

Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:

существует другое
кодовое слово:

полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.

Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.

Например,
пусть кодовое слово ||КС||
=
||011010||.

Его
можно описать полиномом

Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.

Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.

Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.

Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).

Пусть

||A||
= ||011010||,
||В|| =
||110111|.

Тогда

—————————————————————

Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.

Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.

Рассмотрим
умножение на примере умножения полинома
(X³+X¹+X⁰)

на
полином X¹+X⁰

X³
+ 0*X²+X¹+X⁰

*

X¹+X⁰

^{—————————————————}

X³+
0*X²+X¹+Х⁰

X⁴+0*Х³+
X²+Х¹

^{____________________________________}

Х⁴+
X³+
X²+0*X¹+X⁰

Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2

Пример
деления полинома X⁶+X⁴+X³
на полином
X³+X²+1

X⁶+0*X⁵+X⁴
+ X³+0*X²+0*X¹+0
| X³+X²+1

X⁶+X⁵+0*X⁴+X³ результат== |X³+X²

————————————

X⁵
+X⁴
+ 0*X³+0*X²

X⁵
+X⁴
+ 0*X³+
X²

—————————————-

остаток==
X²
=
100

Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xⁿ+1,
если его порядок >
п.

Проверим это на
примере.

Пусть требуется
выполнить циклический сдвиг влево на
одну позицию

коэффициентов
полинома

C(X)=X⁵+Х³+X²+1
→ (101101)

В результате должен
получиться полином

C₁(X)=X⁴+Х³+X¹+1
→ (011011)

Это легко
доказывается:

C₁(X)=C(X)*X-(X⁶+1)=(X⁶+Х⁴+X³+X)+(
X⁶+1)=X⁴+Х³+X¹+1

В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его g_r(X).

Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином g_r(X)

КС_r+k(Х)=g_r(X)+ИС_k(Х).

Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.

ПКС(Х)=КС(Х)+ВО(Х).

где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.

Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):

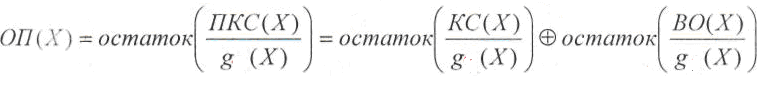
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.

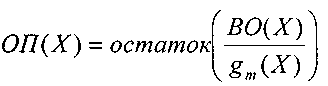
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.

Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.

Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.

Этот недостаток
был устранен следующим образом.

Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.

Эти
дополнительные разряды предлагается
находить по следующей формуле:

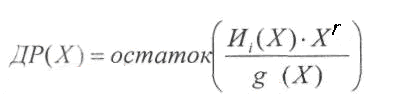
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).

Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:

Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.

Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:

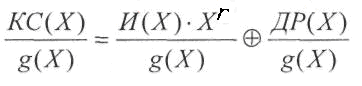
Рассмотрим первое
слагаемое:

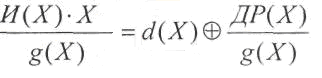
где
d(Х)
— целая
часть результата деления.

Подставим полученную
сумму на место первого слагаемого:

Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).

Значит

—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.

In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.

Hamming Code for Single Error Correction

The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.

Encoding a message by Hamming Code

The procedure used by the sender to encode the message encompasses the following steps −

• Step 1 − Calculation of the number of redundant bits.

• Step 2 − Positioning the redundant bits.

• Step 3 − Calculating the values of each redundant bit.

Once the redundant bits are embedded within the message, this is sent to the destination.

Step 1 − Calculation of the number of redundant bits.

If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2^r states, 2^r must be at least equal to (m + r + 1). Thus the following equation should hold −

2^r ≥ 𝑚 + 𝑟 + 1

Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (2⁴ ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.

Step 2 − Positioning the redundant bits.

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r₁ (at position 1), r₂ (at position 2), r₃ (at position 4), r₄ (at position and so on.

Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.

The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −

• Even Parity − Here the total number of bits in the message is made even.

• Odd Parity − Here the total number of bits in the message is made odd.

Each redundant bit, r_i, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the i^th position except the position of r_i. Thus −

• r₁ is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)

• r₂ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)

• r₃ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)

Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.

Decoding a message in Hamming Code

Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −

• Step 1 − Calculation of the number of redundant bits.

• Step 2 − Positioning the redundant bits.

• Step 3 − Parity checking.

• Step 4 − Error detection and correction

Step 1) Calculation of the number of redundant bits

Using the same formula as in encoding, the number of redundant bits are ascertained.

2^r ≥ 𝑚 + 𝑟 + 1

where m is the number of data bits and r is the number of redundant bits.

Step 2) Positioning the redundant bits

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.

Step 3) Parity checking

Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c₁, c₂, c₃, c₄ etc. Thus

c₁ = parity(1, 3, 5, 7, 9, 11 and so on)

c₂ = parity(2, 3, 6, 7, 10, 11 and so on)

c₃ = parity(4-7, 12-15, 20-23 and so on)

Step 4) Error detection and correction

The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c₁c₂c₃c₄ = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.

Example 4 − Suppose that an incoming message 11110101101 is received.

Step 1 − At first the number of redundant bits are calculated using the formula 2^r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2^r ≥ 12 is 4.

Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −

c₁ = even_parity(1, 3, 5, 7, 9, 11) = 0

c₂ = even_parity(2, 3, 6, 7, 10, 11) = 0

c₃ = even_parity (4, 5, 6, 7) = 0

c₄ = even_parity (8, 9, 10, 11) = 0

Step 4 — Since the value of the check bits c₁c₂c₃c₄ = 0000 = 0, there are no errors in this message.

Hamming Code for double error detection

The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.

Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.

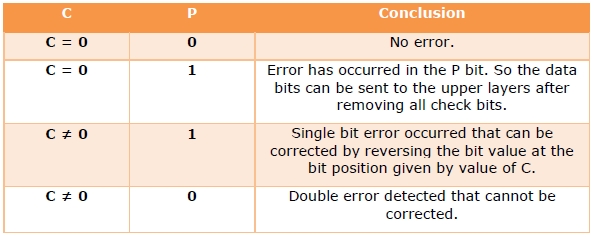
At the receiver’s end, error detection is done as shown in the following table −

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам. 

Теория кодирования. Примеры решений

На этой странице вы найдете готовые примеры заданий по теории кодирования: по Хэммингу, Хаффману, Шеннона-Фано и т.д..

Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.

Задачи и решения по теории кодирования

Задача 1. Закодировать данное слово кодом Хэмминга.
1001 0001 1101 1110 0000 000.

Задача 2. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1111 1011 0010 1100 1101 1100 110.

Задача 3. Построить оптимальный код, пользуясь алгоритмом Хаффмана, найти стоимость кода.

Задача 4. Пусть имеется 6 кодовых символов. С помощью алгоритма Хаффмана построить код Шеннона-Фэно для текстового сообщения STUDENT