Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.
Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.
Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.
Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданному количеству информационных
символов — k,
либо информационных комбинаций N
= 2k
, используя соотношения:
n
= k+m, 2n
(n+1)2k
и
2m
n+1 (14)
m
= [log2
{(k+1)+
[log2(k+1)]}]
вычисляют
основные параметры кода n
и m.
2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2i,
где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.
3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае — 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2k
–1
перечисленных в возрастающем порядке.
Для
m = 3
проверочная матрица имеет вид
 .
.
(15 )
Количество
разрядов m
— определяет количество проверок.
В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b1,
b3,
b5
и т. д.
Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b2,
b3,
b6
и т. д.
В
третью проверку — коэффициенты которые
содержат 1 в третьем разряде и т. д.
Таблица
1
|
Десятичные
(номера
кодовой |
Двоичные |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.
Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.
Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.
Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.
Решение:
1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(4+1)+
[log2(4+1)]}]=3,
при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:
b1
b2
b3
b4
b5
b6
b7
к1
к2
0
к3
1
0 1
3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).
Первая
проверка:
k1
b3
b5
b7
= k1011
будет четной при k1
=
0.
Вторая
проверка:
k2
b3
b6
b7
= k2001
будет четной при k2
=
1.
Третья
проверка:
k3
b5
b6
b7
= k3101
будет четной при k3
=
0.
1
2 3 4 5 6 7
Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1
Допустим
принято: 0 1 1 0 1 0 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.
1)
k1
b3
b5
b7
= 0111 = 1.
2)
k2
b3
b6
b7
= 1101 = 1.
-
k3
b5
b6
b7
= 0101 = 0.
Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.
Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.
Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(9+1)+
[log2(9+1)]}]=4,
при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.
При
этом кодовая комбинация имеет вид:
b1
b2
b3
b4
b5
b6
b7
b8
b9
b10
b11
b12
к1
к2
1
к3
1
0 1 к4
1
0 1 1
3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.
Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью — m.
0001
b1
Количество разрядов m — определяет
количество прове-
0010
b2
верок.
0011
b3
1) к1
b3
b5
b7
b9
а11
=
к111111
=>
0100
b4
четная
при к1=1
0101
b5
2)
к2
b3
b6
b7
b10
b11=
к210101
=>
0110
b6
четная при к2=1
0111
b7
3)
к3
b5
b6
b7
b12
=
к31011=>
1000
b8
четная
при к3=1
1001
b9
4) к4
b9
b10
b11
b12
=
к11011
=>
1010
b10
четная
при к4=1
1011
b11
1100
b12
Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12
1
1 1 1 1 0 1 1 1 0 1 1
Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.
1)
к1
b3
b5
b7
b9
b11
=
110111 =1
2)
к2
b3
b6
b7
b10
b11
=
110101 =0
3)
к3
b5
b6
b7
b12
=
10011 =1
4)
к4
b9
b10
b11
b12
=
11011 =0
Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.
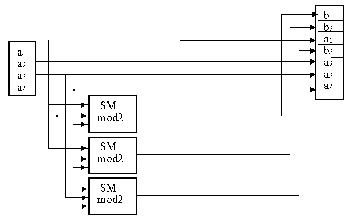
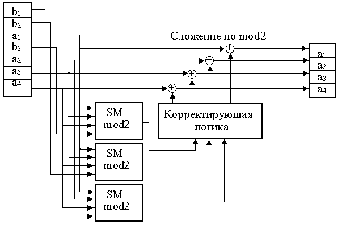
Рис.
1. Схема кодера —а
и декодера –б
для простого (7, 4) кода Хэмминга
Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.
Наибольшее
применение в ЗУ нашли коды Хэмминга с
dmin=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.
Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:
-
автоматическое
исправление ошибки без уведомления
системы;
—
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;
—
не исправление ошибки, а только уведомление
системы об ошибках;
Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.
Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.
В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB — информационное
слово, CB — контрольное слово).
При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.
(22,16)
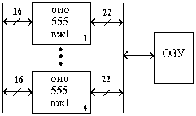
4
схе(72,64)
Рис.2.
Схема контроля
При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.
Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.
Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.
Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.
Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданному количеству информационных
символов — k,
либо информационных комбинаций N
= 2k
, используя соотношения:
n
= k+m, 2n
(n+1)2k
и
2m
n+1 (14)
m
= [log2
{(k+1)+
[log2(k+1)]}]
вычисляют
основные параметры кода n
и m.
2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2i,
где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.
3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае — 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2k
–1
перечисленных в возрастающем порядке.
Для
m = 3
проверочная матрица имеет вид
 .
.
(15 )
Количество
разрядов m
— определяет количество проверок.
В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b1,
b3,
b5
и т. д.
Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b2,
b3,
b6
и т. д.
В
третью проверку — коэффициенты которые
содержат 1 в третьем разряде и т. д.
Таблица
1
|
Десятичные
(номера
кодовой |
Двоичные |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.
Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.
Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.
Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.
Решение:
1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(4+1)+
[log2(4+1)]}]=3,
при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:
b1
b2
b3
b4
b5
b6
b7
к1
к2
0
к3
1
0 1
3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).
Первая
проверка:
k1
b3
b5
b7
= k1011
будет четной при k1
=
0.
Вторая
проверка:
k2
b3
b6
b7
= k2001
будет четной при k2
=
1.
Третья
проверка:
k3
b5
b6
b7
= k3101
будет четной при k3
=
0.
1
2 3 4 5 6 7
Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1
Допустим
принято: 0 1 1 0 1 0 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.
1)
k1
b3
b5
b7
= 0111 = 1.
2)
k2
b3
b6
b7
= 1101 = 1.
-
k3
b5
b6
b7
= 0101 = 0.
Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.
Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.
Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(9+1)+
[log2(9+1)]}]=4,
при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.
При
этом кодовая комбинация имеет вид:
b1
b2
b3
b4
b5
b6
b7
b8
b9
b10
b11
b12
к1
к2
1
к3
1
0 1 к4
1
0 1 1
3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.
Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью — m.
0001
b1
Количество разрядов m — определяет
количество прове-
0010
b2
верок.
0011
b3
1) к1
b3
b5
b7
b9
а11
=
к111111
=>
0100
b4
четная
при к1=1
0101
b5
2)
к2
b3
b6
b7
b10
b11=
к210101
=>
0110
b6
четная при к2=1
0111
b7
3)
к3
b5
b6
b7
b12
=
к31011=>
1000
b8
четная
при к3=1
1001
b9
4) к4
b9
b10
b11
b12
=
к11011
=>
1010
b10
четная
при к4=1
1011
b11
1100
b12
Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12
1
1 1 1 1 0 1 1 1 0 1 1
Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.
1)
к1
b3
b5
b7
b9
b11
=
110111 =1
2)
к2
b3
b6
b7
b10
b11
=
110101 =0
3)
к3
b5
b6
b7
b12
=
10011 =1
4)
к4
b9
b10
b11
b12
=
11011 =0
Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.


Рис.
1. Схема кодера —а
и декодера –б
для простого (7, 4) кода Хэмминга
Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.
Наибольшее
применение в ЗУ нашли коды Хэмминга с
dmin=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.
Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:
-
автоматическое
исправление ошибки без уведомления
системы;
—
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;
—
не исправление ошибки, а только уведомление
системы об ошибках;
Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.
Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.
В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB — информационное
слово, CB — контрольное слово).
При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.
(22,16)

4
схе(72,64)
Рис.2.
Схема контроля
При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.
Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Омский государственный педагогический университет»
(ФГБОУ ВО «ОмГПУ»)
Факультет математики, информатики, физики и технологии
Кафедра прикладной информатики и математики
Курсовая работа
Код Хемминга
Направление: педагогическое образование
Профиль: Информатика и Технология
Дисциплина: Теоретические основы информатики
Выполнила: студентка
32 группы
Коробейникова
Ольга Витальевна
______________________________(подпись)
Научный руководитель:
Курганова
Наталья Александровна
к.п.н., доцент
Оценка _______________
«__» _______________ 20___г.
(подпись)
Омск, 20___
Оглавление
Введение
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
1.2. Характеристика кода Хемминга при помехоустойчивом кодировании
1.3. Алгоритмы использования кода Хемминга для нахождения ошибок
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
ЗАКЛЮЧЕНИЕ
Список литературы
Введение
На сегодняшний день в мире передается огромное количество информации, хотя системы передачи данных отвечают всем требованиям. Они не являются столь совершенными. При передаче данных могут возникать помехи. Помехоустойчивость – способность системы осуществлять прием информации в условиях наличия помех в линии связи и искажений во внутри аппаратных трактах. Помехоустойчивость обеспечивает надежность и достоверность передаваемой информации (данных).Управление правильностью передачи информации выполняется с помощью помехоустойчивого кодирования. Есть коды, обнаруживающие ошибки, и корректирующие коды, которые еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности, дополнительных битов. В симплексных каналах связи устраняют ошибки с помощью корректирующих кодов. В дуплексных–достаточно применения кодов, обнаруживающих ошибки. [1]
История развития помехоустойчивого кодирования началась еще с 1946г., а именно, после публикации монографии американского ученого К. Шеннона «Работы по теории информации и кибернетике».В этой работе он не показал как построить эти коды, а доказал их существование. Важно отметить, что результаты работы К. Шеннона опирались на работы советских ученых, таких как: А. Я. Хинчин, Р.Р. Варшамов и др. На сегодняшний день проблема передачи данных является особо актуальной,т.к. сбой при передаче может вызвать не только искажение сообщения в целом, но и полную потерю информации. Для этого и существуют помехоустойчивые коды, способные предотвратить потерю и искажение информации. В настоящее время существует ряд разновидностей помехоустойчивых кодов, обеспечивающих высокую достоверность при малой величине избыточности и простоте технической реализации кодирующих и декодирующих устройств. Принципиально коды могут быть использованы как для обнаружения, так и для исправления ошибок. Однако удобства построения кодирующих и декодирующих устройств определили преимущественное применение лишь некоторых из них, в частности корректирующего кода Хемминга.
Цель данной курсовой работы: Ознакомление с помехоустойчивым кодированием и изучение кода Хемминга.
Задачи:
1) Ознакомиться с видами помехоустойчивого кодирования;
2) Ознакомиться с кодом Хемминга, как с одним из видов помехоустойчивого кодирования;
3) Изучить алгоритм построения кода Хемминга.
Объект исследования: помехоустойчивое кодирование.
Предмет исследования: код Хемминга.
Данная курсовая работа состоит из титульного листа, оглавления,введения, двух глав (теоретической и практической), заключения и списка литературы.
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
В мире существует немало различных помех и искажений, это могут быть как звуковые искажения, так и на графике. Мы рассмотрим, что понимается под помехой в кодировании информации. Под помехой понимается любое воздействие, накладывающееся на полезный сигнал изатрудняющее его прием. Ниже приведена классификация помех и их источников.
Рис. 1.Помехи и их источники
Внешние источники помех вызывают в основном импульсные помехи, а внутренние –флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевыеи дробления. Краевые искажения связаны со смещением переднего или заднего фронта импульса.Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов [2].
Приведем классификацию помехоустойчивых кодов.
1) Обнаруживающие ошибки:
блоковые:
А) Разделимые:
- с проверкой на четность;
- корреляционные;
- Хэмминга;
- БЧХ;
Б) Неразделимые:
- с постоянным весом;
- Грея.
2) Корректирующие коды:
Непрерывные:
А) С пороговым декодированием;
Б) По макс. правдоподобия;
В) С последовательным декодированием.
Теперь рассмотрим более подробно каждый вид кодирования.
Код с проверкой на четность.
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
В каждом пакет данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
Пример:
Начальные данные: 1111
Данные после кодирования: 11110 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка [3].
Корреляционные коды (код с удвоением).
Элементы данного кода заменяются двумя символами, единица «1» преобразуется в 10, а ноль «0» в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10) [2].
Код с постоянным весом.
Одним из простейших блочных неразделимых кодов является код с постоянным весом. Примером такого кода может служить семибитный телеграфный код МТК–3, в котором каждая разрешенная кодовая комбинация содержит три единицы и четыре нуля (рис.2). Весом кодовой комбинации называют число содержащихся в ней единиц. В рассматриваемом коде вес кодовых комбинаций равен трем.
Число разрешенных кодовых комбинаций в кодах с постоянным весом определяется как количество сочетаний изnсимволов поgи равно
(1)
Где n–длина кодовой комбинации, аg – вес разрешенной кодовой комбинации. Для кода МТК-3 число разрешенных кодовых комбинаций равно. Таким образом, из общего числа комбинаций
только 35 используются для передачи сообщений[4].
Рис.2. Примеры разрешенных и запрещенных комбинаций кода МТК-3
Инверсный код.
К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
|
k |
r |
n |
|
11011 |
11011 |
1101111011 |
|
11100 |
00011 |
1110000011 |
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
|
1) |
11011 11011 |
|
00000 |
|
|
2) |
11111 00100 |
|
11011 |
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k=5, n=10 и . Коэффициент обнаружения будет составлять
[2].
Код Грея.
По сравнению с простым кодом, код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки из-за помех в канале. Обычно этот код применяется для аналогово-цифрового преобразования непрерывных сообщений.
Недостатком кода Грея является его невесомость, т.е. вес единицы не определяется номером разряда. Информацию в таком виде трудно обрабатывать на ЭВМ. Декодирование кода также связано с большими затратами. Поэтому перед вводом в ЭВМ (или перед декодированием) код Грея преобразуется в простой двоичный код, который удобен для ЭВМ и легко декодируется.
Для перевода простого двоичного кода в код Грея нужно:
- под двоичным числом записать такое же число со сдвигом вправо на один разряд (при этом младший разряд сдвигаемого числа теряется);
- произвести поразрядное сложение двух чисел по модулю 2 (четности). [5].
Таким образом, мы рассмотрели виды помехоустойчивого кодирования и увидели, что их существует не так уж и мало. Каждый код по своему уникален и полезен для кодирования информации. Теперь мы ознакомимся с кодом Хемминга подробнее.
1.2.Характеристика кода Хэмминга при помехоустойчивом кодировании
В середине 40-х годов Ричард Хемминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки,скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машине с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.
Р. Хемминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перегружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день мы знаем как код Хемминга.[6.].
Код Хемминга, как и любой (n,k) код, содержит k информационных и избыточных символов. Избыточная часть кода строится таким образом, чтобы при декодировании можно было бы установить не только факт наличия ошибок в принятой – комбинации, но и указать номер позиции, в которой произошла ошибка. Это достигается за счет многократной проверки принятой комбинации на четность. Каждой проверкой должны охватываться часть информационных символов и один из избыточных символов. При каждой проверке получают двоичный контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное число– 1. В результате всех проверок получается p-разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки достаточно лишь изменить значение данного символа на обратное. [7]
К ним обычно относятся коды с минимальным кодовым расстояниемисправляющие все одиночные ошибки, и коды с расстоянием
исправляющие все одиночные и обнаруживающие все двойные ошибки. Длина кода Хэмминга:
(2)
(r – количество проверочных разрядов).
Характерной особенностью проверочной матрицы кода с является то, что ее столбцы представляют собой любые различные ненулевые комбинации длиной r.Например, при r=4 иn=5 для кода (15,11), проверочная матрица может иметь следующий вид (рис.3)
Рис.3. Проверочная матрица
Перестановкой столбцов, содержащих одну единицу, данную матрицу можно привести к виду(рис.4)
Рис. 4.Измененная матрица
Использование такого кода позволяет исправить любую одиночную ошибку или обнаружить произвольную ошибку кратности два.Если информационные и проверочные разряды кода нумеровать слева направо, то в соответствии с матрицей получаем систему проверочных уравнений, с помощью которых вычисляем проверочные разряды(рис.5):
Рис.5. Система проверочных уравнений
где —
-проверочные разряды;
—
-информационные разряды
Двоичный код Хэмминга с кодовым расстоянием получается путем добавления к коду Хэмминга с
одного проверочного разряда, представляющего собой результат суммирования по модулю два всех разрядов кодового слоя. Длина кода при этом
разрядов, из которых
являются проверочными.
Операция кодирования может выполняться в два этапа. На первом этапе определяется кодовая комбинация с использованием матрицы H, соответствующей коду с на втором — добавляется один проверочный разряд, в котором записывается результат суммирования по модулю два всех разрядов кодового слова, полученного на первом этапе. Операция декодирования также состоит из двух этапов. На первом вычисляется синдром, соответствующий коду на втором — проверяется последнее проверочное соотношение.[8]
Таким образом, ознакомившись с характеристикой кода Хемминга, важно сказать, что состоит код из двух частей и предполагает надежную работу нахождения ошибок и корректировки сообщений.
1.3.Алгоритмы использования кода Хэмминга для нахождения ошибок
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
1.По заданному количеству информационных символов – k, либо информационных комбинаций , используя соотношения:
,
(3)
и (4)
(5)
Вычисляют основные параметры кода m и n.
2.Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону , где i= 1,2,3,…т.е. они равны 1,2,4,8,16,…а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно . В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение – 0, в противном случае – 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n -чисел разрядностью – m (табл. 2, для m = 4) или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до
перечисленных в возрастающем порядке.
Количество разрядов m – определяет количество проверок.
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1,b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку –коэффициенты которые содержат 1 в третьем разряде и т.д.
Таблица 2
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
|
|
3 |
21 |
|
|
1 |
0 |
01 |
|
2 |
0 |
10 |
|
3 |
0 |
11 |
|
4 |
1 |
00 |
|
5 |
1 |
01 |
|
6 |
1 |
10 |
|
7 |
1 |
11 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) – разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.[9]
Вывод к главе 1: Таким образом, мы узнали, что такое помехоустойчивость, помехоустойчивое кодирование, ознакомились с видами помехоустойчивого кодирования. Затем рассмотрели код Хемминга, изучили алгоритм построения кода Хемминга. При построении кода важно знать, что код Хемминга ищет и исправляет одиночную ошибку, но двойную ошибку. В итоге, изучив теоретическую часть, мы выяснили, какие существуют виды помехоустойчивого кодирования. Ознакомились подробнее с кодом Хемминга, изучили его алгоритм кодирования.
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
Существует множество различных примеров для нахождения ошибок при помощи кода Хемминга.
Пример 1. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1) 1111 1011 0010 1100 1101 1100 110
РЕШЕНИЕ. Сообщение состоит из 27 символов, из них 22 информационные, а 5 – контрольные. Это разряды b1 = 1, b2 = 1, b4 = 1, b8 = 1, b16=0. Вычислим число J для обнаружения ошибки: Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… – все числа у которых первый разрядравен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… – все числа, у которых второй разрядравен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23 … – все числа, у которых третий разряд равен1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27 … – все числа, у которых четвертый разрядравен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 … – все числа, у которых пятый разрядравен 1.
Разряды числа J определяются следующим образом:
j1 = b1 +b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
j2=b2+b3+b6+b7+b10+b11+b14+b15+b18+b19+b22+b23+b26+b27= 0
j3 = b4+b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23 = 0
j4 =b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27 = 0,
j5 = b16+ b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27 = 1
то есть число J= =
.
Таким образом, ошибка произошла в семнадцатом разряде переданного числа.[10]. В этом примере мы рассмотрели, как можно обнаружить одиночную ошибку. Далее мы проанализируем пример, как можно найти и исправить эту ошибку.
Пример 2.
Построить код Хемминга для передачи сообщений в виде последовательности десятичных цифр, представленных в виде 4 –х разрядных двоичных слов. Показать процесс кодирования, декодирования и исправления одиночной ошибки на примере информационного слова 0101.
Решение:
1. По заданной длине информационного слова (k = 4 ), определим количество контрольных разрядов m, используя соотношение:
,
при этом т. е. получили (7, 4) -код.
2. Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону .
Для рассматриваемой задачи (при n = 7 ) номера контрольных позиций равны 1, 2, 4. При этом кодовая комбинация имеет вид:
b1 b2 b3 b4 b5 b6 b7
k1 k2 0 k2 1 0 1
3. Определяем значения контрольных разрядов (0 или 1), используя проверочную матрицу (рис.3).
Первая проверка:
k1b3 b5 b7 = k1 011 будет четной при k1 = 0.
Вторая проверка:
k2 b3 b6 b7 = k2 001 будет четной при k2 = 1.
Третья проверка:
k3 b5 b6 b7 = k3 101 будет четной при k3 = 0.
1 2 3 4 5 6 7
Передаваемая кодовая комбинация: 0100101
Допустим принято: 0110101
Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, в соответствии с проверочной матрицей результатом которых является двоичное ( ) – разрядное число, называемое синдромом и указывающим на положение ошибки, т. е, номер ошибочной позиции.
1) k1= b3 b5 b7 = 0111 = 1.
2)k2=b3 b6 b7 = 1101 = 1.
3) k3 =b5 b6 b7 = 0101 =0.
Сравнивая синдром ошибки со столбцами проверочной матрицы, определяем номер ошибочного бита. Синдрому 011 соответствует третий столбец, т. е. ошибка в третьем разряде кодовой комбинации. Символ в третьей позиции необходимо изменить на обратный.
Рассмотрев данные задачи, мы выяснили насколько точно код Хемминга может найти и исправить одиночные ошибки.
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
Для обнаружения двойной ошибки следует только добавить еще один проверочный разряд.
Пример 1:
Принята кодовая комбинация С = 101000001001, произошло
искажение 2-го и 5-го разрядов. Обнаружить ошибки.
Решение.
Значения проверок равны:
k1= b1 b3 b5 b7 b9 b11 = 110010= 1
k2= b2 b3 b6 b7 b10 b11= 010000=1
k3=b4 b5 b6 b7 b12= 00001=1
k4= b8 b9 b10 b11 b12= 01001=0
Тогда контрольное число (синдром) ошибкиравен 0111.
Таким образом, при наличии двукратной ошибки декодирование дает
номер разряда с ошибкой в позиции 7, в то время как ошибки произошли
во 2-м и 5-м разрядах. В этом случае составляется расширенный код
Хэмминга, путем добавления одного проверочного символа.
Пример 2 :
Передана кодовая комбинация «01001011», закодированная кодом Хемминга с d = 4. Показать процесс выявления ошибки.
Решение:
Принята комбинация «01001111»:
а) проверка на общую четность указывает на наличие ошибки (число единиц четное);
б) частные проверки производятся так же, как это было в других примерах.
При составлении проверочных сумм последние единицы кодовых комбинаций (дополнительные контрольные символы) не учитываются.
2. Принята комбинация «01101111»:
а) проверка на общую четность показывает, что ошибка не фиксируется;
б) частные проверки (последний символ отбрасывается)
Первая проверка 0 1 1 1 = 1
Вторая проверка 1 1 1 1 = 0
Третья проверка 0 1 1 1 = 1
Таким образом, частные проверки фиксируют наличие ошибки. Она, якобы, имела место на пятой позиции. Но так как при этом первая проверка на общую четность ошибки не зафиксировала, то значит, имела место двойная ошибка. Исправить двойную ошибку такой код не может [14].
Вывод к главе 2: Таким образом, мы показали, как работает код Хемминга на практике. Мы видим, что при одиночной ошибке ее можно исправить, но для этого нам нужно знать, сколько потребуется контрольных разрядов, а двойную ошибку можно лишь обнаружить.
ЗАКЛЮЧЕНИЕ
Высокие требования к достоверности передачи, обработки и хранения информации диктуют необходимость такого кодированияинформации, при котором обеспечивалось бы возможность обнаружения и исправления ошибок. Широкому применению результатов теории помехоустойчивогокодирования в современных системах связи, обработки и хранения информацииследует считать отсутствие достаточно простых решений сложных теоретических достижений теории помехоустойчивого кодирования.В данной работе исследовано помехоустойчивое кодирование, в частности код Хемминга.
Список литературы
- Вернер М. Основы кодирования[Текст].– М.: Техносфера, 2004. – 288 с.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:https://clck.ru/9cWsc,свободный. Дата обращения: 27.11.2015.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:http://habrahabr.ru/post/111336/, свободный. Дата обращения: 05.12.2015.
- Файловый архив для студентов. Лекция: основные понятия кодирования в ЦСПИ [Электронный ресурс]. – Режим доступа: http://www.studfiles.ru/preview/4087325/,свободный. Дата обращения: 27.11.2015.
- Лекция «Простейшие коды» [Электронный ресурс]. – Режим доступа: http://davaiknam.ru/text/lekciya-3-kodirovanie-informacii-prostejshie-kodi, свободный. Дата обращения: 27.11.2015.
- Академик [Электронный ресурс] – Режим доступа: http://dic.academic.ru/dic.nsf/ruwiki/177544, свободный. Дата обращения: 27.11.2015
- Кузьмин И.В.Основы теории информации и кодирования [Текст]. – Киев,1986. – 237 с.
- Научная библиотека. Код Хемминга [Электронный ресурс]. – Режим доступа: http://info.sernam.ru/book_codb.php?id=28, свободный. Дата обращения: 05.12.2015
- Статья корректирующие коды [Электронный ресурс]. – Режим доступа: http://referatwork.ru/refs/source/ref-11094.html#Текст работы, свободный. Дата обращения: 05.12.2015
- МатБюро- решение задач по высшей математике [Электронный ресурс]. – Режим доступа: http://www.matburo.ru/Examples/Files/Hem2.pdf, свободный. Дата обращения: 06.12.2015.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. [Текст]. – Москва, 1986г. –576 с.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования – методы, алгоритмы, применение. [Текст]. – Москва, 2005г.–320 с.
- Р.Хемминг Теория кодирования и теория информации. / Перевод с английского С.Гальфанда. // [Текст]. – Москва, 1983г. – 176 с.
- Портал студентов «Седьмой бит» [Электронный ресурс]. – Режим доступа: http://www.itmo.ru/work/253/page4, открытый. Дата обращения: 20.12.2015.
Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.
In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
Hamming Code for Single Error Correction
The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.
Encoding a message by Hamming Code
The procedure used by the sender to encode the message encompasses the following steps −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Calculating the values of each redundant bit.
Once the redundant bits are embedded within the message, this is sent to the destination.
Step 1 − Calculation of the number of redundant bits.
If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2r states, 2r must be at least equal to (m + r + 1). Thus the following equation should hold −
2r ≥ 𝑚 + 𝑟 + 1
Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (24 ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.
Step 2 − Positioning the redundant bits.
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r1 (at position 1), r2 (at position 2), r3 (at position 4), r4 (at position and so on.
Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.
The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −
-
Even Parity − Here the total number of bits in the message is made even.
-
Odd Parity − Here the total number of bits in the message is made odd.
Each redundant bit, ri, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the ith position except the position of ri. Thus −
-
r1 is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
-
r2 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
-
r3 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)
Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.
Decoding a message in Hamming Code
Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Parity checking.
-
Step 4 − Error detection and correction
Step 1) Calculation of the number of redundant bits
Using the same formula as in encoding, the number of redundant bits are ascertained.
2r ≥ 𝑚 + 𝑟 + 1
where m is the number of data bits and r is the number of redundant bits.
Step 2) Positioning the redundant bits
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.
Step 3) Parity checking
Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c1, c2, c3, c4 etc. Thus
c1 = parity(1, 3, 5, 7, 9, 11 and so on)
c2 = parity(2, 3, 6, 7, 10, 11 and so on)
c3 = parity(4-7, 12-15, 20-23 and so on)
Step 4) Error detection and correction
The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c1c2c3c4 = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.
Example 4 − Suppose that an incoming message 11110101101 is received.
Step 1 − At first the number of redundant bits are calculated using the formula 2r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2r ≥ 12 is 4.
Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −
c1 = even_parity(1, 3, 5, 7, 9, 11) = 0
c2 = even_parity(2, 3, 6, 7, 10, 11) = 0
c3 = even_parity (4, 5, 6, 7) = 0
c4 = even_parity (8, 9, 10, 11) = 0
Step 4 — Since the value of the check bits c1c2c3c4 = 0000 = 0, there are no errors in this message.
Hamming Code for double error detection
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.
At the receiver’s end, error detection is done as shown in the following table −
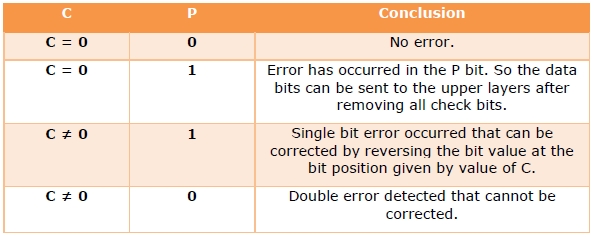
Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.
In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
Hamming Code for Single Error Correction
The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.
Encoding a message by Hamming Code
The procedure used by the sender to encode the message encompasses the following steps −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Calculating the values of each redundant bit.
Once the redundant bits are embedded within the message, this is sent to the destination.
Step 1 − Calculation of the number of redundant bits.
If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2r states, 2r must be at least equal to (m + r + 1). Thus the following equation should hold −
2r ≥ 𝑚 + 𝑟 + 1
Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (24 ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.
Step 2 − Positioning the redundant bits.
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r1 (at position 1), r2 (at position 2), r3 (at position 4), r4 (at position and so on.
Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.
The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −
-
Even Parity − Here the total number of bits in the message is made even.
-
Odd Parity − Here the total number of bits in the message is made odd.
Each redundant bit, ri, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the ith position except the position of ri. Thus −
-
r1 is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
-
r2 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
-
r3 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)
Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.
Decoding a message in Hamming Code
Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Parity checking.
-
Step 4 − Error detection and correction
Step 1) Calculation of the number of redundant bits
Using the same formula as in encoding, the number of redundant bits are ascertained.
2r ≥ 𝑚 + 𝑟 + 1
where m is the number of data bits and r is the number of redundant bits.
Step 2) Positioning the redundant bits
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.
Step 3) Parity checking
Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c1, c2, c3, c4 etc. Thus
c1 = parity(1, 3, 5, 7, 9, 11 and so on)
c2 = parity(2, 3, 6, 7, 10, 11 and so on)
c3 = parity(4-7, 12-15, 20-23 and so on)
Step 4) Error detection and correction
The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c1c2c3c4 = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.
Example 4 − Suppose that an incoming message 11110101101 is received.
Step 1 − At first the number of redundant bits are calculated using the formula 2r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2r ≥ 12 is 4.
Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −
c1 = even_parity(1, 3, 5, 7, 9, 11) = 0
c2 = even_parity(2, 3, 6, 7, 10, 11) = 0
c3 = even_parity (4, 5, 6, 7) = 0
c4 = even_parity (8, 9, 10, 11) = 0
Step 4 — Since the value of the check bits c1c2c3c4 = 0000 = 0, there are no errors in this message.
Hamming Code for double error detection
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.
At the receiver’s end, error detection is done as shown in the following table −

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Омский государственный педагогический университет»
(ФГБОУ ВО «ОмГПУ»)
Факультет математики, информатики, физики и технологии
Кафедра прикладной информатики и математики
Курсовая работа
Код Хемминга
Направление: педагогическое образование
Профиль: Информатика и Технология
Дисциплина: Теоретические основы информатики
Выполнила: студентка
32 группы
Коробейникова
Ольга Витальевна
______________________________(подпись)
Научный руководитель:
Курганова
Наталья Александровна
к.п.н., доцент
Оценка _______________
«__» _______________ 20___г.
(подпись)
Омск, 20___
Оглавление
Введение
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
1.2. Характеристика кода Хемминга при помехоустойчивом кодировании
1.3. Алгоритмы использования кода Хемминга для нахождения ошибок
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
ЗАКЛЮЧЕНИЕ
Список литературы
Введение
На сегодняшний день в мире передается огромное количество информации, хотя системы передачи данных отвечают всем требованиям. Они не являются столь совершенными. При передаче данных могут возникать помехи. Помехоустойчивость – способность системы осуществлять прием информации в условиях наличия помех в линии связи и искажений во внутри аппаратных трактах. Помехоустойчивость обеспечивает надежность и достоверность передаваемой информации (данных).Управление правильностью передачи информации выполняется с помощью помехоустойчивого кодирования. Есть коды, обнаруживающие ошибки, и корректирующие коды, которые еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности, дополнительных битов. В симплексных каналах связи устраняют ошибки с помощью корректирующих кодов. В дуплексных–достаточно применения кодов, обнаруживающих ошибки. [1]
История развития помехоустойчивого кодирования началась еще с 1946г., а именно, после публикации монографии американского ученого К. Шеннона «Работы по теории информации и кибернетике».В этой работе он не показал как построить эти коды, а доказал их существование. Важно отметить, что результаты работы К. Шеннона опирались на работы советских ученых, таких как: А. Я. Хинчин, Р.Р. Варшамов и др. На сегодняшний день проблема передачи данных является особо актуальной,т.к. сбой при передаче может вызвать не только искажение сообщения в целом, но и полную потерю информации. Для этого и существуют помехоустойчивые коды, способные предотвратить потерю и искажение информации. В настоящее время существует ряд разновидностей помехоустойчивых кодов, обеспечивающих высокую достоверность при малой величине избыточности и простоте технической реализации кодирующих и декодирующих устройств. Принципиально коды могут быть использованы как для обнаружения, так и для исправления ошибок. Однако удобства построения кодирующих и декодирующих устройств определили преимущественное применение лишь некоторых из них, в частности корректирующего кода Хемминга.
Цель данной курсовой работы: Ознакомление с помехоустойчивым кодированием и изучение кода Хемминга.
Задачи:
1) Ознакомиться с видами помехоустойчивого кодирования;
2) Ознакомиться с кодом Хемминга, как с одним из видов помехоустойчивого кодирования;
3) Изучить алгоритм построения кода Хемминга.
Объект исследования: помехоустойчивое кодирование.
Предмет исследования: код Хемминга.
Данная курсовая работа состоит из титульного листа, оглавления,введения, двух глав (теоретической и практической), заключения и списка литературы.
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
В мире существует немало различных помех и искажений, это могут быть как звуковые искажения, так и на графике. Мы рассмотрим, что понимается под помехой в кодировании информации. Под помехой понимается любое воздействие, накладывающееся на полезный сигнал изатрудняющее его прием. Ниже приведена классификация помех и их источников.
Рис. 1.Помехи и их источники
Внешние источники помех вызывают в основном импульсные помехи, а внутренние –флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевыеи дробления. Краевые искажения связаны со смещением переднего или заднего фронта импульса.Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов [2].
Приведем классификацию помехоустойчивых кодов.
1) Обнаруживающие ошибки:
блоковые:
А) Разделимые:
- с проверкой на четность;
- корреляционные;
- Хэмминга;
- БЧХ;
Б) Неразделимые:
- с постоянным весом;
- Грея.
2) Корректирующие коды:
Непрерывные:
А) С пороговым декодированием;
Б) По макс. правдоподобия;
В) С последовательным декодированием.
Теперь рассмотрим более подробно каждый вид кодирования.
Код с проверкой на четность.
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
В каждом пакет данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
Пример:
Начальные данные: 1111
Данные после кодирования: 11110 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка [3].
Корреляционные коды (код с удвоением).
Элементы данного кода заменяются двумя символами, единица «1» преобразуется в 10, а ноль «0» в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10) [2].
Код с постоянным весом.
Одним из простейших блочных неразделимых кодов является код с постоянным весом. Примером такого кода может служить семибитный телеграфный код МТК–3, в котором каждая разрешенная кодовая комбинация содержит три единицы и четыре нуля (рис.2). Весом кодовой комбинации называют число содержащихся в ней единиц. В рассматриваемом коде вес кодовых комбинаций равен трем.
Число разрешенных кодовых комбинаций в кодах с постоянным весом определяется как количество сочетаний изnсимволов поgи равно
(1)
Где n–длина кодовой комбинации, аg – вес разрешенной кодовой комбинации. Для кода МТК-3 число разрешенных кодовых комбинаций равно. Таким образом, из общего числа комбинаций
только 35 используются для передачи сообщений[4].
Рис.2. Примеры разрешенных и запрещенных комбинаций кода МТК-3
Инверсный код.
К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
|
k |
r |
n |
|
11011 |
11011 |
1101111011 |
|
11100 |
00011 |
1110000011 |
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
|
1) |
11011 11011 |
|
00000 |
|
|
2) |
11111 00100 |
|
11011 |
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k=5, n=10 и . Коэффициент обнаружения будет составлять
[2].
Код Грея.
По сравнению с простым кодом, код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки из-за помех в канале. Обычно этот код применяется для аналогово-цифрового преобразования непрерывных сообщений.
Недостатком кода Грея является его невесомость, т.е. вес единицы не определяется номером разряда. Информацию в таком виде трудно обрабатывать на ЭВМ. Декодирование кода также связано с большими затратами. Поэтому перед вводом в ЭВМ (или перед декодированием) код Грея преобразуется в простой двоичный код, который удобен для ЭВМ и легко декодируется.
Для перевода простого двоичного кода в код Грея нужно:
- под двоичным числом записать такое же число со сдвигом вправо на один разряд (при этом младший разряд сдвигаемого числа теряется);
- произвести поразрядное сложение двух чисел по модулю 2 (четности). [5].
Таким образом, мы рассмотрели виды помехоустойчивого кодирования и увидели, что их существует не так уж и мало. Каждый код по своему уникален и полезен для кодирования информации. Теперь мы ознакомимся с кодом Хемминга подробнее.
1.2.Характеристика кода Хэмминга при помехоустойчивом кодировании
В середине 40-х годов Ричард Хемминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки,скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машине с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.
Р. Хемминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перегружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день мы знаем как код Хемминга.[6.].
Код Хемминга, как и любой (n,k) код, содержит k информационных и избыточных символов. Избыточная часть кода строится таким образом, чтобы при декодировании можно было бы установить не только факт наличия ошибок в принятой – комбинации, но и указать номер позиции, в которой произошла ошибка. Это достигается за счет многократной проверки принятой комбинации на четность. Каждой проверкой должны охватываться часть информационных символов и один из избыточных символов. При каждой проверке получают двоичный контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное число– 1. В результате всех проверок получается p-разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки достаточно лишь изменить значение данного символа на обратное. [7]
К ним обычно относятся коды с минимальным кодовым расстояниемисправляющие все одиночные ошибки, и коды с расстоянием
исправляющие все одиночные и обнаруживающие все двойные ошибки. Длина кода Хэмминга:
(2)
(r – количество проверочных разрядов).
Характерной особенностью проверочной матрицы кода с является то, что ее столбцы представляют собой любые различные ненулевые комбинации длиной r.Например, при r=4 иn=5 для кода (15,11), проверочная матрица может иметь следующий вид (рис.3)
Рис.3. Проверочная матрица
Перестановкой столбцов, содержащих одну единицу, данную матрицу можно привести к виду(рис.4)
Рис. 4.Измененная матрица
Использование такого кода позволяет исправить любую одиночную ошибку или обнаружить произвольную ошибку кратности два.Если информационные и проверочные разряды кода нумеровать слева направо, то в соответствии с матрицей получаем систему проверочных уравнений, с помощью которых вычисляем проверочные разряды(рис.5):
Рис.5. Система проверочных уравнений
где —
-проверочные разряды;
—
-информационные разряды
Двоичный код Хэмминга с кодовым расстоянием получается путем добавления к коду Хэмминга с
одного проверочного разряда, представляющего собой результат суммирования по модулю два всех разрядов кодового слоя. Длина кода при этом
разрядов, из которых
являются проверочными.
Операция кодирования может выполняться в два этапа. На первом этапе определяется кодовая комбинация с использованием матрицы H, соответствующей коду с на втором — добавляется один проверочный разряд, в котором записывается результат суммирования по модулю два всех разрядов кодового слова, полученного на первом этапе. Операция декодирования также состоит из двух этапов. На первом вычисляется синдром, соответствующий коду на втором — проверяется последнее проверочное соотношение.[8]
Таким образом, ознакомившись с характеристикой кода Хемминга, важно сказать, что состоит код из двух частей и предполагает надежную работу нахождения ошибок и корректировки сообщений.
1.3.Алгоритмы использования кода Хэмминга для нахождения ошибок
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
1.По заданному количеству информационных символов – k, либо информационных комбинаций , используя соотношения:
,
(3)
и (4)
(5)
Вычисляют основные параметры кода m и n.
2.Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону , где i= 1,2,3,…т.е. они равны 1,2,4,8,16,…а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно . В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение – 0, в противном случае – 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n -чисел разрядностью – m (табл. 2, для m = 4) или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до
перечисленных в возрастающем порядке.
Количество разрядов m – определяет количество проверок.
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1,b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку –коэффициенты которые содержат 1 в третьем разряде и т.д.
Таблица 2
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
|
|
3 |
21 |
|
|
1 |
0 |
01 |
|
2 |
0 |
10 |
|
3 |
0 |
11 |
|
4 |
1 |
00 |
|
5 |
1 |
01 |
|
6 |
1 |
10 |
|
7 |
1 |
11 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) – разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.[9]
Вывод к главе 1: Таким образом, мы узнали, что такое помехоустойчивость, помехоустойчивое кодирование, ознакомились с видами помехоустойчивого кодирования. Затем рассмотрели код Хемминга, изучили алгоритм построения кода Хемминга. При построении кода важно знать, что код Хемминга ищет и исправляет одиночную ошибку, но двойную ошибку. В итоге, изучив теоретическую часть, мы выяснили, какие существуют виды помехоустойчивого кодирования. Ознакомились подробнее с кодом Хемминга, изучили его алгоритм кодирования.
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
Существует множество различных примеров для нахождения ошибок при помощи кода Хемминга.
Пример 1. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1) 1111 1011 0010 1100 1101 1100 110
РЕШЕНИЕ. Сообщение состоит из 27 символов, из них 22 информационные, а 5 – контрольные. Это разряды b1 = 1, b2 = 1, b4 = 1, b8 = 1, b16=0. Вычислим число J для обнаружения ошибки: Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… – все числа у которых первый разрядравен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… – все числа, у которых второй разрядравен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23 … – все числа, у которых третий разряд равен1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27 … – все числа, у которых четвертый разрядравен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 … – все числа, у которых пятый разрядравен 1.
Разряды числа J определяются следующим образом:
j1 = b1 +b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
j2=b2+b3+b6+b7+b10+b11+b14+b15+b18+b19+b22+b23+b26+b27= 0
j3 = b4+b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23 = 0
j4 =b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27 = 0,
j5 = b16+ b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27 = 1
то есть число J= =
.
Таким образом, ошибка произошла в семнадцатом разряде переданного числа.[10]. В этом примере мы рассмотрели, как можно обнаружить одиночную ошибку. Далее мы проанализируем пример, как можно найти и исправить эту ошибку.
Пример 2.
Построить код Хемминга для передачи сообщений в виде последовательности десятичных цифр, представленных в виде 4 –х разрядных двоичных слов. Показать процесс кодирования, декодирования и исправления одиночной ошибки на примере информационного слова 0101.
Решение:
1. По заданной длине информационного слова (k = 4 ), определим количество контрольных разрядов m, используя соотношение:
,
при этом т. е. получили (7, 4) -код.
2. Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону .
Для рассматриваемой задачи (при n = 7 ) номера контрольных позиций равны 1, 2, 4. При этом кодовая комбинация имеет вид:
b1 b2 b3 b4 b5 b6 b7
k1 k2 0 k2 1 0 1
3. Определяем значения контрольных разрядов (0 или 1), используя проверочную матрицу (рис.3).
Первая проверка:
k1b3 b5 b7 = k1 011 будет четной при k1 = 0.
Вторая проверка:
k2 b3 b6 b7 = k2 001 будет четной при k2 = 1.
Третья проверка:
k3 b5 b6 b7 = k3 101 будет четной при k3 = 0.
1 2 3 4 5 6 7
Передаваемая кодовая комбинация: 0100101
Допустим принято: 0110101
Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, в соответствии с проверочной матрицей результатом которых является двоичное ( ) – разрядное число, называемое синдромом и указывающим на положение ошибки, т. е, номер ошибочной позиции.
1) k1= b3 b5 b7 = 0111 = 1.
2)k2=b3 b6 b7 = 1101 = 1.
3) k3 =b5 b6 b7 = 0101 =0.
Сравнивая синдром ошибки со столбцами проверочной матрицы, определяем номер ошибочного бита. Синдрому 011 соответствует третий столбец, т. е. ошибка в третьем разряде кодовой комбинации. Символ в третьей позиции необходимо изменить на обратный.
Рассмотрев данные задачи, мы выяснили насколько точно код Хемминга может найти и исправить одиночные ошибки.
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
Для обнаружения двойной ошибки следует только добавить еще один проверочный разряд.
Пример 1:
Принята кодовая комбинация С = 101000001001, произошло
искажение 2-го и 5-го разрядов. Обнаружить ошибки.
Решение.
Значения проверок равны:
k1= b1 b3 b5 b7 b9 b11 = 110010= 1
k2= b2 b3 b6 b7 b10 b11= 010000=1
k3=b4 b5 b6 b7 b12= 00001=1
k4= b8 b9 b10 b11 b12= 01001=0
Тогда контрольное число (синдром) ошибкиравен 0111.
Таким образом, при наличии двукратной ошибки декодирование дает
номер разряда с ошибкой в позиции 7, в то время как ошибки произошли
во 2-м и 5-м разрядах. В этом случае составляется расширенный код
Хэмминга, путем добавления одного проверочного символа.
Пример 2 :
Передана кодовая комбинация «01001011», закодированная кодом Хемминга с d = 4. Показать процесс выявления ошибки.
Решение:
Принята комбинация «01001111»:
а) проверка на общую четность указывает на наличие ошибки (число единиц четное);
б) частные проверки производятся так же, как это было в других примерах.
При составлении проверочных сумм последние единицы кодовых комбинаций (дополнительные контрольные символы) не учитываются.
2. Принята комбинация «01101111»:
а) проверка на общую четность показывает, что ошибка не фиксируется;
б) частные проверки (последний символ отбрасывается)
Первая проверка 0 1 1 1 = 1
Вторая проверка 1 1 1 1 = 0
Третья проверка 0 1 1 1 = 1
Таким образом, частные проверки фиксируют наличие ошибки. Она, якобы, имела место на пятой позиции. Но так как при этом первая проверка на общую четность ошибки не зафиксировала, то значит, имела место двойная ошибка. Исправить двойную ошибку такой код не может [14].
Вывод к главе 2: Таким образом, мы показали, как работает код Хемминга на практике. Мы видим, что при одиночной ошибке ее можно исправить, но для этого нам нужно знать, сколько потребуется контрольных разрядов, а двойную ошибку можно лишь обнаружить.
ЗАКЛЮЧЕНИЕ
Высокие требования к достоверности передачи, обработки и хранения информации диктуют необходимость такого кодированияинформации, при котором обеспечивалось бы возможность обнаружения и исправления ошибок. Широкому применению результатов теории помехоустойчивогокодирования в современных системах связи, обработки и хранения информацииследует считать отсутствие достаточно простых решений сложных теоретических достижений теории помехоустойчивого кодирования.В данной работе исследовано помехоустойчивое кодирование, в частности код Хемминга.
Список литературы
- Вернер М. Основы кодирования[Текст].– М.: Техносфера, 2004. – 288 с.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:https://clck.ru/9cWsc,свободный. Дата обращения: 27.11.2015.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:http://habrahabr.ru/post/111336/, свободный. Дата обращения: 05.12.2015.
- Файловый архив для студентов. Лекция: основные понятия кодирования в ЦСПИ [Электронный ресурс]. – Режим доступа: http://www.studfiles.ru/preview/4087325/,свободный. Дата обращения: 27.11.2015.
- Лекция «Простейшие коды» [Электронный ресурс]. – Режим доступа: http://davaiknam.ru/text/lekciya-3-kodirovanie-informacii-prostejshie-kodi, свободный. Дата обращения: 27.11.2015.
- Академик [Электронный ресурс] – Режим доступа: http://dic.academic.ru/dic.nsf/ruwiki/177544, свободный. Дата обращения: 27.11.2015
- Кузьмин И.В.Основы теории информации и кодирования [Текст]. – Киев,1986. – 237 с.
- Научная библиотека. Код Хемминга [Электронный ресурс]. – Режим доступа: http://info.sernam.ru/book_codb.php?id=28, свободный. Дата обращения: 05.12.2015
- Статья корректирующие коды [Электронный ресурс]. – Режим доступа: http://referatwork.ru/refs/source/ref-11094.html#Текст работы, свободный. Дата обращения: 05.12.2015
- МатБюро- решение задач по высшей математике [Электронный ресурс]. – Режим доступа: http://www.matburo.ru/Examples/Files/Hem2.pdf, свободный. Дата обращения: 06.12.2015.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. [Текст]. – Москва, 1986г. –576 с.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования – методы, алгоритмы, применение. [Текст]. – Москва, 2005г.–320 с.
- Р.Хемминг Теория кодирования и теория информации. / Перевод с английского С.Гальфанда. // [Текст]. – Москва, 1983г. – 176 с.
- Портал студентов «Седьмой бит» [Электронный ресурс]. – Режим доступа: http://www.itmo.ru/work/253/page4, открытый. Дата обращения: 20.12.2015.
Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.
In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
Hamming Code for Single Error Correction
The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.
Encoding a message by Hamming Code
The procedure used by the sender to encode the message encompasses the following steps −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Calculating the values of each redundant bit.
Once the redundant bits are embedded within the message, this is sent to the destination.
Step 1 − Calculation of the number of redundant bits.
If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2r states, 2r must be at least equal to (m + r + 1). Thus the following equation should hold −
2r ≥ 𝑚 + 𝑟 + 1
Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (24 ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.
Step 2 − Positioning the redundant bits.
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r1 (at position 1), r2 (at position 2), r3 (at position 4), r4 (at position  and so on.
and so on.
Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.
The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −
-
Even Parity − Here the total number of bits in the message is made even.
-
Odd Parity − Here the total number of bits in the message is made odd.
Each redundant bit, ri, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the ith position except the position of ri. Thus −
-
r1 is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
-
r2 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
-
r3 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)
Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.
Decoding a message in Hamming Code
Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Parity checking.
-
Step 4 − Error detection and correction
Step 1) Calculation of the number of redundant bits
Using the same formula as in encoding, the number of redundant bits are ascertained.
2r ≥ 𝑚 + 𝑟 + 1
where m is the number of data bits and r is the number of redundant bits.
Step 2) Positioning the redundant bits
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.
Step 3) Parity checking
Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c1, c2, c3, c4 etc. Thus
c1 = parity(1, 3, 5, 7, 9, 11 and so on)
c2 = parity(2, 3, 6, 7, 10, 11 and so on)
c3 = parity(4-7, 12-15, 20-23 and so on)
Step 4) Error detection and correction
The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c1c2c3c4 = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.
Example 4 − Suppose that an incoming message 11110101101 is received.
Step 1 − At first the number of redundant bits are calculated using the formula 2r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2r ≥ 12 is 4.
Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −
c1 = even_parity(1, 3, 5, 7, 9, 11) = 0
c2 = even_parity(2, 3, 6, 7, 10, 11) = 0
c3 = even_parity (4, 5, 6, 7) = 0
c4 = even_parity (8, 9, 10, 11) = 0
Step 4 — Since the value of the check bits c1c2c3c4 = 0000 = 0, there are no errors in this message.
Hamming Code for double error detection
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.
At the receiver’s end, error detection is done as shown in the following table −

