Основные положения теории Шарпа. Коэффициенты регрессии. Измерение ожидаемой доходности и риска портфеля. Дисперсия ошибок. Определение весов ценных бумаг в модели Шарпа. Нахождение оптимального портфеля. Сравнительный анализ методов Г. Марковица и В. Шарпа. [c.335]
Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями. [c.19]
Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров (п дисперсий ошибок регрессии а ) с помощью п наблюдений. [c.161]
Решение. Предположим, что дисперсии ошибок о, связаны уравнением регрессии [c.163]
Вспомним, что наиболее часто употребляемые процедуры устранения гетероскедастичности так или иначе были основаны на предположении, что дисперсия ошибок регрессии ст2 является функцией от каких-то регрессоров. Если а2 существенно зависит от регрессора Z, а при спецификации модели регрессор Z не был включен в модель, стандартные процедуры могут не привести к устранению гетероскедастичности. [c.250]
В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений X должна быть приблизительно равна необъясненной дисперсии для больших значений X, то есть должно быть справедливым следующее равенство [c.125]
Чем ближе к единице отношение / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = Sl / S2 подчиняется F -распределению [c.125]
Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора X и отклика 7. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией. [c.126]
Пятая часть полностью посвящена приложению матричного дифференциального исчисления к линейной регрессионной модели. Она содержит исчерпывающее изложение проблемы оценивания, связанной с неслучайной частью модели при различных предположениях о рангах и других ограничениях. Кроме того, она содержит ряд параграфов, связанных со стохастической частью модели, например оценивание дисперсии ошибок и прогноз ошибок. Включен также небольшой параграф, посвященный анализу чувствительности. Вводная глава содержит необходимые предварительные сведения из теории вероятностей и математической статистики. [c.16]
Дисперсия ошибок прогноза в задаче (3.6) — (3.7) достигает минимума в точке , являющейся основанием перпендикуляра, опущенного из точки т] на подпространство Q, определяемое равенством (3.7). Соотношение (3.10) эквивалентно равенству [c.309]
Ограничение (а) не вызывает претензий. Условие (б) также естественно. Ясно, что механизм сглаживания и прогноза, при котором математическое ожидание или дисперсия ошибок фильтрации или интенсивность искусственного рассеивания достаточно велики, вряд ли рационален и тем более не может быть признан оптимальным. [c.320]
Задача прогнозирования по минимуму дисперсии ошибок при различных статистических характеристиках входных случайных процессов и ошибок измерений подробно обсуждалась в литературе. Имеются и стандартные аналоговые устройства и программы для ЦВМ, реализующие соответствующие схемы. Экстремальная задача, к которой сводится вычисление характеристик генераторов случайных шумов, несомненно, проще исходной вариационной задачи. [c.334]
Матрица корреляции k j R регулируемых ошибок прогноза, оптимального в смысле показателя качества R( k ), может быть получена из корреляционной матрицы kff a ошибок прогноза, оптимальных в смысле минимума дисперсии ошибок в каждой координате в каждый момент времени, по следующей формуле [c.339]
Из (1.14), в частности, следует, что коэффициент корреляции признаков, на которые наложены ошибки измерения, всегда меньше по абсолютной величине, чем коэффициент корреляции исходных признаков. Другими словами, ошибки измерения всегда ослабляют исследуемую корреляционную связь между исходными переменными, и это искажение тем меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих исходных переменных. Формула (1.14) позволяет скорректировать искаженное значение коэффициента корреляции для этого нужно либо знать разрешающие характеристики измерительных приборов (и, следовательно, величины дисперсий ошибок а и а ), либо провести дополнительное исследование по их выявлению. [c.73]
Пример 7.4 ]. Известно, что дисперсия о2, вызванная ошибками измерения, при некоторых видах количественного анализа составляет 0,5. Если заменить измерительный прибор и произвести 10-кратное измерение одного и того же стандартного образца, а затем подсчитать дисперсию, то она составит s2 = 0,25. Может показаться, что дисперсия ошибок измерения изменилась, превысив 5%-ный уровень значимости. Так ли это [c.128]
Теорема Гаусса-Маркова. Оценка дисперсии ошибок сг2 [c.41]
Оценка дисперсии ошибок а2 [c.43]
Формулы (2.11), (2.13) дают дисперсии оценок о, Ь коэффициентов регрессии в том случае, если а2 известно. На практике, как правило, дисперсия ошибок а2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а, Ь. В этом случае вместо дисперсий оценок о, b мы можем получить лишь оценки дисперсий о, 6, заменив а2 на s2 из (2.15) в (2.11), (2.13), (2.14) [c.45]
Распределение оценки дисперсии ошибок s2 [c.47]
Так как оценка дисперсии ошибок s2 является функцией от остатков регрессии et, то для того чтобы доказать независимость s2 и (2,6), достаточно доказать независимость et и (2,6). Оценки 2, 6 так же, как и остатки регрессии et, являются линейными функциями ошибок t (см. (2.4а), (2.46), (2.20)) и поэтому имеют совместное нормальное распределение. Известно (приложение МС, п. 4, N4), что два случайных вектора, имеющие совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость s2 и (а, 6), нам достаточно доказать некоррелированность et и (2,6). [c.48]
Значение Д2 увеличилось по сравнению с первой регрессией. Переход к удельным данным приводит к уменьшению дисперсии ошибок модели. [c.58]
Пусть SML = Y et/ n и OLS — ] et/ (n — 1 — оценки методов максимального правдоподобия и наименьших квадратов для дисперсии ошибок <т2 в классической модели парной регрессии Yt = [c.62]
Оценка дисперсии ошибок а1. Распределение s2 [c.72]
Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]
Тест ранговой корреляции Спирмена использует наиболее общие предположения о зависимости дисперсий ошибок регрессии от значений регрессоров [c.158]
Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности. [c.161]
Наиболее простой и часто употребляемый тест на гетероске-дастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е. [c.161]
Другим недостатком тестов Уайта и Глейзера является то, что факт невыявления ими гетероскедастичности, вообще говоря, не означает ее отсутствия. В самом деле, принимая гипотезу Щ, мы принимаем лишь тот факт, что отсутствует определенного вида зависимость дисперсий ошибок регрессии от значений регрессоров. [c.166]
Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить. [c.57]
Доказано (см., например, [37]), что приведенную задачу оптимального стохастического управления можно разделить на две задачу сглаживания и лрогноза по минимуму дисперсии ошибок и задачу оптимального детерминированного управления. При более сложном критерии качества управления и при дополнительных ограничениях на переменные состояния и управляющие параметры такое разделение не всегда удается я, его, по-видимому, не всегда целесообразно производить. [c.44]
Здесь Paaa(tt, » ) — система функций веса, минимизирующих дисперсию ошибок За(/г-) прогноза W (ti, т) — тождественно не равные нулю функ-22 339 [c.339]
В ходе анализа финансовых данных любой ряд динамики, будь то процентные ставки или цены на финансовые активы, можно разбить на две компоненты, одна из которых изменяется случайным образом, а другая подчиняется определенному закону. Колебания финансовых переменных значительно изменяются во времени бурные периоды с высокой волатильностью переменных сменяют спокойные периоды и наоборот. В некоторых случаях вола-тильность играет ключевую роль в ценообразовании на финансовые активы. В частности, курсы акций напрямую зависят от ожидаемой волатильности доходов корпораций. Все финансовые учреждения без исключения стремятся адекватно оценить волатильность в целях успешного управления рисками. В свое время Трюгве Хаавельмо, нобелевский лауреат по экономике 1989 г., предложил рассматривать изменение экономических переменных как однородный стохастический (случайный) процесс. Вплоть до 1980-х гг. экономисты для анализа финансовых рынков применяли статистические методы, предполагавшие постоянную волатильность во времени. В 1982 г. Роберт Ингл развил новую эконометрическую концепцию, позволяющую анализировать периоды с разной волатильностью. Он ввел кластеризацию данных и условную дисперсию ошибок, которая завесит от времени. Свою разработку Ингл назвал авторегрессионной гетероскедастической моделью , с ее помощью можно точно описать множество временных рядов, встречающихся в экономике. Метод Ингла сегодня применяется финансовыми аналитиками в целях оценки финансовых активов и портфельных рисков. [c.197]
Отметим, что оценки максимального правдоподобия параметров а, 6 совпадают с оценками метода наименьших квадратов OML = SOLS, ML OLS- Это легко видеть из того, что уравнения (2.37а) и (2.376) совпадают с соответствующими уравнениями метода наименьших квадратов (2.2). Оценка максимального правдоподобия для <т2 не совпадает с
несмещенной оценкой дисперсии ошибок. Таким образом, с = ((п — 2)/n)<7OLS является смещенной, но тем не менее состоятельной оценкой <т2. [c.57]
В этом разделе мы рассмотрим частный случай обобщенной регрессионной модели, а именно, модель с гетероскедастичностъю, Это означает, что ошибки некоррелированы, но имеют непостоянные дисперсии. (Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной.) Как уже отмечалось, Гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых. [c.168]
При проведении регрессионного анализа, основанного на методе наименьших квадратов, на практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Как мы отмечали ранее, свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса− Маркова), т. к. при их нарушении МНК может давать оценки с плохими статистическими свойствами. При этом существуют другие методы определения более точных оценок. Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений (см. параграф 5.1, предпосылка 20):
дисперсия случайных отклонений εi постоянна. D(εi)=D(εj) = σ2 для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастич-
ностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
В данной главе мы подробно проанализируем суть гетероскедастичности, ее причины и последствия, а также приведем несколько способов смягчения этих последствий.
8.1. Суть гетероскедастичности
При рассмотрении выборочных данных требование постоянства дисперсии случайных отклонений может вызвать определенное недоумение в силу того, что при каждом i-м наблюдении имеется единственное значение εi. Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной yi и соответственно c определенными случайными отклонениями εi, i = 1, 2, …, n. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую
209
ошибку (отклонение) при одних наблюдениях и меньшую − при других.
Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений εi при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми − при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
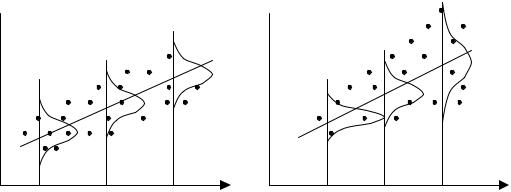
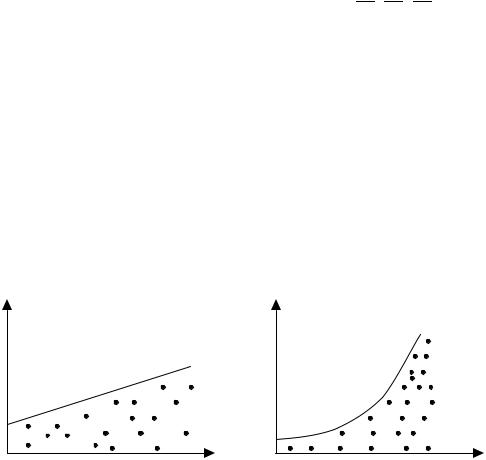
На рис. 8.1 приведены два примера линейной регрессии − зависимости потребления С от дохода I: C = β0 + β1I + ε.
C C
C
|
I1 |
Ik |
In |
I |
I1 |
Ik |
In |
I |
|
а |
б |
Рис. 8.1
В обоих случаях с ростом дохода растет среднее значение потребления. Но если на рис. 8.1, а дисперсия потребления остается одной и той же для различных уровней дохода, то на рис. 8.1, б при аналогичной зависимости среднего потребления от дохода дисперсия потребления не остается постоянной, а увеличивается с ростом дохода. Фактически это означает, что во втором случае субъекты с большим доходом в среднем потребляют больше, чем субъекты с меньшим доходом, и, кроме того, разброс в их потреблении более существенен для большего уровня дохода. Фактически люди с большими доходами имеют больший простор для распределения своего дохода. Реалистичность данной ситуации не вызывает сомнений. Разброс значений потребления вызывает разброс точек наблюдения относительно линии регрессии, что и определяет дисперсию случайных отклонений. Динамика изменения дисперсий (распределений) отклонений для данного примера проиллюстрирована на рис. 8.2. При гомоскедастичности
210
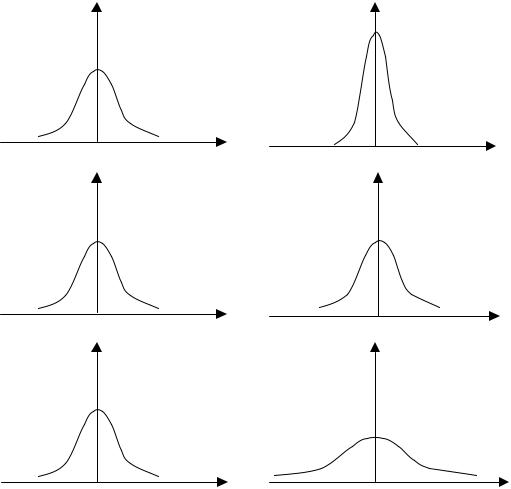
(рис. 8.2, а) дисперсии εi постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии εi изменяются (в нашем примере − увеличиваются).
|
а − гомоскедастичность |
б − гетероскедастичность |
|
Рис. 8.2 |
Проблема гетероскедастичности в большей степени характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Это можно объяснить следующим образом. При перекрестных данных учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли, страны и т. п.), имеющие различные доходы, размеры, потребности и т. д. Но в этом случае возможны проблемы, связанные с эффектом масштаба. Во временных рядах обычно рассматриваются одни и те же показатели в различные моменты времени (например, ВНП, чистый экспорт, темпы инфляции
211
и т. д. в определенном регионе за определенный период времени). Однако при увеличении (уменьшении) рассматриваемых показателей с течением времени может возникнуть проблема гетероскедастичности.
8.2. Последствия гетероскедастичности
Как отмечалось в разделе 5.1, при рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки (BLUE-оценки) лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность): σ2(εi) = σ2 для всех наблюдений i, i = 1, 2, …, n.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими.
1.Оценки коэффициентов по-прежнему остаются несмещенными и линейными.
2.Оценки не будут эффективными (т. е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3.Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что необъясненная уравнением
|
2 |
∑ ei2 |
|||
|
регрессии дисперсия S |
= |
(m − число объясняющих пере- |
||
|
n − m − 1 |
менных), которая используется при вычислении оценок дисперсий всех коэффициентов (см. параграф 6.2, (6.23)), не является более несмещенной.
4.Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися.
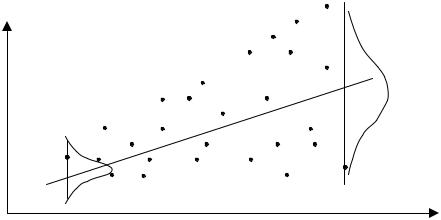
Причину неэффективности оценок МНК при гетероскедастичности легко пояснить следующим примером парной регрессии.
212
y
Из рис. 8.3 видно, что для каждого конкретного значения хi СВ Х переменная Y принимает значение уi из некоторого множества, имеющего свое распределение, отличное одно от другого в силу непостоянства дисперсий (сравните распределения для значений у1 и уn).
По МНК минимизируется сумма квадратов отклонений
∑ei2 = ∑(yi − b0 − b1xi )2.
Но в этом случае каждое конкретное значение ei2 в данной сумме имеет одинаковый “вес” вне зависимости от того, получено оно из распределения с маленькой дисперсией (например, e12 ) или с большой (например, e2n ). Но это противоречит логике, т. к. точка, полученная
из распределения с меньшей дисперсией, более точно определяет направление линии регрессии. Поэтому она должна иметь больший “вес”, чем точка из распределения с большей дисперсией. Следовательно, методы оценивания, учитывающие “веса” точек наблюдений, позволяют получать более точные (эффективные) оценки. Учет “весов” точек характерен, например, для метода взвешенных наименьших квадратов, рассмотренного ниже.
8.3.Обнаружение гетероскедастичности
Вряде случаев на базе знаний характера данных появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.
213
Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, т. к. для знания дисперсий отклонений σ2(еi) необходимо знать распределение СВ Y, соответствующее выбранному значению хi СВ Х. На практике зачастую для каждого конкретного значения хi определяется единственное значение уi , что не позволяет оценить дисперсию СВ Y для данного хi .
Естественно, не существует какого-либо однозначного метода определения гетероскедастичности. Однако к настоящему времени для такой проверки разработано довольно большое число тестов и критериев для них. Рассмотрим наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелда−Квандта.
8.3.1. Графический анализ остатков
Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладывается объясняющая переменная Х (либо линейная комбинация объясняющих переменных Y = b0 + b1X1 + … +
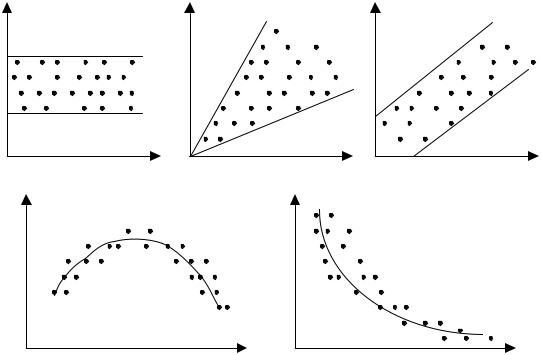
+ bmXm), а по оси ординат либо отклонения еi, либо их квадраты ei2 . Примеры таких графиков приведены на рис. 8.4.
|
а |
xi |
б |
xi |
xi |
|
в |
||||
|
ei2 |
ei2 |
214
На рис. 8.4, а все отклонения ei2 находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит о независимости дисперсий ei2 от значений переменной Х и их постоянстве, т.е. в этом случае мы находимся в условиях гомоскедастичности.
На рис. 8.4, б − г наблюдаются некие систематические изменения в соотношениях между значениями xi переменной Х и квадратами от-
клонений ei2 . Рис. 8.4, б соответствует примеру из параграфа 8.1. На
рис. 8.4, в отражена линейная; 8.4, г − квадратичная; 8.4, д − гиперболическая зависимости между квадратами отклонений и значениями объясняющей переменной Х. Другими словами, ситуации, представленные на рис. 8.4, б − д, отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.
Отметим, что графический анализ отклонений является удобным и достаточно надежным в случае парной регрессии. При множественной регрессии графический анализ возможен для каждой из объясняющих переменных Хj , j = 1, 2, …, m отдельно. Чаще же вместо объясняющих переменных Хj по оси абсцисс откладывают значения yi ,
получаемые из эмпирического уравнения регрессии. Поскольку по уравнению множественной линейной регрессии yi является линейной
комбинацией хij , j = 1, 2, … , m, то график, отражающий зависимость ei2 от yi , может указать на наличие гетероскедастичности аналогично
ситуациям на рис. 8.4, б − д. Такой анализ наиболее целесообразен при большом количестве объясняющих переменных.
8.3.2. Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значения Х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений еi и значения хi СВ Х будут коррелированы. Значения хi и еi ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
|
rx,e = 1− 6 |
∑di2 |
, |
(8.1) |
|
|
n(n2 |
−1) |
|||
где di − разность между рангами хi и ei , i = 1, 2, … , n; n − число наблюдений.
Например, если х20 является 25-м по величине среди всех наблюдений Х; а е20 − является 32-м, то di = 25 − 32= −7.
215
Доказано, что если коэффициент корреляции ρх,е для генеральной совокупности равен нулю, то статистика
|
t = |
rx,e n − 2 |
(8.2) |
|
|
1 − r2 |
|||
|
x,e |
имеет распределение Стьюдента с числом степеней свободы ν = n − 2. Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле (8.2), превышает tкр. = tα,n−2 (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции ρх,е, а следовательно, и об отсутствии гетероскедастичности. В противном
случае гипотеза об отсутствии гетероскедастичности принимается. Если в модели регрессии больше чем одна объясняющая пере-
менная, то проверка гипотезы может осуществляться с помощью t- статистики для каждой из них отдельно.
8.3.3. Тест Парка
Р. Парк предложил критерий определения гетероскедастичности, дополняющий графический метод некоторыми формальными зависимостями. Предполагается, что дисперсия σi2 = σ2(ei ) является функцией i-го значения хi объясняющей переменной. Парк предложил следующую функциональную зависимость
|
уi2 = у2xвi ev i . |
(8.3) |
|
Прологарифмировав (8.4), получим: |
|
|
lnуi2 = lnу2 + вlnxi + vi . |
(8.4) |
Так как дисперсии уi2 обычно неизвестны, то их заменяют оценками квадратов отклонений ei2 .
|
Критерий Парка включает следующие этапы: |
||
|
1. |
Строится уравнение регрессии yi = b0 + b1xi + еi. |
|
|
2. |
Для каждого наблюдения определяются lnei2 |
) |
|
= ln(yi − yi )2 . |
||
|
3. |
Строится регрессия |
|
|
ln ei2 = α + βlnxi + vi , |
(8.5) |
|
|
где α = lnσ2. |
В случае множественной регрессии зависимость (8.5) строится для каждой объясняющей переменной.
216

4. Проверяется статистическая значимость коэффициента β уравнения
(8.5) на основе t-статистики t = в . Если коэффициент β статисти- Sв
чески значим, то это означает наличие связи между lnei2 и lnxi, т. е. гетероскедастичности в статистических данных.
Отметим, что использование в критерии Парка конкретной функциональной зависимости (8.5) может привести к необоснованным выводам (например, коэффициент β статистически незначим, а гетероскедастичность имеет место). Возможна еще одна проблема. Для случайного отклонения vi в свою очередь может иметь место гетероскедастичность. Поэтому критерий Парка дополняется другими тестами.
8.3.4. Тест Глейзера
Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно, более подходящих) зависимостей между дисперсиями отклонений σi и значениями переменной хi. По данному методу оценивается регрессионная зависимость модулей отклонений ei (тесно связанных с σi2) от хi. При этом рассматриваемая зависимость моделируется следующим уравнением регрессии:
|
| ei |= α + βхik + vi . |
(8.6) |
Изменяя значения k, можно построить различные регрессии. Обычно k = …, −1, −0.5, 0.5, 1, … Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий (8.6) коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.
Отметим, что так же, как и в тесте Парка, в тесте Глейзера для отклонений vi может нарушаться условие гомоскедастичности. Однако во многих случаях предложенные модели являются достаточно хорошими для определения гетероскедастичности.
8.3.5.Тест Голдфелда−Квандта
Вданном случае также предполагается, что стандартное отклонение σi = σ(εi) пропорционально значению хi переменной Х в этом
наблюдении, т. е. уi2 = у2 xi2 . Предполагается, что εi имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда−Квандта состоит в следующем:
217
1.Все n наблюдений упорядочиваются по величине Х.
2.Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (n − 2k), k соответственно.
3.Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий от-
клонений значениям Х верно, то дисперсия регрессии (сумма квад-
k
ратов отклонений S1 = ∑ei2 ) по первой подвыборке будет сущест-
i=1
венно меньше дисперсии регрессии (суммы квадратов отклонений
n
S3 = ∑ei2 ) по третьей подвыборке.
i=n-k
4.Для сравнения соответствующих дисперсий строится следующая F-статистика:
|
F = |
S3/(k − m − 1) |
= |
S3 . |
(8.7) |
|
S /(k − m − 1) |
S |
|||
|
1 |
1 |
Здесь (k − m − 1) − число степеней свободы соответствующих выборочных дисперсий (m − количество объясняющих переменных в уравнении регрессии).
При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν1 = ν2 = k − m − 1.
|
5. Если Fнабл.= |
S3 |
> Fкр.= F |
, то гипотеза об отсутствии гетероскеда- |
|
|
S1 |
б;н ;н |
|||
|
1 |
2 |
|||
стичности отклоняется (здесь α − выбранный уровень значимости).
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с σi. При этом k должно быть больше, чем (m + 1). Если нет уверенности относительно выбора переменной Xj, то данный тест может осуществляться для каждой из объясняющих переменных.
Этот же тест может быть использован при предположении об обратной пропорциональности между σi и значениями объясняющей переменной. При этом статистика Фишера примет вид: F = S1/S3.
218
8.4. Методы смягчения проблемы гетероскедастичности
Как отмечалось в разделе 8.2, гетероскедастичность приводит к неэффективности оценок, несмотря на их несмещенность. Это может привести к необоснованным выводам по качеству модели. Поэтому при установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии σi2 отклонений εi .
8.4.1. Метод взвешенных наименьших квадратов (ВНК)
Данный метод применяется при известных для каждого наблюдения значениях σi2. В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. В этом суть метода взвешенных наименьших квадратов.
Для простоты изложения опишем ВНК на примере парной ре-
|
грессии: |
||||||||||||||||
|
yi = β0 + β1xi + εi . |
(8.8) |
|||||||||||||||
|
Разделим обе части (9.7) на известное σi |
= |
уi2 |
: |
|||||||||||||
|
yi |
= в0 |
1 |
+ в1 |
xi + |
еi |
. |
(8.9) |
|||||||||
|
уi |
уi |
уi |
||||||||||||||
|
уi |
||||||||||||||||
|
Положив |
yi |
= уi* , |
xi |
= |
xi*, |
ei |
= vi, |
1 |
= zi, получим уравнение |
|||||||
|
уi |
||||||||||||||||
|
уi |
уi |
уi |
регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с “преобразованным” отклонением v:
|
уi* =β0zi + β1xi* + vi. |
(8.10) |
При этом для vi выполняется условие гомоскедастичности. Действительно,
уi2 (vi ) = M(vi − M(vi ))2 = M(vi2 ) − M2 (vi ) .
|
Так как по предпосылке 10 МНК M(ei) = 0, то M(vi ) = |
1 |
M(ei ) = 0, и |
||||||||
|
уi2 |
||||||||||
|
тогда уi2 (vi ) = M(vi2 ) = |
||||||||||
|
= M( |
ei2 |
) = |
1 |
M(ei2 ) = |
1 |
M(ei − M(ei ))2 = |
1 |
уi2 = 1 = const. |
||
|
уi2 |
уi2 |
|||||||||
|
уi2 |
уi2 |
219
Следовательно, для преобразованной модели (8.10) выполняются предпосылки 10 − 50 МНК. В этом случае оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.
Таким образом, метод взвешенных наименьших квадратов включает следующие этапы:
1.Каждую из пар наблюдений (хi , уi) делят на известную величину σi . Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие “веса”, а с максимальными дисперсиями − наименьшие “веса”. Действительно, наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с большими дисперсиями. Учет этого факта увеличивает вероятность получения более точных оценок.
1 2. По МНК для преобразованных значений
уi
уравнение регрессии без свободного члена с гарантированными качествами оценок.
8.4.2. Дисперсии отклонений не известны
Для применения ВНК необходимо знать фактические значения дисперсий уi2 отклонений. На практике такие значения известны крайне редко. Следовательно, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях уi2 .
Например, может оказаться целесообразным предположить, что дисперсии уi2 отклонений εi пропорциональны значениям хi (рис.8.5, а) или значениям хi2 (рис. 8.5, б).
Рис. 8.5
1. Дисперсии σ i2 пропорциональны хi (рис. 8.5, а).
уi2 = σ2 хi (σ2 − коэффициент пропорциональности).
220
Тогда уравнение (8.9) преобразуется делением его левой и правой частей на xi :
|
yi |
= |
a |
+ b |
xi |
+ |
ei |
yi = a |
1 + b xi + vi . |
(8.11) |
|||
|
xi |
||||||||||||
|
xi |
xi |
xi |
xi |
xi |
||||||||
|
Несложно показать, что для случайных отклонений vi = |
ei |
выпол- |
||||||||||
|
xi |
||||||||||||
няется условие гомоскедастичности. Следовательно, для регрессии (8.11) применим обычный МНК. Действительно, в силу выполнимо-
сти предпосылки уi2 = σ2 (εi) = σ2 хi имеем:
|
у2 (vi ) = у2 ( |
еi |
) = |
1 у2 (еi ) = |
1 у2 xi = у2 = const. |
|
xi |
xi |
xi |
Таким образом, оценив для (8.11) по МНК коэффициенты β0 и β1, затем возвращаются к исходному уравнению регрессии (8.8).
Если в уравнении регрессии присутствует несколько объясняющих переменных, можно поступить следующим образом. Вместо кон-
кретной объясняющей переменной Xj используетсяY исходного уравнения множественной линейной регрессии Y = b0 + b1X1 + … + bmXm ,
т. е. фактически линейная комбинация объясняющих переменных. В этом случае получают следующую регрессию:
|
yi |
1 |
xi1 |
xim |
еi |
||||||
|
= в0 |
) |
+ в1 |
) |
+ … + вm |
) |
+ |
. |
(8.12) |
||
|
) |
) |
|||||||||
|
yi |
yi |
yi |
yi |
yi |
Иногда из всех объясняющих переменных выбирается наиболее подходящая, исходя из графического представления (рис. 8.4).
2. Дисперсия σi2 пропорциональна хi2 (рис. 8.4, б).
В случае, если зависимость σi2 от хi целесообразнее выразить не линейной функцией, а квадратичной, то соответствующим преобразованием будет деление уравнения регрессии (8.8) на хi:
|
yi |
= в0 |
1 |
+ в1 + |
еi |
yi |
= в0 |
1 |
+ в1 + vi |
, где vi = |
еi |
. (8.13) |
|
|
xi |
xi |
|||||||||||
|
xi |
xi |
xi |
xi |
По аналогии с вышеизложенным несложно показать, что для отклонений vi будет выполняться условие гомоскедастичности. После определения по МНК оценок коэффициентов β0 и β1 для уравнения (8.13) возвращаются к исходному уравнению (8.8).
221
Отметим, что для применения описанных выше преобразований существенную роль играют знания об истинных значениях дисперсий отклонений σi2, либо предположения, какими эти дисперсии могут быть. Во многих случаях дисперсии отклонений зависят не от включенных в уравнение регрессии объясняющих переменных, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. В этом случае они должны быть включены в модель. В ряде случаев для устранения гетероскедастичности необходимо изменить спецификацию модели (например, линейную на логлинейную, мультипликативную на аддитивную и т. п.).
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности — достаточно трудоемкая проблема и для ее решения разработано несколько методов (тестов). В случае установления наличия гетероскедастичности ее корректировка также представляет довольно серьезную проблему. Одним из возможных решений является метод взвешенных наименьших квадратов (при этом необходима определенная информация либо обоснованные предположения о величинах дисперсий отклонений). На практике имеет смысл попробовать несколько методов определения гетероскедастичности и способов ее корректировки (преобразований, стабилизирующих дисперсию).
Вопросы для самопроверки
1.В чем суть гетероскедастичности?
2.Какое из следующих утверждений верно, ложно или не определено:
а) вследствие гетероскедастичности оценки перестают быть эффективными и состоятельными; б) оценки и дисперсии оценок остаются несмещенными;
в) выводы по t- и F-статистикам являются ненадежными;
г) при наличии гетероскедастичности стандартные ошибки оценок будут заниженными; д) гетероскедастичность проявляется через низкое значение статистики Дар-
бина−Уотсона DW;
е) не существует общего теста для анализа гетероскедастичности;
ж) тест ранговой корреляции Спирмена основан на использовании t- статистики; з) тест Парка является частным случаем теста Глейзера;
и) использование метода взвешенных наименьших квадратов носит ограниченный характер, т. к. для его использования необходимо знать дисперсии отклонений;
222
к) если в парной регрессии дисперсия случайных отклонений пропорциональна величине объясняющей переменной (х), то для получения эффективных оценок необходимо все наблюдаемые значения поделить на х.
3.Приведите аргументы в пользу графического теста, теста Парка и теста Глейзера.
4.Приведите схему теста Голдфелда−Квандта.
5.В чем суть метода взвешенных наименьших квадратов (ВНК)?
6.Объясните кратко, почему при наличии гетероскедастичности ВНК позволяет получить более эффективные оценки, чем обычный МНК.
7.Есть основание считать, что в регрессии, построенной по квартальным данным, случайные отклонения в первых кварталах больше, нежели отклонения в других кварталах. Как это можно проверить?
Упражнения и задачи
1.Пусть зависимость заработной платы (Y) от стажа работы (X) сотрудника выражена следующим уравнением регрессии:
Y = β0 + β1X + γD + ε,
где D − фиктивная переменная, отражающая пол сотрудника. Как можно проверить предположение о том, что пол сотрудника не влияет на дисперсию случайных отклонений εi?
2.Приведены данные в условных единицах по доходам (Х) и расходам на непродовольственные товары (Y) для тридцати домохозяйств:
|
X |
26.2 |
33.1 |
42.5 |
47.0 |
48.5 |
49.0 |
49.1 |
50.9 |
52.4 |
53.2 |
|
|
Y |
10.0 |
11.2 |
15.0 |
20.5 |
21.2 |
19.5 |
23.0 |
19.0 |
19.5 |
18.0 |
|
|
Х |
54.0 |
54.8 |
59.0 |
61.3 |
62.5 |
63.1 |
64.0 |
66.2 |
70.0 |
71.5 |
|
|
Y |
24.5 |
21.5 |
35.4 |
25.0 |
17.3 |
21.6 |
15.3 |
32.6 |
34.0 |
23.8 |
|
|
Х |
73.2 |
75.4 |
76.0 |
80.6 |
81.2 |
83.3 |
92.0 |
95.5 |
103.2 |
110.4 |
|
|
Y |
22.5 |
27.4 |
40.0 |
23.5 |
20.0 |
40.1 |
15.5 |
39.0 |
47.4 |
21.3 |
а) Определите по МНК оценки парного уравнения регрессии yi = b0+ b1xi+ ei. б) Оцените качество построенного уравнения.
в) Проведите графический анализ остатков.
г) Примените для указанных статистических данных ВНК предположение,
что σ2(ei) = σ2xi2.
д) Примените к полученным в п. а) результатам тест ранговой корреляции Спирмена и тест Парка.
е) Определите, существенно ли повлияла гетероскедастичность на качество оценок в уравнении, построенном по МНК.
223
|
3. |
Для предприятий некоторой отрасли анализируют зависимость заработной |
||||||||
|
платы (Y) сотрудников в зависимости от масштаба (от количества сотрудни- |
|||||||||
|
ков) предприятия (Х). Наблюдения по тридцати случайно отобранным пред- |
|||||||||
|
приятиям представлены следующей таблицей: |
|||||||||
|
Y |
X |
||||||||
|
75.5 |
75.5 |
77.5 |
78.5 |
80.0 |
81.0 |
100 |
|||
|
80.5 |
82.0 |
84.5 |
85.0 |
85.5 |
86.5 |
200 |
|||
|
85.5 |
88.5 |
90.0 |
91.0 |
95.0 |
96.0 |
300 |
|||
|
93.0 |
93.5 |
97.5 |
99.0 |
102.5 |
105.0 |
400 |
|||
|
102.0 |
105.5 |
107.0 |
110.5 |
115.0 |
118.5 |
500 |
а) Постройте уравнение регрессии Y на Х и оцените его качество.
б) Можно ли ожидать наличие гетероскедастичности в данном случае. Ответ поясните.
в) Проверьте наличие гетероскедастичности, используя тест Голдфелда− Квандта. Рекомендуется использовать разбиение, при котором k = 12.
г) Если предположить, что гетероскедастичность имеет место, и дисперсии отклонений пропорциональны значениям Х, то какое преобразование вы предложите, чтобы получить несмещенные, эффективные и состоятельные оценки.
д) Постройте новое уравнение регрессии на основе преобразования, осуществленного в предыдущем пункте, и оцените его качество.
е) Сравните результаты, полученные в пунктах а) и д).
4. Пусть для эмпирического уравнения парной регрессии Y = b0 + b1X + e име-
ет место следующее соотношение M(ei2) = σ2xi. Какое преобразование можно предложить, чтобы устранить проблему гетероскедастичности. Опишите поэтапно предложенную схему.
5. Пусть для регрессии Y = b0 + b1X1 + b2X2 + e, оцениваемой по ежегодным данным (1971−1998), получены следующие результаты: сумма квадратов от-
клонений для данных 1971−1980 гг. равна S1 = ∑ei2 = 15, для данных 1981−
1998 гг. эта сумма равна S2 = ∑ei2 = 50. С помощью теста Голдфелда−Квандта проверьте предположение о том, что дисперсия отклонений не постоянна (в частности, что дисперсия претерпела изменение где-то в 1981 г.).
6. Анализируется объем инвестиций для вымышленной страны. По данным с 1961 по 1990 г. построены два уравнения регрессии:
|
1) |
it = |
52.5 + 0.275gnpt |
− 0.63ct , |
R2 = 0.98. |
|||||||
|
(t) = (12.5) (10.2) |
(6.4) |
||||||||||
|
2) |
it |
= 50.7 |
1 |
+ |
0.27 − |
0.62 |
ct |
, |
|||
|
gnpt |
gnpt |
gnpt |
|||||||||
|
R2 = 0.87, |
|||||||||||
|
(t) |
(13.3) |
(9.3) |
(6.9) |
224
где GNP − валовой национальный продукт; С − совокупное частное потребление; I − объем инвестиций; gnpt, ct, it − значения соответствующих показателей в момент времени t.
а) Что могло послужить причиной преобразования первого уравнения во второе?
б) Если причиной преобразования являлась гетероскедастичность, то какое предположение о дисперсии отклонений являлось основанием для данного преобразования?
в) Можно ли сравнить качества обоих уравнений на основе коэффициентов детерминации? Ответ поясните.
г) Должно ли преобразованное уравнение проходить через начало координат?
7.Выдвигается предположение, что средняя заработная плата наемных рабочих пропорциональна их стажу. Для анализа данного утверждения обследуются по 20 рабочих восьми категорий стажа. Получены следующие статистические данные:
|
Стаж |
[0, 5) [5, 10) [10, 15) [15, 20) [20, 25) [25, 30) [30, 35) [35, 40] |
|
З/п |
10000 12500 14300 18700 25400 29000 32000 34300 |
а) Постройте эмпирическое уравнение регрессии, в котором заработная плата является зависимой переменной, а стаж работы − объясняющей переменной (уравнение строится в предположение, что дисперсии отклонений постоянны).
б) Оцените качество построенной регрессии.
в) Есть ли основания считать, что для данной регрессионной модели весьма вероятна гетероскедастичность? Если да, то почему?
г) Предполагая, что дисперсия отклонений пропорциональна трудовому стажу, постройте на основании тех же данных уравнение по методу взвешенных наименьших квадратов (ВНК).
д) Предполагая, что дисперсия отклонений пропорциональна квадрату величины трудового стажа, постройте по ВНК соответствующее уравнение регрессии.
е) Какое из трех предположений относительно дисперсии отклонений наиболее реалистично с вашей точки зрения?
8.Исследуется зависимость между доходом (Х) домохозяйства и его расходом
(Y) на продукты питания. Выборочные данные по 40 домохозяйствам представлены ниже.
|
X |
25.5 |
26.5 |
27.2 |
29.6 |
35.7 |
38.6 |
39.0 |
39.3 |
40.0 |
41.9 |
42.5 |
44.2 |
44.8 |
45.5 |
|
Y |
14.5 |
11.3 |
14.7 |
10.2 |
13.5 |
9.9 |
12.4 |
8.6 |
10.3 |
13.9 |
14.9 |
11.6 |
21.5 |
10.8 |
|
Х |
45.5 |
48.3 |
49.5 |
52.3 |
55.7 |
59.0 |
61.0 |
61.7 |
62.5 |
64.7 |
69.7 |
71.2 |
73.8 |
74.7 |
|
Y |
13.8 |
16.0 |
18.2 |
19.1 16.3 |
17.5 |
10.9 |
16.1 |
10.5 |
10.6 |
29.0 |
8.2 |
14.3 |
21.8 |
225

Х 75.8 76.9 79.2 81.5 82.4 82.8 83.0 85.9 86.4 86.9 88.3 89.0
Y 26.1 20.0 19.8 21.2 29.0 17.3 23.5 22.0 18.3 13.7 14.5 27.3
а) Постройте эмпирическое уравнение регрессии Y на Х. б) Вычислите отклонения ei.
в) Проведите анализ модели на гетероскедастичность по тесту ранговой корреляции Спирмена.
г) Проведите графический анализ отклонений и выдвиньте предположение о зависимости дисперсии отклонений от значений Х.
д) На основании предыдущего пункта постройте новое уравнение регрессии, используя для этого ВНК.
9.Проводится анализ зависимости средней заработной платы от средней производительности на предприятиях различного масштаба. Проведенное обследование нашло отражение в следующей таблице.
|
Количество сотрудников |
Средняя |
Средняя |
Стандартное |
|
|
предприятия, |
производительность, |
з/п, |
отклонение з/п, |
|
|
n |
X ($) |
Y ($) |
σi ($) |
|
|
1 |
− 4 |
9320 |
3320 |
740 |
|
4 |
− 9 |
8630 |
3640 |
850 |
|
10 |
− 19 |
8050 |
3900 |
730 |
|
20 |
− 49 |
8320 |
4120 |
820 |
|
50 |
− 99 |
8600 |
4090 |
950 |
|
100 |
− 199 |
9120 |
4200 |
1100 |
|
200 |
− 499 |
9540 |
4380 |
1250 |
|
500 |
− 999 |
9730 |
4500 |
1290 |
|
1000 |
− 1999 |
10120 |
4610 |
1350 |
|
2000 |
− 4999 |
10740 |
4800 |
1100 |
|
> 5000 |
11200 |
5000 |
1520 |
а) Постройте уравнение регрессии yi МНК.
б) Постройте уравнение регрессии yi
уi
= b0 + b1xi + ei, используя обычный
|
= b |
1 |
+ b xi |
+ |
ei |
. |
|
|
уi |
||||||
|
0 |
1 уi |
уi |
в) Сравните полученные результаты. Какое из уравнений вы предпочтете и почему?
226
Соседние файлы в папке ЭКОНОМЕТРИКА и математическая экономика
- #
- #
- #
- #
- #
- #
20.04.20152.55 Mб68Кобелев Н.Б. Практика применения экономико-математических методов и моделей. 2000.djvu
- #
- #
Обновлено: 23.06.2023
Тема. ГетероскедастичностьТеоретическая часть
Гетероскедастичность — понятие, означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.
В связи с этимтестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей
В соответствии с одной из предпосылок МНК нужно, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора X остатки е, имеют одну и ту же дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.
ПоследствиягетероскедастичностиПри гетероскедастичности последствия применения МНК будут следующими:
Оценки коэффициентов по-прежнему останутся несмещенными и линейными.
Оценки не будут эффективными (не будут иметь наименьшую дисперсию по сравнению с другими оценками такого же параметра). При увеличении дисперсии оценок снижается вероятность получения максимально точных оценок.
Дисперсии оценок будут рассчитываться со смещением.
Вследствиетого, что было сказано выше, все выводы, получаемые на основе соответствующих t- и F-статистик (критериев Стьюедента и Фишера), а также интервальные оценки будут ненадежными. Значит, статистические выводы, которые получаются при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным выводам по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будутзанижены, следовательно, t-статистики будут завышены. Это может приводить к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющихся.
Определение гетероскедастичностиДля определения гетероскедастичности разработаны несколько тестов и критериев:
Тест ранговой корреляции СпирменаТест Голдфелда-КвандтаТест Парка
Тест ГлайзераТест Уайта
Тест СпирменаПри использовании тестаСпирмена предполагается, что дисперсия отклонения будет или увеличиваться, или уменьшаться с увеличением значений X. Поэтому для регрессии, построенной по методу наименьших квадратах, абсолютные величины отклонений ei и значения xi объясняющей переменной X будут коррелированы. Значения xi и ei ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
Где: di —разность между рангами xi и |ei|, i = 1,…, n ;
6 — число шесть (иногда думают, что это стандартное отклонение).
Доказано, что если коэффициент корреляции ρx,|e| для генеральной совокупности равен нулю, то статистика:
имеет t-распределение Стьюдента с числом степеней свободы v = n — 2.
Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле представленной выше, превышает tкр =tα/2,n-2 (определяется по таблице критических значений распределения Стьюдента), то нужно отклонить гипотезу о равенстве нулю коэффициента корреляции ρx,e, следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощьюt-статистики для каждой из них отдельно.
Тест Парка
Предполагается, что дисперсия σ2 является функцией i-го значения объясняющей переменной. Р. Парк предложил следующую функциональную зависимость:
Так как дисперсии σ2 обычно неизвестны, то их заменяют оценками квадратов отклонений e2.
Критерий Парка включает следующие этапы:
Строится уравнение регрессии: yi = b0+ b1xi + ei.
Оцениваются коэффициенты регрессии:
В случае множественной регрессии зависимость (5.6) строится для каждой объясняющей переменной.
Проверяется статистическая значимость коэффициента b (оценки β) на основе t-статистики t = b/Sb. Если коэффициент b (β) статистически значим, то это означает наличие связи между lne2 и lnx, т.е.
При проведении регрессионного анализа определяются следующие этапы: определение коэффициентов корреляции и детерминации, средней ошибки отклонения и наилучшей модели, анализ данных на гетероскедастичность и автокорреляцию и т. д. На практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса – Маркова), т. к. при их нарушении МНК может давать оценки с плохими статистическими свойствами. При этом существуют другие методы определения более точных оценок. Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: дисперсия случайных отклонений постоянна. для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
В данной курсовой анализируется суть гетероскедастичности, ее причины и последствия, а также приводятся способы ее обнаружения.
ГЛАВА 1. ПОНЯТИЕ ЭКОНОМЕТРИКИ
Постоянно усложняющиеся экономические процессы потребовали создания и совершенствования особых методов изучения и анализа. Широкое распространение получило использование моделирования и количественного анализа. На этом этапе выделилось и сформировалось одно из направлений экономических исследований – эконометрика.
Эконометрика – это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Эконометрика позволяет найти количественное подтверждение либо опровержение того или иного экономического закона либо гипотезы. Одним из важнейших направлений эконометрики является построение прогнозов по различным экономическим показателям.
Эконометрика как научная дисциплина зародилась и получила развитие на основе слияния экономической теории, математической экономики, экономической и математической статистик.
Основные результаты экономической теории носят качественный характер, а эконометрика вносит в них эмпирическое содержание. Математическая экономика выражает экономические законы в виде математических соотношений, а эконометрика осуществляет опытную проверку этих законов. Экономическая статистика дает информационное обеспечение исследуемого процесса в виде исходных (обработанных) статистических данных и экономических показателей, а эконометрика, используя традиционные математико-статистические и специально разработанные методы, проводит анализ количественных взаимосвязей между этими показателями.
К основным задачам эконометрики можно отнести следующие:
· Построение эконометрических моделей, т. е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа.
· Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным.
· Проверка качества найденных параметров модели и самой модели в целом.
· Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Развитие компьютерных систем и эконометрических пакетов, совершенствование методов анализа сделали эконометрику мощнейшим инструментом экономических исследований.
ГЛАВА 2. СУЩНОСТЬ И ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
При рассмотрении выборочных данных требование постоянства дисперсии случайных отклонений может вызвать определенное недоумение в силу того, что при каждом i-м наблюдении имеется единственное значение . Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных имеется дело с конкретными реализациями зависимой переменной и соответственно с определенными случайными отклонениями Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую – при других.
Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми – при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
Динамика изменения дисперсий (распределений) отклонений проиллюстрирована на рис. 1. При гомоскедастичности дисперсии εi постоянны, а при гетероскедастичности дисперсии εi изменяются (на данном рисунке – увеличиваются).

Проблема гетероскедастичности в большей степени характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Это можно объяснить следующим образом. При перекрестных данных учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли, страны и т. п.), имеющие различные доходы, размеры, потребности и т. д. Но в этом случае возможны проблемы, связанные с эффектом масштаба. Во временных рядах обычно рассматриваются одни и те же показатели в различные моменты времени (например, ВНП, чистый экспорт, темпы инфляции и т. д. в определенном регионе за определенный период времени). Однако при увеличении (уменьшении) рассматриваемых показателей с течением времени может возникнуть проблема гетероскедастичности.
При рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность): для всех наблюдений i, i = 1, 2,…, n.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими:
1. Оценки коэффициентов по-прежнему остаются несмещенными и линейными.
2. Оценки не будут эффективными (т. е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3. Дисперсии оценок будут рассчитываться со смещением.
4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися.
ГЛАВА 3. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
3.1. Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшатся с увеличением значения X. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений и значения будут коррелированы. Значения и ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
где — разность между рангами значений и ().
Если соответствующий коэффициент корреляции для генеральной совокупности равен нулю, т. е. гетероскедастичность отсутствует, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией .
Соответствующая тестовая статистика равна:
Следовательно, если значение тестовой статистики, вычисленное по вышеприведенной формуле, превышает 1,96 и 2,58 при уровнях значимости в 5% и 1% соответственно (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции, а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
3.2. Тест Голдфелда – Квандта
В данном случае предполагается, что стандартное отклонение пропорционально значению переменной X в этом наблюдении. Предполагается, что имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда – Квандта состоит в следующем:
1. Все n наблюдений упорядочиваются по величине X по возрастающей.
2. Вся упорядоченная выборка после этого разбивается на две подвыборки размерностей k, (N – 2k), k соответственно.
3. Оцениваются отдельные регрессии для первой подвыборки (kпервых наблюдений) и для второй подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии (сумма квадратов остатков RSS1 ) по первой подвыборке будет существенно меньше дисперсии регрессии (суммы квадратов остатков RSS2 ) по второй подвыборке.
4. Для сравнения соответствующих дисперсий строится следующая F-статистика:
Здесь (k – m – 1) – число степеней свободы соответствующих выборочных дисперсий (m – количество объясняющих переменных в уравнении регрессии).
5. Если , то гипотеза об отсутствии гетероскедастичности отклоняется.
6. Если , то гипотеза об отсутствии гетероскедастичности принимается.
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
Этот же тест может быть использован при предположении об обратной пропорциональности между и значениями объясняющей переменной. При этом F-статистика примет вид: (если X убывает).
3.3. Тест Глейзера
Тест Глейзера предполагает анализ зависимостей между дисперсиями отклонений и значениями переменной :
В качестве зависимой переменной для изучения гетероскедастичности выбирается абсолютная величина остатков, т. е. осуществляется регрессия
где – случайный член.
В качестве функций f обычно выбираются функции вида . Регрессия осуществляется при разных значениях γ, затем выбирается то значение, при котором коэффициент β оказывается наиболее значимым, т. е. имеет наибольшее значение t-статистики. Изменяя значения γ, можно построить различные регрессии. Обычно γ = …, -1, -0.5, 0, 0.5, 1, 1.5, … . Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.
АНАЛИЗ ДАННЫХ ПО РАСХОДАМ НА ПРЕДМЕТ НАЛИЧИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
Выполнить исследование по приведенным исходным данным, основанным на статистике США за годы с 1959-1983. Проанализировать данные на гетероскедастичность и автокорреляцию. Определить наилучшую модель из 3: линейной, степенной и гиперболической. Сделать выводы о модели.
Данные для расчета необходимо взять из табл. 1:
| N | Год | Текущие расходы по газу (x) | Совокупные личные расходы (y) |
| 1 | 1959 | 74,9 | 70,6 |
| 2 | 1960 | 79,8 | 71,9 |
| 3 | 1961 | 80,9 | 72,6 |
| 4 | 1962 | 80,8 | 73,7 |
| 5 | 1963 | 80,8 | 74,8 |
| 6 | 1964 | 81,1 | 75,9 |
| 7 | 1965 | 81,4 | 77,2 |
| 8 | 1966 | 81,9 | 79,4 |
| 9 | 1967 | 81,7 | 81,4 |
| 10 | 1968 | 82,5 | 84,6 |
| 11 | 1969 | 84 | 88,4 |
| 12 | 1970 | 88,6 | 92,5 |
| 13 | 1971 | 95 | 96,5 |
| 14 | 1972 | 100 | 100 |
| 15 | 1973 | 104,5 | 105,7 |
| 16 | 1974 | 117,7 | 116,3 |
| 17 | 1975 | 140,9 | 125,2 |
| 18 | 1976 | 164,8 | 131,7 |
| 19 | 1977 | 195,6 | 139,3 |
| 20 | 1978 | 214,9 | 149,1 |
| 21 | 1979 | 249,2 | 162,5 |
| 22 | 1980 | 297 | 179 |
| 23 | 1981 | 336,8 | 194,5 |
| 24 | 1982 | 404,2 | 206 |
| 25 | 1983 | 473,4 | 213,6 |
1. Найдем линейную модель в виде . Оценки для α и β определяем с помощью метода наименьших квадратов по формулам:
Для этого найдем:
Среднее значение x:
Среднее значение y:
Ковариацию x и y:
Полученная мною линейная модель имеет вид:
В результате выполнения регрессионного анализа мною получено:
TSS –полная сумма квадратов:
RSS – остаточная сумма квадратов:
ESS – оцененная модель суммы квадратов:
Условия правильности моих вычислений на данном этапе проверим по формуле:
49901,17 = 46820,32 + 3080,849
Вычислим коэффициент корреляции и коэффициент детерминации:
Критерием правильности решения задачи является:
Данные параметры характеризуют хорошую линейную зависимость между текущими расходами и совокупными личными расходами на имеющихся статистических данных.
Найдем среднюю ошибку аппроксимации:
Для наглядности представим результаты графически.
Примечание. Прямая линия – уравнение регрессии, а точки – статистические данные.
Определим доверительный интервал для параметров α и β:
Здесь – квантиль t-распределения Стьюдента с (N – p) степенями свободы; p – число параметров, в моем случае он равен 2; и – оценки исследуемых параметров, полученные ранее с использованием метода наименьших квадратов; и – несмещенные оценки для дисперсий случайных величин α и β; γ – уровень значимости.
Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:
Доверительный интервал для 1% уровня значимости:
42,787 2 (εi ) необходимо знать распределение Y, соответствующее выбранному значению xi . На практике зачастую для каждого конкретного значения xi определяется единственное значение yi , что не позволяет оценить дисперсию Y для данного xi .
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности – достаточно трудоемкая проблема и для ее решения разработано несколько методов.
Все они используют в качестве нулевой гипотезы H0 гипотезу об отсутствии гетероскедастичности.
В ходе исследований я получила, что наилучшей моделью является гиперболическая функция, т. к. ей соответствует наименьшая средняя ошибка аппроксимации равная = 5,2%. При проверке полученной модели на возможную гетероскедастичность данных я воспользовалась тестом ранговой корреляции Спирмена и тестом Голдфелда – Квандта. В результате обоих вычислений нулевая гипотеза об отсутствии гетероскедастичности принимается, следовательно мои данные гомоскедастичны.
СПИСОК ЛИТЕРАТУРЫ
1. Бородич С.А. Эконометрика. – Мн.: Новое знание, 2004.
2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1999.
3. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ, 2002.
4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2004.
5. Орлов А.И. Эконометрика. – М.: Экзамен, 2002.
6. Суслов В.И., Ибрагимов Н.М., Талышева Л.П. Эконометрия. – Новосибирск.: СО РАН, 2005.
7. Харин Ю.С., Малюгин В.И., Харин А.Ю. Эконометрическое моделирование. – Мн.: БГУ, 2003.
Поясним данную предпосылку на примере пространственной выборки. Случайная составляющая е, в каждом наблюдении может иметь только одно значение. Как понимать дисперсию Имеется в виду возможное поведение е, до того, как проведено наблюдение, т. е. нет основания ожидать появления особенно больших отклонений в любом наблюдении i = 1,2,…, п. Иными словами, вероятность того, что величина е, примет… Читать ещё >
Понятия и последствия гетероскедастичности ( реферат , курсовая , диплом , контрольная )
Как было показано ранее, при оценке параметров уравнения регрессии применяется традиционный метод наименьших квадратов. При этом должны выполняться определенные предпосылки относительно случайной составляющей ?, и объясняющей переменной х, (предпосылки нормальной линейной регрессионной модели).
Вторая предпосылка гласит:

что означает постоянство дисперсий случайных составляющих для каждого наблюдения i.
Поясним данную предпосылку на примере пространственной выборки. Случайная составляющая е, в каждом наблюдении может иметь только одно значение. Как понимать дисперсию Имеется в виду возможное поведение е, до того, как проведено наблюдение, т. е. нет основания ожидать появления особенно больших отклонений в любом наблюдении i = 1,2,…, п. Иными словами, вероятность того, что величина е, примет какое-то определенное значение, одинакова для всех наблюдений L Это условие известно как условие гомоскедастичности, что означает одинаковый разброс случайной составляющей в,.
Вместе с тем для некоторых выборок можно предположить, что теоретическое распределение случайной составляющей в, является различным для разных наблюдений в выборке, следовательно, различными будут и дисперсии случайных составляющих. Если дисперсии случайных составляющих неодинаковы в разных наблюдениях, т. е.

то имеет место гетероскедастичпость (непостоянство дисперсии отклонений случайных составляющих в;).
Гетероскедастичность может иметь место и при использовании в качестве данных наблюдений временных рядов (хп yt). Если значения xt и yt увеличиваются со временем, то, возможно, и дисперсия случайной составляющей также будет расти со временем (о временных рядах будет рассказано в гл. 10).
Наличие гетероскедастичности можно проследить из графика зависимости квадрата остатков е? от значения объясняющего признака х. Если все отклонения находятся внутри полосы постоянной ширины, параллельной оси абсцисс, гетероскедастичность не наблюдается (рис. 5.1, а). Во всех остальных случаях гетероскедастичность наблюдается (рис. 5.1, б—д)К
- 1) истинная гетероскедастичность. Вызывается непостоянством дисперсии случайного члена, ее зависимостью от различных факторов;
- 2) ложная гетероскедастичность. Вызывается ошибочной спецификацией модели регрессии.
- • оценки коэффициентов по-прежнему останутся несмещенными и линейными;
- • оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра).
- 1 Подробнее см., например, в работе: Гладилин А. В., Герасимов А. II., Громов Е. И. Эконометрика. Ростов н/Д: Феникс, 2011. С. 60.
Они не будут даже асимптотически эффективными, т. е. с увеличением числа наблюдений. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок;
• дисперсии оценок будут рассчитываться со смещением.

Рис. 5.1. Графическое представление отклонений 1.
Поэтому выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки коэффициентов регрессии будут ненадежными. Следовательно, статистические выводы могут быть ошибочными и приводить к неверным заключениям по качеству построенной модели и найденных коэффициентов регрессии.
Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.
При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:
6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
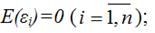
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
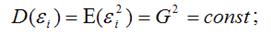
 между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
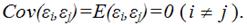
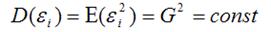
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.
Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.
Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.
Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
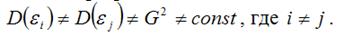
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:
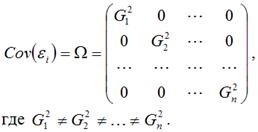
Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:
где Ω – матрица ковариаций случайной ошибки.
Если дисперсии случайных ошибок
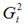
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить.
Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
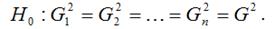
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
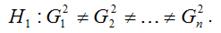
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:
1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;
2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.
Читайте также:
- Теория информационного государства реферат
- Гибель пассажирского лайнера адмирал нахимов реферат
- Реферат на тему казеозная пневмония
- Реферат на тему религия и церковь
- Ампер единица измерения реферат
При проведении регрессионного анализа, основанного на методе наименьших квадратов, на практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Как мы отмечали ранее, свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса− Маркова), т. к. при их нарушении МНК может давать оценки с плохими статистическими свойствами. При этом существуют другие методы определения более точных оценок. Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений (см. параграф 5.1, предпосылка 20):
дисперсия случайных отклонений εi постоянна. D(εi)=D(εj) = σ2 для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастич-
ностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
В данной главе мы подробно проанализируем суть гетероскедастичности, ее причины и последствия, а также приведем несколько способов смягчения этих последствий.
8.1. Суть гетероскедастичности
При рассмотрении выборочных данных требование постоянства дисперсии случайных отклонений может вызвать определенное недоумение в силу того, что при каждом i-м наблюдении имеется единственное значение εi. Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной yi и соответственно c определенными случайными отклонениями εi, i = 1, 2, …, n. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую
209

ошибку (отклонение) при одних наблюдениях и меньшую − при других.
Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений εi при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми − при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
На рис. 8.1 приведены два примера линейной регрессии − зависимости потребления С от дохода I: C = β0 + β1I + ε.
C C
C
|
I1 |
Ik |
In |
I |
I1 |
Ik |
In |
I |
|
а |
б |
Рис. 8.1
В обоих случаях с ростом дохода растет среднее значение потребления. Но если на рис. 8.1, а дисперсия потребления остается одной и той же для различных уровней дохода, то на рис. 8.1, б при аналогичной зависимости среднего потребления от дохода дисперсия потребления не остается постоянной, а увеличивается с ростом дохода. Фактически это означает, что во втором случае субъекты с большим доходом в среднем потребляют больше, чем субъекты с меньшим доходом, и, кроме того, разброс в их потреблении более существенен для большего уровня дохода. Фактически люди с большими доходами имеют больший простор для распределения своего дохода. Реалистичность данной ситуации не вызывает сомнений. Разброс значений потребления вызывает разброс точек наблюдения относительно линии регрессии, что и определяет дисперсию случайных отклонений. Динамика изменения дисперсий (распределений) отклонений для данного примера проиллюстрирована на рис. 8.2. При гомоскедастичности
210

(рис. 8.2, а) дисперсии εi постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии εi изменяются (в нашем примере − увеличиваются).
|
а − гомоскедастичность |
б − гетероскедастичность |
|
Рис. 8.2 |
Проблема гетероскедастичности в большей степени характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Это можно объяснить следующим образом. При перекрестных данных учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли, страны и т. п.), имеющие различные доходы, размеры, потребности и т. д. Но в этом случае возможны проблемы, связанные с эффектом масштаба. Во временных рядах обычно рассматриваются одни и те же показатели в различные моменты времени (например, ВНП, чистый экспорт, темпы инфляции
211
и т. д. в определенном регионе за определенный период времени). Однако при увеличении (уменьшении) рассматриваемых показателей с течением времени может возникнуть проблема гетероскедастичности.
8.2. Последствия гетероскедастичности
Как отмечалось в разделе 5.1, при рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки (BLUE-оценки) лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность): σ2(εi) = σ2 для всех наблюдений i, i = 1, 2, …, n.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими.
1.Оценки коэффициентов по-прежнему остаются несмещенными и линейными.
2.Оценки не будут эффективными (т. е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3.Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что необъясненная уравнением
|
2 |
∑ ei2 |
|||
|
регрессии дисперсия S |
= |
(m − число объясняющих пере- |
||
|
n − m − 1 |
менных), которая используется при вычислении оценок дисперсий всех коэффициентов (см. параграф 6.2, (6.23)), не является более несмещенной.
4.Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися.
Причину неэффективности оценок МНК при гетероскедастичности легко пояснить следующим примером парной регрессии.
212

y
Из рис. 8.3 видно, что для каждого конкретного значения хi СВ Х переменная Y принимает значение уi из некоторого множества, имеющего свое распределение, отличное одно от другого в силу непостоянства дисперсий (сравните распределения для значений у1 и уn).
По МНК минимизируется сумма квадратов отклонений
∑ei2 = ∑(yi − b0 − b1xi )2.
Но в этом случае каждое конкретное значение ei2 в данной сумме имеет одинаковый “вес” вне зависимости от того, получено оно из распределения с маленькой дисперсией (например, e12 ) или с большой (например, e2n ). Но это противоречит логике, т. к. точка, полученная
из распределения с меньшей дисперсией, более точно определяет направление линии регрессии. Поэтому она должна иметь больший “вес”, чем точка из распределения с большей дисперсией. Следовательно, методы оценивания, учитывающие “веса” точек наблюдений, позволяют получать более точные (эффективные) оценки. Учет “весов” точек характерен, например, для метода взвешенных наименьших квадратов, рассмотренного ниже.
8.3.Обнаружение гетероскедастичности
Вряде случаев на базе знаний характера данных появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.
213

Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, т. к. для знания дисперсий отклонений σ2(еi) необходимо знать распределение СВ Y, соответствующее выбранному значению хi СВ Х. На практике зачастую для каждого конкретного значения хi определяется единственное значение уi , что не позволяет оценить дисперсию СВ Y для данного хi .
Естественно, не существует какого-либо однозначного метода определения гетероскедастичности. Однако к настоящему времени для такой проверки разработано довольно большое число тестов и критериев для них. Рассмотрим наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелда−Квандта.
8.3.1. Графический анализ остатков
Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладывается объясняющая переменная Х (либо линейная комбинация объясняющих переменных Y = b0 + b1X1 + … +
+ bmXm), а по оси ординат либо отклонения еi, либо их квадраты ei2 . Примеры таких графиков приведены на рис. 8.4.
|
а |
xi |
б |
xi |
xi |
|
в |
||||
|
ei2 |
ei2 |
214
На рис. 8.4, а все отклонения ei2 находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит о независимости дисперсий ei2 от значений переменной Х и их постоянстве, т.е. в этом случае мы находимся в условиях гомоскедастичности.
На рис. 8.4, б − г наблюдаются некие систематические изменения в соотношениях между значениями xi переменной Х и квадратами от-
клонений ei2 . Рис. 8.4, б соответствует примеру из параграфа 8.1. На
рис. 8.4, в отражена линейная; 8.4, г − квадратичная; 8.4, д − гиперболическая зависимости между квадратами отклонений и значениями объясняющей переменной Х. Другими словами, ситуации, представленные на рис. 8.4, б − д, отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.
Отметим, что графический анализ отклонений является удобным и достаточно надежным в случае парной регрессии. При множественной регрессии графический анализ возможен для каждой из объясняющих переменных Хj , j = 1, 2, …, m отдельно. Чаще же вместо объясняющих переменных Хj по оси абсцисс откладывают значения yi ,
получаемые из эмпирического уравнения регрессии. Поскольку по уравнению множественной линейной регрессии yi является линейной
комбинацией хij , j = 1, 2, … , m, то график, отражающий зависимость ei2 от yi , может указать на наличие гетероскедастичности аналогично
ситуациям на рис. 8.4, б − д. Такой анализ наиболее целесообразен при большом количестве объясняющих переменных.
8.3.2. Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значения Х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений еi и значения хi СВ Х будут коррелированы. Значения хi и еi ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
|
rx,e = 1− 6 |
∑di2 |
, |
(8.1) |
|
|
n(n2 |
−1) |
|||
где di − разность между рангами хi и ei , i = 1, 2, … , n; n − число наблюдений.
Например, если х20 является 25-м по величине среди всех наблюдений Х; а е20 − является 32-м, то di = 25 − 32= −7.
215

Доказано, что если коэффициент корреляции ρх,е для генеральной совокупности равен нулю, то статистика
|
t = |
rx,e n − 2 |
(8.2) |
|
|
1 − r2 |
|||
|
x,e |
имеет распределение Стьюдента с числом степеней свободы ν = n − 2. Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле (8.2), превышает tкр. = tα,n−2 (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции ρх,е, а следовательно, и об отсутствии гетероскедастичности. В противном
случае гипотеза об отсутствии гетероскедастичности принимается. Если в модели регрессии больше чем одна объясняющая пере-
менная, то проверка гипотезы может осуществляться с помощью t- статистики для каждой из них отдельно.
8.3.3. Тест Парка
Р. Парк предложил критерий определения гетероскедастичности, дополняющий графический метод некоторыми формальными зависимостями. Предполагается, что дисперсия σi2 = σ2(ei ) является функцией i-го значения хi объясняющей переменной. Парк предложил следующую функциональную зависимость
|
уi2 = у2xвi ev i . |
(8.3) |
|
Прологарифмировав (8.4), получим: |
|
|
lnуi2 = lnу2 + вlnxi + vi . |
(8.4) |
Так как дисперсии уi2 обычно неизвестны, то их заменяют оценками квадратов отклонений ei2 .
|
Критерий Парка включает следующие этапы: |
||
|
1. |
Строится уравнение регрессии yi = b0 + b1xi + еi. |
|
|
2. |
Для каждого наблюдения определяются lnei2 |
) |
|
= ln(yi − yi )2 . |
||
|
3. |
Строится регрессия |
|
|
ln ei2 = α + βlnxi + vi , |
(8.5) |
|
|
где α = lnσ2. |
В случае множественной регрессии зависимость (8.5) строится для каждой объясняющей переменной.
216

4. Проверяется статистическая значимость коэффициента β уравнения
(8.5) на основе t-статистики t = в . Если коэффициент β статисти- Sв
чески значим, то это означает наличие связи между lnei2 и lnxi, т. е. гетероскедастичности в статистических данных.
Отметим, что использование в критерии Парка конкретной функциональной зависимости (8.5) может привести к необоснованным выводам (например, коэффициент β статистически незначим, а гетероскедастичность имеет место). Возможна еще одна проблема. Для случайного отклонения vi в свою очередь может иметь место гетероскедастичность. Поэтому критерий Парка дополняется другими тестами.
8.3.4. Тест Глейзера
Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно, более подходящих) зависимостей между дисперсиями отклонений σi и значениями переменной хi. По данному методу оценивается регрессионная зависимость модулей отклонений ei (тесно связанных с σi2) от хi. При этом рассматриваемая зависимость моделируется следующим уравнением регрессии:
|
| ei |= α + βхik + vi . |
(8.6) |
Изменяя значения k, можно построить различные регрессии. Обычно k = …, −1, −0.5, 0.5, 1, … Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий (8.6) коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.
Отметим, что так же, как и в тесте Парка, в тесте Глейзера для отклонений vi может нарушаться условие гомоскедастичности. Однако во многих случаях предложенные модели являются достаточно хорошими для определения гетероскедастичности.
8.3.5.Тест Голдфелда−Квандта
Вданном случае также предполагается, что стандартное отклонение σi = σ(εi) пропорционально значению хi переменной Х в этом
наблюдении, т. е. уi2 = у2 xi2 . Предполагается, что εi имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда−Квандта состоит в следующем:
217
1.Все n наблюдений упорядочиваются по величине Х.
2.Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (n − 2k), k соответственно.
3.Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий от-
клонений значениям Х верно, то дисперсия регрессии (сумма квад-
k
ратов отклонений S1 = ∑ei2 ) по первой подвыборке будет сущест-
i=1
венно меньше дисперсии регрессии (суммы квадратов отклонений
n
S3 = ∑ei2 ) по третьей подвыборке.
i=n-k
4.Для сравнения соответствующих дисперсий строится следующая F-статистика:
|
F = |
S3/(k − m − 1) |
= |
S3 . |
(8.7) |
|
S /(k − m − 1) |
S |
|||
|
1 |
1 |
Здесь (k − m − 1) − число степеней свободы соответствующих выборочных дисперсий (m − количество объясняющих переменных в уравнении регрессии).
При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν1 = ν2 = k − m − 1.
|
5. Если Fнабл.= |
S3 |
> Fкр.= F |
, то гипотеза об отсутствии гетероскеда- |
|
|
S1 |
б;н ;н |
|||
|
1 |
2 |
|||
стичности отклоняется (здесь α − выбранный уровень значимости).
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с σi. При этом k должно быть больше, чем (m + 1). Если нет уверенности относительно выбора переменной Xj, то данный тест может осуществляться для каждой из объясняющих переменных.
Этот же тест может быть использован при предположении об обратной пропорциональности между σi и значениями объясняющей переменной. При этом статистика Фишера примет вид: F = S1/S3.
218
8.4. Методы смягчения проблемы гетероскедастичности
Как отмечалось в разделе 8.2, гетероскедастичность приводит к неэффективности оценок, несмотря на их несмещенность. Это может привести к необоснованным выводам по качеству модели. Поэтому при установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии σi2 отклонений εi .
8.4.1. Метод взвешенных наименьших квадратов (ВНК)
Данный метод применяется при известных для каждого наблюдения значениях σi2. В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. В этом суть метода взвешенных наименьших квадратов.
Для простоты изложения опишем ВНК на примере парной ре-
|
грессии: |
||||||||||||||||
|
yi = β0 + β1xi + εi . |
(8.8) |
|||||||||||||||
|
Разделим обе части (9.7) на известное σi |
= |
уi2 |
: |
|||||||||||||
|
yi |
= в0 |
1 |
+ в1 |
xi + |
еi |
. |
(8.9) |
|||||||||
|
уi |
уi |
уi |
||||||||||||||
|
уi |
||||||||||||||||
|
Положив |
yi |
= уi* , |
xi |
= |
xi*, |
ei |
= vi, |
1 |
= zi, получим уравнение |
|||||||
|
уi |
||||||||||||||||
|
уi |
уi |
уi |
регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с “преобразованным” отклонением v:
|
уi* =β0zi + β1xi* + vi. |
(8.10) |
При этом для vi выполняется условие гомоскедастичности. Действительно,
уi2 (vi ) = M(vi − M(vi ))2 = M(vi2 ) − M2 (vi ) .
|
Так как по предпосылке 10 МНК M(ei) = 0, то M(vi ) = |
1 |
M(ei ) = 0, и |
||||||||
|
уi2 |
||||||||||
|
тогда уi2 (vi ) = M(vi2 ) = |
||||||||||
|
= M( |
ei2 |
) = |
1 |
M(ei2 ) = |
1 |
M(ei − M(ei ))2 = |
1 |
уi2 = 1 = const. |
||
|
уi2 |
уi2 |
|||||||||
|
уi2 |
уi2 |
219

Следовательно, для преобразованной модели (8.10) выполняются предпосылки 10 − 50 МНК. В этом случае оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.
Таким образом, метод взвешенных наименьших квадратов включает следующие этапы:
1.Каждую из пар наблюдений (хi , уi) делят на известную величину σi . Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие “веса”, а с максимальными дисперсиями − наименьшие “веса”. Действительно, наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с большими дисперсиями. Учет этого факта увеличивает вероятность получения более точных оценок.
1 2. По МНК для преобразованных значений
уi
уравнение регрессии без свободного члена с гарантированными качествами оценок.
8.4.2. Дисперсии отклонений не известны
Для применения ВНК необходимо знать фактические значения дисперсий уi2 отклонений. На практике такие значения известны крайне редко. Следовательно, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях уi2 .
Например, может оказаться целесообразным предположить, что дисперсии уi2 отклонений εi пропорциональны значениям хi (рис.8.5, а) или значениям хi2 (рис. 8.5, б).
Рис. 8.5
1. Дисперсии σ i2 пропорциональны хi (рис. 8.5, а).
уi2 = σ2 хi (σ2 − коэффициент пропорциональности).
220
Тогда уравнение (8.9) преобразуется делением его левой и правой частей на xi :
|
yi |
= |
a |
+ b |
xi |
+ |
ei |
yi = a |
1 + b xi + vi . |
(8.11) |
|||
|
xi |
||||||||||||
|
xi |
xi |
xi |
xi |
xi |
||||||||
|
Несложно показать, что для случайных отклонений vi = |
ei |
выпол- |
||||||||||
|
xi |
||||||||||||
няется условие гомоскедастичности. Следовательно, для регрессии (8.11) применим обычный МНК. Действительно, в силу выполнимо-
сти предпосылки уi2 = σ2 (εi) = σ2 хi имеем:
|
у2 (vi ) = у2 ( |
еi |
) = |
1 у2 (еi ) = |
1 у2 xi = у2 = const. |
|
xi |
xi |
xi |
Таким образом, оценив для (8.11) по МНК коэффициенты β0 и β1, затем возвращаются к исходному уравнению регрессии (8.8).
Если в уравнении регрессии присутствует несколько объясняющих переменных, можно поступить следующим образом. Вместо кон-
кретной объясняющей переменной Xj используетсяY исходного уравнения множественной линейной регрессии Y = b0 + b1X1 + … + bmXm ,
т. е. фактически линейная комбинация объясняющих переменных. В этом случае получают следующую регрессию:
|
yi |
1 |
xi1 |
xim |
еi |
||||||
|
= в0 |
) |
+ в1 |
) |
+ … + вm |
) |
+ |
. |
(8.12) |
||
|
) |
) |
|||||||||
|
yi |
yi |
yi |
yi |
yi |
Иногда из всех объясняющих переменных выбирается наиболее подходящая, исходя из графического представления (рис. 8.4).
2. Дисперсия σi2 пропорциональна хi2 (рис. 8.4, б).
В случае, если зависимость σi2 от хi целесообразнее выразить не линейной функцией, а квадратичной, то соответствующим преобразованием будет деление уравнения регрессии (8.8) на хi:
|
yi |
= в0 |
1 |
+ в1 + |
еi |
yi |
= в0 |
1 |
+ в1 + vi |
, где vi = |
еi |
. (8.13) |
|
|
xi |
xi |
|||||||||||
|
xi |
xi |
xi |
xi |
По аналогии с вышеизложенным несложно показать, что для отклонений vi будет выполняться условие гомоскедастичности. После определения по МНК оценок коэффициентов β0 и β1 для уравнения (8.13) возвращаются к исходному уравнению (8.8).
221
Отметим, что для применения описанных выше преобразований существенную роль играют знания об истинных значениях дисперсий отклонений σi2, либо предположения, какими эти дисперсии могут быть. Во многих случаях дисперсии отклонений зависят не от включенных в уравнение регрессии объясняющих переменных, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. В этом случае они должны быть включены в модель. В ряде случаев для устранения гетероскедастичности необходимо изменить спецификацию модели (например, линейную на логлинейную, мультипликативную на аддитивную и т. п.).
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности — достаточно трудоемкая проблема и для ее решения разработано несколько методов (тестов). В случае установления наличия гетероскедастичности ее корректировка также представляет довольно серьезную проблему. Одним из возможных решений является метод взвешенных наименьших квадратов (при этом необходима определенная информация либо обоснованные предположения о величинах дисперсий отклонений). На практике имеет смысл попробовать несколько методов определения гетероскедастичности и способов ее корректировки (преобразований, стабилизирующих дисперсию).
Вопросы для самопроверки
1.В чем суть гетероскедастичности?
2.Какое из следующих утверждений верно, ложно или не определено:
а) вследствие гетероскедастичности оценки перестают быть эффективными и состоятельными; б) оценки и дисперсии оценок остаются несмещенными;
в) выводы по t- и F-статистикам являются ненадежными;
г) при наличии гетероскедастичности стандартные ошибки оценок будут заниженными; д) гетероскедастичность проявляется через низкое значение статистики Дар-
бина−Уотсона DW;
е) не существует общего теста для анализа гетероскедастичности;
ж) тест ранговой корреляции Спирмена основан на использовании t- статистики; з) тест Парка является частным случаем теста Глейзера;
и) использование метода взвешенных наименьших квадратов носит ограниченный характер, т. к. для его использования необходимо знать дисперсии отклонений;
222
к) если в парной регрессии дисперсия случайных отклонений пропорциональна величине объясняющей переменной (х), то для получения эффективных оценок необходимо все наблюдаемые значения поделить на х.
3.Приведите аргументы в пользу графического теста, теста Парка и теста Глейзера.
4.Приведите схему теста Голдфелда−Квандта.
5.В чем суть метода взвешенных наименьших квадратов (ВНК)?
6.Объясните кратко, почему при наличии гетероскедастичности ВНК позволяет получить более эффективные оценки, чем обычный МНК.
7.Есть основание считать, что в регрессии, построенной по квартальным данным, случайные отклонения в первых кварталах больше, нежели отклонения в других кварталах. Как это можно проверить?
Упражнения и задачи
1.Пусть зависимость заработной платы (Y) от стажа работы (X) сотрудника выражена следующим уравнением регрессии:
Y = β0 + β1X + γD + ε,
где D − фиктивная переменная, отражающая пол сотрудника. Как можно проверить предположение о том, что пол сотрудника не влияет на дисперсию случайных отклонений εi?
2.Приведены данные в условных единицах по доходам (Х) и расходам на непродовольственные товары (Y) для тридцати домохозяйств:
|
X |
26.2 |
33.1 |
42.5 |
47.0 |
48.5 |
49.0 |
49.1 |
50.9 |
52.4 |
53.2 |
|
|
Y |
10.0 |
11.2 |
15.0 |
20.5 |
21.2 |
19.5 |
23.0 |
19.0 |
19.5 |
18.0 |
|
|
Х |
54.0 |
54.8 |
59.0 |
61.3 |
62.5 |
63.1 |
64.0 |
66.2 |
70.0 |
71.5 |
|
|
Y |
24.5 |
21.5 |
35.4 |
25.0 |
17.3 |
21.6 |
15.3 |
32.6 |
34.0 |
23.8 |
|
|
Х |
73.2 |
75.4 |
76.0 |
80.6 |
81.2 |
83.3 |
92.0 |
95.5 |
103.2 |
110.4 |
|
|
Y |
22.5 |
27.4 |
40.0 |
23.5 |
20.0 |
40.1 |
15.5 |
39.0 |
47.4 |
21.3 |
а) Определите по МНК оценки парного уравнения регрессии yi = b0+ b1xi+ ei. б) Оцените качество построенного уравнения.
в) Проведите графический анализ остатков.
г) Примените для указанных статистических данных ВНК предположение,
что σ2(ei) = σ2xi2.
д) Примените к полученным в п. а) результатам тест ранговой корреляции Спирмена и тест Парка.
е) Определите, существенно ли повлияла гетероскедастичность на качество оценок в уравнении, построенном по МНК.
223
|
3. |
Для предприятий некоторой отрасли анализируют зависимость заработной |
||||||||
|
платы (Y) сотрудников в зависимости от масштаба (от количества сотрудни- |
|||||||||
|
ков) предприятия (Х). Наблюдения по тридцати случайно отобранным пред- |
|||||||||
|
приятиям представлены следующей таблицей: |
|||||||||
|
Y |
X |
||||||||
|
75.5 |
75.5 |
77.5 |
78.5 |
80.0 |
81.0 |
100 |
|||
|
80.5 |
82.0 |
84.5 |
85.0 |
85.5 |
86.5 |
200 |
|||
|
85.5 |
88.5 |
90.0 |
91.0 |
95.0 |
96.0 |
300 |
|||
|
93.0 |
93.5 |
97.5 |
99.0 |
102.5 |
105.0 |
400 |
|||
|
102.0 |
105.5 |
107.0 |
110.5 |
115.0 |
118.5 |
500 |
а) Постройте уравнение регрессии Y на Х и оцените его качество.
б) Можно ли ожидать наличие гетероскедастичности в данном случае. Ответ поясните.
в) Проверьте наличие гетероскедастичности, используя тест Голдфелда− Квандта. Рекомендуется использовать разбиение, при котором k = 12.
г) Если предположить, что гетероскедастичность имеет место, и дисперсии отклонений пропорциональны значениям Х, то какое преобразование вы предложите, чтобы получить несмещенные, эффективные и состоятельные оценки.
д) Постройте новое уравнение регрессии на основе преобразования, осуществленного в предыдущем пункте, и оцените его качество.
е) Сравните результаты, полученные в пунктах а) и д).
4. Пусть для эмпирического уравнения парной регрессии Y = b0 + b1X + e име-
ет место следующее соотношение M(ei2) = σ2xi. Какое преобразование можно предложить, чтобы устранить проблему гетероскедастичности. Опишите поэтапно предложенную схему.
5. Пусть для регрессии Y = b0 + b1X1 + b2X2 + e, оцениваемой по ежегодным данным (1971−1998), получены следующие результаты: сумма квадратов от-
клонений для данных 1971−1980 гг. равна S1 = ∑ei2 = 15, для данных 1981−
1998 гг. эта сумма равна S2 = ∑ei2 = 50. С помощью теста Голдфелда−Квандта проверьте предположение о том, что дисперсия отклонений не постоянна (в частности, что дисперсия претерпела изменение где-то в 1981 г.).
6. Анализируется объем инвестиций для вымышленной страны. По данным с 1961 по 1990 г. построены два уравнения регрессии:
|
1) |
it = |
52.5 + 0.275gnpt |
− 0.63ct , |
R2 = 0.98. |
|||||||
|
(t) = (12.5) (10.2) |
(6.4) |
||||||||||
|
2) |
it |
= 50.7 |
1 |
+ |
0.27 − |
0.62 |
ct |
, |
|||
|
gnpt |
gnpt |
gnpt |
|||||||||
|
R2 = 0.87, |
|||||||||||
|
(t) |
(13.3) |
(9.3) |
(6.9) |
224

где GNP − валовой национальный продукт; С − совокупное частное потребление; I − объем инвестиций; gnpt, ct, it − значения соответствующих показателей в момент времени t.
а) Что могло послужить причиной преобразования первого уравнения во второе?
б) Если причиной преобразования являлась гетероскедастичность, то какое предположение о дисперсии отклонений являлось основанием для данного преобразования?
в) Можно ли сравнить качества обоих уравнений на основе коэффициентов детерминации? Ответ поясните.
г) Должно ли преобразованное уравнение проходить через начало координат?
7.Выдвигается предположение, что средняя заработная плата наемных рабочих пропорциональна их стажу. Для анализа данного утверждения обследуются по 20 рабочих восьми категорий стажа. Получены следующие статистические данные:
|
Стаж |
[0, 5) [5, 10) [10, 15) [15, 20) [20, 25) [25, 30) [30, 35) [35, 40] |
|
З/п |
10000 12500 14300 18700 25400 29000 32000 34300 |
а) Постройте эмпирическое уравнение регрессии, в котором заработная плата является зависимой переменной, а стаж работы − объясняющей переменной (уравнение строится в предположение, что дисперсии отклонений постоянны).
б) Оцените качество построенной регрессии.
в) Есть ли основания считать, что для данной регрессионной модели весьма вероятна гетероскедастичность? Если да, то почему?
г) Предполагая, что дисперсия отклонений пропорциональна трудовому стажу, постройте на основании тех же данных уравнение по методу взвешенных наименьших квадратов (ВНК).
д) Предполагая, что дисперсия отклонений пропорциональна квадрату величины трудового стажа, постройте по ВНК соответствующее уравнение регрессии.
е) Какое из трех предположений относительно дисперсии отклонений наиболее реалистично с вашей точки зрения?
8.Исследуется зависимость между доходом (Х) домохозяйства и его расходом
(Y) на продукты питания. Выборочные данные по 40 домохозяйствам представлены ниже.
|
X |
25.5 |
26.5 |
27.2 |
29.6 |
35.7 |
38.6 |
39.0 |
39.3 |
40.0 |
41.9 |
42.5 |
44.2 |
44.8 |
45.5 |
|
Y |
14.5 |
11.3 |
14.7 |
10.2 |
13.5 |
9.9 |
12.4 |
8.6 |
10.3 |
13.9 |
14.9 |
11.6 |
21.5 |
10.8 |
|
Х |
45.5 |
48.3 |
49.5 |
52.3 |
55.7 |
59.0 |
61.0 |
61.7 |
62.5 |
64.7 |
69.7 |
71.2 |
73.8 |
74.7 |
|
Y |
13.8 |
16.0 |
18.2 |
19.1 16.3 |
17.5 |
10.9 |
16.1 |
10.5 |
10.6 |
29.0 |
8.2 |
14.3 |
21.8 |
225

Х 75.8 76.9 79.2 81.5 82.4 82.8 83.0 85.9 86.4 86.9 88.3 89.0
Y 26.1 20.0 19.8 21.2 29.0 17.3 23.5 22.0 18.3 13.7 14.5 27.3
а) Постройте эмпирическое уравнение регрессии Y на Х. б) Вычислите отклонения ei.
в) Проведите анализ модели на гетероскедастичность по тесту ранговой корреляции Спирмена.
г) Проведите графический анализ отклонений и выдвиньте предположение о зависимости дисперсии отклонений от значений Х.
д) На основании предыдущего пункта постройте новое уравнение регрессии, используя для этого ВНК.
9.Проводится анализ зависимости средней заработной платы от средней производительности на предприятиях различного масштаба. Проведенное обследование нашло отражение в следующей таблице.
|
Количество сотрудников |
Средняя |
Средняя |
Стандартное |
|
|
предприятия, |
производительность, |
з/п, |
отклонение з/п, |
|
|
n |
X ($) |
Y ($) |
σi ($) |
|
|
1 |
− 4 |
9320 |
3320 |
740 |
|
4 |
− 9 |
8630 |
3640 |
850 |
|
10 |
− 19 |
8050 |
3900 |
730 |
|
20 |
− 49 |
8320 |
4120 |
820 |
|
50 |
− 99 |
8600 |
4090 |
950 |
|
100 |
− 199 |
9120 |
4200 |
1100 |
|
200 |
− 499 |
9540 |
4380 |
1250 |
|
500 |
− 999 |
9730 |
4500 |
1290 |
|
1000 |
− 1999 |
10120 |
4610 |
1350 |
|
2000 |
− 4999 |
10740 |
4800 |
1100 |
|
> 5000 |
11200 |
5000 |
1520 |
а) Постройте уравнение регрессии yi МНК.
б) Постройте уравнение регрессии yi
уi
= b0 + b1xi + ei, используя обычный
|
= b |
1 |
+ b xi |
+ |
ei |
. |
|
|
уi |
||||||
|
0 |
1 уi |
уi |
в) Сравните полученные результаты. Какое из уравнений вы предпочтете и почему?
226
Соседние файлы в папке ЭКОНОМЕТРИКА и математическая экономика
- #
- #
- #
- #
- #
- #
20.04.20152.55 Mб68Кобелев Н.Б. Практика применения экономико-математических методов и моделей. 2000.djvu
- #
- #
В предыдущих параграфах данной главы мы рассматривали случай отказа от одной предпосылки классической линейной модели множественной регрессии. Теперь мы расширим наш анализ и откажемся сразу от двух предпосылок: от предпосылок №№4-5 (о постоянстве дисперсии случайной ошибки и о некоррелированности разных случайных ошибок между собой). В техническом смысле этот параграф несколько сложнее предыдущих (в частности, тут более широко используется линейная алгебра). Поэтому, если вы заинтересованы в том, чтобы разобраться только в прикладных аспектах множественной регрессии, а в соответствующих вычислениях готовы полностью довериться эконометрическому пакету, можете его пропустить.
Отказ от указанных двух предпосылок означает, что ковариационная матрица вектора случайных ошибок (таблица, в которой записаны все ковариации между (varepsilon_{i}) и (varepsilon_{j}), см. параграф 3.3) больше не является диагональной матрицей с одинаковыми числами на главной диагонали, как это было в первоначальной классической модели. Теперь ковариационная матрица вектора случайных ошибок Ω — это произвольная ковариационная матрица (разумеется, так как это не совсем любая матрица, а именно ковариационная матрица, то по своим свойствам она является симметричной и положительно определенной).
Модель, в которой сохранены только первые три предпосылки классической линейной модели множественной регрессии, называется обобщенной линейной моделью множественной регрессии.
Проанализируем, к каким последствиям приводит отказ от предпосылок №№4-5.
Во-первых, полученная обычным методом наименьших квадратов оценка ({widehat{beta} = left( {X^{‘}X} right)^{- 1}}X’y) остается несмещенной (это свойство мы доказывали, опираясь как раз лишь на первые три предпосылки).
Во-вторых, МНК-оценки хоть и остаются несмещенными, но больше не являются эффективными.
В-третьих, если мы оцениваем ковариационную матрицу вектора оценок коэффициентов (которая нужна для тестирования всевозможных гипотез), то оценка (widehat{V}{{(widehat{beta})} = left( {X^{‘}X} right)^{- 1}}S^{2}) смещена и больше не является корректной.
Чтобы убедиться в этом, посчитаем ковариационную матрицу от (widehat{beta}) в условиях обобщенной модели (при этом мы используем свойства ковариационной матрицы, перечисленные в параграфе 3.3):
(V{left( widehat{beta} right) = V}{leftlbrack {{({X^{‘}X})}^{- 1}X’y} rightrbrack = V}{leftlbrack {{({X^{‘}X})}^{- 1}X'{({mathit{Xbeta} + varepsilon})}} rightrbrack =})
({}V{leftlbrack {{({{({X^{‘}X})}^{- 1}X’})}varepsilon} rightrbrack = left( {X^{‘}X} right)^{- 1}}X^{‘}Vlbrackvarepsilonrbrack{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega X{({X^{‘}X})}^{- 1})
Так выглядит ковариационная матрица вектора МНК-оценок в обобщенной модели. Ясно, что она не может быть корректно оценена стандартной оценкой (left( {X^{‘}X} right)^{- 1}S^{2}). Следовательно, прежней формулой пользоваться нельзя: если мы будем использовать стандартные ошибки, рассчитанные по обычной формуле (предполагая выполнение предпосылок классической линейной модели), то получим некорректные стандартные ошибки, что может привести нас к неверным выводам по поводу значимости или незначимости тех или иных регрессоров.
Таким образом, последствия перехода к обобщенной модели аналогичны тем, что мы наблюдали для случая гетероскедастичности. Это неудивительно, так как гетероскедастичность — частный случай обобщенной линейной модели.
Поэтому для получения эффективных оценок обычный МНК не подойдет, и придется воспользоваться альтернативным методом — обобщенным МНК (ОМНК, generalized least squares, GLS). Формулу для расчета оценок коэффициентов при помощи ОМНК позволяет получить специальная теорема.
Теорема Айткена
Если
- модель линейна по параметрам и правильно специфицирована
({y = {mathit{Xbeta} + varepsilon}},) - матрица Х — детерминированная матрица, имеющая максимальный ранг k,
- (E{(varepsilon) = overrightarrow{0}}),
- (V{(varepsilon) = Omega}) — произвольная положительно определенная и симметричная матрица,
то оценка вектора коэффициентов модели ({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y) является:
- несмещенной
- и эффективной, то есть имеет наименьшую ковариационную матрицу в классе всех несмещенных и линейных по y оценок.
Предпосылки теоремы Айткена — это предпосылки обобщенной линейной модели множественной регрессии. Из них первые три — стандартные, как в классической модели, а четвертая ничего особого не требует (у вектора случайных ошибок может быть любая ковариационная матрица без каких-либо дополнительных специальных ограничений). Сама теорема Айткена является аналогом теоремы Гаусса — Маркова для случая обобщенной модели.
Докажем эту теорему.
Из линейной алгебры известно: если матрица (Omega) симметрична и положительно определена, то существует такая матрица P, что
(P’bullet{P = Omega^{- 1}}) ⇔ ({P^{‘} = Omega^{- 1}}bullet P^{- 1})
А раз такое представление возможно, то воспользуемся им для замены переменных. От вектора значений зависимой переменной (y), перейдем к вектору (Pbullet y), обозначив его как вектор ({y^{} = P}bullet y). Аналогичным образом введем матрицу ({X^{} = P}bullet X) и вектор ошибок ({varepsilon^{} = P}bulletvarepsilon).
Вернемся к исходной модели, параметры которой нас и интересуют:
({y = X}{beta + varepsilon})
Умножим левую и правую части равенства на матрицу (P):
({mathit{Py} = mathit{PX}}{beta + mathit{Pvarepsilon}})
С учетом новых обозначений это равенство можно записать так:
({y^{} = X^{}}{beta + varepsilon^{}})
Для новой модели (со звездочками) выполняются предпосылки теоремы Гаусса-Маркова. Чтобы в этом убедиться, достаточно показать, что математическое ожидание вектора случайных ошибок является нулевым вектором (третья предпосылка классической модели) и ковариационная матрица вектора случайных ошибок является диагональной с одинаковыми элементами на главной диагонали (четвертая и пятая предпосылки).
Для этого вычислим математическое ожидание нового вектора ошибок:
(E{left( varepsilon^{} right) = E}{left( mathit{Pvarepsilon} right) = P}bullet E{(varepsilon) = P}bullet{overrightarrow{0} = overrightarrow{0}})
Теперь вычислим ковариационную матрицу вектора (varepsilon^{}):
(V{left( varepsilon^{} right) = V}{left( {Pbulletvarepsilon} right) = P}bullet V(varepsilon)bullet{P^{‘} = P}bulletOmegabullet{P^{‘} = P}bulletOmegabulletOmega^{- 1}bullet{P^{- 1} = I_{n}})
Здесь (I_{n}) обозначает единичную матрицу размера n на n.
Следовательно, для модели со звездочками выполняются все предпосылки теоремы Гаусса — Маркова. Поэтому получить несмещенную и эффективную оценку вектора коэффициентов можно, применив к этой измененной модели обычный МНК:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}y^{})
Теперь осталось вернуться к исходным обозначениям, чтобы получить формулу несмещенной и эффективной оценки интересующего нас вектора в терминах обобщенной модели:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}{y^{} = left( {{(mathit{PX})}^{‘}mathit{PX}} right)^{- 1}}left( mathit{PX} right)^{‘}{mathit{Py} = left( {X’P’mathit{PX}} right)^{- 1}}X^{‘}P^{‘}{mathit{Py} =}left( {X’Omega^{- 1}P^{- 1}mathit{PX}} right)^{- 1}X’Omega^{- 1}P^{- 1}{mathit{Py} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y)
Что и требовалось доказать.
Взвешенный МНК, который мы обсуждали ранее, — это частный вариант обобщенного МНК (для случая, когда только предпосылка №4 нарушена, а предпосылка №5 сохраняется).
Как и при использовании взвешенного МНК в ситуации применения ОМНК коэффициент R-квадрат не обязан лежать между нулем и единицей и не может быть интерпретирован стандартным образом.
Слабая сторона ОМНК состоит в том, что для его реализации нужно знать не только матрицу регрессоров X с вектором значений зависимой переменной y, но и ковариационную матрицу вектора случайных ошибок (Omega). На практике, однако, эта матрица почти никогда не известна. Поэтому в прикладных исследованиях практически всегда вместо ОМНК используется, так называемый, доступный ОМНК (его ещё называют практически реализуемый ОМНК, feasible GLS). Идея доступного ОМНК состоит в том, что следует сначала оценить матрицу (Omega) (традиционно обозначим её оценку (widehat{Omega})), а уже затем получить оценку вектора коэффициентов модели, заменив в формуле ОМНК (Omega) на (widehat{Omega}):
({{widehat{beta}}^{} = {({X'{widehat{Omega}}^{- 1}X})}^{- 1}}X'{widehat{Omega}}^{- 1}y.)
Применение этого подхода осложняется тем, что (widehat{Omega}) не может быть оценена непосредственно без дополнительных предпосылок, так как в ней слишком много неизвестных элементов. Действительно, в матрице размер (n) на (n) всего (n^{2}) элементов, и оценить их все, имея всего (n) наблюдений, представляется слишком амбициозной задачей. Даже если воспользоваться тем, что матрица (Omega) является симметричной, в результате чего достаточно оценить только элементы на главной диагонали и над ней, мы все равно столкнемся с необходимостью оценивать (left( {n + 1} right){n/2}) элементов, что всегда больше числа доступных нам наблюдений.
Поэтому процедура доступного ОМНК устроена так:
- Делаются некоторые предпосылки по поводу того, как устроена ковариационная матрица вектора случайных ошибок (Omega). На основе этих предпосылок оценивается матрица (widehat{Omega}).
- После этого по формуле ({({X'{widehat{Omega}}^{- 1}X})}^{- 1}X'{widehat{Omega}}^{- 1}y) вычисляется вектор оценок коэффициентов модели.
Из сказанного следует, что доступный ОМНК может быть реализован только в ситуации, когда есть разумные основания сформулировать те или иные предпосылки по поводу матрицы (widehat{Omega}). Рассмотрим некоторые примеры таких ситуаций.
Пример 5.4. Автокорреляция и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой дисперсия случайных ошибок постоянна, однако наблюдается так называемая автокорреляция первого порядка:
(varepsilon_{i} = {{rho ast varepsilon_{i — 1}} + u_{i}})
Здесь (u_{i}) — независимые и одинаково распределенные случайные величины с дисперсией (sigma_{u}^{2}), а (rhoin{({{- 1},1})}) — коэффициент автокорреляции.
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели, предполагая, что коэффициент (rho) известен.
Примечание: в отличие от гетероскедастичности, автокорреляция случайных ошибок обычно наблюдается не в пространственных данных, а во временных рядах. Для временных рядов вполне естественна подобная связь будущих случайных ошибок с предыдущими их значениями.
Решение:
(а) Используя условие о постоянстве дисперсии случайной ошибки, то есть условие (mathit{var}{{(varepsilon_{i})} = mathit{var}}{(varepsilon_{i — 1})}), найдем эту дисперсию:
(mathit{var}{{(varepsilon_{i})} = mathit{var}}{({{rho ast varepsilon_{i — 1}} + u_{i}})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i — 1})} + mathit{var}}{(u_{i})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i})} + sigma_{u}^{2}})
(mathit{var}{left( varepsilon_{i} right) = frac{sigma_{u}^{2}}{1 — rho^{2}}}.)
Тем самым мы нашли элементы, которые будут стоять на главной диагонали ковариационной матрицы вектора случайных ошибок. Теперь найдем элементы, которые будут находиться непосредственно на соседних с главной диагональю клетках:
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — 1}} right) = mathit{cov}}{left( {{{rho ast varepsilon_{i — 1}} + u_{i}},varepsilon_{i — 1}} right) = {rho ast mathit{cov}}}{left( {varepsilon_{i — 1},varepsilon_{i — 1}} right) + mathit{cov}}{left( {u_{i},varepsilon_{i — 1}} right) = {rho ast mathit{var}}}{{left( varepsilon_{i — 1} right) + 0} = frac{rho ast sigma_{u}^{2}}{1 — rho^{2}}})
По аналогии легко убедиться, что
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — k}} right) = frac{rho^{k} ast sigma_{u}^{2}}{1 — rho^{2}} = frac{sigma_{u}^{2} ast rho^{k}}{1 — rho^{2}}}.)
Следовательно, ковариационная матрица вектора случайных ошибок имеет вид:
({Omega = frac{sigma_{u}^{2}}{1 — rho^{2}}}begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix})
(б) Вектор ОМНК-оценок коэффициентов имеет вид:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}{left( {X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1} ast}X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}y)
Обратите внимание, что дробь (frac{sigma_{u}^{2}}{1 — rho^{2}}) при расчете представленной оценки сокращается. Поэтому для вычисления оценки знать величину (sigma_{u}^{2}) не нужно.
Примечание: если коэффициент автокорреляции (rho) неизвестен, то его можно легко оценить. Например, для этого можно применить обычный МНК к исходной регрессии, получить вектор остатков и оценить регрессию ({widehat{e}}_{i} = {widehat{rho} ast e_{i — 1}}). Полученной оценки (widehat{rho}) достаточно, чтобы вычислить ОМНК-оценку вектора параметров модели. Тем самым в представленном примере для применения доступного ОМНК достаточно оценить всего один параметр ковариационной матрицы вектора оценок коэффициентов.
Пример 5.5. Гетероскедастичность и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой выполнены все предпосылки классической линейной модели множественной регрессии за одним исключением: дисперсия случайной ошибки прямо пропорциональна квадрату некоторой известной переменной
(mathit{var}{left( varepsilon_{i} right) = sigma_{i}^{2} = sigma_{0}^{2}}{z_{i}^{2} > 0}.)
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели.
Решение:
(а) Так как в этом случае нарушена только четвертая предпосылка классической линейной модели множественной регрессии, то вне главной диагонали ковариационной матрицы вектора случайных ошибок будут стоять нули.
(Omega = begin{pmatrix} begin{matrix} {sigma_{0}^{2}z_{1}^{2}} & 0 \ 0 & {sigma_{0}^{2}z_{2}^{2}} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & {sigma_{0}^{2}z_{n}^{2}} \ end{matrix} \ end{pmatrix})
(б) Обратите внимание, что при подстановке в общую формулу для ОМНК-оценки величина (sigma_{0}^{2}) сокращается, следовательно, для оценки вектора коэффициентов знать её не нужно:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}left( {X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1}X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}y)
* * *
Ещё одна важная ситуация, когда с успехом может быть применен доступный ОМНК — это модель со случайными эффектами, которую мы рассмотрим в главе, посвященной панельным данным.
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
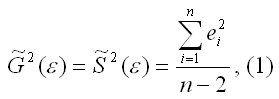
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
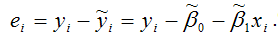
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
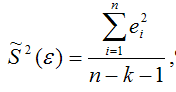
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
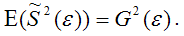
Доказательство. Примем без доказательства справедливость следующих равенств:
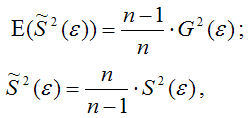
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
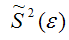
– выборочная оценка дисперсии случайной ошибки.
Тогда:
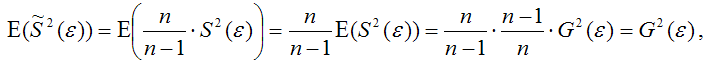
т. е.
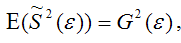
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
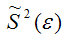
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
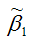
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
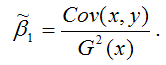
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
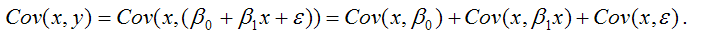
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
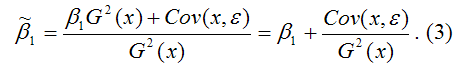
Таким образом, МНК-оценка
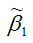
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
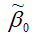
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
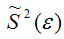
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
В предыдущем параграфе мы научились описывать облако точек некоторой прямой, не делая никаких предположений по поводу природы анализируемых данных. Иными словами, мы не предполагали никакой конкретной модели, описывающей процесс порождения наших данных. Для дальнейшего продвижения, однако, это будет нам необходимо.
Вернемся к нашему примеру с квартирами. Естественно ожидать, что на цену квартиры (y) влияет её площадь (x), а также прочие факторы, например, удаленность квартиры от метро, этаж, наличие балкона и так далее. Обозначим эти прочие факторы переменной (varepsilon ). С учетом этих соображений естественно предположить следующую модель цены квартиры:
( {y}_i = {β}_1 + {β}_2 {x}_i + {ε}_i , i = 1,2 , … , n ).
Здесь — площадь i-ой квартиры в квадратных метрах, — цена i-ой квартиры в миллионах рублей, — прочие факторы, которые оказывают влияние на цену квартиры (y_i). Переменную (varepsilon ) принято называть случайной ошибкой модели. Буквой n будем обозначать число наблюдений в доступной нам выборке.
В целом такая модель выглядит достаточно разумно. Если бы мы знали точные значения коэффициентов (beta _1) и (beta _2), мы могли бы использовать её в практических целях. Например, зная, что (beta _2=0,3), строительная компания могла бы учитывать при планировании продаж, что один дополнительный квадратный метр площади квартиры оценивается рынком в 0,3 млн рублей. К сожалению, на практике значения параметров (beta _1) и (beta _2) нам не известны, зато мы можем собрать статистические данные и получить их (приблизительные) оценки.
Здесь уместно подчеркнуть важное различие между
- параметрами (beta _k) (без «крышек») в выражении (y_i=beta _1+beta _2x_i+varepsilon _i),
- и их оценками (widehat {beta _k})(c «крышками») в выражении .
Это различие состоит в том, что и — это некоторые истинные значения параметров модели, которые на практике никогда не известны исследователю. Все, что исследователь в силах сделать — собрать данные и эти значения оценить приближенно. — это оценки истинных значений, которые мы получаем, используя наши выборочные данные. Так как (widehat {beta _1}text{и}widehat {beta _2}) рассчитываются на основе случайной выборки, то они являются случайными величинами.
Естественно, мы хотим, чтобы оценки были близки к истинным значениям оцениваемых параметров. Поэтому нам важно знать: при каких условиях мы можем доверять этим оценкам, то есть рассчитывать на то, что результат использования МНК будет близок к истине? Эти условия называют предпосылками классической линейной модели парной регрессии.
Предпосылки классической линейной модели парной регрессии (КЛМПР):
- Модель линейна по параметрам и корректно специфицирована
(y_i=beta _1+beta _2x_i+varepsilon _i,i=1,2,{dots},n.) - (x_1,x_2,{dots},x_n) — детерминированные (неслучайные) величины, не все одинаковые.
- Математическое ожидание случайных ошибок равно нулю
(Evarepsilon _i=0). - Дисперсия случайной ошибки одинакова для всех наблюдений (mathit{var}left(varepsilon _iright)=sigma ^2).
- Случайные ошибки, относящиеся к разным наблюдениям, взаимно независимы.
- Случайные ошибки имеют нормальное распределение (varepsilon _iNleft(0,sigma ^2right)).
Мы обсудили выше соображения, исходя из которых может быть сформулирована предпосылка №1. Как мы увидим в дальнейшем, правильная спецификация подразумевает в первую очередь отсутствие среди прочих факторов других переменных, которые одновременно влияют на y и коррелируют с x. Нарушение этого требования приводит к серьезным проблемам, которые мы осветим в конце данной главы.
Предпосылка №2 касается двух важных аспектов. Во-первых, мы предполагаем, что регрессоры (x_i) являются неслучайными величинами. Это техническое предположение, которое упростит некоторые выкладки в этом разделе. Обратите внимание, что (varepsilon _i) в отличие от регрессоров являются случайными величинами, а следовательно, и (y_i) тоже случайны, так как представляют собой сумму неслучайной компоненты (beta _1+beta _2x_i) и случайной величины (varepsilon _i). В терминах нашего примера с квартирами про эту предпосылку можно думать так: представим, что вы собрали случайную выборку из 100 квартир площадью 30 м2, 100 квартир площадью 35 м2 и 100 квартир площадью 40 м2. Если вы соберете другую выборку из трехсот квартир с такими же площадями, то значения регрессоров (x_i) останутся теми же самыми, а вот значения объясняемой переменной (y_i) поменяются, поэтому в данном примере разумно думать про регрессоры как про неслучайные величины, а про величины (y_i) — как про случайные.
Во-вторых, в рамках предпосылки №2 мы предполагаем, что не все значения регрессоров одинаковы. Нетрудно понять, зачем нужно это предположение, если взглянуть на формулу оценки коэффициента
(widehat {beta _2}=frac{widehat {mathit{Cov}}left(x,yright)}{widehat {mathit{Var}}left(xright)}). Обратите внимание, что в знаменателе этой формулы стоит выборочная дисперсия переменной x, но если все значения этой переменной в выборке будут одинаковы, то эта дисперсия окажется равной нулю, и из-за этого мы не сможем рассчитать МНК-оценку (widehat {beta _2}).
Предпосылка №3 говорит о том, что прочие факторы могут приводить к отклонению (y_i) от величины (beta _1+beta _2x_i) как вверх, так и вниз, но в среднем эти отклонения компенсируют друг друга.
Предпосылка №4 требует, чтобы разброс случайных ошибок в среднем был постоянен для всех наблюдений. Её смысл удобно пояснить, используя картинку. Посмотрите на рисунки 2.3а и 2.3б. В первом случае предпосылка о постоянстве дисперсии случайной ошибки выполнена, а во втором — нет, так как разброс точек вокруг линии регрессии растет по мере увеличения объясняющей переменной, следовательно, мы можем заключить, что дисперсия случайной ошибки не является одинаковой для всех наблюдений. Ситуация, когда предпосылка №4 выполнена (то есть ситуация, соответствующая рисунку 2.3а) называется гомоскедастичностью случайных ошибок. Альтернативная ситуация называется гетероскедастичностью случайных ошибок.
Рисунок 2.3а. Гомоскедастичность случайных ошибок
Рисунок 2.3б. Гетероскедастичность случайных ошибок
Из предпосылки №5 следует, что случайные ошибки, относящиеся к разным наблюдениям, не коррелированы друг с другом: (mathit{cov}left(varepsilon _i,varepsilon _jright)=0) при (i{neq}j).
Предпосылка №6 не требуется для обеспечения хороших свойств оценок коэффициентов (обратите внимание, что ниже, в формулировке теоремы Гаусса — Маркова, она не фигурирует), однако будет полезна для тестирования гипотез и построения доверительных интервалов.
Теорема Гаусса — Маркова. Если выполнены предпосылки 1-5 классической линейной модели парной регрессии, то МНК-оценки коэффициентов (widehat {beta _1}text{и}widehat {beta _2}) будут:
(а) несмещенными,
(б) эффективными в классе всех несмещенных и линейных по y оценок1.
Напомним, что оценка называется несмещенной, если её математическое ожидание совпадает с истинным значением оцениваемого параметра: (Ewidehat {beta _2}=beta _2). Свойство эффективности означает, что оценка характеризуется минимальной дисперсией среди всех альтернативных оценок в данном классе, то есть является «наиболее точной» оценкой интересующего нас параметра. Линейность по y означает, что мы рассматриваем все оценки, которые могут быть представлены в виде линейной комбинации значений объясняемой переменной, то есть записаны в виде (sum _{i=1}^nc_i{ast}y_i).
Если переформулировать свойства несмещенности и эффективности нестрого, то можно сказать, что при выполнении предпосылок 1-5 МНК-оценки параметров окажутся хорошими: они будут «в среднем правильными» и наиболее точными. Теорема Гаусса — Маркова дает нам важную мотивацию для того, чтобы оценивать параметры нашей модели именно методом наименьших квадратов, а не каким-то альтернативным способом.
Лирическое отступление о предпосылках
Каждый раз, когда я рассказываю студентам об этой теореме, в моей голове разыгрывается примерно такой диалог между двумя эконометристами (назовем их Филипп и Дима).
Дима: Реалистичны ли предпосылки КЛМПР?
Филипп: Не очень. Например, в реальных исследованиях на пространственных данных ты почти всегда будешь сталкиваться с нарушением требования постоянства дисперсии случайной ошибки (нарушением предпосылки №4). Во многих прикладных исследованиях также окажется более целесообразным думать про регрессоры как про случайные, а не детерминированные случайные величины (это отклонение от предпосылки №2). На нормальность случайных ошибок (предпосылка №6) я бы тоже не рассчитывал…
Дима: Зачем же тогда мы её изучаем? Давайте сразу перейдем к более реалистичной модели.
Филипп: Мы начинаем с КЛМПР, так как это самая простая модель, на примере которой мы можем обсудить ряд важных эконометрических идей и при этом не погрязнуть в технических трудностях. В последующих главах мы будем постепенно отказываться от предпосылок КЛМПР и в результате получим набор моделей и методов, которые хорошо подходят для реальных исследований на живых данных. Кроме того, мы научимся проверять выполнение тех или иных предположений КЛМПР, чтобы понять, когда стоит их использовать, а когда — нет.
В частности, последствия нарушения предпосылки №3 читателю предлагается проанализировать уже в этом параграфе, в одном из заданий для самостоятельного решения.
- Несмещенность и эффективность — это свойства оценок при фиксированном объеме выборки (при фиксированном n). Во многих случаях удобно также использовать асимптотические свойства оценок, то есть свойства, которые имеют место при (nrightarrow {infty}) (например, состоятельность). Об асимптотических свойствах МНК-оценок мы подробно поговорим в одной из последующих глав. ↵
Гетероскедастичность
Случайной ошибкой
называется отклонение в линейной модели
множественной регрессии:
εi=yi–β0–β1x1i–…–βmxmi
В связи с тем, что
величина случайной ошибки модели
регрессии является неизвестной величиной,
рассчитывается выборочная оценка
случайной ошибки модели регрессии по
формуле:
![]()
где ei – остатки
модели регрессии.
Термин
гетероскедастичность в широком смысле
понимается как предположение о дисперсии
случайных ошибок модели регрессии.
При построении
нормальной линейной модели регрессии
учитываются следующие условия, касающиеся
случайной ошибки модели регрессии:
6) математическое
ожидание случайной ошибки модели
регрессии равно нулю во всех наблюдениях:
![]()
7) дисперсия случайной
ошибки модели регрессии постоянна для
всех наблюдений:
![]()
между значениями
случайных ошибок модели регрессии в
любых двух наблюдениях отсутствует
систематическая взаимосвязь, т. е.
случайные ошибки модели регрессии не
коррелированны между собой (ковариация
случайных ошибок любых двух разных
наблюдений равна нулю):
![]()
Второе условие
![]()
означает
гомоскедастичность (homoscedasticity – однородный
разброс) дисперсий случайных ошибок
модели регрессии.
Под гомоскедастичностью
понимается предположение о том, что
дисперсия случайной ошибки βi является
известной постоянной величиной для
всех наблюдений.
Но на практике
предположение о гомоскедастичности
случайной ошибки βi или остатков модели
регрессии ei выполняется не всегда.
Под гетероскедастичностью
(heteroscedasticity – неоднородный разброс)
понимается предположение о том, что
дисперсии случайных ошибок являются
разными величинами для всех наблюдений,
что означает нарушение второго условия
нормальной линейной модели множественной
регрессии:
![]()
Гетероскедастичность
можно записать через ковариационную
матрицу случайных ошибок модели
регрессии:

Тогда можно
утверждать, что случайная ошибка модели
регрессии βi подчиняется нормальному
закону распределения с нулевым
математическим ожиданием и дисперсией
G2Ω:
εi~N(0; G2Ω),
где Ω – матрица
ковариаций случайной ошибки.
Если дисперсии
случайных ошибок
![]()
модели регрессии
известны заранее, то проблема
гетероскедастичности легко устраняется.
Однако в большинстве случаев неизвестными
являются не только дисперсии случайных
ошибок, но и сама функция регрессионной
зависимости y=f(x), которую предстоит
построить и оценить.
Для обнаружения
гетероскедастичности остатков модели
регрессии необходимо провести их анализ.
При этом проверяются следующие гипотезы.
Основная гипотеза
H0 предполагает постоянство дисперсий
случайных ошибок модели регрессии, т.
е. присутствие в модели условия
гомоскедастичности:
![]()
Альтернативная
гипотеза H1 предполагает непостоянство
дисперсиий случайных ошибок в различных
наблюдениях, т. е. присутствие в модели
условия гетероскедастичности:
![]()
Гетероскедастичность
остатков модели регрессии может привести
к негативным последствиям:
1) оценки неизвестных
коэффициентов нормальной линейной
модели регрессии являются несмещёнными
и состоятельными, но при этом теряется
свойство эффективности;
2) существует большая
вероятность того, что оценки стандартных
ошибок коэффициентов модели регрессии
будут рассчитаны неверно, что конечном
итоге может привести к утверждению
неверной гипотезы о значимости
коэффициентов регрессии и значимости
модели регрессии в целом.
Гомоскедастичность
Гомоскедастичность
остатков означает, что дисперсия каждого
отклонения одинакова для всех значений
x. Если это условие не соблюдается, то
имеет место гетероскедастичность.
Наличие гетероскедастичности можно
наглядно видеть из поля корреляции.


Т.к. дисперсия
характеризует отклонение то из рисунков
видно, что в первом случае дисперсия
остатков растет по мере увеличения x, а
во втором – дисперсия остатков достигает
максимальной величины при средних
значениях величины x и уменьшается при
минимальных и максимальных значениях
x. Наличие гетероскедастичности будет
сказываться на уменьшении эффективности
оценок параметров уравнения регрессии.
Наличие гомоскедастичности или
гетероскедастичности можно определять
также по графику зависимости остатков
от теоретических значений
![]() .
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
[c.85]
Основные положения теории Шарпа. Коэффициенты регрессии. Измерение ожидаемой доходности и риска портфеля. Дисперсия ошибок. Определение весов ценных бумаг в модели Шарпа. Нахождение оптимального портфеля. Сравнительный анализ методов Г. Марковица и В. Шарпа.
[c.335]
Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями.
[c.19]
Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров (п дисперсий ошибок регрессии а ) с помощью п наблюдений.
[c.161]
Решение. Предположим, что дисперсии ошибок о, связаны уравнением регрессии
[c.163]
Вспомним, что наиболее часто употребляемые процедуры устранения гетероскедастичности так или иначе были основаны на предположении, что дисперсия ошибок регрессии ст2 является функцией от каких-то регрессоров. Если а2 существенно зависит от регрессора Z, а при спецификации модели регрессор Z не был включен в модель, стандартные процедуры могут не привести к устранению гетероскедастичности.
[c.250]
В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений X должна быть приблизительно равна необъясненной дисперсии для больших значений X, то есть должно быть справедливым следующее равенство [c.125]
Чем ближе к единице отношение / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = Sl / S2 подчиняется F -распределению
[c.125]
Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора X и отклика 7. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией.
[c.126]
Пятая часть полностью посвящена приложению матричного дифференциального исчисления к линейной регрессионной модели. Она содержит исчерпывающее изложение проблемы оценивания, связанной с неслучайной частью модели при различных предположениях о рангах и других ограничениях. Кроме того, она содержит ряд параграфов, связанных со стохастической частью модели, например оценивание дисперсии ошибок и прогноз ошибок. Включен также небольшой параграф, посвященный анализу чувствительности. Вводная глава содержит необходимые предварительные сведения из теории вероятностей и математической статистики.
[c.16]
Дисперсия ошибок прогноза в задаче (3.6) — (3.7) достигает минимума в точке , являющейся основанием перпендикуляра, опущенного из точки т] на подпространство Q, определяемое равенством (3.7). Соотношение (3.10) эквивалентно равенству
[c.309]
Ограничение (а) не вызывает претензий. Условие (б) также естественно. Ясно, что механизм сглаживания и прогноза, при котором математическое ожидание или дисперсия ошибок фильтрации или интенсивность искусственного рассеивания достаточно велики, вряд ли рационален и тем более не может быть признан оптимальным.
[c.320]
Задача прогнозирования по минимуму дисперсии ошибок при различных статистических характеристиках входных случайных процессов и ошибок измерений подробно обсуждалась в литературе. Имеются и стандартные аналоговые устройства и программы для ЦВМ, реализующие соответствующие схемы. Экстремальная задача, к которой сводится вычисление характеристик генераторов случайных шумов, несомненно, проще исходной вариационной задачи.
[c.334]
Матрица корреляции k j R регулируемых ошибок прогноза, оптимального в смысле показателя качества R( k ), может быть получена из корреляционной матрицы kff a ошибок прогноза, оптимальных в смысле минимума дисперсии ошибок в каждой координате в каждый момент времени, по следующей формуле [c.339]
Из (1.14), в частности, следует, что коэффициент корреляции признаков, на которые наложены ошибки измерения, всегда меньше по абсолютной величине, чем коэффициент корреляции исходных признаков. Другими словами, ошибки измерения всегда ослабляют исследуемую корреляционную связь между исходными переменными, и это искажение тем меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих исходных переменных. Формула (1.14) позволяет скорректировать искаженное значение коэффициента корреляции для этого нужно либо знать разрешающие характеристики измерительных приборов (и, следовательно, величины дисперсий ошибок а и а ), либо провести дополнительное исследование по их выявлению.
[c.73]
Пример 7.4 ]. Известно, что дисперсия о2, вызванная ошибками измерения, при некоторых видах количественного анализа составляет 0,5. Если заменить измерительный прибор и произвести 10-кратное измерение одного и того же стандартного образца, а затем подсчитать дисперсию, то она составит s2 = 0,25. Может показаться, что дисперсия ошибок измерения изменилась, превысив 5%-ный уровень значимости. Так ли это [c.128]
Теорема Гаусса-Маркова. Оценка дисперсии ошибок сг2
[c.41]
Оценка дисперсии ошибок а2
[c.43]
Формулы (2.11), (2.13) дают дисперсии оценок о, Ь коэффициентов регрессии в том случае, если а2 известно. На практике, как правило, дисперсия ошибок а2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а, Ь. В этом случае вместо дисперсий оценок о, b мы можем получить лишь оценки дисперсий о, 6, заменив а2 на s2 из (2.15) в (2.11), (2.13), (2.14) [c.45]
Распределение оценки дисперсии ошибок s2
[c.47]
Так как оценка дисперсии ошибок s2 является функцией от остатков регрессии et, то для того чтобы доказать независимость s2 и (2,6), достаточно доказать независимость et и (2,6). Оценки 2, 6 так же, как и остатки регрессии et, являются линейными функциями ошибок t (см. (2.4а), (2.46), (2.20)) и поэтому имеют совместное нормальное распределение. Известно (приложение МС, п. 4, N4), что два случайных вектора, имеющие совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость s2 и (а, 6), нам достаточно доказать некоррелированность et и (2,6).
[c.48]
Значение Д2 увеличилось по сравнению с первой регрессией. Переход к удельным данным приводит к уменьшению дисперсии ошибок модели.
[c.58]
Пусть SML = Y et/ n и OLS — ] et/ (n — 1 — оценки методов максимального правдоподобия и наименьших квадратов для дисперсии ошибок <т2 в классической модели парной регрессии Yt =
[c.62]
Оценка дисперсии ошибок а1. Распределение s2
[c.72]
Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]
Тест ранговой корреляции Спирмена использует наиболее общие предположения о зависимости дисперсий ошибок регрессии от значений регрессоров [c.158]
Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.
[c.161]
Наиболее простой и часто употребляемый тест на гетероске-дастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е.
[c.161]
Другим недостатком тестов Уайта и Глейзера является то, что факт невыявления ими гетероскедастичности, вообще говоря, не означает ее отсутствия. В самом деле, принимая гипотезу Щ, мы принимаем лишь тот факт, что отсутствует определенного вида зависимость дисперсий ошибок регрессии от значений регрессоров.
[c.166]
Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить.
[c.57]
Доказано (см., например, [37]), что приведенную задачу оптимального стохастического управления можно разделить на две задачу сглаживания и лрогноза по минимуму дисперсии ошибок и задачу оптимального детерминированного управления. При более сложном критерии качества управления и при дополнительных ограничениях на переменные состояния и управляющие параметры такое разделение не всегда удается я, его, по-видимому, не всегда целесообразно производить.
[c.44]
Здесь Paaa(tt, » ) — система функций веса, минимизирующих дисперсию ошибок За(/г-) прогноза W (ti, т) — тождественно не равные нулю функ-22 339
[c.339]
В ходе анализа финансовых данных любой ряд динамики, будь то процентные ставки или цены на финансовые активы, можно разбить на две компоненты, одна из которых изменяется случайным образом, а другая подчиняется определенному закону. Колебания финансовых переменных значительно изменяются во времени бурные периоды с высокой волатильностью переменных сменяют спокойные периоды и наоборот. В некоторых случаях вола-тильность играет ключевую роль в ценообразовании на финансовые активы. В частности, курсы акций напрямую зависят от ожидаемой волатильности доходов корпораций. Все финансовые учреждения без исключения стремятся адекватно оценить волатильность в целях успешного управления рисками. В свое время Трюгве Хаавельмо, нобелевский лауреат по экономике 1989 г., предложил рассматривать изменение экономических переменных как однородный стохастический (случайный) процесс. Вплоть до 1980-х гг. экономисты для анализа финансовых рынков применяли статистические методы, предполагавшие постоянную волатильность во времени. В 1982 г. Роберт Ингл развил новую эконометрическую концепцию, позволяющую анализировать периоды с разной волатильностью. Он ввел кластеризацию данных и условную дисперсию ошибок, которая завесит от времени. Свою разработку Ингл назвал авторегрессионной гетероскедастической моделью , с ее помощью можно точно описать множество временных рядов, встречающихся в экономике. Метод Ингла сегодня применяется финансовыми аналитиками в целях оценки финансовых активов и портфельных рисков.
[c.197]
Отметим, что оценки максимального правдоподобия параметров а, 6 совпадают с оценками метода наименьших квадратов OML = SOLS, ML OLS- Это легко видеть из того, что уравнения (2.37а) и (2.376) совпадают с соответствующими уравнениями метода наименьших квадратов (2.2). Оценка максимального правдоподобия для <т2 не совпадает с
несмещенной оценкой дисперсии ошибок. Таким образом, с = ((п — 2)/n)<7OLS является смещенной, но тем не менее состоятельной оценкой <т2.
[c.57]
В этом разделе мы рассмотрим частный случай обобщенной регрессионной модели, а именно, модель с гетероскедастичностъю, Это означает, что ошибки некоррелированы, но имеют непостоянные дисперсии. (Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной.) Как уже отмечалось, Гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.
[c.168]
