Время на прочтение
6 мин
Количество просмотров 61K

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
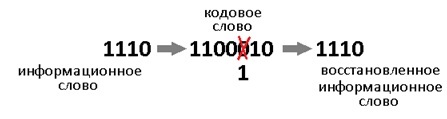
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
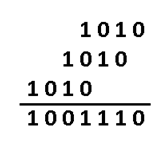
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
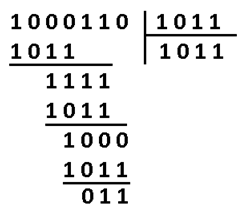
В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):

Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
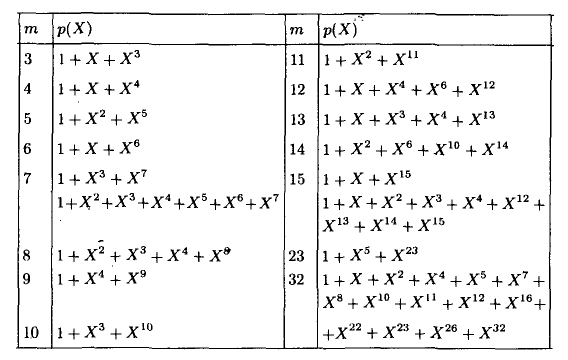
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:

Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Вступление.
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.

На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:
 и
и 
После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:
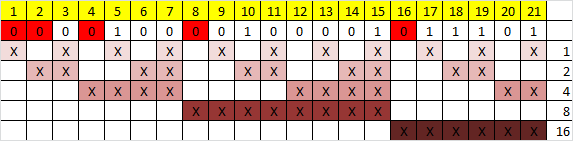
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источники.
1. Википедия
2. Calculating the Hamming Code
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Проблема повышения
верности обусловлена не соответствием
между требованиями, предъявляемыми при
передачи данных и качеством реальных
каналов связи. В сетях передачи данных
требуется обеспечить верность не хуже
10-6— 10-9, а при использовании
реальных каналов связи и простого
(первичного) кода указанная верность
не превышает 10-2— 10-5.
Одним из путей
решения задачи повышения верности в
настоящее время является использование
специальных процедур, основанных на
применении помехоустойчивых
(корректирующих) кодов.
Простые коды
характеризуются тем, что для передачи
информации используются все кодовые
слова (комбинации), количество которых
равно N=qn(q — основание кода, а n —
длина кода). В общем случае они могут
отличаться друг от друга одним символом
(элементом). Поэтому даже один ошибочно
принятый символ приводит к замене одного
кодового слова другим и, следовательно,
к неправильному приему сообщения в
целом.
Помехоустойчивыми
называются коды, позволяющие обнаруживать
и (или) исправлять ошибки в кодовых
словах, которые возникают при передаче
по каналам связи. Эти коды строятся
таким образом, что для передачи сообщения
используется лишь часть кодовых слов,
которые отличаются друг от друга более
чем в одном символе. Эти кодовые слова
называются разрешенными. Все остальные
кодовые слова не используются и относятся
к числу запрещенных.
Построение кода
Хемминга.
Рассмотрим
построение ПУК Хемминга для обнаружения
двух и исправления одной ошибок.
Кодовая группа
состоит из nсимволов,mсимволов используется для передачи
информации, аk=n–mявляются контрольными.
Информационные
символы разбиваются на группы и для
каждой группы при кодировании определяется
контрольный символ (kгрупп).
Контрольные разряды
определяются из позиций кодовой группы
следующим образом:
k1– проверяет все позиции, которые содержат
в 0 разряде 1, т.е. это позиции: 1, 3, 5, 7, 9…
(1, 11, 101, 111, 1001, …);
k2– проверяет все позиции, которые содержат
в 1 разряде 1, т.е. это позиции: 2, 3, 6, 7, 10…
(10, 11, 110, 111, 1010, …);
k3– проверяет все позиции, которые содержат
в 2 разряде 1, т.е. это позиции: 4, 5, 6, 7, 12…
(100, 101, 110, 111, 1100, …) и т.д.
Счёт позиций в ПУК
Хемминга идёт слева направо. Желательно,
чтобы контрольные символы формировались
независимо друг от друга, поэтому
целесообразно их разместить на позициях,
которые встречаются только в одной из
проверяемых групп.
Кодовая группа
выглядит следующим образом:
|
Десятичный |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Двоичный |
0 0 0 0 1 |
0 0 0 1 0 |
0 0 0 1 1 |
0 0 1 0 0 |
0 0 1 0 1 |
0 0 1 1 0 |
0 0 1 1 1 |
0 1 0 0 0 |
0 1 0 0 1 |
0 1 0 1 0 |
0 1 0 1 1 |
0 1 1 0 0 |
0 1 1 0 1 |
0 1 1 1 0 |
0 1 1 1 1 |
1 0 0 0 0 |
1 0 0 0 1 |
1 0 0 1 0 |
1 0 0 1 1 |
1 0 1 0 0 |
|
Символы |
k1 |
k2 |
a1 |
k3 |
a2 |
a3 |
a4 |
k4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
k5 |
a12 |
a13 |
a14 |
a15 |
Контрольные разряды
формируются следующим образом:
k1
= a1
a2
a4
a5
a7
a9
a11
a12
a14…
(входят символы с 1 в 0 разряде
позиции);
k2
= a1
a3
a4
a6
a7
a10
a11
a13
a14…
(входят символы с 1 в 1 разряде
позиции);
k3=a2a3a4a8a9a10a11a15…
(входят символы с 1 во 2 разряде позиции);
k4=a5a6a7a8a9a10a11…
(входят символы с 1 во 3 разряде позиции);
k4=a12a13a14a15…
(входят символы с 1 во 4 разряде позиции).
Построение
циклического ПУК
Циклические ПУК
строятся на основе образующих полиномов
G(x). Образующий
полином должен являться множителем
полиномаxn+1,
гдеn– количество разрядов
кодового слова (k–
количество контрольных разрядов
(разрядностьG(x)
=k+1),m=n–k– количество
информационных разрядов). В каждом
конкретном циклическом ПУК образующий
полином выбирается в соответствии с
корректирующими способностями ПУК.
Строятся циклические
ПУК двумя путями:
-
информационные
разряды помещаются в старшие разряды
кодового слова, а в младшие kразрядов заносится остаток от деленияan-1an-2…an—k00…0
наG(x);
кодовое слово
является результатом умножение
информационного полинома на G(x).
Соседние файлы в папке Госы_2013
- #
- #
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
Слайд 1
Коррекция ошибок при передаче данных
Слайд 2
Символ Двоичный код Кодовое слово 0 1 2 3 4 5 6 7 8 9 Помехоустойчивый код Хемминга основные понятия – кодовое слово
Слайд 3
Символ Двоичный код Кодовое слово 0 0000 0000 1 0001 0001 2 0010 0010 3 0011 0011 4 0100 0100 5 0101 0101 6 0110 0110 7 0111 0111 8 1000 1000 9 1001 1001 Код Хемминга основные понятия – кодовое слово
Слайд 4
Символ Двоичный код Кодовое слово 0 0000 0000 000 1 0001 0001 111 2 0010 0010 110 3 0011 0011 001 4 0100 0100 101 5 0101 0101 010 6 0110 0110 011 7 0111 0111 100 8 1000 1000 011 9 1001 1001 100 Код Хемминга основные понятия – кодовое слово
Слайд 5
Код Хемминга основные понятия – расстояние между двумя словами (количество несовпадений в цифрах) Символ Двоичный код Кодовое слово 0 0000 0000 000 4 1 0001 0001 111 3 2 0010 0010 110 4 3 0011 0011 001 ? 4 0100 0100 101 ? 5 0101 0101 010 3 6 0110 0110 011 ? 7 0111 0111 100 ? 8 1000 1000 011 4 9 1001 1001 100
Слайд 6
Код Хемминга основные понятия – расстояние между двумя словами (количество несовпадений в цифрах) Символ Двоичный код Кодовое слово 0 0000 0000 000 4 1 0001 0001 111 3 2 0010 0010 110 4 3 0011 0011 001 4 4 0100 0100 101 4 5 0101 0101 010 3 6 0110 0110 011 ? 7 0111 0111 100 ? 8 1000 1000 011 4 9 1001 1001 100
Слайд 7
Код Хемминга основные понятия – расстояние между двумя словами (количество несовпадений в цифрах) Символ Двоичный код Кодовое слово 0 0000 0000 000 4 1 0001 0001 111 3 2 0010 0010 110 4 3 0011 0011 001 4 4 0100 0100 101 4 5 0101 0101 010 3 6 0110 0110 011 4 7 0111 0111 100 7 8 1000 1000 011 4 9 1001 1001 100
Слайд 8
АЛГОРИТМ ПОИСКА ПОМЕХ Разделить полученное сообщение на 7-битовые слова 1000011 1001111 0110010 0100101 Сравниваем каждую группу с кодовым словом из кода Хемминга
Слайд 9
1000011 Если полученное слово совпало с кодовым словом в таблице, то сообщение прошло без ошибок Символ Кодовое слово 0 0000 000 1 0001 111 2 0010 110 3 0011 001 4 0100 101 5 0101 010 6 0110 011 7 0111 100 8 1000 011 9 1001 100
Слайд 10
1001111 Если в таблице есть слово, расстояние от которого до полученного равно 1, то полученное слово заменяется на ближайшее к нему из таблицы Символ Кодовое слово 0 0000 000 1 0001 111 2 0010 110 3 0011 001 4 0100 101 5 0101 010 6 0110 011 7 0111 100 8 1000 011 9 1001 100
Слайд 11
0110010 Если в таблице есть слова, расстояние от которого до полученного равно 1, то полученное слово заменяется на ближайшее к нему из таблицы Символ Кодовое слово 0 0000 000 1 0001 111 2 0010 110 3 0011 001 4 0100 101 5 0101 010 6 0110 011 7 0111 100 8 1000 011 9 1001 100
Слайд 12
0100101 Если полученное слово совпало с кодовым словом в таблице, то сообщение прошло без ошибок Символ Кодовое слово 0 0000 000 1 0001 111 2 0010 110 3 0011 001 4 0100 101 5 0101 010 6 0110 011 7 0111 100 8 1000 011 9 1001 100
Слайд 13
Следовательно, передано сообщение: 8164. Если в таблице есть слова, расстояние от которого до полученного равно 2, тогда слово исправить нельзя.
Слайд 14
Практическая часть Реализуйте программу Hemming в системе программирования на Паскале (смотрите стр. 93 — 96). Выполните описанные тесты. ДОМАШНЕЕ ЗАДАНИЕ. § 1.5.3
Помехоустойчивое кодирование. Часть 1: код Хэмминга +33
Программирование
Рекомендация: подборка платных и бесплатных курсов дизайна интерьера — https://katalog-kursov.ru/

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
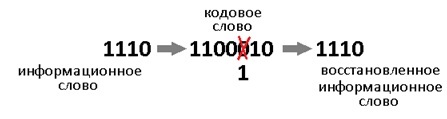
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
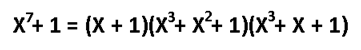
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
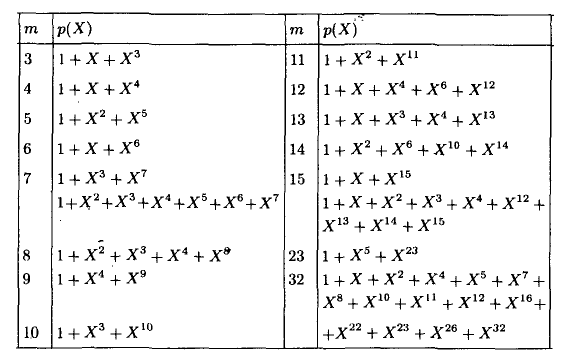
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
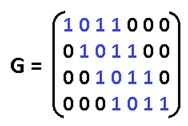
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной 


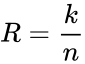
Если исходные 
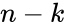
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует 



Это значит, что операция кодирования соответствует умножению исходного 
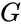
Пусть 

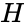

Минимальное расстояние и корректирующая способность
-
Основная статья: Расстояние Хемминга
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 
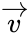


Минимальное расстояние Хемминга 
, округляем «вниз», так чтобы
.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 

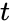
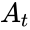


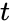

Таким образом получив искажённый код из 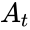

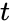
Поясним на примере. Предположим, что есть два кодовых слова 










Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 





Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 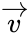
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 


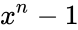
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному 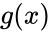
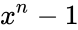
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 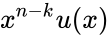
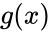
Таким образом, вид полинома 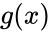
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | 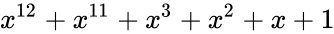
|
| CRC-16 | 16 | 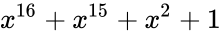
|
| CRC-CCITT | 16 | 
|
| CRC-32 | 32 | 
|
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома 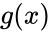
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды
Файл:ECC NASA standard coder.png
Свёрточный кодер (
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
-
Основная статья: Граница Хэмминга
Пусть имеется двоичный блоковый 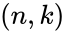
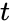
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки
Имеется викиучебник по теме:
Обнаружение и исправление ошибок
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обнаружение и исправление ошибок. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Проблема повышения
верности обусловлена не соответствием
между требованиями, предъявляемыми при
передачи данных и качеством реальных
каналов связи. В сетях передачи данных
требуется обеспечить верность не хуже
10-6— 10-9, а при использовании
реальных каналов связи и простого
(первичного) кода указанная верность
не превышает 10-2— 10-5.
Одним из путей
решения задачи повышения верности в
настоящее время является использование
специальных процедур, основанных на
применении помехоустойчивых
(корректирующих) кодов.
Простые коды
характеризуются тем, что для передачи
информации используются все кодовые
слова (комбинации), количество которых
равно N=qn(q — основание кода, а n —
длина кода). В общем случае они могут
отличаться друг от друга одним символом
(элементом). Поэтому даже один ошибочно
принятый символ приводит к замене одного
кодового слова другим и, следовательно,
к неправильному приему сообщения в
целом.
Помехоустойчивыми
называются коды, позволяющие обнаруживать
и (или) исправлять ошибки в кодовых
словах, которые возникают при передаче
по каналам связи. Эти коды строятся
таким образом, что для передачи сообщения
используется лишь часть кодовых слов,
которые отличаются друг от друга более
чем в одном символе. Эти кодовые слова
называются разрешенными. Все остальные
кодовые слова не используются и относятся
к числу запрещенных.
Построение кода
Хемминга.
Рассмотрим
построение ПУК Хемминга для обнаружения
двух и исправления одной ошибок.
Кодовая группа
состоит из nсимволов,mсимволов используется для передачи
информации, аk=n–mявляются контрольными.
Информационные
символы разбиваются на группы и для
каждой группы при кодировании определяется
контрольный символ (kгрупп).
Контрольные разряды
определяются из позиций кодовой группы
следующим образом:
k1– проверяет все позиции, которые содержат
в 0 разряде 1, т.е. это позиции: 1, 3, 5, 7, 9…
(1, 11, 101, 111, 1001, …);
k2– проверяет все позиции, которые содержат
в 1 разряде 1, т.е. это позиции: 2, 3, 6, 7, 10…
(10, 11, 110, 111, 1010, …);
k3– проверяет все позиции, которые содержат
в 2 разряде 1, т.е. это позиции: 4, 5, 6, 7, 12…
(100, 101, 110, 111, 1100, …) и т.д.
Счёт позиций в ПУК
Хемминга идёт слева направо. Желательно,
чтобы контрольные символы формировались
независимо друг от друга, поэтому
целесообразно их разместить на позициях,
которые встречаются только в одной из
проверяемых групп.
Кодовая группа
выглядит следующим образом:
|
Десятичный |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Двоичный |
0 0 0 0 1 |
0 0 0 1 0 |
0 0 0 1 1 |
0 0 1 0 0 |
0 0 1 0 1 |
0 0 1 1 0 |
0 0 1 1 1 |
0 1 0 0 0 |
0 1 0 0 1 |
0 1 0 1 0 |
0 1 0 1 1 |
0 1 1 0 0 |
0 1 1 0 1 |
0 1 1 1 0 |
0 1 1 1 1 |
1 0 0 0 0 |
1 0 0 0 1 |
1 0 0 1 0 |
1 0 0 1 1 |
1 0 1 0 0 |
|
Символы |
k1 |
k2 |
a1 |
k3 |
a2 |
a3 |
a4 |
k4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
k5 |
a12 |
a13 |
a14 |
a15 |
Контрольные разряды
формируются следующим образом:
k1
= a1
a2
a4
a5
a7
a9
a11
a12
a14…
(входят символы с 1 в 0 разряде
позиции);
k2
= a1
a3
a4
a6
a7
a10
a11
a13
a14…
(входят символы с 1 в 1 разряде
позиции);
k3=a2a3a4a8a9a10a11a15…
(входят символы с 1 во 2 разряде позиции);
k4=a5a6a7a8a9a10a11…
(входят символы с 1 во 3 разряде позиции);
k4=a12a13a14a15…
(входят символы с 1 во 4 разряде позиции).
Построение
циклического ПУК
Циклические ПУК
строятся на основе образующих полиномов
G(x). Образующий
полином должен являться множителем
полиномаxn+1,
гдеn– количество разрядов
кодового слова (k–
количество контрольных разрядов
(разрядностьG(x)
=k+1),m=n–k– количество
информационных разрядов). В каждом
конкретном циклическом ПУК образующий
полином выбирается в соответствии с
корректирующими способностями ПУК.
Строятся циклические
ПУК двумя путями:
-
информационные
разряды помещаются в старшие разряды
кодового слова, а в младшие kразрядов заносится остаток от деленияan-1an-2…an—k00…0
наG(x);
кодовое слово
является результатом умножение
информационного полинома на G(x).
Соседние файлы в папке Госы_2013
- #
- #
Аннотация[править]
Здесь мы рассмотрим основные принципы и методы надёжной и
эффективной передачи данных между двумя машинами, соединёнными
каналом. Под каналом следует понимать любую физическую среду
передачи данных. Посредством этой физической среды
нужно научиться передавать биты так, чтобы они безошибочно
принимались получателем точно в той последовательности,
в какой они были переданы.
Канальный уровень[править]
На уровне канала данных решается ряд проблем, присущих
только этому уровню:
- реализация сервиса для сетевого уровня,
- разбиение потока бит на кадры,
- управление потоком кадров,
- обработка ошибок передачи.
Основная задача канального уровня — обеспечить сервис сетевому уровню,
а это значит помочь передать данные с сетевого уровня одной машины на
сетевой уровень другой машины.
Разбиение на кадры[править]
Сервис, создаваемый канальным уровнем для сетевого, опирается на
сервис, создаваемый физическим уровнем. На физическом уровне
протекают потоки битов. Значение посланного бита не обязательно
равно принятому, и количество посланных битов не обязательно
равно количеству принятых. Всё это требует специальных усилий на
канальном уровне по обнаружению и исправлению ошибок.
Типовой подход к решению этой проблемы — разбиение потока битов
на кадры и подсчёт контрольной суммы для каждого кадра при
посылке данных.
Контрольная сумма — это, в общем смысле, функция от
содержательной части кадра (слова длины 
значений которой — слова фиксированной длины 
Эти r бит добавляются обычно в конец кадра. При приёме
контрольная сумма вычисляется заново и сравнивается с той, что
хранится в кадре. Если они различаются, то это признак ошибки
передачи. Канальный уровень должен принять меры к исправлению
ошибки, например, сбросить плохой кадр, послать сообщение об
ошибке тому кто прислал этот кадр. Разбиение потока битов на
кадры — задача не простая. Один из способов — делать
временную паузу между битами разных кадров. Однако, в сети, где
нет единого таймера, нет гарантии, что эта пауза сохранится или,
наоборот, не появятся новые. Так как временные методы ненадёжны,
то применяются другие. Здесь мы рассмотрим три основных:
- счетчик символов;
- вставка специальных стартовых и конечных символов или последовательностей бит;
- специальная кодировка на физическом уровне.
Первый метод очевиден. В начале каждого кадра указывается сколько
символов в кадре. При приёме число принятых символов
подсчитывается опять. Однако, этот метод имеет существенный
недостаток — счётчик символов может быть искажён при передаче.
Тогда принимающая сторона не сможет обнаружить границы кадра.
Даже обнаружив несовпадение контрольных сумм, принимающая
сторона не сможет сообщить передающей какой кадр надо переслать,
сколько символов пропало. Этот метод ныне используется редко.
Второй метод построен на вставке специальных символов.
Обычно для этого используют управляющие последовательности:
последовательность 
для конца кадра. 

TeXt, 
потеряна граница текущего кадра, надо просто искать
ближайшую последовательность 



нужно избегать появления этих комбинаций внутри самого тела
кадра. Это осуществляется дублированием комбинаций 
встречающихся внутри тела кадра, и удаление дублей после
получения кадра. Недостатком этого метода является
зависимость от кодировки (кодозависимость).
По мере развития сетей эта связь становилась все более и более
обременительной и был предложен новый очевидный кодонезависимый
метод — управляющие последовательности должны быть
бит-ориентированными. В частности, в протоколе 
начинается и заканчивается со специального флаг-байта: 01111110.
Посылающая сторона, встретив последовательно 5 единиц внутри тела
кадра, обязательно вставит 0. Принимающая сторона, приняв 5
последовательных единиц обязательно удалит следующий за ними 0,
если таковой будет. Это называется bit-stuffing. Если
принято шесть и за ними следует ноль, то это управляющий сигнал:
начало или конец кадра, а в случае, когда подряд идут более шести
единиц, — сигнал ожидания или аварийного завершения.
(а) 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 (б) 0 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1
Bit Stuffing. (a) исходные данные (б) посылаемые данные. Жирным отмечены вставленные нули.
Таким образом, кадр легко может быть распознан по
флаг-байту. Если граница очередного кадра по какой-то
причине была потеряна, то все что надо делать — ловить
ближайший флаг-байт.
И наконец, последний метод используется там, где конкретизирована
физическая среда. Например, в случае проводной связи для передачи
одного бита используется два импульса. 1 кодируется как переход
высокое-низкое, 0 — как низкое-высокое. Сочетания низкое-низкое
или высокое-высокое не используются для передачи данных, и их
используют для границ кадра.
На практике используют, как правило, комбинацию этих методов.
Например, счётчик символов с флаг-байтами. Тогда, если число
символов в кадре соответствует кодировке границы кадра, кадр
считается переданным правильно.
Контроль ошибок[править]
Решив проблему разбиения на кадры, мы приходим к следующей
проблеме: как обеспечить, чтобы кадры, пройдя по физическому
каналу с помехами, попадали на сетевой уровень по назначению, в
надлежащей последовательности и в надлежащем виде?
Частичное решение этой проблемы осуществляется посредством
введения обратной связи между отправителем и получателем в
виде кадра подтверждения, а также специального кодирования,
позволяющего обнаруживать или даже исправлять ошибки
передачи конкретного кадра.
Если кадр-подтверждение несет положительную информацию, то
считается что переданные кадры прошли нормально, если там
сообщение об ошибке, то переданные кадры надо передать
заново.
Однако, возможны случаи когда из-за ошибок в канале
кадр исчезнет целиком. В этом случае получатель не будет
реагировать никак, а отправитель будет сколь угодно долго ждать
подтверждения. Для решения этой проблемы на канальном уровне
вводят таймеры. Когда передаётся очередной кадр, то одновременно
устанавливается таймер на определённое время. Этого времени должно
хватать на то, чтобы получатель получил кадр, а отправитель
получил подтверждение. Если отправитель не получит подтверждение
раньше, чем истечёт время, установленное на таймере то он будет
считать, что кадр потерян и повторит его еще раз.
Однако, если кадр-подтверждение был утерян, то вполне возможно, что один и
тот же кадр получатель получит дважды. Как быть? Для решения
этой проблемы каждому кадру присваивают порядковый номер. С
помощью этого номера получатель может обнаружить дубли.
Итак, таймеры, нумерация кадров, флаг-байты,
кодирование и обратная связь — вот основные средства на канальном уровне,
обеспечивающие надёжную доставку каждого кадра до сетевого
уровня в единственном экземпляре. Но и с помощью этих
средств невозможно достигнуть стопроцентной надёжности
передачи.
Управление потоком[править]
Другая важная проблема, которая решается на канальном уровне
— управление потоком. Вполне может
случиться, что отправитель будет слать кадры столь часто, что
получатель не будет успевать их обрабатывать(например, если
машина-отправитель более мощная или загружена слабее, чем
машина-получатель). Для борьбы с такими ситуациями вводят
управления потоком. Это управление предполагает обратную связь
между отправителем и получателем, которая позволяет им
урегулировать такие ситуации. Есть много схем управления потоком
и все они в основе своей имеют следующий сценарий: прежде, чем
отправитель начнёт передачу, он спрашивает у получателя сколько
кадров тот может принять. Получатель сообщает ему определённое
число кадров. Отправитель после того, как передаст это число
кадров, должен приостановить передачу и снова спросить получателя,
как много кадров тот может принять, и т.д.
Помехоустойчивое кодирование[править]
Характеристики ошибок[править]
Физическая среда, по которой передаются данные, не может быть
абсолютно надёжной. Более того, уровень шума бывает очень
высоким, например в беспроводных системах связи и телефонных
системах. Ошибки при передаче — это реальность, которую
надо обязательно учитывать.
В разных средах характер помех разный. Ошибки могут быть
одиночные, а могут возникать группами, сразу по несколько. В
результате помех могут исчезать биты или наоборот — появляться
лишние.
Основной характеристикой интенсивности помех в канале
является параметр шума — p. Это число от 0 до 1, равное
вероятности инвертирования бита, при условии, что он был
передан по каналу и получен на другом конце.
Следующий параметр — 
события, но при условии, что предыдущий бит также был
инвертирован.
Этими двумя параметрами вполне можно ограничиться при построении
теории. Но, в принципе, можно было бы учитывать аналогичные
вероятности для исчезновения бита, а также использовать полную
информацию о пространственной корреляции ошибок, — то есть
корреляции соседних ошибок, разделённых одним, двумя или более
битами.
У групповых ошибок есть свои плюсы и минусы. Плюсы
заключаются в следующем. Пусть данные передаются блоками по
1000 бит, а уровень ошибки 0,001 на бит. Если ошибки
изолированные и независимые, то 63 % (
возникают группами по 100 сразу, то ошибки будут содержать
1 % (
Зато, если ошибки не группируются, то в каждом кадре они невелики,
и есть возможность их исправить. Групповые ошибки портят
кадр безвозвратно. Требуется его повторная пересылка, но в
некоторых системах это в принципе невозможно, — например,
в телефонных системах, использующие цифровое кодирование,
возникает эффект пропадания слов/слогов.
Для надёжной передачи кодов было предложено два основных метода.
Первый — добавить в передаваемый блок данных нескольких «лишних» бит так, чтобы, анализируя
полученный блок, можно было бы сказать, есть в переданном
блоке ошибки или нет. Это так называемые коды с обнаружением ошибок.
Второй — внести избыточность настолько, чтобы,
анализируя полученные данные, можно не только замечать
ошибки, но и указать, где именно возникли искажения. Это
коды, исправляющие ошибки.
Такое деление условно. Более общий вариант — это коды,
обнаруживающие k ошибок и исправляющие l ошибок, где

* Элементы теории передачи информации[править]
Информационным каналом называется пара зависимых
случайных величин 
называется входом другая выходом канала. Если случайные величины
дискретны и конечны, то есть имеют конечные множества событий:
то канал определяется матрицей условных вероятностей


будет значение 
значение 
Входная случайная величина определяется распределением


выходе вычисляется по формуле
Объединённое распределение на

Информация 
канал, есть взаимная информация входа и выхода:
(eq:inf)
где
Если случайные величины 

есть 


((eq:inf)) можно из следующего соображения: энтропия случайной
величины равна информации, которую мы получаем при одном её
измерении. 

содержится по отдельности во входе и в выходе. Но часть этой
информации общая, её нам и нужно найти.
равна величине объединённой информации. В теории
меры[1] есть выражение
аналогичное ((eq:inf)):
Распределение входной случайной величины 
варьировать и получать различные значения I. Её максимум
называется пропускной способностью канала
(eq:cdef)
Эта функция есть решение задачи
Задача 1.
(task:shanon) Каково максимальное количество информации,
которое можно передать с одним битом по каналу

Конец задачи.
Итак, пропускная способность есть функция на множестве стохастических матриц[2].
Стандартный информационный канал это
(eq:sm)
То есть канал с бинарным алфавитом и вероятностью помехи p
(p — вероятность того, что бит будет случайно
инвертирован). Его пропускная способность равна
Эта функция является решением задачи на максимум ((eq:cdef))
для матрицы ((eq:sm)).
begin{figure}[t!]
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/cideal.eps} caption{ 
Пропускная способность канала как функция вероятности
инвертирования бита.} (fig:cideal)
end{figure}
Эта функция 
помехоустойчивого кодирования — если мы хотим с абсолютной
надёжностью передать по каналу с пропускной способностью C
сообщение длиной m, то минимальное количество бит, которое нам
нужно будет передать 
помехоустойчивое кодирование, обеспечивающее вероятность
незамеченной ошибки в переданном слове меньше, чем 
раздувает данные в 
Кодирование, при котором в этом пределе достигается
равенство, называется эффективным. Отметим, что
абсолютно надёжного способа передачи конечного количества
данных по каналу с помехами не существует: то есть

Задача дуальная (task:shanon) формулируется следующим
образом
Задача 2.
(task:dual)
Мы хотим передавать информацию со скоростью V по каналу с
пропускной способностью C. Какова минимальная вероятность
ошибочной передачи одного бита?
Конец задачи.
Решением будет функция заданная неявно




Оказывается, вероятность ошибки растет не так уж и быстро.
Например, если по каналу передавать данных в два раза
больше, чем его пропускная способность, то лишь 11 бит из
ста будут переданы с ошибкой.
begin{figure}[t!]
psfrag{v}{v} psfrag{p}{ 
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/pv.eps} caption{ 
минимальная вероятность ошибки в одном бите как функция от
отношения скорости передачи и пропускной способности 
(fig:pv)
end{figure}
Построение конкретных способов кодирования, приближающихся
по пропускной способности к теоретической границе —
сложная математическая задача.
Метод «чётности» и общая идея[править]
Простым примером
кода с обнаружением одной ошибки является код с битом чётности.
Конструкция его такова: к исходному слову добавляется бит
чётности. Если в исходном слове число единичек чётно, то значение
этого бита 0, если нечётно — 1. Таким образом допустимые слова
этого кода имеют чётное количество единичек. Если получено слово
с нечётным количеством единичек, то при передаче произошла ошибка.
В случае вероятных групповых ошибок эту технику можно
скорректировать. Разобъём передаваемые данные на n слов по k
бит и расположим их в виде матрицы 
каждого столбца вычислим бит чётности и разместим его в
дополнительной строке. Матрица затем передается по строкам. По
получению матрица восстанавливается, и если обнаруживется
несоответствие, то весь блок передается повторно. Этот метод
позволяет обнаружить групповые ошибки длины 
Задача 3.
Слово длиной n с чётным количеством единиц передано по каналу с
уровнем шума p. Покажите, что вероятность того, что при
передаче произошли ошибки и мы их не заметили равна
Что можно привести к виду
Например, при 


Конец задачи.
Следующая задача повышенной сложности.
Задача 4. (task:errmod) Пусть у нас есть возможность контролировать
сумму единичек по модулю d. Тогда вероятность нефиксируемых
ошибок в слове длиной n при передаче его по каналу с шумом p
равна 
Примечание. Интерес здесь представляет неявно
заданная функция 
содержания полезной информации

бит как функция от величины шума и вероятности незамеченных
ошибок. Чем выше желаемая надёжность передачи, то есть чем меньше
вероятность 
полезной информации.
Конец задачи.
Итак, с помощью одного бита чётности мы повышаем надёжность
передачи, и вероятность незамеченной ошибки равна

При 

дублированию каждого бита. Рассмотрим общую идею того, как с
помощью специального кодирования можно добиться сколь угодно
высокой надёжности передачи.
Общая идея На множестве слов длины n определена
метрика Хемминга: расстояние Хемминга между двумя словами
равно количеству несовпадающих бит. Например,
Задача 5.
Докажите, что 
Конец задачи.
Если два слова находятся на расстоянии r по Хеммингу,
это значит, что надо инвертировать ровно r разрядов, чтобы
преобразовать одно слово в другое. В описанном ниже
кодировании Хемминга любые два различных допустимых слова
находятся на расстоянии 
обнаруживать d ошибок, то надо, чтобы слова отстояли друг
от друга на расстояние 
исправлять ошибки, то надо чтобы кодослова отстояли друг от
друга на 
переданное слово содержит d ошибок, оно, как следует из
неравенства треугольника, все равно ближе к правильному
слову, чем к какому-либо еще, и следовательно можно
определить, исходное слово. Минимальное расстояние Хемминга
между двумя различными допустимыми кодовыми словами
называется расстоянием Хемминга данного кода.
Элементарный пример помехоустойчивого кода — это код, у
которого есть только четыре допустимых кодовых слова:
Расстояние по Хеммингу у этого кода 5, следовательно он может
исправлять двойные ошибки и замечать 4 ошибки. Если получатель
получит слово 0001010111, то ясно, что исходное слово имело
вид 0000011111. Коэффициент раздувания равен 5. То есть
исходное слово длины m будет кодироваться в слово длины 
Отметим что имеет смысл говорить о двух коэффициентах:
Первый есть функция от переменной n, а второй, обратный
ему, — от переменной m.
Здесь мы подошли к довольно трудной задаче —
минимизировать коэффициент раздувания для требуемой
надёжности передачи. Она рассматривается в разделе (theory).
Циклические коды[править]
На практике активно применяются полиномиальные коды
или циклические избыточные коды (Cyclic Redundancy Code
— CRC).
CRC коды построены на рассмотрении битовой строки как
строки коэффициентов полинома. k-битовая строка
соответствует полиному степени 
— коэффициент при старшей степени. Например, строка 110001
представляет полином 
принадлежат полю 
Основная идея заключена в том, чтобы пересылать только такие
сообщения, полиномы которых делятся на некоторый фиксированный
полином 
на 
ошибок, если они один допустимый полином (то есть полином
делящийся на 
Полином 
на парах допустимых полиномов.
Есть два очевидных способа кодирования сообщения в полином,
который делится на 
сообщения на 
количество бит так, чтобы результирующий полином делился на

Отправитель и получатель заранее договариваются
о конкретном полиноме-генераторе 

равна l.
Мы добавляем контрольные l бит в конец передаваемого
блоку так, чтобы получился полином кратный генератору

он проверяет его делимость на G. Если есть остаток 
Алгоритм кодирования CRC:
Дано слово W длины m. Ему соответствует полином 
- Добавить к исходному слову W справа r нулей. Получится слово длины
и полином :
- Разделить полином
на
и вычислить остаток от деления
:
- Вычесть остаток (вычитание в
то же самое, что и сложение) из полинома
:
Слово, которое соответствует полиному
, и есть результат.
Рис. (fig:crc) иллюстрирует этот алгоритм для блока
1101011011 и 
begin{figure}[h!]
psfrag{Remainder}{Остаток}
centeringparbox{0.66textwidth}{
begin{tabular}{lcl}
Слово&:&1101011011 \
Результат&:&11010110111110
end{tabular}}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/crc2.eps}
caption{CRC — полиномиальное кодирование}
(fig:crc)
end{figure}
Этот метод позволяет отлавливать одиночные ошибки и
групповые ошибки длины не более степени полинома.
Существует три международных стандарта на вид 

Два остальных — для 8 разрядных. 

одиночные, двойные ошибки, групповые ошибки длины не более 16 и
нечётное число изолированных ошибок с вероятностью 0.99997.
* Теоретический предел[править]
(theory) В примечании
к задаче (task:errmod) было указано как можно получить
значение коэффициента содержания полезной информации (КПС) на
один бит, если передавать данные по каналу с шумом p словами
длиной n бит, при условии, чтобы вероятность незамеченной
ошибки была меньше 
Но ясно, что указанная там функция дает лишь оценку снизу
оптимального значения КПС
— возможно, существует другие методы контролирования
ошибок, для которых он выше. Теория информации позволяет нам
найти точное значение этого коэффициента.
Сформулируем задачу о кодировании, обнаруживающем ошибки.
Для начала предположим, что наличие ошибки фиксируется с
абсолютной точностью.
Задача 6.
(task:err)
Мы хотим передавать информацию блоками, которые содержали
бы m бит полезной информации, так, чтобы
вероятность ошибки в одном бите равнялась p, а
правильность передачи «фиксировалось контрольной суммой». Найти
минимальный размер блока 

Конец задачи.
Решение.
Для передачи m бит с вероятностью ошибки в отдельном бите
p требуется передать 
(см. задачу (task:dual)). Кроме того мы хотим сообщать
об ошибке в передаче. Её вероятность равна 
значит информация, заложенная в этом сообщении,


Конец решения.
Заметим, что 
сообщение об ошибке в нём равносильно передаче самого бита.
Если передавать эти сообщения по каналу с уровнем помех p, то
количество бит на одно сообщение равно 
теоретическая оценка для количества лишних бит равна
Понятно, что данная теоретическая оценка занижена.
Коды Хэмминга[править]
Элементарный пример кода исправляющего ошибки был показан на
странице pageref{simplecode}. Его обобщение очевидно. Для
подобного кода, обнаруживающего одну ошибку, КПС равен 
единице с помощью кодов Хемминга. В частности, при кодировании
11 бит получается слово длинной 15 бит, то есть

Оценим минимальное количество контрольных
разрядов, необходимое для исправления одиночных ошибок. Пусть
содержательная часть составляет m бит, и мы добавляем ещё r
контрольных. Каждое из 
его неправильных вариантов с ошибкой в одном бите. Такими
образом, с каждым из 
слов и эти множества не должны пересекаться. Так как общее число
слов 
Этот теоретический предел достижим при использовании
метода, предложенного Хеммингом. Идея его в следующем: все
биты, номера которых есть степень 2, — контрольные,
остальные — биты сообщения. Каждый контрольный бит
отвечает за чётность суммы некоторой группы бит. Один и тот
же бит может относиться к разным группам. Чтобы определить
какие контрольные биты контролируют бит в позиции k надо
разложить k по степеням двойки: если 
бит относится к трём группам — к группе, чья чётность
подсчитывается в 1-ом бите, к группе 2-ого и к группе 8-ого
бита. Другими словами в контрольный бит с номером
заносится сумма (по модулю 2) бит с номерами, которые имеют
в разложении по степеням двойки степень 
(eq:hem)
Код Хемминга оптимален при 

![{displaystyle m=n-[log _{2}(n+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d24a7d287da182a9c3ab18a6fbd87ef3988a6b9)
![{displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)


n однозначно определяет m).
Пример для 
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle fbox{10110100111}to fbox{fbox{0}fbox{0}1fbox{1}011fbox{0}0100111} }
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle hphantom{fbox{10110100111}to};; lefteqn{,b_1}hphantom{fbox{0}} lefteqn{,b_2}hphantom{fbox{0}} lefteqn{b_3}hphantom{1} lefteqn{;b_4}hphantom{fbox{1}011} lefteqn{,b_8}hphantom{fbox{0}} lefteqn{b_9}hphantom{010011} lefteqn{b_{15}}hphantom{1} }
Получив слово,
получатель проверяет каждый контрольный бит на предмет
правильности чётности и складывая номера контрольных бит, в
которых нарушена чётность. Полученное число, есть XOR номеров
бит, где произошла ошибка. Если ошибка одна, то это число есть
просто номер ошибочного бита.
Например, если в контрольных разрядах 1, 2, 8 обнаружено
несовпадение чётности, то ошибка в 11 разряде, так как
только он связан одновременно с этими тремя контрольными
разрядами.
begin{figure}[h!]
psfrag{Check bits}{hspace{-12mm}Контрольные биты}
centeringincludegraphics[clip=true,
width=0.65textwidth]{pictures/hem.eps} caption{Кодирование
Хемминга} (fig:hem)
end{figure}
Задача 7.
Покажите, что 

Конец задачи.
Код Хемминга может исправлять только единичные ошибки. Однако,
есть приём, который позволяет распространить этот код на случай
групповых ошибок. Пусть нам надо передать k кодослов.
Расположим их в виде матрицы одно слово — строка. Обычно,
передают слово за словом. Но мы поступим иначе, передадим слово
длины k, из 1-ых разрядов всех слов, затем — вторых и т. д. По
приёме всех слов матрица восстанавливается. Если мы хотим
обнаруживать групповые ошибки размера k, то в каждой строке
восстановленной матрицы будет не более одной ошибки. А с
одиночными ошибками код Хемминга справится.
Анализ эффективности[править]
Начнём c небольшого примера. Пусть у нас есть канал с уровнем
ошибок 
передаче блоками по 
10 контрольных бит: 1, 2, dots, 
приходится 1013 бит полезной информации. При передаче 1000
таких блоков потребуется 
В тоже время для обнаружения единичной ошибки достаточно одного
бита чётности. И если мы применим технику повторной передачи, то
на передачу 1000 блоков надо будет потратить 1000 бит
дополнительно и примерно 
повторно. То есть на 1000 блоков приходится один попорченый, и
дополнительная нагрузка линии составляет 

Хемминга плох для такого канала. Надо правильно выбрать длину
блока — если 
Рассмотрим этот вопрос подробнее. Пусть нам нужно передать
информацию M бит. Разобьем её на L блоков по 
и будем передавать двумя способами
— с помощью кодов Хемминга и без них. При этом будем
считать, что в обоих случаях осуществлено предварительное
кодирование, позволяющее с вероятностью
определять ошибочность передачи. Это осуществляется путем
добавления «лишней» информации. Обозначим коэффициент
раздувания для этого кодирования 
этого кодирования каждый блок несёт информацию

1) Без кода Хемминга.
Если пересылать информацию
блоками по 
обнаружения ошибки, то получим, что в среднем нам придётся
переслать D бит:
Где 
повторной передачи равная вероятности ошибки умноженной на
вероятность того, что мы её заметим. Коэффициент раздувания
равен
2) С кодом Хемминга.
При кодировании методом Хемминга слова длины 
(eq:hnm)
Для отдельного блока вероятность
безошибочной передачи равна 
одинарной ошибки 
что произошло более чем одна ошибка, и мы это заметили
— в этом случае требуется повторная передача кадра.
Количество передаваемых данных:
И коэффициент раздувания
где 
функция. Удобно записать соответствующие коэффициенты
полезного содержания:
,
(eq:kps)
Легко обнаружить что при 

оказывается эффективнее, то есть 
begin{figure}[h!]
psfrag{knc}{кпс} psfrag{n}{n}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps.eps}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps2.eps} caption{

в канале с помехами как функция размера элементарного блока.}
parbox{0.85textwidth}{small Светлый график — без кодирования Хемминга;\
Темный график — с кодированием Хемминга;
\Параметры: 

(fig:kps)
end{figure}
begin{figure}[h!]
psfrag{C}{C} psfrag{p}{p}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/kpseff.eps}
caption{
содержания в канале с помехами как функция уровня помех.}
parbox{0.97textwidth}{ small Светлый график — без кодирования Хемминга;\ Темный график — с кодированием Хемминга;\Тонкий график — теоретический
предел, задаваемый функцией 

end{figure}
Значение 
формулах ((eq:kps)) можно оценить как
Напомним, что 
надёжности передачи
— чем меньше 
По определению 
ошибочной передачи блока при условии, что «контрольная сумма
сошлась» и кадр засчитан правильно переданным.
Такое выражение для
получается из формулы
Но это безусловно лишь оценочная формула. Оптимальное
значение 
зависит от p.
Из графика на рисунке (fig:kps) хорошо видно, что при
больших n код Хемминга начинает работать на пользу.
Но зависимость КПС от n не есть критерий эффективности
кода. Эффективность кода определяется функцией
На рисунке (fig:kpseff) показан график этой функции и из
него ясно, что код Хемминга можно использовать с пользой
всегда — при любых 
возможность выбирать подходящее n.
Коды как линейные операторы[править]
То, что на множестве {0,1} есть структура числового поля,
позволяет осуществлять алгебраические интерпретации кодирования.
Заметим, в частности, что как коды Хемминга, так и циклические
коды линейны:\ 1) отношения ((eq:hem)) на
с. pageref{eq:hem}, связывающие контрольные биты кода Хемминга с
другими линейны,\ 2) остаток от деления суммы многочленов на
третий равен сумме остатков.\ То есть кодирование в этих двух
случаях есть линейное отображение из 

матрица кода Хемминга 
соотношения ((eq:hem))). Исходное слово есть

(слова соответствуют столбцам).
Процесс выявления ошибок тоже линейная операция, она
осуществляется с помощью проверочной матрицы 
Пусть принято слово 

случае правильной передачи должно быть равно 000. Значение

слова 
((eq:hem)) и, таким образом, 
бит в которых произошла ошибка, как векторов в 
Заметим, что столбцы проверочной матрицы представляют собой
последовательно записанные в двоичной форме натуральные
числа от 1 до 7.
Вычиcление рабочей матрицы для циклических кодов
основывается на значениях 
её часть равна единичной, так m бит сообщения помещаются
без изменения в начало слова, а нижние r строчек есть m
столбцов высоты r состоящие из коэффициентов многочленов


dots, 




Рабочая и проверочная матрицы равны
то есть
Кроме рабочей и проверочной матриц есть ещё множество порождающих матриц 

слова образуют линейное подпространство 

которой образуют базис этого подпространства, называется
порождающей. В частности, рабочая матрица является порождающей.
Способность обнаруживать и исправлять ошибки однозначно
определяется подпространством L. Порождающих, рабочих и
проверочных матриц соответствующих L несколько.
Действительно, в порождающей и рабочей матрицах можно осуществлять
элементарные операции со столбцами, а в проверочной — со
строчками. Матрицы 

всегда удовлетворяют отношениям
где


Любая порождающая матрица может использоваться как
рабочая.
Декодирующая матрица 

таким свойством может быть несколько. Множество декодирующих
матриц определяется рабочей матрицей:
где 

подпространстве L все декодирующие матрицы действуют одинаково.
Они отличаются на подпространстве ортогональном L. Приведём
декодирующую матрицу для 

К каждой строчке декодирующей матрицы можно добавить любую
линейную комбинацию строчек из проверочной матрицы. Следует
отметить, что процесс исправления ошибок для кодов Хемминга
нелинеен и его нельзя «внедрить» в декодирующую матрицу.
Сформулируем теперь основные моменты, касающиеся линейных кодов.
- Процесс кодирования и декодирования — линейные операторы. :
- Обнаружение ошибок равносильно проверке принадлежности полученного слова подпространству L допустимых слов. Для этого необходимо найти проекцию
(синдром ошибки) полученного слова на
— тоже линейная операция. Для правильно переданного слова
. :
- В случае, когда векторы подпространства L достаточно удалены друг от друга в смысле метрики Хемминга, есть возможность обнаруживать и исправлять некоторые ошибки. В частности, значение синдрома ошибки в случае кода Хемминга равно векторной сумме номеров бит, где произошла ошибка.
- Комбинация (композиция) линейных кодов есть снова линейный код.
Практические методы помехоустойчивого кодирования все основаны на
линейных кодах. В основном это модифицированные CRC, коды
Хемминга и их композиции. Например 
чётность. Такой код может исправлять уже две ошибки. Построение
эффективных и удобных на практике задача сходная с творчеством
художника. На практике важны не только корректирующая способность
кода, но и вычислительная сложность процессов кодирования и
декодирования, а также спектральная характеристика
результирующего аналогового сигнала. Кроме того, важна
способность исправлять специфические для данного физического
уровня групповые ошибки.
Задача 8.
Для данной проверочной матрицы постройте рабочую и декодирующую
матрицу. Докажите, что кодовое расстояние равно 4.
Подсказка
- Это проверочная матрица
плюс условие на чётность числа единичек в закодированном слове вместе с дополнительным восьмым контрольным битом.
- Кодовое расстояние равно минимальному количеству линейно зависимых столбцов в
.
Конец задачи.
Задача 9.
Посторойте декодирующую и проверочную матрицу для циклического
кода с 

рабочей матрицы использовалась матрица
Конец задачи.
*Коды Рида-Соломона[править]
После перехода на язык линейной алгебры естественно возникает
желание изучить свойства линейных кодов над другими конечными
числовыми полями. С помощью такого обобщения появились коды
Рида-Соломона.
Коды Рида-Соломона являются циклическими кодами над
числовым полем отличным от 
Напомним, что существует бесконечное количество конечных полей, и
количество элементов в конечном поле всегда равно степени
простого числа. Если мы зафиксируем число элементов 
найдётся единственное с точностью до изоморфности конечное поле с
таким числом элементов, которое обозначается как

многочленов по модулю неприводимого[3] многочлена 
полем 
многочленов с действительными коэффициентами неприводимыми
многочленами являются только квадратные многочлены с
отрицательным дискриминантом. Поэтому существует только
квадратичное расширение действительного поля — комплексные
числа. А над конечным полем существуют неприводимые многочлены
любой степени. В частности, над 

модулю 

Примеры протоколов канала данных[править]
HDLC протокол[править]
Здесь мы познакомимся с группой протоколов давно известных, но
по-прежнему широко используемых. Все они имеют одного
предшественника — SDLC (Synchronous Data Link Control) —
протокол управления синхронным каналом, предложенным фирмой IBM
в рамках SNA. ISO модифицировала этот протокол и выпустила
под названием HDLC — High level Data Link Control. MKTT
модифицировала HDLC для X.25 и выпустила под именем LAP —
Link Access Procedure. Позднее он был модифицирован в LAPB.
Все эти протоколы построены на одних и тех же принципах. Все
используют технику вставки специальных последовательностей
битов. Различия между ними незначительные.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/frame.eps} caption{Типовая
структура кадра} (fig:frame)
end{figure}
На рис. (fig:frame) показана типовая структура кадра.
Поле адреса используется для адресации терминала, если их
несколько на линии. Для линий точка-точка это поле
используется для различия команды от ответа.
- Поле Control используется для последовательных номеров кадров, подтверждений и других нужд.
- Поле Data может быть сколь угодно большим и используется для передачи данных. Надо только иметь ввиду, что чем оно длиннее тем, больше вероятность повреждения кадра на линии.
- Поле Checksum — это поле используется CRC кодом.
Флаговые последовательности 01111110 используются для
разделения кадров и постоянно передаются по незанятой линии
в ожидании кадра. Существуют три вида кадров: 

Организация поля Control для этих трех видов кадров показана на
рис. (fig:cfield). Как видно из размера поля Seq в окне
отправителя может быть до 7 неподтверждённых кадров. Поле
Next используется для посылки подтверждения вместе с
передаваемым кадром. Подтверждение может быть в форме номера
последнего правильно переданного кадра, а может быть в форме
первого не переданного кадра. Какой вариант будет использован —
это параметр.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/cfield.eps} caption{Cтруктура поля
Control}
parbox{0.66textwidth}{small (а) Информационный кадр (
(б) Управляющий кадр (
кадр (Unnumbered) }
(fig:cfield)
end{figure}
Разряд 
Когда компьютер приглашает терминал к передаче он
устанавливает этот разряд в P. Все кадры, посылаемые
терминалами имеют здесь P. Если это последний кадр,
посылаемый терминалом, то здесь стоит F.

- Тип 0 — уведомление в ожидании следующего кадра (RECEIVE READY). Используется когда нет встречного трафика, чтобы передать уведомление в кадре с данными.
- Тип 1 — негативное уведомление (REJECT) — указывает на ошибку при передаче. Поле Next указывает номер кадра, начиная с которого надо перепослать кадры.
- Тип 2 — RECEIVE NOT READY. Подтверждает все кадры, кроме указанного в Next. Используется, чтобы сообщить источнику кадров об необходимости приостановить передачу в силу каких-то проблем у получателя. После устранения этих проблем получатель шлет RECEIVE REDAY, REJECT или другой надлежащий управляющий кадр.
- Тип 3 — SELECTIVE REJECT — указывает на необходимость перепослать только кадр, указанный в Next. LAPB и SDLC не используют этого типа кадров.
Третий класс кадров — Unnubered. Кадры этого класса иногда
используются для целей управления, но чаще для передачи данных
при ненадёжной передаче без соединения.
Все протоколы имеют команду DISConnect для указания о разрыве
соединения, SNRM и SABM — для установки счётчиков кадров в ноль,
сброса соединения в начальное состояние, установки
соподчинённости на линии. Команда FRMR — указывает на
повреждение управляющего кадра.
- ^ Идея рассмотрения информации как меры на множестве ещё не до конца исчерпала себя — такой меры ещё не построено. Однако доказано, что с помощью этой аналогии можно доказывать неравенства, например
.
- ^ Матрица называется стохастической, если все её элементы неотрицательны и сумма элементов в каждом столбце равна единице.
- ^ Многочлен называется неприводимым, если он не разлагается в произведение многочленов меньшей степени.
























































