Обновлено: 24.06.2023
Свойства физического объекта (явления, процесса) определяются набором количественных характеристик — физических величин . Как правило, результат измерения представляет собой число , задающее отношение измеряемой величины к некоторому эталону . Сравнение с эталоном может быть как прямым (проводится непосредственно экспериментатором), так и косвенным (проводится с помощью некоторого прибора, которому экспериментатор доверяет). Полученные таким образом величины имеют размерность , определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого события, логическое утверждение (да/нет) или даже качественная оценка (сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем, когда результат измерения может быть представлен в виде числа или набора чисел .
Взаимосвязь между различными физическими величинами может быть описана физическими законами , представляющими собой идеализированную модель действительности. Конечной целью любого физического эксперимента (в том числе и учебного) является проверка адекватности или уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат x = x изм . Можно ли утверждать, что x изм — это длина стержня?
Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.
Итак, из нашего примера видно, что никакое физическое измерение не может быть произведено абсолютно точно, то есть у любого измерения есть погрешность .
Об измеренной величине также часто говорят как об оценке , подчеркивая, что эта величина не точна и зависит не только от физических свойств исследуемого объекта, но и от процедуры измерения.
Замечание. Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3 , но для более серьезного понимания следует обратиться к [ 5 ] .
где δ x — абсолютная величина погрешности. Эта запись означает, что исследуемая величина лежит в интервале x ∈ ( x изм — δ x ; x изм + δ x ) с некоторой достаточно большой долей вероятности (более подробно о вероятностном содержании интервалов см. п. 2.2 ). Для наглядной оценки точности измерения удобно также использовать относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с самой измеряемой величиной (её также можно выразить в процентах: ε = δ x x ⋅ 100 % ).
Пример. Штангенциркуль — прибор для измерения длин с ценой деления 0 , 1 мм . Пусть диаметр некоторой проволоки равен 0 , 37 мм. Считая, что абсолютная ошибка составляет половину цены деления прибора, результат измерения можно будет записать как d = 0 , 40 ± 0 , 05 мм (или d = ( 40 ± 5 ) ⋅ 10 — 5 м ). Относительная погрешность составляет ε ≈ 13 % , то есть точность измерения весьма посредственная — поскольку размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x 1 и x 2 и сравним результаты. Можно ли сказать, что стержни одинаковы или различны?
Казалось бы, достаточно проверить, справедливо ли x 1 = x 2 . Но никакие два результата измерения не равны друг другу с абсолютной точностью! Таким образом, без указания погрешности измерения ответ на этот вопрос дать невозможно .
С другой стороны, если погрешность δ x известна, то можно утверждать, что если измеренные длины одинаковы в пределах погрешности опыта , если | x 2 — x 1 | δ x (и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие два измерения, и, следовательно, невозможно сделать никаких значимых выводов по результатам эксперимента: ни о наличии зависимостей между величинами, ни о практической применимости какой-либо теории, и т. п. В связи с этим задача правильной оценки погрешностей является крайне важной, поскольку существенное занижение или завышение значения погрешности (по сравнению с реальной точностью измерений) ведёт к неправильным выводам .
В физическом эксперименте (в том числе лабораторном практикуме) оценка погрешностей должна проводиться всегда (даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых ( однотипных ) измерений одной и той же физической величины (например, многократно приложим линейку к стержню) и получим ряд значений
Что можно сказать о данном наборе чисел и о длине стержня? И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться на практике, величины < x i >почти наверняка окажутся различными . Причиной тому могут быть самые разные обстоятельства, например: у нас недостаточно остроты зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково; стенки стержня могут быть слегка неровными; у стержня может и не быть определённой длины, например, если в нём возбуждены звуковые волны, из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как случайная величина , описываемая некоторым вероятностным законом ( распределением ). Подробнее о случайных величинах и методах работы с ними см. гл. 2 .
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨ x ⟩ = x 1 + x 2 + … + x n n ≡ 1 n ∑ i = 1 n x i . | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений, принято называть выборочным средним. Здесь и далее для обозначения выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Δ x i = x i — ⟨ x ⟩ , i = 1 … n .
Разброс данных относительно среднего принято характеризовать среднеквадратичным отклонением :
| s = Δ x 1 2 + Δ x 2 2 + … + Δ x n 2 n = 1 n ∑ i = 1 n Δ x i 2 | (1.2) |
| s 2 = ⟨ ( x — ⟨ x ⟩ ) 2 ⟩ . | (1.3) |
Значение среднего квадрата отклонения s 2 называют выборочной дисперсией .
Будем увеличивать число измерений n ( n → ∞ ). Если объект измерения и методика достаточно стабильны, то отклонения от среднего Δ x i будут, во-первых, относительно малы, а во-вторых, положительные и отрицательные отклонения будут встречаться примерно одинаково часто. Тогда при вычислении ( 1.1 ) почти все отклонения Δ x i скомпенсируются и можно ожидать, что выборочное среднее при n ≫ 1 будет стремиться к некоторому пределу:
lim n → ∞ 1 n ∑ i = 1 n x i = x ¯ .
Предельную величину среднеквадратичного отклонения при n → ∞ обозначим как
lim n → ∞ 1 n ∑ i = 1 n Δ x i 2 = σ .
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр меняется во времени или в результате самого измерения, либо испытывает слишком большие случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не останавливаемся.
Замечание. Если n мало ( n 10 ), для оценки среднеквадратичного отклонения математическая статистика рекомендует вместо формулы ( 1.3 ) использовать исправленную формулу (подробнее см. п. 5.2 ): s n — 1 2 = 1 n — 1 ∑ i = 1 n Δ x i 2 , (1.4) где произведена замена n → n — 1 . Величину s n — 1 часто называют стандартным отклонением .
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа измерений имеют не слишком большой разброс, так что величина ⟨ x ⟩ может быть использована как приближенное значение ( оценка ) истинного значения ⟨ x ⟩ ≈ x ¯ , а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону распределения (подробнее см. Главу 2 ). Для таких величин могут быть строго доказаны следующие свойства:
при многократном повторении эксперимента бо́льшая часть измерений ( ∼ 68%) попадает в интервал x ¯ — σ x x ¯ + σ (см. п. 2.2 ).
выборочное среднее значение ⟨ x ⟩ оказывается с большей вероятностью ближе к истинному значению x ¯ , чем каждое из измерений < x i >в отдельности. При этом ошибка вычисления среднего убывает пропорционально корню из числа опытов n (см. п. 2.4 ).
Упражнение. Показать, что s 2 = ⟨ x 2 ⟩ — ⟨ x ⟩ 2 . (1.5) то есть дисперсия равна разности среднего значения квадрата ⟨ x 2 ⟩ = 1 n ∑ i = 1 n x i 2 и квадрата среднего ⟨ x ⟩ 2 = ( 1 n ∑ i = 1 n x i ) 2 .
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения, и в каком случае это позволит улучшить результаты опыта, проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить воспроизводимость результатов: повторные измерения в одинаковых условиях, должны давать близкие результаты. В противном случае исследование будет существенно затруднено, если вообще возможно. Таким образом, многократные измерения необходимы для того, чтобы убедиться как в надёжности методики, так и в существовании измеряемой величины как таковой.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе обработки данных, поскольку часть информации о проведении измерений к этому моменту утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего процесса измерений в лабораторном журнале . Подробнее об этом см. п. 4.1.1 .
При многократном повторении измерении одной и той же физической величины погрешности могут иметь систематический либо случайный характер. Назовём погрешность систематической , если она повторяется от опыта к опыту, сохраняя свой знак и величину, либо закономерно меняется в процессе измерений. Случайные (или статистические ) погрешности меняются хаотично при повторении измерений как по величине, так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно выделить
инструментальные (или приборные ) погрешности , связанные с несовершенством конструкции (неточности, допущенные при изготовлении или вследствие старения), ошибками калибровки или ненормативными условиями эксплуатации измерительных приборов;
методические погрешности , связанные с несовершенством теоретической модели явления (использование приближенных формул и моделей явления) или с несовершенством методики измерения (например, влиянием взаимодействия прибора и объекта измерения на результат измерения);
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических явлений, и в той или иной степени проявляется в работе всех без исключения приборов. Случайные погрешности обнаруживаются просто при многократном повторении опыта — в виде хаотичных изменений ( флуктуаций ) значений < x i >.
Если случайные отклонения от среднего в большую или меньшую стороны примерно равновероятны, можно рассчитывать, что при вычислении среднего арифметического ( 1.1 ) эти отклонения скомпенсируются, и погрешность результирующего значения ⟨ x ⟩ будем меньше, чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
с особенностями используемых приборов : техническими недостатками (люфт в механических приспособлениях, сухое трение в креплении стрелки прибора), с естественными (тепловой и дробовой шумы в электрических цепях, тепловые флуктуации и колебания измерительных устройств из-за хаотического движения молекул, космическое излучение) или техногенными факторами (тряска, электромагнитные помехи и наводки);
с особенностями и несовершенством методики измерения (ошибка при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);
с несовершенством объекта измерений (неровная поверхность, неоднородность состава);
со случайным характером исследуемого явления (радиоактивный распад, броуновское движение).
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить, исключить или уменьшить просто многократным повторением измерений. Они могут быть обусловлены, во-первых, неправильной работой приборов ( инструментальная погрешность ), например, сдвигом нуля отсчёта по шкале, деформацией шкалы, неправильной калибровкой, искажениями из-за не нормативных условий эксплуатации, искажениями из-за износа или деформации деталей прибора, изменением параметров прибора во времени из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации результатов ( методическая погрешность ), например, из-за использования слишком идеализированной физической модели явления, которая не учитывает некоторые значимые факторы (так, при взвешивании тел малой плотности в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических цепях может быть необходим учет неидеальности амперметров и вольтметров и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
Известные погрешности, которые могут быть достаточно точно вычислены или измерены. При необходимости они могут быть учтены непосредственно: внесением поправок в расчётные формулы или в результаты измерений. Если они малы, их можно отбросить, чтобы упростить вычисления.
Погрешности известной природы, конкретная величина которых неизвестна, но максимальное значение вносимой ошибки может быть оценено теоретически или экспериментально. Такие погрешности неизбежно присутствуют в любом опыте, и задача экспериментатора — свести их к минимуму, совершенствуя методики измерения и выбирая более совершенные приборы.
Чтобы оценить величину систематических погрешностей опыта, необходимо учесть паспортную точность приборов (производитель, как правило, гарантирует, что погрешность прибора не превосходит некоторой величины), проанализировать особенности методики измерения, и по возможности, провести контрольные опыты.
Погрешности известной природы, оценка величины которых по каким-либо причинам затруднена (например, сопротивление контактов при подключении электронных приборов). Такие погрешности должны быть обязательно исключены посредством модификации методики измерения или замены приборов.
Наконец, нельзя забывать о возможности существования ошибок, о которых мы не подозреваем, но которые могут существенно искажать результаты измерений. Такие погрешности самые опасные, а исключить их можно только многократной независимой проверкой измерений, разными методами и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается, как правило, паспортными погрешностями приборов и теоретическими поправками к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример. Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами: • Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях. • Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока. В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример. Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности: 1. Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления. 2. Систематическая погрешность, связанная с неправильной установкой нуля. 3. Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
Окончательный результат измерения должен быть представлен в стандартной форме записи. Для этого:
1. Абсолютную погрешность измерения округляют до первой значащей цифры, если она не единица;
2. Если первая значащая цифра в абсолютной погрешности единица, то абсолютную погрешность представляют в виде числа с двумя значащими цифрами. Значащими цифрами числа называют все его цифры, начиная с первой слева, отличной от нуля.
3. Числовое значение результата измерения представляется, так чтобы и среднее значение и абсолютная погрешность имели одинаковое число десятичных знаков после запятой. В стандартном виде для записи больших и малых чисел используют следующую запись:
а·10 n , где 1 ≤ а ≤ 10.
Среднее значение результата измерения округляют до того разряда, до которого округлена абсолютная погрешность.
4. Среднее значение результата представляют в виде числа, содержащего до запятой одну значащую цифру, умноженного на десять в соответствующей степени.
Например: (м). Среднее значение измеряемой величины = 6,24·10 -2 (м). Тогда стандартная запись окончательного результата измерений имеет вид:
Пусть в лабораторной работе измеряют силу тока в цепи амперметром, класс точности которого γ = 2,5%, а прибор показывает, что величина силы тока в цепи 2 А. Тогда = 2 А. Шкала прибора односторонняя, диапазон измерения равен 5 А. В этом случае погрешность измерения прибора, согласно соотношению (15) будет равна:
Абсолютная погрешность измерения это величина, всегда имеющая ту же единицу измерения, что и измеряемая физическая величина. Стандартная форма записи окончательного результата имеет вид:
Окончательный результат измерения должен быть представлен в стандартной форме записи. Для этого:
1. Абсолютную погрешность измерения округляют до первой значащей цифры, если она не единица;
2. Если первая значащая цифра в абсолютной погрешности единица, то абсолютную погрешность представляют в виде числа с двумя значащими цифрами. Значащими цифрами числа называют все его цифры, начиная с первой слева, отличной от нуля.
3. Числовое значение результата измерения представляется, так чтобы и среднее значение и абсолютная погрешность имели одинаковое число десятичных знаков после запятой. В стандартном виде для записи больших и малых чисел используют следующую запись:
а·10 n , где 1 ≤ а ≤ 10.
Среднее значение результата измерения округляют до того разряда, до которого округлена абсолютная погрешность.
4. Среднее значение результата представляют в виде числа, содержащего до запятой одну значащую цифру, умноженного на десять в соответствующей степени.
Например: (м). Среднее значение измеряемой величины = 6,24·10 -2 (м). Тогда стандартная запись окончательного результата измерений имеет вид:
Пусть в лабораторной работе измеряют силу тока в цепи амперметром, класс точности которого γ = 2,5%, а прибор показывает, что величина силы тока в цепи 2 А. Тогда = 2 А. Шкала прибора односторонняя, диапазон измерения равен 5 А. В этом случае погрешность измерения прибора, согласно соотношению (15) будет равна:
Абсолютная погрешность измерения это величина, всегда имеющая ту же единицу измерения, что и измеряемая физическая величина. Стандартная форма записи окончательного результата имеет вид:
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.

Рис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то

,
где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в °С, то цена деления Ц = 100/50 = 2 (°С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:

. (7)
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем

. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения

.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины d х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: d х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность d t = 0,2 с;

б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: d х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность d r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и ( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости h рассчитывается по формуле

, (10)
где rш – плотность материала шарика; rж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости h – результат косвенного измерения. Величины rш, rж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения d и зависит от погрешностей прямых измерений d x, d y, d z…и от вида функции (9). Как правило, величину d и можно оценить по формуле вида

, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
| и(х) | kx |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
На практике зависимость (9) чаще всего имеет вид степенной функции

,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность d и оценивается по формуле

, (12)
где – среднее значение величины и; – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и d х) должны быть выражены в одних и тех же единицах.

2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
d S = 0,5 мм = 0,0005 м;
d t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t ) = 2×S 1 ×t – 2 ;
тогда на основании (12) погрешность косвенного измерения ускорения d а определится выражением

.

;

.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность d а равной

Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде

,

где . Тогда для оценки приборной погрешности dh, согласно (12), получим выражение

, (13)

где .

Пренебрегая величиной Еt , проведем расчет по формуле (13):

.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями Ds x и d х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой D, которая, в зависимости от соотношения между величинами Ds x и d х, находится следующим образом.

. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида


с указанием значения доверительной вероятности a . Величины и D выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности

,
выраженное в процентах и округленное до десятых долей.

и запишем окончательный результат измерений:




.
Окончательный результат измерений имеет вид




Пример 6. При определении длины волны l лазерного излучения (работа 5.1) получено: при a = 0,95; dl = 1,86×10 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):

.

Округленное среднее будет равно мм. Оценим полную относительную ошибку

и запишем окончательный результат:


Timeweb — компания, которая размещает проекты клиентов в Интернете, регистрирует адреса сайтов и предоставляет аренду виртуальных и физических серверов. Разместите свой сайт в Сети — расскажите миру о себе!
Виртуальный хостинг
Быстрая загрузка вашего сайта, бесплатное доменное имя, SSL-сертификат и почта. Первоклассная круглосуточная поддержка.
Производительность и масштабируемые ресурсы для вашего проекта. Персональный сервер по цене виртуального хостинга.
Выделенные серверы
Быстрая загрузка вашего сайта, бесплатное доменное имя, SSL-сертификат и почта. Первоклассная круглосуточная поддержка.
В физике и в других науках весьма часто приходится производить измерения различных величин (например, длины, массы, времени, температуры, электрического сопротивления и т. д.).
Измерение – процесс нахождения значения физической величины с помощью специальных технических средств – измерительных приборов.
Измерительным прибором называют устройство, с помощью которого осуществляется сравнение измеряемой величины с физической величиной того же рода, принятой за единицу измерения.
Различают прямые и косвенные методы измерений.
Прямые методы измерений – методы, при которых значения определяемых величин находятся непосредственным сравнением измеряемого объекта с единицей измерения (эталоном). Например, измеряемая линейкой длина какого-либо тела сравнивается с единицей длины – метром, измеряемая весами масса тела сравнивается с единицей массы – килограммом и т. д. Таким образом, в результате прямого измерения определяемая величина получается сразу, непосредственно.
Косвенные методы измерений – методы, при которых значения определяемых величин вычисляются по результатам прямых измерений других величин, с которыми они связаны известной функциональной зависимостью. Например, определение длины окружности по результатам измерения диаметра или определение объема тела по результатам измерения его линейных размеров.
Ввиду несовершенства измерительных приборов, наших органов чувств, влияния внешних воздействий на измерительную аппаратуру и объект измерения, а также прочих факторов все измерения можно производить только с известной степенью точности; поэтому результаты измерений дают не истинное значение измеряемой величины, а лишь приближенное. Если, например, вес тела определен с точностью до 0,1 мг, то это значит, что найденный вес отличается от истинного веса тела менее чем на 0,1 мг.
Точность измерений – характеристика качества измерений, отражающая близость результатов измерений к истинному значению измеряемой величины.
Чем меньше погрешности измерений, тем больше точность измерений. Точность измерений зависит от используемых при измерениях прибо- ров и от общих методов измерений. Совершенно бесполезно стремиться при измерениях в данных условиях перейти за этот предел точности. Можно свести к минимуму воздействие причин, уменьшающих точность измерений, но полностью избавиться от них невозможно, то есть при измерениях всегда совершаются более или менее значительные ошибки (погрешности). Для увеличения точности окончательного результата всякое физическое измерение необходимо делать не один, а несколько раз при одинаковых условиях опыта.
В результате i-го измерения (i – номер измерения) величины «Х”, получается приближенное число Хi, отличающееся от истинного значения Хист на некоторую величину ∆Хi = |Хi – Х|, которая является допущенной ошибкой или, другими словами, погрешностью. Истинная погрешность нам не известна, так как мы не знаем истинного значения измеряемой величины. Истинное значение измеряемой физической величины лежит в интервале
Читайте также:
- Договор аренды земельного участка кратко
- Сет годин лидер есть в каждом кратко
- Экономист по сбыту обязанности кратко
- Латвия географическое положение кратко
- Монако отдых и туризм кратко
![]()
![]() ,
,
где
![]() — абсолютное значение разности между
— абсолютное значение разности между
величинойхi,
полученной вi– том измерении и
средним значением <х>. Абсолютная
погрешность опыта характеризует таким
образом качество проведённых измерений,
т. е. указывает, на сколько истинное
значение измеряемой величины может
отличаться от значения, измеренного в
опыте.
3. Для оценки точности, с которой
определена измеряемая величина,
используется понятие относительной
погрешности:
![]() .
.
Таким образом, относительная погрешность
показывает, какая часть абсолютной
погрешности приходится на каждую единицу
измеряемой величины.
Пример. При измерении толщиныh
стеклянной пластинки с помощью
микрометра было сделано четыре измерения,
результаты которых занесены в табл. 1:
Таблица 1.
Результаты измерений толщины стеклянной
пластинки
-
№ измерения
h,
мм<
h>, ммΔ
hi, ммΔ
h, ммεh,
%1
3,82
3,84
— 0,02
0,03
0,8
2
3,85
+ 0,01
3
3,89
+ 0,05
4
3,80
— 0,04
-
По данным таблицы рассчитываем среднее
значение толщины:
![]()
-
Определяем абсолютную погрешность
опыта (серии измерений):
![]()
-
Определяем относительную погрешность:
![]()
При косвенных измеренияхискомую
величину вычисляют по результатам
прямого измерения других величин,
связанных с искомой определённой
функциональной зависимостьюy = f
(x1,х2,…,хn).
Абсолютная и относительная погрешности
некоторых простейших функций приведены
в табл.2.
Таблица 2
Погрешности при косвенных измерениях
в простейших случаях
-
Вид функции
Абсолютная
погрешность ΔyОтносительная
погрешность
εy1
2
3
x1
+ x2Δ
x1
+ Δ x2
1
2
3
x1
— x2Δ
x1
+ Δ x2
x1
x2x1
Δ x2
+ x2
Δ x1εx1
+ εx2x1
/ x2
εx1
+ εx2xn
nxn-1
Δ xnεx

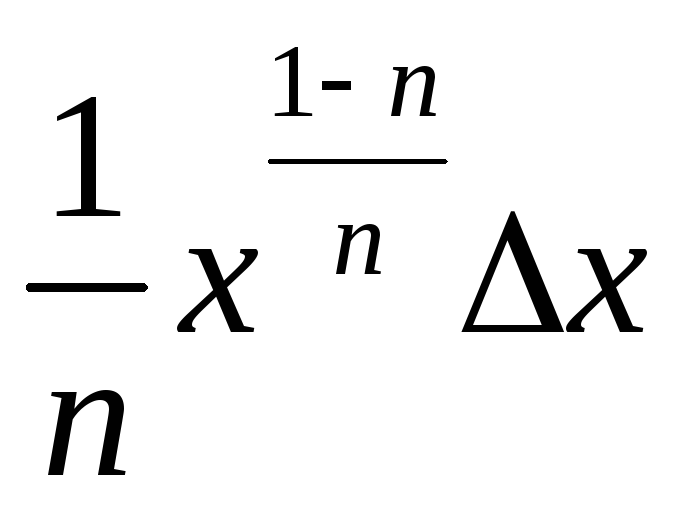

ex
ex
Δ xΔx
Когда функция y = f (x1,х2,…,хn)удобна для логарифмирования, то вначале
лучше рассчитать относительную
погрешность εyфункции (в %) и затем её абсолютную
погрешность
![]() .
.
Пример. Ускорение свободного паденияgопределяется по результатам
измерений периодов колебанийТ1иТ2двух математических
маятников с длинамиl1иl2соответственно (l1>l2)
по формуле
![]() ,
,
где a= l1—l2.
Логарифмирование даёт lng=ln(4π2)
+lna–ln![]() .
.
После дифференцирования lngс заменамиdaна ΔaиdТ на ΔТполучим:
![]()
(предполагается, что погрешности
независимых измерений Δa,ΔТ1и ΔТ2усиливают
друг друга, и поэтому их влияние
учитывается в формуле со знаком плюс).
Затем найдём абсолютную погрешность
![]() ,
,
где![]() .
.
Окончательный результат вычислений
– среднее арифметическое измеряемой
величины записывают в виде числа из
нескольких разрядов. Цифры в этом числе
делятся на значащие и незначащие. К
значащим цифрам относятся все верные
и сомнительные цифры. К незначащим
относятся: а) нули в начале числа,
определяющие разряды десятичных дробей
в числах меньших единицы; б) нули в конце
числа, заменившие цифры после округления;
в) неверные цифры, если они не были
отброшены.
Для определения значащих цифр в
результате измерения необходимо
вычислить абсолютную погрешность опыта,
числовое значение которой тоже может
содержать несколько разрядов. Но
абсолютная погрешность показывает, в
каком разряде полученного результата
содержится неточность. Поэтому её
числовое значение всегда округляется
до одной значащей цифры, кроме того, в
случае когда эта цифра представляет
единицу – в этом случае округление
производится до цифры первого младшего
разряда. Тогда сохранение цифр меньших
разрядов в среднем арифметическом
измеряемой величины теряет смысл.
Пример. В нескольких опытах по
результатам измерений периода колебаний
математического маятника было проведено
с различной погрешностью определение
ускорения свободного падения:
неправильная запись результата
правильная запись результата
g= (10,1835±0,433) м/с2g=
(10,2±0,4) м/с2
g= (9,8167±0,053) м/с2g=
(9,82±0,05) м/с2
g= (9,9423±0,132) м/с2g=
(9,94 ±0,13) м/с2
g= (10,8261±2,026) м/с2g=
(11±2) м/с2
При записи измеренного значения х
последней, таким образом, должна
указываться цифра того десятичного
разряда, который был использован при
указании погрешности. Это правило должно
соблюдаться и в тех случаях, когда
некоторые из цифр являются нулями.
Пусть, например, при вычислении gв
предыдущем опыте было получено значение
9,88 м/с2(точно), а погрешность
составила ± 0,004 м/с2, то окончательный
результат следует представить в таком
виде:
g= 9,880± 0,004 м/с2.
При записи окончательного результата
измерения наряду с основными единицами
СИ и производными от них допускаются к
применению кратные единицы (например,
см, МПа, мВ и т.д.) в тех случаях, когда
это упрощает запись. Полученные в ходе
эксперимента результаты часто изображают
в виде графика.
При построении графика чаще всего
пользуются прямоугольной системой
координат, причем значения аргумента
откладывают по горизонтальной оси, а
значения функции по вертикальной оси.
Начало координат не обязательно должно
совпадать с нулевыми значениями функции
и аргумента. При выборе масштаба величин,
откладываемых на осях координат, исходят
из того, чтобы получить примерно равные
отрезки, которые соответствуют
установленным в опыте интервалам
численных значений функции и аргумента.
Например, по результатам измерения
показателя преломления п водного
раствора глюкозы был построен графикп= п(с), гдес — концентрация
глюкозы (рис.1). На рис.1а график удовлетворяет
необходимым требованиям. На рис. 1б
из-за неудачного выбора масштаба и
начала отсчета дляпзависимостьп(с)почти незаметна, и такой график
бесполезен для практического применения.

Рис. 1
Использование гpафических методов
облегчается в тех случаях, когда гpафик
представляет собой прямую линию. С целью
«спрямления» гpафика исследуемой
зависимости, имеющей сложный характер,
целесообразно использовать нелинейные
шкалы, например, логарифмическую,
квадратичную и т.д. или откладывать не
сами величины аргумента и функции, а их
логарифмы, степени, обратные значения.
Например, в работе «Исследование
теплового излучения чёрного тела» с
целью экспериментальной проверки закона
Стефана – Больцмана
Rэ=σТ4,
где Rэ–
энергетическая светимость тела, аТ– его абсолютная температура, по оси
абсцисс откладывают Т, а по оси ординат
—![]() .
.
Выбрав рациональные масштаб и размеры
гpафика, на координатные оси наносят
деления через 10-20 мм и обозначают их.
Затем наносят экспериментальные точки,
с которыми совмещают прямоугольные
крестики, размеры которых вдоль осей
координат ОхиОуравны удвоенным
погрешностям соответственно 2Δхи
2Δув выбранном масштабе. По отмеченным
точкам проводят линию так, чтобы она
прошла как можно ближе к экспериментальным
точкам, и чтобы равное количество их
оказалось по обе стороны от этой линии.
Для построения графиков, как правило,
используют масштабно-координатную
(миллиметровую) бумагу.
Если в лабораторной работе по графику
определяется какая-либо константа,
например, как угловой коэффициент
экспериментальной прямой y = x0+kx,
то в этом случае тангенс угла α наклона
прямой к оси абсцисс может быть определён
только с учётом соответствующих масштабов
и единиц измерения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: конспект к № 1 теория.docx, отчет Морозова (проверка на ошибки).docx, 3 ошибки, из-за которых тебя отправят служить.pdf, 2.Эконометрика для ИМИТ_ Теоретический материал 5_ Стандартные о, РЕЧЕВЫЕ ОШИБКИ ИИХ ПРЕДУПРЕЖДЕНИЕ.docx, Письменная работа 1 теория управления реферат.docx, Найдите ошибки.docx, Негрубые ошибки.doc, Исправь ошибки (1).docx, рк 1 теория вероятности 19 вариант.pdf
Ч а с т ь I
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная и относительная ошибки
Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность*) измерения х:
х = х – Х. (1)
Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.
Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение является грубым. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:
![]() . (2)
. (2)
Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.
При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно: поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
Случайная и приборная погрешности
Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.
По происхождению ошибки делятся на инструментальные и методические.
Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.
Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.
По характеру проявления ошибки бывают систематические и случайные.
Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х0 , отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х0 .
Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.
Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как s x.
Оценка случайной погрешности. Доверительный интервал
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через ![]() среднеарифметическое значение
среднеарифметическое значение
![]() . (3)
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
![]()
При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение ![]() характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное ![]() » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
» равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).

Рис.1
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения ![]() . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
. «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
![]() , (4)
, (4)
где ![]() .
.
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
![]() . (5)
. (5)
Коэффициент пропорциональности tn, называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина tn, должна быть тем больше, чем выше доверительная вероятность .
С увеличением количества опытов среднее значение приближается к истинному; поэтому при той же вероятности доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффи-циента Стьюдента в зависимости от п и дана в приложениях к настоящему пособию.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины ![]() по формуле (3);
по формуле (3);
2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями ![]() , а также квадрат этой разности (отклонения) ( хi)2 ;
, а также квадрат этой разности (отклонения) ( хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка по формуле (4);
4) по заданной доверительной вероятности и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента tn, и определяется случайная погрешность s x по формуле (5).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл.1.
Таблица 1
Номер опыта |
… | х | х | ( х)2 |
| 1 | … | |||
| 2 | … | |||
| … | … | |||
| п | … | |||
| = | = |
В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с2), коэффициент вязкости жидкости (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение ![]() , получим расчетную формулу
, получим расчетную формулу
![]() . (6)
. (6)
Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним
четвертый столбец значениями ускорения ai и найдем их сумму, которую запишем под этим столбцом в ячейку « = ». Затем рассчитаем среднее значение ![]() по формуле (3)
по формуле (3)
![]() .
.
Таблица 2
| Номер опыта | S,
м |
t,
c |
а,
м/с2 |
а,
м/с2 |
(а)2,
(м/с2)2 |
| 1 | 5 | 2,20 | 2,07 | 0,04 | 0,0016 |
| 2 | 7 | 2,68 | 1,95 | -0,08 | 0,0064 |
| 3 | 9 | 2,91 | 2,13 | 0,10 | 0,0100 |
| 4 | 11 | 3,35 | 1,96 | -0,07 | 0,0049 |
| = | 8,11 | = | 0,0229 |
Вычитая из каждого значения ai среднее, найдем разности ai и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку « = ». По формуле (4) определим среднеквадратичную погрешность:
![]() .
.
Задавшись величиной доверительной вероятности = 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента tn, = 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437 0,139 (м/с2) .
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.
Р
ис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
![]() ,
,
где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
![]() . (7)
. (7)
Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем
![]() . (8)
. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
![]() .
.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;

б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости рассчитывается по формуле
![]() , (10)
, (10)
где ш – плотность материала шарика; ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости – результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида
![]() , (11)
, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
Таблица 3
| и(х) | kx |
|
|
|
|
|
|
|
|
На практике зависимость (9) чаще всего имеет вид степенной функции
![]() ,
,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
![]() , (12)
, (12)
где ![]() – среднее значение величины и;
– среднее значение величины и; ![]() – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
– относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной ![]() . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
. Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t) = 2S 1t – 2 ;
тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением
![]() .
.
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 м; t 3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:
![]() ;
;
![]() .
.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность а равной
![]()
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
![]() ,
,
где ![]() . Тогда для оценки приборной погрешности , согласно (12), получим выражение
. Тогда для оценки приборной погрешности , согласно (12), получим выражение
![]() , (13)
, (13)
где ![]() .
.
Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l 80 cм; D 4 мм; t 10 с; ![]() Пас. Оценим величины, входящие в формулу (13):
Пас. Оценим величины, входящие в формулу (13):

Пренебрегая величиной Еt , проведем расчет по формуле (13):
![]() .
.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами s x и х, находится следующим образом.
Если одна из погрешностей более чем в три раза превышает другую (например, s x > 3х), то полная ошибка принимается равной этой большей величине (в приведенном примере s x). Если же величины s x и х близки между собой, то полная ошибка вычисляется как
![]() . (14)
. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
![]()
с указанием значения доверительной вероятности . Величины ![]() и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
![]() ,
,
выраженное в процентах и округленное до десятых долей.
Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры (примеры: а) 0,2642 0,26; б) 3,177 3,2 3; в) 7,8310 – 7 810 – 7 и т.д.). После этого среднее значение ![]() округляется с той же точностью.
округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения ![]() = 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
= 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
![]()
и запишем окончательный результат измерений:

![]()
![]()
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение ![]() = 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение
= 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение ![]() 343 м/с. Полная относительная погрешность
343 м/с. Полная относительная погрешность
![]() .
.
Окончательный результат измерений имеет вид

![]()
![]()
Пример 6. При определении длины волны лазерного излучения (работа 5.1) получено: ![]() при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
![]() .
.
Округленное среднее будет равно ![]() мм. Оценим полную относительную ошибку
мм. Оценим полную относительную ошибку
![]()
и запишем окончательный результат:

![]()
Е = 4,4 %.
* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.
Подборка по базе: 1. Протокол входного контроля отчетности — Статистика (прочие)_ , измерительные приборы и методика проведения измерений линий кана, Цель проведения измерений.docx, РГР №1. Камеральная обработка разомкнутого нивелирного хода (2)., ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА В МАШИНОСТРОЕНИИ.rtf, Тема 1. Общие сведения о работе личного состава ГДЗС в изолирующ, МДК01.01 Подготовка рабочего места, лабораторных условий, средст, Анализ результатов применения методов увеличения нефтеотдачи пла, практическая обработка эксперементальных данных.pdf, Разработка и заполнение чек-листа соответствия системы оценки до
Часть ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК Абсолютная и относительная ошибки Никакую физическую величину невозможно измерить абсолютно точно как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку или абсолютную погрешность) измерениях х = х – Х. (1) Абсолютная погрешность является размерной величиной она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражениях может быть как положительной, таки отрицательной величиной. Хотя величинах показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами порядка нескольких километров, то точность такого измерения следует признать весьма высокой если же измерялись размеры помещения (не превышающие десятка метров, то измерение является грубым. Для характеристики точности существует понятие относительной ошибки или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине
X
x
E
. (2) Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах. При определении ошибок измерений важно иметь ввиду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно поэтому значениях и Ев принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, те. найти их приближенно стой или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
*
Термины ошибка и погрешность применительно к измерениям имеют один и тот же смысл.
Случайная и приборная погрешности Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, таки по характеру их проявления. По происхождению ошибки делятся на инструментальные и методические. Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штангенциркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом. Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом. По характеру проявления ошибки бывают систематические и случайные. Систематическая погрешность может быть обусловлена как приборами, таки методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта копыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х
, отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х Случайная ошибка также может быть как инструментальной, таки методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта копыту. Значение ее можно уменьшить путем увеличения числа измерений. Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному.
Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам приборная и случайная. Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как
s
x. Оценка случайной погрешности. Доверительный интервал Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины. Пусть в результате проделанных измерений получено п значений величины х х
, х
, …, х
п
. Обозначим через x среднеарифметическое значение
n
i
i
x
n
x
1 1
. (3) В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение x характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата. Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения величинах имеет значение, в точности равное x » равна нулю. Вероятность же утверждения величинах имеет
какое-либо значение равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью
(0 <
< 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина
– доверительной вероятностью или коэффициентом надежности. За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность
x (рис. 1).
Рис Очевидно, что ширина доверительного интервала (а следовательно, и ошибка
s
x) зависит оттого, насколько сильно отличаются отдельные измерения величины хот среднего значения x . Разброс результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой
, которую находят по формуле
n
i
i
x
n
n
1 2
)
(
)
1
(
1
, (4) где Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке
,
n
s
t
x
. (5) Коэффициент пропорциональности t
n,
называется коэффициентом
Стьюдента; он зависит от числа опытов пи доверительной вероятности На риса, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего вероятность накрывания значения Х более широким интервалом выше.
Следовательно, величина t
n,
должна быть тем больше, чем выше доверительная вероятность С увеличением количества опытов среднее значение приближается к истинному поэтому при той же вероятности
доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффициента Стьюдента в зависимости от пи дана в приложениях к настоящему пособию. Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной
задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов ив лабораторном практикуме значение
принимается равным 0,95. Расчет случайной погрешности измерения величины х проводится в следующем порядке
1) вычисляется сумма измеренных значений, а затем – среднее значение величины x по формуле (3);
2) для каждого го опыта рассчитываются разность между измеренными средним значениями
x
x
x
i
i
, а также квадрат этой разности отклонениях) находится сумма квадратов отклонений, а затем – среднеквадратичная ошибка
по формуле (4);
4) по заданной доверительной вероятности
и числу проведенных опытов п из таблицы нас приложений выбирается соответствующее значение коэффициента Стьюдента t
n,
и определяется случайная погрешность
x по формуле (5). Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл. Таблица 1 Номер опытах
х
(
х)
2 1
…
2
…
…
… п
…
=
= В каждом конкретном случае величинах имеет определенный физический смысли соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (мс, коэффициент вязкости жидкости
(Паси т.д. Пропущенные столбцы табл. 1 могут
содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S безначальной скорости. Используя известное соотношение
2 2
t
a
S
, получим расчетную формулу
2 2
t
S
a
. (6) Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним четвертый столбец значениями ускорения a
i
и найдем их сумму, которую запишем под этим столбцом в ячейку « = ». Затем рассчитаем среднее значение a по формуле (3)
)
/
(
03
,
2 4
11
,
8 2
с
м
a
Таблица 2 Номер опытам а, мс а,
м/с
2
(а)
2
, мс 1
5 2,20 2,07 0,04 0,0016 2
7 2,68 1,95
-0,08 0,0064 3
9 2,91 2,13 0,10 0,0100 4
11 3,35 1,96
-0,07 0,0049
=
8,11
=
0,0229 Вычитая из каждого значения a
i
среднее, найдем разности
a
i
и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку « = ». По формуле (4) определим среднеквадратичную погрешность
)
/
(
0437
,
0
)
1 4
(
4 0229
,
0 2
с
м
Задавшись величиной доверительной вероятности
= 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента t
n,
= 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437 0,139 (мс) .
Способы определения приборных ошибок Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электроизмерительных приборов – класс точности. Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА. Рис Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
N
П
Ц
, где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А. Если шкала принадлежит термометру и проградуирована в Сто цена деления Ц = 100/50 = 2 (С. Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы. Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах
100
П
х
К
. (7) Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах. В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм. Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения
D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
13 2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем
100
П
К
x
. (8) Например, для вольтметра с классом точности 2,5 и пределом измерения
600 В абсолютная приборная ошибка измерения напряжения
)
(
15 100 600 В. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, тов зависимости от характера работы прибора возможны два способа определения величины ха указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы х = Ц. Так, при измерении промежутка времени t секундомером сценой деления 0,2 с погрешность
t = 0,2 с б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены делениях Ц. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла. Рис 4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность
r = 0,005 мм.
Погрешности косвенных измерений В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин
x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как и = и, y, z,…). (9) В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости
рассчитывается по формуле
t
D
l
g
ж
ш
2 18
)
(
, (10) где ш – плотность материала шарика ж – плотность жидкости g – ускорение свободного падения D – диаметр шарика t – время его падения в жидкости l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости
– результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры. Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений
x,
y, и от вида функции (9). Как правило, величину и можно оценить по формуле вида
)
(
)
(
)
(
2 2
2
z
k
y
k
x
k
u
z
y
x
, (11) где коэффициенты k
x
, k
y
, k
z
,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций
(a, b, c, n – заданные константы. Таблица 3 их)
k
x
n
x
a
x
u
n
x
n
a
n
1
)
sin(bx
a
)
cos(bx
ab
)
cos(bx
a
)
sin(bx
ab
)
tg(bx
a
)
2
sin(
2
)
(
cos
2
bx
u
b
bx
ab
x
c
b
a
)
ln(b
c
u
)
ln(bx
a
x
a
На практике зависимость (9) чаще всего имеет вид степенной функции
,…)
,
,
(
n
m
k
z
y
x
C
z
y
x
u
, показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
)
(
)
(
)
(
2 2
2
z
y
x
nE
mE
kE
u
u
, (12) где u – среднее значение величины и
,…
,
,
z
z
E
y
y
E
x
x
E
z
y
x
– относительные приборные погрешности прямых измерений величин x, y,
z,… Для подстановки в формулу (12) выбираются наиболее представительные, те. близкие к средним значения x, y, z,… При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, хи х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины (
kE
x
,
mE
y
,
nE
z
,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда передним слева есть хотя бы одна цифра, отличная от нуля. Далее, если одна из этих величин (например, |
kE
x по модулю превышает наибольшую из остальных (
|
mE
y
|
,
|
nE
z
|
,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной
x
kE
u
u
. Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле
(12) ею можно пренебречь. Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой сценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в паб (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 мс. Расчетную формулу (6) можно записать в виде степенной функции
a(
S, t
) = 2S
1
t
– 2
; тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением
2 2
)
2
(
)
1
(
t
S
E
E
a
a
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 мс и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов
000063
,
0 8
0005
,
0
S
S
E
S
;
0067
,
0 3
01 0
2 Очевидно, что в данном случае величиной E
S
можно пренебречь и принять погрешность а равной
).
/
(
0136
,
0 0067
,
0 03
,
2 2
2
с
м
E
a
a
t
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
1 1
2
)
,
,
(
l
t
D
C
l
t
D
, где
g
C
ж
ш
)
(
18 1
. Тогда для оценки приборной погрешности
, согласно (12), получим выражение
2 2
2
)
(
)
2
(
l
t
D
E
E
E
, (13) где Пусть расстояние между метками l измерено сантиметровой лентой сценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда
l = 0,25 см
D = 0,01 мм
t = 0,01 с. Предположим, что измеренные значения равным мм 10 с Пас. Оценим величины, входящие в формулу (13):
0032
,
0 80 25
,
0
;
0010
,
0 10 01
,
0
;
0050
,
0 4
01
,
0 Пренебрегая величиной Е
, проведем расчет по формуле (13):
)
(
00464
,
0 0032
,
0 0050
,
0 784
,
0 2
2
с
Па
Полная ошибка. Окончательный результат измерений В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями
s
x их. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами
s
x их, находится следующим образом. Если одна из погрешностей более чем в три раза превышает другую например,
s
x > х, то полная ошибка принимается равной этой большей величине (в приведенном примере
s
x). Если же величины
s
x их близки между собой, то полная ошибка вычисляется как
2 2
)
(
)
(
x
x
s
. (14) Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
с указанием значения доверительной вероятности
. Величины x и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
%
100
x
E
, выраженное в процентах и округленное до десятых долей. Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится если же вторая значащая цифра
1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры примеры а) 0,2642 0,26; б) 3,177 3,2 3; в 7,8310
– 7
810
– 7 и т.д.). После этого среднее значение x округляется стой же точностью. Пример 4. В результате определения ускорения движения тела примеры 1 и 2) получено среднее значение ускорения a = 2,03 мс, случайная ошибка
s а = 0,139 мс с доверительной вероятностью
= 0,95 и приборная ошибка а = 0,0136 мс. Так как а более чем в десять раз меньше
s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной
s а 0,14 мс. Оценим относительную ошибку
%
8
,
6
%
100 03
,
2 139
,
0
E
и запишем окончательный результат измерений при 03
,
2
(
2
с
м
a
%
8
,
6
E
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты среднее значение
u = 343,3 мс случайная погрешность
s и = 8,27 мс при
= 0,90; абсолютная приборная погрешность и = 1,52 мс. Очевидно, что ив данном случае величиной и можно пренебречь по сравнению сии расчет по формуле (14) не требуется. Полная ошибка после округления равна
s и 8 мс округленное среднее значение u 343 мс. Полная относительная погрешность
%
4
,
2
%
100 3
,
343 Окончательный результат измерений имеет вид при 343
(
с
м
u
%.
4
,
2
Е
Пример 6. При определении длины волны
лазерного излучения работа 5.1) получено
мм
мм
s
5 4
10 17
,
2
;
10 27
,
6
при
= 0,95;
= 1,8610
— 5
мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
)
(
10 3
,
0 10 75
,
2
)
10 86
,
1
(
)
10 17
,
2
(
4 5
2 5
2 5
мм
Округленное среднее будет равно
4 10 3
,
6
мм. Оценим полную относительную ошибку
%
4
,
4
%
100 10 27
,
6 10 75
,
2 и запишем окончательный результат при 3
,
6
(
4
мм
Е = 4,4
%.
1 ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ Задача 1. На платформу весов поставили эталонную гирю весом 1 кг. Весы показали значение 1,005 кг. Определить абсолютную и относительную погрешности измерения. Найти приведенную погрешность весов, если верхний предел измерения (нормирующее значение) равен 5 кг. Решение Абсолютную погрешность находим по формуле
Δ = x
изм
– д где x изм и x д – измеренное и действительное значения величины.
Δ = кг Относительную погрешность определим по формуле д 100%
100%
0,5%
x
1
Определим приведенную погрешность
N
100%
X
верхний предел измерений средства измерений
0,005 100%
0,1 5
Задача 2. При поверке методом сличения последовательно включили поверяемый и эталонный амперметр. Эталонный амперметр показал 2,4 А, поверяемый амперметр показал 2,45 А. Предел измерений поверяемого амперметра 3 А. Для поверяе- мого амперметра определить абсолютную, относительную и приведенную погрешности. Задача 3.
Поверяемый термометр в тающем льду показал С, а в кипящей воде С. Предел измерений термометра С. Определить абсолютные погрешности термометра при этих температурах и максимальную приведенную погрешность термометра. Задача 4. Приведенная погрешность манометра равна 0,5 %, диапазон измерения 0…10 МПа. Определить относительные погрешности измерения давлений 1 МПа и 9 МПа.
2 Задача 5 Определить допустимую приведенную погрешность акселерометра для измерения виброускорения 60 мс с погрешностью ± 2 мс. Диапазон измерения акселерометрам с2bЗадача 6. Напряжение на выводах солнечной батареи должно превышать 1,20 В. При приемочных испытаниях батареи было получено значение 1,21 В. Можно ли обосновано утверждать, что солнечная батарея годна к эксплуатации, если измерение произведено с относительной погрешностью 0,25 %? Задача 7 На бензоколонке заливают бензин с абсолютной систематической погрешностью л. Вычислите относительные погрешности, возникающие при покупке лил бензина.
0,1 100%
0, 25%
40
Задача 8 Основная относительная погрешность измерителя сопротивления равна 0,1
%. Определить относительную погрешность измерителя при температуре 45 С, если его дополнительная относительная погрешность от изменения температуры равна н, где Θ температура окружающей среды н – нормальная температура, равная 20 С. Задание по практическому занятию Каждому студенту предлагается ознакомится с материалами Метрологические характеристики технических измерений и решить приведенные выше задачи. Решенные задачи отправлять на rulev-distant@yandex.ru
. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК Абсолютная и относительная ошибки Никакую физическую величи
Работа добавлена на сайт samzan.net: 2016-03-13
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
11
Ч а с т ь I
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная и относительная ошибки
Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность*) измерения х :
х = х – Х. (1)
Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.
Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение является грубым. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:
. (2)
Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.
При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно: поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
Случайная и приборная погрешности
Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.
По происхождению ошибки делятся на инструментальные и методические.
Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.
Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.
По характеру проявления ошибки бывают систематические и случайные.
Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х0 , отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х0 .
Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.
Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как s x.
Оценка случайной погрешности. Доверительный интервал
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через среднеарифметическое значение
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
Рис.1
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
, (4)
где .
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
. (5)
Коэффициент пропорциональности tn, называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина tn, должна быть тем больше, чем выше доверительная вероятность .
С увеличением количества опытов среднее значение приближается к истинному; поэтому при той же вероятности доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффи-циента Стьюдента в зависимости от п и дана в приложениях к настоящему пособию.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины по формуле (3);
2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями , а также квадрат этой разности (отклонения) ( хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка по формуле (4);
4) по заданной доверительной вероятности и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента tn, и определяется случайная погрешность s x по формуле (5).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл.1.
Таблица 1
|
Номер опыта |
… |
х |
х |
( х)2 |
|
1 |
… |
|||
|
2 |
… |
|||
|
… |
… |
|||
|
п |
… |
|||
|
= |
= |
В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с2), коэффициент вязкости жидкости (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение , получим расчетную формулу
. (6)
Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним
четвертый столбец значениями ускорения ai и найдем их сумму, которую запишем под этим столбцом в ячейку « = ». Затем рассчитаем среднее значение по формуле (3)
.
Таблица 2
|
Номер опыта |
S, м |
t, c |
а, м/с2 |
а, м/с2 |
(а)2, (м/с2)2 |
|
1 |
5 |
2,20 |
2,07 |
0,04 |
0,0016 |
|
2 |
7 |
2,68 |
1,95 |
-0,08 |
0,0064 |
|
3 |
9 |
2,91 |
2,13 |
0,10 |
0,0100 |
|
4 |
11 |
3,35 |
1,96 |
-0,07 |
0,0049 |
|
= |
8,11 |
= |
0,0229 |
Вычитая из каждого значения ai среднее, найдем разности ai и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку « = ». По формуле (4) определим среднеквадратичную погрешность:
.
Задавшись величиной доверительной вероятности = 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента tn, = 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437 0,139 (м/с2) .
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.
Рис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
,
где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
. (7)
Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем
. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;
б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и ( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости рассчитывается по формуле
, (10)
где ш – плотность материала шарика; ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости – результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида
, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
Таблица 3
|
и(х) |
kx |
На практике зависимость (9) чаще всего имеет вид степенной функции
,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
, (12)
где – среднее значение величины и; – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t ) = 2S 1t – 2 ;
тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением
.
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 м; t 3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:
;
.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность а равной
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
,
где . Тогда для оценки приборной погрешности , согласно (12), получим выражение
, (13)
где .
Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l 80 cм; D 4 мм; t 10 с; Пас. Оценим величины, входящие в формулу (13):
Пренебрегая величиной Еt , проведем расчет по формуле (13):
.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами s x и х, находится следующим образом.
Если одна из погрешностей более чем в три раза превышает другую (например, s x > 3 х), то полная ошибка принимается равной этой большей величине (в приведенном примере s x). Если же величины s x и х близки между собой, то полная ошибка вычисляется как
. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
с указанием значения доверительной вероятности . Величины и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
,
выраженное в процентах и округленное до десятых долей.
Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры (примеры: а) 0,2642 0,26; б) 3,177 3,2 3; в) 7,8310 – 7 810 – 7 и т.д.). После этого среднее значение округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения = 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
и запишем окончательный результат измерений:
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение = 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение 343 м/с. Полная относительная погрешность
.
Окончательный результат измерений имеет вид
Пример 6. При определении длины волны лазерного излучения (работа 5.1) получено: при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
.
Округленное среднее будет равно мм. Оценим полную относительную ошибку
и запишем окончательный результат:
Е = 4,4 %.
* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.
. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК Абсолютная и относительная ошибки Никакую физическую величи
Работа добавлена на сайт samzan.net: 2016-03-13
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
11
Ч а с т ь I
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная и относительная ошибки
Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность*) измерения х :
х = х – Х. (1)
Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.
Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение является грубым. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:
. (2)
Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.
При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно: поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
Случайная и приборная погрешности
Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.
По происхождению ошибки делятся на инструментальные и методические.
Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.
Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.
По характеру проявления ошибки бывают систематические и случайные.
Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х0 , отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х0 .
Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.
Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как s x.
Оценка случайной погрешности. Доверительный интервал
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через среднеарифметическое значение
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
Рис.1
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
, (4)
где .
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
. (5)
Коэффициент пропорциональности tn, называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина tn, должна быть тем больше, чем выше доверительная вероятность .
С увеличением количества опытов среднее значение приближается к истинному; поэтому при той же вероятности доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффи-циента Стьюдента в зависимости от п и дана в приложениях к настоящему пособию.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины по формуле (3);
2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями , а также квадрат этой разности (отклонения) ( хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка по формуле (4);
4) по заданной доверительной вероятности и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента tn, и определяется случайная погрешность s x по формуле (5).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл.1.
Таблица 1
|
Номер опыта |
… |
х |
х |
( х)2 |
|
1 |
… |
|||
|
2 |
… |
|||
|
… |
… |
|||
|
п |
… |
|||
|
= |
= |
В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с2), коэффициент вязкости жидкости (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение , получим расчетную формулу
. (6)
Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним
четвертый столбец значениями ускорения ai и найдем их сумму, которую запишем под этим столбцом в ячейку « = ». Затем рассчитаем среднее значение по формуле (3)
.
Таблица 2
|
Номер опыта |
S, м |
t, c |
а, м/с2 |
а, м/с2 |
(а)2, (м/с2)2 |
|
1 |
5 |
2,20 |
2,07 |
0,04 |
0,0016 |
|
2 |
7 |
2,68 |
1,95 |
-0,08 |
0,0064 |
|
3 |
9 |
2,91 |
2,13 |
0,10 |
0,0100 |
|
4 |
11 |
3,35 |
1,96 |
-0,07 |
0,0049 |
|
= |
8,11 |
= |
0,0229 |
Вычитая из каждого значения ai среднее, найдем разности ai и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку « = ». По формуле (4) определим среднеквадратичную погрешность:
.
Задавшись величиной доверительной вероятности = 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента tn, = 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437 0,139 (м/с2) .
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.
Рис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
,
где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
. (7)
Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем
. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;
б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и ( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости рассчитывается по формуле
, (10)
где ш – плотность материала шарика; ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости – результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида
, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
Таблица 3
|
и(х) |
kx |
На практике зависимость (9) чаще всего имеет вид степенной функции
,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
, (12)
где – среднее значение величины и; – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t ) = 2S 1t – 2 ;
тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением
.
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 м; t 3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:
;
.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность а равной
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
,
где . Тогда для оценки приборной погрешности , согласно (12), получим выражение
, (13)
где .
Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l 80 cм; D 4 мм; t 10 с; Пас. Оценим величины, входящие в формулу (13):
Пренебрегая величиной Еt , проведем расчет по формуле (13):
.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами s x и х, находится следующим образом.
Если одна из погрешностей более чем в три раза превышает другую (например, s x > 3 х), то полная ошибка принимается равной этой большей величине (в приведенном примере s x). Если же величины s x и х близки между собой, то полная ошибка вычисляется как
. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
с указанием значения доверительной вероятности . Величины и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
,
выраженное в процентах и округленное до десятых долей.
Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры (примеры: а) 0,2642 0,26; б) 3,177 3,2 3; в) 7,8310 – 7 810 – 7 и т.д.). После этого среднее значение округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения = 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
и запишем окончательный результат измерений:
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение = 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение 343 м/с. Полная относительная погрешность
.
Окончательный результат измерений имеет вид
Пример 6. При определении длины волны лазерного излучения (работа 5.1) получено: при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
.
Округленное среднее будет равно мм. Оценим полную относительную ошибку
и запишем окончательный результат:
Е = 4,4 %.
* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.
Лекция — Погрешности — файл n1.doc
Лекция — Погрешности
скачать (210 kb.)
Доступные файлы (1):
n1.doc
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная и относительная ошибки
Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно не был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность*) измерения х :
х = х – Х. (1)
Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.
Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение проведено очень грубо. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:
![]() . (2)
. (2)
Очевидно, что относительная погрешность – величина безразмерная; чаще всего ее выражают в процентах.
При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно – поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
Случайная и приборная погрешности
Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.
По своему происхождению ошибки делятся на инструментальные и методические.
Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.
Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы, и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.
По характеру проявления ошибки бывают систематические и случайные.
Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна, и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если в отсутствие внешних воздействий стрелка измерительного прибора показывает величину х0 , отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х0 .
Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.
Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как s x.
Оценка случайной погрешности. Доверительный интервал
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через ![]() среднеарифметическое значение
среднеарифметическое значение
![]() . (3)
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
![]()
При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение ![]() характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения “величина х имеет значение, в точности равное ![]() ” равна нулю. Вероятность же утверждения “величина х имеет какое-либо значение” равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
” равна нулю. Вероятность же утверждения “величина х имеет какое-либо значение” равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
Рис.1 (см. конец файла)
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность “накрывания” значения Х более широким интервалом выше). Следовательно, величина tn, должна быть тем больше, чем выше доверительная вероятность .
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения ![]() . “Разброс” результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
. “Разброс” результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
![]() , (4)
, (4)
где ![]() .
.
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
![]() . (5)
. (5)
Коэффициент пропорциональности tn, называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .
С увеличением количества опытов среднее значение становится ближе к истинному; поэтому при той же вероятности доверительный интервал можно взять более узким (см. рис. 1, а,в) – таким образом, с ростом п коэффициент Сьюдента должен уменьшаться.
Таблица значений коэффициента Стьюдента в зависимости от п и дана в приложении к настоящему пособию.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины ![]() по формуле (3);
по формуле (3);
2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями ![]() , а также квадрат этой разности (отклонения) ( хi)2 ;
, а также квадрат этой разности (отклонения) ( хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка по формуле (4);
4) по заданной доверительной вероятности и числу проведенных опытов п из табл. П-1 приложения выбирается соответствующее значение коэффициента Стьюдента tn, и определяется случайная погрешность s x по формуле (5).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, образец которой дан ниже.
Таблица 1
| Номер опыта | … | х | х | ( х)2 |
| 1 | … | |||
| 2 | … | |||
| … | … | |||
| П | … | |||
| = | = |
В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с2), коэффициент вязкости жидкости (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение ![]() , получим расчетную формулу
, получим расчетную формулу
![]() . (6)
. (6)
Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним
четвертый столбец значениями ускорения ai и найдем их сумму, которую запишем под этим столбцом в ячейку “ = ”. Затем рассчитаем среднее значение ![]() по формуле (3):
по формуле (3):
![]() .
.
Таблица 2
| Номер опыта | S,
м |
t,
c |
а,
м/с2 |
а,
м/с2 |
(а)2,
(м/с2)2 |
| 1 | 5 | 2,20 | 2,07 | 0,04 | 0,0016 |
| 2 | 7 | 2,68 | 1,95 | -0,08 | 0,0064 |
| 3 | 9 | 2,91 | 2,13 | 0,10 | 0,0100 |
| 4 | 11 | 3,35 | 1,96 | -0,07 | 0,0049 |
| = | 8,11 | = | 0,0229 |
Вычитая из каждого значения ai среднее, найдем разности ai и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку “ = ”. По формуле (4) определим среднеквадратичную погрешность:
![]() .
.
Задавшись величиной доверительной вероятности = 0,95, для числа опытов п = 4 из табл. П-1 приложения выбираем значение коэффициента Стьюдента tn, = 3,18; наконец, с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437
0,139 (
м/с2
)
.
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом, для электро-измерительных приборов – класс точности.

Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определеяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.
Рис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
![]() ,
,
где N – общее количество делений. Например, на рис. 2 N = 50. Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
![]() . (7)
. (7)
Значение класса точности (без символа “%”) указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись “0,01 мм”. Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем:
![]() . (8)
. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
![]() .
.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;

б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и ( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости рассчитывается по формуле
![]() , (10)
, (10)
где ш – плотность материала шарика; ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости – результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида
![]() , (11)
, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
Таблица 3
| и(х) | kx |
|
|
|
|
|
|
|
|
На практике зависимость (9) чаще всего имеет вид степенной функции
![]() ,
,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
![]() , (12)
, (12)
где ![]() – среднее значение величины и;
– среднее значение величины и; ![]() – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
– относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной ![]() . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
. Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t ) = 2S 1t – 2 ;
тогда, на основании (12), погрешность косвенного измерения ускорения а определится выражением
![]() .
.
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 м; t 3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:
![]() ;
;
![]() .
.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность а равной
![]() .
.
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
![]() ,
,
где ![]() . Тогда для оценки приборной погрешности , согласно (12), получим выражение
. Тогда для оценки приборной погрешности , согласно (12), получим выражение
![]() , (13)
, (13)
где ![]() .
.
Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l 80 cм; D 4 мм; t 10 с; ![]() Пас. Оценим величины, входящие в формулу (13):
Пас. Оценим величины, входящие в формулу (13):

Пренебрегая величиной Еt , проведем расчет по формуле (13):
![]() .
.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами s x и х, находится следующим образом.
Если одна из погрешностей более чем в три раза превышает другую (например, s x > 3 х), то полная ошибка принимается равной этой большей величине (в приведенном примере s x). Если же величины s x и х близки между собой, то полная ошибка вычисляется как
![]() . (14)
. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
![]()
с указанием значения доверительной вероятности . Величины ![]() и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
![]() ,
,
выраженное в процентах и округленное до десятых долей.
Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры (примеры: а) 0,2642 0,26; б) 3,177 3,2 3; в) 7,8310 – 7 810 – 7 и т.д.). После этого среднее значение ![]() округляется с той же точностью.
округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения ![]() = 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
= 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
![]()
и запишем окончательный результат измерений:

![]()
![]()
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение ![]() = 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение
= 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение ![]() 343 м/с. Полная относительная погрешность
343 м/с. Полная относительная погрешность
![]() .
.
Окончательный результат измерений имеет вид

![]()
![]()
Пример 6. При определении длины волны лазерного излучения (работа 5.1) получено: ![]() при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
![]() .
.
Округленное среднее будет равно ![]() мм. Оценим полную относительную ошибку
мм. Оценим полную относительную ошибку
![]()
и запишем окончательный результат:

![]()
Е = 4,4 %.
Л
Л

КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
