В настоящей статье рассматриваются причины и
пути предупреждения у учащихся ошибок,
заключающихся в пропуске цифр частного (потеря
нулей в частном) и в по лучении лишних цифр в
частном.
Основными причинами указанных выше ошибок
являются следующие:
- неумение учащихся осознанно определять
количество цифр в частном; - имеющееся у большинства учащихся представление
о том, что меньшее число не делится даже с
остатком на большее число, а значит, и частного в
этом случае не будет; - формальное усвоение способа образования
неполных делимых; - отсутствие значения о том, что каждое неполное
делимое обязательно дает цифру частного в
соответствующем разряде.
Остановимся на каждой из указанных причин и
путях их устранения.
Обычно определение количества цифр в частном
проводится в результате таких рассуждений:
“Первое неполное делимое 8 сотен, значит, в
частном будет три цифры…”
Однако абсолютное большинство опрошенных
учащихся не смогли объяснить, почему из того, что
если первое неполное делимое 8 сотен, то в частном
будет три цифры. Отсутствие логического перехода
от разряда первого неполного делимого к
количеству цифр частного — основная причина
непонимания учащимися этого шага, а потому и его
невыполнения.
Подробнее объяснение определения количества
цифр частного дано в пособии для учителя при
выполнении деления 936 на 4: “9 сотен — это первое
неполное делимое. Когда разделим сотни, то в
частном получим сотни, а сотни в записи числа
стоят на третьем месте, значит, в частном будет 3
цифры”.
Приведенные рассуждения конкретизируют важное
общее положение: разряд первого неполного
делимого является и высшим разрядом частного.
Указанное общее положение необходимо довести и
до учащихся. Это может быть сделано в результате
обобщения способа определения количества цифр
частного для конкретных случаев деления уже на
уроке ознакомления с алгоритмом деления.
Ниже описан возможный вариант соответствующей
части урока.
После объяснения и выполнения деления
одним-двумя учащимися у доски учитель просит
детей назвать первый шаг алгоритма. Они называют
выделение первого неполного делимого,
определение количества цифр частного. Затем
детям дается задание: для каждого случая деления
(785:5, 434:7, 12360:6, 1736:8) выделить первое неполное
делимое и определить количество цифр частного,
проведя необходимые рассуждения.
Учитель направляет ответы учащихся так, чтобы
количество цифр частного определялось, в
результате примерно таких рассуждений: “Первое
неполное делимое в примере 785:5 будет 7 сотен,
значит, первая цифра частного будет обозначать
сотни. Тогда в частном будут сотни, десятки и
единицы, т. е. три цифры”. “Во втором примере (434:7)
первое неполное делимое 43 десятка, значит, первая
цифра частного будет обозначать десятки (высший
разряд частного – десятки). Значит, частное будет
состоять из десятков и единиц. Частное —
двузначное число”. “В третьем примере (12 360:6)
первое неполное делимое 12 тысяч, значит, высший
разряд частного — тысячи. Тогда частное будет
состоять из тысяч, сотен, десятков и единиц,
значит, в частном — четыре цифры”. “В четвертом
примере (1 736:8) первое неполное делимое 17 сотен,
значит, высший разряд частного — сотни. Поэтому
частное будет содержать сотни, десятки и единицы,
т. е. три цифры”.
При выполнении этого задания полезно на доске
выделить первое неполное делимое, ниже записать
название разряда этого неполного делимого и
название высшего разряда частного, отметить
точками количество цифр частного. Общий вывод —
разряд первого неполного делимого является
высшим разрядом частного — может быть сделан
самим учителем. Требовать запоминания учащимися
определения этого, вывода не нужно.
Далее дети продолжают выполнение
тренировочных упражнений в делении на
однозначное число, комментируя каждый шаг
алгоритма и объясняя способ определения
количества цифр частного.
В дальнейшем полезно в устные упражнения
включать специальные задания на определение
количества цифр частного, например, такие:
1. Сколько цифр будет содержать частное и
почему, если первое неполное делимое 12 десятков? 4
сотни? 57 тысяч? 19 десятков тысяч?
2. Выполняя деление в следующих случаях:
1) 9870:35
2) 136576:64
3) 95345:485
4) 76171:19
5) 720036:36
ученик в частном получил соответственно:
1) трехзначное число; 2) четырехзначное число; 3)
двухзначное число; 4) четырехзначное число; 5)
трехзначное число.
В каких случаях частное найдено неверно?
Почему?
3. Не выполняя действий деления и умножения,
укажите, какие из равенств неверны:
116174:58=203
44172:9 =4908
21476:7 =368
Верно ли, что меньшее число не делится на
большее? Верно, но лишь для деления нацело.
Действительно, разделить нацело одно число на
другое — это значит найти такое третье целое
неотрицательное число, умножив на которое
делитель получим делимое. Если делимое меньше
делителя (но не равно нулю), то такого целого
неотрицательного числа найти нельзя, т. е. для
случая деления, например, 2:7 частного при делении
нацело не существует.
Другое дело, если рассматривается деление с
остатком. В этом случае разделить, например, 3 на 11
означает найти таких два целых неотрицательных
числа — частное и остаток, чтобы сумма
произведения частного на делитель и остатка была
равна делимому. Указанному условию для чисел 3 и 11
удовлетворяют частное и остаток 3. Действительно:
0.11+3=3, т. е. 3:11=0 (ост. 3), где 3<11. Причем это
частное и остаток легко найти, используя
известный прием деления с остатком: “З не
делится нацело на 11. Самое большое число, которое
делится нацело на 11 и меньше 3, есть число 0.
Разделим 0 на 11, получим частное 0. Из делимого 3
вычтем 0, получим 3. Это остаток. Причем 3 меньше 11.
Итак, частное при делении 3 на 11 равно 0, остаток
равен З”.
В каждом шаге алгоритма письменного деления
выполняется именно деление с остатком, так как
при делении неполного делимого на делитель
всегда требуется найти два числа: частное и
остаток. А поэтому и случай, когда неполное
делимое меньше делителя, следует рассматривать
как деление с остатком.
Покажем теперь, как рассуждает ученик, если он
считает, что меньшее число не делится на большее,
т. е. рассматривает это деление как деление
нацело.
Пусть, например, нужно разделить 642 на 6. Найдя
первую цифру частного — 1, учащиеся часто
рассуждают так: “4 на 6 не делится, значит, буду
делить на б число 42. 42 разделить на 6, получится 7.
Частное равно 17”. В этих рассуждениях ошибочным
является утверждение 4 на 6не делится, из которого
уже логически следует оставшаяся часть
рассуждений. Действительно, слова не делится
означают частного не существует, а раз не
существует, то никакой цифры в частном от деления
4 на 6 появиться не должно! Постановка нуля в
частном в этом случае есть нарушение логики.
Появление этой цифры в частном логически
оправдано, если объяснение дается такое: “4
десятка не делится на 6 так, чтобы в частном
получился хотя бы один десяток, поэтому десятков
в частном будет 0”. Однако это объяснение для
слабых учащихся не всегда может быть оправдано,
так как после слов не делится мысль о том, что
частного в этом случае нет, может возникнуть у
них раньше, чем дальнейшие рассуждения. Ведь весь
жизненный опыт учащихся формирует у них (может
быть, неявно) абсолютно верное утверждение:
“Если какое-то действие (в широком смысле) нельзя
выполнить, то и никакого результата у такого
действия не будет!”
Предотвратить возникновение ошибок поможет
рассмотрение деления в случае, когда делимое
меньше делителя, как деления с остатком. Для
этого перед ознакомлением с алгоритмом
письменного деления следует повторить прием
деления с остатком, предлагая учащимся найти
частное и остаток и для выражений вида: 7:23, 2:5, 9:15 и
т. п.
При выполнении письменного деления в
рассмотренном выше случае (642:6 рассуждения
учащихся могут быть такими: “Второе неполное
делимое 4 десятка. 4 десятка разделим на 6. Получим
частное 0 десятков и остаток 4 десятка. 4 меньше,
чем 6, значит, цифра частного найдена верно.
Образуем следующее неполное делимое…”
Формальное усвоение учащимися способа
образования неполных делимых проявляется в том,
что, во-первых, учащиеся не определяют разряд
неполного делимого, а лишь формально
приписывают, сносят цифру полного делимого;
во-вторых, неполными делимыми считают только
числа, большие делителя, а потому при письменном
делении, например, 780 702 указывают только два
неполных делимых: 78 дес. тыс. и 702 ед., хотя в
действительности неполных делимых здесь пять: 78
дес. тыс., ,0 тыс., 7 сот., 70 дес., 702 ед.
Покажем возможные пути устранения
рассматриваемой причины ошибок.
Способ образования неполных делимых состоит из
двух операций: перевода единиц высшего разряда
(перевода остатка) в единицы следующего низшего
разряда и сложение полученного круглого числа с
единицами этого же разряда, имеющимися в полном
делимом.
При ознакомлении с алгоритмом письменного
деления необходимо выделить этот способ для
осознания и запоминания учащимися. Важно при
этом подчеркнуть, что следующее неполное делимое
единицы разряда непосредственно следующего
(низшего) за разрядом предыдущего неполного
делимого, что никаких пропусков и повторений
разрядов не должно быть.
Для закрепления полезно предложить учащимся,
например, такое задание: “При письменном делении
некоторых чисел первое неполное делимое
оказалось равным 28 тысячам. Единицы какого
разряда содержат второе неполное делимое,
третье, четвертое?”
Для осознанного овладения учащимися способом
образования неполных делимых полезно постепенно
осуществлять переход от полных рассуждений при
выполнении письменного деления к кратким,
предлагая учащимся некоторое время проводить
при делении примерно такие рассуждения:
Рисунок 1
“Первое неполное делимое 10 тыс., значит, в
частном будут тысячи, сотни, десятки и единицы, т.
е. четыре цифры. Разделю 10 на 6. Получу в разряде
тысяч в частном I. Умножу 1 на 6. Вычту из 10 число 6.
Второе неполное делимое 43 сотни. 43 разделю на 6.
Получу в частном разряде сотен 7. Умножу 7 на 6 и
вычту 42 из 43. Следующее неполное делимое 15
десятков. 15 делю на 6. В разряде десятков частного
получу 2. Умножу 2 на 6 и вычту 12 из 15. И т. д.”
При рассмотрении первого примера деления с
нулем в частном полезно использовать такую же
запись, как и для случаев без нуля в частном, и
проводить рассуждения так, как это показано ниже:
Рисунок 2
“Первое неполное делимое 4 сотни, значит в
частном будут сотни, десятки и единицы т. е. три
цифры. 4 разделю на 4, в раз ряде сотен получу 1. 1
умножу на 4. Все сотни разделили. Следующее
неполное дели мое 3 десятка. Разделю 3 на 4, получу
в разряде десятков частного 0. 0 умножу на 3, получу
0. Вычту 0 из 3. Остаток 3.
Следующее неполное делимое 32 единицы Разделю 32
на 4, получу 8 в разряде единиц частного. Частное
чисел 432 и 4 равно 108”.
Затем учитель говорит, что умножение нуля на 3 и
вычитание нуля из трех можно выполнить устно, не
записывая результате и показывает сокращенную
запись алгоритма деления для случая деления с
нулем в частном:
Рисунок 3
Рассуждения же проводятся точно так как и при
использовании первой записи.
При рассмотрении случаев деления на двузначное
число с нулем в частном также полезно в записи
иметь каждое из неполных делимых, даже если это
делимое равно нулю. Важно приучить детей к
соблюдению такой последовательности выполнения
деления: после получения неполного делимого
нужно обязательно найти соответствующую цифру
частного, записать ее в частном лишь после этого
образовывать следую неполное делимое. Выработка
у учащихся привычки всегда при выполнении
письменного деления придерживаться указанной
последовательности и есть основной путь
устранения причины ошибок, отмеченной нами выше.
Покажем на примере 480024: 24, как может быть
оформлена запись алгоритма письменного деления
и какими рассуждениями целесообразно ее
сопровождать:
Рисунок 4
“Первое неполное делимое 48 десятков тысяч,
значит, в частном будут десятки тысяч, единицы
тысяч, сотни, десятки и единицы, т. е. пять цифр.
Разделю 48 на 24, получится 2 в разряде десятков
тысяч в частном. Все десятки тысяч разделились,
остаток 0. Образую второе неполное делимое: 0
тысяч. 0 разделю на 24, получится 0 в разряде единиц
тысяч в частном. Следующее неполное делимое 0
сотен. 0 разделю на 24, получится 0 в разряде сотен в
частном. Следующее неполное делимое 2 десятка. 2
разделю на 24, в частном в разряде десятков получу
0, в остатке 2. Следующее неполное делимое 24
единицы. 24 разделю на 24, получится 1 в разряде
единиц частного. Частное чисел 480024 и 24 равно 20001”.
В дальнейшем применяется обычная запись, но в
случае затруднений, ошибок можно прибегать и к
приведенной выше записи или же к такой, как
показано ниже:
Рисунки 5 и 6
В заключение отметим, что формирование любого
навыка идет успешнее, если этот навык осознанный.
Именно поэтому усиление внимания учителей ко
всем отмеченным выше моментам в обучении
алгоритму письменного деления будет
способствовать выработке более прочных
вычислительных навыков.
Деление столбиком используют, когда нужно разделить простые или сложные многозначные числа. Оно помогает найти ответ за счёт разбивания решения на ряд более простых шагов. В статье объясним на примерах, как делить в столбик и дадим пошаговый алгоритм.
Какие арифметические действия используют при делении в столбик
При знакомстве с делением в столбик у школьника могут возникнуть трудности и недопонимания. Отчасти потому, что при сложении в столбик мы только складываем, а при вычитании только вычитаем. Когда же мы делим в столбик, то по очереди выполняем: деление, умножение и вычитание. Кроме того, нужно знать таблицу умножения, уметь делить с остатком и аккуратно писать цифры, каждую в своей клетке, чтобы не ошибиться в расчётах.
Термины «делимое», «делитель», «частное», «неполное делимое»


Делить в столбик двузначные числа на однозначное
Разделим 86 на 2
1. Для начала определим первое неполное делимое и узнаем, сколько будет цифр в частном. 8 можем разделить на 2, значит, 8 — первое неполное делимое, в частном будет первая цифра. После 8 есть ещё одна цифра, значит, и в частном будет ещё одна цифра — всего две цифры.
2. Разделим первое неполное делимое 8 на делитель 2, получим первую цифру частного — 4.
3. Умножим делитель 2 на цифру частного 4, получим ответ — 8. Этот результат записываем под первым неполным делимым.
4. Находим остаток 8 — 8 = 0. Остаток 0 меньше делителя 2, значит, продолжаем вычисления. Остаток 0 можно не писать.
5. Сносим (переписываем) цифру 6 — это новое неполное делимое.
6. Делим неполное делимое 6 на делитель 2, получаем — 3. Результат записываем в частное.
7. Умножаем делитель 2 на новую цифру частного 3, получаем 6. Результат записываем под вторым неполным делимым.
8. Записываем последний остаток 0. Больше мы не можем снести ни одной цифры, значит, неполных делимых не осталось. Деление в столбик закончено.
Делить в столбик трёхзначное число на однозначное
Разделим 486 на 3
1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.
2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.
3. Далее умножим делитель на полученную цифру частного: 3 · 1 = 3. Запишем 3 под первым неполным делителем.
4. Теперь нужно найти остаток при помощи вычитания.
5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.
6. Разделим 18 на 3 и получим вторую цифру частного — 6.
7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.
8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.
9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.
Пример деления с нулём в частном, или сколько раз можно сносить цифру делимого, чтобы получить одно новое неполное делимое
Разделим 816 на 8
1. Первое неполное делимое 8, а за ним ещё две цифры. Значит, в частном будет 3 цифры.
2. Разделим первое неполное делимое 8 на делитель 4 и запишем в частное ответ — 2.
3. Умножим делитель 4 на цифру частного 2, получим 8. Запишем число под первым неполным делимым.
4. Сносим цифру 1 — это новое неполное делимое. Остаток 0 не пишем.
5. Вспомним деление с остатком и разделим 1 на 4. В результате получим 0, остаток — 1. Цифру 0 записываем в частное.
6. Умножим делитель 4 на цифру частного 0, результат 0 запишем под вторым неполным делимым. Остаток 1.
7. Сносим 6 и получаем новое неполное делимое 16. Делим 16 на 4, получаем цифру частного 4.
8. Умножаем делитель 4 на цифру частного 4 и пишем результат под неполным делимым.
9. Записываем последний остаток 0 — деление выполнено.
Как можно сократить запись деления
Когда мы получили неполное делимое 1, которое меньше делителя 4, сносим вторую цифру делимого, чтобы новое неполное делимое было больше делителя. А в частное ставим 0. И далее выполняем деление в установленном порядке.
В этом примере мы дважды сносили цифру делимого, чтобы получить неполное делимое, которое больше делителя.

Надеемся, что теперь у вашего ребёнка не возникнет трудностей с делением в столбик. А если вдруг они есть, наши репетиторы с удовольствием готовы вам помочь!
Влюбляем в обучение на уроках в онлайн-школе Тетрика
Оставьте заявку и получите бесплатный вводный урок
РАБОТА НАД ОШИБКАМИ.
Поупражняемся в делении
столбиком
Цели: учить выполнять работу над
ошибками; формировать умение выполнять деление многозначного числа на
двузначное; решать задачи на деление; формулировать условие задачи по данному
решению; закреплять умение решать уравнение; формулировать условие задачи по
данному уравнению.
Ход урока
I. Устный счет.
1. Восстановите цепочку
вычислений:

2. Прочитайте условие задачи. Три сестры – Алла,
Рита и Лена – собирают открытки. У Аллы их 158, у Риты – в 4 раза больше, чем у
Аллы, а у Лены – на 35 открыток меньше, чем у Риты. Поставьте разумные вопросы
и ответьте на них.
3. Вставьте вместо точек пропущенные цифры и
определите количество цифр в частном.

– В каких разрядах можно брать любые цифры, а в
каких нет?
– От какой цифры зависит, сколько всего будет
цифр в частном?
4. Сколько треугольников изображено на рисунке?

II. Работа по учебнику.
Задание 51. В каждом из данных заданий на деление столбиком покажите
с помощью дуги первое неполное делимое, а с помощью квадратиков – сколько цифр
в неполном частном.

Задание 52. В каждом столбике восстановите полную запись деления
столбиком.

Задание 53. Учащиеся выполняют деление
столбиком для данных чисел.

Задание 54. Прочитайте задачу. Что известно? Что требуется узнать?
Выполните решение задачи.

Ответ: 25 рядов.
Задание 55. Каким может быть первое промежуточное делимое при
делении столбиком трехзначного числа на число 9, если первая цифра неполного
частного равна 4?
![]()
– Запишите самое маленькое и самое большое из возможных таких чисел. (Самое
большое – 44, самое маленькое – 36.)
– Выполните деление столбиком числа 449 на число 9.

Задание 56. Сколько цифр может быть в записи
неполного частного при делении пятизначного числа на однозначное?

– Приведите примеры.

Задание 57. Сколько цифр может быть в записи неполного частного при
делении пятизначного числа на двузначное?

– Приведите примеры.

Задание 58. Учащиеся составляют задачу по выражению.
Привезли – 2850 кг и 3645 кг.
Разложили – в ? ящ. по 15 кг.
Решение:

Ответ: 433 ящика.
Задание 59. Найдите число, которое при делении на число 17 дает в
неполном частном число 3002, а в остатке число 8.
решение: 3002 · 17 + 8 = 51042.
– Выполните деление найденного числа на число 17 столбиком, используя
сокращённую форму записи.

Задание 60. Прочитайте задачу. Что известно? Что требуется узнать?
Выполните краткую запись и решите задачу.
![]()

2) + 2568
214
2782 (дер.) – всего.
Ответ: 2782 дерева.
Задание 61. Учащиеся составляют задачу по уравнению.

Ответ: привезли 302 кг.
III. Итог урока.
– Что нового узнали на уроке?
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
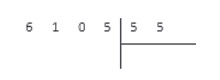
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
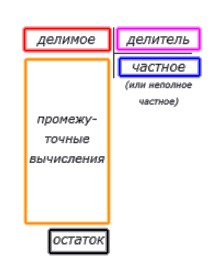
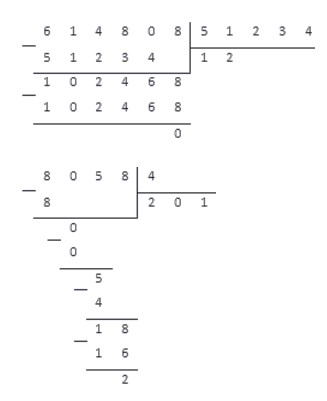
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
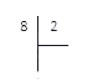
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
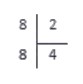
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
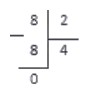
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
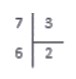
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
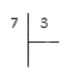
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
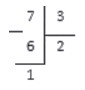
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
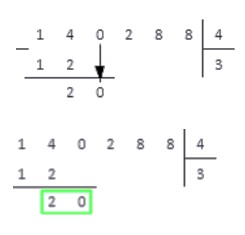
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0. В итоге отмечаем новое рабочее число — 20.
Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
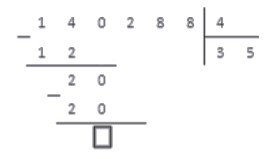
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
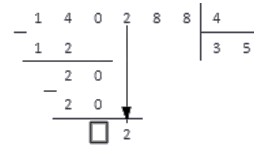
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
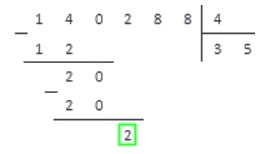
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
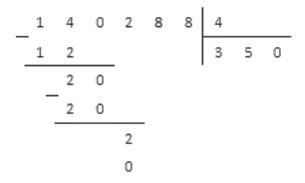
3. Выполняем операцию вычитания и под чертой записываем результат.
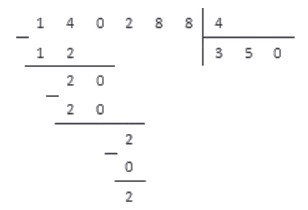
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
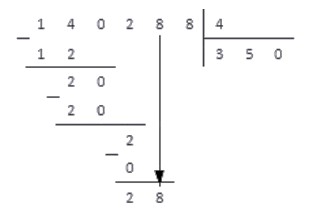
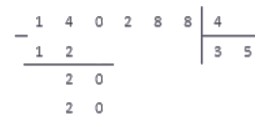
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
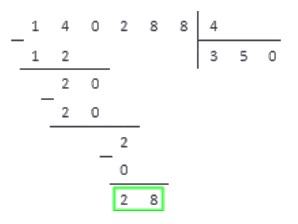
Проделав все по правилам, получаем результат:
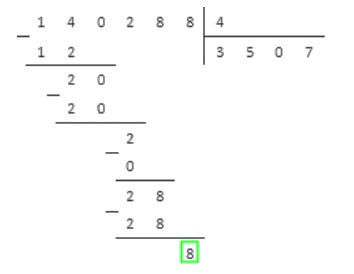
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:
В самой нижней строчке записываем число 0. Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Разделим натуральное число 7136 на натуральное число 9.
Запишем:
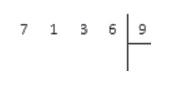
После второго, третьего и четвертого шага алгоритма запись примет вид:
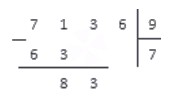
Повторим цикл:
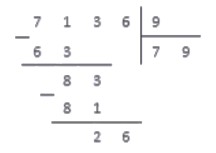
Последний проход, и поучаем результат:
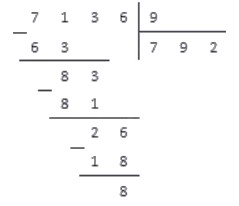
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Разделим число 7042035 на 7.
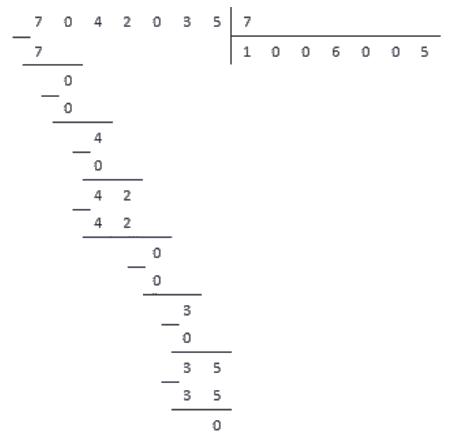
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Разделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
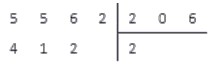
Выполняем вычитание столбиком
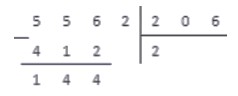
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
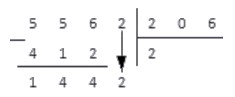
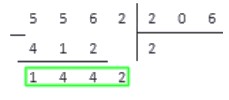
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
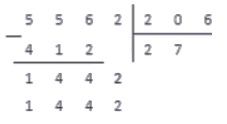
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
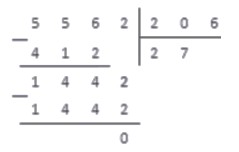
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Разделим натуральное число 238079 на 34.
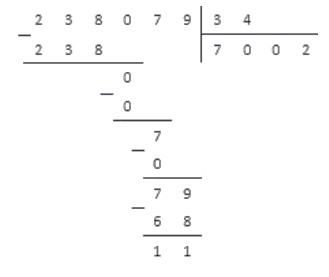
Ответ: 7002
