Еще
много веков назад было отмечено, что
человеческая деятельность не всегда
бывает безукоризненна. Около двух тысяч
лет назад римский философ Цицерон
предупреждал: «Человеку свойственно
ошибаться». Непреложным фактом является
то, что где бы мужчине или женщине не
пришлось работать, когда-нибудь происходят
человеческие ошибки.
В
настоящем пособии «Человеческие ошибки»
профессор Джеймс Ризон определяет
ошибку следующим образом:
«Ошибка
рассматривается как следствие объединяющее
все те случаи, когда запланированная
последовательность умственных или
физических усилий не достигает необходимой
цели и когда все эти провалы не могут
быть отнесены на счет влияния случая».
Ясно,
что обслуживание самолета зависит от
компетенции инженеров исполнителей.
Много примеров описанных в Главе 1
«Инциденты связанные с человеческими
факторами / Человеческими ошибками» и
во всем настоящем пособии освещают
ошибки, которые были допущены инженерами
по обслуживанию самолетов и которые
повлекли за собой авиационные аварии
и инциденты.
В прошлом авиационные
компоненты и системы были относительно
не надежны. Современные самолеты по
сравнению с ними сконструированы и
изготовлены как высоко надежные. Как
следствие, в настоящее время обычно
говорят, что инцидент с самолетом или
авария были вызваны «человеческим
фактором».
Следующее
положение говорит о том, какую ключевую
роль играет инженер по обслуживанию в
поддержании надежности современного
самолета.
«Так
как гражданский самолет сконструирован
для выполнения безопасных полетов в
течение не ограниченного периода
времени, в случае если дефекты
обнаруживаются и устраняются своевременно,
безопасность становится вопросом
определения и ремонта до отказа какой-либо
конструкционной детали (структуры). В
идеальной системе, все дефекты, влияющие
на безопасность полета должны определяться
заранее до момента когда они станут
опасными и устранены эффективным
ремонтом. С этой точки зрения мы изменили
систему безопасности от одного из
физических дефектов в самолете, до одной
из ошибок в комплексной системе с
человеком в центре».
В
оставшейся части настоящей главы
рассматриваются некоторые из различных
путей, по которым определяется
(концептуализируется) человеческая
ошибка. Затем рассматриваются наиболее
распространенные ошибки случающиеся
при обслуживании самолетов и также
рассматриваются возможные пути
предотвращения этих ошибок.
9.8.1 Модели ошибки и
теория.
Для
определения типов ошибок, которые
возможно сделать, исследователи
рассмотрели человеческие ошибки
несколькими путями и предложили различные
модели и теории. Эта попытка обнаружить
природу ошибок и ее характеристики. Для
иллюстрации этого, они предлагают в
качестве моделей и теорий следующие
варианты основных версий:
-
версия
ошибок вызванных конструкцией и ошибки
операторов; -
переменная
версия постоянных ошибок; -
обратимая
версия необратимых ошибок; -
случайные
ошибки; -
ошибки,
связанные со знанием и навыками; -
модель
«Швейцарский сыр».
Версия ошибок вызванных
конструкцией и ошибки операторов.
В
авиации особый упор делается на ошибках
операторов, включая экипажи самолетов,
диспетчеров и персонала по техническому
обслуживанию.
Однако,
ошибки могут быть допущены даже до того
момента когда самолет впервые вылетает
после сборки. Это может означать, что
если самолет собран и летит, как это
предусматривалось конструкцией, полет
этой конструкции может повлиять на
безопасность. Кроме того, правила
управлением самолета введенные компанией
или управлением по организации полетов
могут также приводить к операционным
проблемам.
Издание 1 15 сентября
2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 73
АMIKON
Training Manual Part-66 Human Factors
При
расследовании авиационных инцидентов
часто обнаруживают, что делается более
чем одна ошибка и более чем одним
человеком. Ситуация может складываться
таким образом, что только при определенной
комбинации ошибок и нарушении их защиты
(См. модель «Швейцарский сыр»), нарушается
безопасность.
Переменная версия
постоянных ошибок.
В своей
книге «Человеческие ошибки» профессор
Ризон обсуждает два типа ошибок человека:
переменные и постоянные. Это можно
расссмотреть на Рис.22. Переменные ошибки
(А) случайны по своей природе в то время
как постоянные ошибки (В) сопровождаются
какой то системой и носят систематический
характер. Возникновения постоянных
ошибок может быть предсказано и от них
можно создать защиту, в то время как
переменные ошибки непредсказуемы и,
как правило, приводят к серьезным
последствиям. Если мы знаем достаточно
много о характере операции, окружающей
среде в которой она выполняется и
физическое и моральное состояние
работника, у нас есть высокий шанс
предотвратить ошибки.
Рис.
22 Переменная версия постоянных ошибок.
Мишени
двух стрелков имеющих по десять выстрелов.
Стрелок А не продемонстрировал постоянных
ошибок, все ошибки значительно отличаются
друг от друга; стрелок В продемонстрировал
значительную постоянную ошибку и
небольшую вариацию мелких ошибок.
Последний вариант легче предугадать и
исправить (коррекцией прицела винтовки).
К
сожалению редко удается получить
достаточно информации для точного
предсказания ; мы можем предсказывать
только на уровне «операции по повторной
сборке где ошибки происходят чаще, чем
при операциях по разборке», или «инженер
чаще совершает ошибки после 3-х часов
ночи после того как отработал 12 часов,
чем после 10 утра после того как отработал
только2 часа».
Возможно,
улучшить эти предсказания при получении
большей информации, но все равно ошибки
или непредсказуемые их элементы будут
происходить.
Обратимая версия
необратимых ошибок.
Другой
путь по определению категорий ошибок
это определение обратимые они или нет.
Первые возможно исправить, вторые обычно
нет.
Например,
если пилот не правильно рассчитал
количество топлива для полета, он может
произвести посадку на более близком
аэродроме, но если он резко потерял
топливо, многих возможностей у него не
появится.
Хорошо
сконструированная система или операция
должна означать, что возможные ошибки
инженера по обслуживанию самолета
должны быть обратимыми. Таким образом,
если инженер установил деталь не
правильно, она должна быть определена
контролером и установлена правильно
до выпуска самолета обратно в эксплуатацию.
Случайные ошибки.
Профессор
Ризон определяет понятие «намерение»
при рассмотрении природы ошибок задавая
следующие вопросы:
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 74
АMIKON
Training Manual Part-66 Human Factors
-
Направлялись
ли действия предварительным намерением? -
Происходили
ли действия так как они планировались? -
Достигли
ли они планируемого результата?
Ризон
предложил классификацию ошибок на базе
ответов на эти вопросы (См. Рис.23).
НЕТ
Было ли намерение действовать?
Было ли предварительное
намерение действовать?
Случайное или не
преднамеренное действие

Спонтанное или
вспомогательное действие
ДА
Происходили ли действия как планировалось?
ДА
Не преднамеренное
действие, промах, ошибка
Достигли ли действия ожидаемого
результата?
Намеренное, но
ошибочное действие
Успешное действие

НЕТ
ДА
НЕТ
ДА
Рис.23
Типы ошибок основанные на намерении.
Наиболее
известный тип – промахи, ошибки.
Промахи
— это действия, проведенные не так как
хотелось или планировалось.
Пропущенные
действия , т.е. когда кто то не сделал
что то из-за провала в памяти / или во
внимании (например забыл одеть капот
на двигатель).
Ошибки
– это специфический тип вызванный не
правильным планированием/намерением.
Т.е кто то сделал что то веря что на тот
отрезок времени это правильно, а
практически нет т.е. ошибка в определении
типа болтов для крепления лобового
стекла.
Промахи
обычно случаются в процессе выполнения
операций, ошибки на стадии планирования.
Нарушения
иногда рассматриваются как человеческие
ошибки, но они отличаются от промахов
и ошибок так как они вызваны неправильными
«незаконными» действиями, т.е. сделал
что то, зная что это не по правилам,
например, желая выполнить работу к
сроку.
Операции
должны выполняться строго по правилам,
чтобы сохранять безопасность полетов.
Ошибки, связанные
со знанием и навыками;
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 75
АMIKON
Training Manual Part-66 Human Factors
Поведение
инженера по обслуживанию может быть
подразделено на три отдельные категории:
на основе опыта, на основе правил и на
основе знаний.
На
основе опыта – базируется на усвоенных
человеком навыках и моторных программах,
полученных с опытом практической работы
и выполняемых без особых раздумий.
На
основе правил – базируется на том,
что правила или порядок выполнения
операции выучен. Компонентами этого
типа поведения могут быть отдельные
навыки.
На
основе знаний – для тех, для кого
процедуры не установлены. От авиационного
инженера требуется оценить полученную
информацию и затем использовать свои
знания для определения плана по действиям
в конкретной ситуации.
Для
каждого из этих поведенческих типов
имеются свои ошибки для них характерные.
Примером
ошибок на основе опыта являются промахи
в действиях, воздействие окружающей
среды и обратные действия. Промахи в
действиях это то же самое, что и просто
промахи – это действия, не проведенные,
как следует. Пример дается в Рис.24 когда
инженеру нужен определенный ключ для
окончания операции, но из за того, что
его отвлек коллега, он взял не тот
комплект ключей установленный на другой
момент затяжки и не замечает того, что
он затягивает болты не так как нужно.

Инженер отвлекается
коллегой
Инженер не следит
за выполнением операции
ОШИБКА
Рис.24
Пример промаха в действии.
Примером
влияния окружающей среды может быть
то, когда инженер часто выполняет одну
и ту же операцию в определенном месте.
Например, инженер, выполняющий операцию
по регулировке на самолете А300, может
неосознанно выполнить ее и на другом
самолете А300, хотя это может не
требоваться.
Обратные действия могут
происходить при определенных условиях,
когда привычка хорошо усвоена, ее трудно
забыть, или от нее избавиться. Инженер
может неосознанно выполнить операцию,
которую он выполнял много лет, не смотря
на то, что недавно она была изменена.
Это характерно для работников, которые
не сосредоточены или находятся в
стрессовом состоянии.
Поведение,
основанное на правилах обычно очень
сильное, и поэтому всегда подчеркивается
при выполнении операций по обслуживанию
самолета. Однако происходящие здесь
ошибки обычно связаны с применением
другого правила или не той операции.
Например, нарушение последовательности
выполнения операции.
Ошибки
при поведении, основанном на знаниях,
обычно связаны с неполными или не
правильными знаниями или с не правильной
интерпретацией ситуации. Примером тому
может служить ситуация, когда инженер
ознакомившись с операцией считает, что
он может легко ее выполнить. Если он ее
выполняет, желательно чтобы он обращал
больше внимания на вещи, которые, как
он считает, выполняет всегда успешно,
чтобы не игнорировать очевидность
обратного. (confirmation
bias).
Модель
«Швейцарский сыр»
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 76
АMIKON
Training Manual Part-66 Human Factors
В этом
исследовании Ризон освещает концепцию
защит против человеческих ошибок внутри
организации и дает понятие «защита
изнутри».
Примеры
защиты двойная проверка, предполетная
проверка пилотом и т.д., которые помогают
отловить человеческие ошибки, уменьшая
влияние отрицательных обстоятельств.
Когда эти защиты ослабевают, возникает
возможность инцидента или аварии. Эти
защиты изображены в виде нескольких
барьеров из ломтиков швейцарского сыра
и поэтому эта модель получила название
«Швейцарский сыр» профессора Ризона
Рис.25
Модель «Швейцарский сыр».
Некоторые
проблемы латентны, т.е. они происходили
в прошлом и находятся в спящем режиме.
Они могли быть заложены в конструкцию
или связаны с решением руководства.
Ошибки сделанные персоналом передней
линии, таким, как инженеры по обслуживанию,
являются активными. Больше отверстий
(дырок) в защитах системы, больше
вероятность того, что ошибки приведут
к инциденту или аварии, но это только
при определенных обстоятельствах, когда
все дырки встанут в одну линию. Обычно,
если ошибка прошла защиту на уровне
инженера, она достигает защиты на уровне
диспетчера и исправляется на этой
стадии. Однако, иногда в авиации ошибка
может пройти сквозь все защиты (например,
пилот проигнорировал автоматическое
предупреждение считая его недостоверным)
и возникает катастрофическая ситуация.
Защиты
в области авиационного обслуживания
будут рассматриваться далее
В
Разделе 9.8.4.
Типы ошибок в заданиях
на обслуживание.
Так
как авиационные инженеры это люди,
ошибки в производстве неизбежны.
Каждая
операция, выполняемая на самолете это
возможность совершения ошибки. Ошибки
при техническом обслуживании имеют две
специфических формы:
-
Ошибки
являющиеся результатом специфической
проблемы самолета, которые отсутствовали
до начала операции; -
Ошибки
являющиеся результатом нежелательного
или опасного состояния остававшегося
не обнаруженным при выполнении
обслуживания, направленного на выявление
проблем с самолетом, т.е. что-то было
пропущено.
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 77
АMIKON
Training Manual Part-66 Human Factors
Примеры
ошибок освещенных в предыдущем абзаце
являются неправильная установка
заменяемых узлов (LRU),
не снятие защитного кожуха с гидравлической
линии перед разборкой или повреждение
воздушного тракта используемого в
качестве опоры для ноги чтобы добраться
до места выполнения рабочей операции.
Примеры ошибок в (b)
незамеченные трещины обшивки при
визуальном осмотре или дефектный прибор
авионики, оставленный на самолете при
неправильном определении неисправности,
в результате которой, был заменен другой
прибор. Актуальным типом ошибки может
быть любой освещенный в предыдущем
разделе этого документа.
Ошибки во время
проведения регулярного или менее частого
обслуживания.
Большая
часть заданий по обслуживанию носит
рутинный характер, такие как регулярные
или периодические осмотры самолета.
Таким образом инженеры используют
определенный комплект процедур
сравнительно часто, как отмечалось в
предыдущем разделе, промахи и случайные
ошибки могут случаться при выполнении
заданий в ангаре или в условиях линейного
обслуживания (Раздел 9.6.2).
«Повторяющиеся
ошибки» случаются в случае привыкания
инженера выполнять регулярные, часто
повторяющиеся операции, имеющие
письменные указания в инструкциях по
выполнению. Не реально рассчитывать,
что они будут терять время на постоянное
обращение к хорошо известному материалу
инструкций. Однако, возможны ошибки,
если они не отслеживают внесение
изменений в эти материалы по выполнению
часто используемых операций.
Эти
рутинные операции также подвержены
ошибкам из-за самоуверенности,
окружающей среды и ошибкам из-за
правил (См. выше).
При
выполнении менее частых операций
возможны ошибки из-за неправильной
оценки. Если инженер не знаком или не
вспомнил что действительно нужно
выполнить, он может ошибочно выбрать
не ту операцию или не те детали.
Нарушения при
обслуживании самолетов.
К
сожалению, при обслуживании самолетов
происходят умышленные нарушения.
Большинство выполняют работу должным
образом. Редко возникают акты вандализма
и саботажа. Однако, они представляют
серьезную угрозу безопасности, так как
вся система была разработана на основе
того, что все люди будут выполнять
требования процедур обслуживания.
Существует три типа нарушений:
-
Рутинные
нарушения; -
Нарушения
в зависимости от ситуации; -
Нарушения
вызванные эмоциональным состоянием
человека;
Рутинные нарушения это
вещи которые стали «нормальным путем
выполнения чего-то» среди
рабочей группы людей (бригады). Операции
могут стать рутинными по нескольким
причинам: работники могут считать , что
они слишком глубоко описаны и обходить
их для упрощения (срезание
углов), для
сокращения времени и усилий на выполнение.
Примером рутинного нарушения является
не выполнение гонки двигателя после
бороскопического осмотра («он никогда
не течет»), или не замена кольцевых
уплотнений на коробке передач двигателя
(«Они никогда не повреждаются»).
Нарушения в зависимости от ситуации
– случаются при
наличии определенных факторов
в данное время, таких как авральный
режим работы, высокая рабочая нагрузка,
невыполнимые операции, недостаток
инструмента, плохие рабочие условия.
Это часто случается тогда, когда для
того чтобы работа была выполнена, инженер
считает, что не нужно следовать порядку
выполнения операции. Примером этому
является инцидент, когда дверь на В747
открылась в полете. Инженер очень
торопился. Ему нужен был специальный
лобзик для пропила отверстия в язычке
замка. Лобзика на этот момент не было и
он пропилил отверстие вручную. Если бы
он посмотрел инструкцию, то отложил бы
выполнение операции и самолет вышел бы
из расписания.
Нарушения из-за
эмоционального состояния человека. Это
часто не связано с выполнением заданий.
Человек просто ищет возможность
удовлетворить самого себя. Примером
этому является инженер, который пересекает
аэродром и двигается быстрее чем
разрешено, только для того чтобы приехать
на место скорее. Давление времени и
высокие нагрузки способствуют появлению
нарушений всех типов. Люди сравнивают
возможные риски с возможными преимуществами,
к сожалению, действительные риски
гораздо выше.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 78
АMIKON Training Manual
Part-66 Human Factors
Там
где операция позволяет какие-то
послабления, инженер вырабатывает
собственную стратегию или предпочтительный
путь выполнения. Иногда «хорошим»
правилом или принципом является тот,
который успешно применялся ранее.
Иногда эти правила становятся
предпочтительными для инженера в его
повседневной работе.
Проблемы возникают,
когда принципы и правила применяются
не правильно. На пример соединения
трубок имеют резьбу правого вращения,
но применение этого правила к кислородным
трубопроводам приведет к повреждению
резьбы и трубки. Также существует угроза
применения правил, которые основываются
на предыдущем опыте если, например
философия конструкция аэробусов и
самолетов Боинг отличается. Это может
быть причина в инциденте с запертым
спойлером А320, когда кажущиеся различия
между управлением спойлером на А320 и
Б767 (к которым инженеры достаточно
привыкли) означает, что операции
приемлемые для Боинга не приемлемы для
А320.
В дополнение,
инженеры в процессе своей работы могут
усвоить «плохие
правила»,
ведущие к плохим
привычкам, также
как происходит с водителем после того
как он получил водительские права.
Примером этому может служить инцидент
на Британских железных дорогах с поездом
из Клапхэма, когда применялась практика
загибания старых проводов, вместо замены
их на новые с соответствующей изоляцией.
Ошибки,
связанные с визуальным осмотром.
Имеется также два
особенных типа ошибок присущих визуальным
осмотрам, а именно ошибки
Типа 1 и ошибки Типа 2.
Ошибки типа 1 происходят, когда хорошая
деталь определяется как дефектная.
Ошибки Типа 2 появляются, когда дефектная
деталь утеряна. Ошибки Типа 1 не связаны
с безопасностью, за исключением случаев,
когда это означает что если ресурсы не
будут использоваться более эффективно,
потребуется дополнительная потеря
времени на проверку изделий, которые
не являются очевидно дефектными.
Ошибки Типа 2 наиболее важны так как,
если дефект не обнаружен (трещина) это
может иметь серьезные последствия
(Инцидент с Алоха, когда трещины в обшивке
не были обнаружены).
Исследования
профессора Ризона по техническому
обслуживанию самолетов
Ризон
провел анализ 122 авиационных инцидентов
в крупных авиакомпаниях за три года и
определил основные их причины:
-
Пропуски
(56%) -
Не
правильная установка узлов и деталей
(30%) -
Не
правильные детали (8%) -
Другие
причины (6%)Можно полагать, что выводы
Ризона применимы к техническому
обслуживанию авиации вообще. Пропуски
могут происходить по различным причинам,
таким как забывчивость, отклонение от
порядка выполнения операции. Потеря
масла на двух двигателях В737, когда
крышка ротора не была установлен на
место, является примером пропуска. Не
правильная установка не является
сюрпризом, так как обычно имеется только
один путь как снять деталь и много путей
как ее установить снова. Ризон
иллюстрировал это простым примером
болта и нескольких гаек (Рис.26)задавая
вопрос:
(а) сколькими путями
этот узел может быть разобран? Ответ –
одним путем.
(в) Сколькими путями
узел может быть собран снова? Ответ:
около 40000 исключая ошибки и пропуски
Издание 1 15 сентября 2004 ТОЛЬКО
ДЛЯ ОБУЧЕНИЯ Стр. 79
АMIKON Training Manual
Part-66 Human Factors
В инциденте с ВАС1-11 в июне 1990, ошибкой
была установка не правильных болтов на
иллюминатор. Это иллюстрирует категорию
«не правильные детали».
9.8.3
Вовлечение ошибок (Аварии)
В самых худших случаях человеческие
ошибки в авиационном обслуживании могут
приводить к авариям. Однако, как изображено
на Рис.27, аварии это только видимая часть
изображения ошибок. Как в айсберге, у
которого большая часть находится под
водой, большая часть ошибок не приводит
к авариям и инцидентам.
Рис.27
«Модель Айсберг»
К
счастью большинство ошибок при
обслуживании самолета не приводят к
катастрофическим последствиям. Но это
не означает, что они могут повторяться.
Ошибки, не приводящие к авариям, но
создающие инциденты. Это освещалось в
начале этого документа в Разделе 0.1.2
«Инциденты из-за человеческого
фактора»/Человеческие ошибки, дающим
примеры инцидентов по причине ошибок
при обслуживании. Некоторые инциденты
имеют более высокий уровень чем другие,
создающие проблемы в полете, которые,
благодаря случайности или искусству
летчиков, не привели к авариям. Другие
не стали серьезными благодаря защитам
в системе обслуживания. Однако все
инциденты в авиации являются значительными,
так как могут приводить к будущим авариям
если ошибка произойдет при других
обстоятельствах. Как следствие этому
обо всех инцидентах обязательно
необходимо докладывать авиационным
властям. (Mandatory
Occurance Reporting Scheme (MORS). Эта
информация помогает отслеживать
тенденции и где необходимо, предпринимать
действия по уменьшению ситуации для
возникновения ошибок. В Англии существует
также схема проблемы известны как
Confidentional
Human
Factors
Incident
Reporting
Programme
(CHIPR)
позволяющая информировать об ошибках
конфидециально. Благодаря тому, что
большинство ошибок при обслуживанию
самолетов определяются почти немедленно,
они делаются и исправляются. Инженер
может определить свою собственную
ошибку, или она будет обнаружена его
коллегами, контролером или ОТК. В этих
случаях инженер должен знать о сделанной
ошибке с тем, чтобы не повторять ее в
будущем.Обязательно, чтобы инженер
учился на собственных ошибках и на
ошибках окружающих. Когда случается
ошибка при линейном обслуживании, обычно
признают виновным инженера, кто последним
работал на самолете. Человека могут
наказать, направить на обучение или
просто попросят не повторять подобной
ошибки в будущем.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 80
АMIKON
Training Manual Part-66 Human Factors
Однако, обвинение при обслуживании ВС
не всегда работает как позитивная сила,
это иногда мешает инженерам осознать
ошибки. Они могут скрывать ошибки, или
не докладывать об инциденте. Также не
правильно обвинять инженера, если ошибка
произошла по вине слабости характерной
для системы, которую инженер случайно
обнаружил (например: характерный дефект,
скрытый в конструкции).
9.8.4 Избежание ошибок и управление
ошибками.
В то время как
техническое обслуживание стремится к
тому чтобы ошибки не происходили,
практически не возможно избежать их
полностью. Поэтому все организации по
обслуживанию должны иметь целью
управление ошибками.
Управление ошибками направлено на:
-
предотвращать
появление ошибок; -
снижать или ликвидировать последствия
ошибок.
Ризон определил эти
два компонента управления ошибками
как: (i)
содержание ошибки и (ii)
уменьшение ошибки.
Для
предотвращение появления ошибок
необходимо предугадывать место где они
скорее всего произойдут и принять
превентивные меры. Система рапортов
(такая как MORS)
делает это для производства в целом. В
организации по обслуживанию информация
по инцидентам и авариям должна собираться
в Системе управления безопасностью
(SMS),
которая должна обеспечивать механизм
для определения потенциально слабых
мест или ситуаций, способствующих
появлению ошибок. Результат этого должен
использоваться при обучении персонала,
в процедурах обслуживания, установлении
новых защит или модификации старых.
По исследованию
Ризона, управление ошибками включают
меры по:
-
минимизации
обязательности ошибки работника или
бригады; -
уменьшение
непредсказуемости ошибки в конкретном
задании или его элементах; -
открывать,
вмешиваться и уничтожать факторы
способствующие появлениям ошибок на
рабочем месте; -
проводить
диагноз организационных факторов,
которые создают предпосылки дляошибок работника, бригады, самого
задания и рабочего места; -
проводить поиск
ошибок; -
делать скрытые
условия более видимыми для лиц управляющих
системой;
Очень трудно
составить список всех мер по предотвращению
и минимизации ошибок в деле обслуживания
ВС. Практически во всем этом документе
дается описание этого механизма, начиная
с момента убеждения, что человек подходит
для работы и готов к ней до аттестации
рабочего места по освещенности.
Одним
из факторов наиболее эффективным в деле
предотвращения ошибок, является то что
инженер точно выполняет операции в
соответствии с документацией.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 81
АMIKON
Training Manual Part-66 Human Factors
В обязательном порядке организация по
обслуживанию должна находить разумный
компромисс между расходами на безопасность
– внедрению защитных мер, определению
ошибок и уменьшению их количества и
получением прибыли от деятельности.
Некоторые мероприятия стоят не много
(такие как замена лампочек в ангаре),
другие стоят очень много (например, наем
дополнительного персонала для
распределения рабочей нагрузки).
Инциденты имеют тенденцию приводить к
срочным мерам по исправлению ошибок,
но если в организации в течение длительного
времени инцидентов не было, существует
возможность снижения в ней расходов на
безопасность. Ризон иллюстрирует это
на Рис.28 «лодка на речном пороге»
Рис.28 Путь гипотетической организации
в пространстве производство – защита.
Важно чтобы организация балансировала
прибыль и расходы, и пыталась убедиться,
что расходы на безопасность являются
эффективными, так как идут на снижение
количества ошибок и предотвращение
катастрофических ситуаций. В обязательном
порядке является обязанностью всех и
каждого инженера по обслуживанию очень
внимательно относиться к своей работе
и быть готовым к ошибкам (См. Раздел
9.3.1). В целом, инженеры по обслуживанию
самолетов осознают важность своей
работы и обычно уделяют значительное
внимание и предпринимают усилия на
проведение мероприятий по предотвращению
производственных травм, сохранности
оборудования и безопасности самолета
на котором они работают.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 82
АMIKON
Training Manual Part-66 Human Factors
[c.402]
Модель с ошибками в переменных 403
[c.403]
Лаговые переменные » —Ошибки в переменных -Априорная информация
[c.16]
Стохастические объясняющие переменные, инструментальные переменные и ошибки в переменных
[c.266]
Когда используется метод рентабельности продаж, процентная наценка включает только желаемую величину прибыли. Чтобы этот метод был эффективным, все затраты должны быть распределены по единицам продукции. Поскольку коммерческие, общие и административные расходы труднее отнести на конкретные виды продукции, чем переменные и постоянные производственные затраты, то для их распределения можно использовать произвольные методы. Однако, такое произвольное распределение коммерческих, общих и административных расходов может привести к ошибкам в определении цены изделия. Так как такие внешние факторы, как конкуренция и положение на рынке, должны быть учтены прежде установления окончательной цены, то метод ценообразования на основе рентабельности продаж может быть использован в качестве исходной цены в решении проблемы ценообразования. Для расчетов используются формулы [c.258]
Стохастические связи между различными явлениями и их признаками в отличие от функциональных, жестко детерминированных, характеризуются тем, что результативный признак (зависимая переменная) испытывает влияние не только рассматриваемых независимых факторов, но и подвергается влиянию ряда случайных (неконтролируемых) факторов. Причем полный перечень факторов не известен, так же как и точный механизм их воздействия на результативный признак. В этих условиях значения зависимой переменной тоже не могут быть измерены точно. Их можно определить с определенной вероятностью, поскольку они подвержены случайному разбросу и содержат неизбежные ошибки измерения переменных.
[c.69]
Однако может оказаться, что данные о доходе, полученные в результате опроса, на самом деле являются искаженными, — например, в среднем заниженными, т.е. объясняющие переменные измеряются с систематическими ошибками. В этом случае люди, действительно обладающие доходом X, будут на самом деле тратить на исследуемый товар в среднем величину, меньшую, чем ДА), т.е. в рассмотренном примере объ-
[c.12]
Функциональный учет направлен на выявление реальных затрат, относящихся к обслуживанию каждого предприятия (различных покупателей). Как переменные затраты, так и накладные расходы должны быть разделены на составные части и соотнесены с конкретным покупателем. Компании, которым не удается правильно измерить издержки, не в состоянии и правильно определить свою прибыль, что ведет к ошибкам в маркетинговой деятельности. Кроме того, определение реальных издержек помогает компании установить оптимальную цену на продукцию.
[c.569]
Для достижения успеха на Уолл-стрит инвестору необходимо отыскать оптимальное сочетание двух ключевых переменных— объекта инвестирования и момента инвестирования. Как бы просто и даже банально это ни звучало, но для получения максимальной отдачи инвестор должен сделать правильный выбор объекта инвестирования и определить нужный момент для этого. Ошибка в выборе ценных бумаг и времени их приобретения может обернуться убытками, и различные сочетания двух этих факторов приводят к совершенно разным результатам.
[c.124]
Случайная переменная е, характеризует ошибки в первом уравнении в виду его статистического характера. Параметр а отражает влияние других не учитываемых в данном уравнении факторов потребления (например, цен). Первое уравнение данной системы является сверхидентифицируемым, а второе и третье — определениями.
[c.209]
Таким образом, сначала вместо полной модели с ошибками в уравнении и переменных
[c.78]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных.
[c.80]
Ошибки в именах обычно ограничены разделом внутренние, но могут быть имена переменных, файлов и полей записей. Вероятность ошибки в имени увеличивается, если одно и то же имя используется в нескольких контекстах, или в случае частичного совпадения имен. Заметим, что этот тип ошибок будет часто совпадать с ошибками раздела область (признак ЧТО).
[c.61]
Рассмотрим систему, начинающую работу в момент времени = 0. Система работает до появления ошибки в соответствии с предопределенным критерием. Результаты эксперимента собираются в отрезки времени, за которые могут произойти отказы в работе. Тогда переменная / времени случайного сбоя может быть определена как
[c.238]
Разработка рабочей модели представляет очень трудоемкий процесс, требующий, кроме того, большого внимания, так как достаточно ошибки в одном знаке пр,и коэффициенте переменной, чтобы решение оказалось ошибочным. Поэтому при использовании экономико-математических методов имеет большое значение разработка достаточно эффективных способов проверки записи системы уравнений и информации по переменным.
[c.194]
Хотя первоначальные тесты АРМ обещали больший успех в объяснении различий в доходах, была проведена разделительная линия между использованием этих моделей для объяснения различий в доходах в прошлом и их применением для предсказания будущих доходов. Противники САРМ, с очевидностью, достигли более серьезного успеха в объяснении прошлых доходов, поскольку они не ограничивали себя одним фактором, как это делается в модели САРМ. Подобный учет значительного числа факторов становится более проблематичным, когда мы пытаемся планировать ожидаемые в будущем доходы, поскольку приходится оценивать коэффициенты бета и премии для каждого из этих факторов. Коэффициенты бета и премии для факторов сами по себе изменчивы, поэтому ошибка в оценке может уничтожить все преимущества, которые мы можем получить, переходя от модели САРМ к более сложным моделям. При использовании моделей регрессии, предлагаемых в качестве альтернативы, мы также сталкиваемся с трудностями при оценке, поскольку переменные, прекрасно работающие в
[c.104]
С одной стороны, мы уже знаем (см. (1.30)), что присоединение каждой новой предсказывающей переменной может только увеличить величину множественного коэффициента корреляции R между результирующим показателем т] и предикторами и, следовательно, уменьшить ошибку в предсказании -q (X) (см. (1.26)). С другой стороны, нам известны не точные значения теоретических характеристик R, участвующих в (1.26) — (1.30), а лишь их выборочные аналоги — статистические
[c.191]
Независимые переменные х, Х2,. .., Xk измеряются с пренебрежимо малой ошибкой по сравнению с ошибкой в определении. у-
[c.246]
Существует несколько способов выявления неуверенности руководителя в отношении оценки стоимости (т. е. неопределенность этой оценки) в нашем примере. Допустим, что руководитель представляет себе фактическую стоимость выполнения контракта как сумму оцененной стоимости и некоторой ошибки. В этом случае для нас было бы полезно представить ошибку в виде случайной переменной, среднее значение которой мы примем за меру смещения, а дисперсию — за меру точности процесса оценки. Если среднее значение (математическое ожидание) ошибки равно нулю, мы можем сказать, что процесс дал несмещенные оценки. Если среднее значение ошибки больше нуля, можно было бы вычесть это среднее из каждой оценки и рассматривать исправленные оценки как несмещенные. Но такая простая поправка может улучшить результаты только в том случае, если мы умеем оценивать (т. е. определять точность) способ нахождения оценки.
[c.101]
Если при решении той или иной задачи можно ограничиться линейным приближением, то полный факторный эксперимент типа 2 также оказывается недостаточно эффективным, особенно при большом k. При линейном росте числа независимых переменных число опытов для полного факторного эксперимента растет по показательной функции, в результате слишком много степеней свободы остается на проверку гипотезы адекватности. Например, при k = 2, при линейном приближении, для проверки гипотезы адекватности используется только одна степень свободы, тогда как при k = fj — уже 57 степеней свободы. Правда, при постановке таких больших экспериментов резко снижается ошибка в определении коэффициентов регрессии, так как при факторном планировании все опыты используются для оценки каждого из коэффициентов регрессии. Но это обстоятельство далеко не всегда является достаточным основанием для постановки большого числа опытов. Часто, особенно на первых этапах исследования, бывает нужно получить некоторую, хотя бы и не очень точную, информацию о процессе при минимальной затрате труда на проведение экспериментов. Если можно ограничиться линейным приближением, то число опытов можно резко снизить, используя для планирования так называемые дробные реплики от полного факторного эксперимента [1].
[c.215]
Шестая часть посвящена оценкам максимального правдоподобия, которые, конечно, являются идеальным объектом для демонстрации мощи развиваемой техники. В первых трех главах исследуется несколько моделей, среди которых есть многомерное нормальное распределение, модель с ошибками в переменных и нелинейная регрессионная модель. Рассматриваются методы работы с симметрией и положительной определенностью, специальное внимание уделено информационной матрице. Вторая глава этой части содержит обсуждение одновременных уравнений при условии нормальности ошибок. В ней рассматриваются проблемы оценивания и идентифицируемости параметров при различных (не)линейных ограничениях на параметры. В этой части рассматривается также метод максимального правдоподобия с полной информацией (FIML) и метод максимального правдоподобия с ограниченной информацией (LIML), особое внимание уделено выводу асимптотических ковариационных матриц. Последняя глава посвящена различным проблемам и методам психометрики, в том числе методу главных компонент, мультимодальному компо-
[c.16]
Третий вопрос, на который хотелось бы получат ответ, — как ведут себя различные оценки при разной спецификации ошибок. Например, чего можно ожидать, если возмущения автокоррелированы, если присутствуют ошибки в переменных, если имеет место ощутимая муль-тиколлинеарность, если исключены существенные переменные или при различных комбинациях указанных обстоятельств.
[c.409]
На практике мы молчаливо соглашаемся, как правило, опираться на то, что в действительности является условностью. Суть этой условности — хотя она, конечно, не так уж проста — заключается в допущении, что существующее положение дел будет сохраняться неограниченно долго, если только у нас нет особых оснований ждать перемен. Это не означает, что мы в самом деле верим в неограниченно долгое сохранение существующего положения дел. Весь наш опыт говорит о том, что это совершенно невероятно. Действительные результаты инвестиций за целый ряд лет редко согласуется с первоначальными предположениями. Не подходит и способ рационально обосновать наше поведение ссылкой на то, что для человека, находящегося в полном неведении, ошибки в том или другом направлении равновероятны, так что ему остается сформировать некое среднестатистическое предположение, основывающееся на этих равных вероятностях. Ведь легко показать, что предположение об арифметическом равенстве вероятностей, основывающееся на ситуации полного неведения, ведет к абсурду. На практике мы исходим из того, что существующая рыночная оценка, как бы она ни сложилась, точно отражает имеющиеся у нас знания факторов, которые будут влиять на доход от инвестиций, и что эта оценка меняется лишь в соответствии с изменением наших знаний. Между тем, философски рассуждая, оня не может быть таким единственно правильным отражением, поскольку
[c.65]
Однако, эти результаты достигаются не всегда, если не выполняются следующие условия [334,137] наличие информации об идентичных предпочтениях, общеизвестной структуре капитала и дивидендов, и полной совокупности имущественных прав (т.е. наличие полного спектра производных финансовых инструментов, позволяющих оценить ожидаемые будущие риски). Эти исследования содержат примеры сбоя модели рациональных ожиданий и позволяют предположить, что агрегирование информации является более сложным процессом. В частности, похоже, эффективность рынка, определяемая как полное агрегирование информации, зависит от «сложности» рыночной структуры, обусловленной такими параметрами, как количество акций, обращающихся на рынке, и торговыми периодами [319]. Например, чрезмерная реакция людей на неинформативные сделки может создать, так называемые, самообразующиеся информационные «миражи», которыми, вероятно, можно объяснить явную чрезмерную волатильность биржевых цен.[67]. Более того, эксперименты с рыночными моделями показали, что существует два типа ошибок в оценке рынка ошибки в оценке экзогенных событий, влияющих на стоимость активов, и ошибки в оценке переменных факторов, создаваемых рыночной деятельностью, таких как цены фьючерсных контрактов. Несмотря на существование идеальных условий для обучения, индивидуальные ошибки не устраняются полностью, а, в лучшем случае, иногда сокращаются. [65] Еще одной отличительной особенностью людей, выявленной в ходе экспериментов, является так называемый «эффект избавления», соответствующий тенденции продавать выросшие в цене активы и держать активы, упавшие в цене [446]. Такую тягу к избавлению можно объяснить тем, что люди оценивают прибыль и убытки, привязывая их к какому-либо ориентиру, и склонны идти на риск при наличии опасности потенциального убытка, но стремятся избежать риска при наличии потенциальной возможности получить определенную прибыль. Еще одной важной психологической особенностью человека является то, что многие люди переоценивают свои личные способности и чрезмерно оптимистичны в отношении своего будущего. Как было установлено, эти особенности влияют на экономическое поведение при вступлении в конкурентные игры или при инвестировании на рынке акций [66].
[c.96]
До сих пор мы сравнивали между собой сетевые архитектуры с различным числом скрытых слоев и нейронов, предполагая, что каждый входной сигнал, действительно, влияет на результат. Однако, как уже говорилось, непредвиденная инфляция (UI) и месячное производство (МР) существенно не влияют на среднеквадратичную ошибку. В связи с этим возникает вопрос о том, нельзя ли эти переменные безболезненно изъять из дальнейшего рассмотрения. Явля-
[c.142]
Столбец Выход содержит результаты классификации, выданные сетью, а в столбце Цель указан настоящий номер класса. ABSERR — это абсолютная ошибка классификации, т.е. расстояние до настоящего класса, a DE ISIVN — определенная выше величина решающей способности. На всем материале не произошло ни одной грубой ошибки в классификации— величина ABSERR ни разу не превосходит двух. Переменная временной структуры имеет сильную распознающую роль. Премия за риск, наоборот, представляется лишней переменной. Месячное производство приобрело несколько большее значение, в то время как вклад переменных, выражающих инфляцию, неясен. Результаты такого анализа, которые репрезентативны для всего набора данных, не вполне согласуются с той интерпретацией роли переменных, которую мы получили при изучении погрешности. Однако это противоречие— скорее, кажущееся, по-
[c.148]
Ошибки в определении сущности постоянных затрат, их функциональном назначении порой приводят и к более серьезным заблуждениям. Речь пордет о природе двухставочных тарифов. Обычно и у нас в стране, и за рубежом наличие двухставочного тарифа часто объясняется необходимостью в пиковые часы использовать менее эффективные производственные мощности, потребляющие больше топлива и других переменных затрат на кВт/ч вырабатываемой электрической энергии. На самом деле это не совсем так или совсем не так. Давайте на минуту представим, что неэффективных производственных мощностей в энергетике нет, тогда по логике должна исчезнуть и природа двухставочного тарифа. Однако этого не
[c.18]
Самоконтролирующееся ПО полезно для доказательства надежности программ на различных стадиях разработки. На стадии конструирования и реализации утверждения о соотношении между переменными сделают логические ошибки более очевидными. Это позволяет также повысить уверенность в надежности программы неформальным образом. На стадии тестирования для определения всевозможных аппаратных и программных погрешностей необходимо внедрять разнообразные средства самоконтроля, обеспечивающие локализацию ошибки в системе. История обнаружения ошибки должна < сохраняться для оценки эффективности средств само- » контроля. В системе также должна быть осуществлена Г в широких масштабах оценка стоимостных расходов по различным средствам.
[c.265]
Мультипликатор цена/прибыль (pri e-earnings multiple — РЕ) — наиболее широко распространенный коэффициент, и при этом им же наиболее широко и злоупотребляют. Простота этого показателя придает ему привлекательность во многих сферах применения, начиная от оценки первоначально размещаемых акций и кончая вынесением суждений по поводу относительной ценности. Однако его связь с финансовыми фундаментальными переменными фирмы часто игнорируется, что приводит к серьезным ошибкам в применении. Эта глава позволяет в некоторой степени проникнуть в глубь факторов, определяющих мультипликатор цена/прибыль , и наилучших способов его использования при проведении оценки.
[c.628]
Например, статья в Форбс , написанная Линденом (Linden) и озаглавленная Скучные дни в унылой науке , цитирует Мак-Низа (M Nees, 1983, 1985, 1987, 1988), который изучал экономические прогнозы и нашел, что экономисты делали серьезные ошибки в прогнозах в каждом из поворотных моментов экономического развития, начиная с 70-х годов, когда началась эта работа. Мак-Низ обнаружил также, что в этих поворотных моментах прогнозисты ошибались все вместе. Предсказания, в случае если они сделаны корректно, отражали действительность только в коротком временном интервале. Незначительное изменение только одной переменной может иметь большее влияние, чем это предусматривает теория.
[c.18]
Рассматриваемая нами модель предполагает, что ошибки не зависят от оцениваемых затрат на выполнение контрактов. Ошибки в оценках для крупных контрактов в принципе характеризуются той же степенью неопределенности, что и оценки для контрактов, требующих меньших затрат. Для руководителя может быть разумнее встать на другую точку зрения и рассмотреть относительные ошибки. Он должен чувствовать, что ошибки в долларах будут все-таки больше для крупных контрактов. Можно принять, что фактическая стоимость равна оцененной стоимости, умноженной на некоторую случайную переменную, которая называется коэффициентом ошибки (error ratio). В этом случае несмещенный процесс оценки характеризовался бы коэффициентом ошибки, ожидаемое значение которого равно единице. Подходит ли какая-либо из этих двух моделей и если да, то какая — оставляется на усмотрение руководителя, который руководствуется при этом своим прошлым опытом и фактическими данными относительно качества рассматриваемого процесса оценки. Но какой бы метод он ни выбрал, это, видно, приведет к рассмотрению стоимости выполнения контракта как случайной переменной. Если мы предположим, что руководителю ясно, за какую цену может быть получен контракт, то прибыль становится случайной переменной, определяемой просто как разность между ценой и стоимостью.
[c.102]
В статистике, ошибки-в-переменных модели или измерения модели ошибок являются регрессионные модели, которые учитывают ошибок измерения в независимых переменных . Напротив, стандартные модели регрессии предполагают, что эти регрессоры были точно измерены или наблюдались без ошибок; как таковые, эти модели учитывают только ошибки в зависимых переменных или ответах.

Иллюстрация разбавления регрессии (или систематической ошибки ослабления) с помощью ряда оценок регрессии в моделях с ошибками в переменных. Две линии регрессии (красные) ограничивают диапазон возможностей линейной регрессии. Неглубокий наклон получается, когда независимая переменная (или предиктор) находится на абсциссе (ось x). Более крутой наклон получается, когда независимая переменная находится на ординате (ось y). По соглашению с независимой переменной на оси x получается более пологий наклон. Зеленые контрольные линии — это средние значения в произвольных интервалах по каждой оси. Обратите внимание, что более крутые оценки регрессии для зеленого и красного более согласуются с меньшими ошибками в переменной оси y.
В случае, когда некоторые регрессоры были измерены с ошибками, оценка, основанная на стандартном предположении, приводит к непоследовательным оценкам, что означает, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. Для простой линейной регрессии эффект заключается в занижении коэффициента, известном как смещение затухания . В нелинейных моделях направление смещения, вероятно, будет более сложным.
Мотивирующий пример
Рассмотрим простую модель линейной регрессии вида
где обозначает истинный, но ненаблюдаемый регрессор . Вместо этого мы наблюдаем это значение с ошибкой:
где предполагается, что ошибка измерения не зависит от истинного значения .
Если ‘s просто регрессируют на ‘ s (см. Простую линейную регрессию ), то оценка коэффициента наклона будет
который сходится по мере неограниченного увеличения размера выборки :
Вариации неотрицательны, так что в пределе оценка меньше по величине, чем истинное значение, эффект, который статистики называют ослаблением или разбавлением регрессии . Таким образом, «наивная» оценка методом наименьших квадратов несовместима в этой настройке. Однако оценщик является последовательным оценщиком параметра, необходимого для наилучшего линейного предиктора данного : в некоторых приложениях это может быть то, что требуется, а не оценка « истинного » коэффициента регрессии, хотя это предполагает, что дисперсия ошибки в наблюдении остаются исправленными. Это непосредственно следует из результата, приведенного непосредственно выше, и того факта, что коэффициент регрессии, связывающий ‘s с фактически наблюдаемыми ‘ s, в простой линейной регрессии определяется выражением
Именно этот коэффициент, а не тот, который потребовался бы для построения предиктора на основе наблюдаемого, подверженного шуму.
Можно утверждать, что почти все существующие наборы данных содержат ошибки разной природы и величины, поэтому систематическая ошибка ослабления встречается очень часто (хотя при многомерной регрессии направление систематической ошибки неоднозначно). Джерри Хаусман видит в этом железный закон эконометрики : «Величина оценки обычно меньше ожидаемой».
Технические характеристики
Обычно модели ошибок измерения описываются с использованием подхода скрытых переменных . Если переменная отклика и наблюдаются значения регрессоров, то предполагается, существуют какие — то скрытые переменные и которые следуют «истинной» в модели функциональной зависимости, и таким образом, что наблюдаемые величины их шумные наблюдения:

где находятся в модели параметры и те регрессоры, которые предполагаются свободными от ошибок (например, когда линейная регрессия содержит перехват, регрессор что соответствует константе, безусловно, не имеет «ошибки измерений»). В зависимости от спецификации эти безошибочные регрессоры могут или не могут рассматриваться отдельно; в последнем случае просто предполагается, что соответствующие элементы в матрице дисперсии s равны нулю.
Переменные, , все наблюдали, что означает, что статистик обладает набором данных из статистических единиц, которые следуют за процесс генерирования данных, описанными выше; латентные переменные, , и не наблюдается, однако.

Эта спецификация не охватывает все существующие модели ошибок в переменных. Например, в некоторых из них функция может быть непараметрической или полупараметрической. Другие подходы моделируют отношения между и как распределительные, а не функциональные, то есть они предполагают, что условно on следует за определенным (обычно параметрическим) распределением.
Терминология и предположения
- Наблюдаемая переменная может называться манифестом, индикатором или косвенной переменной .
- Ненаблюдаемая переменная может быть названа скрытой или истинной переменной. Его можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональной моделью ), либо как случайную величину (соответственно структурную модель ).
- Связь между ошибкой измерения и скрытой переменной можно моделировать по-разному:
- Классические ошибки : ошибки не зависят от скрытой переменной. Это наиболее распространенное предположение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
- Независимость от среднего : ошибки равны нулю для каждого значения скрытого регрессора. Это менее ограничительное предположение, чем классическое, поскольку оно допускает наличие гетероскедастичности или других эффектов в ошибках измерения.
- Ошибки Берксона :ошибки не зависят от наблюдаемого регрессора x . Это предположение имеет очень ограниченную применимость. Одним из примеров являются ошибки округления: например, если возраст человека * является непрерывной случайной величиной, тогда как наблюдаемый возраст усекается до следующего наименьшего целого числа, тогда ошибка усечения приблизительно не зависит от наблюдаемого возраста . Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени, скажем, в, тогда реальное измерение может произойти при каком-то другом значении(например, из-за конечного времени реакции ), и такая ошибка измерения обычно не зависит от «наблюдаемого» значения регрессора.
- Ошибки неправильной классификации : частный случай фиктивных регрессоров . Если это индикатор определенного события или состояния (например, лицо мужского / женского пола, какое-либо лечение было / не предоставлено и т. Д.), То ошибка измерения в таком регрессоре будет соответствовать неправильной классификации, аналогичной типу I и типу II. ошибки в статистическом тестировании. В этом случае ошибка может принимать только 3 возможных значения, а ее условное распределение моделируется двумя параметрами:, и . Необходимым условием идентификации является то, что ошибочная классификация не должна происходить «слишком часто». (Эту идею можно обобщить на дискретные переменные с более чем двумя возможными значениями.)
- Классические ошибки : ошибки не зависят от скрытой переменной. Это наиболее распространенное предположение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
Линейная модель
Первыми были изучены линейные модели ошибок в переменных, вероятно, потому, что линейные модели были так широко использованы и они легче нелинейных. В отличие от стандартной регрессии методом наименьших квадратов (OLS), расширение ошибок в регрессии переменных (EiV) с простого случая на многомерный не так просто.
Простая линейная модель
Простая линейная модель ошибок в переменных уже была представлена в разделе «мотивация»:
где все переменные скалярны . Здесь α и β представляют собой интересующие параметры, а σ ε и σ η — стандартные отклонения членов ошибки — являются мешающими параметрами . «Истинный» регрессор x * рассматривается как случайная величина ( структурная модель), не зависящая от ошибки измерения η ( классическое допущение).
Эта модель идентифицируемой в двух случаях: (1) либо латентный регрессор х * является не нормально распределены, (2) или х * имеет нормальное распределение, но ни ε т, ни η т делимы нормальным распределением. То есть параметры α, β могут быть последовательно оценены из набора данных без какой-либо дополнительной информации, при условии, что скрытый регрессор не является гауссовским.
До того, как этот результат идентифицируемости был установлен, статистики пытались применить метод максимального правдоподобия, предполагая, что все переменные являются нормальными, а затем пришли к выводу, что модель не идентифицирована. Предлагаемое решение заключалось в том, чтобы предположить, что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся:
- Регрессия Деминга — предполагается, что отношение δ = σ² ε / σ² η известно. Это может быть подходящим, например, когда ошибки в y и x вызваны измерениями, а точность измерительных устройств или процедур известна. Случай, когда δ = 1, также известен как ортогональная регрессия .
- Регрессия с известным коэффициентом надежности λ = σ² ∗ / ( σ² η + σ² ∗ ), где σ² ∗ — дисперсия скрытого регрессора. Такой подход может быть применим, например, когда доступны повторяющиеся измерения одного и того же устройства, или когда коэффициент надежности известен из независимого исследования. В этом случае непротиворечивая оценка наклона равна оценке методом наименьших квадратов, деленной на λ .
- Регрессия с известным σ² η может произойти, если источник ошибок в x известен и их дисперсия может быть вычислена. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда известно σ² η, мы можем вычислить коэффициент надежности как λ = ( σ² x — σ² η ) / σ² x и свести проблему к предыдущему случаю.
Новые методы оценки, которые не предполагают знания некоторых параметров модели, включают:
- Метод моментов — GMM- оценка, основанная на совместных кумулянтах третьего (или более высокого) порядка наблюдаемых переменных. Коэффициент наклона можно оценить по формуле
где ( n 1, n 2 ) таковы, что K ( n 1 +1, n 2 ) — совместный кумулянт ( x, y ) — не равен нулю. В случае, когда третий центральный момент скрытого регрессора x * отличен от нуля, формула сводится к
- Инструментальные переменные — регрессия, которая требует наличия определенных дополнительных переменных данных z, называемых инструментами . Эти переменные не должны быть коррелированы с ошибками в уравнении для зависимой (итоговой) переменной ( достоверно ), и они также должны быть коррелированы ( релевантны ) с истинными регрессорами x * . Если такие переменные могут быть найдены, то оценка принимает вид
Многопараметрическая линейная модель
Модель с несколькими переменными выглядит точно так же, как простая линейная модель, только на этот раз β, η t, x t и x * t являются векторами k × 1.
В случае, когда ( ε t, η t ) совместно нормально, параметр β не идентифицируется тогда и только тогда, когда существует невырожденная блочная матрица k × k [ a A ], где a — вектор k × 1, такой что a′x * распределяется нормально и независимо от A′x * . В случае, когда ε t, η t1, …, η tk взаимно независимы, параметр β не идентифицируется тогда и только тогда, когда в дополнение к указанным выше условиям некоторые ошибки могут быть записаны как сумма двух независимых переменных один из которых нормальный.
Некоторые из методов оценивания многомерных линейных моделей:
- Всего наименьших квадратов — это расширение регрессии Деминга до многомерной настройки. Когда все k +1 компоненты вектора ( ε, η ) имеют равные дисперсии и независимы, это эквивалентно запуску ортогональной регрессии y по вектору x, то есть регрессии, которая минимизирует сумму квадратов расстояний между точек ( y t, x t ) и k -мерной гиперплоскости «наилучшего соответствия».
- Метод моментов оценки может быть построена на основе условий момента Е [ г т · ( у т — & alpha ; — β’x т )] = 0, где (5 к + 3 ) мерный вектор инструментов г т определен в виде
где обозначает произведение матриц Адамара, а переменные x t, y t были предварительно обнулены. Авторы метода предлагают использовать модифицированную оценку ВА Фуллера.
Этот метод может быть расширен для использования моментов выше третьего порядка, если необходимо, и для учета переменных, измеренных без ошибок.
- Инструментальные переменный подход требует, чтобы найти дополнительные данные переменного г т, которые будут служить в качестве инструментов для mismeasured регрессор х т . Этот метод является наиболее простым с точки зрения реализации, однако его недостатком является то, что он требует сбора дополнительных данных, что может быть дорогостоящим или даже невозможным. Когда инструменты могут быть найдены, оценщик принимает стандартную форму
Нелинейные модели
Общая модель нелинейных ошибок измерения принимает форму
Здесь функция g может быть параметрической или непараметрической. Когда функция g параметрическая, она будет записана как g (x *, β) .
Для общего векторного регрессора x * условия идентифицируемости модели неизвестны. Однако в случае скаляра x * модель идентифицируется, если только функция g не имеет «логарифмически экспоненциальную» форму.
а скрытый регрессор x * имеет плотность
где константы A, B, C, D, E, F могут зависеть от a, b, c, d .
Несмотря на этот оптимистичный результат, в настоящее время не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако есть несколько методов, которые используют некоторые дополнительные данные: либо инструментальные переменные, либо повторные наблюдения.
Методы инструментальных переменных
- Метод моделирования моментов Ньюи для параметрических моделей — требует наличия дополнительного набора наблюдаемых переменных-предикторов z t, так что истинный регрессор может быть выражен как
где π 0 и σ 0 — (неизвестные) постоянные матрицы, а ζ t ⊥ z t . Коэффициент π 0 можно оценить с помощью стандартной регрессии x по z методом наименьших квадратов . Распределение ζ t неизвестно, однако мы можем смоделировать его как принадлежащее гибкому параметрическому семейству — ряду Эджворта :
где ϕ — стандартное нормальное распределение.
Смоделированные моменты могут быть вычислены с использованием алгоритма выборки по важности : сначала мы генерируем несколько случайных величин { v ts ~ ϕ, s = 1,…, S, t = 1,…, T } из стандартного нормального распределения, затем вычисляем моменты при t -м наблюдении как
где θ = ( β, σ, γ ), A — просто некоторая функция инструментальных переменных z, а H — двухкомпонентный вектор моментов
С помощью моментных функций m t можно применить стандартную технику GMM для оценки неизвестного параметра θ .
Повторные наблюдения
В этом подходе доступны два (или, может быть, более) повторных наблюдения регрессора x * . Оба наблюдения содержат собственные ошибки измерения, однако эти ошибки должны быть независимыми:
где x * ⊥ η 1 ⊥ η 2 . Переменные η 1, η 2 не обязательно должны быть одинаково распределены (хотя, если они являются эффективными оценками, их можно немного улучшить). С помощью только этих двух наблюдений можно последовательно оценить функцию плотности x *, используя технику деконволюции Котлярского .
- Метод условной плотности Ли для параметрических моделей. Уравнение регрессии можно записать в терминах наблюдаемых переменных как
где можно было бы вычислить интеграл, если бы мы знали условную функцию плотности ƒ x * | x . Если эта функция может быть известна или оценена, тогда проблема превращается в стандартную нелинейную регрессию, которую можно оценить, например, с помощью метода NLLS .
Предполагая для простоты, что η 1, η 2 одинаково распределены, эту условную плотность можно вычислить как
где с небольшим злоупотреблением обозначениями x j обозначает j -ю компоненту вектора.
Все плотности в этой формуле можно оценить с помощью обращения эмпирических характеристических функций . В частности,Чтобы инвертировать эту характеристическую функцию, необходимо применить обратное преобразование Фурье с параметром обрезки C, необходимым для обеспечения численной стабильности. Например:
- Оценка Шеннаха для параметрической линейной по параметрам нелинейной модели по переменным. Это модель вида
где w t представляет переменные, измеренные без ошибок. Регрессор x * здесь является скалярным (метод можно распространить и на случай вектора x * ).
Если бы не ошибки измерения, это была бы стандартная линейная модель с оценщикомгде
Оказывается, все ожидаемые значения в этой формуле можно оценить с помощью одного и того же трюка с деконволюцией. В частности, для общей наблюдаемой w t (которая может быть 1, w 1 t ,…, w ℓ t или y t ) и некоторой функции h (которая может представлять любые g j или g i g j ) мы имеем
где φ h — преобразование Фурье функции h ( x * ), но с использованием того же соглашения, что и для характеристических функций ,
-
,
а также
Полученная оценка непротиворечива и асимптотически нормальна.
- Оценка Шеннаха для непараметрической модели. Стандартная оценка Надарая – Ватсона для непараметрической модели принимает вид
при подходящем выборе ядра K и пропускной способности h . Оба ожидания здесь можно оценить с помощью той же методики, что и в предыдущем методе.
Рекомендации
дальнейшее чтение
- Догерти, Кристофер (2011). «Стохастические регрессоры и ошибки измерения» . Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. С. 300–330. ISBN 978-0-19-956708-9.
- Кмента, Ян (1986). «Оценка с недостаточными данными» . Элементы эконометрики (второе изд.). Нью-Йорк: Макмиллан. С. 346–391 . ISBN 978-0-02-365070-3.
- Шеннах, Сюзанна . «Погрешность измерения в нелинейных моделях — обзор» . Серия рабочих документов Cemmap . Cemmap . Проверено 6 февраля 2018 года .
Внешние ссылки
- Исторический обзор линейной регрессии с ошибками в обеих переменных, Дж. В. Гиллард, 2006 г.
- Лекция по эконометрики (тема: стохастические регрессоров и ошибки измерения) на YouTube с помощью Mark Thoma .
В статистике модели ошибок в переменных или модели ошибок измерения представляют собой регрессионные модели , которые учитывают ошибки измерения в независимых переменных . Напротив, стандартные регрессионные модели предполагают, что эти регрессоры были точно измерены или наблюдались без ошибок; как таковые, эти модели учитывают только ошибки в зависимых переменных или ответах. [ нужна ссылка ]

Иллюстрация разбавления регрессии (или смещения затухания) рядом оценок регрессии в моделях ошибок в переменных. Две линии регрессии (красные) ограничивают диапазон возможностей линейной регрессии. Пологий наклон получается, когда независимая переменная (или предиктор) находится на оси абсцисс (ось x). Более крутой наклон получается, когда независимая переменная находится на ординате (ось Y). По соглашению, с независимой переменной на оси x получается более пологий наклон. Зеленые опорные линии — это средние значения в произвольных интервалах вдоль каждой оси. Обратите внимание, что более крутые оценки зеленой и красной регрессии лучше согласуются с меньшими ошибками в переменной оси Y.
В случае, когда некоторые регрессоры были измерены с ошибками, оценка, основанная на стандартном предположении, приводит к противоречивым оценкам, означающим, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. Для простой линейной регрессии эффект заключается в недооценке коэффициента, известного как смещение затухания . В нелинейных моделях направление смещения, вероятно, будет более сложным. [1] [2] [3]
Мотивирующий пример
Рассмотрим простую модель линейной регрессии вида
кудаобозначает истинный , но ненаблюдаемый регрессор . Вместо этого мы наблюдаем это значение с ошибкой:
где погрешность измерениясчитается независимым от истинного значения.
Еслипросто регрессируют на‘s (см. простую линейную регрессию ), то оценка коэффициента наклона равна
который сходится как размер выборкинеограниченно возрастает:
Дисперсия неотрицательна, так что в пределе оценка меньше по величине, чем истинное значениеэффект, который статистики называют затуханием или регрессионным разбавлением . [4] Таким образом, «наивная» оценка методом наименьших квадратов несостоятельна в этом случае. Однако оценщик является последовательной оценкой параметра, необходимого для наилучшего линейного предикторадано: в некоторых приложениях это может быть то, что требуется, а не оценка «истинного» коэффициента регрессии, хотя это предполагает, что дисперсия ошибок при наблюденииостается фиксированным. Это следует непосредственно из приведенного выше результата и того факта, что коэффициент регрессии, связывающийк фактически наблюдаемомуs в простой линейной регрессии определяется выражением
Именно этот коэффициент, а не, что потребовалось бы для построения предикторана основе наблюдаемогокоторый подвержен шуму.
Можно утверждать, что почти все существующие наборы данных содержат ошибки разного характера и величины, так что систематическая ошибка затухания встречается чрезвычайно часто (хотя в многомерной регрессии направление систематической ошибки неоднозначно [5] ). Джерри Хаусман видит в этом железный закон эконометрики : «Величина оценки обычно меньше ожидаемой». [6]
Спецификация
Обычно модели ошибок измерения описываются с использованием подхода со скрытыми переменными . Еслипеременная отклика иявляются наблюдаемыми значениями регрессоров, то предполагается, что существуют некоторые скрытые переменныеа такжекоторые следуют «истинным» функциональным отношениям модели , и такие, что наблюдаемые величины являются их зашумленными наблюдениями:
кудаявляется параметром модели и— это те регрессоры, которые считаются безошибочными (например, когда линейная регрессия содержит точку пересечения, регрессор, соответствующий константе, определенно не имеет «ошибок измерения»). В зависимости от спецификации эти безошибочные регрессоры могут обрабатываться или не обрабатываться отдельно; в последнем случае просто предполагается, что соответствующие записи в матрице дисперсииравны нулю.
Переменные,,все наблюдаются , а это означает, что статистик обладает набором данных статистические единицы которые следуют описанному выше процессу генерации данных ; скрытые переменные,,, а такжеоднако не наблюдаются.
Эта спецификация не охватывает все существующие модели ошибок в переменных. Например, в некоторых из них функционируютможет быть непараметрическим или полупараметрическим. Другие подходы моделируют отношения междуа такжедистрибутивной, а не функциональной, т. е. они предполагают, чтоусловно наследует определенному (обычно параметрическому) распределению.
Терминология и предположения
- Наблюдаемая переменнаяможет называться манифестом , индикатором или прокси — переменной .
- Ненаблюдаемая переменнаяможно назвать скрытой или истинной переменной. Ее можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональной моделью ), либо как случайную величину (соответственно структурную модель ). [7]
- Связь между погрешностью измеренияи скрытая переменнаяможно моделировать по-разному:
- Классические ошибки :ошибки не зависят от скрытой переменной. Это наиболее распространенное предположение, оно подразумевает, что погрешности вносятся измерительным прибором и их величина не зависит от измеряемой величины.
- Средняя независимость :ошибки равны среднему нулю для каждого значения скрытого регрессора. Это менее ограничительное предположение, чем классическое [8] , поскольку оно допускает наличие гетероскедастичности или других эффектов в ошибках измерения.
- Ошибки Берксона :ошибки не зависят от наблюдаемого регрессора x . [9] Это предположение имеет очень ограниченную применимость. Одним из примеров являются ошибки округления: например, если возраст человека* является непрерывной случайной величиной , тогда как наблюдаемый возраст усекается до следующего наименьшего целого числа, то ошибка усечения приблизительно не зависит от наблюдаемого возраста . Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени., скажем в, то реальное измерение может происходить при каком-то другом значении(например, из-за ее конечного времени реакции), и такая ошибка измерения, как правило, не будет зависеть от «наблюдаемого» значения регрессора.
- Ошибки неправильной классификации : особый случай, используемый для фиктивных регрессоров . Еслиявляется индикатором определенного события или состояния (например, человек является мужчиной/женщиной, оказано/не оказано какое-либо лечение и т. д.), то ошибка измерения в таком регрессоре будет соответствовать неправильной классификации, аналогичной ошибкам первого и второго рода в статистическом тестировании. В этом случае ошибкаможет принимать только 3 возможных значения, и его распределение зависит отмоделируется двумя параметрами:, а также. Необходимым условием идентификации является то, что, то есть ошибочная классификация не должна происходить «слишком часто». (Эту идею можно обобщить на дискретные переменные с более чем двумя возможными значениями.)
Линейная модель
Линейные модели ошибок в переменных были изучены в первую очередь, вероятно, потому, что линейные модели были настолько широко распространены, и они проще, чем нелинейные. В отличие от стандартной регрессии наименьших квадратов (OLS), распространение ошибок в регрессии переменных (EiV) с простого на случай с несколькими переменными не является простым.
Простая линейная модель
Простая линейная модель ошибок в переменных уже была представлена в разделе «мотивация»:
где все переменные скалярны . Здесь α и β — представляющие интерес параметры, тогда как σ ε и σ η — стандартные отклонения членов ошибки — являются мешающими параметрами . «Истинный» регрессор x* рассматривается как случайная величина ( структурная модель), не зависящая от ошибки измерения η ( классическое предположение).
Эта модель идентифицируема в двух случаях: (1) либо латентный регрессор x* не имеет нормального распределения , (2) либо x* имеет нормальное распределение, но ни ε t , ни η t не делятся на нормальное распределение. [10] То есть параметры α , β можно последовательно оценить по набору данныхбез какой-либо дополнительной информации при условии, что скрытый регрессор не является гауссовским.
Прежде чем этот результат идентифицируемости был установлен, статистики попытались применить метод максимального правдоподобия , предполагая, что все переменные являются нормальными, а затем пришли к выводу, что модель не идентифицируется. Предлагаемое средство защиты заключалось в предположении , что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся [11]
- Регрессия Деминга — предполагает, что отношение δ = σ² ε / σ² η известно. Это может быть уместно, например, когда ошибки в y и x вызваны измерениями, а точность измерительных устройств или процедур известна. Случай, когда δ = 1, также известен как ортогональная регрессия .
- Регрессия с известным коэффициентом достоверности λ = σ² ∗ / ( σ² η + σ² ∗ ), где σ² ∗ — дисперсия латентного регрессора. Такой подход может быть применим, например, когда доступны повторные измерения одной и той же единицы или когда коэффициент достоверности известен из независимого исследования. В этом случае непротиворечивая оценка наклона равна оценке методом наименьших квадратов, деленной на λ .
- Регрессия с известным σ² η может иметь место, когда известен источник ошибок в x’s и можно рассчитать их дисперсию. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда известно σ² η , мы можем вычислить коэффициент надежности как λ = ( σ² x − σ² η ) / σ² x и свести задачу к предыдущему случаю.
Более новые методы оценки, которые не предполагают знания некоторых параметров модели, включают
- Метод моментов — оценка GMM , основанная на совместных кумулянтах третьего (или более высокого) порядка наблюдаемых переменных. Коэффициент наклона можно оценить из [12]
где ( n 1 , n 2 ) таковы, что K ( n 1 +1, n 2 ) — общий кумулянт ( x , y ) — не равен нулю. В случае, когда третий центральный момент латентного регрессора x* отличен от нуля, формула сводится к
- Инструментальные переменные — регрессия, которая требует, чтобы были доступны определенные дополнительные переменные данных z , называемые инструментами . Эти переменные должны быть некоррелированы с ошибками в уравнении для зависимой (исходной) переменной ( действительны ), а также должны быть коррелированы ( релевантны ) с истинными регрессорами x* . Если такие переменные могут быть найдены, то оценка принимает вид
Многомерная линейная модель
Модель с несколькими переменными выглядит точно так же, как и простая линейная модель, только на этот раз β , η t , x t и x * t являются векторами
k × 1.
В случае, когда ( ε t , η t ) совместно нормален, параметр β не идентифицируется тогда и только тогда, когда существует невырожденная блочная матрица размера k × k [ a A ], где a — вектор размера k × 1, такой что a′x* распределяется нормально и независимо от A′x* . В случае, когда ε t , η t1 ,…, η tk взаимно независимы, параметр β не идентифицируется тогда и только тогда, когда в дополнение к указанным выше условиям часть ошибок может быть записана в виде суммы двух независимых переменных, одна из которых является нормальной. [13]
Некоторые из методов оценки для многомерных линейных моделей:
- Суммарный метод наименьших квадратов является расширением регрессии Деминга для многомерной настройки. Когда все компоненты k + 1 вектора ( ε , η ) имеют равные дисперсии и независимы, это эквивалентно запуску ортогональной регрессии y на векторе x , то есть регрессии, которая минимизирует сумму квадратов расстояний между точки ( y t , x t ) и k -мерная гиперплоскость «наилучшего соответствия».
- Метод оценки моментов [14] может быть построен на основе моментных условий E[ z t ·( y t − α − β’x t )] = 0, где (5 k +3)-мерный вектор инструментов z т определяется как
кудаобозначает произведение Адамара матриц, а переменные x t , y t предварительно лишены значения. Авторы метода предлагают использовать модифицированную Фуллером оценку IV. [15]
Этот метод может быть расширен для использования моментов выше третьего порядка, если это необходимо, и для учета переменных, измеренных без ошибок. [16] - Подход с инструментальными переменными требует поиска дополнительных переменных данных z t , которые служили бы инструментами для неправильно измеренных регрессоров x t . Этот метод является наиболее простым с точки зрения реализации, однако его недостатком является то, что он требует сбора дополнительных данных, что может быть дорогостоящим или даже невозможным. Когда инструменты могут быть найдены, оценщик принимает стандартный вид
Нелинейные модели
Общая нелинейная модель ошибки измерения принимает форму
Здесь функция g может быть как параметрической, так и непараметрической. Когда функция g является параметрической, она будет записана как g(x*, β) .
Для общего векторнозначного регрессора x* условия идентифицируемости модели неизвестны. Однако в случае скаляра x* модель идентифицируется, если только функция g не имеет «логарифмически-экспоненциальной» формы [17]
а скрытый регрессор x* имеет плотность
где константы A,B,C,D,E,F могут зависеть от a,b,c,d .
Несмотря на этот оптимистичный результат, на данный момент не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако есть несколько методов, которые используют некоторые дополнительные данные: либо инструментальные переменные, либо повторные наблюдения.
Методы инструментальных переменных
- Метод смоделированных моментов Ньюи [18] для параметрических моделей требует, чтобы существовал дополнительный набор наблюдаемых переменных- предикторов z t , так что истинный регрессор может быть выражен как
где π 0 и σ 0 — (неизвестные) постоянные матрицы, а ζ t ⊥ z t . Коэффициент π 0 можно оценить, используя стандартную регрессию x по z методом наименьших квадратов . Распределение ζ t неизвестно, однако мы можем смоделировать его как принадлежащее гибкому параметрическому семейству — ряду Эджворта :
где ϕ — стандартное нормальное распределение.
Моделируемые моменты можно вычислить с помощью алгоритма выборки важности : сначала мы генерируем несколько случайных величин { v ts ~ ϕ , s = 1,…, S , t = 1,…, T } из стандартного нормального распределения, затем вычисляем моменты при t -м наблюдении как
где θ = ( β , σ , γ ), A — некоторая функция инструментальных переменных z , а H — двухкомпонентный вектор моментов
С функциями моментов m t можно применить стандартный метод GMM для оценки неизвестного параметра θ .
Повторные наблюдения
В этом подходе доступны два (или более) повторяющихся наблюдения регрессора x* . Оба наблюдения содержат свои собственные ошибки измерения, однако эти ошибки должны быть независимыми:
где х* ⊥ η 1 ⊥ η 2 . Переменные η 1 , η 2 не обязательно должны быть одинаково распределены (хотя если они одинаковы, эффективность оценщика может быть немного улучшена). Только с этими двумя наблюдениями можно последовательно оценить функцию плотности x * , используя метод деконволюции Котлярского . [19]
- Метод условной плотности Ли для параметрических моделей. [20] Уравнение регрессии можно записать в терминах наблюдаемых переменных как
где можно было бы вычислить интеграл, если бы мы знали условную функцию плотности ƒ x*|x . Если эту функцию можно было бы узнать или оценить, то задача превращается в стандартную нелинейную регрессию, которую можно оценить, например, методом NLLS .
Полагая для простоты, что η 1 , η 2 одинаково распределены, эту условную плотность можно вычислить как
где с небольшим злоупотреблением обозначениями x j обозначает j -ю компоненту вектора.
Все плотности в этой формуле можно оценить с помощью обращения эмпирических характеристических функций . Особенно,
Чтобы инвертировать эту характеристическую функцию, необходимо применить обратное преобразование Фурье с параметром обрезки C , необходимым для обеспечения численной стабильности. Например:
- Оценка Шеннаха для параметрической линейной по параметрам модели нелинейной по переменным. [21] Это модель вида
где w t представляет переменные, измеренные без ошибок. Регрессор x* здесь скалярный (метод можно распространить и на случай вектора x* ).
Если бы не ошибки измерения, это была бы стандартная линейная модель с оценщиком
куда
Оказывается, все ожидаемые значения в этой формуле можно оценить с помощью одного и того же приема деконволюции. В частности, для общей наблюдаемой w t (которая может быть 1, w 1 t , …, w ℓ t или y t ) и некоторой функции h (которая может представлять любой g j или g i g j ) мы имеем
где φ h — преобразование Фурье h ( x * ), но с использованием того же соглашения, что и для характеристических функций ,
- ,
а также
Полученная оценканепротиворечива и асимптотически нормальна. - Оценка Шеннаха для непараметрической модели. [22] Стандартная оценка Надарая–Ватсона для непараметрической модели принимает вид
для подходящего выбора ядра K и пропускной способности h . Оба ожидания здесь можно оценить с помощью той же методики, что и в предыдущем методе.
Ссылки
- ^ Гриличес, Цви; Рингстад, Видар (1970). «Смещение ошибок в переменных в нелинейных контекстах». Эконометрика . 38 (2): 368–370. дои : 10.2307/1913020 . JSTOR 1913020 .
- ^ Чешер, Эндрю (1991). «Влияние ошибки измерения». Биометрика . 78 (3): 451–462. doi : 10.1093/биомет/78.3.451 . JSTOR 2337015 .
- ^ Кэрролл, Раймонд Дж .; Руперт, Дэвид; Стефански, Леонард А .; Крайничану, Киприан (2006). Ошибка измерения в нелинейных моделях: современная перспектива (второе изд.). ISBN 978-1-58488-633-4.
- ^ Грин, Уильям Х. (2003). Эконометрический анализ (5-е изд.). Нью-Джерси: Прентис Холл. Глава 5.6.1. ISBN 978-0-13-066189-0.
- ^ Вансбик, Т .; Мейер, Э. (2000). «Ошибка измерения и скрытые переменные» . В Baltagi, BH (ред.). Компаньон к теоретической эконометрике . Блэквелл. стр. 162–179. doi : 10.1111/b.9781405106764.2003.00013.x . ISBN 9781405106764.
- ^ Хаусман, Джерри А. (2001). «Неверно измеренные переменные в эконометрическом анализе: проблемы справа и проблемы слева» . Журнал экономических перспектив . 15 (4): 57–67 [с. 58]. doi : 10.1257/jep.15.4.57 . JSTOR 2696516 .
- ^ Фуллер, Уэйн А. (1987). Модели ошибок измерения . Джон Уайли и сыновья. п. 2. ISBN 978-0-471-86187-4.
- ^ Хаяси, Фумио (2000). Эконометрика . Издательство Принстонского университета. стр. 7–8. ISBN 978-1400823833.
- ^ Кул, Хира; Песня, Вэйсин (2008). «Проверка регрессионной модели с ошибками измерения Берксона». Журнал статистического планирования и выводов . 138 (6): 1615–1628. doi : 10.1016/j.jspi.2007.05.048 .
- ^ Рейерсёль, Олав (1950). «Идентифицируемость линейной связи между переменными, которые подвержены ошибкам». Эконометрика . 18 (4): 375–389 [с. 383]. дои : 10.2307/1907835 . JSTOR 1907835 . Несколько более ограничительный результат был установлен ранее Geary, RC (1942). «Внутренние отношения между случайными величинами». Труды Королевской ирландской академии . 47 : 63–76. JSTOR 20488436 . Он показал, что при дополнительном предположении, что ( ε, η ) совместно нормальны, модель не идентифицируется тогда и только тогда, когда x* s нормальны.
- ^ Фуллер, Уэйн А. (1987). «Единая объяснительная переменная» . Модели ошибок измерения . Джон Уайли и сыновья. стр. 1–99. ISBN 978-0-471-86187-4.
- ^ Пал, Маноранджан (1980). «Последовательные оценки моментов коэффициентов регрессии при наличии ошибок в переменных». Журнал эконометрики . 14 (3): 349–364 [стр. 360–1]. doi : 10.1016/0304-4076(80)90032-9 .
- ^ Бен-Моше, Дэн (2020). «Выявление линейных регрессий с ошибками во всех переменных». Эконометрическая теория . 37 (4): 1–31. архив : 1404.1473 . doi : 10.1017/S0266466620000250 . S2CID 225653359 .
- ^ Дагене, Марсель Г .; Дагене, Дениз Л. (1997). «Оценщики более высоких моментов для моделей линейной регрессии с ошибками в переменных». Журнал эконометрики . 76 (1–2): 193–221. CiteSeerX 10.1.1.669.8286 . doi : 10.1016/0304-4076(95)01789-5 . В более ранней статье Пал (1980) рассмотрел более простой случай, когда все компоненты вектора ( ε , η ) независимы и симметрично распределены.
- ^ Фуллер, Уэйн А. (1987). Модели ошибок измерения . Джон Уайли и сыновья. п. 184. ИСБН 978-0-471-86187-4.
- ^ Эриксон, Тимоти; Уайтед, Тони М. (2002). «Двухэтапная оценка GMM модели ошибок в переменных с использованием моментов высокого порядка». Эконометрическая теория . 18 (3): 776–799. doi : 10.1017/s0266466602183101 . JSTOR 3533649 . S2CID 14729228 .
- ^ Шеннах, С .; Ху, Ю .; Льюбель, А. (2007). «Непараметрическая идентификация классической модели ошибок в переменных без дополнительной информации» . Рабочий документ .
- ^ Ньюи, Уитни К. (2001). «Гибкая смоделированная оценка момента нелинейной модели ошибок в переменных». Обзор экономики и статистики . 83 (4): 616–627. дои : 10.1162/003465301753237704 . hdl : 1721.1/63613 . JSTOR 3211757 . S2CID 57566922 .
- ^ Ли, Тонг; Выонг, Куанг (1998). «Непараметрическая оценка модели ошибки измерения с использованием нескольких показателей» . Журнал многомерного анализа . 65 (2): 139–165. doi : 10.1006/jmva.1998.1741 .
- ^ Ли, Тонг (2002). «Надежная и последовательная оценка нелинейных моделей ошибок в переменных». Журнал эконометрики . 110 (1): 1–26. doi : 10.1016/S0304-4076(02)00120-3 .
- ^ Шеннах, Сюзанна М. (2004). «Оценка нелинейных моделей с погрешностью измерения». Эконометрика . 72 (1): 33–75. doi : 10.1111/j.1468-0262.2004.00477.x . JSTOR 3598849 .
- ^ Шеннах, Сюзанна М. (2004). «Непараметрическая регрессия при наличии ошибки измерения». Эконометрическая теория . 20 (6): 1046–1093. doi : 10.1017/S0266466604206028 . S2CID 123036368 .
Дальнейшее чтение
- Догерти, Кристофер (2011). «Стохастические регрессоры и ошибки измерения» . Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. стр. 300–330. ISBN 978-0-19-956708-9.
- Кмента, Ян (1986). «Оценка с недостаточными данными» . Элементы эконометрики (второе изд.). Нью-Йорк: Макмиллан. стр. 346–391 . ISBN 978-0-02-365070-3.
- Шеннах, Сюзанна (2013). «Ошибка измерения в нелинейных моделях — обзор». В Асемоглу, Дарон; Арельяно, Мануэль; Декель, Эдди (ред.). Достижения в области экономики и эконометрики . Издательство Кембриджского университета. стр. 296–337. doi : 10.1017/CBO9781139060035.009 . hdl : 10419/79526 . ISBN 9781107017214.
Внешние ссылки
- Исторический обзор линейной регрессии с ошибками в обеих переменных , Дж. В. Гиллард, 2006 г.
- Лекция по эконометрике (тема: Стохастические регрессоры и ошибка измерения) на YouTube Марка Тома .
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
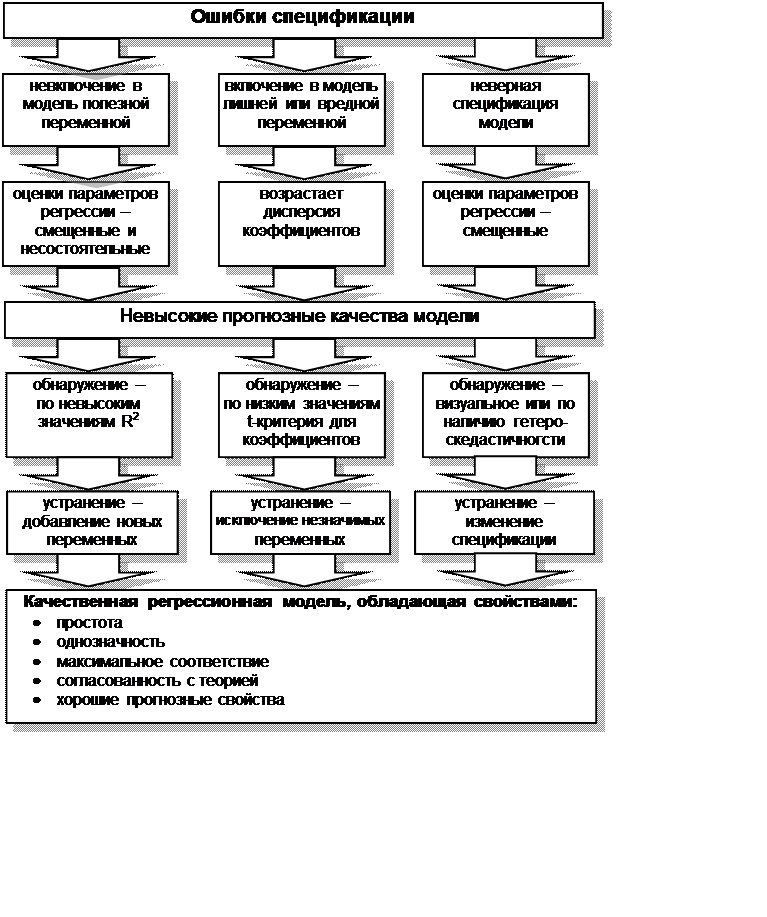
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Еще
много веков назад было отмечено, что
человеческая деятельность не всегда
бывает безукоризненна. Около двух тысяч
лет назад римский философ Цицерон
предупреждал: «Человеку свойственно
ошибаться». Непреложным фактом является
то, что где бы мужчине или женщине не
пришлось работать, когда-нибудь происходят
человеческие ошибки.
В
настоящем пособии «Человеческие ошибки»
профессор Джеймс Ризон определяет
ошибку следующим образом:
«Ошибка
рассматривается как следствие объединяющее
все те случаи, когда запланированная
последовательность умственных или
физических усилий не достигает необходимой
цели и когда все эти провалы не могут
быть отнесены на счет влияния случая».
Ясно,
что обслуживание самолета зависит от
компетенции инженеров исполнителей.
Много примеров описанных в Главе 1
«Инциденты связанные с человеческими
факторами / Человеческими ошибками» и
во всем настоящем пособии освещают
ошибки, которые были допущены инженерами
по обслуживанию самолетов и которые
повлекли за собой авиационные аварии
и инциденты.
В прошлом авиационные
компоненты и системы были относительно
не надежны. Современные самолеты по
сравнению с ними сконструированы и
изготовлены как высоко надежные. Как
следствие, в настоящее время обычно
говорят, что инцидент с самолетом или
авария были вызваны «человеческим
фактором».
Следующее
положение говорит о том, какую ключевую
роль играет инженер по обслуживанию в
поддержании надежности современного
самолета.
«Так
как гражданский самолет сконструирован
для выполнения безопасных полетов в
течение не ограниченного периода
времени, в случае если дефекты
обнаруживаются и устраняются своевременно,
безопасность становится вопросом
определения и ремонта до отказа какой-либо
конструкционной детали (структуры). В
идеальной системе, все дефекты, влияющие
на безопасность полета должны определяться
заранее до момента когда они станут
опасными и устранены эффективным
ремонтом. С этой точки зрения мы изменили
систему безопасности от одного из
физических дефектов в самолете, до одной
из ошибок в комплексной системе с
человеком в центре».
В
оставшейся части настоящей главы
рассматриваются некоторые из различных
путей, по которым определяется
(концептуализируется) человеческая
ошибка. Затем рассматриваются наиболее
распространенные ошибки случающиеся
при обслуживании самолетов и также
рассматриваются возможные пути
предотвращения этих ошибок.
9.8.1 Модели ошибки и
теория.
Для
определения типов ошибок, которые
возможно сделать, исследователи
рассмотрели человеческие ошибки
несколькими путями и предложили различные
модели и теории. Эта попытка обнаружить
природу ошибок и ее характеристики. Для
иллюстрации этого, они предлагают в
качестве моделей и теорий следующие
варианты основных версий:
-
версия
ошибок вызванных конструкцией и ошибки
операторов; -
переменная
версия постоянных ошибок; -
обратимая
версия необратимых ошибок; -
случайные
ошибки; -
ошибки,
связанные со знанием и навыками; -
модель
«Швейцарский сыр».
Версия ошибок вызванных
конструкцией и ошибки операторов.
В
авиации особый упор делается на ошибках
операторов, включая экипажи самолетов,
диспетчеров и персонала по техническому
обслуживанию.
Однако,
ошибки могут быть допущены даже до того
момента когда самолет впервые вылетает
после сборки. Это может означать, что
если самолет собран и летит, как это
предусматривалось конструкцией, полет
этой конструкции может повлиять на
безопасность. Кроме того, правила
управлением самолета введенные компанией
или управлением по организации полетов
могут также приводить к операционным
проблемам.
Издание 1 15 сентября
2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 73
АMIKON
Training Manual Part-66 Human Factors
При
расследовании авиационных инцидентов
часто обнаруживают, что делается более
чем одна ошибка и более чем одним
человеком. Ситуация может складываться
таким образом, что только при определенной
комбинации ошибок и нарушении их защиты
(См. модель «Швейцарский сыр»), нарушается
безопасность.
Переменная версия
постоянных ошибок.
В своей
книге «Человеческие ошибки» профессор
Ризон обсуждает два типа ошибок человека:
переменные и постоянные. Это можно
расссмотреть на Рис.22. Переменные ошибки
(А) случайны по своей природе в то время
как постоянные ошибки (В) сопровождаются
какой то системой и носят систематический
характер. Возникновения постоянных
ошибок может быть предсказано и от них
можно создать защиту, в то время как
переменные ошибки непредсказуемы и,
как правило, приводят к серьезным
последствиям. Если мы знаем достаточно
много о характере операции, окружающей
среде в которой она выполняется и
физическое и моральное состояние
работника, у нас есть высокий шанс
предотвратить ошибки.
Рис.
22 Переменная версия постоянных ошибок.
Мишени
двух стрелков имеющих по десять выстрелов.
Стрелок А не продемонстрировал постоянных
ошибок, все ошибки значительно отличаются
друг от друга; стрелок В продемонстрировал
значительную постоянную ошибку и
небольшую вариацию мелких ошибок.
Последний вариант легче предугадать и
исправить (коррекцией прицела винтовки).
К
сожалению редко удается получить
достаточно информации для точного
предсказания ; мы можем предсказывать
только на уровне «операции по повторной
сборке где ошибки происходят чаще, чем
при операциях по разборке», или «инженер
чаще совершает ошибки после 3-х часов
ночи после того как отработал 12 часов,
чем после 10 утра после того как отработал
только2 часа».
Возможно,
улучшить эти предсказания при получении
большей информации, но все равно ошибки
или непредсказуемые их элементы будут
происходить.
Обратимая версия
необратимых ошибок.
Другой
путь по определению категорий ошибок
это определение обратимые они или нет.
Первые возможно исправить, вторые обычно
нет.
Например,
если пилот не правильно рассчитал
количество топлива для полета, он может
произвести посадку на более близком
аэродроме, но если он резко потерял
топливо, многих возможностей у него не
появится.
Хорошо
сконструированная система или операция
должна означать, что возможные ошибки
инженера по обслуживанию самолета
должны быть обратимыми. Таким образом,
если инженер установил деталь не
правильно, она должна быть определена
контролером и установлена правильно
до выпуска самолета обратно в эксплуатацию.
Случайные ошибки.
Профессор
Ризон определяет понятие «намерение»
при рассмотрении природы ошибок задавая
следующие вопросы:
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 74
АMIKON
Training Manual Part-66 Human Factors
-
Направлялись
ли действия предварительным намерением? -
Происходили
ли действия так как они планировались? -
Достигли
ли они планируемого результата?
Ризон
предложил классификацию ошибок на базе
ответов на эти вопросы (См. Рис.23).
НЕТ
Было ли намерение действовать?
Было ли предварительное
намерение действовать?
Случайное или не
преднамеренное действие

Спонтанное или
вспомогательное действие
ДА
Происходили ли действия как планировалось?
ДА
Не преднамеренное
действие, промах, ошибка
Достигли ли действия ожидаемого
результата?
Намеренное, но
ошибочное действие
Успешное действие

НЕТ
ДА
НЕТ
ДА
Рис.23
Типы ошибок основанные на намерении.
Наиболее
известный тип – промахи, ошибки.
Промахи
— это действия, проведенные не так как
хотелось или планировалось.
Пропущенные
действия , т.е. когда кто то не сделал
что то из-за провала в памяти / или во
внимании (например забыл одеть капот
на двигатель).
Ошибки
– это специфический тип вызванный не
правильным планированием/намерением.
Т.е кто то сделал что то веря что на тот
отрезок времени это правильно, а
практически нет т.е. ошибка в определении
типа болтов для крепления лобового
стекла.
Промахи
обычно случаются в процессе выполнения
операций, ошибки на стадии планирования.
Нарушения
иногда рассматриваются как человеческие
ошибки, но они отличаются от промахов
и ошибок так как они вызваны неправильными
«незаконными» действиями, т.е. сделал
что то, зная что это не по правилам,
например, желая выполнить работу к
сроку.
Операции
должны выполняться строго по правилам,
чтобы сохранять безопасность полетов.
Ошибки, связанные
со знанием и навыками;
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 75
АMIKON
Training Manual Part-66 Human Factors
Поведение
инженера по обслуживанию может быть
подразделено на три отдельные категории:
на основе опыта, на основе правил и на
основе знаний.
На
основе опыта – базируется на усвоенных
человеком навыках и моторных программах,
полученных с опытом практической работы
и выполняемых без особых раздумий.
На
основе правил – базируется на том,
что правила или порядок выполнения
операции выучен. Компонентами этого
типа поведения могут быть отдельные
навыки.
На
основе знаний – для тех, для кого
процедуры не установлены. От авиационного
инженера требуется оценить полученную
информацию и затем использовать свои
знания для определения плана по действиям
в конкретной ситуации.
Для
каждого из этих поведенческих типов
имеются свои ошибки для них характерные.
Примером
ошибок на основе опыта являются промахи
в действиях, воздействие окружающей
среды и обратные действия. Промахи в
действиях это то же самое, что и просто
промахи – это действия, не проведенные,
как следует. Пример дается в Рис.24 когда
инженеру нужен определенный ключ для
окончания операции, но из за того, что
его отвлек коллега, он взял не тот
комплект ключей установленный на другой
момент затяжки и не замечает того, что
он затягивает болты не так как нужно.

Инженер отвлекается
коллегой
Инженер не следит
за выполнением операции
ОШИБКА
Рис.24
Пример промаха в действии.
Примером
влияния окружающей среды может быть
то, когда инженер часто выполняет одну
и ту же операцию в определенном месте.
Например, инженер, выполняющий операцию
по регулировке на самолете А300, может
неосознанно выполнить ее и на другом
самолете А300, хотя это может не
требоваться.
Обратные действия могут
происходить при определенных условиях,
когда привычка хорошо усвоена, ее трудно
забыть, или от нее избавиться. Инженер
может неосознанно выполнить операцию,
которую он выполнял много лет, не смотря
на то, что недавно она была изменена.
Это характерно для работников, которые
не сосредоточены или находятся в
стрессовом состоянии.
Поведение,
основанное на правилах обычно очень
сильное, и поэтому всегда подчеркивается
при выполнении операций по обслуживанию
самолета. Однако происходящие здесь
ошибки обычно связаны с применением
другого правила или не той операции.
Например, нарушение последовательности
выполнения операции.
Ошибки
при поведении, основанном на знаниях,
обычно связаны с неполными или не
правильными знаниями или с не правильной
интерпретацией ситуации. Примером тому
может служить ситуация, когда инженер
ознакомившись с операцией считает, что
он может легко ее выполнить. Если он ее
выполняет, желательно чтобы он обращал
больше внимания на вещи, которые, как
он считает, выполняет всегда успешно,
чтобы не игнорировать очевидность
обратного. (confirmation
bias).
Модель
«Швейцарский сыр»
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 76
АMIKON
Training Manual Part-66 Human Factors
В этом
исследовании Ризон освещает концепцию
защит против человеческих ошибок внутри
организации и дает понятие «защита
изнутри».
Примеры
защиты двойная проверка, предполетная
проверка пилотом и т.д., которые помогают
отловить человеческие ошибки, уменьшая
влияние отрицательных обстоятельств.
Когда эти защиты ослабевают, возникает
возможность инцидента или аварии. Эти
защиты изображены в виде нескольких
барьеров из ломтиков швейцарского сыра
и поэтому эта модель получила название
«Швейцарский сыр» профессора Ризона
Рис.25
Модель «Швейцарский сыр».
Некоторые
проблемы латентны, т.е. они происходили
в прошлом и находятся в спящем режиме.
Они могли быть заложены в конструкцию
или связаны с решением руководства.
Ошибки сделанные персоналом передней
линии, таким, как инженеры по обслуживанию,
являются активными. Больше отверстий
(дырок) в защитах системы, больше
вероятность того, что ошибки приведут
к инциденту или аварии, но это только
при определенных обстоятельствах, когда
все дырки встанут в одну линию. Обычно,
если ошибка прошла защиту на уровне
инженера, она достигает защиты на уровне
диспетчера и исправляется на этой
стадии. Однако, иногда в авиации ошибка
может пройти сквозь все защиты (например,
пилот проигнорировал автоматическое
предупреждение считая его недостоверным)
и возникает катастрофическая ситуация.
Защиты
в области авиационного обслуживания
будут рассматриваться далее
В
Разделе 9.8.4.
Типы ошибок в заданиях
на обслуживание.
Так
как авиационные инженеры это люди,
ошибки в производстве неизбежны.
Каждая
операция, выполняемая на самолете это
возможность совершения ошибки. Ошибки
при техническом обслуживании имеют две
специфических формы:
-
Ошибки
являющиеся результатом специфической
проблемы самолета, которые отсутствовали
до начала операции; -
Ошибки
являющиеся результатом нежелательного
или опасного состояния остававшегося
не обнаруженным при выполнении
обслуживания, направленного на выявление
проблем с самолетом, т.е. что-то было
пропущено.
Издание
1 15 сентября 2004 ТОЛЬКО ДЛЯ ОБУЧЕНИЯ
Стр. 77
АMIKON
Training Manual Part-66 Human Factors
Примеры
ошибок освещенных в предыдущем абзаце
являются неправильная установка
заменяемых узлов (LRU),
не снятие защитного кожуха с гидравлической
линии перед разборкой или повреждение
воздушного тракта используемого в
качестве опоры для ноги чтобы добраться
до места выполнения рабочей операции.
Примеры ошибок в (b)
незамеченные трещины обшивки при
визуальном осмотре или дефектный прибор
авионики, оставленный на самолете при
неправильном определении неисправности,
в результате которой, был заменен другой
прибор. Актуальным типом ошибки может
быть любой освещенный в предыдущем
разделе этого документа.
Ошибки во время
проведения регулярного или менее частого
обслуживания.
Большая
часть заданий по обслуживанию носит
рутинный характер, такие как регулярные
или периодические осмотры самолета.
Таким образом инженеры используют
определенный комплект процедур
сравнительно часто, как отмечалось в
предыдущем разделе, промахи и случайные
ошибки могут случаться при выполнении
заданий в ангаре или в условиях линейного
обслуживания (Раздел 9.6.2).
«Повторяющиеся
ошибки» случаются в случае привыкания
инженера выполнять регулярные, часто
повторяющиеся операции, имеющие
письменные указания в инструкциях по
выполнению. Не реально рассчитывать,
что они будут терять время на постоянное
обращение к хорошо известному материалу
инструкций. Однако, возможны ошибки,
если они не отслеживают внесение
изменений в эти материалы по выполнению
часто используемых операций.
Эти
рутинные операции также подвержены
ошибкам из-за самоуверенности,
окружающей среды и ошибкам из-за
правил (См. выше).
При
выполнении менее частых операций
возможны ошибки из-за неправильной
оценки. Если инженер не знаком или не
вспомнил что действительно нужно
выполнить, он может ошибочно выбрать
не ту операцию или не те детали.
Нарушения при
обслуживании самолетов.
К
сожалению, при обслуживании самолетов
происходят умышленные нарушения.
Большинство выполняют работу должным
образом. Редко возникают акты вандализма
и саботажа. Однако, они представляют
серьезную угрозу безопасности, так как
вся система была разработана на основе
того, что все люди будут выполнять
требования процедур обслуживания.
Существует три типа нарушений:
-
Рутинные
нарушения; -
Нарушения
в зависимости от ситуации; -
Нарушения
вызванные эмоциональным состоянием
человека;
Рутинные нарушения это
вещи которые стали «нормальным путем
выполнения чего-то» среди
рабочей группы людей (бригады). Операции
могут стать рутинными по нескольким
причинам: работники могут считать , что
они слишком глубоко описаны и обходить
их для упрощения (срезание
углов), для
сокращения времени и усилий на выполнение.
Примером рутинного нарушения является
не выполнение гонки двигателя после
бороскопического осмотра («он никогда
не течет»), или не замена кольцевых
уплотнений на коробке передач двигателя
(«Они никогда не повреждаются»).
Нарушения в зависимости от ситуации
– случаются при
наличии определенных факторов
в данное время, таких как авральный
режим работы, высокая рабочая нагрузка,
невыполнимые операции, недостаток
инструмента, плохие рабочие условия.
Это часто случается тогда, когда для
того чтобы работа была выполнена, инженер
считает, что не нужно следовать порядку
выполнения операции. Примером этому
является инцидент, когда дверь на В747
открылась в полете. Инженер очень
торопился. Ему нужен был специальный
лобзик для пропила отверстия в язычке
замка. Лобзика на этот момент не было и
он пропилил отверстие вручную. Если бы
он посмотрел инструкцию, то отложил бы
выполнение операции и самолет вышел бы
из расписания.
Нарушения из-за
эмоционального состояния человека. Это
часто не связано с выполнением заданий.
Человек просто ищет возможность
удовлетворить самого себя. Примером
этому является инженер, который пересекает
аэродром и двигается быстрее чем
разрешено, только для того чтобы приехать
на место скорее. Давление времени и
высокие нагрузки способствуют появлению
нарушений всех типов. Люди сравнивают
возможные риски с возможными преимуществами,
к сожалению, действительные риски
гораздо выше.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 78
АMIKON Training Manual
Part-66 Human Factors
Там
где операция позволяет какие-то
послабления, инженер вырабатывает
собственную стратегию или предпочтительный
путь выполнения. Иногда «хорошим»
правилом или принципом является тот,
который успешно применялся ранее.
Иногда эти правила становятся
предпочтительными для инженера в его
повседневной работе.
Проблемы возникают,
когда принципы и правила применяются
не правильно. На пример соединения
трубок имеют резьбу правого вращения,
но применение этого правила к кислородным
трубопроводам приведет к повреждению
резьбы и трубки. Также существует угроза
применения правил, которые основываются
на предыдущем опыте если, например
философия конструкция аэробусов и
самолетов Боинг отличается. Это может
быть причина в инциденте с запертым
спойлером А320, когда кажущиеся различия
между управлением спойлером на А320 и
Б767 (к которым инженеры достаточно
привыкли) означает, что операции
приемлемые для Боинга не приемлемы для
А320.
В дополнение,
инженеры в процессе своей работы могут
усвоить «плохие
правила»,
ведущие к плохим
привычкам, также
как происходит с водителем после того
как он получил водительские права.
Примером этому может служить инцидент
на Британских железных дорогах с поездом
из Клапхэма, когда применялась практика
загибания старых проводов, вместо замены
их на новые с соответствующей изоляцией.
Ошибки,
связанные с визуальным осмотром.
Имеется также два
особенных типа ошибок присущих визуальным
осмотрам, а именно ошибки
Типа 1 и ошибки Типа 2.
Ошибки типа 1 происходят, когда хорошая
деталь определяется как дефектная.
Ошибки Типа 2 появляются, когда дефектная
деталь утеряна. Ошибки Типа 1 не связаны
с безопасностью, за исключением случаев,
когда это означает что если ресурсы не
будут использоваться более эффективно,
потребуется дополнительная потеря
времени на проверку изделий, которые
не являются очевидно дефектными.
Ошибки Типа 2 наиболее важны так как,
если дефект не обнаружен (трещина) это
может иметь серьезные последствия
(Инцидент с Алоха, когда трещины в обшивке
не были обнаружены).
Исследования
профессора Ризона по техническому
обслуживанию самолетов
Ризон
провел анализ 122 авиационных инцидентов
в крупных авиакомпаниях за три года и
определил основные их причины:
-
Пропуски
(56%) -
Не
правильная установка узлов и деталей
(30%) -
Не
правильные детали (8%) -
Другие
причины (6%)Можно полагать, что выводы
Ризона применимы к техническому
обслуживанию авиации вообще. Пропуски
могут происходить по различным причинам,
таким как забывчивость, отклонение от
порядка выполнения операции. Потеря
масла на двух двигателях В737, когда
крышка ротора не была установлен на
место, является примером пропуска. Не
правильная установка не является
сюрпризом, так как обычно имеется только
один путь как снять деталь и много путей
как ее установить снова. Ризон
иллюстрировал это простым примером
болта и нескольких гаек (Рис.26)задавая
вопрос:
(а) сколькими путями
этот узел может быть разобран? Ответ –
одним путем.
(в) Сколькими путями
узел может быть собран снова? Ответ:
около 40000 исключая ошибки и пропуски
Издание 1 15 сентября 2004 ТОЛЬКО
ДЛЯ ОБУЧЕНИЯ Стр. 79
АMIKON Training Manual
Part-66 Human Factors
В инциденте с ВАС1-11 в июне 1990, ошибкой
была установка не правильных болтов на
иллюминатор. Это иллюстрирует категорию
«не правильные детали».
9.8.3
Вовлечение ошибок (Аварии)
В самых худших случаях человеческие
ошибки в авиационном обслуживании могут
приводить к авариям. Однако, как изображено
на Рис.27, аварии это только видимая часть
изображения ошибок. Как в айсберге, у
которого большая часть находится под
водой, большая часть ошибок не приводит
к авариям и инцидентам.
Рис.27
«Модель Айсберг»
К
счастью большинство ошибок при
обслуживании самолета не приводят к
катастрофическим последствиям. Но это
не означает, что они могут повторяться.
Ошибки, не приводящие к авариям, но
создающие инциденты. Это освещалось в
начале этого документа в Разделе 0.1.2
«Инциденты из-за человеческого
фактора»/Человеческие ошибки, дающим
примеры инцидентов по причине ошибок
при обслуживании. Некоторые инциденты
имеют более высокий уровень чем другие,
создающие проблемы в полете, которые,
благодаря случайности или искусству
летчиков, не привели к авариям. Другие
не стали серьезными благодаря защитам
в системе обслуживания. Однако все
инциденты в авиации являются значительными,
так как могут приводить к будущим авариям
если ошибка произойдет при других
обстоятельствах. Как следствие этому
обо всех инцидентах обязательно
необходимо докладывать авиационным
властям. (Mandatory
Occurance Reporting Scheme (MORS). Эта
информация помогает отслеживать
тенденции и где необходимо, предпринимать
действия по уменьшению ситуации для
возникновения ошибок. В Англии существует
также схема проблемы известны как
Confidentional
Human
Factors
Incident
Reporting
Programme
(CHIPR)
позволяющая информировать об ошибках
конфидециально. Благодаря тому, что
большинство ошибок при обслуживанию
самолетов определяются почти немедленно,
они делаются и исправляются. Инженер
может определить свою собственную
ошибку, или она будет обнаружена его
коллегами, контролером или ОТК. В этих
случаях инженер должен знать о сделанной
ошибке с тем, чтобы не повторять ее в
будущем.Обязательно, чтобы инженер
учился на собственных ошибках и на
ошибках окружающих. Когда случается
ошибка при линейном обслуживании, обычно
признают виновным инженера, кто последним
работал на самолете. Человека могут
наказать, направить на обучение или
просто попросят не повторять подобной
ошибки в будущем.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 80
АMIKON
Training Manual Part-66 Human Factors
Однако, обвинение при обслуживании ВС
не всегда работает как позитивная сила,
это иногда мешает инженерам осознать
ошибки. Они могут скрывать ошибки, или
не докладывать об инциденте. Также не
правильно обвинять инженера, если ошибка
произошла по вине слабости характерной
для системы, которую инженер случайно
обнаружил (например: характерный дефект,
скрытый в конструкции).
9.8.4 Избежание ошибок и управление
ошибками.
В то время как
техническое обслуживание стремится к
тому чтобы ошибки не происходили,
практически не возможно избежать их
полностью. Поэтому все организации по
обслуживанию должны иметь целью
управление ошибками.
Управление ошибками направлено на:
-
предотвращать
появление ошибок; -
снижать или ликвидировать последствия
ошибок.
Ризон определил эти
два компонента управления ошибками
как: (i)
содержание ошибки и (ii)
уменьшение ошибки.
Для
предотвращение появления ошибок
необходимо предугадывать место где они
скорее всего произойдут и принять
превентивные меры. Система рапортов
(такая как MORS)
делает это для производства в целом. В
организации по обслуживанию информация
по инцидентам и авариям должна собираться
в Системе управления безопасностью
(SMS),
которая должна обеспечивать механизм
для определения потенциально слабых
мест или ситуаций, способствующих
появлению ошибок. Результат этого должен
использоваться при обучении персонала,
в процедурах обслуживания, установлении
новых защит или модификации старых.
По исследованию
Ризона, управление ошибками включают
меры по:
-
минимизации
обязательности ошибки работника или
бригады; -
уменьшение
непредсказуемости ошибки в конкретном
задании или его элементах; -
открывать,
вмешиваться и уничтожать факторы
способствующие появлениям ошибок на
рабочем месте; -
проводить
диагноз организационных факторов,
которые создают предпосылки дляошибок работника, бригады, самого
задания и рабочего места; -
проводить поиск
ошибок; -
делать скрытые
условия более видимыми для лиц управляющих
системой;
Очень трудно
составить список всех мер по предотвращению
и минимизации ошибок в деле обслуживания
ВС. Практически во всем этом документе
дается описание этого механизма, начиная
с момента убеждения, что человек подходит
для работы и готов к ней до аттестации
рабочего места по освещенности.
Одним
из факторов наиболее эффективным в деле
предотвращения ошибок, является то что
инженер точно выполняет операции в
соответствии с документацией.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 81
АMIKON
Training Manual Part-66 Human Factors
В обязательном порядке организация по
обслуживанию должна находить разумный
компромисс между расходами на безопасность
– внедрению защитных мер, определению
ошибок и уменьшению их количества и
получением прибыли от деятельности.
Некоторые мероприятия стоят не много
(такие как замена лампочек в ангаре),
другие стоят очень много (например, наем
дополнительного персонала для
распределения рабочей нагрузки).
Инциденты имеют тенденцию приводить к
срочным мерам по исправлению ошибок,
но если в организации в течение длительного
времени инцидентов не было, существует
возможность снижения в ней расходов на
безопасность. Ризон иллюстрирует это
на Рис.28 «лодка на речном пороге»
Рис.28 Путь гипотетической организации
в пространстве производство – защита.
Важно чтобы организация балансировала
прибыль и расходы, и пыталась убедиться,
что расходы на безопасность являются
эффективными, так как идут на снижение
количества ошибок и предотвращение
катастрофических ситуаций. В обязательном
порядке является обязанностью всех и
каждого инженера по обслуживанию очень
внимательно относиться к своей работе
и быть готовым к ошибкам (См. Раздел
9.3.1). В целом, инженеры по обслуживанию
самолетов осознают важность своей
работы и обычно уделяют значительное
внимание и предпринимают усилия на
проведение мероприятий по предотвращению
производственных травм, сохранности
оборудования и безопасности самолета
на котором они работают.
Издание 1 15 сентября 2004 ТОЛЬКО ДЛЯ
ОБУЧЕНИЯ Стр. 82
АMIKON
Training Manual Part-66 Human Factors
Модель с ошибками в переменных 403 [c.403]
Таким образом, сначала вместо полной модели с ошибками в уравнении и переменных [c.78]
А, С не выполняется. Например, эти условия не выполняются, если в i -м уравнении какая-нибудь из объясняющих переменных коррелирована с ошибкой в этом уравнении. Последнее характерно для моделей с ошибками в измерении объясняющих переменных и для моделей «одновременных уравнений», о которых мы будем говорить ниже. Пока же приведем пример, показывающий, к каким последствиям приводит нарушение условия некоррелированности объясняющих переменных с ошибками. [c.106]
Модели с ошибками в измерении объясняющих переменных [c.111]
Как и в случае регрессионной модели с одной независимой переменной, вариацию Y (Ut У)2 можно разбить на две части объясненную регрессионным уравнением и необъясненную (т. е. связанную с ошибками е) — см. (2.25) [c.74]
Отметим, что в соответствии с этой моделью цена и величина спроса-предложения определяются одновременно (отсюда и термин одновременные уравнения ) и поэтому обе эти переменные должны считаться эндогенными. В отличие от них доход yt является экзогенной переменной. Подчеркнем, что деление переменных на экзогенные и эндогенные определяется содержательной стороной модели. Предполагается, что в каждом уравнении экзогенные переменные некоррелированы с ошибкой. В то же время эндогенные переменные, стоящие в правых частях уравнений, как [c.224]
В главе 2 рассматривается возможность получения подходящих оценок параметров в ситуациях, когда объясняющие переменные, входящие в уравнение регрессии, коррелированы с ошибкой в этом уравнении. Именно такое положение наблюдается в имеющих широкое применение моделях, известных под названием «системы [c.7]
Приведенные здесь выкладки можно почти дословно повторить и в том случае, если в модели присутствует объясняющая переменная X, не коррелирующая с ошибками регрессии. Приведем их окончательный результат. Оценка (8.20) сходится по вероятности к величине вида [c.202]
Другой тонкий симптом подстройки можно определить только путем сравнения форвардного показателя эффективности торговой модели с ее доходностью в реальной торговле. Вспомните, что форвардный показатель эффективности — это отношение средней годовой форвардной прибыли к средней годовой оптимизационной прибыли. Реальная доходность должна быть сравнительно близка к форвардной доходности. Если она кардинально отличается от последней в течение достаточно продолжительного периода времени, то скорее всего это симптом подстройки. Однако, обычно ситуации такого рода поправимы. Если модель прошла форвардный тест, то по всей вероятности она работоспособна. Работоспособная модель может быть слегка подстроенной, если возникают небольшие расхождения в результатах реальной и тестовой торговли. Например, возможно, недостаточно большой была выборка данных, число степеней свободы было на пределе возможного или диапазоны сканирования переменных были слишком короткими. Такие ошибки могут быть исправлены, а исходные тестовые процедуры — модифицированы и выполнены заново. [c.167]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Найденная с помощью уравнения (7.53) (его параметры можно искать обычным МНК) оценка у, может служить в качестве инструментальной переменной для фактора уг Эта переменная, во-первых, тесно коррелирует с у, ь во-вторых, как показывает соотношение (7.53), она представляет собой линейную комбинацию переменной х, х, для которой не нарушается предпосылка МНК об отсутствии зависимости между факторным признаком и остатками в модели регрессии. Следовательно, переменная у, также не будет коррелировать с ошибкой и,. [c.326]
Хотя первоначальные тесты АРМ обещали больший успех в объяснении различий в доходах, была проведена разделительная линия между использованием этих моделей для объяснения различий в доходах в прошлом и их применением для предсказания будущих доходов. Противники САРМ, с очевидностью, достигли более серьезного успеха в объяснении прошлых доходов, поскольку они не ограничивали себя одним фактором, как это делается в модели САРМ. Подобный учет значительного числа факторов становится более проблематичным, когда мы пытаемся планировать ожидаемые в будущем доходы, поскольку приходится оценивать коэффициенты бета и премии для каждого из этих факторов. Коэффициенты бета и премии для факторов сами по себе изменчивы, поэтому ошибка в оценке может уничтожить все преимущества, которые мы можем получить, переходя от модели САРМ к более сложным моделям. При использовании моделей регрессии, предлагаемых в качестве альтернативы, мы также сталкиваемся с трудностями при оценке, поскольку переменные, прекрасно работающие в [c.104]
Во многих задачах регрессионного типа разбиение переменных на две жесткие группы (в первую входят переменные, наблюдаемые с ошибкой, во вторую — переменные, значения которых известны точно) оказывается неадекватным реальному положению дел все переменные наблюдаются или фиксируются с некоторыми ошибками. К настоящему времени в литературе предложен ряд моделей, описывающих подобные ситуа- [c.250]
Ошибки в измерениях зависимой переменной. Предположим, что истинной является модель (8.1), но вектор у измеряется с ошибкой, т. е. наблюдается вектор у — у + и, где и — ошибки, имеющие нулевое математическое ожидание и не зависящие от е и X. Тогда нетрудно понять, что построение МНК-оценок на основании у эквивалентно регрессии [c.214]
Нетрудно понять, что в общем случае эндогенные переменные и ошибки в структурной системе коррелированы (пример 1 данной главы), поэтому, как уже неоднократно отмечалось, применение к какому-либо из уравнений метода наименьших квадратов даст смещенные и несостоятельные оценки структурных коэффициентов. В то же время коэффициенты приведенной формы могут быть состоятельно оценены, поскольку переменные Xt некоррелированы со структурными ошибками et и, следовательно, с ошибками приведенной формы модели vt. [c.233]
Использование эндогенных условий переключения режимов в модели, которая имеет эндогенные объясняющие переменные, коррелированные с ошибками, ведет к чрезмерному усложнению и серьезным проблемам, связанным с оцениванием. Кроме того, возникает проблема рефлексии, или так называемой круговой причинности , во взаимосвязи переменных YH+I и 1ц+. Чтобы избежать этих проблем, были использованы экзогенные детерминированные годовые и региональные условия переключения режимов. Для этих целей выборка наблюдений S была разделена на две подгруппы Si и [c.70]
Модели, в которых некоторые объясняющие переменные коррелированы с ошибкой [c.111]
В такой форме модели ошибка vit состоит из двух компонент щ и uit. Как и в модели с фиксированными эффектами, случайные эффекты at также отражают наличие у субъектов исследования некоторых индивидуальных характеристик, не изменяющихся со временем в процессе наблюдений, которые трудно или даже невозможно наблюдать или измерить. Однако теперь значения этих характеристик встраиваются в состав случайной ошибки, как это делается в классической модели регрессии, в которой наличие случайных ошибок интерпретируется как недостаточность включенных в модель объясняющих переменных для полного объяснения изменений объясняемой переменной. К прежним предположениям о том, что [c.249]
После получения оценки для р производится преобразование переменных, призванное получить модель с независимыми ошибками. Наконец, в рамках преобразованной модели производится обычный анализ на фиксированные или случайные эффекты. [c.274]
Отметим также следующее обстоятельство. Если остатки ряда модели подчинены процессу скользящей средней, уравнение с нормально распределенными ошибками будет содержать бесконечное число лагов переменной Y. Коэффициенты при них убывают в геометрической прогрессии, и можно ограничиться несколькими первыми членами. В этом случае метод максимального правдоподобия практически равносилен нелинейному методу наименьших квадратов. [c.205]
Соответственно оценки параметров аи b могут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка е мультипликативно связана с объясняющей переменной х. Если же модель представить в виде у = а х + е, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. [c.70]
Хотя коэффициент детерминации по модели, параметры которой были рассчитаны обычным МНК, несколько выше, однако стандартные ошибки коэффициентов регрессии в модели, полученной с учетом ограничений на полиномиальную структуру лага, значительно снизились. Кроме того, модель, полученная обычным МНК, обладает более существенным недостатком коэффициенты регрессии при лаговых переменных этой модели xt и х, 3 нельзя считать статистически значимыми. [c.305]
Шестая часть посвящена оценкам максимального правдоподобия, которые, конечно, являются идеальным объектом для демонстрации мощи развиваемой техники. В первых трех главах исследуется несколько моделей, среди которых есть многомерное нормальное распределение, модель с ошибками в переменных и нелинейная регрессионная модель. Рассматриваются методы работы с симметрией и положительной определенностью, специальное внимание уделено информационной матрице. Вторая глава этой части содержит обсуждение одновременных уравнений при условии нормальности ошибок. В ней рассматриваются проблемы оценивания и идентифицируемости параметров при различных (не)линейных ограничениях на параметры. В этой части рассматривается также метод максимального правдоподобия с полной информацией (FIML) и метод максимального правдоподобия с ограниченной информацией (LIML), особое внимание уделено выводу асимптотических ковариационных матриц. Последняя глава посвящена различным проблемам и методам психометрики, в том числе методу главных компонент, мультимодальному компо- [c.16]
Заметим, что переменные X не коррелируют с ошибками Е, так что, применив обратное преобразование Койка, мы решили проблему коррелированности регрессоров со случайными членами. Однако применение обычного метода наименьших квадратов к модели (8.32) оказывается на практике невозможным из-за бесконечно большого количества регрессоров. Разумеется, в силу того, что коэффициенты входящего в модель ряда убывают в геометрической прогрессии, и, стало быть, сам ряд быстро сходится, можно было бы ограничиться сравнительно небольшим числом лагов. Однако и в этом случае мы столкнулись бы по крайней мере с двумя трудно решаемыми проблемами. Во-первых, возникла бы сильная мультиколлинеарность, так как естественно ожидать, что лаговые переменные сильно коррели-рованы. Во-вторых, уравнение оказалось бы неидентифицируемым. В модели на самом деле присутствует всего четыре параметра. Между тем как, взяв всего лишь три лага, мы бы получили оценки пяти параметров. [c.203]
Однако, эти результаты достигаются не всегда, если не выполняются следующие условия [334,137] наличие информации об идентичных предпочтениях, общеизвестной структуре капитала и дивидендов, и полной совокупности имущественных прав (т.е. наличие полного спектра производных финансовых инструментов, позволяющих оценить ожидаемые будущие риски). Эти исследования содержат примеры сбоя модели рациональных ожиданий и позволяют предположить, что агрегирование информации является более сложным процессом. В частности, похоже, эффективность рынка, определяемая как полное агрегирование информации, зависит от «сложности» рыночной структуры, обусловленной такими параметрами, как количество акций, обращающихся на рынке, и торговыми периодами [319]. Например, чрезмерная реакция людей на неинформативные сделки может создать, так называемые, самообразующиеся информационные «миражи», которыми, вероятно, можно объяснить явную чрезмерную волатильность биржевых цен.[67]. Более того, эксперименты с рыночными моделями показали, что существует два типа ошибок в оценке рынка ошибки в оценке экзогенных событий, влияющих на стоимость активов, и ошибки в оценке переменных факторов, создаваемых рыночной деятельностью, таких как цены фьючерсных контрактов. Несмотря на существование идеальных условий для обучения, индивидуальные ошибки не устраняются полностью, а, в лучшем случае, иногда сокращаются. [65] Еще одной отличительной особенностью людей, выявленной в ходе экспериментов, является так называемый «эффект избавления», соответствующий тенденции продавать выросшие в цене активы и держать активы, упавшие в цене [446]. Такую тягу к избавлению можно объяснить тем, что люди оценивают прибыль и убытки, привязывая их к какому-либо ориентиру, и склонны идти на риск при наличии опасности потенциального убытка, но стремятся избежать риска при наличии потенциальной возможности получить определенную прибыль. Еще одной важной психологической особенностью человека является то, что многие люди переоценивают свои личные способности и чрезмерно оптимистичны в отношении своего будущего. Как было установлено, эти особенности влияют на экономическое поведение при вступлении в конкурентные игры или при инвестировании на рынке акций [66]. [c.96]
В случае с многими переменными может быть больше одного вектора коинтеграции. Следовательно, нужна методология, которая бы определила структуру всех векторов коинтеграции. Такой процесс был разработан Йохансеном (1988) и Йохансеном и Йезулиусом (1990). Он определяет множество временных рядов в качестве векторного авторегрессионного (VAR) процесса. Модель исправления ошибки разрабатывается следующим образом. [c.344]
Стандартные ошибки предсказания могут быть рассчитаны с помощью добавления в модель фиктивных переменных по методу Сал-кевера. Пусть имеется возможность получения статистических данных за р моментов на прогнозном периоде. Тогда строится такая же регрессия для совокупного набора данных выборки и прогнозного периода, но с добавлением фиктивных переменных Dt+i, Dt+2,. . ., Dt+p. При этом Dt+i = 1 только для момента наблюдения (t + i). Для всех других моментов Dt+i = 0. Доказано, что оценки коэффициентов и их стандартные ошибки для всех количественных переменных Xj в точности совпадают со значениями, полученными по регрессии, построенной только по данным выборки. Коэффициент при фиктивной переменной Dt+i будет равен ошибке предсказания в момент (t + i). A стандартная ошибка коэффициента равна стандартной ошибке предсказания. [c.295]
Использование взвешенного метода в статистических пакетах, где предоставлена возможность задавать веса вручную, позволяет регулировать вклад тех или иных данных в результаты построения моделей. Это необходимо в тех случаях, когда мы априорно знаем о нетипичности какой-то части информации, т.е. на зависимую переменную оказывали влияние факторы, заведомо не включаемые в модель. В качестве примера такой ситуации можно привести случаи стихийных бедствий, засух. При анализе макроэкономических показателей (ВНП и др.) данные за эти годы будут не совсем типичными. В такой ситуации нужно попытаться исключить влияние этой части информации заданием весов. В разных статистических пакетах приводится возможный набор весов. Обычно это числа от О до 100. По умолчанию все данные учитываются с единичными весами. При указании веса меньше 1 мы снижаем вклад этих данных, а если задать вес больше единицы, то вклад этой части информации увеличится. Путем задания весового вектора мы можем не только уменьшить влияние каких — либо лет из набора данных, но и вовсе исключить его из анализа. Итак, ключевым моментом при применении этого метода является выбор весов. В первом приближении веса могут устанавливаться пропорционально ошибкам невзвешенной регрессии. [c.355]
В предыдущих разделах предполагалось, что независимые переменные (матрица X) являются неслучайными. Ясно, что такое условие выполнено не всегда, например, во многих ситуациях при измерении независимых переменных могут возникать случайные ошибки. Кроме того, при анализе временных рядов значение исследуемой величины в момент t может зависеть от ее значений в предыдущие моменты времени, т. е. в некоторых уравнениях эти значения выступают в качестве независимых, а в других — в качестве зависимых переменных (модели с лагированными переменными). Поэтому возникает необходимость рассматривать модели со стохастическими регрессорами. [c.149]
Рассматривая реализацию (12.4), (12.5) модели (12.3) с помощью ненаблюдаемой переменной у, мы предполагали, что ошибки t одинаково распределены, в частности, гомоскедастичны. Известно (п. 6.1), что при нарушении этого условия, т.е. при наличии гетероскедастичности, оценки метода наименьших квадратов в линейных регрессионных моделях перестают быть эффективными, но остаются несмещенными и состоятельными. В нашем случае гетероскедастичность, вообще говоря, приводит к нарушению состоятельности и асимптотической несмещенности. На содержательном уровне это нетрудно понять, исходя из следующих соображений. Пусть ошибки t, t — 1,. . . , п распределены нормально с нулевым средним и дисперсиями at, t — 1,. .., п (гетероскедастичность) и предположим, что выполнено (12.5). Тогда, повторяя выкладки (12.6), получим [c.328]
Во-вторых, наличие ошибки предсказаний Qit+ приводит к корреляции между ошибкой и переменной инвестиций Iit+i в момент t+1. Из-за корреляции ошибок с объясняющими переменными применение OLS и GLS также приводит к несостоятельным оценкам. Эти проблемы имеют место для любой спецификации модели как для фиксированных, так и для случайных эффектов. Для оценки (4.10) могут быть применены несколько альтернативных процедур, связанных с использованием инструментальных переменных, среди которых метод инструментальных переменных, обобщенный метод инструментальных переменных, обобщенный метод моментов (GMM). Среди перечисленных методов обобщенный метод моментов является единственным, который обеспечивает эффективные оценки параметров, поэтому предпочтение было отдано методу GMM ( Verbeek M., 2000 Baltagi В. Н., 1995). [c.61]
Когда критерии смещения и стандартного отклонения объединяются в критерии среднеквадратической ошибки, возникает в некотором смысле смешанная картина. Вагнер, проведя сопоставление по этому критерию, обнаружил, что для трех параметров его модели обыкновенный метод наименьших квадратов примерно эквивалентен методу ограниченной информации и он лучше этого метода для оставшихся ч еты-рех параметров. Нагар установил приблизительную эквивалентность обыкновенного и двухшагового методов наименьших квадратов для двух параметров его модели, преимущество обыкновенного метода для двух других параметров и преимущество двухшагового метода для двух оставшихся. Басман обнаружил, что обыкновенному методу наименьших квадратов соответствует меньшая, чем двухшаговому, среднеквад-ратическая ошибка в четырех случаях из пяти (весьма значительное превосходство) и что оба метода дают лучшие результаты, чем метод ограниченной информации. Более основательные доказательства, базирующиеся на исследовании Саммерса, приведены в табл. 13.5. Для каждого параметра каждый оператор оценивания получил ранг 1, 2, 3 или 4 в зависимости от величины среднеквадратической ошибки (по возрастанию), а затем все ранги, соответствующие одному методу, суммировались по рассматриваемой группе экспериментов. Таким образом, меньшая величина ранга соответствует лучшему оператору оценивания. Для правильно специфицированной модели в случае независимых экзогенных переменных лучшим оказался метод максимального правдоподобия с полной информацией, на втором месте — двухшаговый [c.414]
В качестве переменных параметров в модели планирования геологоразведочных работ использовались объемы запасов нефти различных категорий на отдельных месторождениях затраты, связанные с переводом запасов в другую категорию и добычей единицы запасов временные показатели, определяющие очередность отбора запасов, сроки перевода запасов и т. д. Кроме того, ряд характеристик отражал подтверждаемость запасов, их достоверность. Совокупность условий, характеризующих баланс запасов с учетом возможности перевода нефти из одной категории в другую, наличие остатков, прирост запасов и добычи нефти из месторождений и т. д. связывал эти параметры в соотношения, из которых можно было найти искомые переменные и тем самым обосновать объем потребных геологоразведочных работ. Необходимо отметить, что, несмотря на полноту охвата всех производственных этапов перевода запасов из низших категорий в высшие, определение некоторых используемых в модели показателей (коэффициентов подтверждаемости запасов, их достоверности и т. п.) с приемлемой ошибкой (т. е. с высокой надежностью) является весьма трудной задачей, и в этом смысле построенная модель информационно не обеспечена. [c.202]
Стандартные модели и симуляции сценариев экстремальных событий служат многочисленными источниками ошибки, каждая из которых может иметь отрицательное воздействие на действительность предсказаний [232]. Некоторые из вероятностных переменных находятся под контролем в процессе моделирования -они обычно подразумевают балансирование между более полным описанием и реализуемостью вычислений. Другие источники ошибки находятся вне контроля, поскольку они свойственны методологии моделирования в определенных научных дисциплинах. Обе известных стратегии моделирования ограничены в этом отношении аналитические теоретические предсказания находятся вне досягаемости для большинства сложных проблем. Грубая сила числового решения уравнений (когда они известны) или сценариев, дает надежные результаты лишь в «центре распределения», то есть в режиме, далеком от крайностей, где может быть накоплена хорошая статистика. Кризисы — это чрезвычайные события, которые происходят редко, хотя и с экстраординарными последствиями. Таким образом, редкие катасторофические события полностью не имеют статистической выборки и не укладываются в рамки какой-либо модели. Даже появление «терра» суперкомпьютеров качественно не меняет этого фундаментального ограничения. [c.33]
Денежные потоки в любой организации, без преувеличения, можно назвать ее кровеносной системой. В то же время этот показатель, как никакой другой, труден для прогнозирования. Эта глава посвящена проблеме управления активами и пассивами Министерства финансов Голландии (далее — MoF). Особое внимание будет уделено оценке суммы ежемесячного валового сбора налогов. Мы рассмотрим и сравним различные методы, в том числе, и модель ARIMA — собственную разработку MoF. Так как нейронные сети превосходят другие методы по показателю среднеквадратичной ошибки (MSE) на вновь предъявляемых образцах, мы будем выделять различные типы индивидуального и совместного поведения переменных с помощью анализа первичных весов, тестов на чувствительность и выделения кластеров среди векторов весов-состояния. [c.94]
В скобках указаны стандартные ошибки параметров уравнения регрессии. Применение метода инструментальных переменных привело к статистической незначимости параметра С[ = 0,109 при переменной yf . Это произошло ввиду высокой мультиколлинеарности факторов, иyt v. Несмотря на то что результаты, полученные обычным МНК, на первый взгляд лучше, чем результаты применения метода инструментальных переменных, результатам обычного МНК вряд ли можно доверять вследствие нарушения в данной модели его предпосылок. Поскольку ни один из методов не привел к получению достоверных результатов расчетов параметров, следует перейти к получению оценок параметров данной модели авторегрессии методом максимального правдоподобия. [c.328]
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.

Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат









![hat { beta} xrightarrow {p} frac { operatorname {Cov} [, x_t, y_t ,]} { operatorname {Var} [, x_t ,]} = frac { beta sigma ^ 2_ {x ^ *}} { sigma_ {x ^ *} ^ 2 + sigma_ eta ^ 2} = frac { beta} {1 + sigma_ eta ^ 2 / sigma_ {x ^ * } ^ 2} ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9c0402eadca9ed6bcb72418d8683aacd8a5b09a)



![beta _ {x} = { frac { operatorname {Cov} [, x_ {t}, y_ {t} ,]} { operatorname {Var} [, x_ {t} ,]}} .](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f85337e7adf5dc85f1151b5a21149c1549d60fd)









![operatorname {E} [ eta | x ^ *] , = , 0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/f582199baa64e433bfbc070f6ca1cd14d582c8a4)


![alpha = operatorname {Pr} [ eta = -1 | х ^ * = 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aae13c5226fe0e441d7f99d96c73f7d90e9eb647)
![beta = operatorname {Pr} [ eta = 1 | х ^ * = 0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/df26f5a1c5afa4b64bc34a1225a30fdcaee4d0e0)







![begin {align} & z_t = left (1 z_ {t1}' z_ {t2}' z_ {t3}' z_ {t4}' z_ {t5}' z_ {t6}' z_ {t7}' right)', quad text {где} & z_ {t1} = x_t circ x_t & z_ {t2} = x_t y_t & z_ {t3} = y_t ^ 2 & z_ {t4} = x_t circ x_t circ x_t - 3 big ( operatorname {E} [x_tx_t'] circ I_k big) x_t & z_ {t5} = x_t circ x_t y_t - 2 big ( operatorname {E} [y_tx_t'] circ I_k big) x_t - y_t big ( operatorname {E} [x_tx_t'] circ I_k big) iota_k & z_ {t6} = x_t y_t ^ 2 - operatorname {E} [y_t ^ 2] x_t - 2y_t operatorname {E} [x_ty_t] & z_ {t7} = y_t ^ 3 - 3y_t operatorname {E} [y_t ^ 2] end {выровнять}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17ecb7ca4ed41a50e2b152d1f7e7fca5a40d909b)










![operatorname {E} [, y_ {t} | x_ {t} ,] = int g (x_ {t} ^ {*}, beta) f _ {{x ^ {*} | x}} ( x_ {t} ^ {*} | x_ {t}) dx_ {t} ^ {*},](https://wikimedia.org/api/rest_v1/media/math/render/svg/27918e2a9b583e2315d252b3d42b6875f6a67eda)




![hat { beta} = big ( hat { operatorname {E}} [, xi_t xi_t',] big) ^ {- 1} hat { operatorname {E}} [, xi_t y_t ,],](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f3ff27dccb72aa60aa497f76cbd82a2f1bc3ff)

![operatorname {E} [, w_ {t} h (x_ {t} ^ {*}) ,] = { frac {1} {2 pi}} int _ {{- infty}} ^ { infty} varphi _ {h} (- u) psi _ {w} (u) du,](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c77215b400b8a31c6083ae054e5eb0885cb4f9)
![psi_w (u) = operatorname {E} [, w_te ^ {iux ^ *} ,] = frac { operatorname {E} [w_te ^ {iux_ {1t}}]} { operatorname {E} [e ^ {iux_ {1t}}]} exp int_0 ^ ui frac { operatorname {E} [x_ {2t} e ^ {ivx_ {1t}}]} { operatorname {E} [e ^ { ivx_ {1t}}]} dv](https://wikimedia.org/api/rest_v1/media/math/render/svg/10012101ed93d980603ae2b70bb8f2f6115cea6b)

![hat {g} (x) = frac { hat { operatorname {E}} [, y_tK_h (x ^ * _ t - x) ,]} { hat { operatorname {E}} [, K_h (x ^ * _ t - x) ,]},](https://wikimedia.org/api/rest_v1/media/math/render/svg/be0ab49c7a4dad7b326a206f00968cf528eb1302)