Quantum error correction (QEC) is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is theorised as essential to achieve fault tolerant quantum computing that can reduce the effects of noise on stored quantum information, faulty quantum gates, faulty quantum preparation, and faulty measurements. This would allow algorithms of greater circuit depth.[1]
Classical error correction employs redundancy. The simplest albeit inefficient approach is the repetition code. The idea is to store the information multiple times, and—if these copies are later found to disagree—take a majority vote; e.g. suppose we copy a bit in the one state three times. Suppose further that a noisy error corrupts the three-bit state so that one of the copied bits is equal to zero but the other two are equal to one. Assuming that noisy errors are independent and occur with some sufficiently low probability p, it is most likely that the error is a single-bit error and the transmitted message is three ones. It is possible that a double-bit error occurs and the transmitted message is equal to three zeros, but this outcome is less likely than the above outcome. In this example, the logical information was a single bit in the one state, the physical information are the three copied bits, and determining what logical state is encoded in the physical state is called decoding. Similar to classical error correction, QEC codes do not always correctly decode logical qubits, but their use reduces the effect of noise.
Copying quantum information is not possible due to the no-cloning theorem. This theorem seems to present an obstacle to formulating a theory of quantum error correction. But it is possible to spread the (logical) information of one qubit onto a highly entangled state of several (physical) qubits. Peter Shor first discovered this method of formulating a quantum error correcting code by storing the information of one qubit onto a highly entangled state of nine qubits.
Classical error correcting codes use a syndrome measurement to diagnose which error corrupts an encoded state. An error can then be reversed by applying a corrective operation based on the syndrome. Quantum error correction also employs syndrome measurements. It performs a multi-qubit measurement that does not disturb the quantum information in the encoded state but retrieves information about the error. Depending on the QEC code used, syndrome measurement can determine the occurrence, location and type of errors. In most QEC codes, the type of error is either a bit flip, or a sign (of the phase) flip, or both (corresponding to the Pauli matrices X, Z, and Y). The measurement of the syndrome has the projective effect of a quantum measurement, so even if the error due to the noise was arbitrary, it can be expressed as a combination of basis operations called the error basis (which is given by the Pauli matrices and the identity). To correct the error, the Pauli operator corresponding to the type of error is used on the corrupted qubit to revert the effect of the error.
The syndrome measurement provides information about the error that has happened, but not about the information that is stored in the logical qubit—as otherwise the measurement would destroy any quantum superposition of this logical qubit with other qubits in the quantum computer, which would prevent it from being used to convey quantum information.
Bit flip code[edit]
The repetition code works in a classical channel, because classical bits are easy to measure and to repeat. This approach does not work for a quantum channel in which, due to the no-cloning theorem, it is not possible to repeat a single qubit three times. To overcome this, a different method has to be used, such as the three-qubit bit flip code first proposed by Asher Peres in 1985.[2] This technique uses entanglement and syndrome measurements and is comparable in performance with the repetition code.

Consider the situation in which we want to transmit the state of a single qubit 





Let 







The channel acts on 






Comparison of output minimum fidelities, with (red) and without (blue) error correcting via the three qubit bit flip code. Notice how, for 
Let us assume for simplicity that 
This reveals which qubits are different from the others, without at the same time giving information about the state of the qubits themselves. If the outcome corresponding to 


Note that, while this procedure perfectly corrects the output when zero or one flips are introduced by the channel, if more than one qubit is flipped then the output is not properly corrected. For example, if the first and second qubits are flipped, then the syndrome measurement gives the outcome 





![{displaystyle [(1-p)^{3}+3p(1-p)^{2}],vert psi 'rangle langle psi 'vert +(...)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/339e43e84be56445c2eb3f56a60d1b32febe38bd)

This fidelity is to be compared with the corresponding fidelity obtained when no error-correcting protocol is used, which was shown before to equal 


Sign flip code[edit]

Flipped bits are the only kind of error in classical computer, but there is another possibility of an error with quantum computers, the sign flip. Through the transmission in a channel the relative sign between 



The original state of the qubit
will be changed into the state
In the Hadamard basis, bit flips become sign flips and sign flips become bit flips. Let 


Shor code[edit]
The error channel may induce either a bit flip, a sign flip (i.e., a phase flip), or both. It is possible to correct for both types of errors on any one qubit using a QEC code, which can be done using the Shor code published in 1995.[4][5]: 10 This is equivalent to saying the Shor code corrects arbitrary single-qubit errors.

Quantum circuit to encode a single logical qubit with the Shor code and then perform bit flip error correction on each of the three blocks.
Let 


If a bit flip error happens to a qubit, the syndrome analysis will be performed on each block of qubits (1,2,3), (4,5,6), and (7,8,9) to detect and correct at most one bit flip error in each block.
If the three bit flip group (1,2,3), (4,5,6), and (7,8,9) are considered as three inputs, then the Shor code circuit can be reduced as a sign flip code. This means that the Shor code can also repair a sign flip error for a single qubit.
The Shor code also can correct for any arbitrary errors (both bit flip and sign flip) to a single qubit. If an error is modeled by a unitary transform U, which will act on a qubit 

where 



If U is equal to I, then no error occurs. If 


Bosonic codes[edit]
Several proposals have been made for storing error-correctable quantum information in bosonic modes.[clarification needed] Unlike a two-level system, a quantum harmonic oscillator has infinitely many energy levels in a single physical system. Codes for these systems include cat,[6][7][8] Gottesman-Kitaev-Preskill (GKP),[9] and binomial codes.[10][11] One insight offered by these codes is to take advantage of the redundancy within a single system, rather than to duplicate many two-level qubits.
Binomial code[10][edit]
Written in the Fock basis, the simplest binomial encoding is
where the subscript L indicates a «logically encoded» state. Then if the dominant error mechanism of the system is the stochastic application of the bosonic lowering operator 


Cat code[6][7][8][edit]
Schrödinger cat states, superpositions of coherent states, can also be used as logical states for error correction codes. Cat code, realized by Ofek et al.[13] in 2016, defined two sets of logical states: 

Those two sets of states differ from the photon number parity, as states denoted with 



Still, cat qubits are not protected against two-photon loss 


General codes[edit]
In general, a quantum code for a quantum channel 



where 


A non-degenerate code is one for which different elements of the set of correctable errors produce linearly independent results when applied to elements of the code. If distinct of the set of correctable errors produce orthogonal results, the code is considered pure.[14]
Models[edit]
Over time, researchers have come up with several codes:
- Peter Shor’s 9-qubit-code, a.k.a. the Shor code, encodes 1 logical qubit in 9 physical qubits and can correct for arbitrary errors in a single qubit.
- Andrew Steane found a code that does the same with 7 instead of 9 qubits, see Steane code.
- Raymond Laflamme and collaborators found a class of 5-qubit codes that do the same, which also have the property of being fault-tolerant. A 5-qubit code is the smallest possible code that protects a single logical qubit against single-qubit errors.
- A generalisation of the technique used by Steane, to develop the 7-qubit code from the classical [7, 4] Hamming code, led to the construction of an important class of codes called the CSS codes, named for their inventors: Robert Calderbank, Peter Shor and Andrew Steane. According to the quantum Hamming bound, encoding a single logical qubit and providing for arbitrary error correction in a single qubit requires a minimum of 5 physical qubits.
- A more general class of codes (encompassing the former) are the stabilizer codes discovered by Daniel Gottesman, and by Robert Calderbank, Eric Rains, Peter Shor, and N. J. A. Sloane; these are also called additive codes.
- Two dimensional Bacon–Shor codes are a family of codes parameterized by integers m and n. There are nm qubits arranged in a square lattice.[15]
- A newer idea is Alexei Kitaev’s topological quantum codes and the more general idea of a topological quantum computer.
- Todd Brun, Igor Devetak, and Min-Hsiu Hsieh also constructed the entanglement-assisted stabilizer formalism as an extension of the standard stabilizer formalism that incorporates quantum entanglement shared between a sender and a receiver.
That these codes allow indeed for quantum computations of arbitrary length is the content of the quantum threshold theorem, found by Michael Ben-Or and Dorit Aharonov, which asserts that you can correct for all errors if you concatenate quantum codes such as the CSS codes—i.e. re-encode each logical qubit by the same code again, and so on, on logarithmically many levels—provided that the error rate of individual quantum gates is below a certain threshold; as otherwise, the attempts to measure the syndrome and correct the errors would introduce more new errors than they correct for.
As of late 2004, estimates for this threshold indicate that it could be as high as 1–3%,[16] provided that there are sufficiently many qubits available.
Experimental realization[edit]
There have been several experimental realizations of CSS-based codes. The first demonstration was with nuclear magnetic resonance qubits.[17] Subsequently, demonstrations have been made with linear optics,[18] trapped ions,[19][20] and superconducting (transmon) qubits.[21]
In 2016 for the first time the lifetime of a quantum bit was prolonged by employing a QEC code.[13] The error-correction demonstration was performed on Schrodinger-cat states encoded in a superconducting resonator, and employed a quantum controller capable of performing real-time feedback operations including read-out of the quantum information, its analysis, and the correction of its detected errors. The work demonstrated how the quantum-error-corrected system reaches the break-even point at which the lifetime of a logical qubit exceeds the lifetime of the underlying constituents of the system (the physical qubits).
Other error correcting codes have also been implemented, such as one aimed at correcting for photon loss, the dominant error source in photonic qubit schemes.[22][23]
In 2021, an entangling gate between two logical qubits encoded in topological quantum error-correction codes has first been realized using 10 ions in a trapped-ion quantum computer.[24][25] 2021 also saw the first experimental demonstration of fault-tolerant Bacon-Shor code in a single logical qubit of a trapped-ion system, i.e. a demonstration for which the addition of error correction is able to suppress more errors than is introduced by the overhead required to implement the error correction as well as fault tolerant Steane code.[26][27][28]
In 2022, researchers at the University of Innsbruck have demonstrated a fault-tolerant universal set of gates on two logical qubits in a trapped-ion quantum computer. They have performed a logical two-qubit controlled-NOT gate between two instances of the seven-qubit colour code, and fault-tolerantly prepared a logical magic state.[29]
In February 2023 researchers at Google claimed to have decreased quantum errors by increasing the qubit number in experiments, they used a fault tolerant surface code measuring an error rate of 3.028% and 2.914% for a distance-3 qubit array and a distance-5 qubit array respectively.[30][31][32]
Quantum error-correction without encoding and parity-checks[edit]
Also in 2022, research at University of Engineering and Technology Lahore demonstrated error-cancellation by inserting single-qubit Z-axis rotation gates into strategically chosen locations of the superconductor quantum circuits.[33] The scheme has been shown to effectively correct errors that would otherwise rapidly add up under constructive interference of coherent noise. This is a circuit-level calibration scheme that traces deviations (e.g. sharp dips or notches) in the decoherence curve to detect and localize the coherent error, but does not require encoding or parity measurements.[34] However, further investigation is needed to establish the effectiveness of this method for the incoherent noise.[33]
See also[edit]
- Error detection and correction
- Soft error
References[edit]
- ^ Cai, Weizhou; Ma, Yuwei (2021). «Bosonic quantum error correction codes in superconducting quantum circuits». Fundamental Research. 1 (1): 50–67. doi:10.1016/j.fmre.2020.12.006.
A practical quantum computer that is capable of large circuit depth, therefore, ultimately calls for operations on logical qubits protected by quantum error correction
- ^ Peres, Asher (1985). «Reversible Logic and Quantum Computers». Physical Review A. 32 (6): 3266–3276. Bibcode:1985PhRvA..32.3266P. doi:10.1103/PhysRevA.32.3266. PMID 9896493.
- ^ Nielsen, Michael A.; Chuang, Isaac L. (2000). Quantum Computation and Quantum Information. Cambridge University Press.
- ^ Shor, Peter W. (1995). «Scheme for reducing decoherence in quantum computer memory». Physical Review A. 52 (4): R2493–R2496. Bibcode:1995PhRvA..52.2493S. doi:10.1103/PhysRevA.52.R2493. PMID 9912632.
- ^ Devitt, Simon J; Munro, William J; Nemoto, Kae (2013-06-20). «Quantum error correction for beginners». Reports on Progress in Physics. 76 (7): 076001. arXiv:0905.2794. Bibcode:2013RPPh…76g6001D. doi:10.1088/0034-4885/76/7/076001. ISSN 0034-4885. PMID 23787909. S2CID 206021660.
- ^ a b Cochrane, P. T.; Milburn, G. J.; Munro, W. J. (1999-04-01). «Macroscopically distinct quantum-superposition states as a bosonic code for amplitude damping». Physical Review A. 59 (4): 2631–2634. arXiv:quant-ph/9809037. Bibcode:1999PhRvA..59.2631C. doi:10.1103/PhysRevA.59.2631. S2CID 119532538.
- ^ a b Leghtas, Zaki; Kirchmair, Gerhard; Vlastakis, Brian; Schoelkopf, Robert J.; Devoret, Michel H.; Mirrahimi, Mazyar (2013-09-20). «Hardware-Efficient Autonomous Quantum Memory Protection». Physical Review Letters. 111 (12): 120501. arXiv:1207.0679. Bibcode:2013PhRvL.111l0501L. doi:10.1103/physrevlett.111.120501. ISSN 0031-9007. PMID 24093235. S2CID 19929020.
- ^ a b Mirrahimi, Mazyar; Leghtas, Zaki; Albert, Victor V; Touzard, Steven; Schoelkopf, Robert J; Jiang, Liang; Devoret, Michel H (2014-04-22). «Dynamically protected cat-qubits: a new paradigm for universal quantum computation». New Journal of Physics. 16 (4): 045014. arXiv:1312.2017. Bibcode:2014NJPh…16d5014M. doi:10.1088/1367-2630/16/4/045014. ISSN 1367-2630. S2CID 7179816.
- ^ Daniel Gottesman; Alexei Kitaev; John Preskill (2001). «Encoding a qubit in an oscillator». Physical Review A. 64 (1): 012310. arXiv:quant-ph/0008040. Bibcode:2001PhRvA..64a2310G. doi:10.1103/PhysRevA.64.012310. S2CID 18995200.
- ^ a b c Michael, Marios H.; Silveri, Matti; Brierley, R. T.; Albert, Victor V.; Salmilehto, Juha; Jiang, Liang; Girvin, S. M. (2016-07-14). «New Class of Quantum Error-Correcting Codes for a Bosonic Mode». Physical Review X. 6 (3): 031006. arXiv:1602.00008. Bibcode:2016PhRvX…6c1006M. doi:10.1103/PhysRevX.6.031006. S2CID 29518512.
- ^ Albert, Victor V.; Noh, Kyungjoo; Duivenvoorden, Kasper; Young, Dylan J.; Brierley, R. T.; Reinhold, Philip; Vuillot, Christophe; Li, Linshu; Shen, Chao; Girvin, S. M.; Terhal, Barbara M.; Jiang, Liang (2018). «Performance and structure of single-mode bosonic codes». Physical Review A. 97 (3): 032346. arXiv:1708.05010. Bibcode:2018PhRvA..97c2346A. doi:10.1103/PhysRevA.97.032346. S2CID 51691343.
- ^ a b Sun, L.; Petrenko, A.; Leghtas, Z.; Vlastakis, B.; Kirchmair, G.; Sliwa, K. M.; Narla, A.; Hatridge, M.; Shankar, S.; Blumoff, J.; Frunzio, L.; Mirrahimi, M.; Devoret, M. H.; Schoelkopf, R. J. (July 2014). «Tracking photon jumps with repeated quantum non-demolition parity measurements». Nature. 511 (7510): 444–448. arXiv:1311.2534. Bibcode:2014Natur.511..444S. doi:10.1038/nature13436. ISSN 1476-4687. PMID 25043007. S2CID 987945.
- ^ a b Ofek, Nissim; Petrenko, Andrei; Heeres, Reinier; Reinhold, Philip; Leghtas, Zaki; Vlastakis, Brian; Liu, Yehan; Frunzio, Luigi; Girvin, S. M.; Jiang, L.; Mirrahimi, Mazyar (August 2016). «Extending the lifetime of a quantum bit with error correction in superconducting circuits». Nature. 536 (7617): 441–445. Bibcode:2016Natur.536..441O. doi:10.1038/nature18949. ISSN 0028-0836. PMID 27437573. S2CID 594116.
- ^ Calderbank, A. R.; Rains, E. M.; Shor, P. W.; Sloane, N. J. A. (1998). «Quantum Error Correction via Codes over GF(4)». IEEE Transactions on Information Theory. 44 (4): 1369–1387. arXiv:quant-ph/9608006. doi:10.1109/18.681315. S2CID 1215697.
- ^ Bacon, Dave (2006-01-30). «Operator quantum error-correcting subsystems for self-correcting quantum memories». Physical Review A. 73 (1): 012340. arXiv:quant-ph/0506023. Bibcode:2006PhRvA..73a2340B. doi:10.1103/PhysRevA.73.012340. S2CID 118968017.
- ^ Knill, Emanuel (2004-11-02). «Quantum Computing with Very Noisy Devices». Nature. 434 (7029): 39–44. arXiv:quant-ph/0410199. Bibcode:2005Natur.434…39K. doi:10.1038/nature03350. PMID 15744292. S2CID 4420858.
- ^ Cory, D. G.; Price, M. D.; Maas, W.; Knill, E.; Laflamme, R.; Zurek, W. H.; Havel, T. F.; Somaroo, S. S. (1998). «Experimental Quantum Error Correction». Phys. Rev. Lett. 81 (10): 2152–2155. arXiv:quant-ph/9802018. Bibcode:1998PhRvL..81.2152C. doi:10.1103/PhysRevLett.81.2152. S2CID 11662810.
- ^ Pittman, T. B.; Jacobs, B. C.; Franson, J. D. (2005). «Demonstration of quantum error correction using linear optics». Phys. Rev. A. 71 (5): 052332. arXiv:quant-ph/0502042. Bibcode:2005PhRvA..71e2332P. doi:10.1103/PhysRevA.71.052332. S2CID 11679660.
- ^ Chiaverini, J.; Leibfried, D.; Schaetz, T.; Barrett, M. D.; Blakestad, R. B.; Britton, J.; Itano, W. M.; Jost, J. D.; Knill, E.; Langer, C.; Ozeri, R.; Wineland, D. J. (2004). «Realization of quantum error correction». Nature. 432 (7017): 602–605. Bibcode:2004Natur.432..602C. doi:10.1038/nature03074. PMID 15577904. S2CID 167898.
- ^ Schindler, P.; Barreiro, J. T.; Monz, T.; Nebendahl, V.; Nigg, D.; Chwalla, M.; Hennrich, M.; Blatt, R. (2011). «Experimental Repetitive Quantum Error Correction». Science. 332 (6033): 1059–1061. Bibcode:2011Sci…332.1059S. doi:10.1126/science.1203329. PMID 21617070. S2CID 32268350.
- ^ Reed, M. D.; DiCarlo, L.; Nigg, S. E.; Sun, L.; Frunzio, L.; Girvin, S. M.; Schoelkopf, R. J. (2012). «Realization of Three-Qubit Quantum Error Correction with Superconducting Circuits». Nature. 482 (7385): 382–385. arXiv:1109.4948. Bibcode:2012Natur.482..382R. doi:10.1038/nature10786. PMID 22297844. S2CID 2610639.
- ^ Lassen, M.; Sabuncu, M.; Huck, A.; Niset, J.; Leuchs, G.; Cerf, N. J.; Andersen, U. L. (2010). «Quantum optical coherence can survive photon losses using a continuous-variable quantum erasure-correcting code». Nature Photonics. 4 (10): 700. arXiv:1006.3941. Bibcode:2010NaPho…4..700L. doi:10.1038/nphoton.2010.168. S2CID 55090423.
- ^ Guo, Qihao; Zhao, Yuan-Yuan; Grassl, Markus; Nie, Xinfang; Xiang, Guo-Yong; Xin, Tao; Yin, Zhang-Qi; Zeng, Bei (2021). «Testing a quantum error-correcting code on various platforms». Science Bulletin. 66 (1): 29–35. arXiv:2001.07998. Bibcode:2021SciBu..66…29G. doi:10.1016/j.scib.2020.07.033. PMID 36654309. S2CID 210861230.
- ^ «Error-protected quantum bits entangled for the first time». phys.org. 2021-01-13. Retrieved 2021-08-30.
- ^ Erhard, Alexander; Poulsen Nautrup, Hendrik; Meth, Michael; Postler, Lukas; Stricker, Roman; Stadler, Martin; Negnevitsky, Vlad; Ringbauer, Martin; Schindler, Philipp; Briegel, Hans J.; Blatt, Rainer; Friis, Nicolai; Monz, Thomas (2021-01-13). «Entangling logical qubits with lattice surgery». Nature. 589 (7841): 220–224. arXiv:2006.03071. Bibcode:2021Natur.589..220E. doi:10.1038/s41586-020-03079-6. ISSN 1476-4687. PMID 33442044. S2CID 219401398.
- ^ Bedford, Bailey (2021-10-04). «Foundational step shows quantum computers can be better than the sum of their parts». phys.org. Retrieved 2021-10-05.
- ^ Egan, Laird; Debroy, Dripto M.; Noel, Crystal; Risinger, Andrew; Zhu, Daiwei; Biswas, Debopriyo; Newman, Michael; Li, Muyuan; Brown, Kenneth R.; Cetina, Marko; Monroe, Christopher (2021-10-04). «Fault-tolerant control of an error-corrected qubit». Nature. 598 (7880): 281–286. Bibcode:2021Natur.598..281E. doi:10.1038/s41586-021-03928-y. ISSN 0028-0836. PMID 34608286. S2CID 238357892.
- ^ Ball, Philip (2021-12-23). «Real-Time Error Correction for Quantum Computing». Physics. 14. 184. Bibcode:2021PhyOJ..14..184B. doi:10.1103/Physics.14.184. S2CID 245442996.
- ^ Postler, Lukas; Heuβen, Sascha; Pogorelov, Ivan; Rispler, Manuel; Feldker, Thomas; Meth, Michael; Marciniak, Christian D.; Stricker, Roman; Ringbauer, Martin; Blatt, Rainer; Schindler, Philipp; Müller, Markus; Monz, Thomas (2022-05-25). «Demonstration of fault-tolerant universal quantum gate operations». Nature. 605 (7911): 675–680. arXiv:2111.12654. Bibcode:2022Natur.605..675P. doi:10.1038/s41586-022-04721-1. PMID 35614250. S2CID 244527180.
- ^ Google Quantum AI (2023-02-22). «Suppressing quantum errors by scaling a surface code logical qubit». Nature. 614 (7949): 676–681. Bibcode:2023Natur.614..676G. doi:10.1038/s41586-022-05434-1. ISSN 1476-4687. PMC 9946823. PMID 36813892.
- ^ Boerkamp, Martijn (2023-03-20). «Breakthrough in quantum error correction could lead to large-scale quantum computers». Physics World. Retrieved 2023-04-01.
- ^ Conover, Emily (2023-02-22). «Google’s quantum computer reached an error-correcting milestone». ScienceNews. Retrieved 2023-04-01.
- ^ a b Ahsan, Muhammad; Naqvi, Syed Abbas Zilqurnain; Anwer, Haider (2022-02-18). «Quantum circuit engineering for correcting coherent noise». Physical Review A. 105 (2): 022428. arXiv:2109.03533. Bibcode:2022PhRvA.105b2428A. doi:10.1103/physreva.105.022428. ISSN 2469-9926. S2CID 237442177.
- ^ Steffen, Matthias (2022-10-20). «What’s the difference between error suppression, error mitigation, and error correction?». IBM Research Blog. Retrieved 2022-11-26.
Further reading[edit]
- Daniel Lidar and Todd Brun, ed. (2013). Quantum Error Correction. Cambridge University Press.
- La Guardia, Giuliano Gadioli, ed. (2020). Quantum Error Correction: Symmetric, Asymmetric, Synchronizable, and Convolutional Codes. Springer Nature.
- Frank Gaitan (2008). Quantum Error Correction and Fault Tolerant Quantum Computing. Taylor & Francis.
- Freedman, Michael H.; Meyer, David A.; Luo, Feng (2002). «Z2-Systolic freedom and quantum codes». Mathematics of quantum computation. Comput. Math. Ser. Boca Raton, FL: Chapman & Hall/CRC. pp. 287–320.
- Freedman, Michael H.; Meyer, David A. (1998). «Projective plane and planar quantum codes». Found. Comput. Math. 2001 (3): 325–332. arXiv:quant-ph/9810055. Bibcode:1998quant.ph.10055F.
External links[edit]
- Error-check breakthrough in quantum computing[permanent dead link]
- «Topological Quantum Error Correction». Quantum Light. University of Sheffield. 2018-09-28. Archived from the original on 2021-12-22 – via YouTube.
Как пространство и время могут быть квантовым кодом исправления ошибок
Время на прочтение
10 мин
Количество просмотров 13K
Те же самые коды, требующиеся для предотвращения ошибок в квантовых компьютерах, могут придавать ткани пространства-времени присущую ей прочность

В игрушечных «голографических» вселенных (даже если и не в нашей, настоящей) ткань пространства-времени возникает на основе сети квантовых частиц. Физики обнаружили, что это работает по принципу квантового исправления ошибок.
В 1994-м математик из исследовательского подразделения AT&T по имени Питер Шор мгновенно прославил квантовые компьютеры (КК), открыв, что эти гипотетические устройства могли бы быстро раскладывать большие числа на множители – тем самым ломая большую часть современной криптографии. Но на пути реального создания КК стояла фундаментальная проблема: естественная неустойчивость их физических компонентов.
В отличие от двоичных битов информации обычных компьютеров, кубиты состоят из квантовых частиц, у которых есть вероятность нахождения в одном из двух состояний, обозначаемых |0> и |1>, в одно и то же время. При взаимодействии кубитов их возможные состояния становятся взаимозависимыми, и шансы оказаться в состояниях |0> и |1> зависят друг от друга. Пропорциональные вероятности растут тем более, чем сильнее после каждой операции кубиты становятся запутанными друг с другом. Поддержка и управление этим экспоненциально растущим количеством одновременных возможностей и делают КК теоретически мощными.
Однако кубиты безумно подвержены ошибкам. Слабейшее магнитное поле или случайный микроволновый импульс заставляет их «перебрасывать биты», меняя их шансы оказаться равными |0> или |1> по отношению к другим кубитам, или «переворачивать фазы», что обращает математическое отношение двух их состояний. Чтобы КК смогли работать, учёным нужно найти способы защищать информацию даже при повреждении отдельных кубитов. Более того, эти способы должны обнаруживать и исправлять ошибки, не измеряя сами кубиты напрямую, поскольку измерение приводит к коллапсу сосуществующих возможностей кубита в определённую реальность – а старые добрые 0 и 1 не могут поддерживать квантовые вычисления.
В 1995 году Шор вслед за своим алгоритмом разложения опубликовал ещё одно поразительное доказательство, о существовании «кодов, исправляющих квантовые ошибки». Специалисты по информатике Дорит Ааронова и Майкл Бен-Ор (а также другие независимые исследователи) годом позже доказали, что эти коды теоретически могут довести количество ошибок почти до нуля. «Это было важнейшее открытие 90-х, убедившее людей, что масштабируемые квантовые вычисления в принципе возможны, — сказал Скотт Ааронсон, ведущий специалист по квантовым компьютерам из Техасского университета. – И что это просто сложнейшая инженерная задача».

Питер Шор, Дорит Ааронова и Майкл Бен-Ор
Сегодня, хотя небольшие КК материализуются в лабораториях по всему миру, полезных КК, способных превзойти по производительности обыкновенные, остаётся ждать ещё несколько лет или даже десятилетий. Требуются куда как более эффективные коды исправления ошибок, чтобы справляться с обескураживающе большим количеством ошибок, выдаваемым реальными кубитами. Попытки разработать улучшенные коды – «один из важнейших вопросов в области», как сказал Ааронсон, наравне с совершенствованием железа.
Однако в рамках настойчивых поисков этих кодов, проходивших в последние 25 лет, в 2014-м году произошло нечто забавное – физики нашли свидетельство глубоких связей между квантовым исправлением ошибок и природой пространства, времени и гравитации. В общей теории относительности Альберта Эйнштейна гравитация определяется, как искривление ткани пространства и времени – или «пространства-времени» — вокруг массивных объектов. Мяч, подброшенный в воздух, перемещается по прямой линии в пространстве-времени, а оно уже изгибается по направлению к Земле. Однако, несмотря на всю мощь теории Эйнштейна, физики считают, что у гравитации должно быть более глубокое, квантовое происхождение, из которого каким-то образом появляется нечто похожее на ткань пространства-времени.
В 2014-м трое молодых исследователей квантовой гравитации пришли к невероятному результату. Они работали в любимой теоретиками области: игрушечной вселенной, известной, как «антидеситтеровское пространство», которая работает как голограмма. Искривлённая ткань пространства-времени внутри вселенной возникает как проекция запутанных квантовых частиц, существующих на её внешней границе. Ахмед Альмейри, Си Дон и Даниель Харлоу провели вычисления, из которых следует, что это голографическое «проявление» пространства-времени работает точно как квантовый код исправления ошибок. В журнале физики высоких энергий они опубликовали предположение о том, что само пространство-время является кодом – по крайней мере, в антидеситтеровском пространстве. Работа породила целую волну активности в сообществе исследователей квантовой гравитации, и были открыты новые квантовые коды исправления ошибок, включающие в себя больше свойств пространства-времени.
Джон Прескил, физик-теоретик из Калифорнийского технологического института, говорит, что квантовое исправление ошибок объясняет надёжность пространства-времени, несмотря на то, что оно соткано из хрупкого квантового вещества. «Нам не приходится обходиться с этой идеей слишком осторожно, чтобы не развалить геометрию, — сказал Прескил. – Я думаю, эта связь с квантовым исправлением ошибок – глубочайшее объяснение из всех, что у нас есть».
Язык квантового исправления ошибок также начинает позволять исследователям изучать загадки чёрных дыр: сферических участков, в которых пространство-время так сильно искривляется к центру, что оттуда не может убежать даже свет. «Все следы ведут к чёрным дырам», — сказал Альмейри, работающий в данное время в Институте передовых исследований в Принстоне. В этих наполненных парадоксами местах гравитация достигает своего пика, а общая теория относительности Эйнштейна перестаёт работать. «Есть некоторые признаки того, что если мы поймём, какой код использует пространство-время, — сказал он, — это может помочь нам понять внутреннее строение чёрных дыр».
В качестве бонуса исследователи надеются, что голографическое пространство-время сможет подсказать и способ масштабировать КК, реализовав давнюю мечту Шора и других. «Пространство-время умнее нас, — сказал Альмейри. – В эти конструкции встроен очень эффективный квантовый код исправления ошибок».

Ахмед Альмейри, Си Дон и Даниель Харлоу
Как как же работают квантовые коды исправления ошибок? Секрет сохранения информации в неспокойных кубитах состоит в том, чтобы хранить её не в отдельных кубитах, а в системе множества запутанных кубитов.
В качестве простого примера рассмотрим код для трёх кубитов: они использует три «физических» кубита для защиты одного «логического» кубита информации от переворачивания битов. Такой код не особенно полезен для квантового исправления ошибок, поскольку не защищает от переворота фаз, но объясняющую функцию выполняет. Состояние логического кубита |0> соответствует нахождению всех трёх физических кубитов в состоянии |0>, а состояние |1> соответствует тому, что все три находятся в состоянии |1>. Система находится в суперпозиции этих состояний, что записывается, как |000> + |111>. Но, допустим, у одного из кубитов перебросился бит. Как обнаружить и исправить ошибку, не измеряя кубиты напрямую?
В квантовый контур кубит можно ввести через два шлюза. Один проверяет «чётность» первого и второго физических кубитов – одинаковые они или различные – а другой проверяет чётность первого и третьего. Когда ошибок нет (то есть, кубиты находятся в состоянии |000> + |111>), измеряющие чётность шлюзы определяют, что первый и второй, а также первый и третий кубиты идентичны. Однако если у первого кубита случайно перебрасывается бит, это приводит к состоянию |100> + |011>, и шлюз определяет различие в обеих парах. Переброс бита во втором кубите даёт |010> + |101>, шлюзы определяют, что первый и второй кубит отличаются, а второй и третий совпадают; в случае переброса третьего кубита результат будет «совпадают; различаются». Эти уникальные результаты показывают, какая именно корректирующая хирургия необходима, и необходима ли она вообще – то есть, операция переброса назад первого, второго или третьего физического кубита, не приводящая к коллапсу логического кубита. «Квантовое исправления ошибок кажется мне магией», — сказал Альмейри.
Лучшие коды исправления обычно могут восстановить всю закодированную информацию на основе чуть большего количества физических кубитов, чем половина, даже если все остальные повреждены. Именно это натолкнуло Альмейри, Дона и Харлоу в 204 году на мысль о возможном наличии связи между квантового исправления ошибок и тем, как антидеситтеровское пространство (АдС) возникает из квантовой запутанности.
Важно отметить, что АдС пространство отличается от геометрии пространства-времени нашего, деситтеровского пространства. Наша Вселенная насыщена положительной энергией вакуума, заставляющей её расширяться без границ, в то время, как в АдС пространстве энергия вакуума отрицательна, из-за чего оно приобретает гиперболическую геометрию, похожую на «Предел – круг» М. К. Эшера. Мозаичные существа Эшера становятся всё меньше, распространяясь от центра круга, в итоге исчезая на периметре. Точно так же пространственное измерение, исходящее из центра АдС пространства, постоянно сжимается и в итоге исчезает, обозначая внешнюю границу вселенной. АдС пространство стало популярным у физиков-теоретиков, изучающих квантовую гравитацию, в 1997, после того, как известный физик Хуан Малдасена открыл, что его изогнутая ткань пространства-времени «голографически дуальна» квантовой теории частиц, существующих на границе, свободной от гравитации и с меньшим числом измерений.

Гиперболическая геометрия на гравюре Эшера 1959 года «Предел – круг III» изображает АдС пространство
Изучая, как работает дуальность, как и сотни других физиков в последние пару десятилетий, Альмейри с коллегами заметили, что любую точку внутри АдС пространства можно создать на основе чуть больше половины границы – точно так же, как оптимальный квантовый код исправления ошибок.
В их работе, предполагающей, что голографическое пространство-время и квантовое исправление ошибок суть одно и то же, они описали, как даже простейший код можно представить в виде двумерной голограммы. Она состоит из трёх «кутритов» – частиц, существующих в одном из трёх состояний – находящихся на равных расстояниях друг от друга по кругу. Запутанное трио кутритов кодирует один логический кутрит, соответствующий одной точке пространства-времени в центре круга. Код защищает точку от стирания любого из трёх кутритов.
Конечно, одна точка – это так себе вселенная. В 2015 году Харлоу, Прескил, Фернандо Паставский и Бени Йошида обнаружили ещё один голографический код, названный HaPPY, перенимающий больше свойств АдС пространства. Код делит пространство на пятисторонние плитки – «как маленькие детальки конструктора Tinkertoy», сказал Патрик Хейден из Стэнфордского университета, руководитель исследований. Каждая деталька представляет одну точку пространства-времени. «Эти плитки играли бы роль рыб в мозаике Эшера», — сказал Хейден.
В коде HaPPY и других открытых голографических схемах исправления ошибок, всё внутри региона пространства-времени, называемого «клином запутанности» [entanglement wedge], можно воссоздать из кубитов, находящихся в регионе, соседнем с границей. У перекрывающиеся регионов на границе будут накладываться клинья запутанности, сказал Хейден, точно так же, как логический кубит в КК можно воссоздать из множества различных подмножеств физических кубитов. «И вот здесь вступает в игру свойство исправления ошибок».
«Квантовое исправление ошибок даёт нам обобщённое представление о геометрии в этом кодовом языке», — сказал Прескил. Тот же язык, сказал он, «вероятно, можно применять и к более обобщённым ситуациям», — в частности, к такой деситтеровской вселенной, как наша. Но оказалось, что деситтеровское пространство, у которого нет границ, гораздо сложнее представить в виде голограммы.
Пока что такие исследователи, как Альмейри, Харлоу и Хейден, работают с АдС пространством, поскольку у него много общих черт с деситтеровским миром, но при этом оно легче поддаётся изучению. Геометрии пространства-времени обоих пространств подчиняются теории Эйнштейна, они просто изгибаются в разных направлениях. И что, вероятно, гораздо важнее, во вселенных обоих типов есть чёрные дыры. «Самое фундаментальное свойство гравитации – наличие чёрных дыр», — сказал Харлоу, сейчас работающий адъюнкт-профессором физики в MIT. «Именно это отличает гравитацию от всех остальных взаимодействий. Поэтому с квантовой гравитацией так тяжело».
Язык квантового исправления ошибок обеспечил новый способ описания чёрных дыр. Наличие чёрной дыры определяется, как «отказ исправляемости», сказал Хейден: «Когда у вас появляется так много ошибок, что вы уже не можете отслеживать, что происходит в большом количестве пространства-времени, вы приходите к чёрной дыре. Это что-то типа сливного отверстия для невежества».
Невежество неизбежно накапливается в отношении внутренностей чёрных дыр. Откровение Стивена Хокинга 1974-го года о том, что ЧД излучают тепло, и, следовательно, рано или поздно испаряются, породило печально известный «парадокс исчезновения информации в ЧД», который спрашивает, что происходит со всей проглоченной ЧД информацией. Эта проблема может быть связана с космологией и рождением Вселенной, поскольку расширение сингулярности Большого взрыва очень похоже на гравитационный коллапс ЧД в обратном воспроизведении.
АдС пространство упрощает вопрос об информации. Поскольку граница АдС вселенной голографически дуальна всему, что в ней есть – всем ЧД и прочему – то информация, падающая в ЧД, гарантированно не потеряется; она всегда будет голографически закодирована на границе вселенной. Расчёты показывают, что для реконструкции информации о внутренностях чёрной дыры на основе кубитов на границе, вам потребуется доступ к запутанным кубитам примерно на трёх четвертях границы. «Чуть больше половины уже недостаточно», — сказал Альмейри. Он добавил, что требование трёх четвертей должно сообщать что-то важное о квантовой гравитации, но вопрос о том, почему получается именно такая доля, «всё ещё остаётся открытым».
В первой заявке Альмейри от 2012 года, высокий худой физик из ОАЭ и три его соратника углубили информационный парадокс. Их рассуждения предполагали, что информация вообще может не попадать внутрь ЧД, поскольку её остановит «файервол» на горизонте событий ЧД.
Как и большинство физиков, Альмейри не верит в то, что файерволы ЧД реально существуют, однако обойти это понятие оказалось сложно. Сейчас он считает, что формированию файерволов препятствует квантовое исправление ошибок, защищающая информацию даже после пересечения горизонта ЧД. В его последней самостоятельной работе, появившейся в октябре, он сообщил, что квантовое исправление ошибок «необходима для поддержки гладкости пространства-времени на горизонте» чёрной дыры из двух составных частей, известной, как червоточина. Он предполагает, что квантовое исправление ошибок не только предотвращает файерволы, но и позволяет кубитам убегать из ЧД после падения в неё, поскольку нити запутанности между внутренней и наружней частями ЧД сами похожи на миниатюрные червоточины. Это объяснило бы парадокс Хокинга.
В этом году министерство обороны выделило финансирование на исследования голографического пространства-времени, в частности потому, что подвижки в этой области могут привести к появлению более эффективных кодов исправления ошибок для квантовых компьютеров.
Физике же ещё придётся разобраться с тем, можно ли описать деситтеровскую вселенную, например, нашу, при помощи голограммы и в терминах кубитов и кодов. «Вся эта связь известна для мира, который очевидно не является нашим», — сказал Ааронсон. В работе от прошлого года Дон, сейчас работающий в Калифорнийском университете в Санта-Барбаре, и его соавторы Ева Сильверстейн и Гонзало Торроба, сделали шаг в деситтеровском направлении, пытаясь создать примитивное голографическое описание. Исследователи пока ещё изучают это предложение, но Прескил считает, что язык квантового исправления ошибок в итоге всё же будет перенесён в реальное пространство-время.
«На самом деле пространство удерживается благодаря запутанности, — сказал он. – Если вы хотите сшить пространство-время из маленьких кусочков, их надо правильно запутать. А правильно будет сделать это, создав квантовый код исправления ошибок».
Как квантовые компьютеры будут исправлять свои ошибки

В 1994 году Питер Шор, математик из Bell Labs в Нью-Джерси, доказал, что квантовый компьютер способен решать некоторые задачи экспоненциально быстрее, чем классический компьютер. Вопрос был в том, можно ли построить квантовый компьютер? Скептики утверждали, что квантовые состояния слишком хрупкие — окружающая среда неизбежно перемешает информацию в квантовом компьютере, сделав его совсем неквантовым.
Год спустя Шор ответил. Классические схемы измеряли отдельные биты для проверки на наличие ошибок, но этот подход не работал бы для квантовых битов или «кубитов», поскольку любое измерение разрушило бы квантовое состояние и, следовательно, вычисления. Шор нашел способ определить, произошла ли ошибка, без измерения состояния самого кубита. Код Шора положил начало области квантовой коррекции ошибок.
Раздел квантовой коррекции ошибок расцвел. Большинство физиков видят в нём единственный путь к созданию чрезвычайно мощного квантового компьютера. «Без коррекции ошибок мы не сможем масштабировать квантовые компьютеры до такой степени, чтобы они могли решать действительно сложные задачи», — сказал Джон Прескилл, физик из Калифорнийского технологического института.
Как и в случае с квантовыми вычислениями в целом, одно дело разработать код, исправляющий ошибки, и совсем другое — реализовать его на работающей машине. Но в начале октября исследователи под руководством Криса Монро, физика из Университета Мэриленда, сообщили, что они продемонстрировали многие ингредиенты, необходимые для работы схемы Шора с исправлением ошибок.
Так как же Шору удалось разгадать загадки, с которыми он столкнулся? Он использовал дополнительную сложность квантовой механики в своих интересах.
Повтор повтор повтор
Шор смоделировал свой протокол по образцу классического кода повторителя, который включает создание копий каждого бита информации, а затем периодическое сравнение этих копий друг с другом. Если один из битов отличается от других, компьютер может исправить ошибку и продолжить расчет.
Шор разработал квантовую версию этого протокола. Он использовал три отдельных «физических» кубита для кодирования одного кубита информации — «логического» кубита. Однако код квантового повторителя Шора не мог точно совпадать с классической версией. Существенная мощность квантовых вычислений проистекает из того факта, что кубиты могут существовать в «суперпозиции», находясь в комбинации 0 и 1 одновременно. Поскольку измерение квантового состояния разрушило бы суперпозицию, не было простого способа проверить, произошла ли ошибка.
Вместо этого Шор нашел способ определить, находятся ли три физических кубита в одном и том же состоянии. Если один из кубитов отличается, это означает, что произошла ошибка.
Задача мало чем отличается от решения простой логической головоломки. Вам даны три шара, которые выглядят одинаково, но один из шаров может иметь другой вес. У вас также есть простые весы. Какие измерения позволят вам определить, есть ли среди шаров отличающийся, и если да, то какой именно?

Ответ состоит в том, чтобы сначала взвесить два шара, затем заменить один из шаров оставшимся шаром и снова взвесить. Если весы были сбалансированы оба раза, то все шары идентичны. Если весы были сбалансированы только один раз, то один из замененных шаров отличается. Если вес оба раза отличается, то виноват третий шар.
Код Шора заменяет весы двумя дополнительными «вспомогательными» кубитами. Первый из них сравнивает первый и второй физические кубиты; другой сравнивает второй и третий. Измеряя состояния этих вспомогательных кубитов, вы узнаете, находятся ли три содержащих информацию кубита в идентичных состояниях, не нарушая состояния любого из них.
Этот код защищает от переключения битов, который является единственной возможной ошибкой, возникающей в классических вычислениях. Но у кубитов есть еще один потенциальный источник ошибок.
Суперпозиции — это ключ к квантовым вычислениям, но важно не только значение кубита. Относительная «фаза» между кубитами тоже имеет значение. Вы можете думать об этой фазе как о волне — она сообщает вам местоположение пиков и впадин волны. Когда две волны находятся в фазе, их пики синхронизированы. Если они столкнутся, они интерферируют, сливаясь в единую волну вдвое большего размера. Но если волны не в фазе, тогда одна волна находится на пике, другая — во впадине, и они нейтрализуют друг друга.
Квантовый алгоритм использует это фазовое соотношение между кубитами. Это создает ситуацию, когда правильный ответ вычислений конструктивно интерферирует и, следовательно, усиливается, в то время как неправильный ответ подавляется деструктивной интерференцией.
Но если ошибка приводит к изменению фазы, тогда деструктивная интерференция может переключиться на конструктивную интерференцию, и квантовый компьютер начнет усиливать неправильный ответ.
Шор обнаружил, что он может исправлять фазовые ошибки, используя принцип, аналогичный тому, который он использовал для переключения битов. Каждый логический кубит кодируется в три кубита, и дополнительные кубиты проверяют, не изменилась ли одна из фаз.
Затем Шор объединил два кода. Результатом стал код, переводящий один логический кубит в девять физических кубитов, который предлагал как битовую, так и фазовую проверку.
Устойчивость к ошибкам
Код Шора в принципе защищает отдельный логический кубит от ошибок. Но что, если произошла ошибка в самих измерениях ошибки? Пытаясь исправить несуществующую ошибку, вы переключите бит и невольно внесете настоящую ошибку. В некоторых случаях это может вызвать каскад ошибок, распространяющихся по коду.
Код Шора также не учитывал, как он будет управлять квантовым компьютером, построенным из его логических кубитов. «Нам нужен какой-то способ выполнять вычисления с закодированными состояниями без потери этой защиты. И это непросто», — сказал Дэниел Готтесман, ученый-теоретик из Университета Мэриленда.
Тогда в 1996 году Шор придумал понятие отказоустойчивости. Отказоустойчивый код может иметь дело с ошибками, вносимыми средой, несовершенными операциями с кубитами и даже самими этапами исправления ошибок — при условии, что частота возникновения этих ошибок ниже определенного порога.
В прошлом месяце Монро и его группа объявили, что они использовали защищенную от сбоев версию кода Шора, называемую кодом Бэкона-Шора, для демонстрации почти всех инструментов, необходимых для полностью отказоустойчивого квантового компьютера. Они закодировали логический кубит в квантовые состояния девяти ионов, а затем, используя четыре вспомогательных кубита, показали, что могут безотказно выполнять все операции с одним кубитом, необходимые для квантовых вычислений. Результат показывает, что отказоустойчивый квантовый компьютер возможен.
Однако создание квантового компьютера ещё не близко. Монро считает, что преимущества, предоставляемые исправлением ошибок, не будут заметны до тех пор, пока квантовые компьютеры не достигнут примерно 100 логических кубитов. Для такой машины потребуется около 1300 физических кубитов, поскольку каждому логическому кубиту нужно девять физических кубитов плюс четыре вспомогательных (в настоящее время самый крупный квантовый процессор, недавно анонсированный IBM Eagle, имеет 127 физических кубитов). На данном этапе «мы собираемся начать создавать фабрику кубитов, а затем внедрить исправление ошибок», — сказал Монро. «Но не раньше».
Те же самые коды, что защищают от ошибок квантовые компьютеры, возможно, обеспечивают и внутреннюю устойчивость самой ткани пространства-времени.
В 1994 году «квантовые компьютеры» мгновенно обрели широчайшую известность, когда математик из AT&T Labs Research по имени Питер Шор (Peter Shor) обнаружил, что эти гипотетические устройства могут быстро разлагать на множители большие числа и тем самым революционизировать современную криптографию. Однако на пути создания квантовых компьютеров встала фундаментальная проблема: их физические компоненты по своей природе крайне неустойчивы.
В отличие от бинарных битов информации обычных компьютеров, «кубиты» состоят из квантовых частиц, которые с некоторой вероятностью способны пребывать сразу в двух состояниях, обозначаемых как |0⟩ и |1⟩. При взаимодействии кубитов их возможные состояния становятся взаимозависимыми, шансы любого из них находиться в каком-то из двух состояний зависят от шансов других. Количество обусловленных таким образом возможностей растёт по мере того, как кубиты с каждой операцией становятся всё более и более «запутанными». Способность поддерживать экспоненциально растущее число одновременно существующих возможностей и манипулировать ими — вот что теоретически делает квантовые компьютеры чрезвычайно мощными.
Однако кубиты безумно часто создают ошибки. При малейшем воздействии магнитного поля или рассеянного микроволнового импульса они совершают «битовые кульбиты» (bit-flips), меняющие их шансы пребывать в состоянии |0⟩ или |1⟩ по отношению к другим кубитам, или «фазовые кульбиты» (phase-flips), которые инвертируют математические отношения между двумя их состояниями. Чтобы в квантовом компьютере даже тогда, когда отдельные кубиты повреждены, информация оставалась защищённой, нужны особые схемы её защиты. Эти схемы должны выявлять и исправлять ошибки, не прибегая к прямому измерению кубитов, поскольку такие измерения сводят сосуществующие возможности кубитов к жёстко определённой реальности — к старым добрым значениям 0 или 1, которые не способны поддерживать квантовые вычисления.
В 1995 году Шор вслед за своим алгоритмом разложения на множители выдал ещё одну сенсацию: доказал существование «квантовых кодов, исправляющих ошибки». Год спустя учёные-компьютерщики Дорит Ааронова (ивр. דורית אהרונוב, англ. Dorit Aharonov) и Майкл Бен-Ор (ивр. מיכאל בן-אור, англ. Michael Ben-Or) (а также другие исследователи, работавшие независимо) установили, что теоретически эти коды могут свести процент ошибок почти до нуля. «Это было главным открытием 90-х годов, — считает Скотт Ааронсон (Scott Aaronson), ведущий разработчик квантовых компьютеров Техасского университета в Остине (University of Texas at Austin). — Оно показало, что масштабируемые квантовые вычисления принципиально возможны, — что это просто чрезвычайно трудная инженерная проблема».
В лабораториях разных стран уже материализуются квантовые компьютеры, но сейчас они маленькие и существенно превзойти обычные смогут лишь через годы, а то и десятилетия. Для решения проблемы пугающе частых ошибок реальных кубитов нужны квантовые коды, которые гораздо эффективнее тех, что используются ныне. По словам Ааронсона, наряду с совершенствованием компьютерного «железа» разработка более совершенных кодов, исправляющих ошибки, является «одним из главных направлений деятельности в данной области исследований».
В последние два с половиной десятилетия шла упорная борьба за создание таких кодов. И тут — хоть плачь, хоть смейся — в 2014 году физики обнаружили глубокую связь между квантовой коррекцией ошибок и природой пространства, времени и гравитации. В общей теории относительности Альберта Эйнштейна гравитация определяется как ткань пространства и времени (или «пространства-времени»), искривляемая массивными объектами. (Шарик, брошенный в воздух, движется по прямой, но в пространстве-времени, искривлённом к Земле). Однако физики, опираясь на теорию Эйнштейна, считают, что у гравитации должно быть глубокое, квантовое происхождение, благодаря чему каким-то образом возникает видимая пространственно-временная ткань.
Итак, в 2014 году три молодых исследователя квантовой гравитации пришли к удивительному открытию. Они работали на игровой площадке физиков-теоретиков: в игрушечной вселенной, которая называется «антидеситтеровским пространством» и функционирует, как голограмма. Искривлённая пространственно-временная ткань внутри данного мира — это проекция, возникающая из живущих на его внешней границе запутанных квантовых частиц. Ахмед Альмхеири (Ahmed Almheiri), Си Дун (Xi Dong) и Дэниел Харлоу (Daniel Harlow) провели расчёты, исходя из того, что это голографическое «проявление» пространства-времени работает так же, как квантовый код, исправляющий ошибки. В Journal of High Energy Physics они предположили, что само пространство-время есть код — по меньшей мере, в антидеситтеровских (AdS) вселенных. Их статья так взбудоражила сообщество исследователей квантовой гравитации, что были открыты новые квантовые коды, исправляющие ошибки, которые более полно охватывают свойства пространства-времени.
По мнению Джона Прескилла (John Phillip Preskill), физика-теоретика из Калифорнийского технологического института (California Institute of Technology), квантовая коррекция ошибок объясняет, каким образом пространство-время достигает «внутренней устойчивости», несмотря на то, что соткано из хрупких квантовых элементов. «Нам не нужно осторожничать, боясь развалить эту геометрию, — говорит Прескилл. — Почему дело обстоит именно так? Я думаю, на данный момент лучшее объяснение — связь с квантовой коррекцией ошибок».
Кроме того, язык квантовой коррекции ошибок стал помогать исследовать тайны чёрных дыр — сферических объектов, в которых пространство-время так круто искривляется по направлению к их центру, что даже свет не в состоянии вырваться. «Все дороги ведут к чёрным дырам», — говорит Альмхеири, ныне сотрудник Института перспективных исследований (Institute for Advanced Study) в Принстоне, штат Нью-Джерси. В этих парадоксальных объектах гравитация достигает максимума, а общая теория относительности Эйнштейна терпит провал. «Кое-какие факты, — утверждает принстонский исследователь, — указывают на то, что, выяснив, какой код реализует пространство-время, легче понять интерьер чёрной дыры».
А ещё исследователи надеются на бонус: голографическое пространство-время может показать дорогу к масштабируемым квантовым вычислениям, воплощающим давнее предсказание Шора и других. «Пространство-время намного умнее нас, — говорит Альмхеири. — Исправляющий ошибки квантовый код, реализованный в такого рода конструкциях, очень эффективен».
А как работает квантовый код коррекции ошибок? Чтобы, несмотря на пугливость кубитов, защищать содержащуюся в них информацию, нужно исхитриться хранить её не в отдельных кубитах, а в паттернах их запутывания.
В качестве простого примера рассмотрим трёхкубитовый код. В нём для защиты от битовых кульбитов одного «логического» кубита информации используются три «физических» кубита. (Такой код не может защитить от фазовых кульбитов, поэтому для квантовой коррекции ошибок толку от него мало, но ознакомиться с ним полезно). Состояние логического кубита (|0⟩ или |1⟩) соответствует такому же состоянию всех трёх физических кубитов. Данная система пребывает в «суперпозиции» этих состояний, обозначаемой как |000⟩ + |111⟩. Пусть один из кубитов совершил битовый кульбит. Как обнаружить и исправить эту ошибку без прямого измерения какого-либо из кубитов?
Кубиты можно вводить через два гейта в квантовой цепи. Один гейт проверяет «чётность» (parity) первого и второго физических кубитов (являются ли они одинаковыми), а другой — чётность первого и третьего. Когда ошибки нет (это означает, что кубиты пребывают в состоянии |000⟩ + |111⟩), гейты измерения чётности отмечают, что как первый и второй, так и первый и третий кубиты чётны (одинаковы). Однако если первый кубит случайно совершил битовый кульбит и создал состояние |100⟩ + |011⟩, гейты обнаруживают в обеих парах разницу — отсутствие чётности. При битовом кульбите второго кубита, дающем состояние |010⟩ + |101⟩, гейты измерения чётности отмечают, что первый и второй кубиты нечётны, а первый и третий чётны, при битовом кульбите третьего кубита — что кубиты первой пары чётны, а второй — нечётны. Когда возникает ошибка, эти неповторяющиеся результаты показывают, какую нужно внести поправку, не разрушая при этом логический кубит, — какой из физических кубитов (первый, второй или третий) следует заставить совершить обратный кульбит. «По мне, квантовая коррекция ошибок сродни волшебству», — говорит Альмхеири.

Кубиты, основные элементы квантовых компьютеров, способны одновременно пребывать в нескольких состояниях, но при этом склонны ошибаться. Квантовый код, исправляющий эти ошибки, выявляет их и вносит соответствующие поправки, не разрушая «суперпозицию» состояний, необходимую для квантовых вычислений.
Наиболее эффективные коды, исправляющие ошибки, способны восстановить всю закодированную информацию даже тогда, когда повреждена почти половина физических кубитов. В 2014 году этот факт навёл Альмхеири, Дуна и Харлоу на мысль, что квантовая коррекция ошибок может иметь отношение к тому, как из квантовой запутанности возникает антидеситтеровское пространство-время.
Важно отметить, что у пространства AdS и пространства-времени нашей «деситтеровской» вселенной разная геометрия. Если положительная вакуумная энергия, которая пронизывает нашу вселенную, вынуждает её бесконечно расширяться, то отрицательная вакуумная энергия антидеситтеровского пространства, напротив, делает его геометрию гиперболической — такой, как на одной из композиций М. К. Эшера (нидерл. Maurits Cornelis Escher) из серии Circle Limit. Мозаичные существа Эшера по мере удаления от центра круга становятся всё меньше и меньше и, в конце концов, исчезают на его границе; аналогично, пространственное измерение, которое излучает центр пространства AdS, постепенно сжимается и в конечном итоге исчезает, образуя внешнюю границу вселенной. Пространство AdS приобрело популярность в теории квантовой гравитации после того, как в 1997 году известный физик Хуан Малдасена (Juan Maldacena) обнаружил, что, согласно квантовой теории, искривлённая пространственно-временная ткань в своём интерьере «голографически дуальна» по отношению к частицам, живущим на безгравитационной границе с меньшей мерностью.

Изучая, как и сотни других физиков за последние два десятилетия, особенности функционирования этой дуальности, Альмхеири и его коллеги заметили, что любую точку интерьера пространства AdS можно построить на основе частиц, занимающих чуть больше половины границы этого мира — как и в случае эффективного квантового кода, исправляющего ошибки.
В своей статье эти учёные, предполагая, что голографическое пространство-время и квантовая коррекция ошибок — одно и то же, описали, как даже простой код можно представить в виде двухмерной голограммы. Такой код состоит из трёх «кутритов» — частиц, способных пребывать в любом из трёх состояний. Кутриты занимают равноудалённые точки на границе круга и, составляя вместе запутанное трио, кодируют один логический кутрит, соответствующий одной-единственной точке пространства-времени, находящейся в центре круга. Код защищает данную точку при выходе из строя любого из трёх кутритов.
Конечно, одна-единственная точка — весьма скромная вселенная. В 2015 году Харлоу, Прескилл, Фернандо Паставски (Fernando Pastawski) и Бени Ёсида (Beni Yoshida) описали ещё один голографический код, получивший прозвище «HaPPY». В нём свойства пространства AdS представлены шире. Код HaPPY использует для построения пространства пятиугольные кирпичики, напоминающие детали детского конструктора «Tinkertoy», — «тинкертойчики», как выразился Патрик Хейден (Patrick Hayden) из Стэнфордского университета (Stanford University), ведущего учебного заведения в данной области исследований. Каждый тинкертойчик репрезентирует одну точку пространства-времени. «В мозаике Эшера эти кирпичики играли бы роль рыб», — говорит Хейден.
В коде HaPPY и других известных ныне голографических схемах исправления ошибок всё, что находится внутри некоторой части интерьера пространства-времени, называемой «клином запутанности» (entanglement wedge), восстановимо с помощью кубитов соответствующего участка границы. По словам Хейдена, перекрывающиеся клинья запутанности можно воспроизводить перекрывающимися участками границы так же, как логический кубит квантового компьютера воспроизводим посредством многих подмножеств физических кубитов. «Именно здесь проявляется способность исправлять ошибки».
«Квантовая коррекция ошибок даёт нам более общий взгляд на геометрию, соответствующую данному кодовому языку», — заявляет Прескилл. Этот же язык, считает калифорнийский физик, «должен иметь более широкое применение». В частности, его следует применять к деситтеровской вселенной, подобной нашей. Но безграничное пространство де Ситтера (нидерл. Willem de Sitter) всё ещё не удаётся осмыслить как голограмму.
Пока что такие исследователи, как Альмхеири, Харлоу и Хейден, работают с пространством AdS, у которого много существенных свойств деситтеровского мира и которое легче исследовать. В обоих случаях пространственно-временная геометрия подчиняется теории Эйнштейна, просто разное искривление. И, что, возможно, важнее всего, оба вида вселенных содержат чёрные дыры. «Самым фундаментальным свойством гравитации является существование чёрных дыр», — утверждает Харлоу, который в настоящее время является доцентом кафедры физики в Массачусетском технологическом институте (Massachusetts Institute of Technology). — Это то, что отличает силу тяжести от всех других сил и делает трудной для понимания квантовую гравитацию».
Язык квантовой коррекции ошибок предоставил физикам новый способ описания чёрных дыр. По словам Хейдена, присутствие чёрной дыры определяется «крахом корректности»: «Когда так много ошибок, что вы теряете способность отслеживать, что происходит в данном объёме [пространстве-времени], вы получаете чёрную дыру. Это вроде клоаки для вашего невежества».
Невежество неизменно зашкаливает при попытках осмыслить интерьер чёрной дыры. В 1974 году на Стивена Хокинга (Stephen Hawking) снизошло прозрение, согласно которому чёрные дыры излучают тепло и, стало быть, в конечном итоге испаряются. В результате возник печально известный «информационный парадокс чёрных дыр», вынуждающий искать ответа на вопрос, что происходит с информацией, поглощённой чёрными дырами. Квантовая теория гравитации должна помочь физикам выяснить, как то, что попадает в чёрную дыру, ещё и выходит оттуда. Эта проблема может быть связана с космологией и рождением вселенной, поскольку расширение из сингулярности при Большом взрыве очень похоже на процесс, противоположный гравитационному коллапсу, происходящему при падении в чёрную дыру.
Пространство AdS делает более простым объяснение информационного парадокса. То, что граница вселенной AdS голографически дуальна по отношению к интерьеру этого мира, — к чёрным дырам и всему остальному, — гарантирует сохранность информации, попавшей в чёрную дыру: ведь граница вселенной всегда голографически кодирует эту информацию. Согласно расчётам, для реконструкции данных об интерьере чёрной дыры необходим доступ к запутанным кубитам границы на её участке, протяжённость которого составляет примерно три четверти всей её длины. «Чуть больше половины здесь уже недостаточно», — отмечает Альмхеири. Потребность в трёх четвертях, добавляет он, по-видимому, говорит о квантовой гравитации что-то важное, но почему нужна именно такая часть границы, «до сих пор непонятно».
В 2012 году Альмхеири впервые сделал заявку на мировую известность: этот высокий худощавый физик из Эмиратов и три его помощника углубили информационный парадокс. Они предположили, что можно предотвратить поглощение информации чёрной дырой, и здесь, в первую очередь, следует использовать «файрвол» на горизонте событий данного объекта.
Как и большинство физиков, Альмхеири не очень-то верит в существование файрволов чёрных дыр. Однако оказалось, что обойтись без них очень трудно. Теперь исследователь считает, что формированию файрволов мешает квантовая коррекция ошибок, которая защищает информацию даже в тех случаях, когда она пересекает горизонты чёрных дыр. Как заявляет Альмхеири в своей последней, сольной работе, опубликованной в октябре, квантовая коррекция ошибок «необходима для поддержания гладкости пространства-времени на горизонте» двухустной (two-mouthed) чёрной дыры, именуемой червоточиной. Согласно предположению принстонского исследователя, квантовая коррекция ошибок, как и предотвращение ею формирования файрволов, объясняет, каким образом кубиты, попавшие в чёрную дыру, выходят из неё по нитям запутанности между внутренней и внешней сторонами, которые сами похожи на миниатюрные червоточины. Это разрешило бы парадокс Хокинга.
В наступившем году министерство обороны США финансирует исследования голографического пространства-времени — по меньшей мере отчасти потому, что побочным результатом успешного продвижения на этом направлении научной деятельности может стать появление более эффективных кодов, исправляющих ошибки квантовых компьютеров.
Что касается физиков, то они всё ещё пытаются выяснить, можно ли описывать вселенные де Ситтера, в том числе и нашу, голографически, в терминах кубитов и кодов. «Всё, что мы знаем о скрепах мира, явно не является знанием о нашем мире», — подчёркивает Ааронсон. В статье, опубликованной прошлым летом, Дун, ныне сотрудник Калифорнийского университета в Санта-Барбаре (University of California, Santa Barbara), и его соавторы Ева Сильверстайн (Eva Silverstein) и Гонсало Торроба (Gonzalo Torroba) сделали шаг в направлении вселенной де Ситтера, попытавшись дать её простейшее голографическое описание. Физики-теоретики всё ещё изучают эту попытку, однако, по мнению Прескилла, язык квантовой коррекции ошибок, в конце концов, утвердится в сфере исследования реального пространства-времени.
«То, что скрепляет пространство, — это не что иное, как запутанность, — убеждён он. — Если вы хотите сплести пространство-время из маленьких нитей, вы должны правильно их запутать. А чтобы это получилось правильно, нужно создать квантовый код, исправляющий ошибки».
Рис. 4. Сравнение временных затрат Рис. 5. Сравнение критерия адекватности
Анализ результатов эксперимента показывает, что применение предварительной ориентации контуров сокращает время последующей деформации и приближает значения критерия адекватности к его максимальному значению. В рамках дальнейших исследований планируется модифицировать процедуру предварительной ориентации применительно к сплайновому представлению контуров и представления трехмерных объектов как сплошных тел.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. McInerney T., Terzopoulos D. Deformable Models in Medical Image Analysis: A Survey. Medical Image Analysis, 1996, 1(2):91-108
2. Christopher Lee. Wyatt Extending the geometric deformable model for use in medical image analysis. PhD dissertation, Wake forest university, 2000. — 56 p.
3. Бабков В.С. Застосування методу “деформованих моделей“ для реконструкції органів в КТ за умови обмеженої кількості вхідної інформації. Вісник Житомирського інженерно-технологічного інституту. Спеціальний випуск за матеріалами Міжнародної науково-технічної конференції “ІКТ-2002”. — 207-214 сс
4. Samuel D. Fenster Training, Evaluation and Local Adaptation in Deformable Models. PhD dissertation, Columbia university, 2000. — 91 p.
С. М. Гушанский, Р. А. Погорелов КВАНТОВЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОШИБКИ
Практическая реализация квантовых вычислений в настоящее время ограничена рядом проблем, среди которых следует выделить погрешность измерения состояния квантовой системы, нестабильность квантовых состояний вследствие декогерентности. Невозможность полной изоляции кубитов приводит к возникновению в них разнотипных ошибок (битовых, фазовых, битофазовых). Поэтому столь актуальным сейчас является создание эффективных методов квантовой коррекции. Использование квантовых кодов коррекции ошибок позволяет бороться с декогерентностью, восстанавливая квантовые состояния, уменьшая одновременно погрешность измерений.
В силу специфики пространства состояний кубита, считается, что его взаимодействие с окружающей средой может привести к ошибке одного из трех возможных типов [1]:
1) битовые ошибки, приводящие к перебросу кубита |0 ® Ц, Ц ® |0. Их иначе еще называют X — ошибками, так как их можно представить, как результат произведения матрицы Паули Ух и вектора состояния кубита;
2) фазовые ошибки, приводящие к перевороту фазы кубита |0 ® |0,
1 ® _| 1. Их называют Z — ошибками (соответствующая матрица Паули У г);
3) смешанные битофазовые ошибки, приводящие одновременно и к перебросу кубита и перевороту фазы |0 ® Ц, Ц ®-|0 . Их называют Y — ошибками
(соответствующая матрица Паули Уу ).
Таким образом, принимая во внимание факт, что взаимодействие с окружающей средой может и не повлиять на квантовое состояние, любую квантовую ошибку в единичном кубите можно представить в виде линейной комбинации всех видов ошибок. Если через у обозначить произвольное состояние единичного
кубита, то возникновение ошибки можно представить следующей схемой [2]:
у) ® (e1I + e2X + ^ + е4Z)|у) = ^eiEi у) ,
i
где I — единичная матрица (отсутствие ошибки), X, Y, 2 — соответствуют, как уже было сказано, матрицам Паули Уг, Уу , Уг. е1…е4 — некоторые коэффициенты, в
общем случае комплексные, Е{ — общее обозначение матриц элементарных преобразований.
Понятно, что процесс появления ошибок вследствие декогерентности может протекать с разной интенсивностью. Сделаем ряд важных предположений, жестко регламентирующий круг ошибок, с которыми можно бороться, используя квантовые коды коррекции:
— воздействие окружающей среды на квантовую систему будем считать ограниченным. То есть существует такое конечное время Д/, в течение которого вероятность, что ошибка появится в двух или более кубитах, бесконечно мала.
— все ошибки будем считать слабокоррелированными. Это означает, что ошибка, возникающая в одном кубите, не влияет на состояние другого.
— будем полагать, что все ошибки носят случайный характер, т.е. отсутствуют так называемые систематические ошибки.
Если возникающие ошибки удовлетворяют этим условиям, то для их обнаружения и устранения возможно использование квантовых кодов коррекции.
Идея отказоустойчивых кодов заимствована из классической теории информации, однако их реализация в случае кодирования квантовых состояний заметно отличается от классической ситуации.
Пусть £ — произвольное состояние в гильбертовом пространстве М. Кодом называется изометрическое отображение V : М ® N , переводящее состояния £ в кодирующие состояния VS в гильбертовом пространстве N [3].
Квантовый код V может обнаружить возникновение ошибки, если размерность гильбертова пространства N больше размерности пространства М. Иными словами, как и в классическом случае, любой отказоустойчивый квантовый код базируется на принципе избыточного кодирования.
Пусть преобразование квантового состояния в ходе кодирования и последующего возникновения ошибки описывается следующей схемой [3]:
£ ® V£ ®Ф(V£),
где Фё Е — оператор ошибки, определенного класса Е.
Тогда код V называется кодом, исправляющим ошибки, если существует такой оператор ^, что
¥[Ф( VS)]® с (Ф) 5,
для любого Фё Е. Здесь с (Ф) — некоторая константа, зависящая от оператора
ошибки [3]. Ее называют анциллой синдрома ошибки, так как ее значение зависит только от вида ошибки и ее локализации.
Система | )
Кодирующая
0)
Рис. 1. Базовая схема построения квантовых кодов коррекции
Полученная на основании этих утверждений схема любого отказоустойчивого кода приведена на рис. 1 [4]. Здесь под кодирующей анциллой понимается совокупность кубитов, посредством которых происходит кодирование состояния квантовой системы. Процесс кодирования превращает состояние кодирующей ан-циллы в отображение состояния исходной квантовой системы. Анцилла синдрома ошибки является также ансамблем из нескольких кубитов. Она введена с целью определения типа возникшей ошибки и ее локализации. Процесс коррекции ошибок является двухступенчатым:
— посредством квантовых схем, индивидуальных для каждого кода коррекции, анализируется состояние кодирующей анциллы, в ходе чего происходит изменение состояния анциллы синдрома;
— состояние анциллы синдрома измеряется, и, в зависимости от него, с кодирующей анциллой осуществляются те или иные преобразования. Т ак как ошибка единичного кубита определяется унитарным преобразованием, то для восстановления состояния достаточно лишь повторно применить к ошибочному кубиту преобразование, вызвавшее ошибку.
По аналогии с классическим кодированием, для обозначения квантовых кодов коррекции используется обозначение вида [[п, к, ^]. Здесь п — определяет полное число кубитов кода, к — число информационных кубитов, d — называется минимальным кодовым расстоянием кода, определяется как минимальное расстояние Хемминга [5] между всеми возможными парами кодовых слов (двойные скобки отличают квантовый код от классического).
Всё многообразие квантовых кодов коррекции принято разделять на три класса [4]:
1) аддитивные стабилизирующие (симплексные) коды. Наиболее обширный класс кодов базируется на классических кодах коррекции, в связи с чем и получили наибольшее развитие. Стабилизирующие коды можно проклассифицировать по минимальному кодовому расстоянию [8]:
— класс кодов с кодовым расстоянием два. Общее обозначение [[n, n-2, 2]];
— класс кодов с кодовым расстоянием три. Общее обозначение [[2, 2-/-2, 3]];
— класс кодов с кодовым расстоянием четыре. Общее обозначение [[2, 2-2j-2, 4]].
Здесь j может принимать произвольные целые значения. Такая классификация стабилизирующих кодов не является единственной и общепринятой. Чаще можно встретиться с классификацией по виду матрицы стабилизатора кода:
• циклические коды;
• CSS — коды;
• Амплитудно-защищающие коды они же “code over GF(4)”;
2) неаддитивные коды, не являющиеся стабилизирующими;
3) каскадные или Клиффорд-коды. Вероятность ошибки для них намного ниже, чем для двух предыдущих, за что приходится платить многоуровневой структурой кода, а как следствие увеличением числа кубитов. Каскадные коды являются обобщением аддитивных стабилизирующих кодов. В классической теории кодирования они имеют себе аналог, называемый сверточными кодами.
В основе квантового помехоустойчивого кодирования лежит код Хемминга, который представляет собой код коррекции ошибки единичного бита [5]. Длина кодового слова равна 7 битам: 4 информационных бита, 3 — контрольных. Суть кодирования заключается в установке контрольных битов по определенному правилу в зависимости от информационных.
Для обнаружения ошибки в кодовом слове используется так называемая матрица проверки, имеющая вид
0 0 0 1 1 1 1
0 1 1 0 0 1 1
1 0 1 0 1 0 1
V /
Если кодовое слово представить в виде матрицы столбца, то произведение матрицы H на этот столбец даст столбец из трех бит (при умножении матриц сложение заменяется сложением по модулю два), который определяет номер переброшенного бита или говорит об отсутствии ошибки (если он нулевой).
На основе кода Хемминга рассмотрим пример несложного, но важного се-микубитового кода, предложенного Эндрю Стином. Он позволяет, ориентируясь на классическое кодирование, наглядно рассмотреть общий принцип действия квантовых кодов коррекции. Данный код позволяет кодировать пространство состояний единичного кубита, используя для этого 7 кубитов. Иными словами, мы имеем дело с отображением произвольного состояния двумерного комплексного гильбертового пространства в состояние в 128 — мерном гильбертовом пространстве. Код Стина относится к уже упомянутому классу CSS — кодов. Предполагается, что любой вид ошибки может произойти в любом из семи кубитов, но только в одном (ограниченность воздействия окружающей среды). При кодировании состояния кубита кодом Стина используют суперпозицию только тех базисных векторов 128 — мерного комплексного гильбертового пространства, которые соответствуют множеству безошибочных кодовых слов кода Хемминга. Причем, при кодировании 10 используются только комбинации с четным числом единиц, а при
кодировании Ц , наоборот, с нечетным [6].
10
2^2
X И
ееп фе Р
V
^ (10000000) + | 0001111 + 1 °110011) + | 0111100)
242
|1010101) +11011010) +|1100110) +11101001))
2у12
ойй фе Р
V
^ (11111111 +11110000) +|1001100) +11000011) +
242
+ |0101010) + |0100101 + 10011001 +10010110)
Используя такой метод кодирования можно, как и в классическом случае, определить, в каком из кубитов произошла ошибка, однако обнаруженной может быть только X — ошибка. Процесс обнаружения ошибки запишем как
ф)®) ®|ф)®| Иф) ,
‘ / I / апс I ‘ / I ‘ / апс
вектор Иф) аналогичен трехбитовому столбцу для кода Хемминга, следова-
I ‘ ‘апс
тельно, он также однозначно задает локализацию X — ошибки.
рис.2.
Определение X — ошибки для семикубитового кода Стина приведено на
+
с 1
с > с > г > о
и и и и и и Ш г л г л С л с Л
с и и и и и и и к К К Э
Рис. 2
Теперь мы можем привести квантовую схему, позволяющую обнаружить X
— ошибку в любом из семи кубитов кода (рис. 2). В схеме используются общепринятые обозначения для управляемых гейтов (точкой обозначается управляющий кубит, а кружком с крестиком — управляемый). Данная схема позволяет понять, как происходит выявление синдрома ошибки для кода Стина. Каждый кубит ан-циллы синдрома есть результат суммирования по модулю 2 определенных кубитов кода. Причем если сравнить матрицу проверки кода Хемминга и схему (рис. 2), то видно, что именно матрица проверки и определяет номера кубитов кода, суммируемых (по модулю 2) в каждом кубите анциллы.
Однако понятно, что помимо X — ошибок необходимо бороться и с 2 -ошибками (если можно будет ликвидировать оба типа этих ошибок, то У — ошибки автоматически также будут ликвидированы, так как их можно представить как результат последовательного действия первых двух). Как известно, понятия битовая и фазовая ошибки уместны лишь при введенном базисе. Смена базиса определенным образом превращает битовую ошибку в фазовую и наоборот. Преобразование, осуществляющее поворот базиса, называется преобразованием Адамара [7]
R = V2
1 1
1 -1
Преобразование Адамара переводит кодирующие состояния |о и h в
I / code I / code
новые кодирующие состояния
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
l 0^c0de 42 ^ 0code ^1 code ) ’
^ code 42 ^ ^ code ^ 1 code )
Учитывая, что преобразование Адамара унитарно, т.е. двукратное его применение переведет систему в исходное состояние, то возможная реализация схемы, позволяющей обнаружить любые ошибки в семикубитном коде Стина, будет иметь вид (рис. 3).
Определение любой ошибки для кода Стина показано на рис. 3.
е 5 ; Pi У -ч э-е
г ) v Г i г > Г
О . ) к. ) 1 ) V
— R -« »_ О А
— R -i 1- R 4
— R -t р 1
— R ч R
Г л г > г >
U J L U L U L и > л г л >
Z к ) К i—У ) L X э
|я )
I / СИ
я
Рис. 3
В предложенном варианте квантовой схемы (рис. 3) используются две ан-циллы (анцилла X — ошибки и анцилла 2 — ошибки). Так как по нашему предположению ошибка может произойти лишь в одном кубите, то возможно 4 исхода обнаружения ошибки:
1) обе анциллы нулевые: ошибки не произошло;
2) анциллаX нулевая, а анцилла 2 нет: произошла 2 — ошибка в кубите, чей номер содержится в анцилле 2;
3) анцилла 2 нулевая, а анцилла X нет: произошла X — ошибка в кубите, чей номер содержится в анцилле X;
4) обе анциллы ненулевые и содержат одно и то же значение: произошла У
— ошибка в кубите, чей номер содержится в анцилле X и 2.
Если установлен тип ошибки и ее локализация, то процесс коррекции заключается лишь в применении к ошибочному кубиту соответствующего преобразования: X, У, или 2.
Рассмотрим процесс обнаружения ошибки на примере. Пусть имеется исходное состояние единичного кубита:
И-tjI»)+$!>>•
тогда закодированное состояние, согласно правилам кодирования кода Стина, будет иметь вид
1 ¡2 1
И cd — ^1°) code + ^l1) code — ^ (I 0000000) + l 0001111) + l 0110011) + l O1111O0 +
+ | 1010101 +11011010 +11100110 + (1101001) ) + —U (11111111 +11110000 +11001100) +
2V3
+ | 1000011 + 10101010 + | 0100101 + 10011001 + 10010110 )
Предположим, что ошибка представляет собой просто X — преобразование, примененное к третьему кубиту кода, т.е. оператор ошибки равен
Ф = IÄIÄ X ÄIÄIÄIÄI,
тогда в результате ошибки закодированное состояние примет вид
ф|у)^ — -V (10010000) + | 0011111 + | 0100011 + | 0101100) +11000101 +11001010) +
co e 2V6
+ (1110110 + (1111001) + ~Г» (11101111 + (1100000 + (1011100 + (1010011 + 10111010 + 2V3 + |0110101 + 10001001 + 10000110)
обозначим состояние анциллы синдрома как (ccc), первоначально c1 — c2 — c3 — 0. Осуществив преобразования, согласно схеме (рис. 3), получим для нашего случая
c1 — x4 @ x5 @ x6 @ x7 — 0
c2 — x2 @ x3 @ x6 @ x7 -1 ■
c3 — x1 @ x3 @ x5 @ x7 -1
Видно, что состояние анциллы синдрома |011) однозначно указывает на X
— ошибку в третьем кубите. Для ее устранения достаточно лишь повторно применить оператор ошибки Ф к закодированному состоянию.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Стин Э. Квантовые вычисления. —Москва-Ижевск: РХД, 2000.
2. Рифель Е. Полак В. Основы квантовых вычислений.
3. ХолевоА. С. Введение в квантовую теорию информации. —Москва: МЦНМО, 2002. — 128 с.
4. GrassM. Quantum Error-Correcting Codes.
5. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ.- Москва: Мир, 1986.
6. Preskill J. Fault-Tolerant Quantum Computation. arXiv:quant-ph/9712048 v1 19 Dec 1997.
7. Steane A. M. Error correcting codes in quantum theory, Phys. Rev. Lett. 77, 793 1996.
8. Gottesman D. Stabilizer Codes and Quantum Error Correction. arXiv:quant-ph/9705052 v1 28 May 1997.
Quantum Error Correction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
7.3.6 Distance Properties of Quantum Error Correction Codes
A QECC is defined by the encoding operation of mapping K qubits into N qubits. The QECC [N,K] can be interpreted as a 2K-dimensional subspace Cq of N-qubit Hilbert space HN2, together with corresponding recovery operation R. As mentioned above, this subspace (Cq) is called the code space, the kets belonging to Cq are known as codewords, and the encoded computational basis kets are called the basis codewords. The basis for single-qubit errors is given by {I,X,Y,Z}, as described above. Because any error, be either discrete or continuous, can be represented as a linear combination of base errors, the linear combination of correctable errors will also be a correctable error. The basis for N-qubit quantum errors is obtained by forming all possible direct products:
(7.42)E=jlO1⊗…⊗ON=jl′X(a)Z(b);a=a1…aN;b=b1⋯bN;ai,bi=0,1;l,l′=0,1,2,3X(a)≡X1a1⊗…⊗XNaN;Z(b)≡Z1b1⊗…⊗ZNbN;Oi∈{I,X,Y,Z}.
The weight of an error operator E(a,b) is defined to be the number of qubits different from the identity operator. Necessary and sufficient conditions for a quantum error correction code to correct a set of errors E = {Ep}, given by Eq. (7.41), can be consolidated as follows:
(7.43)〈i¯|Ep†Eq|j¯〉=Cpqδi¯j¯,
where the matrix elements Cpq satisfy the condition Cpq = Cqp∗, so that the square matrix C = (Cpq) is Hermitian. A QECC for which matrix C is singular is said to be degenerate. If we interpret Ep†Eq as a new error operator E, Eq. (7.43) can be rewritten as
(7.44)〈i¯|E|j¯〉=CEδi¯j¯.
We say that a QECC has a distance D if all errors of weight less than D satisfy Eq. (7.44), and there exists at least one error of weight D to violate it. In other words, the distance of QECC is the weight of the smallest weight D of error E that cannot be detected by the code. Similarly to classical codes, we can relate the distance D to the error correction capability t as follows: D ≥ 2t + 1. Namely, since E=Ep†Eq the weight of error operator E will be wt(Ep†Eq)=2t. If we are only interested in detecting errors but not correcting them, the error detection capability d is related to the distance D by D ≥ d + 1. Since we are interested only in detection of errors we can set Ep = I to obtain wt(Ep†Eq)=wt(Eq)=d. If we are interested in simultaneously detecting d errors and correcting t errors, the distance of the code must be D ≥ d + t + 1. The following theorem can be used to determine if a given quantum code Cq of quantum distance D is degenerate or not.
Theorem 7.4. The quantum code Cq of distance D is a degenerate code if and only if its stabilizer S contains an element with weight less than D (excluding the identity element).
The theorem can be proved as follows. If the code Cq is a degenerate code of distance D, there will exist two correctable errors E1, E2 such that their action on a CB codeword is the same: E1|i¯〉=E2|i¯〉. By multiplying by E2† from the left we obtain E2†E1|i¯〉=|i¯〉, which indicates that the error E2†E1∈S. Since any correctable error satisfies 〈i¯|E|j¯〉=CEδi¯j¯, we obtain 〈i¯|E2†E1|j¯〉=C12δi¯j¯. Because the Cq code has a distance D it is clear that wt(E2†E1)<D. On the other hand, if there exists an s ∈ S with wt(s) < D, we can find another sa ∈ S so that sas = sb ∈ S. By multiplying both sides by sa†, we obtain s=sa†sb. From the definition of stabilizer codes we know that s|i¯〉=|i¯〉,∀s∈S. By expressing s=sa†sb, we obtain sa†sb|i¯〉=|i¯〉, which by multiplying by sa from the left becomes sb|i¯〉=sa|i¯〉, which is equivalent to (sa−sb)|i¯〉=0. Since the matrix Sab is singular, the code Cq is degenerate.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000071
Entanglement-Assisted Quantum Error Correction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
9.7 Summary
This chapter has considered entanglement-assisted quantum error correction codes, which use pre-existing entanglement between transmitter and receiver to improve the reliability of transmission. A key advantage of EA quantum codes compared to CSS codes is that EA quantum codes do not impose the dual-containing constraint. Therefore, arbitrary classical codes can be used to design EA quantum codes. The number of required ebits has been determined by e = rank(HHT), where H is the parity-check matrix of the corresponding classical code. A general description of entanglement-assisted quantum error correction was provided in Section 9.1. In Section 9.2, we studied entanglement-assisted canonical code and its error correction capability. In Section 9.3, the concept of EA canonical code to arbitrary EA code was generalized. We also described how to design EA codes from classical codes, in particular classical quaternary codes. In Section 9.4, encoding for EA quantum codes was discussed. In Section 9.5, the concept of operator quantum error correction, also known as subsystem codes, was introduced. Entanglement-assisted operator quantum error correction was discussed in Section 9.6.
In the following section, we provide a set of problems that will help the reader gain better understanding of the material in this chapter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000095
Introduction to Quantum Information Processing
Shikhar Uttam, in Quantum Information Processing and Quantum Error Correction, 2012
4.7 Conclusion
In this chapter the key ideas and concepts that lie at the heart of information processing tasks and quantum mechanics in general have been introduced. We have presented the quantum idea of superposition of states and how it leads to quantum parallelism, the no-cloning theorem and our inability to reliably distinguish non-orthogonal quantum states. The mathematical formalism and the physical idea behind quantum entanglement have also been presented. The reader will see that all these concepts resurface in all later chapters as they underpin the algorithms and protocols discussed therein. The operator-sum representation is also crucial for understanding communication over quantum channels. We have discussed some of these quantum channels here. They will arise again in later chapters when quantum error correction codes are discussed.
This introductory chapter is by no means a thorough examination of the concepts that lie herein. In fact, we have barely scratched the surface. But the ideas outlined here are crucial to understanding the rest of this book. If the reader is interested in delving into the details of each individual topic, we would encourage the reader to consult the references. References [1–5] are seminal works on information theory both from Shannon’s probabilistic/statistical point of view [1–3] and Kolmogorov’s complexity point of view [3,5]. Landauer’s important work [4] provides an important connection between classic physics, information theory, and reversible and irreversible computation. References [6–8] detail Alan Turing’s groundbreaking work that founded the field of computer science. References [9–17] list a series of papers that established the theoretical foundations of quantum mechanics. Reference [18] is J. J. Sakurai’s eloquent exposition of the field of quantum mechanics. The jump from quantum mechanics to quantum computation began when Feynman proposed the idea of a quantum computer in his keynote address in 1981 at the California Institute of Technology [19]. References [21–25] are papers that discuss, for the first time, the practical feasibility of quantum computing.
Finally, Refs [26–31] present the fundamental debate regarding nonlocal interactions and qubit entanglement and how it was settled, thereby establishing quantum mechanics as a legitimate physical theory. Quantum entanglement is a complex field and the subject of current research. Reference [32] discusses the various aspects of quantum entanglement.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000046
Introduction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
1.6 Quantum Error Correction Concepts
The QIP relies on delicate superposition states, which are sensitive to interactions with the environment, resulting in decoherence. Moreover, the quantum gates are imperfect and the use of quantum error correction coding (QECC) is necessary to enable fault-tolerant computing and to deal with quantum errors [18–23]. QECC is also essential in quantum communication and quantum teleportation applications. The elements of quantum error correction codes are shown in Figure 1.12a. The (N,K) QECC code performs encoding of the quantum state of K qubits, specified by 2K complex coefficients αs, into a quantum state of N qubits, in such a way that errors can be detected and corrected, and all 2K complex coefficients can be perfectly restored, up to the global phase shift. This means that, from quantum mechanics (see Chapter 2), we know that two states |ψ〉 and ejθ|ψ〉 are equal up to a global phase shift as the results of measurement on both states are the same. A quantum error correction consists of four major steps: encoding, error detection, error recovery, and decoding. The sender (Alice) encodes quantum information in state |ψ〉 with the help of local ancillary qubits |0〉, and then sends the encoded qubits over a noisy quantum channel (say, a free-space optical channel or optical fiber). The receiver (Bob) performs multi-qubit measurement on all qubits to diagnose the channel error and performs a recovery unitary operation R to reverse the action of the channel. Quantum error correction is essentially more complicated than classical error correction. The difficulties in quantum error correction can be summarized as follows: (i) the no-cloning theorem indicates that it is impossible to make a copy of an arbitrary quantum state; (ii) quantum errors are continuous and a qubit can be in any superposition of the two bases states; and (iii) the measurements destroy the quantum information. The quantum error correction principles will be more evident after a simple example given below.

FIGURE 1.12. (a) Quantum error-correction principle. (b) The bit-flipping quantum channel model. (c) Three-qubit flip-error correction code encoder.
Assume we want to send a single qubit |ψ〉 = α|0〉 + β|1〉 through the quantum channel in which during transmission the transmitted qubit can be flipped to X|ψ〉 = β|0〉 + α|1〉 with probability p. Such a quantum channel is called a bit-flip channel and it can be described as shown in Figure 1.12b. The three-qubit flip code sends the same qubit three times, and therefore represents the repetition code equivalent. The corresponding codewords in this code are |0¯〉=|000〉 and |1¯〉=|111〉. The three-qubit flip-code encoder is shown in Figure 1.12c. One input qubit and two ancillaries are used at the input encoder, which can be represented by |ψ123〉=α|000〉+β|100〉. The first ancillary qubit (the second qubit at the encoder input) is controlled by the information qubit (the first qubit at encoder input) so that its output can be represented by CNOT12(α|000〉+β|100〉)=α|000〉+β|110〉 (if the control qubit is |1〉 the target qubit gets flipped, otherwise it stays unchanged). The output of the first CNOT gate is used as input to the second CNOT gate in which the second ancillary qubit (the third qubit) is controlled by the information qubit (the first qubit), so that the corresponding encoder output is obtained as CNOT13(α|000〉+β|110〉)=α|000〉+β|111〉, which indicates that basis codewords are indeed |0¯〉 and |1¯〉. With this code, we are able to correct a single qubit-flip error, which occurs with probability (1 − p)3 + 3p(1 − p)2 = 1 − 3p2 + 2p3. Therefore, the probability of an error remaining uncorrected or wrongly corrected with this code is 3p2 − 2p3. It is clear from Figure 1.12c that the three-qubit flip-code encoder is a systematic encoder in which the information qubit is unchanged, and the ancillary qubits are used to impose the encoding operation and create the parity qubits (the output qubits 2 and 3).
Let us assume that a qubit flip occurred on the first qubit, leading to received quantum word |ψr〉 = α|100〉 + β|011〉. In order to identify the error it is necessary to perform the measurements on the observables Z1Z2 and Z2Z3, where the subscript denotes the index of qubit on which a given Pauli gate is applied. The result of the measurement is the eigenvalue ±1, and corresponding eigenvectors are two valid codewords, namely |000〉 and |111〉. The observables can be represented as follows:
(1.62)Z1Z2=(|00〉〈11|+|11〉〈11|)⊗I−(|01〉〈01|+|10〉〈10|)⊗IZ2Z3=I⊗(|00〉〈11|+|11〉〈11|)−I⊗(|01〉〈01|+|10〉〈10|).
It can be shown that 〈ψr|Z1Z2|ψr〉=−1,〈ψr|Z2Z3|ψr〉=+1, indicating that an error occurred on either the first or second qubit, but not on the second or third qubit. The intersection reveals that the first qubit was in error. By using this approach we can create the three-qubit look-up table (LUT), given in Table 1.1.
Table 1.1. The three-qubit flip-code LUT
| Z1Z2 | Z2Z3 | Error |
|---|---|---|
| +1 | +1 | I |
| +1 | −1 | X3 |
| −1 | +1 | X1 |
| −1 | −1 | X2 |
Three-qubit flip-code error detection and error correction circuits are shown in Figure 1.13. The results of measurements on ancillaries (see Figure 1.13a) will determine the error syndrome [±1 ±1], and based on the LUT given in Table 1.1, we identify the error event and apply the corresponding Xi gate on the ith qubit being in error, and the error is corrected since X2 = I. The control logic operation is described in Table 1.1. For example, if both outputs of the measurements circuits are −1, the operator X2 is activated. The last step is to perform decoding as shown in Figure 1.13b by simply reversing the order of elements in the corresponding encoder.

FIGURE 1.13. (a) Three-qubit flip-code error detection and error correction circuit. (b) Decoder circuit configuration.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000010
Quantum control of bosonic modes with superconducting circuits
Wen-Long Ma, … Liang Jiang, in Science Bulletin, 2021
1 Introduction
Quantum computation holds the promise of solving some specific problems, such as factorization of large integers and simulation of quantum many-body problems [1], much faster than any known classical computer. To build such a quantum computer, the physical platform should work in the quantum regime with long coherence time, fast quantum operations and good scalability, which are daunting obstacles for current technologies. The promising strategies to overcome such obstacles are quantum error correction (QEC) [2–4] and fault-tolerant (FT) quantum computation [5], where the coherence time of the quantum memories can be extended and the quantum operations can tolerate some low-probability errors (including errors in the QEC circuit) below a certain threshold.
In the prototypical model for quantum computation – the quantum circuit model, a quantum bit of information (qubit) is encoded into a two-level system, called a physical qubit, and the usual approach for QEC is to encode a logical qubit into some subspace of multiple physical qubits, so that different error processes lead to distinguishable syndromes and can therefore be corrected. However, the increased number of physical qubits for a logical qubit introduces more decoherence for the system to correct. Moreover, the logical gate operations become quite complicated since multiple physical systems need to be addressed simultaneously. Hence, it is still an outstanding experimental challenge to build a more robust quantum register using multiple physical qubits.
An alternative scheme is to encode the quantum information into bosonic modes such as harmonic oscillators [6,7]. A single bosonic mode already provides an infinitely large Hilbert space, from which we choose a logical subspace for an error-correcting code [8–13]. Such bosonic QEC modes can be hardware-efficient compared to the conventional QEC codes based on multiple qubits. Moreover, the bosonic modes often have relatively simple decoherece processes (mainly bosonic excitation loss channel) during which the bosonic excitations are lost one by one [14]. There have been several error-correcting encoding schemes in a single bosonic mode proposed to date, including the Gottesman-Kitaev-Preskill (GKP) codes [10,15,16], cat codes [11,17,18], binomial codes [12], rotation-symmetric codes [19] and other variations [13,20]. The GKP codes, consisting of superpositions of highly squeezed states, are not only protected against small shifts in position but also have been shown to perform well against the more realistic amplitude damping channel [13]. The cat codes use superpositions of coherent states evenly distributed around a circle in phase space, which can be protected against (single or multiple) bosonic excitation loss and dephasing errors. The binomial codes exploit superpositions of Fock states weighted with binomial coefficients, which can exactly correct the bosonic excitation loss, gain and dephasing errors up to a specific degree.
For bosonic modes, the standard operations (e.g., displacement operation, phase rotation, one-mode squeezing, beam splitting, and two-mode squeezing) are all Gaussian operations, which can only transform Gaussian states into Gaussian states [6,21]. However, universal control of a single bosonic mode can be achieved by adding a single nonlinear operation [21]. When such a direct nonlinear operation is difficult to realize directly, it is still possible to implement an indirect nonlinear interaction by coupling the bosonic mode to a finite-level ancilla. Moreover, quantum non-demolition (QND) measurement of the ancilla enables measurement-based feedback control and therefore arbitrary operation on the bosonic mode. Here, we will review recent advances in the approaches for universal control and arbitrary operation of bosonic modes (Table 1), including unitary control, quantum feedback control, driven-dissipative control and holonomic control (Fig. 1a). In the first two approaches, an ancilla qubit is coupled to a single bosonic mode to introduce nonlinear interaction and feedback control, while in the remaining two approaches, a special coupling between the bosonic mode and reservoir or a special Hamiltonian of the bosonic mode is engineered to support some stabilized manifold, consisting of all coherent superpositions of multiple steady states that are free of any nonunitary effect caused by the reservoir.
Table 1. Recent theoretical and experimental advances in quantum control of bosonic modes in circuit QED.
| Unitary control | Unitary & feedback | Unitary & dissipation |
|---|---|---|
| Ancilla-induced nonlinearity | Quantum adaptive control | Quantum Zeno dynamics |
| Theory: — SNAP gate [22] — Optimal control [23,24] — E-SWAP gate [25] — CPHASE gate [26] |
Theory: — CPTP maps [27] — Teleported gate [28] — ET gate [29,30] — PI gate [31] |
Theory: — Dissipative cat [32] — Kerr cat [33] — FT syndrome detection [34] — Bias-preserving Kerr cat [35] — Bias-preserving dissipative cat [36] — Holonomic gatea [37] |
| Experiments: — SNAP gate [38] — Optimal control [23] — CNOT gate [39] — CZ gate [40] — E-SWAP gate [41] |
Experiments: — QEC [42–44] — CPTP simulation [45,46] — Teleported CNOT gate [47] — FT parity measurement [48] — PI SNAP gate [49] — ET phase gate [50] |
Experiments: — Dissipative cat [51–53] — Kerr cat [54] |
- a
- This scheme uses only dissipation.

Fig. 1. (Color online) (a) Schematic of various approaches for controlling a quantum system: (i) unitary control on the system alone or both the system and an ancilla; (ii) quantum feedback control based on measurement of the ancilla; (iii) driven-dissipative control with either engineered dissipation or Hamiltonian engineering; (iv) holonomic quantum control based on only engineered dissipation. (b), (c) Schematic and device photograph of a circuit QED system modeled as a coupled qubit-oscillator system. The storage cavity with long coherence time is used to encode quantum information, the transmon qubit acts as an ancilla for universal control of the storage cavity, and the readout cavity with short coherence time is used for qubit readout. Both the storage cavity and transmon qubit can be addressed by microwave control fields. Reprinted with permission from Refs. [27,55].
The physical platform we consider is circuit quantum electrodynamics (circuit QED) [14,56–61], which is an analog of cavity QED [62] using superconducting circuits [63,64]. Cavity QED engineers the environment of the atoms by placing them in a cavity that supports only discrete bosonic modes of the electromagnetic field. Examples of cavity QED systems include alkali atoms in optical cavities [65] and Rydberg atoms in microwave cavities [66]. Circuit QED uses superconducting qubits as artificial atoms coupled to microwave resonators. A key advantage of circuit QED is the extremely strong coupling between the superconducting qubits and the cavity. Corresponding to the two encoding schemes based on qubits or bosonic modes, there are two main routes in superconducting quantum computing with circuit QED.
Qubits can be encoded into the first two levels of superconducting artificial atoms, such as the most widely used transmons [67–69], while the cavity resonators are used for qubit readout. Arbitrary single qubit rotations can be realized with resonant voltage drives at the qubit frequencies [56,70], and gate errors can be reduced below 10-3 by pulse shaping techniques [71,72]. Two-qubit gates can be realized by either capacitive coupling [71] or using the resonator as a mediator [56,70,73], with current error rates being less than one percent [74,75]. Recent experimental developments include implementations of quantum search algorithms [76], quantum teleportation [77], simulations of topological transitions [78], digitized adiabatic quantum computing [79], variational quantum algorithms [80], supervised learning with quantum-enhanced feature spaces [81], quantum reservoir engineering [82], quantum walks [83], advances towards quantum error correction [84–87], building cloud-based devices and demonstrating quantum supremacy with several tens of qubits [88].
Alternatively, a storage cavity resonator as a bosonic mode with long coherence time can encode the quantum information, while the transmon qubits can act as ancillas to aid universal control of the storage cavity (Fig. 1b, c). Such an encoding scheme can make use of various bosonic QEC codes, which are hardware-efficient compared to more standard qubit-based codes such as surface codes. Moreover, bosonic QEC codes often have specific noise resilience [36], and therefore can be concatenated with conventional QEC codes to reduce the hardware overhead [36,89,90]. Recently there has been significant experimental progress in bosonic QEC. QEC based on cat codes or binomial codes in superconducting cavities have reached or approached the break-even point [42,43], at which the lifetime of the logical qubit exceeds that of the single best physical qubit within the logical qubit. The encoding based on GKP codes has also been demonstrated in trapped-ion mechanical oscillators [91,92] and superconducting cavities [44]. However, compared to conventional one-qubit and two-qubit control, universal control of single and multiple bosonic modes requires the introduction of nonlinearity and therefore is more complex. This will be the main topic of this review.
This review is organized as follows. In Section 2, we review the universal control of a single bosonic mode with the aid of an ancilla qubit dispersively coupled to it. Then we introduce, in Section 3, the extension from the universal unitary control to quantum feedback control and arbitrary quantum channel construction for the bosonic mode by QND measurement of the ancilla. In Section 4, it is shown that reservoir engineering and Hamiltonian engineering can be promising strategies to realize universal quantum computation in some unitarily evolving subspace of the bosonic mode. In Section 5, the combination of reservoir engineering and holonomic quantum control is introduced to realize universal control of bosonic modes. Then in Section 6, we introduce the quantum control schemes to entangle different bosonic modes for universal quantum computation. In Section 7, we briefly summarize the review and outline some future directions for quantum control of the bosonic modes. For convenience, we take the reduced Plank constant as ℏ=1 throughout this review.
Read full article
URL:
https://www.sciencedirect.com/science/article/pii/S2095927321004011
Quantum Error Correction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
7.3.6 Distance Properties of Quantum Error Correction Codes
A QECC is defined by the encoding operation of mapping K qubits into N qubits. The QECC [N,K] can be interpreted as a 2K-dimensional subspace Cq of N-qubit Hilbert space HN2, together with corresponding recovery operation R. As mentioned above, this subspace (Cq) is called the code space, the kets belonging to Cq are known as codewords, and the encoded computational basis kets are called the basis codewords. The basis for single-qubit errors is given by {I,X,Y,Z}, as described above. Because any error, be either discrete or continuous, can be represented as a linear combination of base errors, the linear combination of correctable errors will also be a correctable error. The basis for N-qubit quantum errors is obtained by forming all possible direct products:
(7.42)E=jlO1⊗…⊗ON=jl′X(a)Z(b);a=a1…aN;b=b1⋯bN;ai,bi=0,1;l,l′=0,1,2,3X(a)≡X1a1⊗…⊗XNaN;Z(b)≡Z1b1⊗…⊗ZNbN;Oi∈{I,X,Y,Z}.
The weight of an error operator E(a,b) is defined to be the number of qubits different from the identity operator. Necessary and sufficient conditions for a quantum error correction code to correct a set of errors E = {Ep}, given by Eq. (7.41), can be consolidated as follows:
(7.43)〈i¯|Ep†Eq|j¯〉=Cpqδi¯j¯,
where the matrix elements Cpq satisfy the condition Cpq = Cqp∗, so that the square matrix C = (Cpq) is Hermitian. A QECC for which matrix C is singular is said to be degenerate. If we interpret Ep†Eq as a new error operator E, Eq. (7.43) can be rewritten as
(7.44)〈i¯|E|j¯〉=CEδi¯j¯.
We say that a QECC has a distance D if all errors of weight less than D satisfy Eq. (7.44), and there exists at least one error of weight D to violate it. In other words, the distance of QECC is the weight of the smallest weight D of error E that cannot be detected by the code. Similarly to classical codes, we can relate the distance D to the error correction capability t as follows: D ≥ 2t + 1. Namely, since E=Ep†Eq the weight of error operator E will be wt(Ep†Eq)=2t. If we are only interested in detecting errors but not correcting them, the error detection capability d is related to the distance D by D ≥ d + 1. Since we are interested only in detection of errors we can set Ep = I to obtain wt(Ep†Eq)=wt(Eq)=d. If we are interested in simultaneously detecting d errors and correcting t errors, the distance of the code must be D ≥ d + t + 1. The following theorem can be used to determine if a given quantum code Cq of quantum distance D is degenerate or not.
Theorem 7.4. The quantum code Cq of distance D is a degenerate code if and only if its stabilizer S contains an element with weight less than D (excluding the identity element).
The theorem can be proved as follows. If the code Cq is a degenerate code of distance D, there will exist two correctable errors E1, E2 such that their action on a CB codeword is the same: E1|i¯〉=E2|i¯〉. By multiplying by E2† from the left we obtain E2†E1|i¯〉=|i¯〉, which indicates that the error E2†E1∈S. Since any correctable error satisfies 〈i¯|E|j¯〉=CEδi¯j¯, we obtain 〈i¯|E2†E1|j¯〉=C12δi¯j¯. Because the Cq code has a distance D it is clear that wt(E2†E1)<D. On the other hand, if there exists an s ∈ S with wt(s) < D, we can find another sa ∈ S so that sas = sb ∈ S. By multiplying both sides by sa†, we obtain s=sa†sb. From the definition of stabilizer codes we know that s|i¯〉=|i¯〉,∀s∈S. By expressing s=sa†sb, we obtain sa†sb|i¯〉=|i¯〉, which by multiplying by sa from the left becomes sb|i¯〉=sa|i¯〉, which is equivalent to (sa−sb)|i¯〉=0. Since the matrix Sab is singular, the code Cq is degenerate.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000071
Entanglement-Assisted Quantum Error Correction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
9.7 Summary
This chapter has considered entanglement-assisted quantum error correction codes, which use pre-existing entanglement between transmitter and receiver to improve the reliability of transmission. A key advantage of EA quantum codes compared to CSS codes is that EA quantum codes do not impose the dual-containing constraint. Therefore, arbitrary classical codes can be used to design EA quantum codes. The number of required ebits has been determined by e = rank(HHT), where H is the parity-check matrix of the corresponding classical code. A general description of entanglement-assisted quantum error correction was provided in Section 9.1. In Section 9.2, we studied entanglement-assisted canonical code and its error correction capability. In Section 9.3, the concept of EA canonical code to arbitrary EA code was generalized. We also described how to design EA codes from classical codes, in particular classical quaternary codes. In Section 9.4, encoding for EA quantum codes was discussed. In Section 9.5, the concept of operator quantum error correction, also known as subsystem codes, was introduced. Entanglement-assisted operator quantum error correction was discussed in Section 9.6.
In the following section, we provide a set of problems that will help the reader gain better understanding of the material in this chapter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000095
Introduction to Quantum Information Processing
Shikhar Uttam, in Quantum Information Processing and Quantum Error Correction, 2012
4.7 Conclusion
In this chapter the key ideas and concepts that lie at the heart of information processing tasks and quantum mechanics in general have been introduced. We have presented the quantum idea of superposition of states and how it leads to quantum parallelism, the no-cloning theorem and our inability to reliably distinguish non-orthogonal quantum states. The mathematical formalism and the physical idea behind quantum entanglement have also been presented. The reader will see that all these concepts resurface in all later chapters as they underpin the algorithms and protocols discussed therein. The operator-sum representation is also crucial for understanding communication over quantum channels. We have discussed some of these quantum channels here. They will arise again in later chapters when quantum error correction codes are discussed.
This introductory chapter is by no means a thorough examination of the concepts that lie herein. In fact, we have barely scratched the surface. But the ideas outlined here are crucial to understanding the rest of this book. If the reader is interested in delving into the details of each individual topic, we would encourage the reader to consult the references. References [1–5] are seminal works on information theory both from Shannon’s probabilistic/statistical point of view [1–3] and Kolmogorov’s complexity point of view [3,5]. Landauer’s important work [4] provides an important connection between classic physics, information theory, and reversible and irreversible computation. References [6–8] detail Alan Turing’s groundbreaking work that founded the field of computer science. References [9–17] list a series of papers that established the theoretical foundations of quantum mechanics. Reference [18] is J. J. Sakurai’s eloquent exposition of the field of quantum mechanics. The jump from quantum mechanics to quantum computation began when Feynman proposed the idea of a quantum computer in his keynote address in 1981 at the California Institute of Technology [19]. References [21–25] are papers that discuss, for the first time, the practical feasibility of quantum computing.
Finally, Refs [26–31] present the fundamental debate regarding nonlocal interactions and qubit entanglement and how it was settled, thereby establishing quantum mechanics as a legitimate physical theory. Quantum entanglement is a complex field and the subject of current research. Reference [32] discusses the various aspects of quantum entanglement.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000046
Introduction
Ivan Djordjevic, in Quantum Information Processing and Quantum Error Correction, 2012
1.6 Quantum Error Correction Concepts
The QIP relies on delicate superposition states, which are sensitive to interactions with the environment, resulting in decoherence. Moreover, the quantum gates are imperfect and the use of quantum error correction coding (QECC) is necessary to enable fault-tolerant computing and to deal with quantum errors [18–23]. QECC is also essential in quantum communication and quantum teleportation applications. The elements of quantum error correction codes are shown in Figure 1.12a. The (N,K) QECC code performs encoding of the quantum state of K qubits, specified by 2K complex coefficients αs, into a quantum state of N qubits, in such a way that errors can be detected and corrected, and all 2K complex coefficients can be perfectly restored, up to the global phase shift. This means that, from quantum mechanics (see Chapter 2), we know that two states |ψ〉 and ejθ|ψ〉 are equal up to a global phase shift as the results of measurement on both states are the same. A quantum error correction consists of four major steps: encoding, error detection, error recovery, and decoding. The sender (Alice) encodes quantum information in state |ψ〉 with the help of local ancillary qubits |0〉, and then sends the encoded qubits over a noisy quantum channel (say, a free-space optical channel or optical fiber). The receiver (Bob) performs multi-qubit measurement on all qubits to diagnose the channel error and performs a recovery unitary operation R to reverse the action of the channel. Quantum error correction is essentially more complicated than classical error correction. The difficulties in quantum error correction can be summarized as follows: (i) the no-cloning theorem indicates that it is impossible to make a copy of an arbitrary quantum state; (ii) quantum errors are continuous and a qubit can be in any superposition of the two bases states; and (iii) the measurements destroy the quantum information. The quantum error correction principles will be more evident after a simple example given below.

FIGURE 1.12. (a) Quantum error-correction principle. (b) The bit-flipping quantum channel model. (c) Three-qubit flip-error correction code encoder.
Assume we want to send a single qubit |ψ〉 = α|0〉 + β|1〉 through the quantum channel in which during transmission the transmitted qubit can be flipped to X|ψ〉 = β|0〉 + α|1〉 with probability p. Such a quantum channel is called a bit-flip channel and it can be described as shown in Figure 1.12b. The three-qubit flip code sends the same qubit three times, and therefore represents the repetition code equivalent. The corresponding codewords in this code are |0¯〉=|000〉 and |1¯〉=|111〉. The three-qubit flip-code encoder is shown in Figure 1.12c. One input qubit and two ancillaries are used at the input encoder, which can be represented by |ψ123〉=α|000〉+β|100〉. The first ancillary qubit (the second qubit at the encoder input) is controlled by the information qubit (the first qubit at encoder input) so that its output can be represented by CNOT12(α|000〉+β|100〉)=α|000〉+β|110〉 (if the control qubit is |1〉 the target qubit gets flipped, otherwise it stays unchanged). The output of the first CNOT gate is used as input to the second CNOT gate in which the second ancillary qubit (the third qubit) is controlled by the information qubit (the first qubit), so that the corresponding encoder output is obtained as CNOT13(α|000〉+β|110〉)=α|000〉+β|111〉, which indicates that basis codewords are indeed |0¯〉 and |1¯〉. With this code, we are able to correct a single qubit-flip error, which occurs with probability (1 − p)3 + 3p(1 − p)2 = 1 − 3p2 + 2p3. Therefore, the probability of an error remaining uncorrected or wrongly corrected with this code is 3p2 − 2p3. It is clear from Figure 1.12c that the three-qubit flip-code encoder is a systematic encoder in which the information qubit is unchanged, and the ancillary qubits are used to impose the encoding operation and create the parity qubits (the output qubits 2 and 3).
Let us assume that a qubit flip occurred on the first qubit, leading to received quantum word |ψr〉 = α|100〉 + β|011〉. In order to identify the error it is necessary to perform the measurements on the observables Z1Z2 and Z2Z3, where the subscript denotes the index of qubit on which a given Pauli gate is applied. The result of the measurement is the eigenvalue ±1, and corresponding eigenvectors are two valid codewords, namely |000〉 and |111〉. The observables can be represented as follows:
(1.62)Z1Z2=(|00〉〈11|+|11〉〈11|)⊗I−(|01〉〈01|+|10〉〈10|)⊗IZ2Z3=I⊗(|00〉〈11|+|11〉〈11|)−I⊗(|01〉〈01|+|10〉〈10|).
It can be shown that 〈ψr|Z1Z2|ψr〉=−1,〈ψr|Z2Z3|ψr〉=+1, indicating that an error occurred on either the first or second qubit, but not on the second or third qubit. The intersection reveals that the first qubit was in error. By using this approach we can create the three-qubit look-up table (LUT), given in Table 1.1.
Table 1.1. The three-qubit flip-code LUT
| Z1Z2 | Z2Z3 | Error |
|---|---|---|
| +1 | +1 | I |
| +1 | −1 | X3 |
| −1 | +1 | X1 |
| −1 | −1 | X2 |
Three-qubit flip-code error detection and error correction circuits are shown in Figure 1.13. The results of measurements on ancillaries (see Figure 1.13a) will determine the error syndrome [±1 ±1], and based on the LUT given in Table 1.1, we identify the error event and apply the corresponding Xi gate on the ith qubit being in error, and the error is corrected since X2 = I. The control logic operation is described in Table 1.1. For example, if both outputs of the measurements circuits are −1, the operator X2 is activated. The last step is to perform decoding as shown in Figure 1.13b by simply reversing the order of elements in the corresponding encoder.

FIGURE 1.13. (a) Three-qubit flip-code error detection and error correction circuit. (b) Decoder circuit configuration.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123854919000010
Quantum control of bosonic modes with superconducting circuits
Wen-Long Ma, … Liang Jiang, in Science Bulletin, 2021
1 Introduction
Quantum computation holds the promise of solving some specific problems, such as factorization of large integers and simulation of quantum many-body problems [1], much faster than any known classical computer. To build such a quantum computer, the physical platform should work in the quantum regime with long coherence time, fast quantum operations and good scalability, which are daunting obstacles for current technologies. The promising strategies to overcome such obstacles are quantum error correction (QEC) [2–4] and fault-tolerant (FT) quantum computation [5], where the coherence time of the quantum memories can be extended and the quantum operations can tolerate some low-probability errors (including errors in the QEC circuit) below a certain threshold.
In the prototypical model for quantum computation – the quantum circuit model, a quantum bit of information (qubit) is encoded into a two-level system, called a physical qubit, and the usual approach for QEC is to encode a logical qubit into some subspace of multiple physical qubits, so that different error processes lead to distinguishable syndromes and can therefore be corrected. However, the increased number of physical qubits for a logical qubit introduces more decoherence for the system to correct. Moreover, the logical gate operations become quite complicated since multiple physical systems need to be addressed simultaneously. Hence, it is still an outstanding experimental challenge to build a more robust quantum register using multiple physical qubits.
An alternative scheme is to encode the quantum information into bosonic modes such as harmonic oscillators [6,7]. A single bosonic mode already provides an infinitely large Hilbert space, from which we choose a logical subspace for an error-correcting code [8–13]. Such bosonic QEC modes can be hardware-efficient compared to the conventional QEC codes based on multiple qubits. Moreover, the bosonic modes often have relatively simple decoherece processes (mainly bosonic excitation loss channel) during which the bosonic excitations are lost one by one [14]. There have been several error-correcting encoding schemes in a single bosonic mode proposed to date, including the Gottesman-Kitaev-Preskill (GKP) codes [10,15,16], cat codes [11,17,18], binomial codes [12], rotation-symmetric codes [19] and other variations [13,20]. The GKP codes, consisting of superpositions of highly squeezed states, are not only protected against small shifts in position but also have been shown to perform well against the more realistic amplitude damping channel [13]. The cat codes use superpositions of coherent states evenly distributed around a circle in phase space, which can be protected against (single or multiple) bosonic excitation loss and dephasing errors. The binomial codes exploit superpositions of Fock states weighted with binomial coefficients, which can exactly correct the bosonic excitation loss, gain and dephasing errors up to a specific degree.
For bosonic modes, the standard operations (e.g., displacement operation, phase rotation, one-mode squeezing, beam splitting, and two-mode squeezing) are all Gaussian operations, which can only transform Gaussian states into Gaussian states [6,21]. However, universal control of a single bosonic mode can be achieved by adding a single nonlinear operation [21]. When such a direct nonlinear operation is difficult to realize directly, it is still possible to implement an indirect nonlinear interaction by coupling the bosonic mode to a finite-level ancilla. Moreover, quantum non-demolition (QND) measurement of the ancilla enables measurement-based feedback control and therefore arbitrary operation on the bosonic mode. Here, we will review recent advances in the approaches for universal control and arbitrary operation of bosonic modes (Table 1), including unitary control, quantum feedback control, driven-dissipative control and holonomic control (Fig. 1a). In the first two approaches, an ancilla qubit is coupled to a single bosonic mode to introduce nonlinear interaction and feedback control, while in the remaining two approaches, a special coupling between the bosonic mode and reservoir or a special Hamiltonian of the bosonic mode is engineered to support some stabilized manifold, consisting of all coherent superpositions of multiple steady states that are free of any nonunitary effect caused by the reservoir.
Table 1. Recent theoretical and experimental advances in quantum control of bosonic modes in circuit QED.
| Unitary control | Unitary & feedback | Unitary & dissipation |
|---|---|---|
| Ancilla-induced nonlinearity | Quantum adaptive control | Quantum Zeno dynamics |
| Theory: — SNAP gate [22] — Optimal control [23,24] — E-SWAP gate [25] — CPHASE gate [26] |
Theory: — CPTP maps [27] — Teleported gate [28] — ET gate [29,30] — PI gate [31] |
Theory: — Dissipative cat [32] — Kerr cat [33] — FT syndrome detection [34] — Bias-preserving Kerr cat [35] — Bias-preserving dissipative cat [36] — Holonomic gatea [37] |
| Experiments: — SNAP gate [38] — Optimal control [23] — CNOT gate [39] — CZ gate [40] — E-SWAP gate [41] |
Experiments: — QEC [42–44] — CPTP simulation [45,46] — Teleported CNOT gate [47] — FT parity measurement [48] — PI SNAP gate [49] — ET phase gate [50] |
Experiments: — Dissipative cat [51–53] — Kerr cat [54] |
- a
- This scheme uses only dissipation.

Fig. 1. (Color online) (a) Schematic of various approaches for controlling a quantum system: (i) unitary control on the system alone or both the system and an ancilla; (ii) quantum feedback control based on measurement of the ancilla; (iii) driven-dissipative control with either engineered dissipation or Hamiltonian engineering; (iv) holonomic quantum control based on only engineered dissipation. (b), (c) Schematic and device photograph of a circuit QED system modeled as a coupled qubit-oscillator system. The storage cavity with long coherence time is used to encode quantum information, the transmon qubit acts as an ancilla for universal control of the storage cavity, and the readout cavity with short coherence time is used for qubit readout. Both the storage cavity and transmon qubit can be addressed by microwave control fields. Reprinted with permission from Refs. [27,55].
The physical platform we consider is circuit quantum electrodynamics (circuit QED) [14,56–61], which is an analog of cavity QED [62] using superconducting circuits [63,64]. Cavity QED engineers the environment of the atoms by placing them in a cavity that supports only discrete bosonic modes of the electromagnetic field. Examples of cavity QED systems include alkali atoms in optical cavities [65] and Rydberg atoms in microwave cavities [66]. Circuit QED uses superconducting qubits as artificial atoms coupled to microwave resonators. A key advantage of circuit QED is the extremely strong coupling between the superconducting qubits and the cavity. Corresponding to the two encoding schemes based on qubits or bosonic modes, there are two main routes in superconducting quantum computing with circuit QED.
Qubits can be encoded into the first two levels of superconducting artificial atoms, such as the most widely used transmons [67–69], while the cavity resonators are used for qubit readout. Arbitrary single qubit rotations can be realized with resonant voltage drives at the qubit frequencies [56,70], and gate errors can be reduced below 10-3 by pulse shaping techniques [71,72]. Two-qubit gates can be realized by either capacitive coupling [71] or using the resonator as a mediator [56,70,73], with current error rates being less than one percent [74,75]. Recent experimental developments include implementations of quantum search algorithms [76], quantum teleportation [77], simulations of topological transitions [78], digitized adiabatic quantum computing [79], variational quantum algorithms [80], supervised learning with quantum-enhanced feature spaces [81], quantum reservoir engineering [82], quantum walks [83], advances towards quantum error correction [84–87], building cloud-based devices and demonstrating quantum supremacy with several tens of qubits [88].
Alternatively, a storage cavity resonator as a bosonic mode with long coherence time can encode the quantum information, while the transmon qubits can act as ancillas to aid universal control of the storage cavity (Fig. 1b, c). Such an encoding scheme can make use of various bosonic QEC codes, which are hardware-efficient compared to more standard qubit-based codes such as surface codes. Moreover, bosonic QEC codes often have specific noise resilience [36], and therefore can be concatenated with conventional QEC codes to reduce the hardware overhead [36,89,90]. Recently there has been significant experimental progress in bosonic QEC. QEC based on cat codes or binomial codes in superconducting cavities have reached or approached the break-even point [42,43], at which the lifetime of the logical qubit exceeds that of the single best physical qubit within the logical qubit. The encoding based on GKP codes has also been demonstrated in trapped-ion mechanical oscillators [91,92] and superconducting cavities [44]. However, compared to conventional one-qubit and two-qubit control, universal control of single and multiple bosonic modes requires the introduction of nonlinearity and therefore is more complex. This will be the main topic of this review.
This review is organized as follows. In Section 2, we review the universal control of a single bosonic mode with the aid of an ancilla qubit dispersively coupled to it. Then we introduce, in Section 3, the extension from the universal unitary control to quantum feedback control and arbitrary quantum channel construction for the bosonic mode by QND measurement of the ancilla. In Section 4, it is shown that reservoir engineering and Hamiltonian engineering can be promising strategies to realize universal quantum computation in some unitarily evolving subspace of the bosonic mode. In Section 5, the combination of reservoir engineering and holonomic quantum control is introduced to realize universal control of bosonic modes. Then in Section 6, we introduce the quantum control schemes to entangle different bosonic modes for universal quantum computation. In Section 7, we briefly summarize the review and outline some future directions for quantum control of the bosonic modes. For convenience, we take the reduced Plank constant as ℏ=1 throughout this review.
Read full article
URL:
https://www.sciencedirect.com/science/article/pii/S2095927321004011
Физики разработали код коррекции ошибок в квантовых вычислениях, который работает при вдвое большем уровне шума, чем его предшественник. Авторы показали, как ведет себя новый код при разных типах ошибок и как с его помощью можно уменьшить число физических кубитов в системе, а эксперименты подтвердили все его преимущества. Работа опубликована в журнале Nature communications.
Второй важной задачей на пути к воплощению квантовых вычислений помимо создания долгожданного устройства, можно считать разработку кода коррекции ошибок. Базовые элементы квантовых компьютеров (кубиты, вентили) не идеальны: кубиты могут находиться в неправильном состоянии, а вентили — вносить ошибку в выходной кубит. Поэтому ученым приходится придумывать способы как с этим бороться. Известный из классической информатики вариант — коррекция возникающих ошибок. Тут есть несколько разных способов — можно несколько раз измерять полученную информацию и потом обрабатывать полученный набор, либо использовать для кодирования 1 кубита (логического) несколько физических кубитов. Для современных квантовых устройств время жизни кубитов не позволяет использовать первый метод, поэтому для реализации вычислений без ошибок требуется большее число кубитов, чем задействовано в самих вычислениях. Использование нескольких (часто трех) кубитов вместо одного позволяет получить правильный ответ, даже если один из кубитов оказался «битым», ведь остальные будут верными. Вероятность того, что два кубита одновременно ошибочны, очень мала.
Среди множества кодов коррекции ошибок существуют так называемые поверхностные коды. Для их представления используется двумерная решетка, на ребрах которой расположены кубиты. Часть из них участвует в вычислениях, а другая часть помогает выявлять и исправлять ошибки. Измерение дополнительных кубитов можно проводить в разных базисах: чаще всего, набор однокубитных измерений ограничен матрицами Паули. В случае поверхностного кода используют операторы XXXX и ZZZZ (называются стабилизаторами), которые действуют сразу на 4 кубита, а на решетке располагаются в виде креста. Поверхностные коды работают при высоком уровне шума, то есть могут получить верный логический кубит несмотря на большой процент ошибок в физических. Тем не менее, платят за это своей размерностью — требуется много дополнительных кубитов, для реализации такого кода.
Домашнее задание студента из университета Сиднея по улучшению поверхностных кодов для коррекции ошибок вылилось в полномасштабное исследование. Вместе с другими учеными под руководством Бенджамина Брауна (Benjamin J. Brown) ему удалось разработать код, который оказался в два раза эффективнее существующего. Авторы протестировали его на небольших системах из кубитов и показали, что новый код требует меньше дополнительных физических кубитов для коррекции ошибок и в некоторых случаях превосходит теоретическую оценку.
Интересно, что к достижению весомых результатов привело небольшое и, казалось бы, незначительное изменение в поверхностном коде: авторы предложили использовать операторы XZZX вместо привычных стабилизаторов. Такой подход оказался более информативным в плане обнаружения ошибок системы. Авторы сравнивали его не только с поверхностным кодом, но и с теоретическим пределом (хэшированием). Они рассмотрели общую модель шума, который может быть в системе: в нем с определенной вероятностью p возникает ошибка, источником которой может быть один из трех операторов X, Y или Z. Каждый оператор вносит свой вклад r в общую ошибку, в крайних случаях преобладать может шум только от одного оператора (смещенный шум). Как раз в таких случаях для операторов X и Z XZZX-код имеет в пять раз более высокий порог ошибки.
После обнаружения описанной выше особенности кода, авторы начали проверять как от смещения шума (преобладания одной из матриц Паули в шуме) зависит его помехоустойчивость. С увеличением смещения порог шума растет, все дальше и дальше удаляясь от порога для поверхностного кода. Но это не все. Важно, что начиная с какого-то смещения, результат для XZZX кода превосходит теоретическую оценку.
Ученые были заинтересованы в том, чтобы показать, как на практике может быть полезен большой возможный порог шума. Они кодировали логические кубиты с двух разных кодов коррекции ошибок — XZZX и поверхностного. После этого интерпретировали полученный результат с помощью метода максимального правдоподобия: если на выходе получается набор физических кубитов, который не соответствует ни одному логическому (например, логическая 1 — это 111, 0 — это 000, а на выходе получилось 110), то ему присваивается ближнее значения логического кубита (то есть 110 — это логическая 1, а не логический 0). Полученные результаты помогали авторам выявлять характер масштабируемости решеток, увеличения его размерности в зависимости от смещения шума и его порога. Как и ожидалось, благодаря устойчивости к шуму, XZZX коды оказываются перспективны для применения в больших системах, где они будут требовать значительно меньше дополнительных кубитов.
Авторы подчеркивают, что наиболее важный результат их работы состоит не в преимуществе над поверхностными кодами, а в том, что они смогли показать, что модификации в существующих кодах коррекции ошибок могут дать результат лучше, чем предсказывает теория. А, значит, можно создавать и придумывать коды ошибок, которые существенно упростят работу квантовых устройств.
Поверхностные коды активно использует Google в своих сверхпроводящих устройствах на несколько десятков кубитов, которые не менее активно пытается масштабировать. Поэтому интересно будет увидеть, какие коды коррекции придут на смену существующим в больших квантовых вычислителях.
Оксана Борзенкова
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Повышение надежности
передачи и хранения информации достигается
посредством избыточности. Например, в
трехбитовом коде каждый логический бит
информации задаётся тремя физическими
битами
![]()
В рассматриваемом
случае реализуется мажоритарная система
исправления ошибок (принятие решения
на основе большинства голосов). В случае
трехбитового кодирования сообщение
(логический бит) передаётся правильно,
если число ошибок в физических битах
равно нулю или единице. Соответственно,
сообщение может быть передано неверно,
если ошибок две или три.
Рассмотрим в
качестве простого введения двоичный
симметричный канал. Пусть
—
вероятность ошибки в одном физическом
бите: вероятность превращения нуля в
единицу (![]()
),
либо наоборот, единицы в нуль (![]()
).
Будем считать обе эти вероятности
одинаковыми (отсюда название- симметричный
канал). Вероятность безошибочной передачи
информации (![]()
, либо
![]()
),
соответственно, равна
![]()
.
Задача 5.18
Покажите, что классический трёхбитовый
код характеризуется следующей вероятностью
ошибки передачи одного логического
бита информации
![]()
Покажите далее,
что избыточность увеличивает надежность
передачи информации (т.е.
![]()
,
если
![]()
).
Перейдем теперь
к рассмотрению квантового бита (кубита).
Рассмотрим вначале так называемый канал
с классической ошибкой (название
«классическая ошибка» довольно условно).
Такая ошибка
описывается действием оператора
(NOT),
когда состояние 0 меняется на 1, а состояние
1 меняется на 0:
![]()
,
т.е.
![]()
Таким образом,
действие ошибки описывается следующим
преобразованием состояния кубита
![]()
Трёхбитовый код
в квантовом исполнении (резервирование
одного логического кукубита тремя
физическими кубитами) выглядит следующим
образом:
![]()
,
т.е.
![]()
![]()
Реализация
рассматриваемого способа кодирования
посредством квантовой схемы представлена
на рисунке.
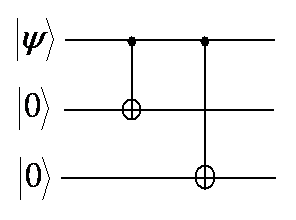
Рис. 5.11 Квантовая
схема кодирования для защиты от
классической ошибки
Квантовая схема
обеспечивает следующую последовательность
преобразований
![]()
Рассмотрим каким
образом добавление вспомогательной
системы из двух кубитов в исходном
состоянии ноль позволяет детектировать
возможное наличие ошибки.
Дополним схему
кодирования схемой декодирования и
измерения вспомогательной системы.
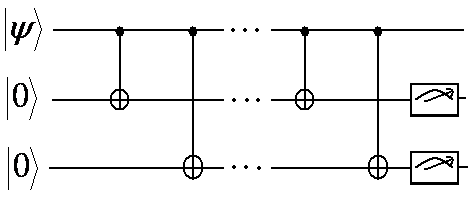
Рис. 5.12 Квантовая
схема кодирования, дополненная схемой
декодирования и измерения.
Специфика квантового
исправления ошибок состоит в том, что
мы не можем подвергать измерениям
кубиты, несущие информацию (в противном
случае эта информация будет утеряна в
результате редукции состояния). Вместо
измерения информационной системы
производится измерение вспомогательной
системы. Измерение вспомогательной
системы позволяет идентифицировать
возможную ошибку и исправить её.
Оказывается, что
измерение двух вспомогательных (второго
и третьего) кубитов допускает 4 следующие
возможности: 11 (когда произошла ошибка
в первом кубите), 00 (когда ошибок нет),
10 (ошибка во втором кубите), 01 (ошибка в
третьем кубите).
Предположим,
например, что возникла ошибка в первом
(информационном) кубите, т.е.
![]()
Тогда, декодирование
(правая часть рисунка) приведёт к
следующей последовательности
преобразований:
![]()
Измерение второго
и третьего кубитов дадут результат 11.
Это будет означать, что в первом
(информационном) кубите произошла
ошибка. Для исправления этой ошибки
нужно выполнить преобразование
над информационным кубитом.
Рассмотрим три
остальных случая. Если ошибок нет, то
последовательность преобразований
будет следующей:
![]()
Убеждаемся, что в
результате преобразований информационный
кубит не изменился, а вспомогательная
система оказалась в состоянии 00.
Если возникла
ошибка во втором кубите, то имеем цепочку
преобразований:
![]()
Снова информационный
кубит не изменился, а вспомогательная
система оказалась теперь в состоянии
10.
Если возникла
ошибка в третьем кубите, то аналогично
получим:
![]()
Информационный
кубит опять не изменился, а вспомогательная
система оказалась теперь в состоянии
01.
Таким образом,
рассматриваемые четыре возможности
идентифицируют 4 ситуации (отсутствие
ошибок, либо ошибка в одном из трёх
кубитов).
Рассмотрим теперь
случай двух ошибок. Пусть, например,
ошибки возникли в 1-ом и 2-ом кубитах.
Тогда
![]()
Если мы будем
действовать по схеме, указанной выше,
то мы ошибочно сделаем вывод о наличии
ошибки в третьем кубите и, таким образом,
не сможем идентифицировать ошибку в
информационном кубите.
Мы видим, что
рассмотренный трёхкубитовый код
исправляет гарантированно не более
одной ошибки.
Рассмотрим теперь
так называемую фазовую ошибку. Эта
ошибка сводится к несанкционированному
действию оператора сдвига фазы
.
Таким образом, действие фазовой ошибки
описывается следующим преобразованием
состояния кубита (меняется знак у
базисного состояния
)
![]()
Покажем, что
рассмотрение фазовой ошибки можно
свести к рассмотрению классической
ошибки:
Выполнив
преобразование Адамара, перейдем к
новому базису:
![]()
![]()
Мы видим, что в
новом базизе действие фазовой ошибки
сводится к тому, что состояния
![]()
и
![]()
переходят друг в друга (![]()
,
![]()
).
Таким образом, в новом базисе фазовая
ошибка сводится к классической ошибке.
Схема кодирования
фазовой ошибки изображена на рисунке.
Она представляет собой схему кодирования
классической ошибки, дополненную
преобразованием Адамара для каждого
кубита
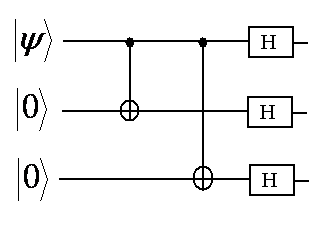
Рис. 5.13 Квантовая
схема кодирования для защиты от фазовой
ошибки
СПИСОК ЛИТЕРАТУРЫ
-
Нильсен М, Чанг
И. Квантовые вычисления и квантовая
информация: Пер. с англ. Под ред. М.Н.
Вялого и П.М. Островского с предисловием
К.А. Валиева. — М.: Мир. 2006. 824 с. -
Валиев К.А.,
Кокин А.А.
Квантовые компьютеры: Надежды и
реальность. 2-е изд., исп. М.–Ижевск: НИЦ
РХД, 2002. 320 с.
-
Физика квантовой
информации. Квантовая криптография.
Квантовая телепортация. Квантовые
вычисления // Под. ред. Д.Боумейстера,
А.Экерта, А. Цайлингера;
Пер. с англ. под ред. С.П.Кулика
и Т.А.Шмаонова.
М. Постмаркет. 2002. 376с. -
Прескилл Дж. Квантовая информация
и квантовые вычисления. Том.1. М.-Ижевск.
РХД. 2008. 464с. -
Валиев К.А.
Квантовые компьютеры и квантовые
вычисления // Успехи Физических Наук.
2005. Т.175. №1. С.3-39. -
Ожигов Ю.И.
Квантовые
вычисления. М. МГУ. 2003. -
Feynman
R.
Simulating Physics with Computers // Int. J. Theor. Phys.
1982. V.21.
№6/7. P.467-488.
См. перевод Фейнман
Р. Моделирование
физики на компьютерах // сб. «Квантовый
компьютер и квантовые вычисления».
Т.2. Ижевск. РХД. 1999. с.96-124. -
Feynman
R.
Quantum Mechanical Computers // Found. of Phys. 1986. V.16.
№6. P.507-531.
См. перевод Фейнман
Р.
Квантовомеханические компьютеры // сб.
«Квантовый компьютер и квантовые
вычисления». Т.2. Ижевск. РХД. 1999. с.125-156. -
Манин Ю.И.
Вычислимое и невычислимое. М. Советское
Радио. 1980. 128с. -
Китаев А., Шень
А., Вялый М.
Классические и квантовые вычисления
М. МЦНМО. ЧеРо. 1999. 192 с. -
Grover
L.K.
Quantum Mechanics Help in Searching for a Needle in a Haystack //
Phys. Rev.
Lett.
1997. V.78.
№2. P.325-328.
См. перевод Гровер
Л.К. Квантовая
механика помогает найти иголку в стоге
сена // сб. «Квантовый компьютер и
квантовые вычисления». Т.1. Ижевск. РХД.
1999. с.101-109. -
Shor
P.
Polynomial-Time Algorithms for Prime Factorization and Discrete
Logarithms on a Quantum Computer. LANL Report quant-ph/
9508027.1995. 28p. -
Deutsch
D.
Quantum Theory, the Church- Turing Principle and the Universal
Quantum Computer // Proc. Roy. Soc. London.
1985. V.A400.
№1818. P.97-117.
См. перевод Дойч
Д. Квантовая
теория принципа Черча- Тьюринга и
универсальный квантовый компьютер //
сб. «Квантовый компьютер и квантовые
вычисления». Т.2. Ижевск. РХД. 1999. с.157-189. -
Barenco
A., Bennett C.H., Cleve C., DiVincenzo D.P., Margolus N., Shor P.,
Sleater T., Smolin J.A., Weinfurter H.
Elementary Gates for Quantum Computation // Phys. Rev. A. 1995.
V.52. №5.
P.3457-3467. -
Preskill
J.
Fault-tolerant quantum computation. LANL Report quant-ph/
9712048.1997. 58p. -
Kim
Y.H., Kulik S.P., Shih Y.H. Quantum
teleportation of a polarization state with a complete Bell state
measurement // Phys. Rev. Lett. 2001. V.86. P.1370-1373 -
Bartlett
S.D., Munro W.J.
Quantum Teleportation of Optical Quantum Gates // Phys. Rev. Lett.
2003. V.90. 117901. -
Mattle
K., Weinfurter H., Kwiat P.G., and Zeilinger A.
Dense Coding in Experimental Quantum Communication // Phys. Rev.
Lett. 1996. V76. P.4656-4659. -
Kim
Y.H., Kulik S.P., Shih Y.H. Bell
state preparation using pulsed nondegenerate two-photon
entanglement // Phys. Rev.A. 2001. V.63. 060301. 4p. -
Kim
Y.H.,
Chekhova
M.V., Kulik S.P.,
Rubin
M., Shih Y.H. Interferometric
Bell state preparation using femtosecond pulse pumped spontaneous
parametric down-conversion. 2001. // Phys. Rev. A. V.63. 062301.
11p. -
Cavity
Quantum Electrodynamics. Advances in atomic, molecular and optical
physics // Berman
P.
(editor). Academic Press. San Diego. 1994. 497 p. -
Münstermann
P., Fischer T., Maunz P., Pinkse P.W.H., and Rempe G.
Observation
of cavity-mediated long-range light forces between strongly coupled
atoms // Phys. Rev. Lett. 2000. V.84.
P.4068-4071. -
Beige
A.
Ion-trap quantum computing in the presence of cooling // Phys. Rev.
A. 2004. V.69. 012303. 11p. -
Pachos
J., Walther H.
Quantum computation with trapped ions in an optical cavity // Phys.
Rev. Lett. 2002. V.89. 187903. 4p. -
Childs
A., Chuang I.L.
Universal quantum computation with two-level trapped ions // Phys.
Rev. A. 2001. V.63. 012306. 4p. -
Gershenfeld
N.A.,
Chuang I.L. Bulk Spin-Resonance Quantum Computation // Science.
1997. V. 275. №1. P.350-356. -
Vandersypen
L.M.K., Steffen
M., Breyta
G., Yannoni
C.S., Sherwood
M.H., Chuang
I.L.
Experimental realization of Shor’s quantum factoring algorithm using
nuclear magnetic resonance // Nature. Dec. 2001. V.414. P. 883-887. -
Кокин А.А.
Твердотельные квантовые компьютеры
на ядерных спинах. Институт компьютерных
исследований. Москва- Ижевск. 2004. 204 с. -
Bohr N.
Discussion with Einstein on epistemological problems in atomic
physics // in Schilp P.A. (editor), Albert Einstein,
Philosopher-Scientist (Library of Living Philosophers, Evanston,
Illinois, 1949), P.200-241. Перевод
на русский язык: Бор
Н. Дискуссия
с Эйнштейном по проблемам теории
познания в атомной физике. Избранные
научные труды в 2-х томах. Т.2. С. 399-433. М.
Наука. 1971. -
Богданов Ю.И.
Многопараметрические статистические
модели в задачах квантовой информатики
// Труды ФТИАН. М. Наука. 2005. Т.18. с.91-118 -
Крамер
Г. Математические
методы статистики. М.: Мир, 1975. 648 с. -
Lukacs
E.
Characteristic Functions.
London. Charles Griffin & Company Limited. 1960.216 p. -
Прохоров Л.В.
Квантовая
механика- проблемы и парадоксы. СПб.
НИИХ СПбГУ. 2003. 120 с. -
Владимиров В.С.
Обобщенные
функции в математической физике. М.
Наука. 1979. 320с. -
Robertson
H.P. An
Indeterminacy Relation for Several Observables and Its Classical
Interpretation // Phys.Rev. 1934. V.46. P.794-801 -
Холево А.С.
Статистическая структура квантовой
теории. М.Ижевск:
Ин-т комп. исслед., 2003. 192 с. -
Богданов А.Ю.,
Богданов Ю.И., Валиев К.А.
Информация Шмидта и запутанность
квантовых систем //Вестн. Моск. ун-та.
Сер.15. Вычислительная математика и
кибернетика. 2007.№1; LANL
report
quant-ph/0512062 -
Кендалл М.,
Стьюарт А.
Статистические выводы и связи. М. Наука.
1973. 900 с. -
Вероятность и
математическая статистика. Энциклопедия.
// Под ред. Ю.В.
Прохорова. М:.
Большая Российская энциклопедия, 1999.
911 с. -
Крянев А.В., Лукин
Г.В. Математические
методы обработки неопределенных данных.
М. Физматлит. 2003. 216 с. -
Богданов Ю.И.
Основная задача статистического анализа
данных: Корневой подход. М.:
МИЭТ,
2002. 96с.
Пер.
на
англ.:
Bogdanov
Yu. I.
Fundamental problem of statistical data analysis: Root approach.
M.: MIEE, 2002. 84 p.; Bogdanov
Yu. I.
Statistical inverse problem // LANL E-print, 2002, arXiv:
phys/0211109. 39p. -
Bogdanov
Yu.I.
Quantum mechanical view of mathematical statistics // Proceedings of
SPIE. 2006. V.6264. 62640E; LANL E-print, 2003, arXiv:
quant-ph/0303013. 26 p; New Topics in Quantum Physics Research.
Nova Science. 2006. pp. 1-36. -
Ю.И. Богданов,
Унифицированный
метод статистического восстановления
квантовых состояний, основанный на
процедуре очищения // ЖЭТФ. 2009. Т.135.
Вып.6.с.1068-1078. -
Богданов Ю.И.,
Кривицкий Л.А., Кулик С.П. Статистическое
восстановление квантовых состояний
оптических трехуровневых систем //
Письма в ЖЭТФ. 2003. Т. 78, вып. 6. С. 804809. -
Bogdanov
Yu.I., Chekhova M.V., Kulik S.P.
et al.
Statistical reconstruction of qutrits // Phys. Rev. A. 2004. Vol.
70. 042303. 16 p. -
Bogdanov
Yu.I., Chekhova M.V., Kulik S.P.
et al.
Qutrit state engineering with biphotons // Phys. Rev. Lett. 2004.
Vol. 93. 230503. 4p. -
Bogdanov Yu.I., Brida G, Genovese M., Kulik
S.P., Moreva E.V., Shurupov A.P. Statistical
Estimation of the Efficiency of Quantum State Tomography Protocols
// Phys. Rev. Lett. 2010. V.105. 010404. 4p. -
Дирак П.А.М.
Принципы квантовой механики // Собрание
научных трудов. Т.1: Квантовая теория.
М.: Физматлит, 2002. С. 7320. -
Von
Neumann J.
Mathematische Grudlagen der Quantenmechanik. Berlin.
Springer.
1932. См. перевод Фон
Нейман И.
Математические основы квантовой
механики. М. Наука. 1964. 368с. -
Dirac
P.A.M.
Relativity and Quantum Mechanics // Fields and Quanta. 1972.
V3.
P.139-164.
(см. перевод Дирак
П.А.М. Теория
относительности и квантовая механика
// Собрание научных трудов. Том III.
М. Физматлит. 2004. с. 141-152.) -
Bogdanov
Yu.I.
Root estimator of quantum states // LANL E-print, 2003, arXiv:
quant-ph/0303014. 26 p; New Topics in Quantum Physics Research.
Nova Science. 2006. pp. 129-162. -
Богданов
Ю. И.
Основные
понятия классической и квантовой
статистики: Корневой подход // Оптика
и спектроскопия. 2004. Т.96, №5. С.735746. -
Einstein
A., Podolsky B., Rosen N.
Can
quantum-mechanical description of physical reality be considered
complete? // Phys. Rev.
1935. V.47.
P.777-780.
Перевод на русский язык: Эйнштейн А.,
Подольский Б., Розен Н. Можно ли считать
квантовомеханическое описание физической
реальности полным? А. Эйнштейн Собрание
научных трудов в 4-х томах. Т.3. С. 604-611.
М. Наука. 1966. -
Гнеденко Б.В.
Курс теории
вероятностей. М. Эдиториал УРСС. 2005. 448
с. -
Коэн-Таннуджи
К., Диу Б., Лалоэ Ф.
Квантовая механика // Пер. с фр. Л.Н.
Новикова. В 2-х т. Екатеринбург. Изд-во
Урал. Ун-та. 2000. -
Ландау Л.Д.,
Лифшиц Е.М. Квантовая
механика. Нерелятивистская теория М.
Наука. 1974. 752 с. -
Ehrenfest
P. Bemerkung
über die angenaherte Gültigkeit der klassischen Mechanik innerhalb
der Quanten Mechanik // Z. Phys. 1927. 45.
S.
455-457. См. перевод: Эренфест
П. Замечание
о приближенной справедливости
классической механики в рамках квантовой
механики // в сб. Эренфест
П.
Относительность. Кванты. Статистика.
Сборник статей. М. Наука. 1972. с.82- 84. -
Гильберт
Д. Математические
проблемы // Избранные труды. Т2. М.
Факториал. 1998. с.401- 436. -
Zee
H.D. Roots
and Fruits of Decoherence // Seminaire Poincare. 2005. p.115-129.;
Zurek
W.H.
Decoherence and the Transition from Quantum to Classical-
Revisited// Ibid. p.1-23. -
Больцман Л.
Дальнейшие
исследования теплового равновесия
между молекулами газа // Избранные
труды. М. Наука. 1984. с.125-189. -
Гильберт
Д. Основы
общей теории линейных интегральных
уравнений. Глава XXII
Обоснование кинетической теории газов
// Избранные труды. Т2. М. Факториал. 1998.
с.350- 364. -
Гейзенберг В.
О квантовотеоретической интерпретации
кинематических и механических
соотношений. Избранные труды. М. УРСС.
2001. с. 86-98. -
Борн М., Иордан
П. К квантовой
механике. Там же. С. 99-126. -
Гейзенберг В.,
Борн М., Иордан П. К
квантовой механике. II.
Там же. С. 127-175. -
Hilbert
D., Neumann J., Nordheim L. Űber
die Grundlagen der Quantenmechanik. 1928.
Math. Ann. Bd. 98. s. 1-30. -
Bell
J.S.
Speakable and unspeakable in quantum mechanics. Collected papers on
quantum phylosophy. Cambridge University Press. 1993. -
Холево А.С.
Введение в квантовую теорию информации.
М. МЦНМО. 2002. 128с. -
Холево А.С.
Вероятностные и статистические аспекты
квантовой теории. Издание 2-е, дополненное.
Москва- Ижевск. Институт компьютерных
исследований. 2003. 410 с. -
Гнеденко Б.В. К
шестой проблеме Гильберта // Проблемы
Гильберта (сб. статей под ред. Александрова
П.С.)
М. УРСС. 2000. с.117- 119. -
Блейхут
Р.
Быстрые алгоритмы цифровой обработки
сигналов. М. Мир, 1989. 448 с. -
Килин
С.Я. Квантовая
информация // Успехи Физических Наук.
1999. Т.169. №5. С.507-527.
|
Содержание |
стр. |
|
Введение |
3 |
|
Глава 1. Квантовая |
|
|
1.1. Статистическая |
8 |
|
1.2. Принцип |
10 |
|
1.3. Характеристическая |
13 |
|
1.4. Операторы |
17 |
|
1.П. Приложение |
19 |
|
Глава 2. Точность |
|
|
2.1. Неравенство |
22 |
|
2.2. Неравенство |
25 |
|
2.3. Соотношение |
27 |
|
2. 4. Соотношение |
29 |
|
2.5. Многомерное |
32 |
|
2.6. Информация |
35 |
|
2.7. Неравенство |
36 |
|
2.8. Многомерное |
40 |
|
Глава3. Принципы |
|
|
3.1 Постулаты |
44 |
|
3.2 От квантовой |
53 |
|
3.3. Шестая проблема |
60 |
|
3.4. Обсуждение |
63 |
|
3.П. Приложение. |
65 |
|
Глава 4. Основные |
|
|
4.1 Квантовые биты |
71 |
|
4.2. Реализация |
78 |
|
4.3. Система кубитов |
79 |
|
4.4. Измерение |
82 |
|
4.5. Простейшие |
84 |
|
4.6. |
87 |
|
4.7. Теорема о |
88 |
|
4.8. Состояния |
91 |
|
4.9. Парадокс |
92 |
|
4.10. Неравенство 4.11. Физическая |
94 103 |
|
Глава 5. Некоторые |
|
|
5.1 Сверхплотное |
108 |
|
5.2. Телепортация |
112 |
|
5.3. Квантовый |
113 |
|
5.4. Квантовое |
125 |
|
5.5. Нахождение |
130 |
|
5.6. Факторизация |
134 |
|
5.7. Квантовая 5.8. Алгоритм 5.9. Введение в |
139 143 148 |
|
СПИСОК ЛИТЕРАТУРЫ |
154 |
152
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как пространство и время могут быть квантовым кодом исправления ошибок +15
Научно-популярное, Физика, Квантовые технологии
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/
Те же самые коды, требующиеся для предотвращения ошибок в квантовых компьютерах, могут придавать ткани пространства-времени присущую ей прочность

В игрушечных «голографических» вселенных (даже если и не в нашей, настоящей) ткань пространства-времени возникает на основе сети квантовых частиц. Физики обнаружили, что это работает по принципу квантового исправления ошибок.
В 1994-м математик из исследовательского подразделения AT&T по имени Питер Шор мгновенно прославил квантовые компьютеры (КК), открыв, что эти гипотетические устройства могли бы быстро раскладывать большие числа на множители – тем самым ломая большую часть современной криптографии. Но на пути реального создания КК стояла фундаментальная проблема: естественная неустойчивость их физических компонентов.
В отличие от двоичных битов информации обычных компьютеров, кубиты состоят из квантовых частиц, у которых есть вероятность нахождения в одном из двух состояний, обозначаемых |0> и |1>, в одно и то же время. При взаимодействии кубитов их возможные состояния становятся взаимозависимыми, и шансы оказаться в состояниях |0> и |1> зависят друг от друга. Пропорциональные вероятности растут тем более, чем сильнее после каждой операции кубиты становятся запутанными друг с другом. Поддержка и управление этим экспоненциально растущим количеством одновременных возможностей и делают КК теоретически мощными.
Однако кубиты безумно подвержены ошибкам. Слабейшее магнитное поле или случайный микроволновый импульс заставляет их «перебрасывать биты», меняя их шансы оказаться равными |0> или |1> по отношению к другим кубитам, или «переворачивать фазы», что обращает математическое отношение двух их состояний. Чтобы КК смогли работать, учёным нужно найти способы защищать информацию даже при повреждении отдельных кубитов. Более того, эти способы должны обнаруживать и исправлять ошибки, не измеряя сами кубиты напрямую, поскольку измерение приводит к коллапсу сосуществующих возможностей кубита в определённую реальность – а старые добрые 0 и 1 не могут поддерживать квантовые вычисления.
В 1995 году Шор вслед за своим алгоритмом разложения опубликовал ещё одно поразительное доказательство, о существовании «кодов, исправляющих квантовые ошибки». Специалисты по информатике Дорит Ааронова и Майкл Бен-Ор (а также другие независимые исследователи) годом позже доказали, что эти коды теоретически могут довести количество ошибок почти до нуля. «Это было важнейшее открытие 90-х, убедившее людей, что масштабируемые квантовые вычисления в принципе возможны, — сказал Скотт Ааронсон, ведущий специалист по квантовым компьютерам из Техасского университета. – И что это просто сложнейшая инженерная задача».

Питер Шор, Дорит Ааронова и Майкл Бен-Ор
Сегодня, хотя небольшие КК материализуются в лабораториях по всему миру, полезных КК, способных превзойти по производительности обыкновенные, остаётся ждать ещё несколько лет или даже десятилетий. Требуются куда как более эффективные коды исправления ошибок, чтобы справляться с обескураживающе большим количеством ошибок, выдаваемым реальными кубитами. Попытки разработать улучшенные коды – «один из важнейших вопросов в области», как сказал Ааронсон, наравне с совершенствованием железа.
Однако в рамках настойчивых поисков этих кодов, проходивших в последние 25 лет, в 2014-м году произошло нечто забавное – физики нашли свидетельство глубоких связей между квантовым исправлением ошибок и природой пространства, времени и гравитации. В общей теории относительности Альберта Эйнштейна гравитация определяется, как искривление ткани пространства и времени – или «пространства-времени» — вокруг массивных объектов. Мяч, подброшенный в воздух, перемещается по прямой линии в пространстве-времени, а оно уже изгибается по направлению к Земле. Однако, несмотря на всю мощь теории Эйнштейна, физики считают, что у гравитации должно быть более глубокое, квантовое происхождение, из которого каким-то образом появляется нечто похожее на ткань пространства-времени.
В 2014-м трое молодых исследователей квантовой гравитации пришли к невероятному результату. Они работали в любимой теоретиками области: игрушечной вселенной, известной, как «антидеситтеровское пространство», которая работает как голограмма. Искривлённая ткань пространства-времени внутри вселенной возникает как проекция запутанных квантовых частиц, существующих на её внешней границе. Ахмед Альмейри, Си Дон и Даниель Харлоу провели вычисления, из которых следует, что это голографическое «проявление» пространства-времени работает точно как квантовый код исправления ошибок. В журнале физики высоких энергий они опубликовали предположение о том, что само пространство-время является кодом – по крайней мере, в антидеситтеровском пространстве. Работа породила целую волну активности в сообществе исследователей квантовой гравитации, и были открыты новые квантовые коды исправления ошибок, включающие в себя больше свойств пространства-времени.
Джон Прескил, физик-теоретик из Калифорнийского технологического института, говорит, что квантовое исправление ошибок объясняет надёжность пространства-времени, несмотря на то, что оно соткано из хрупкого квантового вещества. «Нам не приходится обходиться с этой идеей слишком осторожно, чтобы не развалить геометрию, — сказал Прескил. – Я думаю, эта связь с квантовым исправлением ошибок – глубочайшее объяснение из всех, что у нас есть».
Язык квантового исправления ошибок также начинает позволять исследователям изучать загадки чёрных дыр: сферических участков, в которых пространство-время так сильно искривляется к центру, что оттуда не может убежать даже свет. «Все следы ведут к чёрным дырам», — сказал Альмейри, работающий в данное время в Институте передовых исследований в Принстоне. В этих наполненных парадоксами местах гравитация достигает своего пика, а общая теория относительности Эйнштейна перестаёт работать. «Есть некоторые признаки того, что если мы поймём, какой код использует пространство-время, — сказал он, — это может помочь нам понять внутреннее строение чёрных дыр».
В качестве бонуса исследователи надеются, что голографическое пространство-время сможет подсказать и способ масштабировать КК, реализовав давнюю мечту Шора и других. «Пространство-время умнее нас, — сказал Альмейри. – В эти конструкции встроен очень эффективный квантовый код исправления ошибок».

Ахмед Альмейри, Си Дон и Даниель Харлоу
Как как же работают квантовые коды исправления ошибок? Секрет сохранения информации в неспокойных кубитах состоит в том, чтобы хранить её не в отдельных кубитах, а в системе множества запутанных кубитов.
В качестве простого примера рассмотрим код для трёх кубитов: они использует три «физических» кубита для защиты одного «логического» кубита информации от переворачивания битов. Такой код не особенно полезен для квантового исправления ошибок, поскольку не защищает от переворота фаз, но объясняющую функцию выполняет. Состояние логического кубита |0> соответствует нахождению всех трёх физических кубитов в состоянии |0>, а состояние |1> соответствует тому, что все три находятся в состоянии |1>. Система находится в суперпозиции этих состояний, что записывается, как |000> + |111>. Но, допустим, у одного из кубитов перебросился бит. Как обнаружить и исправить ошибку, не измеряя кубиты напрямую?
В квантовый контур кубит можно ввести через два шлюза. Один проверяет «чётность» первого и второго физических кубитов – одинаковые они или различные – а другой проверяет чётность первого и третьего. Когда ошибок нет (то есть, кубиты находятся в состоянии |000> + |111>), измеряющие чётность шлюзы определяют, что первый и второй, а также первый и третий кубиты идентичны. Однако если у первого кубита случайно перебрасывается бит, это приводит к состоянию |100> + |011>, и шлюз определяет различие в обеих парах. Переброс бита во втором кубите даёт |010> + |101>, шлюзы определяют, что первый и второй кубит отличаются, а второй и третий совпадают; в случае переброса третьего кубита результат будет «совпадают; различаются». Эти уникальные результаты показывают, какая именно корректирующая хирургия необходима, и необходима ли она вообще – то есть, операция переброса назад первого, второго или третьего физического кубита, не приводящая к коллапсу логического кубита. «Квантовое исправления ошибок кажется мне магией», — сказал Альмейри.
Лучшие коды исправления обычно могут восстановить всю закодированную информацию на основе чуть большего количества физических кубитов, чем половина, даже если все остальные повреждены. Именно это натолкнуло Альмейри, Дона и Харлоу в 204 году на мысль о возможном наличии связи между квантового исправления ошибок и тем, как антидеситтеровское пространство (АдС) возникает из квантовой запутанности.
Важно отметить, что АдС пространство отличается от геометрии пространства-времени нашего, деситтеровского пространства. Наша Вселенная насыщена положительной энергией вакуума, заставляющей её расширяться без границ, в то время, как в АдС пространстве энергия вакуума отрицательна, из-за чего оно приобретает гиперболическую геометрию, похожую на «Предел – круг» М. К. Эшера. Мозаичные существа Эшера становятся всё меньше, распространяясь от центра круга, в итоге исчезая на периметре. Точно так же пространственное измерение, исходящее из центра АдС пространства, постоянно сжимается и в итоге исчезает, обозначая внешнюю границу вселенной. АдС пространство стало популярным у физиков-теоретиков, изучающих квантовую гравитацию, в 1997, после того, как известный физик Хуан Малдасена открыл, что его изогнутая ткань пространства-времени «голографически дуальна» квантовой теории частиц, существующих на границе, свободной от гравитации и с меньшим числом измерений.

Гиперболическая геометрия на гравюре Эшера 1959 года «Предел – круг III» изображает АдС пространство
Изучая, как работает дуальность, как и сотни других физиков в последние пару десятилетий, Альмейри с коллегами заметили, что любую точку внутри АдС пространства можно создать на основе чуть больше половины границы – точно так же, как оптимальный квантовый код исправления ошибок.
В их работе, предполагающей, что голографическое пространство-время и квантовое исправление ошибок суть одно и то же, они описали, как даже простейший код можно представить в виде двумерной голограммы. Она состоит из трёх «кутритов» – частиц, существующих в одном из трёх состояний – находящихся на равных расстояниях друг от друга по кругу. Запутанное трио кутритов кодирует один логический кутрит, соответствующий одной точке пространства-времени в центре круга. Код защищает точку от стирания любого из трёх кутритов.
Конечно, одна точка – это так себе вселенная. В 2015 году Харлоу, Прескил, Фернандо Паставский и Бени Йошида обнаружили ещё один голографический код, названный HaPPY, перенимающий больше свойств АдС пространства. Код делит пространство на пятисторонние плитки – «как маленькие детальки конструктора Tinkertoy», сказал Патрик Хейден из Стэнфордского университета, руководитель исследований. Каждая деталька представляет одну точку пространства-времени. «Эти плитки играли бы роль рыб в мозаике Эшера», — сказал Хейден.
В коде HaPPY и других открытых голографических схемах исправления ошибок, всё внутри региона пространства-времени, называемого «клином запутанности» [entanglement wedge], можно воссоздать из кубитов, находящихся в регионе, соседнем с границей. У перекрывающиеся регионов на границе будут накладываться клинья запутанности, сказал Хейден, точно так же, как логический кубит в КК можно воссоздать из множества различных подмножеств физических кубитов. «И вот здесь вступает в игру свойство исправления ошибок».
«Квантовое исправление ошибок даёт нам обобщённое представление о геометрии в этом кодовом языке», — сказал Прескил. Тот же язык, сказал он, «вероятно, можно применять и к более обобщённым ситуациям», — в частности, к такой деситтеровской вселенной, как наша. Но оказалось, что деситтеровское пространство, у которого нет границ, гораздо сложнее представить в виде голограммы.
Пока что такие исследователи, как Альмейри, Харлоу и Хейден, работают с АдС пространством, поскольку у него много общих черт с деситтеровским миром, но при этом оно легче поддаётся изучению. Геометрии пространства-времени обоих пространств подчиняются теории Эйнштейна, они просто изгибаются в разных направлениях. И что, вероятно, гораздо важнее, во вселенных обоих типов есть чёрные дыры. «Самое фундаментальное свойство гравитации – наличие чёрных дыр», — сказал Харлоу, сейчас работающий адъюнкт-профессором физики в MIT. «Именно это отличает гравитацию от всех остальных взаимодействий. Поэтому с квантовой гравитацией так тяжело».
Язык квантового исправления ошибок обеспечил новый способ описания чёрных дыр. Наличие чёрной дыры определяется, как «отказ исправляемости», сказал Хейден: «Когда у вас появляется так много ошибок, что вы уже не можете отслеживать, что происходит в большом количестве пространства-времени, вы приходите к чёрной дыре. Это что-то типа сливного отверстия для невежества».
Невежество неизбежно накапливается в отношении внутренностей чёрных дыр. Откровение Стивена Хокинга 1974-го года о том, что ЧД излучают тепло, и, следовательно, рано или поздно испаряются, породило печально известный «парадокс исчезновения информации в ЧД», который спрашивает, что происходит со всей проглоченной ЧД информацией. Эта проблема может быть связана с космологией и рождением Вселенной, поскольку расширение сингулярности Большого взрыва очень похоже на гравитационный коллапс ЧД в обратном воспроизведении.
АдС пространство упрощает вопрос об информации. Поскольку граница АдС вселенной голографически дуальна всему, что в ней есть – всем ЧД и прочему – то информация, падающая в ЧД, гарантированно не потеряется; она всегда будет голографически закодирована на границе вселенной. Расчёты показывают, что для реконструкции информации о внутренностях чёрной дыры на основе кубитов на границе, вам потребуется доступ к запутанным кубитам примерно на трёх четвертях границы. «Чуть больше половины уже недостаточно», — сказал Альмейри. Он добавил, что требование трёх четвертей должно сообщать что-то важное о квантовой гравитации, но вопрос о том, почему получается именно такая доля, «всё ещё остаётся открытым».
В первой заявке Альмейри от 2012 года, высокий худой физик из ОАЭ и три его соратника углубили информационный парадокс. Их рассуждения предполагали, что информация вообще может не попадать внутрь ЧД, поскольку её остановит «файервол» на горизонте событий ЧД.
Как и большинство физиков, Альмейри не верит в то, что файерволы ЧД реально существуют, однако обойти это понятие оказалось сложно. Сейчас он считает, что формированию файерволов препятствует квантовое исправление ошибок, защищающая информацию даже после пересечения горизонта ЧД. В его последней самостоятельной работе, появившейся в октябре, он сообщил, что квантовое исправление ошибок «необходима для поддержки гладкости пространства-времени на горизонте» чёрной дыры из двух составных частей, известной, как червоточина. Он предполагает, что квантовое исправление ошибок не только предотвращает файерволы, но и позволяет кубитам убегать из ЧД после падения в неё, поскольку нити запутанности между внутренней и наружней частями ЧД сами похожи на миниатюрные червоточины. Это объяснило бы парадокс Хокинга.
В этом году министерство обороны выделило финансирование на исследования голографического пространства-времени, в частности потому, что подвижки в этой области могут привести к появлению более эффективных кодов исправления ошибок для квантовых компьютеров.
Физике же ещё придётся разобраться с тем, можно ли описать деситтеровскую вселенную, например, нашу, при помощи голограммы и в терминах кубитов и кодов. «Вся эта связь известна для мира, который очевидно не является нашим», — сказал Ааронсон. В работе от прошлого года Дон, сейчас работающий в Калифорнийском университете в Санта-Барбаре, и его соавторы Ева Сильверстейн и Гонзало Торроба, сделали шаг в деситтеровском направлении, пытаясь создать примитивное голографическое описание. Исследователи пока ещё изучают это предложение, но Прескил считает, что язык квантового исправления ошибок в итоге всё же будет перенесён в реальное пространство-время.
«На самом деле пространство удерживается благодаря запутанности, — сказал он. – Если вы хотите сшить пространство-время из маленьких кусочков, их надо правильно запутать. А правильно будет сделать это, создав квантовый код исправления ошибок».
Исследователи, финансируемые армией и военно-воздушными силами США, сделали шаг в создании отказоустойчивого квантового компьютера. Он обеспечит расширенные возможности обработки данных.
Читайте «Хайтек» в
Квантовые вычисления — путь к новым вычислительным возможностям того Он также может способствовать открытию материалов, искусственному интеллекту , биохимической инженерии и многим другим дисциплинам, необходимым для будущих военных; однако, поскольку кубиты, фундаментальные строительные блоки квантовых компьютеров, по своей сути хрупки, давним препятствием для квантовых вычислений была эффективная реализация квантовой коррекции ошибок. Кроме того, военные планируют «сражаться и побеждать» в так называемых многодоменных операциях как раз используя квантовые вычисления, сообщает Научно-исследовательская лаборатория армии США.
Исследователи из Массачусетского университета в Амхерсте определили способ защиты квантовой информации от общего источника ошибок в сверхпроводящих системах, одной из ведущих платформ для реализации крупномасштабных квантовых компьютеров. В исследовании, опубликованном в журнале Nature, ученые реализовали новый способ спонтанного исправления квантовых ошибок.
Сегодняшние компьютеры построены с транзисторами, представляющими классические биты, либо 1, либо 0. В свою очередь, квантовые вычисления — это новая парадигма вычислений с использованием квантовых битов или кубитов, где квантовая суперпозиция и запутанность могут использоваться для экспоненциального увеличения вычислительной мощности.
Существующие демонстрации квантовой коррекции ошибок активны. Это значит, что они требуют периодической проверки на наличие ошибок и их немедленного исправления. В свою очередь, это требует аппаратных ресурсов и, таким образом, препятствует масштабированию квантовых компьютеров.
Напротив, в эксперименте исследователей достигается пассивная квантовая коррекция ошибок путем корректировки трения, или диссипации, испытываемой кубитом. Поскольку трение обычно считается важным препятствием квантовой когерентности, этот результат может показаться неожиданным. Хитрость в том, что диссипация должна быть спроектирована специально квантовым образом.
Эта общая стратегия была известна в теории около двух десятилетий, но практический способ получить такую диссипацию и использовать ее для квантовой коррекции ошибок было сложной задачей.
«Демонстрация таких нетрадиционных подходов, мы надеемся, подтолкнет к появлению более умных идей для преодоления некоторых из самых сложных проблем квантовой науки», — объясняет Грейс Меткалф, женщина-программный руководитель отдела квантовой информатики в AFOSR.
Исследователи заявили, что подразумевается, что может быть больше способов защитить кубиты от ошибок и сделать это с меньшими затратами.
«Хотя наш эксперимент все еще является довольно элементарной демонстрацией, мы наконец реализовали эту противоречивую теоретическую возможность диссипативных QEC, — сказал доктор Чен Ван, физик из Массачусетского университета в Амхерсте. — Этот эксперимент поднимает перспективу создания полезного отказоустойчивого квантового компьютера в среднесрочной и долгосрочной перспективе».
Читать далее
Физики создали аналог черной дыры и подтвердили теорию Хокинга. К чему это приведет?
Уран получил статус самой странной планеты в Солнечной системе. Почему?
Научный прибор SuperCam с ровера Perseverance прислал на Землю первые результаты
Рис. 4. Сравнение временных затрат Рис. 5. Сравнение критерия адекватности
Анализ результатов эксперимента показывает, что применение предварительной ориентации контуров сокращает время последующей деформации и приближает значения критерия адекватности к его максимальному значению. В рамках дальнейших исследований планируется модифицировать процедуру предварительной ориентации применительно к сплайновому представлению контуров и представления трехмерных объектов как сплошных тел.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. McInerney T., Terzopoulos D. Deformable Models in Medical Image Analysis: A Survey. Medical Image Analysis, 1996, 1(2):91-108
2. Christopher Lee. Wyatt Extending the geometric deformable model for use in medical image analysis. PhD dissertation, Wake forest university, 2000. — 56 p.
3. Бабков В.С. Застосування методу “деформованих моделей“ для реконструкції органів в КТ за умови обмеженої кількості вхідної інформації. Вісник Житомирського інженерно-технологічного інституту. Спеціальний випуск за матеріалами Міжнародної науково-технічної конференції “ІКТ-2002”. — 207-214 сс
4. Samuel D. Fenster Training, Evaluation and Local Adaptation in Deformable Models. PhD dissertation, Columbia university, 2000. — 91 p.
С. М. Гушанский, Р. А. Погорелов КВАНТОВЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОШИБКИ
Практическая реализация квантовых вычислений в настоящее время ограничена рядом проблем, среди которых следует выделить погрешность измерения состояния квантовой системы, нестабильность квантовых состояний вследствие декогерентности. Невозможность полной изоляции кубитов приводит к возникновению в них разнотипных ошибок (битовых, фазовых, битофазовых). Поэтому столь актуальным сейчас является создание эффективных методов квантовой коррекции. Использование квантовых кодов коррекции ошибок позволяет бороться с декогерентностью, восстанавливая квантовые состояния, уменьшая одновременно погрешность измерений.
В силу специфики пространства состояний кубита, считается, что его взаимодействие с окружающей средой может привести к ошибке одного из трех возможных типов [1]:
1) битовые ошибки, приводящие к перебросу кубита |0 ® Ц, Ц ® |0. Их иначе еще называют X — ошибками, так как их можно представить, как результат произведения матрицы Паули Ух и вектора состояния кубита;
2) фазовые ошибки, приводящие к перевороту фазы кубита |0 ® |0,
1 ® _| 1. Их называют Z — ошибками (соответствующая матрица Паули У г);
3) смешанные битофазовые ошибки, приводящие одновременно и к перебросу кубита и перевороту фазы |0 ® Ц, Ц ®-|0 . Их называют Y — ошибками
(соответствующая матрица Паули Уу ).
Таким образом, принимая во внимание факт, что взаимодействие с окружающей средой может и не повлиять на квантовое состояние, любую квантовую ошибку в единичном кубите можно представить в виде линейной комбинации всех видов ошибок. Если через у обозначить произвольное состояние единичного
кубита, то возникновение ошибки можно представить следующей схемой [2]:
у) ® (e1I + e2X + ^ + е4Z)|у) = ^eiEi у) ,
i
где I — единичная матрица (отсутствие ошибки), X, Y, 2 — соответствуют, как уже было сказано, матрицам Паули Уг, Уу , Уг. е1…е4 — некоторые коэффициенты, в
общем случае комплексные, Е{ — общее обозначение матриц элементарных преобразований.
Понятно, что процесс появления ошибок вследствие декогерентности может протекать с разной интенсивностью. Сделаем ряд важных предположений, жестко регламентирующий круг ошибок, с которыми можно бороться, используя квантовые коды коррекции:
— воздействие окружающей среды на квантовую систему будем считать ограниченным. То есть существует такое конечное время Д/, в течение которого вероятность, что ошибка появится в двух или более кубитах, бесконечно мала.
— все ошибки будем считать слабокоррелированными. Это означает, что ошибка, возникающая в одном кубите, не влияет на состояние другого.
— будем полагать, что все ошибки носят случайный характер, т.е. отсутствуют так называемые систематические ошибки.
Если возникающие ошибки удовлетворяют этим условиям, то для их обнаружения и устранения возможно использование квантовых кодов коррекции.
Идея отказоустойчивых кодов заимствована из классической теории информации, однако их реализация в случае кодирования квантовых состояний заметно отличается от классической ситуации.
Пусть £ — произвольное состояние в гильбертовом пространстве М. Кодом называется изометрическое отображение V : М ® N , переводящее состояния £ в кодирующие состояния VS в гильбертовом пространстве N [3].
Квантовый код V может обнаружить возникновение ошибки, если размерность гильбертова пространства N больше размерности пространства М. Иными словами, как и в классическом случае, любой отказоустойчивый квантовый код базируется на принципе избыточного кодирования.
Пусть преобразование квантового состояния в ходе кодирования и последующего возникновения ошибки описывается следующей схемой [3]:
£ ® V£ ®Ф(V£),
где Фё Е — оператор ошибки, определенного класса Е.
Тогда код V называется кодом, исправляющим ошибки, если существует такой оператор ^, что
¥[Ф( VS)]® с (Ф) 5,
для любого Фё Е. Здесь с (Ф) — некоторая константа, зависящая от оператора
ошибки [3]. Ее называют анциллой синдрома ошибки, так как ее значение зависит только от вида ошибки и ее локализации.
Система | )
Кодирующая
0)
Рис. 1. Базовая схема построения квантовых кодов коррекции
Полученная на основании этих утверждений схема любого отказоустойчивого кода приведена на рис. 1 [4]. Здесь под кодирующей анциллой понимается совокупность кубитов, посредством которых происходит кодирование состояния квантовой системы. Процесс кодирования превращает состояние кодирующей ан-циллы в отображение состояния исходной квантовой системы. Анцилла синдрома ошибки является также ансамблем из нескольких кубитов. Она введена с целью определения типа возникшей ошибки и ее локализации. Процесс коррекции ошибок является двухступенчатым:
— посредством квантовых схем, индивидуальных для каждого кода коррекции, анализируется состояние кодирующей анциллы, в ходе чего происходит изменение состояния анциллы синдрома;
— состояние анциллы синдрома измеряется, и, в зависимости от него, с кодирующей анциллой осуществляются те или иные преобразования. Т ак как ошибка единичного кубита определяется унитарным преобразованием, то для восстановления состояния достаточно лишь повторно применить к ошибочному кубиту преобразование, вызвавшее ошибку.
По аналогии с классическим кодированием, для обозначения квантовых кодов коррекции используется обозначение вида [[п, к, ^]. Здесь п — определяет полное число кубитов кода, к — число информационных кубитов, d — называется минимальным кодовым расстоянием кода, определяется как минимальное расстояние Хемминга [5] между всеми возможными парами кодовых слов (двойные скобки отличают квантовый код от классического).
Всё многообразие квантовых кодов коррекции принято разделять на три класса [4]:
1) аддитивные стабилизирующие (симплексные) коды. Наиболее обширный класс кодов базируется на классических кодах коррекции, в связи с чем и получили наибольшее развитие. Стабилизирующие коды можно проклассифицировать по минимальному кодовому расстоянию [8]:
— класс кодов с кодовым расстоянием два. Общее обозначение [[n, n-2, 2]];
— класс кодов с кодовым расстоянием три. Общее обозначение [[2, 2-/-2, 3]];
— класс кодов с кодовым расстоянием четыре. Общее обозначение [[2, 2-2j-2, 4]].
Здесь j может принимать произвольные целые значения. Такая классификация стабилизирующих кодов не является единственной и общепринятой. Чаще можно встретиться с классификацией по виду матрицы стабилизатора кода:
• циклические коды;
• CSS — коды;
• Амплитудно-защищающие коды они же “code over GF(4)”;
2) неаддитивные коды, не являющиеся стабилизирующими;
3) каскадные или Клиффорд-коды. Вероятность ошибки для них намного ниже, чем для двух предыдущих, за что приходится платить многоуровневой структурой кода, а как следствие увеличением числа кубитов. Каскадные коды являются обобщением аддитивных стабилизирующих кодов. В классической теории кодирования они имеют себе аналог, называемый сверточными кодами.
В основе квантового помехоустойчивого кодирования лежит код Хемминга, который представляет собой код коррекции ошибки единичного бита [5]. Длина кодового слова равна 7 битам: 4 информационных бита, 3 — контрольных. Суть кодирования заключается в установке контрольных битов по определенному правилу в зависимости от информационных.
Для обнаружения ошибки в кодовом слове используется так называемая матрица проверки, имеющая вид
0 0 0 1 1 1 1
0 1 1 0 0 1 1
1 0 1 0 1 0 1
V /
Если кодовое слово представить в виде матрицы столбца, то произведение матрицы H на этот столбец даст столбец из трех бит (при умножении матриц сложение заменяется сложением по модулю два), который определяет номер переброшенного бита или говорит об отсутствии ошибки (если он нулевой).
На основе кода Хемминга рассмотрим пример несложного, но важного се-микубитового кода, предложенного Эндрю Стином. Он позволяет, ориентируясь на классическое кодирование, наглядно рассмотреть общий принцип действия квантовых кодов коррекции. Данный код позволяет кодировать пространство состояний единичного кубита, используя для этого 7 кубитов. Иными словами, мы имеем дело с отображением произвольного состояния двумерного комплексного гильбертового пространства в состояние в 128 — мерном гильбертовом пространстве. Код Стина относится к уже упомянутому классу CSS — кодов. Предполагается, что любой вид ошибки может произойти в любом из семи кубитов, но только в одном (ограниченность воздействия окружающей среды). При кодировании состояния кубита кодом Стина используют суперпозицию только тех базисных векторов 128 — мерного комплексного гильбертового пространства, которые соответствуют множеству безошибочных кодовых слов кода Хемминга. Причем, при кодировании 10 используются только комбинации с четным числом единиц, а при
кодировании Ц , наоборот, с нечетным [6].
10
2^2
X И
ееп фе Р
V
^ (10000000) + | 0001111 + 1 °110011) + | 0111100)
242
|1010101) +11011010) +|1100110) +11101001))
2у12
ойй фе Р
V
^ (11111111 +11110000) +|1001100) +11000011) +
242
+ |0101010) + |0100101 + 10011001 +10010110)
Используя такой метод кодирования можно, как и в классическом случае, определить, в каком из кубитов произошла ошибка, однако обнаруженной может быть только X — ошибка. Процесс обнаружения ошибки запишем как
ф)®) ®|ф)®| Иф) ,
‘ / I / апс I ‘ / I ‘ / апс
вектор Иф) аналогичен трехбитовому столбцу для кода Хемминга, следова-
I ‘ ‘апс
тельно, он также однозначно задает локализацию X — ошибки.
рис.2.
Определение X — ошибки для семикубитового кода Стина приведено на
+
с 1
с > с > г > о
и и и и и и Ш г л г л С л с Л
с и и и и и и и к К К Э
Рис. 2
Теперь мы можем привести квантовую схему, позволяющую обнаружить X
— ошибку в любом из семи кубитов кода (рис. 2). В схеме используются общепринятые обозначения для управляемых гейтов (точкой обозначается управляющий кубит, а кружком с крестиком — управляемый). Данная схема позволяет понять, как происходит выявление синдрома ошибки для кода Стина. Каждый кубит ан-циллы синдрома есть результат суммирования по модулю 2 определенных кубитов кода. Причем если сравнить матрицу проверки кода Хемминга и схему (рис. 2), то видно, что именно матрица проверки и определяет номера кубитов кода, суммируемых (по модулю 2) в каждом кубите анциллы.
Однако понятно, что помимо X — ошибок необходимо бороться и с 2 -ошибками (если можно будет ликвидировать оба типа этих ошибок, то У — ошибки автоматически также будут ликвидированы, так как их можно представить как результат последовательного действия первых двух). Как известно, понятия битовая и фазовая ошибки уместны лишь при введенном базисе. Смена базиса определенным образом превращает битовую ошибку в фазовую и наоборот. Преобразование, осуществляющее поворот базиса, называется преобразованием Адамара [7]
R = V2
1 1
1 -1
Преобразование Адамара переводит кодирующие состояния |о и h в
I / code I / code
новые кодирующие состояния
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
l 0^c0de 42 ^ 0code ^1 code ) ’
^ code 42 ^ ^ code ^ 1 code )
Учитывая, что преобразование Адамара унитарно, т.е. двукратное его применение переведет систему в исходное состояние, то возможная реализация схемы, позволяющей обнаружить любые ошибки в семикубитном коде Стина, будет иметь вид (рис. 3).
Определение любой ошибки для кода Стина показано на рис. 3.
е 5 ; Pi У -ч э-е
г ) v Г i г > Г
О . ) к. ) 1 ) V
— R -« »_ О А
— R -i 1- R 4
— R -t р 1
— R ч R
Г л г > г >
U J L U L U L и > л г л >
Z к ) К i—У ) L X э
|я )
I / СИ
я
Рис. 3
В предложенном варианте квантовой схемы (рис. 3) используются две ан-циллы (анцилла X — ошибки и анцилла 2 — ошибки). Так как по нашему предположению ошибка может произойти лишь в одном кубите, то возможно 4 исхода обнаружения ошибки:
1) обе анциллы нулевые: ошибки не произошло;
2) анциллаX нулевая, а анцилла 2 нет: произошла 2 — ошибка в кубите, чей номер содержится в анцилле 2;
3) анцилла 2 нулевая, а анцилла X нет: произошла X — ошибка в кубите, чей номер содержится в анцилле X;
4) обе анциллы ненулевые и содержат одно и то же значение: произошла У
— ошибка в кубите, чей номер содержится в анцилле X и 2.
Если установлен тип ошибки и ее локализация, то процесс коррекции заключается лишь в применении к ошибочному кубиту соответствующего преобразования: X, У, или 2.
Рассмотрим процесс обнаружения ошибки на примере. Пусть имеется исходное состояние единичного кубита:
И-tjI»)+$!>>•
тогда закодированное состояние, согласно правилам кодирования кода Стина, будет иметь вид
1 ¡2 1
И cd — ^1°) code + ^l1) code — ^ (I 0000000) + l 0001111) + l 0110011) + l O1111O0 +
+ | 1010101 +11011010 +11100110 + (1101001) ) + —U (11111111 +11110000 +11001100) +
2V3
+ | 1000011 + 10101010 + | 0100101 + 10011001 + 10010110 )
Предположим, что ошибка представляет собой просто X — преобразование, примененное к третьему кубиту кода, т.е. оператор ошибки равен
Ф = IÄIÄ X ÄIÄIÄIÄI,
тогда в результате ошибки закодированное состояние примет вид
ф|у)^ — -V (10010000) + | 0011111 + | 0100011 + | 0101100) +11000101 +11001010) +
co e 2V6
+ (1110110 + (1111001) + ~Г» (11101111 + (1100000 + (1011100 + (1010011 + 10111010 + 2V3 + |0110101 + 10001001 + 10000110)
обозначим состояние анциллы синдрома как (ccc), первоначально c1 — c2 — c3 — 0. Осуществив преобразования, согласно схеме (рис. 3), получим для нашего случая
c1 — x4 @ x5 @ x6 @ x7 — 0
c2 — x2 @ x3 @ x6 @ x7 -1 ■
c3 — x1 @ x3 @ x5 @ x7 -1
Видно, что состояние анциллы синдрома |011) однозначно указывает на X
— ошибку в третьем кубите. Для ее устранения достаточно лишь повторно применить оператор ошибки Ф к закодированному состоянию.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Стин Э. Квантовые вычисления. —Москва-Ижевск: РХД, 2000.
2. Рифель Е. Полак В. Основы квантовых вычислений.
3. ХолевоА. С. Введение в квантовую теорию информации. —Москва: МЦНМО, 2002. — 128 с.
4. GrassM. Quantum Error-Correcting Codes.
5. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ.- Москва: Мир, 1986.
6. Preskill J. Fault-Tolerant Quantum Computation. arXiv:quant-ph/9712048 v1 19 Dec 1997.
7. Steane A. M. Error correcting codes in quantum theory, Phys. Rev. Lett. 77, 793 1996.
8. Gottesman D. Stabilizer Codes and Quantum Error Correction. arXiv:quant-ph/9705052 v1 28 May 1997.
Физики показали как можно уменьшить число кубитов для коррекции ошибок в квантовых вычислителях. Они предложили код коррекции ошибок, в котором шум спадает экспоненциально в зависимости от числа кубитов и рассчитали вклады разных типов ошибок. Работа опубликована в журнале Nature.
Коррекция ошибок в квантовых вычислителях — не менее важная задача, чем создание работоспособного устройства. Полностью избавиться от шума на практике невозможно, а научиться корректировать работу вычислителя с учетом шума возможно, хоть и непросто. Сложности в создании кодов коррекции ошибок возникают из-за ограничений — нельзя сильно увеличивать число кубитов, задействованных в коррекции ошибок, но при этом следить за тем, чтобы вероятность ошибки оставалась небольшой. Необходимость использовать дополнительные кубиты связана с тем, что один логический кубит кодируется несколькими физическими — первый несет нужную информацию, а остальные (измеряемые) «следят» за возникновением ошибок в нем. Понятно, что сто физических кубитов в качестве одного логического позволят очень точно отслеживать и исправлять ошибки, но такой подход только добавляет сложностей в создании экспериментального устройства. Поэтому хороший метод коррекции ошибок не просто должен снижать шум, но и делать это с помощью наименьшего числа вспомогательных кубитов.
Ученые из Google AI во главе с Джулианом Келли (Julian Kelly) показали, что уровень ошибок может падать экспоненциально с увеличением числа кубитов. Они разработали код, для которого возникает такая зависимость, сравнили его с поверхностным кодом для квантовой коррекции ошибок и подробно изучили вклады разных типов ошибок.
Для моделирования и экспериментов физики использовали 54-кубитной сверхпроводящий вычислитель Sycamore, известный благодаря статье о квантовом превосходстве. Он представляет собой двумерную матрицу кубитов, каждый из которых связан с четырьмя соседями и позволяет реализовывать два типа кодов коррекции ошибок: код с повторением и поверхностный. Работа первого использует цепочку из физических кубитов и получается, что на каждый информативный кубит есть два соседа, которые следят за ошибками, а второй «расползается» по поверхности и на каждый кубит приходится по 4 следящих соседа. Так как ошибки могут возникать не только в самом кубите, но и в операциях (вентилях), которым он подвергается, то поверхностный код кажется эффективнее — в отличие от кода-цепочки он может контролировать более сложные двухкубитные операции. Помимо этого, как можно догадаться, код с повторением требует повторения фиксированного набора итераций, а время жизни кубита ограничено. С другой, для поверхностного кода нужно большее число кубитов, что на данный момент непросто.
Авторы применяли первый тип коррекции ошибок для цепочки из 21 кубита (11 информативных) и смогли получить заданное состояние кубитов с ошибкой около 0.5 процентов и откалибровать систему так, чтобы уровень ошибки в операции CZ (контролируемый Z-вентиль) оказался 0.62 процента. Кроме этого, процент ошибок оказался стабильным — он не менялся в течение 50 циклов коррекции.
В повторяющихся кодах можно выделить три типа самых распространенных ошибок — пространственная, временная и пространственно-временная. Индикатор первой — ошибка в одном и том же цикле в двух кубитах-соседях к информативному, вторая возникает в разных временных циклах, а третья — комбинация первых двух. Для того чтобы оценить влияние каждой из них и проверить наличие других неучтенных ошибок, ученые следили за корреляциями между всеми измеряемыми кубитами в цепочке. В идеальной цепочке без ошибок и возможных связей между кубитами корреляции не должно быть. Наличие корреляций в соседних по времени и пространству кубитах говорит об ошибках в вычислителе. Как оказалось, именно эти два типа ошибок вносят основной вклад, в то время как пространственно-временная встречается почти в десять раз реже, как и еще два других типа ошибок. Первый связан с тем, что цепочка не расположена вдоль одной прямой, а загибается, поэтому некоторые кубиты оказываются рядом, хоть и различаются номерами больше чем на 1. А второй возникает между разными циклами и, по мнению физиков, связан с применением вентилей и термализацией.
Для того чтобы показать преимущество исследуемого кода, авторы получили зависимость итогового процента ошибок от числа кубитов. Эта зависимость оказалась экспоненциальной (быстро спадает), то есть при увеличении числа кубитов от 5 до 21 вероятность ошибки падает в 100 раз. Экспериментальная проверка одномерного и двумерного поверхностного кодов коррекции подтвердила результаты моделирования и показала, что архитектура Sycamore имеет процент ошибок значительно меньший, чем пороговое значения для поверхностного кода.
Несмотря на то, что авторам удалось показать быстрое спадание уровня ошибок при увеличении числа кубитов для разработанного кода и выявить ошибки, которые вносят наибольший вклад, для реальных устройств этого пока еще недостаточно. Поэтому ученые планируют дальнейшие исследования для нивелирования ошибок и механизмов их возникновения.
Физики исследуют и другие типы кодов для коррекции ошибок: изначально в Google использовали торический код для матрицы 7 на 7, а домашнее задание студента из университета Сиднея вылилось в разработку эффективного поверхностного кода.
Оксана Борзенкова
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.











