Как свести влияние систематических ошибок к минимуму путем

Лекции по дисциплине Геодезия (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Такая наука, как геодезия тесно связана с измерениями, которые сопровождаются неизбежными ошибками. Если обозначим:

У – истинное значение измеряемой величины;

у – результат измерений;

— истинная ошибка.

то истинная ошибка может быть вычислена по формуле:

(15)

2 Виды ошибок измерений

По источникам и характеру ошибки делятся на грубые, систематические и случайные.

Грубые ошибки являются, как правило, следствие промахов, просчетов в измерениях, неисправностями инструментов и приборов, резким ухудшением внешних условий и пр. Они обнаруживаются при несоблюдении допусков и контролей и исключаются повторными измерениями.

Систематические – те, которые знаком или величиной однообразно повторяются в многократных измерениях. Их источниками являются неисправности в применяемых инструментах, неточная установка инструментов, личные физиологические особенности наблюдателя, влияние внешних факторов и т. п.

Примеры систематических ошибок:

— ошибка в измеренном значении длины линии на местности из-за отклонения мерной ленты от створа;

— ошибка в определении длины мерного прибора (ошибка компарирования).Эта ошибка постоянна и действует пропорционально измеренному расстоянию;

— систематическая ошибка нанесения шрихов лимба теодолита.

Влияние систематических ошибок сводят к допустимому минимуму путем тщательной поверки инструментов, применения соответствующей методики измерений, а также путем введения поправок в результаты измерений.

Некоторые рекомендации по уменьшению влияния систематических ошибок измерения:

— устанавливают закон появления систематической ошибки, после чего ошибку устраняют введением поправки в результаты измерений. Например, эталонирование мерного прибора и введение потом поправок за длину и температуру;

— применяют соответствующую методику измерений, чтобы систематические ошибки меняли знак. Например:

1) отсчитывание по диаметрально противоположным штрихам лимба, что приводит к исключению влияния эксцентриситета алидады;

2) перестановка лимба между приёмами на угол 180˚/n, где n-число приёмов ( при этом ослабевает влияние систематических ошибок штрихов лимба);

— используют определённую методику обработки результатов измерений. Например, углы и координаты вытянутого теодолитного хода уравнивают раздельно. Это ведёт к ослаблению влияния систематических ошибок угловых и линейных измерений.

Таким образом, будем считать, что результаты измерений содержат только слуайные ошибки, т. е. такие, размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным.

3 Свойства случайных ошибок

Величину и знак случайных погрешностей установить нельзя.

Примеры случайных ошибок:

— ошибки отсчитывания по угломерному кругу;

— часть ошибки визирования, обусловленную колебаниями изображения;

— случайные ошибки нанесения штрихов лимба;

— влияние вибрации сигнала;

— ошибка отсчитывания по нивелирной рейке;

— ошибка за округление чисел при вычислениях.

Если результаты измерений содержат только случайные ошибки (грубые и систематические исключают), то

Чем ближе результат измерений к истинному значению, тем он точнее. Чем меньше ошибки, тем выше точность.

4 Обработка рядя равноточных измерений.

По точности результаты измерений разделяют на равноточные и неравноточные.

Под равноточными понимают однородные результаты, полученные при измерениях одним и тем же инструментом, одинаковым числом приемов, одним и тем же или равноценными методами и в одинаковых условиях.

5 Критерии оценки точности результатов измерений.

В геодезии необходиом уметь оценивать точность результатов измерений. Основным критерием точности в геодезии является средняя квадратическая ошибка (СКО). Ее математическое выражение:

, (16)

то есть квадрат СКО равен математическому ожиданию квадрата истинной ошибки.

Для оценки точности отдельного измерения применяется формула Гаусса:

или (17)

— случайная ошибка, тоже истинная, но

θ- истинная ошибка в более широком смысле. Она может состоять из случайной и систематической частей.

СПРАВКА: (1777 – 1855гг) – немецкий математик. Автор работ по астрономии. геодезии. физике. Разработал математические основы высшей геодезии, вычисляя погрешности при измерениях, разработал метод наименьших квадратов.

Кроме основной характеристики m, характеризующей влияние случайных ошибок на результаты измерений. иногда применяют дополнительную характеристику – среднюю ошибку

,

но СКО имеет ряд преимуществ по сравнению со средней квадратической погрешностью:

— на величину СКО сильнее влияют большие по абсолютной величине ошибки;

— СКО – устойчивая характеристика, даже при небольшом числе измерений даёт надёжные результаты.

Если — среднее арифметическое или арифметическая средина, то СКО арифметической средины М находится по формуле

где n – число измерений;

m – СКО одного измерения.

Для решения практических задач используется предельная ошибка ∆пред. Для серии ошибок в качестве ∆пред принимается утроенная СКО.

Это допуск, предел, больше которого не должно быть ошибки.

На практике во многих работах для повышения требований к точности измерений за предельную ошибку принимают удвоенную СКО.

Все приведённые выше ошибки называются абсолютными ошибками. Кроме абсолютных бывают относительные ошибки fотн, которыми называют отношение абсолютной ошибки к среднему значению измеряемой величины. Относительная ошибка выражается дробью, числитель которой равен 1, а знаменатель – отношение среднего значения измеряемой величины к абсолютной ошибке.

Приведенная выше формула Гаусса 17 применима для случаев, когда известны истинные значения измеряемых величин (или истинные ошибки). Эти случаи в практике редки. Известны они могут быть например, при моделировании, или за истинные значения принимают результаты измерений более высокой точности.

6 Арифметическая средина и ее средняя квадратичная ошибка

Как правило, истинные значения измеряемых величин неизвестны, но из измерений можно получить наиболее надежный результат – арифметическую средину по формуле:

(18)

=

Вычислив уклонение отдельных измерений от арифметической средины

, (19)

можно СКО одного измерения определить по формуле Бесселя:

(20)

Справка: (1784 – 1846гг) – немецкий астроном. член Берлинской АН. Он один из первых определил расстояние до звёзд. Реформировал методы учёта инструментальных и других ошибок, что повысило точность астрономических измерений.

7Средние квадратичные ошибки функций измеренных величин.

Формулы Гаусса и Бесселя определяют СКО непосредственно измеренных величин. Если определяемая величина является функцией других непосредственно измеряемых величин, то СКО функции может быть найдена по формуле:

где — СКО функции;

— функция многих независимых аргументов ;

— частные производные от функции по каждой переменной (результату измерений);

— СКО каждого результата измерений.

8 Неравноточные измерения.

9 Понятие о весе.

На практике часто производятся неравноточные измерения, которые выполнены в различных условиях, приборами различной точности, различным числом приемов и т. д. В этом случае уже нельзя ограничиваться простым арифметическим средним, а необходимо учитывать степень надежности каждого результата измерений. Надежность результата, выраженная числом, называется его весом. Чем надежнее результат, тем больше его вес. Следовательно, вес связан с точностью результата измерения, которая характеризуется СКО. Поэтому вес результата измерения принимают обратно пропорциональным квадрату СКО, то есть:

, (22)

где — некоторая постоянная величина, коэффициент пропорциональности;

— СКО измерения.

Таким образом, вес – относительная характеристика точности измерений. Использование веса вместо СКО облегчает. упрощает формулы математической обработки в случае неравноточных измерений. Необходим вес и потому, что более точные измерения в большей степени должны влиять на окончательный результат. (Для облегчения задачи отыскивания весов обычно вес какого-либо результата принимают за единицу и относительно его вычисляют веса остальных неизвестных.)

Если вес результат какого-либо измерения принять равным единице, а СКО измерения его обозначить через , то общее выражение веса примет вид:

, (23)

где — ср. кв. ош-ка единицы веса.

В практике геодезических работ в качестве весов принимают:

— при обработке результатов угловых измерений одним и тем же прибором – величины, пропорциональные количеству измерений каждого угла; для суммы углов в ходе, имеющем ni вершин,

— при обработке линейных измерений одним и тем же мерным прибором вес вычисляется по формуле

где si – длина линии;

— при обработке превышений из геометрического нивелирования — величины, обратно пропорциональные длине ходов или числу станций;

— при тригонометрическом нивелировании вес вычисляется по формуле

где si – расстояние между пунктами.

Принципы уравнивания геодезических сетей

1 Уравнивание геодезических сетей по МНК коррелатным способом.

2 Средняя квадратичная ошибка единицы веса

Геодезические измерения характерны тем, что их всегда больше, чем необходимо для определения искомых величин. Необходимыми называют такие измерения, которые позволяют однократно, бесконтрольно найти определяемые величины. Избыточными измерениями называются те, которые выполняют сверх необходимых. Например, для решения треугольника измеряют три угла, тогда как было бы достаточно измерить два угла.

Избыточные измерения позволяют:

— проконтролировать результаты измерений;

— в среднем повысит точность определяемых величин;

— выполнить оценку точности этих величин.

Число избыточных измерений определяется по формуле , (24)

где — число всех измерений в сети;

— число необходимых измерений.

Геодезические измерения ведутся в создаваемых на местности геодезических построениях, истинные элементы которых, в том числе и измеряемые, связаны между собой Математическими зависимостями.

Каждое избыточное измерение приводит к появлению математического соотношения с другими измеренными величинами. Неизбежные ошибки в измерениях приводят к появлению невязок в этих соотношениях. Для устранения невязок необходимо уравнивание результатов измерений.

Уравнивание – это математическая обработка результатов измерений, позволяющая:

— найти наиболее надежные (вероятнейшие) значения неизвестных с оценкой точности полученных результатов;

— исключить все математические противоречия в зависимостях, существующих между измеряемыми величинами.

ВЫВОД: сама задача уравнивания может быть поставлена только при наличии в сети избыточных измерений.

Целью уравнивания является:

— нахождение таких поправок к результатам измерений, которые не только компенсировали бы невязки, но и наилучшим образом приблизили уравненные значения измеренных величин к их истинным значениям;

— повышение точности всех измеренных величин;

— выполнение оценки точности по материалам уравнивания.

Может быть найдено множество систем поправок (множество вариантов), ликвидирующих невязки, но только одна система поправок позволяет найти вероятнейшие (т. е. наиболее приближённые к истинным) значения определяемых величин (и их функций).

Такая система поправок находится под условиями 25 и 26:

— для равноточных измерений,

(условие Лежандра) (25)

-для неравноточных измерений)

(условие Гаусса) (26)

Первое условие – сумма квадратов поправок в непосредственные измерения должна быть минимальной.

Второе условие – сумма произведений квадратов поправок на веса соответствующих результатов измерений должна быть минимальной.

Уравнивание под условиями 25 и 26 называют уравниванием по методу наименьших квадратов (МНК), а условия (25) и (26) – принципом наименьших квадратов.

Уравнивание по МНК – строгое. Другие способы нахождения поправок – приближённое уравнивание.

Для решения задачи уравнивания по МНК применяются два основных способа:

— коррелатный, основанный на способе Лагранжа с неопределенными множителями для нахождения условного экстремума;

— параметрический – способ абсолютного экстремума, при котором все измеренные величины представляют в виде функций некоторых независимых неизвестных параметров.

Существуют также комбинированные способы уравнивания – коррелатный с дополнительными неизвестными и параметрический с избыточными параметрами.

1 Уравнивание геодезических сетей по МНК коррелатным способом

Пусть выполнено измерений их которых — необходимых.

— результаты измерений;

— истинные значения измеренных величин;

— установленная система весов результатов измерений;

— обратные веса.

Связь между ними может быть выражена следующими соотношениями:

, (27)

где

— случайные ошибки;

. (28)

Число избыточных измерений , где .

Каждое избыточное измерение приводит к математическому соотношению между истинными значениями измеренных величин, т. е. в геодезической сети возникает условий:

, (29)

где

( т. е. здесь r функций: ).

Эта исходная система условных уравнений связи включает только независимые уравнения, число которых равно

Вследствие неизбежных ошибок в измерениях, эти же функции, но от измеренных величин примут вид:

где — невязки.

Это выражение называется системой условных уравнений связи от измеренных значений.

(31)

Отдельные ошибки неизвестны, но их совокупность (сумма) в каждом условии может быть вычислена.

Необходимо найти такие поправки к результатам измерений, которые ликвидируют невязки, то есть должно выполняться равенство:

, (32)

где поправки к результатам измерений;

Уравненные результаты измерений находят по формуле:

(33)

Тогда система условных уравнений связи от уравненных значений примет вид:

(34)

где

В правой части опять нули, т. к. невязки компенсировались поправками.

Систему (34) приводят к линейному виду, раскладывая каждое уравнение в ряд Тейлора, и пренебрегая при этом малыми (нелинейными) членами разложения:

Первое слагаемое согласно формуле (30) является невязкой , поэтому выражение (35) примет вид:

Обозначим частные производные от первой функции буквой , от второй —, от третьей —и т. д. То есть:

, ,…,;

, ,…, (37)

, ,…,

С учетом (37) система (36) примет вид:

(38)

Это система условных уравнений поправок. В ней:

— невязки;

— коэффициенты при поправках;

— неизвестные поправки, которые надо найти, решив систему (38).

Так как в системе (38) число уравнений меньше числа неизвестных поправок , то такая система имеет множество решений, т. е. не решается однозначно. Чтобы из множества вариантов выбрать один, наилучший, необходимо поставить дополнительное условие. Это условие:

(39)

является принципом наименьших квадратов.

Вывод нормальных уравнений коррелат представляется в матричной форме. Система (38) условных уравнений поправок

решается под условием (39) МНК

,

где — матрица коэффициентов при поправках условных уравнений поправок;

— вектор поправок;

— трансформированный вектор поправок;

— вектор свободных членов;

— матрица весов результатов измерений;

Используя метод Лагранжа с неопределенными множителями, называемыми в геодезии коррелатами, представленными в виде вектора коррелат (40)

составляют функцию Лагранжа (41)

чтобы найти min, находят производную от этой функции (42)

, (43)

(44)

где — трансформированная матрица коэффициентов при поправках;

— вектор коррелат.

Полагая, что , как симметричная матрица, получим коррелатное уравнение поправок, выражающее поправки в виде функций коррелат

(45)

— матрица обратных весов результатов измерений;

— обратный вес результата измерений;

— единичная матрица – т. е. уравнение (45) можно представить в виде

(46)

Выражение (46) является коррелатным уравнением поправок.

Подставив (46) в (38), получают систему нормальных уравнений коррелат:

(47)

,

где — матрица коэффициентов нормальных уравнений.

Коэффициенты, стоящие на главной диагонали, называются квадратичными, они всегда положительны, остальные – неквадратичные.

(48)

В системе нормальных уравнений коррелат (48) — неизвестные коррелаты. Их число r, как и число уравнений, поэтому система (48) решается однозначно.

Способы решения могут быть различны:

— по схеме Гаусса;

— методом исключения, когда из последнего уравнения выражается последнее неизвестное, подставляется в предыдущее уравнение и т. д.;

— на ЭВМ, по готовым программам.

Из решения нормальных уравнений находят коррелаты , а по ним поправки:

(49)

Выражение (49) называется коррелатным уравнением поправок.

Контролем вычисления поправок является равенство:

(50)

После этого вычисляют уравненные значения результатов измерений

, () (51)

и делают контроль уравнивания путем подстановки уравненных измерений в условные уравнения связи

(52)

2 Средняя квадратическая ошибка единицы веса

Оценка точности по результатам уравнивания, то есть по поправкам, может быть выполнена по формуле:

, (53)

где — средняя квадратическая ошибка единицы веса, то есть ошибка измерения с весом .

Чтобы оценить какой-либо элемент сети (отметку, координату, угол и т. д.) необходимо составить функцию, то есть математически выразить этот элемент.

(54)

где — средняя квадратическая ошибка функции;

— вес функции.

1 Уравнивание одиночного нивелирного хода коррелатным способом

Рассмотрим нивелирный ход

Рисунок 9 — Нивелирный ход

— исходные пункты;

— отметки исходных пунктов;

— измеренные превышения;

— длины секций;

— определяемые пункты, отметки которых необходимо найти.

Уравнивание нивелирного хода начинается с подсчета числа избыточных измерений по формуле

(55)

В ходе, представленном на рисунке 9, число измеренных превышений . Число необходимых измерений — по числу определяемых пунктов. Поэтому .

Контроль вычисления производится по формуле , (56)

где — число замкнутых полигонов;

— число исходных пунктов.

Таким образом, в нивелирном ходе возникает только одно условие и соответственно одно условное уравнение связи:

(57)

где — невязка.

Так как , то, согласно общей теории уравнивания, составляется одно нормальное уравнение коррелат

, (58)

где — обратные веса;

при , обратные веса ;

— коэффициенты при поправках условного уравнения поправок

(59)

Коэффициенты находятся как частные производные от функции по результатам измерений , т. е. , ,…, .

Коррелатный способ уравнивания

Коррелатный способ основан на использовании функциональной связи между собой элементов геодезических построений X_i (i = 1, n). Эти уравнения связи называются условными уравнениями:

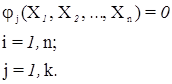
При коррелатном способе уравнивания вначале составляется система условных уравнений AV + W = 0,

где А – матрица коэффициентов системы условных уравнений;

V – вектор поправок в измеренные значения элементов сети;

W – вектор невязок условных уравнений.

При этом коэффициенты a_ij условных уравнений поправок определяются по формуле:

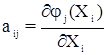
а невязки уравнений – по формуле:

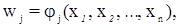
где x_i (i = 1, n) – измеренные значения элементов геодезических построений.

При известной весовой матрице Р вначале вычисляют обратную весовую матрицу Q = P -1 , а затем от системы условных уравнений переходят к системе нормальных уравнений:

Определив коррелаты К = — (AQA T ) W, вычисляют поправки V = QA T K и уравненные значения измеренных элементов сети x* = x + v,

где х* – вектор уравненных значений;

х – вектор измеренных значений элементов геодезических построений.

Дата добавления: 2016-06-02 ; просмотров: 1885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Примеры коррелатного способа уравнивания

В этом разделе приводятся примеры уравнивания некоторых геодезических построений. В примерах рассматривается алгоритм решения задачи уравнивания для разных вариантов геодезических построений со сравнительно небольшим числом измеренных величин, как это часто имеет место, например, в практике геодезических и маркшейдерских работ на земной поверхности при создании опорных сетей либо в горных выработках при обработке результатов измерений в системах полигонометрических ходов. Уравнивание систем нивелирных ходов обычно производится при точных и высокоточных измерениях, например, при наблюдениях за деформациями горных выработок и наземных сооружений, что тоже имеет место и в практике геодезических и маркшейдерских работ.

В примерах рассмотрены сравнительно простые схемы геодезических построений, однако принцип расчётов и в сложных системах точно такой же, как и в простых.

137.1. Уравнивание углов в полигоне

В полигоне, состоящем из четырёх вершин (рис. 14.7), неравноточно измерены горизонтальные углы: А = β₁ , В = β₂ , С = β₃ , D = β₄ (табл. 14.4).

Выполнить уравнивание углов без учёта измерения длин сторон.

Предварительно найдем веса p_i и обратные веса q_i, приняв м (см. табл. 14.4) без учёта величин измеренных углов, считая их практически примерно одинаковыми (значения весов определяются по условию возможной погрешности в направлениях из-за центрирования теодолита; для веса угла применяется правило сложения обратных весов направлений):

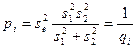, (14.91)

где s₁ и s₂ – стороны, образующие данный угол.

Шаг 1. Общее число измеренных величин n = 4, число необходимых измерений k = 3, число избыточных измерений r = 1.

Шаг 2. Составим условное уравнение (условие сумм углов полигона).

Всего одно уравнение, поскольку r = 1.

Шаг 3. Приводим условное уравнение к линейному виду, для чего продифференцируем его и найдем частные производные функции по аргументам β_i . Очевидно, что

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (таблица 14.5).

Рис. 14.7. Уравнивание углов в полигоне.

Обозначение	Значение угла	Вес pi	Обратный вес qi
β1	80 0 16′ 44,3″	0,221	4,520
β2	91 0 45′ 00,7″	0,459	2,181
β3	69 0 25′ 56,8″	0,473	2,113
β4	118 0 32′ 25,2″	0,225	4,452

Матрица коэффициентов, весов и обратных весов

i→ j↓
+ 1	+ 1	+ 1	+ 1
рi	0,221	0,459	0,473	0,225
qi	4,520	2,181	2,113	4,452

Свободный член уравнения

Шаг 4. Найдём коэффициенты b_jj нормальных уравнений (в данном случае – уравнений коррелат):

, (14.92)

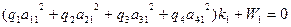. (14.93)

Для приведенного примера, с учётом значений a_ij и q_i , 13,266 k₁ + 7 = 0, откуда k₁ = — 0,528.

Шаг 5. Составляем условное уравнение поправок

(14.94)

и формулы для вычисления поправок (с вычислением их значений):

Контроль по формуле (14.94): условие выполнено! (проверьте сами). Отступление при округлениях значений поправок на 0,1″ является допустимым.

Вспомните загадку, которая прозвучала в начале этой главы. А если забыли, то возвратитесь к этому началу. Вот оно, что «под конец тонко» — это и есть хвостик решения всей задачи уравнивания: маленькие поправочки в измеренные величины. Ну а что тут было зелено, да посерёдке толсто – это уж понятно из решения данной задачи. Правда, приведенная задача – одна из самых простых. Дальше будет корнеплод посложнее. Но, всему своё время. А сейчас – закончим решение приведенной задачи.

Шаг 6. Вычисляем уравненные значения углов:

β₁ ‘ = 80° 16′ 44,3″ – 2,4″ = 80° 16′ 41,9″; β₂ ‘ = 91° 45′ 00,7″ – 1,1″ = 91° 44′ 59,6″;

β₃ ‘ = 69° 25′ 56,8″ – 1,2″ = 69° 25′ 55,6″; β₄ ‘ = 118° 32′ 25,2″ – 2,4″ = 181° 32′ 22,8″.

Контроль: подстановка уравненных значений углов в уравнение (14.91) – условие выполнено! (проверьте это условие).

Очевидно, что при равноточных измерениях углов для них были бы получены одинаковые поправки, т.е. невязка была бы распределена поровну во все углы.

137.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками

На местности пройдена система нивелирных ходов с четырьмя узловыми точками 1, 2, 3 и 4 (рис. 14.8). В результате измерений образовано 9 секций, превышения в которых по указанному направлению приведены непосредственно на схеме. Указаны также высоты исходных реперов Р10, Р20 и Р30. В табл. 14.6 приведены длины ходов в секциях и значения весов и обратных весов превышений в секциях, вычисленные по формулам:

Рис. 14.8. Схема нивелирных ходов с четырьмя узловыми точками.

№ секции	Превышение h, мм	Длина хода s в секции, км	Вес p пре-вышения	Обратный вес q пре-вышения
+3586	0,84	2,38	0,42
+2841	1,36	1,47	0,68
-752	2,15	0,93	1,08
-1243	0,78	2,56	0,39
+509	2,63	0,76	1,32
+5338	2,05	0,98	1,03
-5863	3,02	0,66	1,51
+4639	3,44	0,58	1,72
-3024	2,38	0,84	1,19

, (14.95)

где

Требуется определить уравненные значения высот узловых точек.

Шаг 1. Общее число измерений n = 9, число необходимых измерений k = 4, число избыточных измерений r = 5.

Шаг 2. Составим r = 5 условных уравнений:

Шаг 3. Приведём условные уравнения к линейному виду, продифференцировав их по аргументам h_i. Получим коэффициенты a_ij условных уравнений поправок:

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (табл. 14.7).

Матрица коэффициентов и обратных весов

→ i j↓
+1	-1	+1
-1	+1	+1
+1	+1	+1
+1	+1	-1
+1	+1	+1
qi	0,42	0,68	1,08	0,39	1,32	1,03	1,51	1,72	1,19

Вычислим свободные члены (в мм), подставив в уравнения (14.96) измеренные значения h_i в секциях:

Шаг 4. Найдём по формулам (14.88) коэффициенты b_jj нормальных уравнений коррелат:

(14.97)

После подстановки значений a_ij и q_i в уравнения (14.97) получим исходные нормальные уравнения коррелат:

Из решения системы уравнений (14.98) одним из способов получим:

Контроль вычисления коррелат выполняем подстановкой их значений в исходные уравнения (14.98):

1. 2,18 (-2,137) – 1,08 (-11,552) + 0,42 (-1,945) – 7 = + 0,001;

2. -1,08(-2,137) + 2,79(-11,552) + 1,32(+9,606) + 0,39(-1,945) + 18 = -0,001;

3. 1,32(-11,552) + 3,86(+9,606) + 1,51(-3,882) – 16 = — 0,031;

4. 1,51(+9,606) + 4,42(-3,882) + 1,72(-1,945) + 6 = +0,001;

5. 0,42(-2,137) + 0,39(-11,552) + 1,72(-3,882) + 2,53(-1,945) + 17 = -0,001.

Сравнительно большее невыполнение условия мы видим в уравнении 3. Это вызвано погрешностями округлений. При вычислении с большими значащими цифрами этого не наблюдалось бы. При этом результаты вычислений принимаем удовлетворительными, поскольку поправки в измеренные значения превышений для данных условий будут в дальнейшем округляться до 1 мм, а вычисления проведены с большим запасом точности.

Шаг 5. Составляем условные уравнения поправок v_i, пользуясь формулами (14.86) и табл. 14.7:

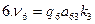
(14.99)

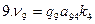
1. v₁ = 0,42 ∙1∙ (-2,137) + 0,42∙1∙ (-1,945) = — 1,714 = — 2 мм;

2. v₂ = 0,68 ∙ (-1) ∙ (-2,137) = + 1,453 = + 1 мм;

3. v₃ = 1,08 ∙ 1 ∙ (2,137) + 1,08 ∙ (-1) ∙ (-11,552) = +10,168 = + 10 мм;

4. v₄ = 0,39 ∙ 1 ∙ (-11,552) + 0,39 ∙1 ∙ (-1,945) = — 5,264 = — 5 мм;

5. v₅ = 1,32 ∙1∙ (-11,552) + 1,32 ∙ 1 ∙ (+9,606) = — 2,569 = — 3 мм;

6. v₆ = 1,03 ∙1 ∙ (+9,606) = + 9,894 = + 10 мм;

7. v₇ = 1,51 ∙ 1 ∙ (+9,606) + 1,51 ∙1 ∙ (-3,882) = + 8,643 = + 9 мм;

8. v₈ = 1,72 ∙ 1 ∙ (-3,882) + 1,72 ∙ 1 ∙ (-1,945) = — 10,022 = — 10 мм;

9. v₉ = 1,19 ∙ (-1) ∙ (-3,882) = + 4,620 = + 5 мм.

Контроль вычисления поправок можно выполнить по формулам (14.96), подставив в них вместо превышений значения поправок (суммы поправок должны быть равны значениям соответствующих невязок с обратным знаком):

Шаг 6. Вычисляем уравненные значения превышений в секциях и контролируем уравнивание по выполнению условия (14.96):

h₆ ‘= + 5338 + 10 = + 5348 мм;

Подстановка в уравнения (14.96) подтверждает выполнение указанного условия.

Вычисляем уравненные значения высот узловых точек 1, 2 , 3 и 4:

Контроль вычислений здесь можно выполнить вторичным получением высот искомых точек по другим направлениям. Должны получиться те же результаты. Например, H₁ = H_P30 – h₈‘ – h₄‘ = 85,301 – 4,629 + 1,248 = 81,920 м.

137.3. Уравнивание системы полигонометрических ходов с двумя узловыми точками

Уравнивание таких систем полигонометрических ходов аналогично уравниванию как одиночного полигонометрического хода, так и системы полигонометрических ходов с одной узловой точкой. В такой системе (рис. 14.9) образуется три независимых полигонометрических хода [(1), (2), (3)], в которых возникает по три условия: три условия дирекционных углов и шесть условий координат, т.е. получается девять условных уравнений.

Рис. 14.9. Система полигонометрических ходов с двумя узловыми точками.

В табл. 14.8, 14.9 и 14.10 приведены необходимые исходные данные для решения задачи уравнивания, заключающейся в определении уравненных значений координат точек 1, 2, 3, M, N, а также уравненного значения дирекционного угла узловой линии MN. (В данном примере узловые точки M и N образуют и узловую линию).

Часто между узловыми точками прокладывают полигонометрический ход в две и более линии. Тогда понятие узловой линии не будет иметь места. Ею может быть любая линия с началом в какой-либо узловой точке).

Горизонтальные углы измерены равноточно с погрешностью m_β = 2,0″. Расстояния измерены светодальномером с погрешностью, примерно одинаковой для всех линий (m_s = 18 мм = 1,8 см). В соответствии с указанной точностью измерения расстояний и углов веса углов принимаем равными единице (p_β = 1; q_β = 1), а веса расстояний –

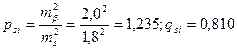
Координаты исходных пунктов

Координаты, м	B	C	F	G
Х	7183,652	8137,565	6124,924	7894,521
Y	4380,124	6463,782	4718,048	7173,596

Исходные дирекционные углы

αАВ	71º 08′ 14,3″	α BA	251º 08′ 14,3″
α CD	118º 19′ 14,7″	α DC	298º 19′ 14,7″
α EF	324º 21′ 18,0″	α FE	144º 21′ 18,0″
α GH	159º 58′ 14,2″	α HG	339º 58′ 14,2″

Измеренные горизонтальные углы и расстояния

Обозначение угла	Значение угла	Обозначение расстояния	Значение расстояния, м
β 1	226º 15′ 25″	s 1	475,885
β 2	201º 36′ 36″	s 2	693,027
β 3	85º 02′ 31″	s 3	857,338
β 4	170º 15′ 07″	s 4	401,239
β 5	172º 53′ 18″	s 5	841,215
β 6	271º 07′ 58″	s 6	625,329
β 7	280º 34′ 07″	s 7	573,421
β 8	84º 46′ 52″	s 8	989,716
β 9	337º 03′ 44″
β 10	178º 54 26″
β 11	78º 21 28″

Выполним предварительные вычисления в полигонометрических ходах (1), (2) и (3), т.е. определим координаты точек ходов, используя только измеренные величины (табл. 14.11).

Шаг 1. Общее число измерений n = 19 (11 углов и 8 расстояний), число необходимых измерений k = 10, число избыточных измерений r = 9.

№№ точек	Гориз.углы β	Дирекц.углы α	Рассто-яния s , м	Приращения координат, м	Координаты, м	№№ точек
Δх	Δу	Х	Y
A	Ход (1)
71°08’14,3″
B	226°15’25»	7183,652	4380,124	B
117°23’39,3″	475,885	-218,960	+422,520
201°36’36»	6964,692	4802,644
139°00’15,3″	693,027	-523,068	+454,628
M	280°34’07»	6441,624	5257,272	M
239°34’22,3″	625,329	-316,693	-539,205
F	84°46’52»	6124,931 6124,924 +0,7 см	4718,067 4718,048 +1,9 см	F o FИСХ
144°21’14,3″ 144°21’18,0″ -3,7″
E
Ход (2)
A
71°08’14,3″
B	226°15’25»	7183,652	4380,124	B
117°23’39,3″	475,885	-218,960	+422,520
201°36’36»	6964,692	4802,644	1
139°00’15,3″	693,027	-523,068	+454,628
M	85°02’31»	6441,624	5257,272	M
44°02’46,3″	857,338	+616,237	+596,054
N	170°15’07»	7057,861	5853,326	N
34°17’53,3″	401,239	+331,470	+226,098
172°53’18»	7389,331	6079,424
27°11’11,3″	841,215	+748,281	+384,341
C	271°07’58»	8137,612 8137,565	6463,765 6463,782	C o СИСХ
118°19’09,3″ 118°19’14,7″ -5,4″
D	+4,7 см	-1,7 см
Ход (3)
H
339°58’14,2″
G	78°21’28»	7894,521	7173,596	G
238°19’42,2″	573,421	-301,075	-488,022
178°54’26»	7593,446	6685,574
237°14’08,2″	989,716	-535,620	-832,255
N	337°03’44»	7057,826	5853,320	N
34°17’52,2″	401,239	+331,471	+226,096
172°53’18»	7389,297	6079,415
27°11’10,2″	841,215	+748,283	+384,337
C	271°07’58»	8137,580 8137,565	6463,752 6463,782	C o СИСХ
118°19’08,2″ 118°19’14,7″ -6,5″
D	+1,5 см	-3,0 см

Шаг 2. Составление условных уравнений.

Для трёх независимых ходов, будем иметь три условных уравнения для дирекционных углов и шесть условных уравнений для координат ( три – для абсцисс, три – для ординат).

1.

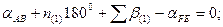
2.

3.

4.

5. (14.100)

6.

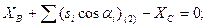
7.

8.

9.

В уравнениях (14.100) индексы (1), (2) и (3) относятся к соответствующим ходам (см. табл. 14.11), например, n₍₁₎ = 4, n₍₂₎ = 6, n₍₃₎ = 5.

Приведём условные уравнения к линейному виду по правилам, изложенным выше. В полученные выражения введём знак гауссовых сумм.

1.

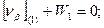
2.

3.

4.

5. 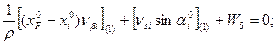(14.101)

6.

7.

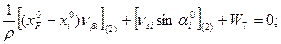
8.

9.

В уравнениях (14.101) значения координат берут в километрах, а значение ρ = 206265″ уменьшают на 100000.

Вычислим значения невязок в уравнениях (14.101) с учётом данных измерений и предварительных вычислений:

где T_i o – результат вычисления исходной величины T_i(исх).

W₁ = 144º 21′ 14,3″ – 144º 21′ 18,0″ = — 3,7″ ;

W₂ = 118º 19′ 09,3″ – 118º 19′ 14,7″ = — 5,4″ ;

W₃ = 118º 19′ 08,2″ – 118º 19′ 14,7″ = — 6,5″ ;

W₄ = 6124,931 – 6124,924 = +0,007 м = + 0,7 см;

W₅ = 4718,067 – 4718,048 = + 0,019 м = + 1,9 см;

W₆ = 8137,612 – 8137,565 = + 0,047м = + 4,7 см;

W₇ = 6463,765 – 6463,782 = — 0,017 м = — 1,7 см;

W₈ = 8137,580 – 8137,565 = + 0,015 м = + 1,5 см;

W₉ = 6463,752 – 6463,782 = — 0,030 м = — 3.0 см .

По данным табл. 14.11 составим табл. 14.12 значений синусов и косинусов дирекционных углов и разностей абсцисс и ординат. Получим окончательные условные уравнения поправок:

Значения синусов и косинусов дирекционных углов, значения разностей координат

№№ точек	Sin αi	Cos αi	(хn 0 -xi 0 ), км	(yn 0 -yi 0 ), км
Ход 1
В	(В-1) 0,8879	-0,4601	-1,0587	0,3379
(1-М) 0,6560	-0,7548	-0,8398	-0,0846
М	(M-F) -0,8623	-0,5064	-0,3167	-0,5392
F
Ход 2
В	(В-1) 0,8879	-0,4601	0,9540	2,0836
(1-М) 0,6560	-0,7548	1,1729	1,6611
М	(M-N) 0,6952	0,7188	1,6960	1,2065
N	(N-2) 0,5635	0,8261	1,0798	0,6104
(2-C) 0,4569	0,8895	0,7483	0,3843
C
Ход 3
G	(G-3)-0,8511	-0,5250	0,2431	-0,7098
(3-N)-0,8409	-0,5412	0,5441	-0,2218
N	(N-2)0,5635	0,8261	1,0798	0,6104
(2-C)0,4569	0,8895	0,7483	0,3843
C

Составим матрицу коэффициентов a_ij и обратных весов q_i , необходимую для определения коэффициентов нормальных уравнений коррелат (табл. 14.13).

Матрица коэффициентов и обратных весов

i→ j↓	β1	β2	β3	β4	β5	β6	β7	β8	β9
-0,1638	0,0410	0,2614
-0,5133	-0,4071	-0,1535
-1,0102	-0,8053	-0,5849	-0,2959	-0,1863
0,4625	0,5686	0,8222	0,5235	0,3628
-0,1863	-0,2959
0,3628	0,5235
qi

(продолжение табл. 14.13)

β10	β11	s1	s2	s3	s4	s5	s6	s7	s8
-0,4601	-0,7548	-0,5064
0,8879	0,6560	-0,8623
-0,4601	-0,7548	0,7188	0,8261	0,8895
0,8879	0,6560	0,6952	0,5635	0,4569
0,1076	0,3441	0,8261	0,8895	-0,5250	-0,5412
0,2638	0,1178	0,5635	0,4569	-0,8511	-0,8409
0,810	0,810	0,810	0,810	0,810	0,810	0,810	0,810

Шаг 4. Составление нормальных уравнений коррелат.

Систематическая погрешность измерения— это составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины. Систематические
погрешности разделяются на постоянные
(например, погрешность из-за смещения
нуля прибора) и переменные (например,
погрешность, обусловленная изменением
температуры окружающей среды). Рассмотрим
основные методы уменьшения систематических
погрешностей измерения.

3.2.1. Уменьшение постоянных систематических погрешностей

Для уменьшения постоянной систематической
погрешности наибольшее распространение
получили следующие методы: введение
поправок, метод замещения, метод
компенсации погрешности по знаку.

Введение поправок является широко
используемым методом исключения
систематических погрешностей. Поправкой
называют величину, которую надо прибавить
к результату измерения с целью
исключения систематической погрешности.

Рассмотрим введение поправки, если
результат измерения содержит аддитивную
₀, мультипликативную_Sи обе составляющие погрешности.

В случае наличия аддитивной погрешности
она устраняется алгебраическим сложением
результата измерения Y и поправки а =
-₀,
то есть

X = Y + а = Y —
₀.
(3.4)

Если систематическая погрешность
является мультипликативной, то она
может быть исключена умножением
результата измерения Y на поправочный
коэффициент, который равен b= S/(S +S) [7]. В
этом случае имеем

Х = Y b = Y[S/(S +
S)],
(3.5)

где S — чувствительность средства
измерения; S —
абсолютная мультипликативная погрешность
(погрешность чувствительности).

При наличии обеих составляющих
погрешности результат измерения может
быть исправлен с помощью поправки и
поправочного коэффициента

Х = (Y
+ a)b. (3.6)

Поправки могут быть определены различными
способами: расчетным путем (например,
поправки на погрешность от собственного
потребления мощности средством
измерения); по результатам поверки
средств измерений в рабочих условиях,
что дает возможность учесть все
систематические погрешности без
выяснения причин их возникновения.

Метод
замещения (метод разновременного
сравнения) является одним из наиболее
распространенных методов устранения
большинства систематических погрешностей
и заключается в том, что воздействие на
измерительный прибор измеряемой величины
заменяется эквивалентным, известным
воздействием на прибор регулируемой
меры. Измерение осуществляется в два
этапа. При сохранении условий эксперимента
неизменными за результат измерения
принимается значение известной величины,
определяемое по указателю переменной
меры. Погрешность измерения при этом
будет определяться погрешностью меры
и случайной погрешностью измерительного
прибора, умноженной на2.
Метод замещения широко используется
для повышения точности измерения
величин, для которых существуют точные
регулируемые меры (например, при
измерении сопротивлений, емкостей и
др.) [4].

Метод компенсации погрешности по
знакуприменяется для исключения
известных по природе, но неизвестных
по значению погрешностей, источники
которых имеют направленное действие
(погрешности от влияния магнитных
полей, термоЭДС и др.). Для устранения
таких погрешностей измерения проводят
дважды (или четное число раз) так, чтобы
систематическая погрешность входила
в результаты измерений с противоположными
знаками. Среднее значение из двух
полученных результатов является
окончательным результатом измерения
[4].

Реализация этого метода может
осуществляться двумя способами:

1) Изменением знака систематической
погрешностипри неизменном значении
измеряемой величины (например, для
исключения влияния внешнего магнитного
поля на показания магнитоэлектрического
прибора изменение знака погрешности
достигают поворотом прибора на 180⁰).

Х = (Y₁+
Y₂)/2 = (Х +_С+Х -_С),
(3.7)

где Y₁= Х +_С;
Y₂= Х -_С— результаты двух измерений величины
Х, содержащие систематическую погрешность_С, природа
которой известна.

2) Инвертированием входного сигналапри сохранении знака и значения
систематической погрешности (например,
при измерении постоянного напряжения
для исключения погрешности от термоЭДС
производится повторное измерение при
одновременном изменении полярности
измеряемого напряжения). При этом
результаты двух измерений Y₁ и
-Y₂, содержащих систематическую
погрешность, могут быть представлены
в виде

Y₁= Х +_С;
-Y₂= -Х +_С,
(3.8)

где Х и (-Х) — значение измеряемой
величины.

Окончательный результат измерения
определяется по формуле 3.7.

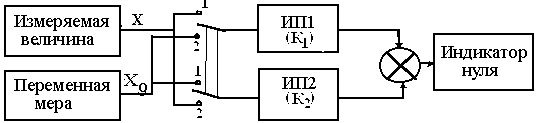Метод
противопоставленияпозволяет
исключить мультипликативную составляющую
систематической погрешности. Для этого
проводят два измерения. В первом —
измеряемую величину Х подают на вход
измерительного преобразователя ИП1
(рис. 3.1) с коэффициентом преобразования
К₁, а на вход второго преобразователя
ИП2 с коэффициентом преобразования
К₂(К₁К₂) подают величину, воспроизводимую
мерой Х₀. Затем изменением Х₀производят уравновешивание. При этом
Х^.К₁, = Х₀₁^.К₂.
При втором измерении объект измерения
и меру меняют местами и вновь производят
уравновешивание Х^.К₂=
Х_О2^.К₁, (Х_О1и Х_О2— значения величин, воспроизводимых
мерой, которым соответствует нулевое
показание индикатора нуля).

Рис. 3.1

Если отношение коэффициентов преобразования
К₁/К₂остается постоянным,
то результат измерения Х не содержит
мультипликативной погрешности и его
можно определить как [7]

Х =Х_О1Х_О2. (3.9)

При незначительном отличии
коэффициентов преобразования К₁и К₂друг от друга для определения
измеряемой величины Х можно использовать
приближенное выражение

Х (Х_О1+Х_О2)/2.
(3.10)

Примером метода противопоставления
является взвешивание на равноплечих
весах, при котором уравновешивание
весов осуществляется дважды. Во втором
случае взвешиваемое тело и гири меняются
местами. При этом устраняется погрешность,
обусловленная неравноплечестью весов.

Под погрешностью измерений понимают:
А) среднее арифметическое результатов измерений;
В) просчеты по измерительным приборам;
С) разность между результатом измерения и истинным значением измеряемой величины;
Д) результаты измерений по определенной геометрической закономерности;
Е) нет правильного ответа;

По характеру действия погрешности бывают:
средние, грубые, элементарные;
грубые, систематические, случайные;
грубые, математические, интегральные;
систематические, погодные, вероятные;
случайные, средние, вероятные;

Грубые погрешности это:
когда результаты измерения каждого отдельного участка не влияет на конечный результат;
погрешности, размер и влияние которых на каждый отдельный результат измерения остается неизвестным;
погрешности, превосходящие по абсолютной величине некоторый, установленный для данных условий измерений, предел;
погрешности, которые по знаку или величине однообразно повторяются в многократных измерениях
нет правильного ответа;

Как избежать грубых ошибок при геодезических измерениях?
А) путем введение поправки;
В) путем повторного измерения;
С) путем вычисления квадратической ошибки;
Д) путем вычисление предельной ошибки;
Е) путем вычисления арифметической середины.

Случайные погрешности это:
А) когда результаты измерения каждого отдельного участка не влияет на конечный результат;
В) погрешности, размер и влияние которых на каждый отдельный результат измерения остается неизвестными;
С) погрешности, превосходящие по абсолютной величине некоторый, установленный для данных условий измерений, предел;
Д)погрешности, результаты измерений которых меняется по определенной математической закономерности;
Е) нет правильного ответа.

Характеристикой точности случайных погрешностей отдельного измерения применяют:
А) среднюю кубическую погрешность;
В) среднюю квадратическую погрешность;
С) среднюю геометрическую погрешность;
Д) среднюю географическую погрешность;
Е) среднюю тригонометрическую погрешность.

Квадратическая предельная погрешность для данного ряда измерений не должна превышать:
А) 4m;
В) 5m;
С) 6m;
Д) 3m;
Е) 1m.

Систематические погрешности это:
А) когда результаты измерения каждого отдельного участка не влияет на конечный результат;
В) погрешности, размер и влияние которых на каждый отдельный результат измерения остается неизвестными;
С) погрешности, превосходящие по абсолютной величине некоторый, установленный для данных условий измерений, предел;
Д) погрешности, результаты измерений которых меняется по определенной математической закономерности;
Е) нет правильного ответа;

Как свести влияние систематических ошибок к минимуму?
А) путем повторного измерения;
В) путем введения поправки к результату измерения;
С) путем нахождение квадратичной ошибки;
Д) путем нахождение предельной ошибки;
Е) путем нахождение вероятнейшим значением.

При определенных условиях измерений случайные погрешности по абсолютной величине не могут превышать:
Среднего отклонения;
Средне алгебрического;
Известного предела;
Математической закономерности;
Источника происхождения;

Отношение абсолютной погрешности к значению самой измеряемой величины называется:
А) случайной погрешностью;
В) относительной погрешностью;
С) грубой погрешностью;
D) систематической погрешностью;
E) равноточной погрешностью;

Исключение систематических погрешностей

• Выше было подчеркнуто, что систематические ошибки могут вызвать смещение результатов измерений. Наибольшую опасность в этом отношении представляют систематические ошибки, которые остаются незамеченными, Подозреваемый. Это была не случайная ошибка, а систематическая ошибка, которая стала причиной ложных научных выводов, установления ложных физических законов и неудовлетворительного проектирования измерительных приборов и дефектных изделий. Методы устранения и учета систематических ошибок можно разделить на четыре основные группы: 1.

Устранение причины ошибок перед началом измерения (предотвращение ошибок). 2. Замена, компенсация ошибок знаком, контраст, устранение ошибок процесса измерения симметричным наблюдением (исключение ошибок экспериментом). 3. Внесение известных исправлений в результаты измерений (устранение ошибок расчета). 4. Оцените границы систематических ошибок, если они не могут быть исключены.

Пневматический прибор надежен, он оборудован с измеряя соплом малого размера, его можно установить в труднодоступные места, он может легко получить сумму и разницу сигналов.
Людмила Фирмаль

Устранение причин ошибок перед измерением Этот метод устранения систематических ошибок является наиболее разумным, поскольку он устраняет необходимость устранения ошибок в процессе измерения и расчета результатов с учетом поправок. Другими словами, устранение источника ошибок значительно упрощает и ускоряет процесс измерения. Устраняя причину ошибки, необходимо понимать как ее прямое устранение (например, удаление источника тепла), так и защиту измерительного прибора и объекта измерения от воздействия этих причин.

Причины ошибок прибора, характерные для данного экземпляра прибора, могут быть устранены во время калибровки или ремонта перед началом измерения, и необходимость устанавливается во время проверки. Таким образом, вы можете сделать вывод, что прибор должен быть проверен до начала измерения (один, серия или в течение определенного периода времени). Выполнимость вопроса ремонта или наладки определяется по результатам проверки. Причину ошибок из-за неправильной установки часто можно устранить до начала измерения. Устранить температурные эффекты.

Так называемые термостаты широко используются для предотвращения температурных ошибок. Это гарантирует определенную температуру окружающей среды с определенным допуском. Термостат большой комнаты (мастерская, лаборатория), маленькой комнаты (комната, комната), измеритель Цельные или отдельные детали (резистивные катушки, нормальные элементы, свободный конец термопары, стабилизатор частоты кристалла и т. Д.) В зависимости от жестких требований температурных условий используются разные методы контроля температуры. Прежде всего, нужно вызвать естественный термостат.

Другими словами, изоляция поддерживает определенную температуру в комнате. Примером такого термостата является часть помещения Всесоюзного ордена профсоюза Красного флага в Институте метрологии. Д. И. Ленинградский Менделеев (ВНИИМ). Эти объекты находятся в центре здания и имеют огромные капитальные стены. Вокруг них большой коридор, образованный вторым рядом капитальных стен, за которым следуют лаборатория и кабинет с самыми большими наружными стенами. Это окно имеет тройной кадр. Аккумулятор радиатора размещается вдоль наружной стены.

Благодаря устройству этого здания центральная комната поддерживается постоянной температуры. Небольшие колебания температуры происходят очень медленно. Во многих случаях подвалы используются для создания комнаты с термостатическим управлением, но это накладывает много требований (таких как недостаток влаги). Чем глубже подвал, тем ниже степень, необходимая для поддержания постоянной естественной температуры и ее искусственного поддержания. Затопление Земли также используется для небольшого контроля температуры.

По этой причине свободные концы термопар и отправная точка медных проводов от них часто размещаются в небольших коробках, расположенных на земле под полом здания. Поддержание необходимого уровня температуры, естественно, не всегда возможно. Чаще полагайтесь на искусственное поддержание температуры — нагревание или охлаждение. При наличии электрической сети нагревательное устройство не вызывает серьезных проблем. Выполнение контролируемого охлаждения намного сложнее.

Поэтому, если позволяет измерительное оборудование, выбирается стабильный уровень температуры, чтобы исключить необходимость охлаждения и использовать только нагреватели. Температура стабильна на уровне 30-40 ° С или выше. В небольших количествах используются не только воздушные термостаты, но и жидкости, которые окружают измерительное устройство или объект измерения водой, маслом или другими жидкостями. Это значительно снижает температурные колебания и облегчает поддержание постоянного уровня.

Это, вообще говоря, способы устранения несоответствия температуры между измерительным прибором и средой, окружающей объект, что является одним из наиболее опасных источников ошибок. Сегодня термостаты часто заменяются кондиционерами. Во время кондиционирования поддерживается не только температура на требуемом уровне, но и другие параметры окружающего воздуха, особенно влажность. Термостаты и кондиционеры обеспечивают отличную защиту от прямого воздействия тепла.

Однако неправильное расположение нагревателя в термостате или в помещении, контролируемом термостатом, и отсутствие устройства (такого как смеситель), которое равномерно распределяет тепло по объему, само по себе может привести к ошибкам. Во многих современных измерительных приборах источник тепла находится в корпусе. Например, потребляемая мощность многих электронных измерительных устройств может достигать 1 кВт или более. Такие устройства обычно прогреваются на некоторое время, прежде чем проводить измерения. Устранение эффектов магнитного поля.

Эффекты магнитных полей не всегда легко обнаружить. Степень влияния поля на значения измерений различных приборов также различна. Рассмотрим меры, принятые для устранения воздействия магнитных полей. Поскольку магнитное поле Земли низкое, значительный риск удара возникает только в устройствах, которые характеризуются повышенной чувствительностью. Единственным средством защиты устройства от воздействия магнитного поля Земли является устройство с закрытым непрерывным экраном из магнитомягкого материала.

Линии магнитного поля перемещаются вокруг экранированного пространства, а небольшие зазоры в магнитной цепи экрана (неточная подгонка соединений компонентов) могут значительно снизить эффективность экрана. В настоящее время экран от воздействия магнитного поля Земли и экран от магнитного поля, образованного постоянным током и переменным током, распространяются. Этому способствовало изобретение магнитомягких сплавов (таких как пермаллой) с большой начальной проницаемостью и низкой коэрцитивной силой.

Устройства с магнитным экранированием имеют нежелательные явления даже при использовании пермаллоя. Если вы измените конфигурацию линий внешнего магнитного поля, экран также повлияет на конфигурацию линии внутреннего ( действия ) магнитного поля и, в некоторых случаях, на показания прибора. Помните, что экран не идеален и внешнее магнитное поле может воздействовать на экранированное измерительное устройство. Стандарты (такие как ГОСТ 1845-59) установили различные категории защиты от воздействия внешних магнитных полей. Экранирование от высокочастотных электромагнитных полей немного проще.

В этом случае возможно и наиболее целесообразно использовать материалы с высокой проводимостью. Этот эффект достигается вихревыми токами и создаваемым ими обратным электромагнитным полем. Кроме того, такие экраны защищают механизм от электрических полей. Удалить вредные вибрации и тремор. Эти эффекты устраняются амортизацией инструмента и его компонентов. В зависимости от частоты этих вибраций и чувствительности прибора к этим воздействиям для амортизации используются различные типы поглотителей вибрации.

Например, Оттепель резиновая в сочетании с различными видами упругих подвесок (струны, пружины) Устранение других видов вредных воздействий. Влияние таких факторов, как изменение атмосферного давления простыми средствами, не может быть исключено. Если соблюдение определенных требований является обязательным, следует использовать камеру давления с регулируемым давлением. Как правило, эти камеры могут контролировать влажность и температуру одновременно. Регулировка давления в помещении во время кондиционирования требует принудительной герметизации помещения, что делает установку очень сложной.

Устранить систематические ошибки в процессе измерения Устранение систематических ошибок в процессе измерения является эффективным способом устранения многих вредных воздействий. Нет необходимости в специальных установках или устройствах. Как правило, эти или их методы измерения могут не только устранить ошибки, возникающие в результате воздействия, но и оценить их степень. Исключением из этого метода являются в основном ошибки оборудования, ошибки установки и ошибки от внешних воздействий.

Некоторые постоянные ошибки субъективного характера могут быть устранены только в процессе измерения путем повторных измерений несколькими людьми. Особенности метода устранения ошибок процесса измерения, рассмотренные ниже, в основном применяются к измерению стабильных параметров и являются ленивыми, потому что он требует повторных измерений. Метод замены. Это один из самых распространенных способов устранения ошибок. Дело в том, что измеряемый объект заменяется известной мерой. Это в то же время это было в то же время Я сам.

Давайте рассмотрим некоторые из наиболее типичных примеров использования альтернативных методов. Точное взвешивание часто выполняется с использованием следующего жирного метода: Поместите взвешенную массу на одну чашу весов. Весы уравновешиваются путем применения другой нагрузки (негигроскопичной, неиспаряющейся и т. Д.), Например, некоторой нагрузки, которая не изменяется во время измерения. Когда равновесие достигнуто, взвешенная масса удаляется, и вес помещается на место до достижения равновесия.

Общий вес весов, необходимый для восстановления равновесия, соответствует значению взвешенного веса. Поэтому можно сделать исключение из результатов взвешивания ошибок, вызванных неоднородностями баланса. Этот метод был усовершенствован Д. И. Менделеевым. Все взвешивания прикреплены к чаше весов для взвешивания, а весы уравновешены любой нагрузкой. Затем поместите груз на чашку, в которую он был помещен, и удалите часть веса, чтобы восстановить равновесие. Общая масса полученных весов соответствует значению взвешенной массы.

Этот вариант метода замены не только устраняет ошибки из несбалансированного баланса, но также сохраняет неизменной чувствительность при взвешивании различных масс. Степень чувствительности рычажной шкалы зависит от нагрузки. В результате только одна нагрузка может обеспечить постоянную чувствительность. В настоящее время лабораторные весы, построенные по этому принципу, производятся в Советском Союзе и за рубежом и используются для снятия гирь с помощью рычага с внешним управлением и для подсчета значения массы взятых гирь.

Он оснащен. Методы замены широко используются при измерении электрических параметров — сопротивления, емкости и индуктивности. Процедура измерения в основном такая же, как и во время взвешивания. Объект, электрическое сопротивление, индуктивность или емкость которого подлежат измерению, содержится в той или иной измерительной цепи. В большинстве случаев метод нулевого баланса (мост, компенсация и т. Д.) Используется для выполнения электрического баланса цепи. После балансировки переменные значения измерения включаются вместо объекта измерения без изменения схемы.

Сопротивление накопителя, емкость, индуктивность. Переменный конденсатор или индуктивность. Изменяя свою стоимость, они достигают восстановления цепного равновесия. В этом случае метод замены устраняет остаточные дисбалансы в мостовой схеме, влияние магнитных и электрических полей на цепь, взаимное влияние отдельных элементов цепи, а также утечки и другие паразитные явления. Другим примером является определение характеристик источника света путем сравнения его со стандартной лампой накаливания с использованием фотометра.

Фотометр наблюдает за двумя смежными белыми полями (визуально или с использованием фотоэлементов), одно из которых освещается исследуемым источником света, а другое освещается так называемой лампой сравнения. Отрегулируйте оба поля, чтобы иметь одинаковое освещение. Затем вместо исследуемого источника света будет установлена примерная лампа, и будет достигнуто равномерное восстановление освещенности обоих полей фотометра без изменения настройки лампы сравнения. В этом случае альтернативный способ исключает влияние изменения степени поглощения света в обоих оптических каналах фотометра.

Приведенный выше пример не исчерпывает возможности использования метода замещения для устранения многих ошибок, возникающих во время измерения. Метод исправления знаковых ошибок. Способ устранения этой ошибки состоит в том, что измерение выполняется дважды. Поэтому ошибка, которая изначально неизвестна по размеру, включена в результат с обратным знаком. Ошибки исключаются при расчете среднего значения.

В алгебраической форме это может быть выражено как: Пусть X1 и x2 — результаты двух измерений. A — Систематическая ошибка, природа которой известна. Важность неизвестна. Ся — это безошибочное значение измерения. тогда X1 = xl + b Xa = xd-A. Среднее значение — = * + * = (Xd + D) + (x, -D) X 2 2 Чтобы повысить точность результата и оценить его уровень, выполняется серия повторных измерений, и все ошибки с положительным знаком равны одинаковому количеству отрицательных ошибок, чтобы устранить указанную ошибку. Так что должно быть выполнено четное количество измерений. Этот метод ограничен.

Используется для исключения только тех ошибок, в которых источник имеет указанное действие. Типичным примером компенсации является устранение ошибок, вызванных воздействием магнитного поля Земли. Этот метод применяется. Известно (или предполагается), что показания могут быть подвержены ошибкам под воздействием магнитного поля Земли при использовании приборов для измерений. (VI. ) Первое измерение может быть выполнено, когда прибор находится в любом положении.

Перед выполнением второго измерения поверните прибор на 180 ° в горизонтальной плоскости. В первом случае магнитное поле Земли, добавленное к магнитному полю прибора, вызывает положительную ошибку, и если оно поворачивается на 180 °, магнитное поле Земли оказывает противоположный эффект, вызывая отрицательную ошибку, равную начальной величине. Дальнейшее внимание может быть уделено применению метода для исправления ошибки знака, чтобы устранить ошибки, вызванные воздействием магнитных полей различного происхождения. Имейте в виду, что поле от источника неоднородно, даже если не очень близко.

• Часть измерительного прибора, которая воздействует на магнитное поле, может быть размещена в другом месте. Ошибка, вызванная влиянием магнитного поля, в этом случае меняет не только знак, но и размер. Кроме того, внешнее магнитное поле может меняться со временем. Описанный метод, безусловно, полезен для обнаружения воздействия магнитных полей на измерительный прибор. Повторяя его, вы также можете проверить, являются ли эти эффекты постоянными и стабильными.

Использование метода, который исправляет ошибки знака, устраняет ошибки, вызванные явлениями гистерезиса (такими как магнитный гистерезис в ферромагнитных материалах и механический гистерезис в упругих материалах). Контрастный метод. Этот метод очень похож на исправление ошибок знака. Это связано с тем, что, поскольку измерение выполняется дважды, причина первой ошибки измерения будет отрицательно влиять на результат второго измерения. Примером является взвешивание равновесного равновесия (метод, предложенный Гауссом для устранения ошибок из-за остаточной неравномерности).

Единицей светового потока является люмен, равный световому потоку, излучаемому точечным источником под твердым углом 1 СР со светимостью 1 кд.
Людмила Фирмаль

При первом взвешивании масса x, помещенная в одну чашку весов, уравновешивается весом общей массы pi, помещенной в другую чашку. тогда Где 1g 11 — фактическое соотношение плеч. Взвешенная масса затем переносится в чашку, в которую помещается вес, и масса переносится в чашку, где размещается вес. Поскольку отношение плеч 4 A не совсем равно 1, баланс нарушается, и для баланса массы x необходимо использовать общую массу вес Ig. (U1.3) Разделив уравнение (V1.2) на уравнение (V1.3), получаем x = Или ГП и если немного отличается друг от друга Это уравнение и уравнение (U1.1) совпадают.

Однако уравнение (U1.1), полученное путем исправления ошибки со знаком, точно отражает суть исключения ошибки. В этом случае формула является приблизительной. Сравнивая оба метода с формулой, вы можете увидеть, что метод исправления ошибок включает в себя ошибку, которая удаляется как термин (алгебраически), а не как коэффициент. Особенностью противоположного метода является то, что фактическая пропорция плеча может быть определена.

Следовательно, умножение уравнений (VI.2) и (Y1.3) в примере взвешивания по Гауссу дает: Основной областью применения метода оппозиции является устранение ошибок при сравнении измерений с измерениями примерно равных значений. Методы контрастирования используются, например, в равновеликих мостах для измерения параметров электрических цепей, главным образом при измерении электрического сопротивления постоянному току. Пример. Сопротивление x измеряется с использованием равного плеча моста, где каждый рычаг r2 и r3 (см. Гл. X на рисунке 34) равен 1000 Ом.

Мостовое равновесие было достигнуто при r = 1000,4 Ом. После изменения положения x и r равновесие достигалось при Г1 = 1000.2 Ом. x-D-4 + 2 a1 , 3 Ом. Определите фактическую пропорцию плеча 1000.4-1000.2 = г, 2 1000, 2 Симметричный метод наблюдения. Симметричные методы наблюдения используются для устранения прогрессивных ошибок, которые являются линейными функциями времени (или другой величины). Такую функцию можно нарисовать в виде графика (рисунок 14).

Время нанесено на абсциссу, В зависимости от прогрессивной ошибки и характеристик измерительного прибора, прогрессивная ошибка может увеличиваться с момента первого измерения. После этого это происходит по всем вторым, третьим и последующим измерениям. Уже включает прогрессив Греховность. Симметричные методы наблюдения состоят в том, что измерения производятся непрерывно через равные промежутки времени. При обработке используйте свойства результата любых двух наблюдений. Симметричная относительная средняя точка интервала наблюдения.

Это свойство Ошибка, полученная в результате пары симметричных наблюдений, равна ошибке, соответствующей средней точке интервала. Например, было проведено 5 измерений. Началось в то время, когда ошибка была T1 1 (см. Рисунок 14). Легко показать, что = ^ y- * = m. Количество измерений Может быть. тогда ch-n x + 14 2 2 2 Три измерения (минимальное количество измерений) и нулевая начальная ошибка упрощают расчет. Если начальная неоднородность постепенно увеличивается, рассмотрим пример применения симметричного метода наблюдения при взвешивании по методу Боде (метод замещения).

Четыре взвешивания выполняются. 1. Взвешенная масса x уравновешена массой g. Предположим, что это соответствует точке А согласно расписанию (см. Рисунок 13). Где 12 11 — коэффициент плеча этих весов, когда на них не влияет причина прогрессивной ошибки. 2. Удалите массу x и уравновесите массу g и массу (их общая масса обозначена I1). Происходит во время 2 = + ч) г- 3. Балансировка повторяется таким образом, чтобы значение веса балансировочного веса считалось равным 1z, когда ошибка достигает значения tz. В результате общая масса t2, которая уравновешивает массу g, изменяется.

Удалите ожоги и поместите взвешенную массу * в чашку. Поскольку неравномерность изменилась и ошибка достигла m4 к времени 4, одна из чашек должна добавить некоторую массу в виде веса для достижения равновесия. Знак плюс перед m указывает, что эта масса добавлена в чашку с массой x, и что знак минус добавлен в чашку с массой r.

Среднее из первого и четвертого измерений (U1.4) Для второго и третьего взвешивания t1 + t, H-NZH, 2 и 2 на (U1.5) Поскольку средняя ошибка результата пары симметричных измерений равна друг другу, h + t4 g, + -s3 2 2 Правые части равенства (U1.4) и (U1.5) также равны. В результате левая часть этих уравнений также равна (U1.6) Оказывается, исключаются не только прогрессивные ошибки из-за изменений неравенства, но также некоторые ошибки из неравенства ( hM).

Как уже указывалось, одной из причин прогрессирующей ошибки в электрических измерениях является постепенное падение напряжения батареи или батареи, питающей схему измерения. Рисунок 15. Схема потенциометра постоянного тока Рассмотрим пример устранения прогрессивной погрешности потенциометра постоянного тока из падения напряжения батареи B (Рисунок 15). Сделайте три измерения. Сначала включите гальванометр G в цепь ЭДС.

Регулировка сопротивления r нормального элемента (переключатель 7 в положении 7) уравновешивает падение напряжения и падение напряжения на сопротивлении образца напряжением от рабочего тока I. Медленное снижение рабочего тока по, Затем поверните переключатель P в положение 2, чтобы отрегулировать сопротивление Ex и измерить требуемое напряжение Ex. Повторите первое измерение здесь. Из-за постепенной ошибки достигается равновесие с новыми значениями рабочего тока и модельного сопротивления E.

Принимая это во внимание, после соответствующего преобразования получите значение Ex без какой-либо прогрессивной ошибки. + Если не ясно, есть ли прогрессивная ошибка, рекомендуется использовать симметричный метод наблюдения. Многие измерения, выполненные в порядке, показанном в сочетании с каким-либо методом для исключения определенных ошибок, могут выявить и устранить любые прогрессивные ошибки. Известная коррекция результатов измерений Результат измерения корректируется расчетом.

Наиболее распространенным случаем коррекции является алгебраическое сложение результатов измерений и коррекций (с учетом их знака). Числовая поправка равна систематической ошибке, а знак противоположен. В других случаях ошибка устраняется путем умножения результата измерения на поправочный коэффициент. Поправочный коэффициент может быть немного больше или меньше 1. Только когда коррекция мала по сравнению с измеренным значением или когда поправочный коэффициент близок к 1, может быть рассчитана высокая точность результата коррекции.

Предположим, что поправочный коэффициент включает одно и два десятичных знака, причем первая цифра равна нулю. Первый десятичный знак (1,1) соответствует 10% -ной ошибке, и такая большая ошибка встречается редко. Поэтому поправочный коэффициент часто составляет 1,01. 1,02; 1,03 литра и т. Д. Чтобы умножить такое число на результат измерения, умножьте на 1 100, переместите запятую на два символа влево и добавьте ее к значению результата. Например, показание прибора составляет 85, а поправочный коэффициент равен 1,02. Одна половина 85 — 1,70.

Скорректированный результат измерения составляет 85 + 1,7 = 86,7. Этот прием также следует использовать, когда поправочный коэффициент меньше 1. Например, 0,96 = 1-0,04 поправочный коэффициент. Чтобы умножить показания устройства на него, вам нужно получить 4 100 устройства. 85 0,96 = 85 (1-0,04) = 85-3,4 = 81,6. Во многих случаях показания прибора должны быть умножены на коэффициент, называемый преобразованием (2; 2,5; 3; 5; 10; 20 и т. Д.). Не объединяйте поправочный коэффициент с коэффициентом пересчета, потому что это усложняет вычисление результатов измерения. Числовой пример.

В результате комбинации был получен коэффициент 2,88. Трудно умножить это число на число в вашем уме. Если вы используете каждый фактор отдельно, умножение не вызовет проблем. Множитель 2,88 является результатом умножения коэффициента преобразования 3 на поправочный коэффициент 0,96. Значение считывания измерительного устройства составляет 115. тогда 115-0,96 = 115 (1-0,04) = 115-4,6 = 110,4; 110.4-3 = 331.2 (как вы знаете, порядок умножения на коэффициенты не играет роли).

В отличие от поправок, поправочные коэффициенты используются, когда погрешность пропорциональна показаниям прибора в определенном диапазоне измерений. В некоторых случаях удобнее указывать фактический размер каждого номинального размера (или дисплея прибора), то есть размер, для которого коррекция уже была введена. Этот модифицированный метод учета в основном используется в качестве контрмеры. Преимущество особенно заметно при применении ряда мер. Фактический размер комплекта, составленного В процессе измерения получается суммирование фактических размеров мер, входящих в комплект.

Сумма этих размеров немного сложнее, чем номинальный размер, но обычно компенсируется номинальным размером. Поскольку операция добавления исключена, результат коррекции быстрее. Кроме того, уменьшается вероятность ошибок расчета. Может указывать фактический размер и ошибку. В этом нет необходимости, поскольку вы можете более уверенно определять признаки коррекции.

Чтобы исправить результаты измерений любым из описанных методов, вы должны сначала определить эти поправки. Чтобы исключить ошибки метода, необходимо знать параметры прибора, который может рассчитать коррекцию результата измерения (если он может быть рассчитан) справочная формула (U1.5) Пример. В случае измерения сопротивления x согласно схеме, показанной на рисунке 10b, были получены следующие измеренные значения амперметра и вольтметра.

Исправьте сопротивление амперметра. Это 0,2 Ом. Фактическое значение сопротивления xd = 2,5-0,2 = = 2,3 Ом. Как правило, ошибки измерительного прибора и другие данные и зависимости, необходимые для определения и создания поправок, идентифицируются до измерения. Однако это можно определить после измерения, но это не следует считать неправильным. В качестве примера мы можем сослаться на точное определение времени на основе астрономических наблюдений и измерений. Коррекция в этом случае определяется после измерения.

Оценка границ систематической ошибки В некоторых случаях систематическое устранение ошибок практически невозможно. Прежде всего, речь идет о методе измерения, и его систематическая ошибка не совсем понятна. Кроме того, существует большая группа приборов, для которых систематические ошибки были изучены и могут быть измерены и определены, но не могут быть использованы для корректировки результатов измерений. Это интегрированная группа инструментов, чаще всего называемая счетчиками.

Скорее, показания счетчиков могут корректироваться только в очень ограниченных случаях, которые не характерны для их применения и предполагаемых условий. Давайте проанализируем вышеупомянутые детали на примере счетчика электрической энергии (обычно называемого электрическим счетчиком). Как правило, угловая скорость каждого встречного диска Текущий момент пропорционален потребляемой мощности. На практике, однако, он не строго пропорционален мощности, и, как следствие, существуют разные нагрузки , то есть разные систематические ошибки для разных мощностей.

На рисунке 13 показана зависимость погрешности счетчика от потребляемой мощности, выраженная в процентах от номинальной мощности (соответствует номинальным значениям тока и напряжения). Каждое значение мощности соответствует определенной ошибке. Однако эти ошибки можно использовать для исправления индикации только в том случае, если значение мощности не изменилось в течение всего процесса измерения. Если измерения с использованием счетчика выполняются с переменными значениями мощности, это очень сложно и в большинстве случаев невозможно рассчитать поправку.

Если систематические ошибки не могут быть исключены (даже если они известны, как в примере выше), оценить возможные границы систематических ошибок. Ошибки счетчика иногда считаются случайными, потому что причина их появления неизвестна, но это не так, потому что каждой величине энергопотребления соответствует конкретная ошибка. Потребляемая мощность не является случайной величиной, а зависит от режима работы электрического устройства, потребляющего энергию. В большинстве случаев ошибка измерения энергии счетчика меньше максимальной ошибки.

Эта ошибка является наибольшей только тогда, когда режим энергопотребления всегда одинаков и ошибка соответствует наиболее важному моменту (см. Рисунок 12). Этот случай маловероятен. При изменении нагрузки признаки ошибок могут меняться, что приводит к частичной компенсации в целом. Поэтому нет способа определить результирующую ошибку, и необходимо внести исправление. Обратите внимание, что если погрешность измерительной системы не превышает ± 2%, ошибка измерения энергии в конечном итоге составит менее 2%.

То, что было сказано об электрических счетчиках, также можно отнести к другим встроенным измерительным приборам и измерениям, проводимым с их помощью. Повторим еще раз: при разработке новых методов измерения и новых инструментов необходимо выявить и исследовать все возможные систематические ошибки.

Смотрите также:

Решение задач по метрологии