Ошибка в примере по вычислению среднего арифметического
- Главная
- Вопросы
В примере по вычислению среднего арифметического от 0 до 100 дан неверный код, который приводит к неверному результату.
Ср.арифметическое (1+2+3+…+100) / 100 = 50.5, а не 50.0, как в уроке (можете проверить ручками или он-лайн калькулятором).
Ошибка состоит в том, что при последнем проходе цикла в значении count = 100 после последнего суммирования count инкрементируется еще раз и на выходе из цикла его значение = 101.
Исправить это можно только отняв лишнюю единицу уже при вычислении итогового результата, потому как, меняя условие на строгое неравенство, мы получаем на выходе правильный count, но недосчитанную на последнее число 100 sum.
Ну или вводом дополнительного условия внутри цикла с break, но это лишний объем кода.
Есть еще варианты?
public class Loop {
public static void main(String[] args) {
int sum = 0;
int count = 1;
while (count <= 100) {
sum += count;
count++;
}
float result = sum / (float) (count - 1);
System.out.println(result);
}
}- Активные
- Старые
- Голоса
Привет, не помню в деталях эту задачу когда проходил, но если задача стоит как вычисление среднего арифметического от 0 до 100 — то здесь 101 число получается 0,1,2,3,…,100, соответвенно и сумму всех чисел делить надо не на 100 как у вас, а на 101. Или что-то я не так понял/прочитал…?
Pavel Lazarev
2 years ago
Привет! Спасибо за ответ, да, это я наоборот не учла, что 0 как слагаемое хоть ничего не добавляет к сумме, но как элемент учитывается все равно и даже в ряде 0+0+1 придется делить на 3 элемента.
2 ответов
|
Lintrix 0 / 0 / 0 Регистрация: 01.05.2013 Сообщений: 61 |
||||
|
1 |
||||
Расчет среднего арифметического01.05.2013, 16:29. Показов 15551. Ответов 5 Метки нет (Все метки)
Расчет среднего арифметического. Здравствуйте, подскажите пожалуйста где в следующей программе ошибка.
__________________ 0 |
|
Vemp 23 / 23 / 3 Регистрация: 18.06.2012 Сообщений: 61 |
||||
|
01.05.2013, 16:34 |
2 |
|||
0 |
|
Fler 212 / 214 / 44 Регистрация: 20.12.2011 Сообщений: 635 |
||||
|
01.05.2013, 16:36 |
3 |
|||
|
среднее арифметическое от количества чисел может быть? или цифр одного числа?
замените свой цикл этим кодом Добавлено через 1 минуту
rezult = sum / n; смысл на каждой итерации цикла вычислять result? 1 |
|
23 / 23 / 3 Регистрация: 18.06.2012 Сообщений: 61 |
|
|
01.05.2013, 16:38 |
4 |
|
смысл на каждой итерации цикла вычислять result? исправил уже ) 1 |
|
0 / 0 / 0 Регистрация: 01.05.2013 Сообщений: 61 |
|
|
01.05.2013, 16:48 [ТС] |
5 |
|
Спасибо за ответы уже разобрался.Как я понял ошибка была в том что нужно было проинициализировать переменные sum и rezult. Может кто-то обьяснить новичку с чем это связано. 0 |
|
212 / 214 / 44 Регистрация: 20.12.2011 Сообщений: 635 |
|
|
01.05.2013, 16:52 |
6 |
|
код Ваш редактировал не забивая в IDE 1 |
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
![]()
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
![]()
Используя более привычные обозначения, формулу записывают как:
![]()
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
![]()
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
![]()
Формула стандартной ошибки средней при использовании выборочной дисперсии
![]()
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
![]()
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
В этой статье вы узнаете, как написать программу, вычисляющая среднее арифметическое значение.
Примечание! Скомпилировать программу через Visual Studio,скорее всего не удастся. Все дело в том, что clrscr() — это тема Борланда, поэтому если компилируешь Студией у тебя ничего не получится.Она поддерживается только Борландовскими компиляторами (программа Borland C++).
Содержание
- Вычислить среднее арифметическое в C++
- Программа на C++ определяющая среднее арифметическое значение
- Рассчитать среднее арифметическое на C
- Программный код на С для расчета среднего арифметического
- Определить среднее арифметическое на Java
- Найти среднее число в Python
- Программный код Python для вычисления среднего числа
Чтобы вычислить среднее арифметическое чисел в программировании на C++ , вы должны попросить пользователя ввести размер числа, а затем попросить ввести числа этого размера.
Чтобы вычислить среднее арифметическое для всех чисел, сначала выполните сложение всех чисел, затем возьмите переменную, отвечающую за среднее арифметическое, и поместите добавление / размер в переменную, скажем armean (среднее арифметическое), а затем отобразите результат на экране вывода, как показано здесь в следующей программе.
Программа на C++ определяющая среднее арифметическое значение
После программы на C++ попросите пользователя ввести размер числа (скажем, n ), затем попросите ввести n чисел для вычисления и отображения среднего арифметического всех чисел:
Вычислить среднее арифметическое на C++
/ * Программа C ++ — Вычислить среднее арифметическое * /
#include<iostream.h>
#include<conio.h>
void main()
{
clrscr();
int n, i, arr[50], sum=0;
cout<<"How many number you want to enter ?n";
cin>>n;
cout<<"Enter "<<n<<" Numbers :";
for(i=0; i<n; i++)
{
cin>>arr[i];
sum=sum+arr[i];
}
int armean=sum/n;
cout<<"Arithmetic Mean = "<<armean;
getch();
}
Когда вышеупомянутая программа C++ компилируется и выполняется, она даст следующий результат:
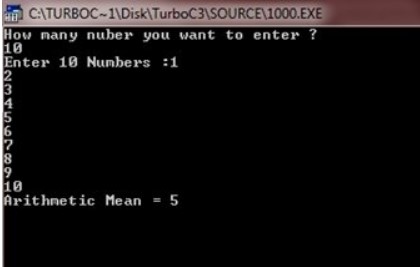
Рассчитать среднее арифметическое на C
Чтобы вычислить среднее арифметическое чисел в программировании на С, вы должны попросить пользователя ввести размер числа, затем попросить ввести числа этого размера для выполнения сложения, затем назначить переменную, отвечающую за среднее и поместить сложение / размер в среднем, затем отобразить результат
Программный код на С для расчета среднего арифметического
Следуя программе на C, попросите пользователя ввести «Сколько цифр он / она хочет ввести», затем попросить ввести все числа для вычисления и отображения среднего арифметического:
Вычислить среднее арифметическое на C
/ * Программа C — Вычислить среднее арифметическое * /
#include<stdio.h>
#include<conio.h>
void main()
{
clrscr();
int n, i, arr[50], sum=0;
printf("How many number you want to enter ?n");
scanf("%d",&n);
printf("Enter %d Numbers :",n);
for(i=0; i<n; i++)
{
scanf("%d",&arr[i]);
sum=sum+arr[i];
}
int armean=sum/n;
printf("Arithmetic Mean = %d",armean);
getch();
}
Когда вышеупомянутая программа c скомпилирована и выполнена, она выдаст следующий результат:

Определить среднее арифметическое на Java
Чтобы вычислить среднее арифметическое некоторых чисел в Java-программировании, вы должны попросить пользователя ввести размер числа, затем попросить ввести числа этого размера для выполнения сложения, а затем назначить переменную, отвечающую за среднее и место сложения / размера. в среднем, затем отобразите результат на экране вывода.
Программный код Java для вычисления среднего или среднего арифметического
Следуя Java-программе, попросите пользователя ввести «Сколько чисел он хочет ввести», затем попросите ввести все числа для вычисления и отображения среднего арифметического:
/ * Пример Java-программы — Вычислить среднее арифметическое * /
import java.util.Scanner;
public class JavaProgram
{
public static void main(String args[])
{
int n, i, sum=0, armean;
int arr[] = new int[50];
Scanner scan = new Scanner(System.in);
System.out.print("How many Number you want to Enter ? ");
n = scan.nextInt();
System.out.print("Enter " +n+ " Numbers : ");
for(i=0; i<n; i++)
{
arr[i] = scan.nextInt();
sum = sum + arr[i];
}
armean = sum/n;
System.out.print("Arithmetic Mean = " +armean);
}
}
Когда вышеуказанная Java-программа компилируется и выполняется, она выдаст следующий вывод:
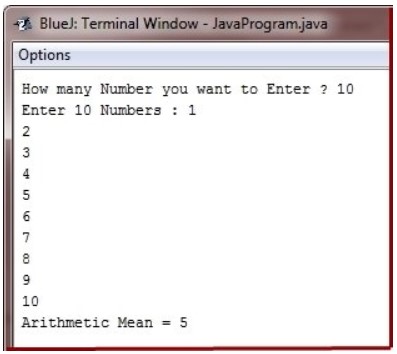
Найти среднее число в Python
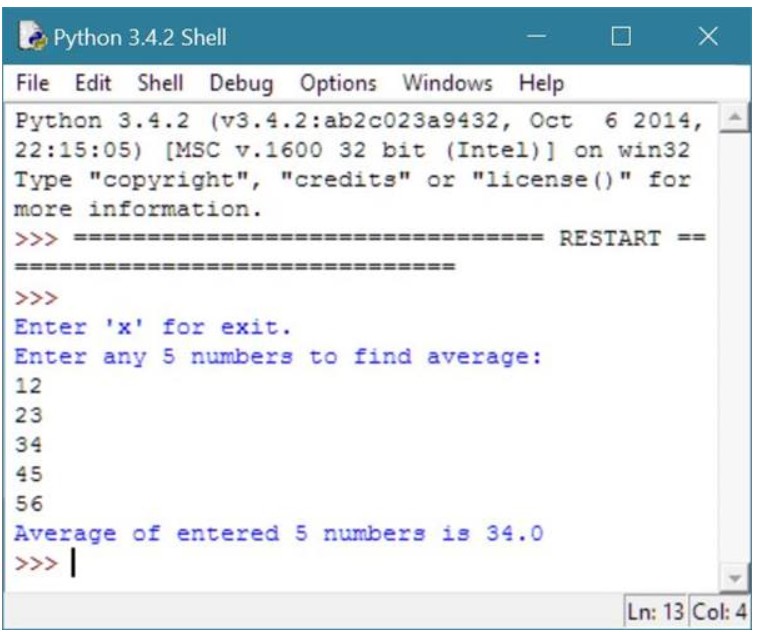
Чтобы рассчитать среднее и арифметическое среднее число чисел в Python, вы должны попросить пользователя ввести некоторый набор чисел, скажем, 5 чисел, чтобы найти среднее из этих чисел, как показано в программе, приведенной здесь.
Программный код Python для вычисления среднего числа
Следующая программа python попросит пользователя ввести 5 цифр, чтобы найти среднее значение всех чисел:
Рассчитать среднее число на Python
# Python Program — Рассчитать среднее число на Python
print("Enter 'x' for exit.");
print("Enter any 5 numbers to find average: ");
n1 = input();
if n1 == 'x':
exit();
else:
n2 = input();
n3 = input();
n4 = input();
n5 = input();
number1 = int(n1);
number2 = int(n2);
number3 = int(n3);
number4 = int(n4);
number5 = int(n5);
sum = number1 + number2 + number3 + number4 + number5;
average = sum/5;
print("Average of entered 5 numbers is",average);
Вот пример запуска вышеуказанной программы Python, показывающий, как рассчитать и напечатать среднее число:
Выше приведен начальный вывод, запрашивающий у пользователя ввести любые пять чисел, чтобы найти среднее значение для всех заданных 5 чисел пользователями, как показано в приведенном ниже примере вывода:
Вот та же самая программа, написанная напрямую и работающая на оболочке Python:
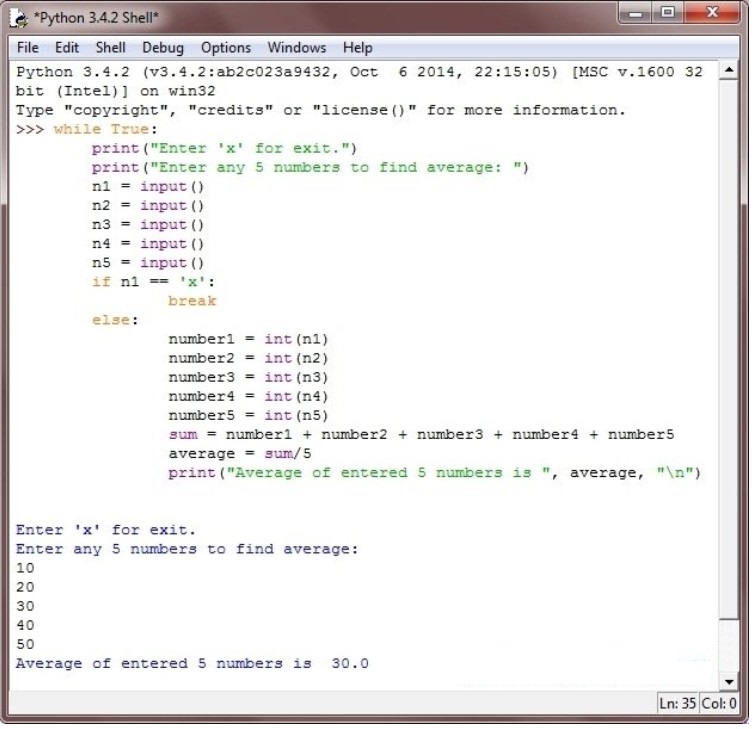
Интересные записи:
Примеры программ на C++
Как написать программу на языке программирования C ++
10 интересных фактов о языке программирования Python
Какова важность математики в информатике?
C ++ теперь более популярен, чем язык программирования Python
Самые востребованные языки программирования
Условное
обозначение средней арифметической
величины через М (от латинского слова
Media) чаще применяется в медицинских и
педагогических исследованиях. В
математической статистике предпочитают
обозначение через ![]() .
.
Средняя арифметическая величина является
производной, обобщающей количественные
признаки ряда однородных показателей
(совокупности). Выражая одним числом
определенную совокупность, она как бы
ослабляет влияние случайных индивидуальных
отклонений, и акцентирует некую обобщенную
количественную характеристику, наиболее
типичное свойство изучаемого ряда
показателей.
Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.
1.
Средняя арифметическая величина может
характеризовать только те признаки
изучаемого объекта, которые присущи
всей совокупности, но в разной
количественной мере (например, уровень
развития быстроты движений характерен
для каждого человека, хотя и в разной
количественной мере). Средняя арифметическая
величина не может характеризовать
количественную меру тех признаков,
которые одной части совокупности
присущи, а другой нет, т. е. она не может
отражать присутствие или отсутствие
того или иного признака (например, умение
или неумение выполнять то или иное
двигательное действие).
2.
Средняя арифметическая величина должна
включать все показатели, полученные в
данном исследовании. Произвольное
исключение даже некоторых из них
неизбежно приведет к искажению конечного
результата.
3.
Средняя арифметическая величина обязана
отражать только однородную совокупность.
Нельзя, например, определять средний
уровень физического развития школьников,
не разделив их предварительно по возрасту
и полу.
4.
Средняя арифметическая величина должна
вычисляться на достаточно большой
совокупности, размеры которой определяются
в каждом конкретном случае отдельно
(см. «Подбор исследуемых»).
5.
Необходимо стремиться к тому, чтобы
средняя арифметическая величина имела
четкие и простые свойства, позволяющие
легко и быстро ее вычислять.
6.
Средняя арифметическая величина должна
обладать достаточной устойчивостью к
действию случайных факторов. Только в
этом случае она будет отражать
действительное состояние изучаемого
явления, а не его случайные изменения.
7.
Точность вычисления средней арифметической
величины должна соответствовать
содержанию изучаемого педагогического
явления. В некоторых случаях нет
необходимости в расчетах с большой
точностью, в других — большая точность
нужна при вычислениях, но совершенно
не нужна в выводах. Например, при расчете
средних величин числа подтягиваний на
перекладине можно пользоваться и сотыми
долями целого, но представлять и выводах,
что исследуемые в среднем подтянулись
7,83 раза, было бы неграмотна, так как
невозможно измерение с подобной
точностью. В этом случае необходимо в
выводах представлять числа, округленные
до целых единиц.
В
простейшем случае этот показатель
вычисляется путем сложения всех
полученных значений (которые называются
вариантами) и деления суммы на число
вариант:
![]()
где
S — знак суммирования;
V
— полученные в исследовании значения
(варианты);
п
— число вариант.
По
этой формуле вычисляется так называемая
простая средняя арифметическая величина.
Применяется она в тех случаях, когда
имеется небольшое число вариант.
При
большом числе вариант прибегают к
вычислению так называемой взвешенной
средней арифметической величины. С этой
целью строят ряд распределения, или
вариационный ряд, который представляет
собой ряд вариант и их частот,
характеризующих какой-нибудь признак
в убывающем или возрастающем порядке.
Например, в нашем случае измерение
точности попадания мячом в цель дало
125 вариант, т. е. в группе I, где применялась
методика обучения «А», одноразово
исследовалось 125 детей с числовым
выражением от 0 (точное попадание в цель)
до 21,5 см (максимальное отклонение от
цели). Каждое числовое выражение
встречалось в исследовании один и более
раз, например «0» встретился 28 раз.
Другими словами, 28 участников эксперимента
точно попали в цель. Этот показатель
называется числом наблюдений или
частотой вариант и условно обозначается
буквой «Р» (число наблюдений составляет
часть числа вариант).
Для
упрощения числовых операций все 125
вариант разбиваются на классы с величиной
интервала 1,9 см. Число классов зависит
от величины колебаний вариант (разности
между максимальной и минимальной
вариантами), наличия вариант для каждого
класса (если, например, для первого
класса — «0 — 1,9» — нет соответствующих
вариант, т.е. ни один исследуемый не имел
точных попаданий или отклонений от цели
в пределах от 0 до 1,9 см, то подобный класс
не вносится в вариационный ряд) и,
наконец, требуемой точности вычисления,
(чем больше классов, тем точность
вычисления выше). Вполне понятно, что
чем больше величина интервала, тем
меньше число классов при одной и той же
величине колебаний вариант.
После
разбивки вариант по классам в каждом
классе определяется срединная варианта
«Vc»,
и для каждой срединной варианты
проставляется число наблюдений. Пример
этих операций, и дальнейший ход вычислений
приведены в следующей таблице:
|
Классы |
Серединные |
Число |
VCP |
VC-M=d |
d2 |
d2P |
|
0 |
1 |
28 |
28 |
-4.6 |
21.16 |
592.48 |
|
2 |
3 |
29 |
87 |
-2.6 |
6.76 |
196.04 |
|
4 |
5 |
22 |
110 |
-0.6 |
0.36 |
7.92 |
|
6 |
7 |
13 |
91 |
1.4 |
1.96 |
25.48 |
|
8 |
9 |
11 |
99 |
3.4 |
11.56 |
127.16 |
|
10 |
11 |
13 |
143 |
5.4 |
29.16 |
379.08 |
|
12 |
13 |
4 |
52 |
7.4 |
54.76 |
219.04 |
|
14 |
15 |
2 |
30 |
9.4 |
88.36 |
176.72 |
|
16 |
17 |
1 |
17 |
11.4 |
130.00 |
130.00 |
|
18 |
19 |
1 |
19 |
13.4 |
179.60 |
179.60 |
|
20 |
21 |
1 |
21 |
15.4 |
237.20 |
237.20 |
|
125 |
697 |
2270.72 |
Очередность
числовых операций:
1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);
2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);
3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);
4)
вычислить взвешенную среднюю арифметическую
величину по формуле:
![]()
Средняя
арифметическая величина позволяет
сравнивать и оценивать группы изучаемых
явлений в целом. Однако для характеристики
группы явлений только этой величины
явно недостаточно, так как размер
колебаний вариант, из которых она
складывается, может быть различным.
Поэтому в характеристику группы явлений
необходимо ввести такой показатель,
который давал бы представление о величине
колебаний вариант около их средней
величины.
Вычисление
средней ошибки среднего арифметического.
Условное обозначение средней ошибки
среднего арифметического — т. Следует
помнить, что под «ошибкой» в статистике
понимается не ошибка исследования, а
мера представительства данной величины,
т. е. мера, которой средняя арифметическая
величина, полученная на выборочной
совокупности (в нашем примере — на 125
детях), отличается от истинной средней
арифметической величины, которая была
бы получена на генеральной совокупности
(в нашем примере это были бы все дети
аналогичного возраста, уровня
подготовленности и т. д.). Например, в
приведенном ранее примере определялась
точность попадания малым мячом в цель
у 125 детей и была получена средняя
арифметическая величина примерно равная
5,6 см. Теперь надо установить, в какой
мере эта величина будет характерна,
если взять для исследования 200, 300, 500 и
больше аналогичных детей. Ответ на этот
вопрос и даст вычисление средней ошибки
среднего арифметического, которое
производится по формуле:
![]()
Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:
![]()
Следовательно,
M±m = 5,6±0,38. Это означает, что полученная
средняя арифметическая величина (M =
5,6) может иметь в других аналогичных
исследованиях значения от 5,22 (5,6 — 0,38 =
5,22) до 5,98 (5,6+0,38 = 5,98).
Соседние файлы в предмете Ветеринарная генетика
- #
- #
- #
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-

1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-

1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-

1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-

1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?

To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?

The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?

The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 995,237 times.
Did this article help you?
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-

1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-

1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-

1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-

1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?

To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?

The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?

The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 995,237 times.
Did this article help you?
Содержание
- Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
- Вопросы и ответы

Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.
Расчет ошибки средней арифметической
Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.
В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.
Способ 1: расчет с помощью комбинации функций
Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.
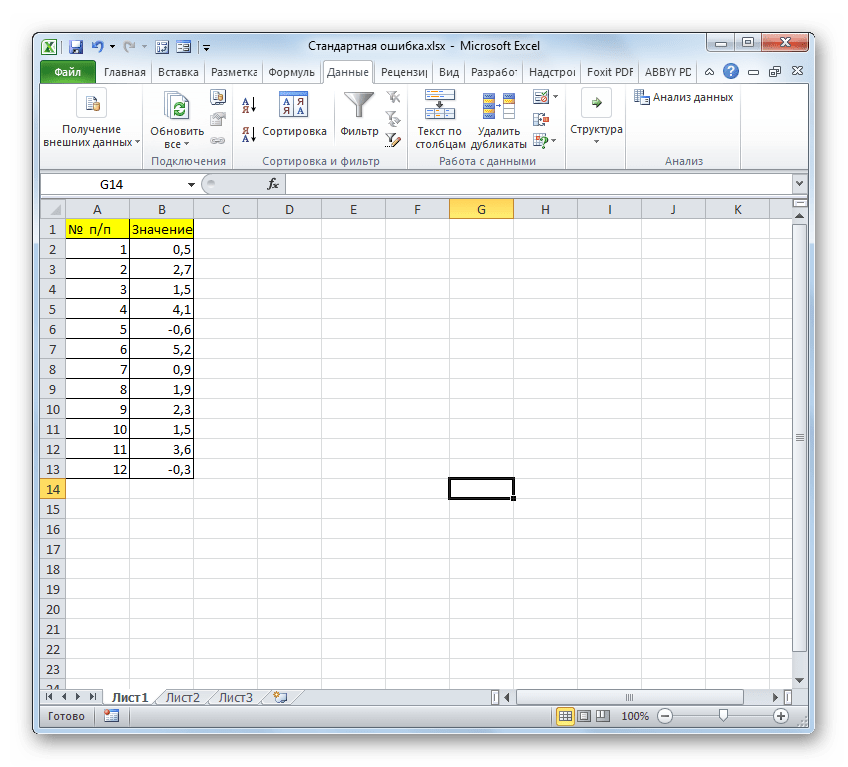
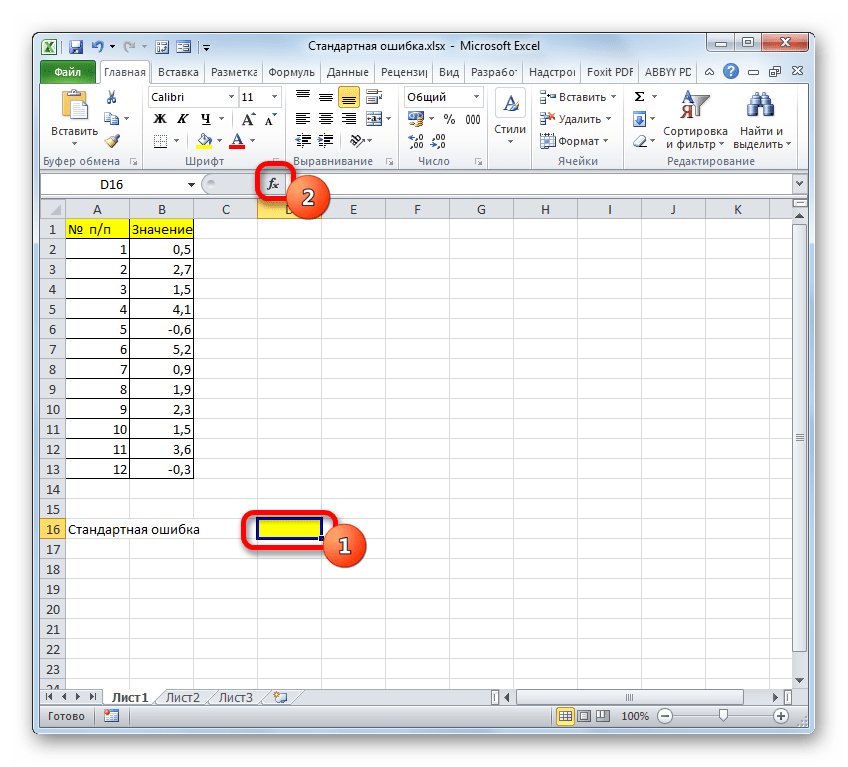
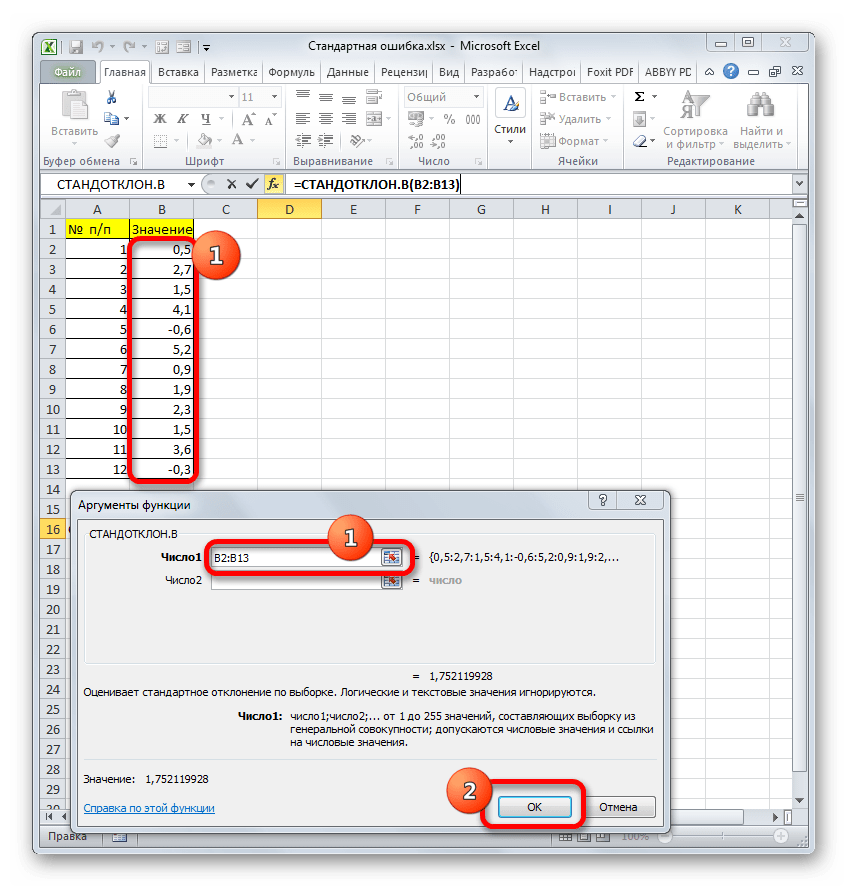
- Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».
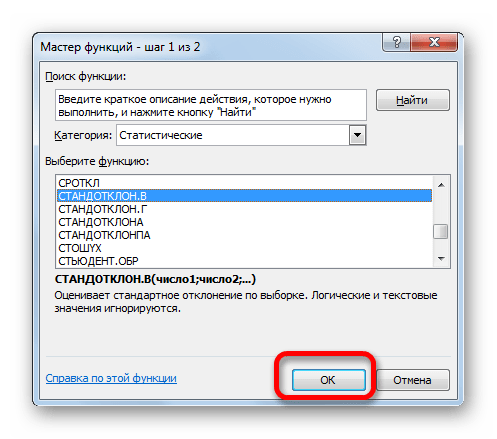
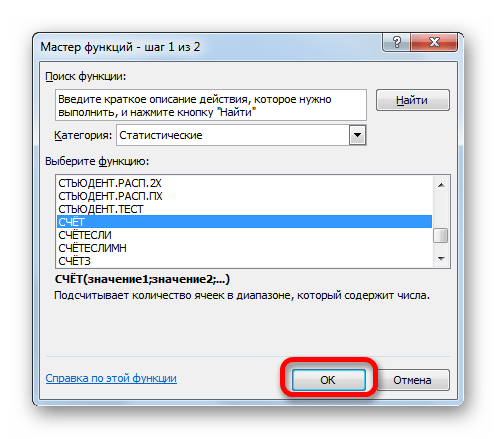
- Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».
- Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».
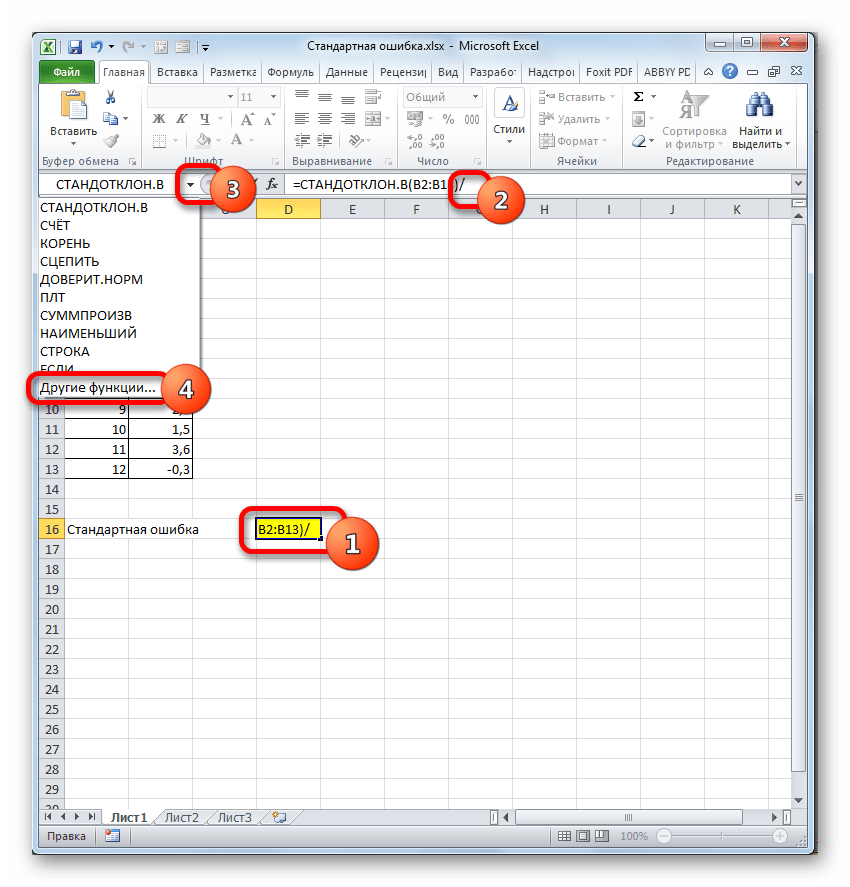
- В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».
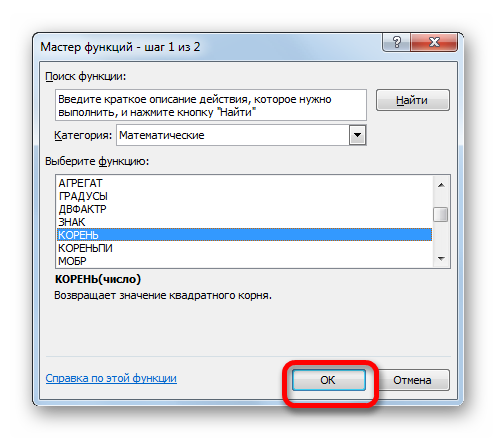
- Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».
- Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)
Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.
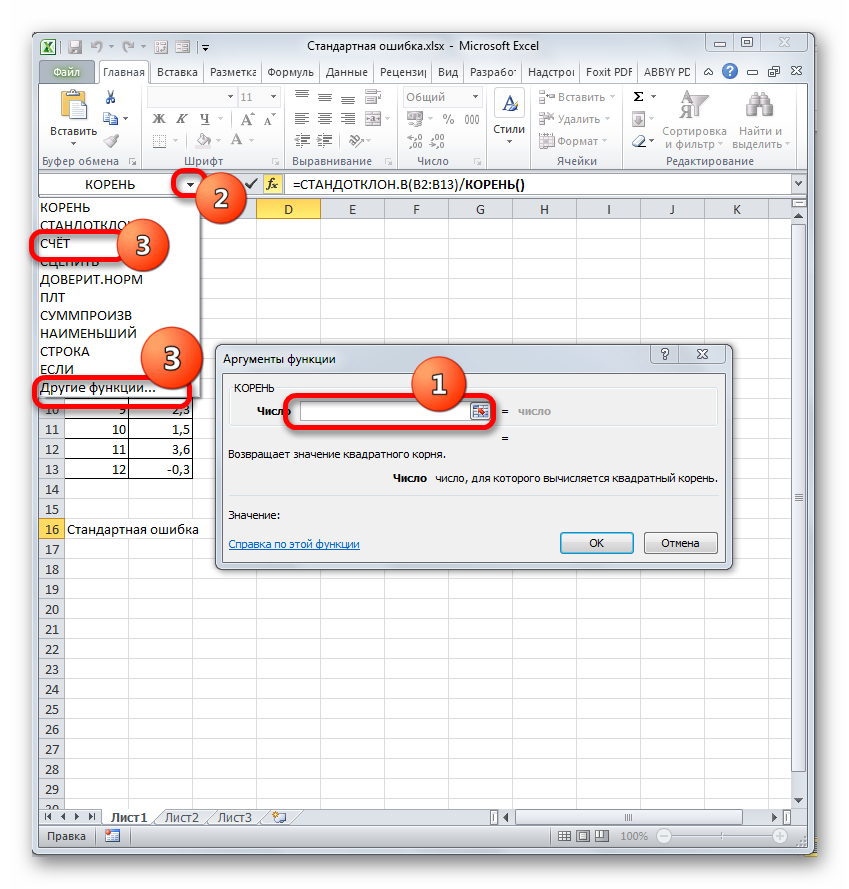
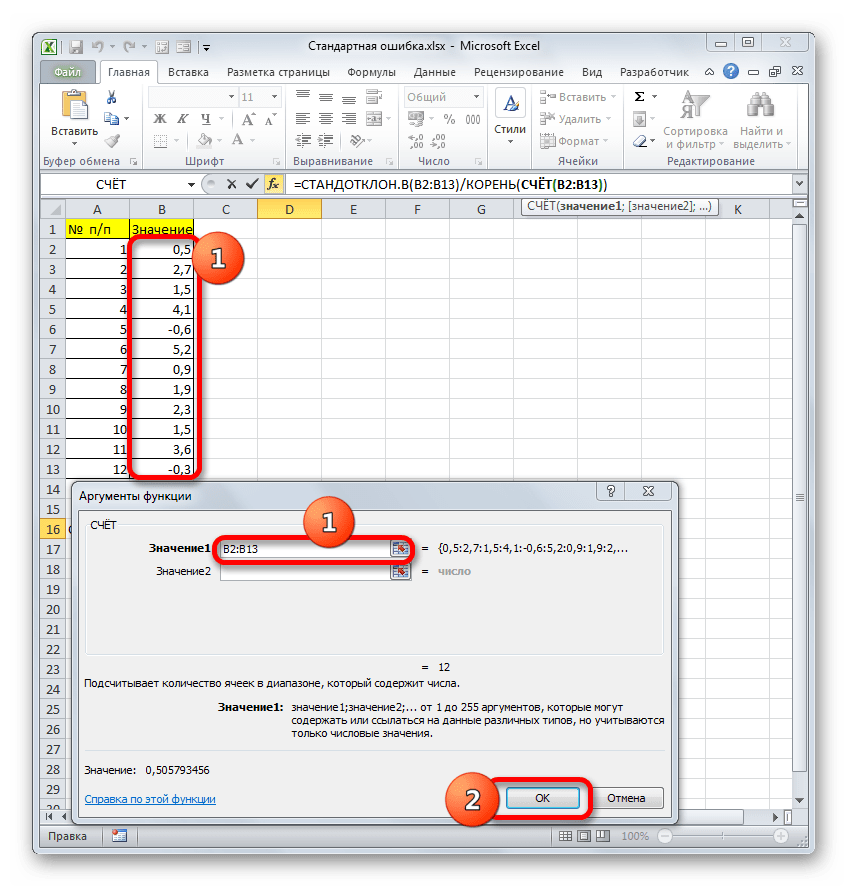
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».
- В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».
- Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».
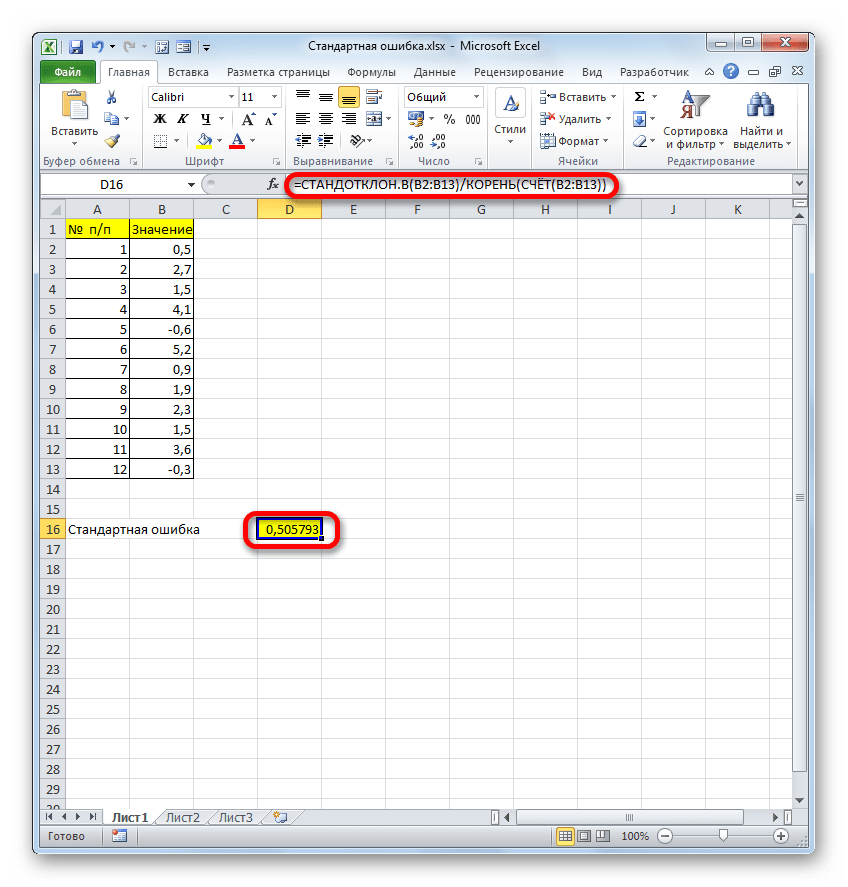
- После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.
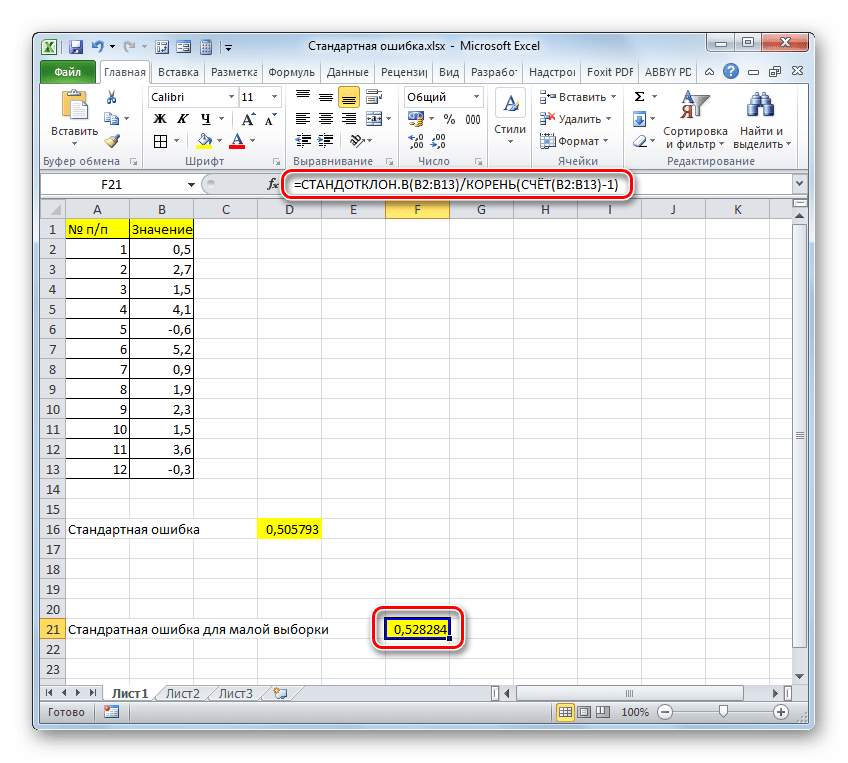
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)
Урок: Статистические функции в Экселе
Способ 2: применение инструмента «Описательная статистика»
Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.
Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.
- После того, как открыт документ с выборкой, переходим во вкладку «Файл».
- Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».
- Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».
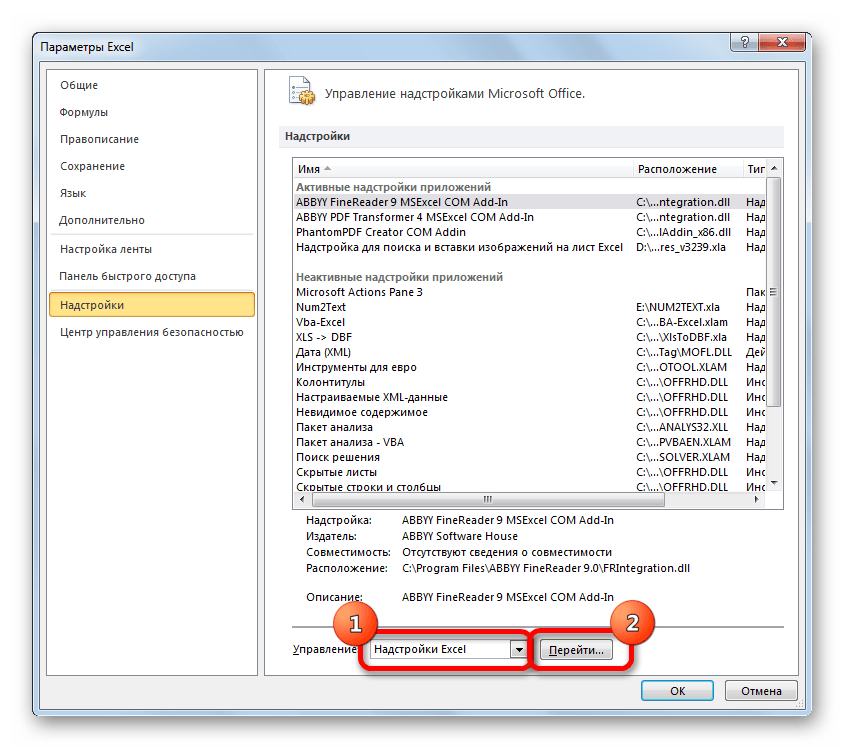
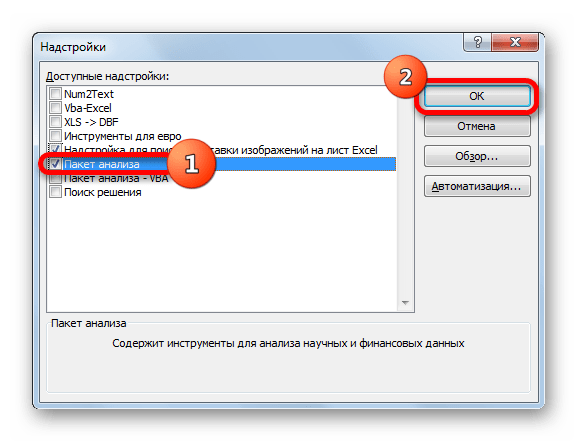
- В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.
- Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.
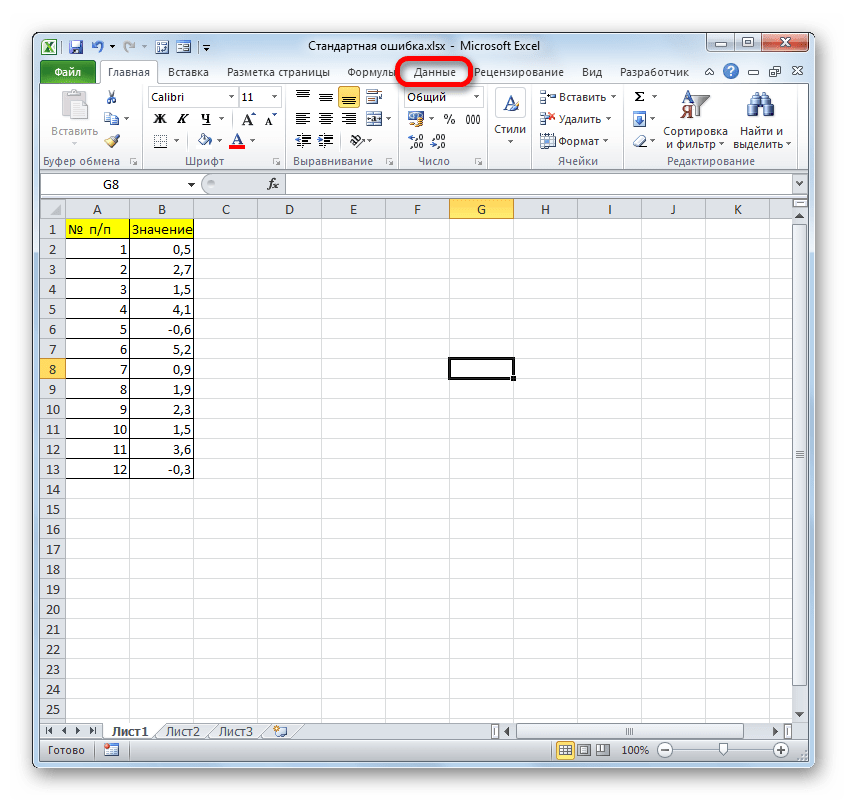
- После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».
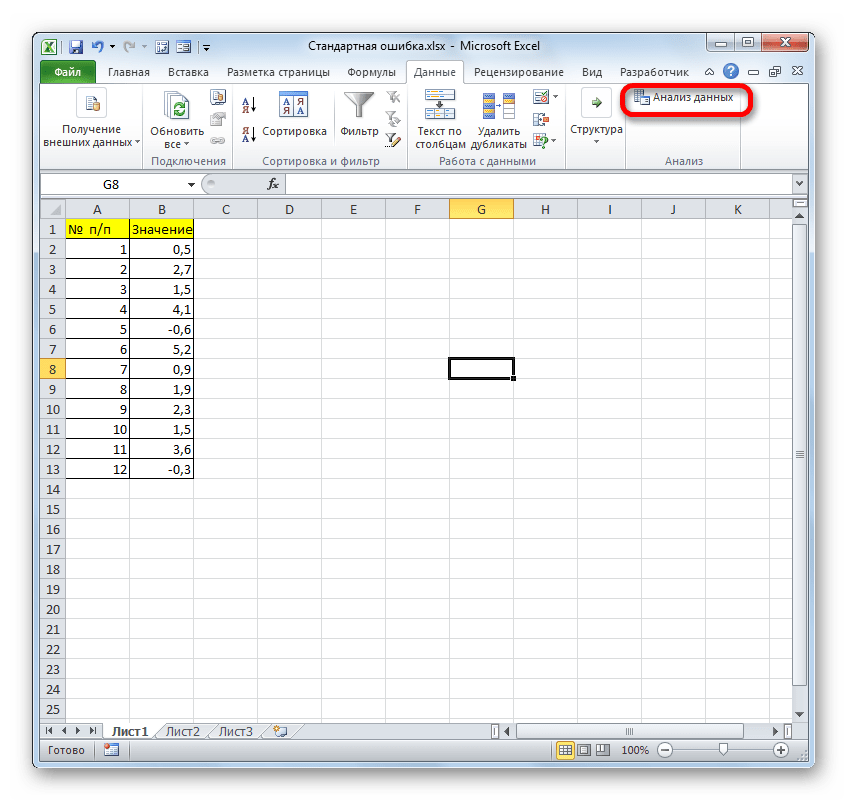
- После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.
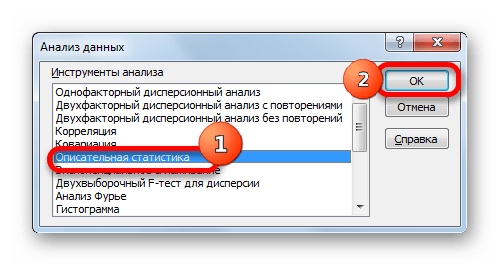
- Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.
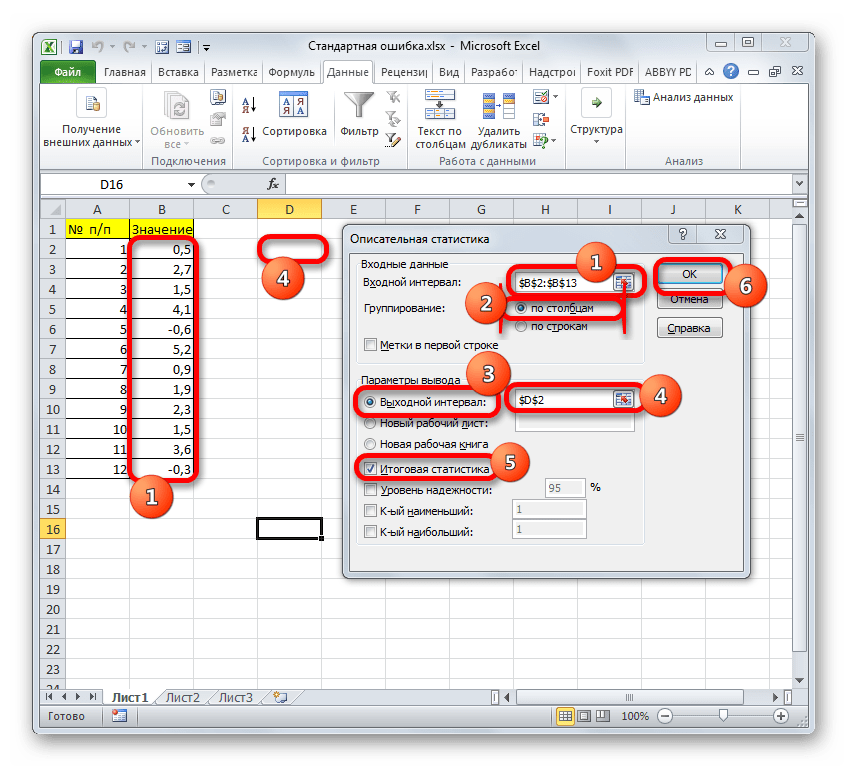
- Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.
В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.
Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.
Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.
Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.
После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.
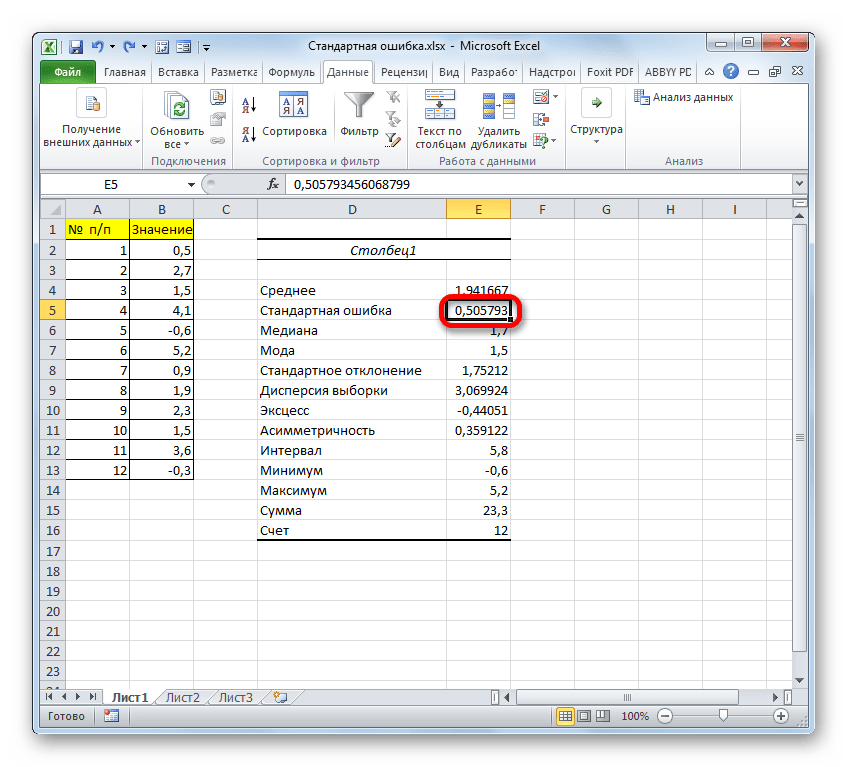
- После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.
Урок: Описательная статистика в Экселе
Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.
|
Lintrix 0 / 0 / 0 Регистрация: 01.05.2013 Сообщений: 61 |
||||
|
1 |
||||
Расчет среднего арифметического01.05.2013, 16:29. Показов 16883. Ответов 5 Метки нет (Все метки)
Расчет среднего арифметического. Здравствуйте, подскажите пожалуйста где в следующей программе ошибка.
0 |
|
Vemp 23 / 23 / 3 Регистрация: 18.06.2012 Сообщений: 61 |
||||
|
01.05.2013, 16:34 |
2 |
|||
0 |
|
Fler 212 / 214 / 44 Регистрация: 20.12.2011 Сообщений: 635 |
||||
|
01.05.2013, 16:36 |
3 |
|||
|
среднее арифметическое от количества чисел может быть? или цифр одного числа?
замените свой цикл этим кодом Добавлено через 1 минуту
rezult = sum / n; смысл на каждой итерации цикла вычислять result?
1 |
|
23 / 23 / 3 Регистрация: 18.06.2012 Сообщений: 61 |
|
|
01.05.2013, 16:38 |
4 |
|
смысл на каждой итерации цикла вычислять result? исправил уже )
1 |
|
0 / 0 / 0 Регистрация: 01.05.2013 Сообщений: 61 |
|
|
01.05.2013, 16:48 [ТС] |
5 |
|
Спасибо за ответы уже разобрался.Как я понял ошибка была в том что нужно было проинициализировать переменные sum и rezult. Может кто-то обьяснить новичку с чем это связано.
0 |
|
212 / 214 / 44 Регистрация: 20.12.2011 Сообщений: 635 |
|
|
01.05.2013, 16:52 |
6 |
|
код Ваш редактировал не забивая в IDE
1 |
a =[]
n= 3
num=0
summ=0
avrg=0
for i in range (0,n):
a.append (int(input()))
if a[i] < 0:
num = num + 1;
if a[i] < 0:
summ = summ + a[i];
avrg=summ/num
print (avrg)
в результате дает последнее число, а не среднее арифметическое всех чисел массива
задан 7 ноя 2017 в 18:41
![]()
toxicarchonttoxicarchont
451 золотой знак1 серебряный знак6 бронзовых знаков
5
Вы хотите каждое вводящие число тестировать на отрицательность и только тогда увеличить их сумму и количество.
Так как вы делаете это сразу после загрузки каждого числа, вам не нужно сохранять их в массиве. Тоже не надо инициализировать переменную avrg:
n = 3
num = 0
summ = 0
for __ in range (0, n):
a = int(input())
if a < 0:
num += 1
summ += a
if num != 0:
avrg = summ / num
print (avrg)
else:
print ('Нет хи одного отрицательного числа.')
Примечания:
-
В цикле
forнам не надо переменной, потому что мы ее не будем использовать — и так вместоiпишем__. -
Мы будем делить на
num— это возможно только для ненулевого значения, потому заключительныйif-тест.
ответ дан 8 ноя 2017 в 6:03
MarianDMarianD
14.2k3 золотых знака18 серебряных знаков29 бронзовых знаков
Во первых, у вас сейчас условия не входят в цикл. То есть выполняются только по последнему значению i на выходе из цикла. Во вторых, избыток условных конструкций. В третьих, можно записать короче. В четвертых, избыточное использование точек с запятой. Они не нужны, если конструкции указываются на разных строках.
В итоге, должно получиться следующее:
a = []
n = 3
num=0
summ=0
avrg=0
for i in range (0,n):
a.append (int(input()))
if a[i] < 0:
num += 1
summ += a[i]
avrg=summ/num
print (avrg)
ответ дан 8 ноя 2017 в 1:19
![]()
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
![]()
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
![]()
Используя более привычные обозначения, формулу записывают как:
![]()
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
![]()
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
![]()
Формула стандартной ошибки средней при использовании выборочной дисперсии
![]()
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
![]()
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:
Стандартная ошибка среднего = s / √n
куда:
- s : стандартное отклонение выборки
- n : размер выборки
В этом руководстве объясняются два метода, которые вы можете использовать для вычисления стандартной ошибки среднего значения для набора данных в Python. Обратите внимание, что оба метода дают одинаковые результаты.
Способ 1: используйте SciPy
Первый способ вычислить стандартную ошибку среднего — использовать функцию sem() из библиотеки SciPy Stats.
Следующий код показывает, как использовать эту функцию:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29]
#calculate standard error of the mean
sem(data)
2.001447
Стандартная ошибка среднего оказывается равной 2,001447 .
Способ 2: использовать NumPy
Другой способ вычислить стандартную ошибку среднего для набора данных — использовать функцию std() из NumPy.
Обратите внимание, что мы должны указать ddof=1 в аргументе этой функции, чтобы вычислить стандартное отклонение выборки, а не стандартное отклонение генеральной совокупности.
Следующий код показывает, как это сделать:
import numpy as np
#define dataset
data = np.array([3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29])
#calculate standard error of the mean
np.std(data, ddof= 1 ) / np.sqrt (np.size (data))
2.001447
И снова стандартная ошибка среднего оказывается равной 2,001447 .
Как интерпретировать стандартную ошибку среднего
Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 150 ]
#calculate standard error of the mean
sem(data)
6.978265
Обратите внимание на скачок стандартной ошибки с 2,001447 до 6,978265.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:
from scipy.stats import sem
#define first dataset and find SEM
data1 = [1, 2, 3, 4, 5]
sem(data1)
0.7071068
#define second dataset and find SEM
data2 = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]
sem(data2)
0.4714045
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.
Дополнительные ресурсы
Как рассчитать стандартную ошибку среднего в R
Как рассчитать стандартную ошибку среднего в Excel
Как рассчитать стандартную ошибку среднего в Google Sheets


 изначально в последней строке ошибка компиляции должна была быть. а связано это с тем, что цикл(в котором переменная result у Вас получала значения) теоретически мог ни разу не выполниться(если бы n было < 1), а в последней строке вы пытаетесь вывести неопределенную переменную
изначально в последней строке ошибка компиляции должна была быть. а связано это с тем, что цикл(в котором переменная result у Вас получала значения) теоретически мог ни разу не выполниться(если бы n было < 1), а в последней строке вы пытаетесь вывести неопределенную переменную