Вычитание операция обратная сложению логика ошибка

Логические значения, операции, выражения

Код ОГЭ: 1.3.3. Логические значения, операции, выражения

Алгебра логики, логические высказывания

Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.

Форма мышления — это способ выражения мыслей или форма, по которой они строятся.

Форма, обозначающая какой–либо объект или отличающий его признак, называется понятием. Примеры понятий: «компьютер», «планета», «длина», «профессия».

Форма, утверждающая или отрицающая что–либо о свойствах понятий и отношений между ними, называется утверждением (высказыванием, суждением). Примеры логических утверждений: «Декодирование — процесс восстановления информации из закодированного представления»; «В двоичной системе используются две цифры: 0 и 1»; «Париж — столица Франции». Утверждения могут быть истинными или ложными. Так, высказывание «Шанхай — столица Франции» является ложным утверждением.

Форма, в которой из двух или нескольких высказываний получают новое утверждение, называется умозаключением. Пример умозаключения: «Периферийные устройства компьютера — это устройства для ввода или вывода информации. Сканер — устройство для переноса текста и изображений с бумаги в компьютер. Следовательно, сканер — периферийное устройство».

Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.

Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.

Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно. Вопросительные и повелительные предложения не являются логическими высказываниями. Но и не каждое повествовательное предложение является логическим высказыванием. Например, суждение «Лето было очень дождливым» не является однозначным, для утверждения «Существует несколько Вселенных» нельзя однозначно определить истинность; поэтому такие предложения не являются логическими высказываниями (утверждениями).

Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.

В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.

Сложные высказывания представляют собой объединение простых высказываний с помощью логических связок. В качестве логических связок используются слова «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний. Например, из простых высказываний «Офис фирмы находится в Мадриде» и «Офис фирмы находится в Берлине» можно составить сложные: «Офис фирмы находится в Мадриде или Берлине», «Офис фирмы находится в Мадриде и Берлине», «Если офис фирмы находится в Мадриде, то он находится в Берлине». Истинность первого из них означает, что офис фирмы находится в одном из названных городов или же имеются офисы в обоих городах. Ложность его означает, что ни в одном из этих городов офиса нет. Второе составное утверждение истинно тогда, когда в обоих городах имеется офис фирмы. Если же офис существует только в Берлине или только в Мадриде, — второе составное высказывание ложно.

В классической, двузначной алгебре логики логических значений всего два: истина (True) и ложь (False). Им соответствует цифровое представление — 1 и 0. Иногда эти значения записывают как «да» и «нет». Факт истинности или ложности некоторого высказывания А записывают соответственно как А = 1 или А = 0.

Логические операции

В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.

Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.

Логическое отрицание (инверсия) — логическая операция, в результате которой из данного высказывания получается новое высказывание — отрицание исходного. Обозначается символически чертой сверху (Ā) или условными обозначениями ¬А, not А, не А (читается «отрицание А», «не А», «А ложно», «неверно, что А»).

Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.

Таблица истинности операции отрицания

Если обозначить через А высказывание «Арбуз является ягодой», то ¬А соответствует высказыванию «Арбуз не является ягодой» («Неверно, что арбуз — ягода»).

Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.

Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.

Логическое умножение (конъюнкция) — операция, соединяющая два или более высказываний при помощи связки «и». Эта связка символически обозначается с помощью знака ∧ и читается «А и В». Для обозначения конъюнкции также применяются знаки: А • В, А & В, А и В, А and В, а иногда между высказываниями не ставится никакого знака: АВ.

Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.

Таблица истинности операции конъюнкции

Например, высказывания «Лондон расположен севернее Лиссабона» и «Лондон расположен восточнее Лиссабона» истинны. Тогда истинным будет и составное логическое высказывание «Лондон расположен севернее и восточнее Лиссабона». Высказывания «Лондон расположен не севернее и восточнее Лиссабона», «Лондон расположен севернее и не восточнее Лиссабона», «Лондон расположен не севернее и не восточнее Лиссабона» — ложны.

Логическое сложение (дизъюнкция) — операция, соединяющая два или более высказываний при помощи связки « или». Эта связка символически обозначается с помощью знака v и читается «А или В». Для обозначения дизъюнкции также применяются знаки: А + В, А или В, А or В, А | B.

Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.

Таблица истинности операции дизъюнкции

Например, высказывания «Виктор старше Ольги» и «Виктор — однофамилец Ольги» истинны. Тогда истинными будут и составные логические высказывания «Виктор старше Ольги или Виктор — однофамилец Ольги», «Виктор младше Ольги или Виктор — однофамилец Ольги», «Виктор старше Ольги или Виктор — не однофамилец Ольги». Высказывание «Виктор младше Ольги или Виктор — не однофамилец Ольги» — ложно, поскольку ложны оба составляющие его простые высказывания.

Исключающее сложение (исключающая дизъюнкция, строгая дизъюнкция, сложение по модулю два, дизъюнкция строго–разделительная) — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле (называется также исключающее «или»). Операция символически обозначается с помощью знака ⊕ и читается «либо А, либо В».

Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.

Таблица истинности операции строгой дизъюнкции

Например, результат исключающей дизъюнкции двух высказываний «Виктор не старше Ольги» и «Виктор младше Ольги» всегда будет истиной, кто бы из них не был старше.

Логическое следование (импликация) — логическая операция, соединяющая два высказывания при помощи связки «если… то» в сложное высказывание. Операция символически обозначается с помощью знака → и читается «Если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяются также знаки ⊃ или ⇒. Первое логическое высказывание является условием (посылкой), а второе — следствием (заключением).

Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.

Таблица истинности операции импликации

Для высказываний «Луна — спутник Земли» и «Сумма углов треугольника не равна 180°» (первое истинно, второе ложно) составное высказывание «Если Луна — спутник Земли, то сумма углов треугольника не равна 180°» будет ложным. Однако истинными будут высказывания «Если Луна — спутник Земли, то сумма углов треугольника равна 180°», «Если Луна — не спутник Земли, то сумма углов треугольника не равна 180°» и «Если Луна — не спутник Земли, то сумма углов треугольника равна 180°». Этот пример наглядно демонстрирует, что в алгебре логики смысл высказываний не учитывается, а рассматриваются только их истинность или ложность.

Логическое равенство (эквивалентность, следование, двойная импликация, равнозначность) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В (читается «А эквивалентно B»). Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Для обозначения эквивалентности применяются знаки ~, ⇔.

Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.

Таблица истинности операции эквивалентности

Для высказываний «Линейное уравнение всегда имеет решение» и «Кит — млекопитающее» их эквивалентность всегда будет истиной, так как оба простые утверждения истинны.

Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:

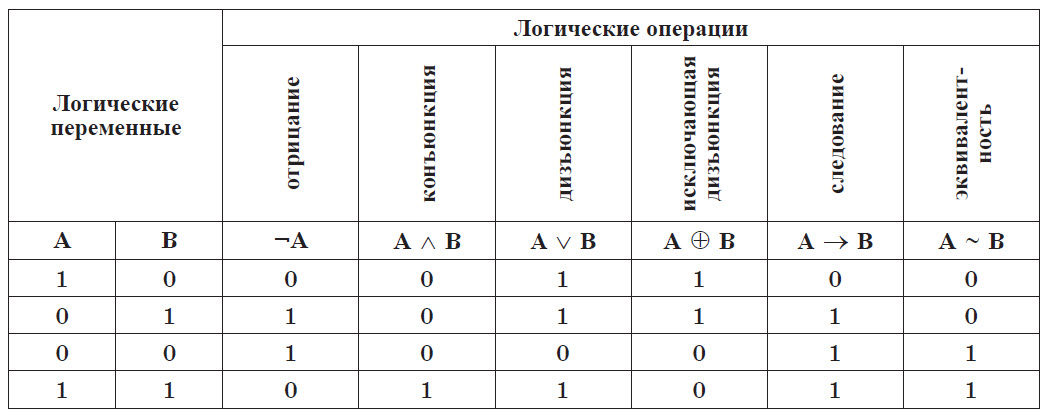
Логические выражения

Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.

Правила построения логических выражений:

• любая логическая переменная или константа (истина и ложь) являются логическим выражением;
• если А — , то ¬А — тоже логическое выражение;
• если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А ~ В — тоже логические выражения.

Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.

Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.

Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В ~ ¬В.

Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.

Приоритет выполнения логических операций в логических выражениях

Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В

Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий:

Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.

Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)

1) Олег   2) Марианна  3) Светлана   4) Ольга.

Решение.

1.  В соответствии с приоритетом выполнения операций сначала нужно вычислить результат операции отрицания: «Длина имени больше 5 букв». Такие имена — Марианна, Светлана.
2. Затем необходимо рассчитать результат конъюнкции (связка И) второго и третьего высказываний. Конъюнкция истинна только тогда, когда истинны оба высказывания. Следовательно, нужно выбрать имена, в которых и первая буква гласная, и длина имени больше 5 букв — таких имен среди вариантов нет.
3. Результат дизъюнкции (связка ИЛИ) истинен только тогда, когда истинно или одно, или второе, или одновременно оба простые высказывания. Первое простое высказывание истинно для имени Марианна, второе ложно для указанных имен. Таким образом, верный вариант ответа — 2.

Ответ: 2) Марианна.

СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ

Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности можно выразить через операции отрицания, логического сложения и умножения, что отражено в следующей таблице.

Связь между логическими операциями

Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.

Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.

РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.

Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.

Пример 3
Проверить равносильность выражений А ~ E и (Ā ∧ Ē) v (A ∧ E).

Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.

Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.

Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.

Основные законы алгебры логики

Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.

Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.

Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.

Тождественные преобразования логических выражений

Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.

Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.

Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).

1) A         2) A ∧ B          3) Ā ∧ B           4) B

Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше <, больше или равно ≥, меньше или равно ≤, равно =, не равно ≠), также являются логическими выражениями. Кроме операций сравнения и логических операций такие выражения могут включать функции и алгебраические операции. Приоритет выполнения этих операций таков:

1. Вычисление значений функций.
2. Выполнение алгебраических операций (вначале возведение в степень, затем умножение и деление, после чего вычитание и сложение).
3. Выполнение операций сравнения (в порядке записи).
4. Выполнение логических операций (сначала операции отрицания, затем операции логического умножения, потом операции логического сложения, последними выполняются операции импликации и эквивалентности).

Если в логическом выражении используются скобки, то сначала выполняются заключенные в них операции.

Пример 5
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1          2) 2         3) 3        4) 4

Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М < 10. Получим выражение М < 10 ∧ M > 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.

Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.

Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1           2) 2         3) 3        4) 4

Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:

Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.

Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?

Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март < Апрель) ∧ (Апрель < Май) v (Июнь > 80).

Введем обозначения:
А = (Март < Апрель)
В = (Апрель < Май)
С = (Июнь > 80)

Тогда выражение можно записать как А ∧ В v С.

Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март < Апрель) и (Апрель < Май)). Значение выражения дизъюнкции будет истинным, если хотя бы одно из составляющих его простых высказываний будет истинным.

Составим таблицу истинности для исходных данных.

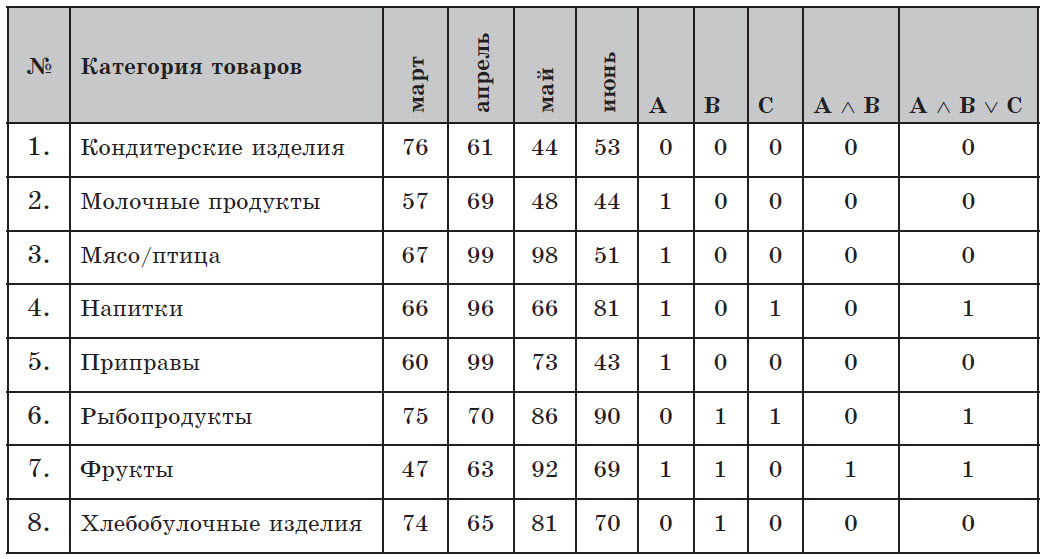
Логическому выражению удовлетворяют 3 записи — 4–я, 6–я и 7–я.
Ответ: 3.

Конспект урока по информатике «Логические значения, операции, выражения».

Вернуться к Списку конспектов по информатике.

Прежде чем говорить о физическом смысле арифметических операций напомним основные понятия арифметики:

Операнд – величина, представляющая собой объект операции.

Операции определяют действия, которые надо выполнить над операндами (+, –, ×, :).

Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a + b.

Вычитание – действие, обратное сложению (См. Сложение); задачей В. является определение одного из двух слагаемых, когда даны сумма и другое слагаемое. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, результат действия — разностью. В области положительных чисел В. не всегда выполнимо (из меньшего числа нельзя вычесть большее). Это обстоятельство является формальным поводом для введения в арифметику нуля и отрицательных чисел; в расширенной таким образом числовой области В. всегда однозначно выполнимо.

Умножение – операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. Умножение обозначается знаком «×» (ввёл англ. математик У. Оутред в 1631) или «•» (ввёл нем. учёный Г. Лейбниц в 1698); в буквенном обозначении эти знаки опускаются и вместо а × b или а • b пишут ab. Умножение имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. Умножение целых положительных чисел есть, по определению, действие, относящее числам а и b третье число с, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а + … + а (b слагаемых). Число а называется множимым, b – множителем.

Деление – действие, обратное умножению (См. Умножение); заключается в нахождении одного из двух сомножителей, если известны произведение и др. сомножитель. Т. о., разделить а на b — это значит найти такое х, что bx = а или xb = а. Результат Д. х называется частным, или отношением, a и b. Заданное произведение а называется делимым, а заданный множитель b — делителем. Для обозначения Д. употребляют знаки двоеточия (а : b) или горизонтальной (иногда наклонной) черты (a/b).

Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте. Последовательность всех натуральных чисел, расположенных в порядке их возрастания, называется натуральным рядом. Существуют два подхода к определению натуральных чисел — это числа, возникающие при: подсчёте (нумерации) предметов (первый, второй, третий) или при обозначении количества предметов (нет предметов, один предмет, два предмета). В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход.

Нуль – (нем. Null, от латин, nullus – никакой). Арабская цифра, сама по себе, ничего не значащая, но показывающая отсутствие того разряда цифр (в нумерации), на месте которого она стоит (правильнее сказать отсутствие цифр в разряде – авт.); поставленная после значащих цифр обозначает десятки, сотни, тысячи и т. д.

Для простоты будем рассматривать действия с натуральными числами.  

***

Хотя математика является всего лишь языком физики, практически все математики давно забыли об этом и провозгласили математику царицей наук, стоящей даже выше физики. Поэтому мы предлагаем вашему вниманию давно забытые математиками физические основы арифметических операций и причины, по которым математики иногда вполне обоснованно нарушают их в пользу своих математических абстракций. Однако при этом сами математики, как это ни странно, уже не в состоянии объяснить правомерность своих же собственных правил по причине отрыва от физики.   

В природе количество предметов изменяется либо в процессе физико–химических взаимодействий материи, либо в результате её механического движения. При этом любое изменение количества предметов должно строго соответствовать закону сохранения материи и энергии, что подразумевает изменение количества в строгом соответствии с реальными физическими действиями с ними.

В арифметике определение общего количества предметов осуществляется путём их сквозной нумерации (счёта) с присвоением каждому последующему элементу счёта порядкового номера на единицу большего, чем предыдущий. При этом сам процесс счёта фактически представляет собой операцию сложения, простейшим слагаемым которого является одна единица счёта или нумерации. А суммой является последний порядковый номер счёта.

Совершенно очевидно, что сквозная нумерация не зависит от любых внутренних перестановок предметов внутри их общей суммы в любом их сочетании и количестве, что и определяет все известные свойства сложения и их соответствие законам природы. На этих физических свойствах собственно и основаны все остальные арифметические операции, являющиеся всего лишь различными алгоритмами сложения или обратного ему действия вычитания.

Таким образом, сложение является базовой операцией определения количества чего–либо в природе.

В математике существуют также более сложные математические операции: возведение в степень, извлечение корней, логарифмы, экспоненты и т.д. Однако все они так или иначе построены на простейших арифметических операциях, т.е. в конечном итоге на базовом сложении, что отражено в определении их количественного результата «столбиком».

Таким образом, базовой арифметической операцией, лежащей в основе всех математических операций, является операция сложения, физической основой которой является сквозная нумерация или счёт.

Рассмотрим физический смысл простейших арифметических операций на примере операций с нулём, которым обозначают отсутствие количества предметов счёта и действий с ним, т.к. именно такие операции и вызывают наибольшее количество вопросов по физическому смыслу арифметических операций.

Итак, обо всём по порядку.

Сложение. По определению общая сумма должна определяться общим счётом, т.е. последовательной нумерацией предметов счёта, содержащихся, как минимум в двух числах, что определяет свойство бинарности сложения. При этом в случае сложения одного значащего числа с нулём свойство бинарности формально нарушается, т.к. нуль – это символ, обозначающий отсутствие числа. Однако вопреки официальному определению сложения и в частности свойству бинарности, суммой в математике однозначно признаётся даже один единственный значащий операнд, о чём свидетельствует существующее сложение с нулём:

0 + Х = Х + 0 = Х

По официальной версии один операнд просто не с чем складывать. Однако физически даже один операнд имеет собственную сквозную нумерацию, конечный номер которой определяет его собственную сумму. Она же фактически является и общей суммой операции сложения с нулём, если уж признавать такую не бинарную операцию с нулём правомерной. Однако, как это ни странно, официальная математика отрицает это вполне правомерное физическое объяснение свойства бинарности в операциях сложения с нулём.

Рис. 6.1.1

На рисунке (6.1.1) показано, что сумма нуля со значащим операндом, представляющим собой мешок с деньгами, равна собственному счёту денег в мешке при любом порядке сложения этих операндов. Некоторые наши оппоненты утверждают, что результат такой фактически несостоявшейся операции с бездействующим и беспредметным нулём не может считаться результатом самой операции, как таковой, т.к. она не состоялась.

Но во–первых, при этом сохраняется результат сквозного счёта значащего операнда.

А, во–вторых, результат – это итоговое знание существующей реальности, которое включает в себя, в том числе и знание того, состоялось ли что–то или не состоялось.

Что касается бинарности, то даже, если единственный значащий операнд представляет собой одну единственную единицу счёта, например, одну монету, то и это теоретически не отменяет суммарного итога такой не бинарной операции, поскольку одна единица счёта одновременно является первичным структурным элементом суммы. А поскольку конечность деления материи на сегодняшний день наукой не установлена, то вопрос бинарности это ещё и вопрос выбора единиц измерения или масштаба счёта. Даже одиночные предметы перестают быть единицами счёта при изменении его масштаба.

Таким образом, бинарность в физике – это всего лишь вопрос выбора единиц измерения предметов счёта, а в математике – масштаба единиц счёта, мельчайшая из которых в любом случае является элементом счёта и соответственно первичным структурным элементом суммы.

Некоторые математики не видят нарушения свойства бинарности в операциях сложения с нулём совсем по другой причине. Они считают нуль таким же полноправным числом, как и значащие числа, а значит и полноправным операндом операции сложения. Однако не меньшее количество математиков так не считают. Но математика, как язык физики, не может опираться на личные предпочтения математиков. Поэтому здесь и далее мы будем исходить только из физических соображений.

Число – это не просто второе лингвистическое название, т.е. синоним операнда. Физически любое число отражает количество предметов. И хотя официально цифры в математике не считаются числами, количество заложено также и во все цифры от 1 до 9, кроме нуля. Нуль – это единственная цифра, или символ, обозначающий отсутствие количества по определению. Следовательно, физически, а значит и математически нуль – это не число. Нуль – это цифра, символизирующая отсутствие чего–либо, т.е. это символ несуществующей сущности, в том числе и несуществующего действия.

Но дело вовсе не в названии. Даже если назвать нуль числом, он так и останется особым, пустым «числом», обозначающим пустой операнд, не способный ничего изменить ни в какой операции. В представленной выше иллюстрации (см. Рис. 6.1.1) таким пустым операндом является сам мешок, который не способен изменить общий счёт денег, задействованных в операции. Можно, конечно, дорисовать нуль или нулевой пустой мешок и в правой части равенств, изображённых на рисунке (6.1.2), однако на суммарном количестве денег это никак не отразится. Поэтому в правой части пустые мешки, эквивалентные пустому числу нуль, мы просто опускаем.

Рис. 6.1.2

То же самое можно принципиально сделать и в левой части, в которой пустой мешок или нуль сохранён исключительно только для обозначения последовательности математических преобразований исходного выражения, в результате которых его члены могут и обнуляться, в том числе. При этом в математике нулевые члены без каких–либо противоречий физическому счёту могут быть опущены только в операциях сложения и вычитания.

В умножении принципиально такая же операция опускания одинаковых членов выполняется делением на одинаковые члены, что уже принципиально отличается от простого «опускания» и соответственно называется несколько другим словом — «сокращение». Причём в отношении нулевых членов эти различия принципиально одинаковых действий над принципиально одинаковыми операциями, опирающимися на общее базовое сложение, необъяснимы с физической точки зрения.

Если в сложении и вычитании сократить или просто опустить нулевые операнды можно безо всяких последствий для итогового счёта или суммы, то в умножении и делении просто так без последствий избавиться от несуществующих операндов, обозначенных нулём, не получится. Существующее умножение на нуль совершенно не естественным, т.е. не физическим образом обнуляет весь предыдущий счёт, а сокращение или деление на нуль в математике вообще запрещено, что противоречит физическому смыслу базовой операции сложения! Ё!

Более подробно мы рассмотрим это вопрос ниже в разделе «умножение» и «деление».

Вычитание — обратно сложению. В вычитании ничего не значащая по определению цифра – нуль также не считается нарушением свойства бинарности:

Х — 0 = Х + (–0)) и (0 — Х = 0 + (–Х)

Справедливость этих равенств не зависимо от свойства бинарности проиллюстрировано на рисунке (6.1.3). Конечно же, последнее равенство на рисунке (6.1.3) можно представить, как мешок с деньгами со знаком минус или как пустой мешок, что означает мнимое число денег, т.е. долг. Тем не менее заметим, что вернуть–то в любом случае нужно положительное количество денег. Следовательно, мнимое отрицательное число долга количественно по абсолютной величине равно значащему операнду, что и отражено в последнем равенстве на рисунке (6.1.3) без знака минус.

Рис. 6.1.3

На рисунке (6.1.4) символическая запись долга показана в виде мнимого отрицательного мешка с деньгами в верхнем равенстве или в виде пустого мешка в нижнем равенстве.  Это вопрос всего лишь условных обозначений, но никак не физики процесса.

Рис. 6.1.4

Но даже формальное нарушение свойства бинарности в базовом сложении и вычитании с нулём – это ничто по сравнению с физическими противоречиями арифметических операций умножения и деления с нулём. Несмотря на то, что эти операции ничем принципиально не отличаются от базовой для них операции сложения, пустое число нуль в них является настолько значимым, что только он один целиком и полностью определяет результат счёта даже для значимых операндов.

Итак, перейдём к физическому смыслу операций умножения и деления на нуль.

    Умножение. По определению умножение – это сложение одинаковых операндов равных по величине умножаемому в количестве равном множителю.

Как видно, по своему физическому смыслу операция умножения, которую можно представить в виде сложения одинаковых операндов, ничем принципиально не отличается от операции базового сложения. Однако если в сложении и вычитании нуль не влияет на конечный результат, то в результате операции умножения значащего числа с нулём получается нуль, что совершенно необоснованно с физической точки зрения:

Х * 0 = 0 * Х = 0                                   

Можно показать, что если нуль обозначает величину умножаемого (0 * Х), то аналогия классического умножения с нулём, как алгоритма повторяющегося сложения, в котором есть (Х) одинаковых нулевых слагаемых со сложением, хотя бы формально сохраняется:

0 * Х = 0 + 0 + … + 0 = 0

Это является самым распространённым в математике формальным доказательством нулевого результата при умножении на нуль. А формальность этого доказательства заключается в следующем:

Во–первых, повторение несуществующей сущности возможно только абстрактно математически. В реальной действительности, как ничто ни повторяй, ничто и получится. Точнее ничего не получится. Поэтому нулевой символ, обозначающий отсутствующую сущность, так и останется единственным и не повторённым, причём только в начальных условиях операции, т.к. саму операцию с нулём следует считать не состоявшейся. А результат этой не состоявшейся операции ничем не будет отличаться от результата операции базового сложения с нулём:

0 + Х = 0 * Х = Х

Во всяком случае значащий операнд x, присутствующий в исходных условиях игнорировать, как ничего не значащий 0, нельзя. Тем более что раз операция не состоялась, то с (х) в итоге ничего не может произойти в принципе.

Во-вторых, само по себе не повторение должно оставлять всё, что есть без изменения, т.к. нет никаких физических оснований считать, что ни разу не повторённый значащий операнд вдруг исчезает, превратившись в нуль, безо всяких действий над ним. При этом, чтобы факт несостоявшейся операции никого не смущал, операцию с бездействующим нулём целесообразно считать вполне состоявшейся охранной операцией по запрещению действия, хотя бы в противовес официальному физическому беспределу по необоснованному уничтожению значащих операндов при умножении их на нуль.  В этом случае, операция умножения числа на нуль будет строго соответствовать базовой операции сложения с нулём:

Х + 0 = Х * 0 = Х

Но молчат математики, нет у них вразумительного объяснения, что это за странное правило такое и откуда оно взялось.

В-третьих, повторение нуля (0 * Х = 0 + 0 + … + 0 = 0) не только не возможно физически, о чём говорится в пункте 1. Это противоречит результату не повторения значащего операнда (Х * 0 = Х), т.е. фактически переместительному свойству умножения. Следовательно, более правдоподобной является охранная операция по запрещению действия с нулём, т.е. с ничем, в результате которой сохраняется (охраняется) значащий операнд (Х * 0 = Х). А невозможность повторения незначащего операнда не отменяет значащий операнд, присутствующий в начальных условиях.

В–четвёртых, поскольку, как показано в первых двух пунктах, в операциях умножения и деления на нуль символ нуля физически не соответствует своей ничтожной физической сущности не только количественно, но и в качестве действия, то очевидно, что в этих операциях он наделён в классической физике не свойственными для него качествами действия искусственно вопреки своему определению.

Очевидно, что физически бездействие нуля в умножении не должно принципиально отличается от бездействия нуля в базовом для умножения сложении.  Поэтому в результате умножения с нулём точно также, как и при сложении с нулём, а также при умножении с единицей, которая всего лишь оставляет то, что есть в единичном экземпляре, что также эквивалентно бездействию не только нуля, но и единицы, физически должен получаться именно значащий операнд:

Х * 0 = 0 * Х = Х * 1 = 1 * Х = Х

Причём это не противоречит ни физическому смыслу базового сложения, ни определению умножения, в котором естественно для классической арифметики не оговаривается эквивалентность умножения на нуль и единицу, ни определению нуля и единицы. Дело в том, что эквивалентность умножения на нуль и на единицу вовсе не означает физического равенства нуля и единицы. Равны только результаты операций с их участием. Но и в этом также нет никаких противоречий.

Оставить всё, как есть при умножении на ничего не значащий нуль – это абсолютно то же самое, что и оставить то, что есть в единственном экземпляре при умножении на вполне значащую единицу.

Всё выше сказанное относится, в том числе и к делению на нуль (Х / 0 = Х), что будет показано ниже в разделе «деление». А пока покажем правомерность физического умножения на нуль в нашей версии на конкретном примере.

 Умножение с нулём, эквивалентное умножению на единицу, а также переместительное свойство умножения, совершенно очевидно следует из сквозной нумерации базового сложения ячеек одной и той же таблицы. Естественно, что от перемены мест сомножителей, роль которых играют столбцы и строки таблицы, общее количество её ячеек, определяющееся её сквозной нумерацией, не изменится. Именно так в официальной арифметике популярно объясняют переместительное свойство умножения детям.  За исключением, конечно же, умножения с нулём, о чём мы поговорим ниже.

Итак, пусть имеется таблица, состоящая из (х) строк и (у) столбцов. В качестве исходных данных условимся также, что строка должна состоять как минимум из двух ячеек по горизонтали, а столбец из двух ячеек по вертикали. В противном случае количество строк или столбцов равно нулю. Это, кстати, общепринятое понимание строк и столбцов. Например, в кроссвордах строку, состоящую из (n) букв никто не называет буквами, расположенными в (n) столбцах, а вертикальную надпись никто не называет буквами, расположенными в (n) строк. Математика, конечно не кроссворды, но логика, тем не менее, вещь упрямая и универсальная.

Общее количество ячеек таблицы (N) в полном соответствии с определением умножения, основанном на базовом сложении равно:

N = х * у = у * х

Далее

1. Квадрат — равносторонний четырехугольник,
у которого стороны попарно параллельны.

2. Безбилетным считается пассажир,
который не име­ет никаких проездных
документов, а также тот, который не
прокомпостировал свой проездной талон
до следую­щей после его входа в
транспорт остановки. (Из объяв­ления
в трамвае.)

3. Кража — тайное похищение какого-либо
имущества.

4. Кандидат — лицо, выдвигаемое для
избрания в де­путаты.

5. Домохозяйка — это не профессия.

6. Ядовитыми растениями называются
растения, со­держащие ядовитые
вещества.

7. Вычитание — операция, обратная сложению

9. Альт — низкий детский голос.

10. Обвиняемый — лицо, в отношении которого
в установленном законом порядке принято
постановление о привлечении его к
следствию в качестве обвиняемого

11 Сделка — действие, направленное на
установле­ние, изменение или прекращение
гражданских прав и обязанностей.

12. Допрос — следственное или судебное
действие, состоящее в получении от
свидетеля или потерпевшего устного
показания об известных ему обстоятельствах
дан­ного дела.

13. Голография — это метод получения
объемного изо­бражения объекта,
основанный на использовании голографических
средств.

7. Проверьте правильность приводи­мых ниже определений. Укажите, в чем состоит ошибка в неправильных определениях.

1. Прямая — кратчайшая линия между
точками.

2. Планета — небесное тело, вращающееся
во­круг солнца.

3. Человек — это звучит гордо.

4. Аудитория — помещение для лекций.

5. Феодал — крупный землевладелец.

6. Кит — рыба, превосходящая остальных
сво­ими размерами.

7. Химия есть наука, которую преподает
мой дядя.

8. Бином Ньютона есть то, что я никак не
могу понять.

9. Остров — часть суши, со всех сторон
окру­женная водой.

10. Простое число есть число, которое,
кроме единицы и самого себя, не имеет
других делителей.

11. «Человек — смеющееся животное» (Аль
Фараби).,

8. Правильно ли построены определения?

1. Озеро — замкнутый в берегах большой
естественный водоем с пресной водой.

2. Философ — это человек, разрабатывающий
научную методологию.

3. «Материализм — теория, которая
рассматривает все­ленную как нечто,
состоящее только из твердых объектов».
(Определение материализма, данное
американским фило­софом Роном Хаббардом
в книге «Дорога к счастью» ).

4. Как известно, категориями называются
такие поня­тия, в которых отражаются
и фиксируются действительные связи и
отношения наиболее широкой общности.

5. Что такое возможность? — Потенциальная
действи­тельность. Что такое
действительность? — Реализованная
возможность.

6. Прекрасное есть закон в его ограниченном
временем, пространством и конкретной
исторической формой проявления.

7. Сущность — это суть вещи, выражающая
её существенные признаки.

8. Дадаизм — художественное хулиганство.

9. Человек — это живое существо, имеющее
мягкие мочки ушей.

10. Метагалактика — это совокупность
звездных систем-га­лактик, движущихся
в наблюдаемой нами части Вселенной.

11. Либеральный человек — это человек,
имеющий ли­беральные убеждения.

12. Преступление — предусмотренное
уголовным зако­ном общественно опасное
действие, посягающее на обще­ственный
или государственный строй, систему
хозяйства, собственность, личность,
политические, трудовые, иму­щественные
и другие права граждан, а равно иное,
пося­гающее на правопорядок общественно
опасное действие, предусмотренное
уголовным законом.

13. Бразилия — страна неожиданностей.

14. «Пространство как философская
категория обозна­чает универсальную
структуру (порядок) взаиморасположе­ния
и протяжения материальных объектов в
их существова­нии, движении и развитии.
Время как философская категория
обозначает универ­сальную структуру
(порядок) необходимой смены событий,
последовательности и деления процессов
и объектов в их существовании, движении
и развитии» (Очерки по диалек­тическому
материализму. М., 1988. С. 104—105).

15. «Человек — животное, способное к
совершению ку­пли и продажи»
(Аль-Фараби).

16. Ёж — это существо, колючее на ощупь.

17. Документ по уголовному или гражданскому
делу — это письменное доказательство,
которое заверено компетент­ным органом
вустановленном законом порядке и
содержит необходимые реквизиты (дату
выдачи, указание организа­ции или
органа, выдавшего документ, подпись
должност­ного лица и т. д.).

18. Ночное время — это время с 22 до 6 часов
по местно­му времени.

19. Возможность «есть то, что существенно
для действи­тельности, но она существенна
таким образом, что она вместе с тем есть
только возможность; возможность есть
абстракт­ный момент действительности».
(Философская энциклопе­дия. Т. 1. Ст.
«Возможность».)

20. «Душа — то, что у человека болит, когда
тело здоро­во» (Андрей Кураев).

21. Притвориться — принять вид, не
соответствующий действительности.

22. Глагол — самая огнепышащая, самая
живая часть речи, В глаголе струится
самая алая, самая свежая, артериальная
кровь языка,

23. Противозаконное действие — это
действие, запре­щенное законом.

24. Прибыль — разница между выручкой
предприятия за реализованную продукцию
и издержками на ее производство.

25. Комар — мелкое двукрылое насекомое
с тонким тель­цем, больно кусающееся.

26. Отрицание является функтором, которым
просто от­рицается определенное
высказывание.

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

САМОСТОЯТЕЛЬНОЕ АНАЛИТИЧЕСКОЕ ЗАДАНИЕ

Найдите в периодической печати или художественной литературе пример доказательства или опровержения (2-3страницы) и проанализируйте его: найдите тезис, выделите и охарактеризуйте аргументы, определите их связь с тезисом и их корректность.

МАТЕРИАЛ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

Семинар № 1. Понятие. Логические операции с понятиями

I.Вопросы для подготовки:

1. Что такое понятие? Содержание и объем понятия.
2. Соотношения между сравнимыми понятиями, изображение их с помощью кругов Эйлера.
3. Операции обобщения и ограничения понятия.
4. Определение понятия как логическая операция; правила ее осуществления.
5. Операция деления понятия, правила ее осуществления.

II.Практические задания

Задание № 1

Определите соотношения между понятиями и изобразите их с помощью круговых схем:

1. Христианство, православие, религия.
2. Берёза, липа, дерево, лиственное дерево.
3. Друг, враг.
4. Рассказ, рассказ М. Шолохова, новелла, повесть, литературное произведение.
5. Милиционер, токарь, студент-заочник.
6. Имя собственное, существительное, одушевлённый предмет.
7. Верующий, неверующий.
8. Писатель, учёный.
9. Час, минута, секунда.
10. Самолёт, реактивный самолёт, реактивный двигатель.

Задание № 2

Обобщите и ограничьте понятия:

1. Автомобиль
2. Озеро
3. Стихотворение
4. Писатель
5. Сосна
6. Золото
7. Кислород
8. Хирург
9. Контрольная работа
10. Шкаф

Задание № 3

Установите правильность определения и в случае ошибки укажите, какое правило определения нарушено

1. Квадрат – равносторонний четырехугольник, у которого стороны попарно параллельны.
2. Медицина – наука, изучающая человеческие болезни.
3. Вычитание – операция, обратная сложению.
4. Безличными называются предложения, сказуемое которых не допускает при себе подлежащего.
5. Ядовитыми растениями называют растения, содержащие ядовитые вещества.
6. Футуризмом называют одно из декадентских художественных течений XX века.
7. Феодализм – общественный строй, основанный на эксплуатации.
8. Оговор – показание свидетеля, ложно изобличающее другое лицо в совершении преступления.

Задание № 4

Установите правильность деления и в случае ошибки укажите, какое правило деления нарушено

1. Договоры делятся на устные, письменные и безвозмездные.
2. Понятия делятся на единичные и общие.
3. Животные делятся на позвоночных, беспозвоночных и млекопитающих.
4. Удочка делится на удилище, лесу, поплавок, грузило, поводок и крючок.
5. «Читающих было два рода: старожилы из местной интеллигенции, – их было большинство, – и люди из простого народа» (Пастернак Б.П.).
6. Художник может быть живописцем, портретистом или пейзажистом.
7. Политический режим различных государств может быть демократическим и недемократическим.
8. К ценным бумагам относятся акции и чеки.

Семинар № 2. Индуктивные и дедуктивные умозаключения

I.Вопросы для подготовки:

1. Умозаключение как форма речемыслительной деятельности. Классификация умозаключений.
2. Индуктивные умозаключения и их виды.
3. Дедуктивные умозаключения, их классификация.
4. Простой категорический силлогизм: состав, правила построения и проверка.

II.Практические задания

Задание № 1

Сделайте полный разбор силлогизма: укажите заключение и посылки, средний, меньший и больший термины, меньшую и большую посылки. Изобразите в круговых схемах отношение между терминами

1. Лицо, совершившее кражу, привлекается к уголовной ответственности. Обвиняемый совершил кражу, поэтому он привлечён к уголовной ответственности.
2. Любой материальный объект может существовать только благодаря взаимодействию его элементов. Атом – материальный объект, значит, он может существовать только благодаря этому взаимодействию.
3. Федеральное Собрание РФ состоит из двух палат и является постоянно действующим органом. Значит, некоторые постоянно действующие органы стоят из двух палат.
4. Доказательство, полученное с нарушением закона, не имеет юридической силы. Данное доказательство не имеет юридической силы, потому что оно получено с нарушением закона.
5. Каждый участник общей долевой собственности имеет право на чуждение своей доли другому лицу. Р. не является участником общей долевой собственности, так как он не имеет права на отчуждение своей доли другому лицу.
6. Суждение «Некоторые птицы не являются перелётными» не обращаются, так как оно является частноотрицательным, а частоотрицательное суждения не обращаются.

Задание № 2

В условной посылке укажите основание и следствие, сделайте вывод, определите модус, постройте схему

1. Если туман не рассеется, вылет будет задержан. Вылет не задержали.
2. Договор был бы заключён, если бы между договаривающимися сторонами было достигнуто соглашение. Однако договор заключён не будет.
3. Обмен жилого помещения не допускается, если он носит корыстный или фиктивный характер. Данный обмен носит фиктивный характер.
4. Ни одно предприятие, цех, участок, производство не могут быть приняты и введены в эксплуатацию, если на них не обеспечены здоровые и безопасные условия труда. Сборочный цех может быть принят и введён в эксплуатацию.
5. В состав суда, рассматривающего уголовное дело, не могут входить лица, если они состоят в родстве между собой. Р. и П. – родственники.
6. Если граждане моложе 16 лет не являются лицами, участвующими в деле, или свидетелями, то они не допускаются в зал судебного заседания.

Задание № 3

Сделайте вывод из посылки разделительно – категорического умозаключения, определите модус, постройте его схему, укажите вид дизъюнкции: строгая или нестрогая, полная или неполная

1. Доказательство бывает прямым или косвенным. Это не прямое доказательство.
2. Правонарушения делятся на преступления и проступки. Данное правонарушение – проступок.
3. Выдвинутая гипотеза доказывается или отвергается. Данная гипотеза доказана.
4. Покупатель, которому продана вещь ненадлежащего качества, если её недостатки не были оговорены продавцом, вправе по своему выбору потребовать или замены вещи, определённой в договоре родовыми признаками, вещью надлежащего качества, либо соразмерного уменьшения покупной цены, либо безвозмездного устранения недостатков вещи продавцом, или возмещения расходов покупателя на их исправление, либо расторжение договора с возмещением покупателю убытков. Покупатель потребовал замены вещи.

Задание № 4

Укажите умозаключения полной и неполной индукции, в последней определите степень вероятности обобщения («маловероятно», «равновероятно», «более вероятно, чем нет», «весьма вероятно»). Выделите умозаключения по аналогии

1. Для выступления с докладами на общеинститутской студенческой конференции подготовились 6 членов кружка по философии: Алексеев, Борисова, Круглов, Морозов, Константинов и Новиков. Студент Алексеев выступил с докладом на пленарном заседании. Студенты Борисова, Круглов, Морозов, Константинов и Новиков выступили с докладами на секциях. Таким образом, все члены кружка по философии, приготовившие доклады, выступили на конференции.
2. На первом курсе института 8 студенческих групп. Анализ итогов сессии показал, что студенты 1-, 2-, 3-, 8 – й групп успешно сдали все экзамены. На этом основании был сделан вывод о том, что все студенты первого курса успешно сдали все экзамены.
3. В 1581 г. Ермак начал освоение Сибири. В 1639 г. Иван Москвитин достиг Охотского моря и первым из европейцев увидел с востока Тихий океан. В 1648 г. Семен Дежнев вместе с Поповым проплыл от устья Колымы в Тихий океан, обогнул Чукотский полуостров, открыл пролив между Азией и Америкой.
4. Всё это говорит о том, что наши соотечественники ещё в XVI – XVII вв. прокладывали морские пути, обследовали далёкие северные просторы.
5. При освобождении бойцами ОМОН заложников, захваченных преступниками, в завязавшейся схватке один бандит был убит, двое ранены, остальные сдались. Ни один из заложников не пострадал. Таким образом, все заложники были освобождены, бандиты обезврежены.
6. Осматривая место происшествия, где выстрелом из охотничьего ружья был убит гр –н Петухов, следователь нашёл пыж. Он оказался самодельным, изготовленным из обрывка газеты. Развернув его, следователь убедился, что он сделан из клочка бумаги, оторванного от газеты «Труд». У. Савельева, подозреваемого в убийстве, при обыске изъяли ружьё и патроны. При вскрытии последних были изъяты пыжи. Они оказались самодельными и изготовленными из газеты «Труд». Следователь развернул все пыжи и приложил один к другому по линии отрывов. В результате удалось составить около ¾ листа газеты. Следователь решил проверить, не совпадает ли с отобранными пыжами и тот, который был найден на месте убийства. Оказалось, что и этот пыж по линии отрыва совпал с пыжами, изъятыми у Савельева; одной стороны – с одним пыжом, а другой – с другим. На этом основании следователь сделал вывод, что пыж, найденный на месте убийства, изготовлен из той же газеты, обрывки которой найдены в патронах, изъятых у Савельева.
7. Крестьянская война 874 – 901 гг. в Китае потерпела поражение. Крестьянская война 1524 – 1526 гг. в Германии потерпела поражение. Потерпела поражение крестьянская война в Китае в 1628 – 1645 гг., а также крестьянская война в России в XVII в. и крестьянская война под предводительством Е. Пугачёва в 1773 – 1775 гг. Следовательно, все крестьянские войны терпели поражение.
8. Осматривая извлечённый из реки труп неизвестного мужчины, следователь отметил ряд отметил ряд характерных примет, в том числе татуировку, золотые коронки во рту. Опираясь на эти приметы, следователь предложил, что убитый мог быть ранее судимым или каким – то образом связанным с преступным миром (уж очень красноречивыми были упомянутые татуировки). Большое количество ранений на трупе давало основание предложить, что убийство могли совершить ранее судимые. Кроме того последнее обстоятельство наталкивало на мысль, что преступление совершенно из мести. Ограбление можно было предположить с меньшим основанием, так как на руке убитого были часы.
9. Кинокомедии Э. Рязанова «Карнавальная ночь», «Берегись автомобиля», «Служебный роман» и другие пользуются большим успехом. Очевидно, что такое отношение зрителя можно отнести ко всем фильмам этого талантливого кинорежиссёра, включая и те, которые не вышли на экран.
10. Русские юристы последней трети XIX в. Александров и Спасович были выдающимися судебными ораторами. То же можно сказать и о юристах этого периода Арсеньеве, Андреевском, Карабачевском, Плевако, Урусове. Из этого следует, что все русские юристы последней трети XIX в. были выдающимися ораторами.

Семинар № 3. Доказательство и опровержение

I.Вопросы для подготовки:

1. Логические основы аргументации. Состав аргументации: субъекты, структура.
2. Правила и ошибки в аргументации.

II.Практические задания

Задание № 1

Определите вид ошибки, допущенной в доказательствах

1. Мы перешли улицу и вскоре оказались у бывшего жилища святой Вероники. Когда Спаситель проходил здесь, она вышла ему навстречу, полная истинного женского сострадания, и, не страшась улюлюканья и угроз черни, сказала ему жалостливые слова и своим платком отерла пот с его лица. <…>. Но самое странное в случае со святой вероникой, из-за чего она, собственно, и прославилась, заключается в том, что, когда она отирала пот, на ее платке отпечаталось лицо Спасителя, точный его портрет, и отпечаток этот сохранился и по сей день. Мы знаем это, ибо видели этот платок в парижском соборе, в одном из соборов Испании и в двух итальянских.
2. Вопрос: Значит, древнейшие гоминиды пользовались орудиями?

Ответ: Мы предполагаем, что да. У них, как у шимпанзе, была такая потенциальная способность, и они сохранили её, покинув лес.

Вопрос: Но что стимулировало её развитие?

Ответ: На открытой местности им требовались орудия, чтобы защищаться от врагов, так как клыки у них были небольшими.

Вопрос: А почему клыки у них были небольшими?

Ответ: Потому что большие клыки им уже не были нужны. Оружие позволяло им успешнее защищаться, и большие клыки утратили своё значение как средство защиты.

1. Они доказывают это с помощью следующего силлогизма: слова только ветер; знание же не что иное, как слова; следовательно, знание есть не что иное, как ветер.
2. — Сними свою шляпу, — сказал Король Болванщику.

— Она не моя, — ответил Болванщик.

— Украдена! — закричал Король с торжеством и повернулся к присяжным.

Присяжные взялись за грифели.

— Я их держу для продажи, — сказал Болванщик. — Я Шляпных Дел Мастер. Знаете пословицу: сапожник без сапог, шляпник без шляпы…

1. Адвокат пытается доказать, что подсудимый не совершал вменяемое ему преступление, рассуждая так: «Если бы обвиняемый был богат, то этот автомобиль он купил бы. Если ж обвиняемый был бесчестен, то он украл бы его. Однако обвиняемый не богат и уж ни в коем случае его нельзя отнести к бесчестным. Следовательно, обвиняемый не покупал и не крал этого злополучного автомобиля».
2. После революции в сибирской деревне комиссар в кожаной куртке вёл беседу: «Бога нет, а человек произошёл от обезьяны». Крестьяне сказали: «Докажи, что человек произошёл от обезьяны». Комиссар ответил: «Месяц назад на Кавказе обезьяна родила человека». Крестьяне поверили. Они привыкли верить друг другу.
3. Если темпаратура у вас не повышена, то вы не больной, а симулянт.
4. В гробнице египетских фараонов была найдена проволока. На этом основании один «египтолог» высказал предположение, что в Древнем Египте был известен телеграф. Услышав об этом, другой «исследователь» заключил, что, поскольку в гробницах ассирийских царей никакой проволоки не найдено, в Древней Ассирии был уже известен беспроволочный телеграф.

Задание № 2

Найдите тезис, аргументы и демонстрацию в следующих рассуждениях

1. Спекуляция является общественно опасным деянием, так как она – преступление, а всякое преступление представляет собой общественно опасное деяние.
2. В категорическом силлогизме средний термин должен быть распределен по крайней мере в одной из посылок, а как известно, термины распределены, когда они являются субъектами общих суждений либо предикатами отрицательных. Значит, в силлогизме средний термин по крайней мере однажды должен быть взят либо в качестве субъекта общего, либо предиката отрицательного суждения.
3. По данному проводнику не проходит электрический ток, так как вокруг него не возникает магнитное поле. Известно, что если по проводнику проходит электрический ток, то вокруг него возникает магнитное поле.
4. Страсти вводят нас в заблуждение, так как они сосредотачивают всё наше внимание на одной стороне рассматриваемого предмета и не дают нам возможности исследовать его всесторонне.

Задание № 3

Определите вид уловки или ошибки, допущенной в рассуждениях

1. Адвокат пытался доказать, что подсудимый не совершал вменяемое ему преступление, рассуждая так: «Если бы обвиняемый был богат, то этот автомобиль он купил бы. Если ж обвиняемый был бесчестен, то он украл бы его. Однако обвиняемый не богат и уж ни в коем случае его нельзя отнести с бесчестным. Следовательно, обвиняемый не покупал и не крал этого злополучного автомобиля».
2. «Ах, батюшки мои! Да чем же он плут, скажи, пожалуйста! Каждый праздник он в церковь ходит, да придёт-то раньше всех; посты держит; великим постом и чаю не пьёт-с. Так-то, голубчик! Не то, что ты. А если и обманет кого, так что за беда! Не он первый, не он последний; человек коммерческий. Тем, Антипушка, и торговля-то держится. Не помимо пословица-то говорится: “не обмануть – не продать”» (А.Островский. Семейная Картина).
3. «Вы сочинили и напечатали в своём умном сочинении, как сказал мне Герасимов, что будто бы на самом величайшем светиле, на солнце, есть чёрные пятнушки. Этого не может быть, потому что этого не может быть никогда. Как Вы могли видеть на солнце пятны, если на солнце нельзя глядеть простыми человеческими глазами, и для чего на нём пятны, если и без них можно обойтиться? Из какого мокрого тела сделаны эти самые пятны, если они не сгорают?» (А.Чехов. Письмо ученому соседу).
4. Одна из партий на выборах оказалась в большинстве местных дум преобладающей партией. Вступив в блок с другими родственными ей партиями, она не дала ни одного места враждебным партиям в местных управах. Члены последних доказывали, что имеют право требовать известное число мест: выборы были пропорциональные, следовательно, и места в управах должны быть распределены согласно тому же принципу.

Господствующая партия отвергла этот довод как непригодный и неправильный.

Однако случилось, что в некоторых районах она все же оказалась непреобладающей. Враждебные партии воспользовались этим и, составив между собою блок, в свою очередь не дали ей ни одного места в управе. Тогда она прибегла к тому же доводу, к какому прибегали в других думах ее «враги». Здесь он казался пригодным и правильным.

1. Пётр Николаевич иной раз привозил с собой двух-трёх философов для вставок, иными словами, отдельных предложений в соответствии с их профессиональной ориентацией. Один из таких философов замучил нас вставками по поводу развития национальных отношений в стране путём поощрения межнациональных браков. Ему представлялась это главным средством сближения и даже слияния наций. Он настойчиво и даже настырно пытался пропихнуть за общим редакционным столом свои вставки и изрядно надоел всем, даже уравновешенному и спокойному Петру Николаевичу. Тот как-то попросил меня взять предлагаемые страницы и, отредактировав их, вернуть за общий стол. А я, вместо того, чтобы заниматься текстом, который считал совершенно непригодным, решил ограничиться шуткой и к сакраментальной формулировке автора «лучшим путём сближения наций является развитие брачных отношений» добавил: «и иных форм половых отношений между представителями различных наций». Когда эта формула была зачитана за общим столом, она вызвала гомерический хохот, и Пётр Николаевич, невзирая на горячие протесты, выбросил весь текст целиком без всякой жалости.
2. Наука доказала, что Бога нет.
3. Некто взялся доказать, что 3 раза по 2 будет не 6, а 4. Выполняя свою странную затею, он взял в руки обыкновенную спичку и попросил присутствующих внимательно следить за ходом его мысли.

— Переломив спичку пополам, — заявил странный математик, — мы будем иметь один раз 2. Проделав то же самое над одной из половинок, мы будем иметь второй раз 2. Наконец, проделав эту же операцию над второй из половинок, получим третий раз 2. Итак, беря три раза по 2, мы получим 4, а не 6, как принято думать.

1. « — Что думаете вы, — спросил я его, — о новых колясках, изобретенных в Англии, на которых можно ездить без лошадей?..

— О! — сказал мой ученый. — Это вещь невозможная.

— Почему это?

— Я много в жизни путешествовал, — отвечал он, — и опытом удостоверился, что ездить без лошадей на земле почти так же невозможно, как быть сыту не евши.

— О! Это убедительное доказательство.

1. Однажды русский старообрядец яростно доказывал представителю официальной церкви, что официальная церковь и ее представители – еретики. Находчивый оппонент не растерялся и тут же задал вопрос: «Вот как! Значит и наш Государь Император еретик»?
2. «Фидиа. Посмотри на петухов и остальных животных, как они дерутся с отцами. А разница между нами и ими не в том ли только, что они не издают писаных законов.

Стрепсиад. Гм! Если хочешь брать пример с петухов, почему же не ешь навозу и не спишь на шестке?

Фидиа. Это, милейший, совсем к делу не относится, как согласился бы и Сократ» (Аристофан. Облака).