Вывод формулы для вычисления вероятности ошибки при регистрации методом стробирования
Рассмотрим
случай, когда регистрация единичных
элементов осуществляется методом
стробирования. На рисунке 10 приведен
единичный элемент 0
, отмечен оптимальный момент регистрации
МР.

Рисунок
11 – График распределения плотностей
вероятности.
Плотность
вероятностей смещения левой и правой
границ единичного элемента обозначены
соответственно Wл(δ)
и Wпр(δ).
Ошибочная регистрация элемента 0
произойдет в следующих случаях: левая
или правая граница единичного элемента
сместится вправо на величину |δ|≥μ,
одновременно обе границы сместятся
внутрь единичного элемента и смещение
превысит исправляющую способность
приемника μ.
Вероятность
ошибочной регистрации Pош
=
P1
+P2
– P1P2
, где P1и
P2
– соответственно вероятности смещения
левой и правой границ на величину больше
μ.
Как видно из рисунка 11:
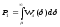

Устройство
поэлементной синхронизации вырабатывает
синхроимпульсы с некоторым смещением
(погрешностью ε). В этом случае:



Плотности
вероятности смещения левой и правой
границ единичного элемента. Т.к.
Т.к.
Wл(δ)
и Wпр(δ)
описываются Гауссовским законом с
параметрами а и σ, то Р1
и Р2
можно выразить через функцию Крампа:
 ,
,
что и было сделано раньше.

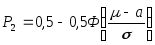
![]()
Решение задач
Задача№1.Начертить
временную диаграмму сигнала на выходе
модулятора, вид модуляции и передаваемая
последовательность приведены в таблице.
Дано:
Вид
модуляции: Двукратная относительно —
фазовая модуляция.
Передаваемая
последовательность: 001011 01 10 11
Решение:
При
ДОФМ два соседних сигнала могут отличаться
по фазе на одно из четырех возможных
значений. Диаграмма ДОФМ на сигнальной
плоскости выглядит так:

Рисунок
12 –
Диаграмма ДОФМ.
Вычислим
фазы сигнала для каждой пары единичных
элементов:
|
φ1 φ2 φ3=900+900=1800 φ4 φ5 φ6 φ1 |
Рисунок |
Задача№2.
Начертить
временные диаграммы сигналов на выходе
каждого из элементов регистрирующего
устройства, если используется интегральный
(N-четное) или метод
стробирования (N-нечетное),
а так же заданы значащие моменты сигнала
на входе регистрирующего устройства
(в таблице – первый ЗМ означает переход
от «0» к «1», общая длительность сигнала
составляет 10τ0).
Стробирующий импульс предполагается
бесконечно узким, длительностью которого
можно пренебречь. Длительность единичного
элемента выбрать самостоятельно.
Дано:
Метод
регистрации: интегральный.
Значащие
моменты:
|
0,1τ0 |
3,3 |
4,0 |
5,2 |
5,9 |
6,7 |
7,3 |
7,8 |
8,7 |
9,3 |
Решение:

Рисунок
14 – Схема регистрирующего устройства.
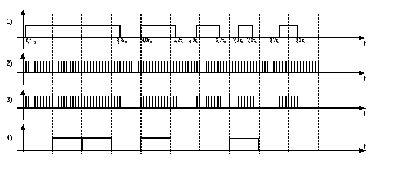 Рисунок
Рисунок
15 – Временные
диаграммы сигналов на выходе каждого
из элементов регистрирующего устройства.
Синхронизация в системах пдс Классификация систем поэлементной синхронизации
Различают
поэлементную, групповую и цикловую
синхронизацию. Поэлементная синхронизация
позволяет на приеме правильно отделить
один элемент от другого и обеспечить
наилучшие условия для его регистрации.
Групповая синхронизация обеспечивает
правильное разделение принятой
последовательности на кодовые комбинации,
а цикловая синхронизация — правильное
разделение циклов временного объединения
элементов на приеме. Обычно задачи
цикловой и групповой решаются одними
и теми же методами.
Системы
синхронизации можно классифицировать
последующим признакам:
а)
прохождение синхросигналов.
б)
способ формирования синхросигналов.
Прохождение
синхросигналов
Синхронизирующие
импульсы в пункте приема могут быть
получены тремя способами: от
высокостабильного источника колебаний,
который является эталоном отсчетов
времени, путем передачи отсчетов времени
(синхронизирующие импульсы) от передатчика
к приемнику по отдельному каналу
(синхроканалу) и путем получения
информации об отсчетах времени из
информационной последовательности
единичных элементов.
Первый
способ применим в тех случаях, когда
время сеанса связи, включая время
вхождения в связь, не превышает время
сохранения синфазности. Второй способ
достаточно эффективен, однако требует
создания отдельного канала синхронизации,
что снижает пропускную способность
канала связи. Как правило, этот способ
применяется в групповых многоканальных
синхронных системах связи. Третий способ
позволяет более эффективно использовать
пропускную способность системы связи
и обеспечить приспособляемость
(адаптацию) устройств фазирования и
синхронизации к изменяющимся параметрам
канала связи. Основной недостаток
способа состоит в зависимости точности
синхронизации от искажений принимаемых
информационных сигналов и структуры
информационных последовательностей
единичных элементов. Несмотря на
указанные недостатки, третий способ
нашел преимущественное применение в
системах передачи дискретной информации
и телеграфной техники.
Способ
формирования синхросигналов
По
этому способу системы синхронизации
разделяют на разомкнутые (без обратной
связи) и замкнутые (с обратной связью).
В разомкнутых СС синхросигнал (тактовые
импульсы) формируются либо из сигналов,
принимаемых по специальному выделенному
синхроканалу (рисунок16а), либо из
информационных сигналов с помощью
анализатора сигнала АС и формирователя
синхронного сигнала (рисунок16б). АС
предназначен для извлечения из
информационного сигнала сведений о
положении ЗМ. ФСС под действием сигналов
с АС формирует синхросигналы в определенной
фазе по отношению к информационным
сигналам.
В
замкнутых СС синхросигнал вырабатывается
генератором синхроимпульсов. В АС
производится сравнение фазового
положения синхроимпульсов и положения
ЗМ приходящих информационных сигналов.
При рассогласовании фаз вырабатывается
управляющий сигнал, корректирующий
работу синхроимпульсов. Таким образом,
АС представляет собой устройство с ФАПЧ
и состоит из фазового дискриминатора
и управляющего устройства. Различают
замкнутые СС с непосредственным
воздействием на частоту генератора
(рисунок17а) и без непосредственного
воздействия на частоту генератора
(рисунок17б). В первом случае корректирующее
фазы синхросигналов достигается
изменением параметров колебательного
контура генератора синхросигналов, во
втором — воздействием на промежуточный
преобразователь частоты, как правило,
на делитель частоты. Весьма существенно,
что замкнутые СС предусматривают только
режим непрерывной синхронизации, т.е.
могут использоваться лишь в синхронных
системах связи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: диломная работа Бурнашева Артура.docx, Статистика 2 работа.docx, менеджмент 4 работа.docx, Практическая работа по социальной психологии.docx, Памятка этические основы деловой коммуникации.docx, Курсовая работа Микроэкономика 1 семестр.docx, Контрольная работа, налоги.docx, Самостоятельная работа по Бухгалтерскому учету.docx, Титульный лист основы.doc, Домашняя работа АНГЛ.pdf
Studlancer.net — закажи реферат, курсовую, диплом!
Курсовая работа
По дисциплине: Основы построения телекоммуникационных систем и сетей
Вариант 07
Содержание
Введение
1. Методы регистрации
1.1 Регистрация посылок методом стробирования
1.2 Интегральный метод регистрации
1.3 Сравнение методов регистрации
1.3.1 Задача №1
2.Синхронизация в системах ПДС
2.1 Устройства синхронизации с добавлением и вычитанием импульсов
2.2 Параметры системы синхронизации с добавлением и вычитанием импульсов
2.3 Расчет параметров системы синхронизации с добавлением и вычитанием импульсов
2.3.1 Задача № 2
2.3.2 Задача № 3
2.3.3 Задача № 4
3. Корректирующее кодирование в системах ПДС
3.1 Циклические коды
3.2 Построение кодера и декодера
3.2.1 Задача № 5
4.Системы ПДС с обратной связью
4.1 Системы с информационной обратной связью
4.2 Системы с решающей обратной связью
4.2.1 Задача № 6
4.2.2 Задача №7
Список литературы
Введение
Теория передачи дискретных сообщений представляет наиболее разработанную часть общей теории связи. Основной проблемой этой теории является отыскание методов передачи и приема, обеспечивающих получение требуемой верности принятого сообщения, повышение скорости передачи и понижение ее стоимости. Эти задачи нельзя рассматривать в отрыве друг от друга. Действительно, каждую из них можно было бы решать за счет остальных. Так, например, можно легко повысить верность принятого сообщения, уменьшая скорость передачи, либо увеличивая мощность сигнала и т. д. Поэтому только учет всех указанных факторов позволяет правильно сформулировать задачу оптимального построения системы связи. В зависимости от конкретных условий постановка этой задачи различна. В одних случаях требуется обеспечить наибольшую экономичность (или наименьшую затрачиваемую мощность) при заданных верности и скорости передачи. В других случаях заданными являются скорость передачи и мощность сигнала и требуется обеспечить максимальную верность и т. д.
Такие задачи постоянно возникают перед инженерами. проектирующими и эксплуатирующими различные системы и линии передачи сообщении, а также разрабатывающими соответствующую аппаратуру. Для их решения необходимо четкое знание теории, позволяющей находить оптимальные (или близкие к ним) условия путем сравнительно простых расчетов, не прибегая к дорогостоящим экспериментам.
1. Методы регистрации
Сигнал, поступающий с выхода полунепрерывного канала или КПТ, должен быть отождествлен с “1” или “0”. Процесс определения и запоминания значащей позиции сигнала данных – называется регистрацией.
Наиболее распространены для регистрации методы стробирования и интегрирования. дискретный сообщение стробирование синхронизация
1.1 Регистрация посылок методом стробирования
Метод стробирования – значащая позиция принимаемого элемента определяются на основании анализа знака импульса в середине единичного интервала.
Если индивидуальное КИ не превышает ![]() , то элемент регистрируются правильно.
, то элемент регистрируются правильно.
Говорят идеальная исправляющая способность 50%.
Исправляющая способность – это величина, на которую допускаются смещения ЗМ, не вызывающее неправильный прием элемента.

Схема состоит из входного устройства, двух ключей и RS-триггера. Входное устройство имеет два выхода на один транслируется входной сигнал без изменений, а на другой с инверсией (точки 1 и 2). Стробирующие импульсы открывают ключи на время своего существования. Через ключи высокий потенциал поступает на один из входов тригера и переводит его в соответствующее состояние. Последовательность 4 – устанавливает триггер в “1”, а 5 – сбрасывает триггер в “0”.
1.2 Интегральный метод регистрации
Решение о виде принятого элемента выносится на основании анализа напряжения на всем единичном интервале.
В идеальном случае (если единичный. элемент не искажен), то Uвых= 1
решением о “1” принимается при ![]() ;
;
решением о “0” принимается при ![]() .
.
В цифровом виде интегральный метод может быть реализован на основе многократного стробирования.
Структурная схема интегрального метода.
На ключ поступают стробирущие импульсы. Управление ключом производится сигналом с выхода порогового устройства. Импульсы прошедшие ключ подсчитываются счетчиком. По приходу тактового импульса решающее устройство считывает показание счетчика, сравнивает его с пороговым значением и принимает решение о значащей позиции на текущем интервале.
Алгоритм принятия решения:
Пусть за время неискаженной токовой посылки появляется N тактовых импульсов, тогда:
если показание счетчика ![]()
![]() +1 – решение “1”
+1 – решение “1”
если меньше, то “0”
Временные диаграммы работы данной схемы приведены на следующем рисунке
1.3 Сравнение методов регистрации
1. Вероятность ошибки при действии КИ у метода стробирования меньше ![]() [стробирование лучше].
[стробирование лучше].
2. При дроблениях лучше интегральный метод ![]() .
.
1.3.1 Задача №1
Вычислить вероятность ошибки при регистрации методом стробирования, в соответствии с приложением 1.
| N | 0, 6 | 1, 7 | 2, 8 | 3, 9 | 4 | 5 |
| m | 48 | 50 | 43 | 47 | 40 | 45 |
| s | 20 | 15 | 10 | |||
| А | N | N+1 | N+10 |
Решение.![]()

![]()
![]()
2. Синхронизация в системах ПДС
Синхронизация – это процедура установления и поддержания определенных временных соотношений между двумя и более процессами.
Различают поэлементную, групповую и цикловую синхронизацию.
При поэлементной синхронизации устанавливаются и поддерживаются требуемые фазовые соотношения между значащими моментами переданных и принятых единичных элементов цифровых сигналов данных. Поэлементная синхронизация позволяет на приеме правильно отделить один единичный элемент от другого и обеспечить наилучшие условия для его регистрации.
Групповая синхронизация – обеспечивает правильное разделение принятой последовательности на кодовые комбинации.
Цикловая синхронизация – обеспечивает правильное разделение циклов временного объединения.
2.1 Устройства синхронизации с добавлением и вычитанием импульсов
Устройство относится к классу без непосредственного воздействия на частоту генератора и является 3-х позиционным.
При работающей системе синхронизации возможны три случая:
Импульсы генератора без изменения проходят на вход делителя частоты.
К последовательности импульсов добавляется 1 импульс.
Из последовательности импульсов вычитается 1 импульс.

Задающий генератор вырабатывает относительно высокочастотную последовательность импульсов. Данная последовательность проходит через делитель с заданным коэффициентом деления. Тактовые импульсы с выхода делителя обеспечивают работу блоков системы передачи и также поступают в фазовый дискриминатор для ставнения.
Фазовый дискриминатор определяет знак расхождения по фазе ЗМ и ТИ задающего генератора.
Если частота ЗГ приема больше, то ФД формирует сигнал вычитания импульса для УДВИ, по которому запрещается прохождение одного импульса.
Если частота ЗГ приема меньше, то импульс добавляется.
В результате тактовая последовательность на выходе Dk сдвигается на ![]() .
.
Следующий рисунок иллюстрирует изменение положения тактового импульса в результате добавления и исключения импульсов.
ТИ2 – в результате добавления, ТИ3 – в результате вычитания.

Роль реверсивного счетчика:
В реальной ситуации принимаемые элементы имеют краевые искажения, которые изменяются случайным образом положение значащих моментов в разные стороны от идеального ЗМ. Это может вызвать ложную подстройку синхронизации.
При действии КИ смещения ЗМ как в сторону опережения, так и в сторону отставания равновероятны.
При смещении ЗМ по вине устройства синхронизации фаза стабильно смещается в одну сторону.
Поэтому для уменьшения влияния КИ на погрешность синхронизации ставят реверсивный счетчик емкости S. Если подряд придет S сигналов на добавление импульса, говорящих об отставании генератора приема, то импульс добавится и следующий ТИ появится раньше на ![]() .
.
Если сначала придет S-1 сигнал об опережении, потом S-1 об отставании, то добавления и вычитания не будет.
2.2 Параметры системы синхронизации с добавлением и вычитанием импульсов
К основным параметрам системы синхронизации относятся:
1.
Погрешность синхронизации ![]() —
—
— максимальное отклонение синхросигналов от их идеального положения, которое может произойти при работе устройства синхронизации с заданной вероятностью. (выражается в долях единичного интервала).
Погрешность синхронизации – складывается из статической ![]() , определяемой нестабильностью генераторов
, определяемой нестабильностью генераторов ![]() и шагом коррекции
и шагом коррекции ![]() и динамической
и динамической ![]() , определенной краевыми искажениями.
, определенной краевыми искажениями.
![]() -коэффициент деления, где
-коэффициент деления, где ![]() — длительность единичного элемента,
— длительность единичного элемента, ![]() — шаг коррекции
— шаг коррекции
В силу конечности шага коррекции возникает погрешность: ![]()
Вследствие нестабильности генераторов, между двумя подстройками накапливается погрешность равная![]()
где ![]() – среднее число принимаемых подряд элементов одного знака
– среднее число принимаемых подряд элементов одного знака
Период корректирования – время между двумя подстройками, в общем случае определяется так: ![]() ,
,
однако нужно понимать, что ![]() – случайная величина и определяется структурой сообщения.
– случайная величина и определяется структурой сообщения.
Таким образом, общее выражение для статической погрешности: .
.
Динамическая погрешность синхронизации
Динамическая погрешность вызывается краевыми искажениями единичных элементов.
Краевые искажения имеют случайный характер со среднеквадратичным значением![]()
![]() . Следовательно, динамическая погрешность также случайная величина. Она подчиняется нормальному закону и имеет свое среднеквадратическое значение
. Следовательно, динамическая погрешность также случайная величина. Она подчиняется нормальному закону и имеет свое среднеквадратическое значение ![]() .
. .
.
Окончательно погрешность синхронизации определяется выражением: .
.
2.
Время синхронизации (или вхождения в синхронизм) ![]() —
—
— время необходимое для корректирования первоначального отклонения синхроимпульсов относительно границ единичных принимаемых элементов.
В момент включения расхождение по фазе между тактовыми импульсами передачи и приема – случайно и имеет в пределах от 0 до ![]() .
.
Выбирая наихудший случай, когда сдвиг фаз равен ![]() получим время синхронизации равное
получим время синхронизации равное![]() . Так как
. Так как ![]() ,
, ![]() , то окончательно:
, то окончательно:
![]() .
.
3.
Время поддержания синхронизма ![]() —
—
— время, в течение которого отклонение синхроимпульсов от границ единичных элементов не превысит допустимый предел (![]() ) при прекращении работы устройства синхронизации по подстройке фазы.
) при прекращении работы устройства синхронизации по подстройке фазы.
Эта задача аналогична задаче об автономных генераторах, рассмотренной нами выше, поэтому можно записать![]() .
.
В качестве ![]() — выбирают теоретическую исправляющую способность приемника
— выбирают теоретическую исправляющую способность приемника ![]() уменьшенную на погрешность синхронизации. Поэтому окончательно:
уменьшенную на погрешность синхронизации. Поэтому окончательно:![]() .
.
4.
Вероятность срыва синхронизма ![]() —
—
— вероятность того, что под действием помех отклонение синхроимпульсов от границ единичных элементов превысит половину единичного интервала ![]() .
.
![]() -можно уменьшить увеличив время усреднения сигналов коррекции фазы. Т.е. увеличив емкость реверсивного счетчика.
-можно уменьшить увеличив время усреднения сигналов коррекции фазы. Т.е. увеличив емкость реверсивного счетчика.
Особенности синхронизации при старт-стопной передаче.
Каждая кодовая комбинация начинается со ”старта” и оканчивается ”стопом”. Генератор приема (приемный распределитель) запускается при поступлении каждого сигнала ”старт” и останавливается по сигналу ”стоп”
Накопившееся за время кодовой комбинации расхождения фазы каждый раз ликвидируется.
+ Высокая стабильность генераторов не требуется
+ Быстрое вхождение в синхронизм.
2.3 Расчет параметров системы синхронизации с добавлением и вычитанием импульсов
2.3.1 Задача № 2
Коэффициент нестабильности задающего генератора устройства синхронизации и передатчика К=10-6 . Исправляющая способность приемника m =40%. Краевые искажения отсутствуют. Постройте зависимость времени нормальной работы (без ошибок) приемника от скорости телеграфирования после выхода из строя фазового детектора устройства синхронизации. Будут ли возникать ошибки, спустя минуту после отказа фазового детектора, если скорость телеграфирования В = 9600 Бод?
Решение.
Время ![]() , за которое расхождение по фазе достигнет e процентов от длительности единичного интервала, равно
, за которое расхождение по фазе достигнет e процентов от длительности единичного интервала, равно![]()

Зависимость времени нормальной работы (без ошибок) приемника от скорости телеграфирования
При скорости телеграфирования В = 9600 Бод время безошибочной работы равно![]() ,
,
т.е. спустя минуту после отказа фазового детектора будут возникать ошибки.
2.3.2 Задача № 3
В системе передачи данных используется устройство синхронизации без непосредственного воздействия на частоту задающего генератора. Скорость модуляции равна В. Шаг коррекции должен быть не более D j к. Определите частоту задающего генератора и число ячеек делителя частоты, если коэффициент деления каждой ячейки равен двум. Значения В, D j к определите для своего варианта по формулам:
B = 1000 + 10N=1070,
D j к = 0,01 + 0,003N=0,031.
Решение.
Частота задающего генератора![]()
Коэффициент деления делителя![]()
Число ячеек делителя частоты![]() .
.
2.3.3 Задача № 4
Рассчитать параметры устройства синхронизации без непосредственного воздействия на частоту задающего генератора со следующими характеристиками: время синхронизации не более 1 с, время поддержания синфазности не менее 10 с, погрешность синхронизации не более 10% единичного интервала t 0, среднеквадратическое значение краевых искажений равно 10%t 0 , исправляющая способность приемника 45%, коэффициент нестабильности генераторов k=10-6 . Определить реализуемо ли устройство синхронизации без непосредственного воздействия на частоту задающего генератора, обеспечивающее погрешность синхронизации e = 2,5% при данных условиях. Скорость модуляции для своего варианта рассчитайте по формуле: В=(600 + 10N)=670 Бод.
Решение.
Задано.
— погрешность синхронизации ![]() =0,1;
=0,1;
— скорость телеграфирования ![]() =670;
=670;
— среднеквадратическое значение краевых искажений ![]() =0,1;
=0,1;
— исправляющая способность приемника ![]() =0,45;
=0,45;
— время синхронизации ![]() =1с;
=1с;
— время поддержания синфазности ![]() =10c.
=10c.
— коэффициент нестабильности генераторов k=10-6
Подлежат расчету:
— частота задающего генератора ![]() ;
;
— коэффициент деления делителя m;
— емкость реверсивного счетчика S.
Расчет параметров сводится по существу к решению системы уравнений (7), (8), (9). Можно предложить следующий порядок расчета.
1. Допустимая величина коэффициента нестабильности задающего генератора. ![]() , т.е. заданные генераторы удовлетворяют условию.
, т.е. заданные генераторы удовлетворяют условию.
2. Утроенное значение радикала
3. Емкость реверсивного счетчика
4. Коэффициент деления делителя![]()
5. Частота задающего генератора ![]()
3. Корректирующее кодирование в системах ПДС
От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность.
Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение.
Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов.
В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО.
Пусть имеется источник сообщений с объемом алфавита К.
Поставим в соответствие каждому сообщению n — элементную двоичную последовательность. Всего последовательностей из n — элементов может быть ![]() .
.
Если ![]() , то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.
, то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.
Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки.
Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия ![]() , при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.
, при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.
Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных.
3.1 Циклические коды
Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов:
если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.![]() .
.
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.
Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.
Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов).
В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде![]() .
.
где ![]() ={0,1}, причем
={0,1}, причем ![]() = 0 соответствуют нулевым элементам комбинации, а
= 0 соответствуют нулевым элементам комбинации, а ![]() = 1 — ненулевым.
= 1 — ненулевым.
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так, ![]() ,
,
поскольку ![]() .
.
Следует отметить, что действия над коэффициентами полинома (сложение и умножение) производятся по модулю 2.
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация — разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки, ее местоположении и исправить ошибку.
Формирование базиса (производящей матрицы) циклического кода возможно как минимум двумя путями.
Вариант первый.
Составить единичную матрицу для простого исходного кода.
Определить для каждой кодовой комбинации исходного кода группу проверочных элементов и дописать их в соответствующие строки матрицы. 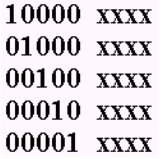
Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).
Вариант второй.
Дописать слева от КК, соответствующей образующему полиному циклического кода нули так, чтобы длина разрешенной кодовой комбинации равнялась n.
Получить остальные разрешенные кодовые КК базиса, используя циклический сдвиг исходной. (В базисе должно быть k – строк)
В данном случае код будет неразделимым.
Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом ![]()
3.2 Построение кодера и декодера
Рассмотрим код (9,5) образованный полиномом![]() .
.
Разрешенная комбинация циклического кода ![]() образуется из комбинации простого (исходного) кода путем умножения ее на
образуется из комбинации простого (исходного) кода путем умножения ее на ![]() и прибавления остатка R(x) от деления
и прибавления остатка R(x) от деления ![]() на образующий полином
на образующий полином![]() .
.
Умножение полинома на одночлен ![]()
эквивалентно добавлению к двоичной последовательности соответствующей G(x) , r — нулей справа.
Пусть ![]()
тогда ![]()
Для реализации операции добавления нулей используется r-разрядный регистр задержки.
Рассмотрим более подробно операцию деления: 
Как видим из примера, процедура деления одного двоичного числа на другое сводится к последовательному сложению по mod2 делителя [10011] с соответствующими членами делимого [10101], затем с двоичным числом, полученным в результате первого сложения, далее с результатом второго сложения и т.д., пока число членов результирующего двоичного числа не станет меньше числа членов делителя.
Это двоичное число и будет остатком ![]() .
.
Построение формирователя остатка циклического кода.
Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.
Сформулируем правила построения ФПГ.
Число ячеек памяти равно степени образующего полинома r.
Число сумматоров на единицу меньше веса кодирующей комбинации образующего полинома.
Место установки сумматоров определяется видом образующего полинома.![]()

Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.
4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.
Структурная схема кодера циклического кода (9,5).
Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.

Рассмотрим работу этой схемы
1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4
2. Во время пятого такта К2 – замыкается а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.
За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток
3. К2 – размыкается, К1 – замыкается и в след за информационными в линию уйдут элементы проверочной группы.
4. Одновременно идет заполнение регистров новой комбинацией.
Второй вариант построения кодера ЦК.
Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.
Устройство деления на производящий полином ![]() можно реализовать в следующем виде:
можно реализовать в следующем виде: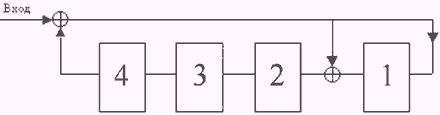
За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).
За эти же 5 тактов информационные разряды, выданные сразу на модулятор.
Далее в след за информационными уходят проверочные из ячеек устройств деления.
Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.
Окончательно структурная схема экономичного кодера выглядит так.
— На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.
— После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;
— на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.
Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.
Пример декодирования комбинации ЦК.
Положим, получена комбинация H(х)=111011010
Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х8 на производяший полином P(x)=X4+X+1
X8 X2+X+1
X8+X5+X4 x4+x+1
X5+X4
X5+X2+X
X4+X2+X
X4+X+1
X2+1=R0(X)=0101
Разделим принятую комбинацию на образующий полином
H(x) · x
1110110100 10011
10011 111111
5-т 11101
10011
6-т 11100
10011
7-т 11111
10011
8-т 11000
10011
9-т 10110 = R(X) ![]() R0(X)
R0(X)
10011
10-т 0101=R0(x)
Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.
Декодер циклического кода с исправлением ошибки
Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ.
Если во втором по старшинству то после 10го;
в третьем по старшинству то после 11го;
в четвертом по старшинству то после 12го
в пятом по старшинству то после 13го
в шестом по старшинству то после 14го
в седьмом по старшинству то после 15го
в восьмом по старшинству то после 16го
в девятом по старшинству то после 17го.
На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.
Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.
В нашем случае инвертируется второй разряд на 11 такте.
3.2.1 Задача № 5
Записать кодовую комбинацию циклического кода для случая, когда производящий полином имеет вид Р(х)=х3+х2+1 (для N= 0,1,2,3,4) и Р(х)=х3+х+1 (для N=5,6,7,8,9). Кодовая комбинация, поступающая от источника сообщений имеет К=4 элементов и записывается в двоичном виде как число, соответствующее (N+3=10) для N=6¸ 9. Нарисовать кодирующее и декодирующее устройство с обнаружением ошибок и «прогнать» через кодирующее устройство исходную кодовую комбинацию с целью формирования проверочных элементов.
Решение.
Определение остатка от деления

Кодовая комбинация G(x)=1010011
Кодирующее устройство.
| Такт | Вх | 1 | 2 | 3 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | |
| 6 | 0 | 0 | 1 | |
| 7 | 1 | 1 | 0 |
Результат «прогона» через кодирующее устройство исходной кодовой комбинации
Декодер с обнаружением ошибок
4. Системы ПДС с обратной связью
В зависимости от назначения ОС различают системы:
с решающей ОС (РОС)
с информационной (ИОС)
Общее в алгоритме работы систем с ОС в простейшем случае, то что после передачи некоторой порции информации передатчик прямого канала ожидает сигнала, либо на выдачу следующей порции, либо на повторную передачу предыдущей.
Принципиальное отличие систем РОС и ИОС состоит в том, где принимается решение о дальнейшем поведении системы.
В системах с РОС решение принимается на приёме, а в системах с ИОС – на передаче.
Для организации обратной связи и в тех и в других системах используется обратный канал.
4.1 Системы с информационной обратной связью
Рассмотрим структуру системы ПДС с ИОС
Алгоритм. Кодовые комбинации, поступающие в приёмник передаются по обратному каналу в передатчик. На передающей стороне сравниваются комбинации, которые передавались – с возвращёнными. Если они совпадают, то решающее устройство формирует сигнал на продолжение передачи и в прямой канал выдаются новые данные, а приёмник выдаёт принятые кодовые комбинации получателю. Если при сравнении обнаруживаются отличия, то передатчик вновь повторяет переданные ранее КК.
Информация передаваемая по каналу с ОС – называется квитанцией.
Системы с ИОС в которых осуществляется полная передача принятых кодовых комбинаций по обратному каналу называются ретрансляционные.
Чаще приёмник формирует специальные сигналы, имеющие меньший объём, чем полезная информация переданная по прямому каналу т. е. квитанция меньше – укороченная ИОС.
4.2 Системы с решающей обратной связью
Наиболее распространёнными среди систем с РОС являются :
системы с ожиданием (РОС — ОЖ);
с непрерывной передачей информации и блокировкой
с адресным переспросом
Рассмотрим более подробно систему (РОС — ОЖ)
В данной системе после передачи кодовой комбинации система ожидает сигнала подтверждения, и только после этого происходит передача следующей КК.
Структурная схема СПД с РОС – ОЖ
Алгоритм работы:
КК выдаваемая ИС поступает в кодер, и одновременно в накопитель передачи Н пер. Кодер добавляет проверочные разряды в соответствии с алгоритмом ПУ кодирования. Далее КК модулируется (УПС) и выдаётся в прямой канал связи. Спустя некоторое время, необходимое для передачи по каналу tp , КК поступает в приёмник.
После УПС приёма информационная часть КК записываются в накопитель приёма, и одновременно с этим вся КК поступает в ПУ декодер.
Если декодер не обнаружил ошибку, то РУ принимает решение о качестве приёма и выдаёт соответствующий сигнал на УУ.
УУ – формирует сигнал для выдачи принятой порции информации получателю и команду для формирования сигнала »подтверждения».
Данный сигнал пройдя через ОК дешифруется ДСОС и поступает в УУ пер. По его приходу УУ передачи стирает старую комбинацию из Н пер и сигнализирует ИС о выдачи следующей порции информации (КК).
Если в результате декодирования обнаружена ошибка, то решающее устройство выдаёт соответствующий сигнал в УУ приёма. УУ стирает принятую КК из Н пр и даёт команду на формирование сигнала »переспрос».
После получения сигнала »переспрос» УУ пер запрещает ИС выдавать следующую КК, и подаёт сигнал накопителю, который посылает записанную в нём КК в декодер – повторно.
4.2.1 Задача № 6
Рассчитать скорость передачи информации для системы РОС с ОЖ. Ошибки в канале не зависимы Pош=(N/2)-10-3. Построить графики зависимости R(g 1,g 2,g 3) от длины блока. Найти оптимальную длину блока. Если время ожидания tош=0,6× tбл (при к=8). Блок передаваемый в канал имеет значения: к=8,16,24,32,40,48,56. Число проверочных элементов: r=6. Длина блока в канале определяется по формуле n=ki+r.
Решение.
Коэффициенты уменьшения скорости.![]()
 , т.к.
, т.к. ![]() , а tбл=nτ0 , то
, а tбл=nτ0 , то

![]()
Скорость передачи информации

Зависимость скорости передачи информации от длины блока
Оптимальная длина блока – 8 элементов.
4.2.2 Задача №7
Определить вероятность неправильного приема в системе с РОС-ОЖ в зависимости от длины блока и построить график. Блок передаваемый в канал имеет значения: к=8,16,24,32,40,48,56. Число проверочных элементов: r=6. Длина блока в канале определяется по формуле n=ki+r. Ошибки в канале считать независимыми. Вероятность ошибки на элемент Pош=(N/2)-10-3.
Решение.
Вероятность неправильного приема
![]()

Список литературы
1. Передача дискретных сообщений: Учебник для вузов / В. П. Шувалов, Н. В. Захарченко, В. О. Шварцман и др.; Под ред. В. П. Шувалова. – М.: Радио и связь, 1990-464с.
2. Конспект лекций по курсу “Основы построения телекоммуникационных систем и сетей” СибГУТИ.
Курсовая Курсовая по ПДС
Работа добавлена на сайт bukvasha.com: 2015-10-25
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Министерство РФ по связи
и информатизации.
СибГУТИ.
Кафедра ПДС
Курсовая работа по ПДС
Выполнил:
Студент гр. А-85
Соломагин Д. А.
Проверил:
Шувалов В. П.
—
Новосибирск 2000
—
Содержание:
1.
Методы регистрации.
1.1.
Теоретические основы.
1.1.1. Регистрация посылок методом стробирования.
1.1.2. Интегральный метод.
1.1.3. Комбинированный способ регистрации посылок.
1.1.4. Регистрация посылок со стиранием.
1.1.5. Сравнение помехоустойчивости методов регистрации.
1.2.
Вывод формулы для вычисления вероятности ошибки при регистрации методом стробирования и вычисление вероятности ошибки для заданных а,
s
,
m
..
2.
Синхронизация в системах ПДС.
2.1.
Классификация систем синхронизации.
2.1.1. Прохождение синхросигналов.
2.1.2. Способ формирования синхросигналов.
2.2.
Поэлементная синхронизация с добавлением и вычитанием импульсов.
2.3.
Параметры системы синхронизации с добавлением и вычитанием импульсов.
2.4.
Расчет параметров системы синхронизации с добавлением и вычитанием импульсов.
3.
Кодирование в системах ПДС.
3.1.
Классификация кодов.
3.2.
Циклические коды.
3.3.
Построение кодера и декодера.
4.
Системы ПДС с ОС.
5.
Заключение.
6.
Список литературы.
1. Методы регистрации
1.1.
Теоретические основы.
Процесс регистрации посылок состоит в выявлении правильного знака (полярности) принятой посылки даже при наличии в них искажений: как краевых так и дроблений. Наибольшее распространение получили три способа регистрации, способ стробирования, способ интегрирования и комбинированный способ. Кроме перечисленных способов в последнее время все чаще используется способ регистрации посылок со стиранием, который применяется в системах с обнаружением ошибки на приеме.
1.1.
1
. Регистрация посылок методом стробирования.
Сущность способа регистрации стробирования состоит в том, что накопительный элемент наборного устройства приемника подключается на время, которое значительно меньше длительности элементарной посылки. Момент подключения накопительного элемента к входному устройству часто называется моментом регистрации или временем регистрации. Очевидно, что момент регистрации посылки должен совпадать с приходом из канала связи наиболее устойчивой части посылки. При наличии краевых искажений наиболее устойчива средняя часть посылки. Именно в момент средней части посылки ее целесообразно регистрировать.
Регистрация методом стробирования может быть реализована на электронных элементах. Схема устройства для регистрации методом стробирования показана на рисунке 1.
Рис. 1. Регистрация методом стробирования.
Временные диаграммы поясняющие принцип работы регистрирующего устройства, изображенного на рисунке 1, приведены ниже на рисунке 2.
Рисунок 2. Временные диаграммы работы регистрирующего устройства
Передается последовательность 10101. На выходе входного устройства Вх.У. импульсы постоянного тока имеют прямоугольную форму, но искажены по длительности (штриховой линией показаны неискаженные сигналы). Ключи Кл.1 и Кл.2 открываются одновременно на время поступления стробимпульса. Поступление импульса
U
б
в моменты, соответствующие серединам единичных интервалов, обеспечивается применением устройств поэлементной синхронизации. При этом сигнал
U4 (U5)
появляется на выходе Кл.1 (точка 4), или Кл.2 (точка 5). В зависимости от этого выходное устройство Вых.У. фиксирует «1» или «0». Если смещение ЗМ относительно идеального положения не превышает 0,5
t
0
, то элемент сигнала регистрируется правильно. Величина, на которую допускается смещение ЗМ, не вызывающее неправильный прием, определяет исправляющую способность приемника. В нашем случае исправляющая способность (теоретическая) равна 0,5
t
0
или 50%. Из рис.2. видно, что из-за смещения ЗМ относительно идеального положения на величину, превышающую 0,5
t
0
5 элемент принят неправильно.
1.1.
2
. Интегральный метод.
Сущность интегрального метода регистрации состоит в том, что во время приема на накопительном элементе происходит накопление энергии посылки в течении времени длительности неискаженной посылки
t
0
и решение в виде принятого элемента выносится на основе анализа сигнала
U
вых
, определяемого выражением:
где
U
вх
(
t)-
сигнал на входе регистрирующего устройства. Этот сигнал является дискретной функции непрерывного времени.
Пусть
Uвх(t)
принимает на интервале анализа как значение
U
вх
(t)=0
, так и
Uвх(t)=1
. Тогда решение о приеме «1» должно выносится, если
U
вых
>
0,5. Очевидно, что ошибка при передаче «1» будет в том случае, когда
U
вых
<
0,5.
Интегральный метод часто реализуется на основе многократного стробирования сигнала
U
вх
(
t)
в
N
точках. Схема, поясняющая принцип действия такого устройства регистрации, а также диаграммы поясняющие принцип регистрации интегральным методом приведены соответственно на рис.3. и рис.4.
Рис.3. Регистрация интегральным методом.
Рис.4. Диаграммы поясняющие принцип регистрации интегральным методом.
Сигнал U1(t1)
(точка 1) управляет ключом Кл. При открытом ключе, когда U
вх(t)=1
, тактовые импульсы U5(t)
(стробимпульсы) проходят на вход счетчика С4. За время действия неискаженной токовой посылки U1(t)
(на интервале
t
0
) на выходе Кл. (точка 3) появляется N
тактовых импульсов. Если на выходе Кл. на единичном интервале появится 0,5N+1
и более стробимпульсов, то можно сделать вывод о том, что принята «1». Емкость счетчика достаточно взять равной 0,5N
+1. В конце единичного интервала, определяемого с помощью устройства поэлементной синхронизации, показания счетчика считываются, и он обнуляется.
1.1.3. Комбинированный способ регистрации посылок.
Сущность комбинированного способа регистрации состоит в том, что приходящую посылку стробируют в нескольких точках, например в трех. Если в двух или в трех точках регистрации зафиксирован знак «1», то т выходное устройство перейдет в состояние «1». Нетрудно заметить, что при стробировании только в центре посылки комбинированный способ регистрации переходит в регистрацию стробированием и при очень большом количестве проб в интервале длительности посылки
t
0
– в интегральный способ регистрации.
1.1.4. Регистрация посылок со стиранием.
В рассмотренных выше способах регистрации регистрирующее устройство давало однозначный ответ о том, какой знак посылки принят «1» или «0». В условиях сильных помех в канале связи могут часто возникать случаи, когда смещение ЗМ превысят предельно допустимую величину или же будут действовать смещение ЗМ и дробления, изменяющие знак принимаемой посылки на интервале времени, превышающем
t
0
/2. В этих случаях при методе регистрации стробированием и интегрированием произойдет неправильная регистрация посылки. Для уменьшения случаев неправильной регистрации используют способ регистрации со стиранием.
Если возникает сомнение в правильности принятого знака, то на выход регистрирующего устройства поступает специальный сигнал – стирание. Кодовая комбинация в этом случае в дешифратор не поступает, а стирается. Стертую комбинацию переспрашивают до тех пор, пока она не будет зарегистрирована правильно. Наиболее просто реализовать способ регистрации со стиранием, используя устройства комбинированного способа регистрации. Однако здесь определение знака производится не по большинству, а по обязательному совпадению всех трех проб. Если хотя бы одна из трех проб определила противоположный знак регистрируемой посылки, то посылка (а следовательно, и кодовая комбинация) стирается. Качество приема посылок при этом резко повышается. Разумеется, что повышение качества приема приводит к частым переспросам комбинаций, которые вызывают сомнения, что сопряжено с некоторой потерей пропускной способности.
1.1.5. Сравнение помехоустойчивости способов регистрации.
Сравним помехоустойчивость методом стробирования и интегрального при действии краевых искажений. Поскольку при регистрации методом стробирования посылка регистрируется в середине, то допускается смещение любого из ЗМ на величину, не превращающую 0,5
t
0
. При регистрации интегральным методом суммарное смещение границ не должно превышать 0,5
t
0
. Очевидно что последнее условие выполняется с меньшей вероятностью, то есть р(и)ош.к.>
р(с)ош.к., где р(и)ош.к., р(с)ош.к. – соответственно вероятности неправильного приема при краевых искажениях и регистрации интегральным методом и методом стробирования.
Рассмотрим действия дробления. Будем считать, что на единичный интервал приходится только одно дробление. Обозначим длительность дробления t
др.
очевидно, что все дробления могут быть подразделены на две группы t
др.>
t
0
/2 и tдр.<
t0
/2. Если t
др.<
t0
/2, то при интегральном методе прием будет правильным, так как искажается менее половины ИПТ. Если t
др.>
t
0
/2 и при этом искажено более половины ИПТ, то при интегральном методе будет неправильный прием. Однако поскольку искажено более половины посылки, то будет искажена и ее середина. Следовательно, будет неправильный прием и при регистрации методом стробирования. Таким образом, если при регистрации методом стробирования неправильный прием возможен как в случае, если t
др.<
t0/2
, так и при t
др.>
t0
/2,
то при интегральном методе только при t
др.>
t0
/2. Поэтому р(и)ош.д.<
р(с)ош.д.. Вероятность ошибки будет тем больше, чем чаще появляется дробление, а также чем больше средняя длительность дробления и дисперсия длительности дробления.
1.2. Вывод формулы для вычисления вероятности ошибки при регистрации методом стробирования и вычисление вероятности ошибки для заданных а,
s
,
m
.
Рассмотрим элемент сигнала, поступающего от источника, имеющий длительность τ0 и два значащих момента (ЗМ1 и ЗМ2). При передаче по каналу связи элементы сигнала искажается по длительности (действуют краевые искажения), в результате чего ЗМ смещаются на величину Δ
t
в сторону отставания (Δ
t1
) или опережения (Δ
t2
) (рис.1.2.1.). Регистрация элементов осуществляется методом стробирования.
Поскольку при регистрации методом стробирования посылка регистрируется в середине, то допускается смещение любого значащего момента на величину 0,5τ0 = μ, где μ – исправляющая способность приемника (теоретическая). Элемент сигнала регистрируется неправильно в том случае, если левая или правая его граница сместится во внутрь на величину, превышающую исправляющую способность приемника. Вероятности этих событий обозначим соответственно р1 и р2. Неправильная регистрация имеет место также и в том случае, если обе границы одновременно сместятся на величину, большую μ. Вероятность этого события в предположении независимости смещения определим как р1р2. Тогда вероятность ошибки при регистрации методом стробирования определится следующим образом:
Предполагается, что краевые искажения δ подчиняются гауссовскому закону распределения:
,
где а – математическое ожидание δ, σ 2 – дисперсия δ.
Так как элемент сигнала ограничен с обеих сторон моментами ЗМ1 и ЗМ2, то имеем:
,
,
где
W1(
δ
), W2(
δ
) – плотность распределения искажений для левого и правого ЗМ соответственно (рис.1.2.2.).
Рис.1.2.2. Распределение вероятностей искажений для левого и правого ЗМ.
Очевидно, что
,
,
где
–
функция Крампа, .
Определив таким образом р1 и р2 нетрудно определить и .
Вычислим вероятность неправильной регистрации, если заданы
μ = 43%, а = 13%, σ = 15%.
.
Зная
Z
, по таблице
[3]
находим р1 и р2:
р1 = р2 =0,02275; далее, подставляя значения р1 и р2 в формулу (1.2.1.), получаем .
2. Синхронизация в системах ПДС
Синхронизация есть процесс установления и поддержания определенных временных соотношений между двумя и более процессами. Различают поэлементную, групповую и цикловую синхронизацию. Поэлементная синхронизация позволяет на приеме правильно отделить один элемент от другого и обеспечить наилучшие условия для его регистрации. Групповая синхронизация обеспечивает правильное разделение принятой последовательности на кодовые комбинации, а цикловая синхронизация – правильное разделение циклов временного объединения на приеме. Обычно задачи цикловой и групповой синхронизации решаются одними и теми же методами.
2.1. Классификация систем синхронизации.
Системы синхронизации можно классифицировать по следующим признакам:
а) прохождение синхроимпульсов;
б) способ формирования синхросигналов;
2.1.1. Прохождение сихросигналов.
Синхронизирующие импульсы в пункте приема могут быть получены тремя способами: от высокостабильного источника колебаний, который является эталоном отсчетов времени, путем передачи отсчетов времени (синхронизирующие импульсы) от передатчика к приемнику по отдельному каналу (синхроканалу) и путем получения информации об отсчетах времени из информационной последовательности единичных элементов.
Первый способ применим в тех случаях. Когда время сеанса связи, включая время вхождения в связь, не превышает время сохранения симфазности. Второй способ достаточно эффективен, однако требует создания отдельного канала синхронизации, что снижает пропускную способность канала связи. Как правило, этот способ применяется в групповых многоканальных синхронных системах связи. Третий способ позволяет более эффективно использовать пропускную способность системы связи и обеспечить приспособляемость (адаптацию) устройств фазирования и синхронизации к изменяющимся параметрам канала связи. Основной недостаток способа состоит в зависимости точности синхронизации от искажений принимаемых информационных сигналов и структуры информационных последовательностей единичных элементов. Несмотря на указанные недостатки, третий способ нашел преимущественное применение в системах передачи дискретной информации и телеграфной техники.
2.1.2. Способ формирования синхросигналов.
По этому способу системы синхронизации разделяют на разомкнутые (без обратной связи) и замкнутые (с обратной связью). В разомкнутых системах связи синхросигнал (тактовые импульсы) формируются либо их сигналом, применяемых по специальному выделенному синхроканалу (рис.5а), либо из информационных сигналов с помощью анализатора сигнала (АС) и формирователя синхронного сигнала (ФСС) (рис. 5б). АС предназначен для извлечения из информационного сигнала сведений о положении ЗМ. ФСС под действием сигналов с АС формирует синхросигналы в определенной фазе по отношению к информационным сигналам.
В замкнутых СС синхросигнал вырабатывается генератором синхроимпульсов. В АС производится сравнение фазового положения синхроимпульсов и положения ЗМ приходящих информационных сигналов. При рассогласовании фаз вырабатывается управляющий сигнал, корректирующий работу синхроимпульсов. Таким образом, АС представляет собой устройство с ФАПЧ и состоит из фазового дискриминатора и управляющего устройства. Различают замкнутые СС с непосредственным воздействием на частоту генератора (рис. 6а) и без непосредственного воздействия на частоту генератора (рис. 6б). В первом случае корректирующие фазы синхросигналов достигается изменением параметров колебательных контура генератора синхросигналов, во втором – воздействием на промежуточный преобразователь частоты, как правило, на делитель частоты. Весьма существенно, что замкнутые СС предусматривают только режим непрерывной синхронизации, т.е. могут использоваться лишь в синхронных системах связи.
Рис. 5а. Формирование Рис. 5б. Формирование синхросигнала из
синхросигнала по информационных сигналов
выделенному синхросигналу.
Рис. 6а. Структурная схема СС с Рис. 6б. Структурная схема СС
воздействием на частоту генератора. без воздействия на частоту
генератора.
2.2. Поэлементная синхронизация с добавлением и вычитанием импульсов (принцип действия).
В системах синхронизации без непосредственного воздействия на частоту генератора фаза подстраивается в промежуточном преобразователе ПП, через который проходит местное тактовое колебание (генерируемая последовательность тактовых импульсов). В качестве ПП чаще всего используется делитель частоты следования импульсов. Устройства синхронизации с делителем частоты возможно реализовать целиком на дискретных элементах, что упрощает их изготовление, настройку и эксплуатацию. Часто такие устройства называют устройствами с дискретным управлением (или дискретными устройствами синхронизации). Принцип изменения фазы в процессе деления частоты можно пояснить, пользуясь, рис.7а.
Рис. 7а. Структурная схема деления частоты.
f
вч
=m*f
т
fвч
б)
f
г
f
вч
в)
f
т
f
вч
г)
f
т
Рис. 7.
б) Нормальный процесс деления
в) Добавление импульса
г) Исключение импульса
Генератор вырабатывает колебание высокой частоты, в m
раз больше тактовой частоты: f
вч
=m*f
т, где m
– коэффициент деления делителя. Формирователь превращает синусоидальное колебание в последовательность импульсов с частотой следования f
вч
. Далее частота этой последовательности делится на определенное число m
, например, делителем в виде цепочки из двоичных счетчиков. Процесс деления иллюстрируется временной диаграммой, представленной на рис. 7б. На рисунке изображены исходная последовательность импульсов с частотой f
вч
и получаемая на выходе тактовая последовательность с частотой f
т
. Коэффициент деления m=
6. В этом случае на выход выдается каждый шестой импульс входной последовательности импульсов.
Если на вход делителя подать дополнительный импульс через СДИИ, то фаза выходных импульсов (рис. 7в) сместится в сторону опережения на величину, равную периоду колебаний генератора:
Dt=1/f
вч
. Дополнительные импульсы не должны совпадать во времени с импульсами высокочастотного генератора. Если один из импульсов, подаваемых на делитель, исключить, то фаза выходных импульсов стремится на ту же величину
Dt
в сторону отставания (рис.7г). Таким образом, добавлением и исключением импульсов легко изменять фазу тактовой последовательности в нужную сторону.
2.3. Параметры системы синхронизации с добавлением и вычитанием импульсов.
Рассмотрим основные параметры систем синхронизации:
1.
Шаг коррекции
j
к
– выражение в долях единичного элемента смещение фазы тактовых импульсов на выходе делителя при добавлении или исключении одного импульса:
2.
Минимальный период корректирования tmin
– наименьшее время, в течении которого корректирование не производится. Это время зависит от длительности единичного элемента
t
0
и времени усреднения в инерционном элементе (емкости реверсивного счетчика S
). При получении информационной последовательности типа 1:1 сигнал на выходе реверсивного счетчика РС появиться после получения S
импульсов одного и того же знака с выхода ФД.
Поэтому , где В – скорость модуляции, Бод.
3.
Погрешность (точность) синхронизации
e
— величина характеризующая наибольшее отклонение фазы синхросигналов (ТИ) от их оптимального положения, которое с заданной вероятностью может произойти при работе СС. Погрешность синхронизации рассматривается как сумма двух погрешностей – статической и динамической:
Статическая погрешность
e
ст.
– выраженное в долях единичного элемента
t
0
фазовое отклонение ТИ при приеме неискаженной информационной последовательности элементов. Величина
e
ст.
определяется параметрами СС:
e
ст.
=
j
к
+
j
г
, где
j
к
– шаг коррекции;
j
г
– относительное смещение фазы тактовых сигналов из-за нестабильности генераторов передачи и приема за время между сигналами управления. Очевидно, что при передаче комбинации 1:1 промежуток времени между сигналами управления составил t=
t0*S
, что соответствует tmin
. При передаче единичных элементов одного и того же знака промежуток времени между сигналами управления бесконечен. Выражение для
e
ст.
можно представить в виде:
Динамическая погрешность
e
дин.
– выраженное в долях единичного элемента фазовое смещение ТИ, вызванное искажениями элементов информационного сигнала (смещениями ЗМ). Искажения длительности принимаемых элементов могут вызвать появление ложных сигналов управления на выходе ФД, а, следовательно, и на выходе инерционного элемента. Эти сигналы могут осуществить ложное корректирование СС в сторону рассогласования фаз. При нормальном распределении смещений ЗМ входящей последовательности со средним значением, равным нулю, и среднеквадратическим отклонением
s
0
случайная величина
e
дин.
Также распределена по нормальному закону с дисперсией:
4.
Время синхронизации t
с
– время, необходимое для корректирования первоначального расхождения фаз
D
j
между ТИ (синхроимпульсами) и входящей последовательностью информационных сигналов. Первоначальное расхождение фаз случайно и может лежать в пределах от 0 до +
p
(от 0 до +
t
0
/2).
Рассмотрим граничный случай, когда
D
j
максимален и равен
t
0
/2. При приеме информационной последовательности типа 1:1 и y=1
: tcmax=S*m*
t0
/2. При приеме текста (у=0,5) время синхронизации: tcmax=S*m*
t0
.
5. Время поддержания синфазности t
п.с.
– время, в течении которого фаза синхросигнала не выйдет за допустимые пределы рассогласования
e
доп.
При прекращении работы СС по подстройке фазы. Подстройка может прекратиться по причине обрыва канала связи или резкого ухудшения его качества, а также в случае долговременного поступления на вход приемника информационных элементов одного и того же знака. Следовательно, время t
п.с.
определяет допустимое время обрыва в канале связи, при котором ранее установленная синфазность сохраняется. Время t
п.с.
может быть определено по формуле: t
п.с.
=
e
доп.
/2kB
. Величина
e
доп.
Определяется исправляющей способностью приемника
m
(способностью приемника правильно регистрировать единичные элементы при наличии искажений). Тогда t
п.с.
=
m
/2kB
. Увеличение t
п.с.
при заданной скорости модуляции может быть достигнуто уменьшением коэффициента нестабильности задающих генераторов (т.к. величина
m
определяется схемой аппаратуры ПДИ и способом регистрации элементов и заранее известна).
6. Вероятность срыва синхронизации Рс.с. – вероятность того, что фаза синхросигналов под действием помех сдвинется на величину большую |
t
0
/2|
. Подобный переход фазы ТИ в соседний элемент полностью нарушает работу синхронной системы связи, т.к. распределители передачи и приема «разойдутся» на элементы, что приведет к нарушению фазирования по циклам. Уменьшить величину Рс.с. можно увеличением времени усреднения сигналов, поступающих с ФД, т.е. увеличением емкости реверсивного счетчика S
. Это в свою очередь приводит к увеличению времени синхронизации tc
и снижению периода корректирования. Поэтому задача снижения Рс.с. и выбора периода усреднения (емкости S)
является вариационной. В результате ее решения необходимо определить оптимальную характеристику того параметра, который наиболее важен в данных условиях.
2
.4.
Расчет параметров системы синхронизации с добавлением и вычитанием импульсов.
Задача №1
Коэффициент нестабильности задающего генератора устройства синхронизации
k = 10-6,
исправляющая способность μ
=
40%. Краевые искажения отсутствуют. Построить зависимость времени нормальной работы (без ошибок) приемника от скорости телеграфирования В после выхода из строя фазового детектора (ФД) устройства синхронизации. Будут ли возникать ошибки спустя минуту после отказа ФД, если скорость телеграфирования В = 9600 Бод?
Решение
Рассматривается устройство синхронизации без непосредственного воздействия на частоту генератора, структурная схема которого приведена на рис. 2.4.1.
Рис.2.4.1 Устройство синхронизации с добавлением и исключением импульсов.
При выходе из строя ФД перестает осуществляться подстройка фазы. Некоторое время после этого система еще работает без ошибок, а потом синхронизм нарушается, система перестает работать. В данной задаче требуется определить это время, т.е. время поддержания синхронизма
t
п.с.
для разных значений скорости телеграфирования В и построить график зависимости
t
п.с
=
f(B)
. Время поддержания синхронизма рассчитывается по следующей формуле:
, где μ – исправляющая способность приемника.
Рассчитаем значение
tп.с для следующих значений скорости телеграфирования В = 600, 1200, 2400, 4800, 7200, 9600 Бод.
Для В = 600 Бод:
Аналогичным образом рассчитаем
t
п.с
для остальных значений В и результаты расчета сведем в таблицу:
| В, Бод | 600 | 1200 | 2400 | 4800 | 7200 | 9600 |
| t п.с, с |
333,33 | 166,67 | 83,33 | 41,67 | 27,78 | 20,83 |
Построим график зависимости
t
п.с
=
f (B)
:
Рис.2.4.2 График зависимости времени поддержания синхронизма от скорости телеграфирования В.
Из графика видно, что с увеличением скорости телеграфирования время поддержания синхронизма системой уменьшается.
 Будут ли возникать ошибки спустя минуту после отказа ФД, если скорость телеграфирования В = 9600 Бод?
Будут ли возникать ошибки спустя минуту после отказа ФД, если скорость телеграфирования В = 9600 Бод?
Ответ: спустя минуту после отказа ФД при скорости телеграфирования 9600 Бод будут возникать ошибки, так как время поддержания синхронизма системой
t
п.с.
= 20,83 с
, что меньше 1
минуты.
Задача №2
В системе передачи данных используется устройство синхронизации без непосредственного воздействия на частоту генератора. Скорость модуляции В, шаг коррекции Δф. Определить частоту задающего генератора и число ячеек
n
делителя частоты, если коэффициент деления каждой ячейки равен 2.
В = 1000 + 20
N;
Δф
= 0
,01 + 0,003
N,
где
N
– номер в журнале группы.
N = 16,
В = 1000 + 2
0∙16 = 1320 Бод,
Δф
= 0
,01 + 0,003
∙16 = 0,058.
Решение
Коэффициент деления делителя
m и шаг коррекции Δф
связаны между собой следующим соотношением: .
.
Так как коэффициент деления одной ячейки равен 2, то коэффициент деления самого делителя должен быть равным 2
n
, где
n –
число ячеек
В нашем случае число ячеек должно равняться
n =
5, а
m = =
2
5
= 32.
Теперь, зная
m
, определяем частоту ЗГ:
fзг = mB = 32∙1320 = 42240
Гц.
Задача №3
Рассчитать параметры устройства синхронизации без непосредственного воздействия на частоту задающего генератора со следующими характеристиками : время синхронизации
tс < 1c
, время поддержания синфазности
tп.с. < 10c, погрешность синхронизации ε < 10%
от τ0
, исправляющая способность
μ
= 45%, коэффициент нестабильности генераторов k = 10-6, скорость модуляции В = 600 + 20N
, среднеквадратическое значение краевых искажений σкр. = 10% от τ0 .
Решение
В данной задаче требуется рассчитать следующие параметры:
m – коэффициент деления делителя частоты;
S – емкость реверсивного счетчика;
fзг –
частота задающего генератора.
Требуемые параметры найдем, решив систему:
.
Далее, найдя
m и S, найдем fзг = mВ.
Из первого уравнения системы выражаем m:
и подставляем во второе уравнение:
.
Проделав несложные преобразования, выражаем и находим
S:
.
Зная
S
, находим
m:
Далее вычисляем
fзг :
Задача №4
Определить, реализуемо ли устройство синхронизации без непосредственного воздействия на частоту задающего генератора, обеспечивающее погрешность синхронизации
ε= = 2,5% при условиях предыдущей задачи.
Решение
Чтобы определить, реализуемо ли устройство синхронизации, обеспечивающее
ε = =2,5% при условиях предыдущей задачи,
рассчитаем его параметры для
ε = 2,5%.
Емкость счетчика:
Емкость счетчика получилась отрицательной величиной, что не может иметь место на практике. Отсюда, не определяя остальные параметры, можно сделать вывод, что при условиях предыдущей задачи устройство синхронизации, обеспечивающее погрешность синхронизации
ε = 2,5%, не реализуемо.
Задача №5
В системе передачи данных используется устройство синхронизации без непосредственного воздействия на частоту генератора с коэффициентом нестабильности
k = 10-5
. Коэффициент делителя
m = 10, емкость реверсивного счетчика S = 10.
Смещение ЗМ подчинено нормальному закону распределения с нулевым математическим ожиданием и СКО , длительности единичного интервала. Рассчитать вероятность ошибки при регистрации методом стробирования без учета и с учетом погрешности синхронизации. Исправляющую способность считать равной μ = 50%.
.
Решение
Рассмотрим рис. 2.4.3, на котором приведен приведен единичный элемент длительностью τ0 , отмечен оптимальный момент регистрации МР (время регистрации
tр = 0 и исправляющая способность приемника μ ≈ 50%)
. Плотности вероятностей смещения левой и правой границ единичного элемента обозначены соответственно
W1(δ)
и
W2(δ). Ошибочная регистрация элемента произойдет в следующих случаях: левая или правая граница единичного элемента сместится вправо на величину | δ | ≥ μ
, одновременно обе границы сместятся внутрь единичного элемента, и смещение превысит исправляющую способность приемника
μ.
Рис.2.4.3. Плотности вероятностей смещения левой и правой границ единичного элемента.
Вероятность ошибочной регистрации , где р1 и р2 – соответственно вероятности смещения левой и правой границ на величину больше μ. Если устройство синхронизации работает идеально (ε = 0), то, как видно из рис. 2.4.3.,
;
.
Наличие статической и динамической составляющих погрешности корректирования приведет к уменьшению верности приема единичного элемента.
Пусть устройство поэлементной синхронизации вырабатывает синхроимпульсы (стробимпульсы) с некоторым смещением (погрешностью ε) (рис. 2.4.3.). В этом случае:
Так как плотности распределения вероятностей
W1(δ)
и
W2(δ) описываются гауссовским законом с параметрами акр. и σкр., то вероятности
р1 и р2 можно выразить через функцию Крампа
:
Рассчитаем вероятность ошибочной регистрации без учета и с учетом погрешности синхронизации.
1). Без учета погрешности синхронизации:
.
По таблице находим р1 = р2 = 0,01578.
.
2). С учетом погрешности синхронизации.
Рассчитаем погрешность синхронизации по формуле:
.
С учетом этого:
,
.
По таблице находим р1 = 0,000968 и р2 = 0,11507;
По результатам расчетов делаем вывод: погрешность синхронизации вызывает увеличение вероятности неправильной регистрации элементов сигнала.
3. Кодирование в системах ПДС.
3.1.
Классификация кодов.
Помехоустойчивые коды делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению отводится блок из
n символов (разрядов) или блоки с разным числом символов. В связи с этим блочные коды делятся на равномерные и неравномерные. Широкое практическое применение нашли равномерные коды. К неравномерным кодам относятся, например, код Морзе. Непрерывные коды, к которым относятся рекуррентные (сверточные), представляют собой непрерывные последовательности единичных элементов, не разделенные на блоки. В таких кодах избыточные разряды помещаются в определенном порядке между информационными разрядами.
Равномерные блочные коды делятся на разделимые и неразделимые. Разделимые коды в свою очередь делятся на систематические (линейные) и несистематические (нелинейные). Код называется линейным, если любая разрешенная кодовая комбинация может быть получена в результате линейной операции под набором не нулевых линейно – независимых КК. В систематических кодах проверочные элементы формируются линейным преобразованием информационных.
Нелинейные коды указанным выше свойством не обладают и применяются значительно реже. Примером несистематического кода является код с контрольным суммированием.
Различают два метода формирования проверочной группы: поэлементной и в целом; последний характерен для широко распространенных полиномиальных кодов (и их разновидности – циклических). Среди систематических кодов большое применение нашли коды Хэмминга. Эти коды, обеспечивающие
d0=3, позволяют исправить одну ошибку. Помехоустойчивость коды могут иметь основание (значность) и больше 2. Однако в связи со сложностью построения кодирующих и декодирующих устройств они на практике применяются значительно реже двоичных.
3.2.
Циклические коды.
Широкое распространение получил класс линейных кодов, которые называются циклическими. Название этих кодов происходит от их основного свойства: если кодовая комбинация
а1, а2,……, а
n-1,
an принадлежит циклическому коду, то комбинации
an, a1,a2,……, an-1; an, an-1, a1, a2,……, an-2 и т.д., полученные циклической перестановкой элементов, также принадлежат этому коду.
Общим свойством всех разрешенных КК ЦК (как полиномов) является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой КК на этот полином. Описание циклических кодов и их построения обычно проводят с помощью многочленов (полиномов). Цифры двоичного кода можно рассматривать как коэффициенты многочлена переменной х.
Поскольку любое число в произвольной системе счисления можно записать в виде
an-1xn-1+an-2xn-2+…..+a0x0, где х – основание системы счисления,
an-1,…., a0 – цифры этой системы, то переход от двоичного числа к записи в виде многочлена осуществляется следующим образом:
КК ЦК описываются полиномами обладающими определенными свойствами. Последние определяются свойствами и операциями той алгебраической системы, к которой принадлежит множество полиномов. Например, в алгебраической системе, которая носит название поля Галуа (
GF(x)), действие над коэффициентами полиномов (сложение, вычитание) производится по модулю два. Умножение полиномов должно производиться по модулю некоторого полинома Р
r
(x). Эти два условия определяют замкнутость указанных операций: их применение не приводит к кодовым комбинациям, длина которых больше длинны заданного кода
n.
В циклических кодах разрешенными КК являются те, которые делятся на образующий полином без остатка из всех возможных полиномов степени
n(2n) только 2к полиномов (
k=n-r) имеют нулевой остаток при делении. Они и образуют множество различных КК ЦК.
ЦК являются блочными, равномерными и линейными, линейность кодов вытекает из того, что если кодовые слова принадлежат ЦК, то их линейная комбинация будет также принадлежать ЦК, т.е. обязательно делится без остатка на производящий полином. Это свойство существенно упрощает аппаратурную реализацию кода.
3.3. Построение кодера и декодера ЦК
Задача №1.
Нарисовать кодер циклического кода, для которого производящий полином задан числом (2
N +1)
, где
N = 16.
Решение
Производящий полином задан числом 33, которому соответствует число в двоичной системе счисления 100001, следовательно,
Р(х) = х5 + 1.
Степень производящего полинома определяет число проверочных элементов (
r)
в кодовой комбинации циклического кода. В нашем случае
r = 5.
Кодирующее устройство (кодер) состоит из регистра с обратными связями, число ячеек памяти которого равно числу проверочных элементов, и сумматоров по модулю два, число которых на единицу меньше числа ненулевых членов производящего полинома Р(х), и в нашем случае равно 1.
На рис. 3.3.1. приведена схема кодера циклического кода, производящий полином которого имеет вид: Р(х) = х5 + 1.
Рис.3.3.1 Схема кодера циклического кода.
Задача №2.
Записать кодовую комбинацию циклического кода для случая, когда производящий полином имеет вид Р(х) = х3 + х + 1. Кодовая комбинация, поступающая от источника сообщений имеет
k
= 4 элементов и записывается в двоичном виде как число, соответству
—
ющее
(
N –  = 16 – 8 = 8.
= 16 – 8 = 8.
Решение
Кодовая комбинация, поступающая от источника, имеет вид 1000, т.е.
Q(x) =
х3 .
Сформируем кодовую комбинацию циклического кода путем деления
Q(x)
х
3
на производящий полином Р(х).
;
Далее выполняем операцию деления:
Остаток от деления
R(x)
=
.
Это значит, что проверочными элементами для данной кодовой комбинации являются
101
.
Таким образом, получена кодовая циклического кода
1000101
.
Задача №3.
Нарисовать кодирующее и декодирующее устройство с обнаружением ошибок и «прогнать» через кодирующее устройство исходную кодовую комбинацию с целью формирования проверочных элементов.
Решение
Кодовая комбинация, поступающая от источника –
1000
; производящий полином имеет вид: Р(х) = х3 + х + 1.
Схема кодирующего устройства приведена на рис. 3.3.2.
Рис.3.3.2. Схема кодирующего устройства.
Схема работает по правилу: «новый элемент записывается, старый сдвигается».
Составим таблицу:
| № такта | Инф. элементы | 3 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 2 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 1 |
При считывании проверочных элементов необходимо разорвать цепь обратной связи. Это делается с помощью ключа К.
Декодирующее устройство представлено на рис. 3.3.3.
Обнаружение ошибок в циклическом коде производится путем деления принятой кодовой комбинации на производящий полином. Если остаток от деления окажется равным нулю, то вероятнее всего, ошибок нет. Если же получен ненулевой остаток, то имеет место ошибка.
Рис.3.3.3. Схема декодирующего устройства.
Задача №4.
Вычислить вероятность неправильного приема кодовой комбинации (режим исправления ошибок) в предположении, что ошибки независимы, а вероятность неправильного приема на элемент соответствует вычисленной в главе 2 (с учетом погрешности синхронизации и без учета погрешности синхронизации).
Решение
Если код используется в режиме исправления ошибок и кратность исправляемых ошибок равна
t
и.о.,
то вероятность неправильного приема кодовой комбинации определяется следующим образом:
Здесь рош. – вероятность неправильного приема единичного элемента;
n
– длина кодовой комбинации;
t
и.о.
–
кратность исправляемых ошибок;
.
Кратность исправляемых. ошибок
t
и.о
определяется как , где
d
0
–
кодовое расстояние. Для кода (7,4), заданного в задаче №3,
d
0
= 3 и
t
и.о.
= 1, т.е. данный код способен исправлять однократные ошибки.
Расчет вероятности неправильного приема без учета погрешности синхронизации.
Вероятность ошибки на элемент без учета погрешности синхронизации равна
рош. = 0,
031311.
Расчет вероятности неправильного приема с учетом погрешности синхронизации.
Вероятность ошибки на элемент с учетом погрешности синхронизации равна рош= = 0,
115927
Глядя на результаты расчетов, можно сделать вывод о том, что при наличии погрешности поэлементной синхронизации вероятность неправильного приема кодовой комбинации увеличивается.
4. Системы ПДС с ОС.
В системах с ОС ввод в передаваемую информацию избыточности производится с учетом состояния дискретного канала. С ухудшением состояния дискретного канала вводимая избыточность увеличивается, и наоборот, по мере улучшения состояния канала она уменьшается.
В зависимости от назначения ОС различают системы:
ü с решающей обратной связью (РОС)
ü информационной обратной связью (ИОС)
ü с комбинированной обратной связью (КОС)
Структурная схема системы ПД с ОС
РОС
ИОС
В системе с РОС приемник, приняв кодовую комбинацию и проанализировав ее на наличие ошибок, принимает окончательное решение о выдаче комбинации потребителю информации или о ее стирании и посылке по обратному каналу сигнала о повторной передаче этой кодовой комбинации. Поэтому системы с РОС часто называют системами с переростом или системами с автоматическим запросом ошибок (АЗО). В случае принятия кодовой комбинации без ошибок приемник формирует и направляет в канал ОС сигнал подтверждения, получив который, передатчик ПКпер передает следующую кодовую комбинацию. Таким образом в системах с РОС активная роль принадлежит приемнику, а по обратному каналу передаются вырабатываемые им сигналы решения.
В системах с ИОС по обратному каналу передаются сведения о поступающих на приемник кодовых комбинаций до их окончательной обработки и принятия заключительных решений. Частным случаем ИОС является полная ретрансляция поступающих на приемную сторону КК или их элементов. Эти системы получили название ретрансляционных. Если количество информации, передаваемое по каналу ОС равно количеству инфомации в сообщении, передаваемому по прямому каналу, то ИОС называется полной. Если содержащаяся в квитанции информация отражает лишь некоторые признаки сообщения, то ИОС называется информационной.
Полученная по каналу ОС информация анализируется передатчиком, и по результатам анализа передатчик принимает решение о передаче следующей КК или о повторении ранее переданных. После этого передатчик передает служебные сигналы о принятых решениях, а затем соответствующие КК. Приемник ПКпр или выдает накопленную кодовую комбинацию получателю, или стирает ее и запоминает вновь переданную. В система с укороченной ИОС меньше загрузка обратного канала, но больше вероятность появления ошибок по сравнению с полной ИОС.
В системах с КОС решение о выдаче КК получателю информации или о повторной передаче может приниматься и в приемнике, и в передатчике системы ПДС, а канал ОС используется для передачи как квитанций, так и решений.
Системы ОС:
ü с ограниченным числом повторений (КК повторяется не более
L раз)
ü с неограниченным числом повторений (КК повторяется до тех пор, пока приемник или передатчик не примет решение о выдаче этой комбинации потребителю).
Системы с ОС могут отбрасывать либо использовать информацию, содержащуюся в забракованных КК, с целью принятия более правильного решения. Система первого типа называется системой без памяти, а второго система с памятью.
Системы с ОС являются адаптивными: темп передачи информации по каналам связи автоматически приводится в соответствие с конкретными условиями прохождения сигналов.
Наличие ошибок в каналах ОС приводит к тому, что в системах с РОС возникают специфические потери верности, состоящие в появлении лишних КК — вставок и пропаданий КК — выпадений.
Задача №1.
Построить временные диаграммы для системы с РОС-ОЖ (ошибки в канале независимы). В канал передаются кодовые комбинации 1,2,3,4,5,6. Искажена 2 кодовая комбинация. На третьей кодовой комбинации Да → Нет (искажение сигнала с подтверждением).
Решение
Решение данной задачи приведено на рис. 4.1.
1)
Кодовые комбинации от источника сообщения;
2)
Кодовые комбинации, посылаемые передатчиком в канал;
3)
Кодовые комбинации, полученные приемником из канала;
4)
Сигналы на выходе устройства формирования управляющих сигналов;
5)
Сигналы на входе устройства приема управляющих сигналов;
6)
Кодовые комбинации, передаваемые получателю сообщения.
Рис.4.1 Временные диаграммы работы системы РОС-ОЖ.
Задача №2.
Рассчитать скорость передачи информации для системы РОС-ОЖ. Ошибки в канале независимы, . Построить графики зависимости
R(R1
,
R2
,
R3) от длины блока. Найти оптимальную длину блока. Если время ожидания tож = 0
,6
∙tбл. (при k = 
. Блок, передаваемый в канал имеет значения:
k
= 8,16,24,32,40,48,56. Число проверочных элементов
r = 6.
Длина блока в канале определяется по формуле
n = ki + r
.
Решение
.
Скорость передачи информации определяется по формуле
R = R1
∙
R2
∙
R3,
где R1
– потери скорости засчет введения избыточности;
R2
–
потери скорости, обусловленные ожиданием;
R3
– потери, обусловленные повторными передачами.
;
;
.
Здесь:
n –
общее число элементов в кодовой комбинации;
k –
блок, передаваемый в канал,
n = ki + r
;
tож – время ожидания;
tбл. – длина блока;
Ро.о. – вероятность обнаружения ошибки.
Рассчитаем
R1
в зависимости от длины блока и результаты расчета сведем в таблицу:
| n | 14 | 22 | 30 | 38 | 46 | 54 | 62 |
| k | 8 | 16 | 24 | 32 | 40 | 48 | 56 |
| R1 | 0,571 | 0,727 | 0,800 | 0,842 | 0,869 | 0,889 | 0,905 |
Рассчитаем
R2
. Сначала находим отношение в зависимости от длины блока. Пусть
n0 = 14 (k = 8
)
, тогда
;
.
Результаты расчета сведем в таблицу:
| n | 14 | 22 | 30 | 38 | 46 | 54 | 62 |
| t ож. /t бл. |
0,6 | 0,381 | 0,280 | 0,221 | 0,182 | 0,155 | 0,135 |
| R2 | 0,625 | 0,724 | 0,781 | 0,818 | 0,845 | 0,865 | 0,881 |
Вероятность обнаружения ошибки определяем по формуле:
,
где
Рош. – вероятность ошибки на элемент.
Рассчитаем
R3
и результаты сведем в таблицу:
| n | 14 | 22 | 30 | 38 | 46 | 54 | 62 |
| Ро.о . |
0,106 | 0,162 | 0,214 | 0,263 | 0,309 | 0,352 | 0,392 |
| R3 | 0,894 | 0,838 | 0,768 | 0,737 | 0,691 | 0,648 | 0,608 |
Далее определяем
R в зависимости от длины блока:
| n | 14 | 22 | 30 | 38 | 46 | 54 | 62 |
| R | 0,3 19 |
0,4 4 1 |
0, 480 |
0, 508 |
0,5 07 |
0, 498 |
0, 485 |
Построим графики зависимости R = R1
∙
R2
∙
R3 от длины блока.
Рис.4.2 График зависимости скорости передачи
R
и относительных скоростей передачи
R1, R2, R3 от длины блока n.
Оптимальная длина блока
n = 38
элементов, так как при этом достигается максимальная скорость передачи информации.
Задача №3.
Определить вероятность неправильного приема в системе с РОС-ОЖ в зависимости от длины блока и построить график. Ошибки в канале считать независимыми. Вероятность ошибки на элемент
Решение
.
При работе системы ПДС с РОС-ОЖ возможны следующие состояния (рис. 4.3.2).
Рис.4.3. Граф состояний системы РОС-ОЖ.
Вероятность неправильного приема в системе с РОС-ОЖ определится следующим образом:
где
.
.
.
Рассчитаем значение вероятности неправильного приема для разных значений
n.
Остальными слагаемыми можно пренебречь, так как они очень малы и не внесут значительных изменений в сумму.
Остальными слагаемыми можно пренебречь, так как они очень малы и не внесут значительных изменений в сумму.
Сведем результаты расчетов в таблицу и построим график (рис. 4.4).
| п | 14 | 22 | 30 | 38 | 46 | 54 | 62 | |||
| 1 – Ро.о . | 0,894 | 0,838 | 0,768 | 0,737 | 0,691 | 0,648 | 0,608 | |||
| Рн.о. х10-5 | 0, 2726 |
1,099 | 2 , 763 |
5 , 475 |
9 , 396 |
1 4 , 464 |
21,3 | |||
|
Рн.о.* х10-5 |
0, 305 |
1 , 311 |
3 , 598 |
7 , 429 |
13 , 598 |
22 , 321 |
35,033 |
Рис. 4.4 График зависимости вероятности не обнаружения ошибки от длины блока
n.
Глядя на полученный график, видно, что с увеличением длины блока увеличивается вероятность его поражения помехами, а следовательно, увеличивается вероятность неправильного приема.
5. Заключение
В работе рассмотрены способы расчета систем синхронизации и кодирования. По результатам расчетов видно, что краевые искажения в каналах связи влияют на верность передачи информации, так же влияние оказывает и погрешность системы синхронизации. Одним из методов борьбы с ошибками может являться применение помехоустойчивых кодов, один из вариантов которых — циклический рассмотрен в этой работе
6. Список литературы
ü Буга Н.Н., Основы теории связи и передачи данных, ЛВИКА им. Можайского, 1970.
ü Шувалов В.П., Захарченко Н.В., Шварцман В.О., Передача дискретных сообщений/ Под ред. Шувалова В.П.-М.: Радио и связь — 1990.

