2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка
выборки
показывает, насколько отклоняется в
среднем параметр выборочной
совокупности
от соответствующего параметра генеральной.
Если рассчитать среднюю из ошибок всех
возможных выборок определенного вида
заданного объема (n),
извлеченных из одной и той же генеральной
совокупности,
то получим их обобщающую характеристику
среднюю
ошибку выборки
().
В
теории выборочного наблюдения
выведены формулы для определения ,
которые индивидуальны для разных
способов отбора (повторного и
бесповторного), типов используемых
выборок и видов оцениваемых статистических
показателей.
Например, если
применяется повторная собственно
случайная выборка, то
определяется как:
![]()
при
оценивании среднего значения признака;
![]()
если
признак альтернативный, и оценивается
доля.
При бесповторном
собственно случайном отборе в формулы
вносится поправка
![]()
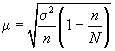
для
среднего значения признака;
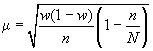
для
доли.
Вероятность
получения именно такой величины ошибки
всегда равна 0,683. На практике же
предпочитают получать данные с большей
вероятностью, но это приводит к возрастанию
величины ошибки выборки.
Предельная
ошибка выборки ()
равна t-кратному
числу средних ошибок выборки (в теории
выборки принято коэффициент t
называть
коэффициентом доверия):
t
.
Если ошибку выборки
увеличить в два раза (t
2), то получим гораздо большую вероятность
того, что она не превысит определенного
предела (в нашем случае
двойной средней ошибки)
0,954. Если взять t
3, то доверительная вероятность составит
0,997
практически достоверность.
Уровень предельной
ошибки выборки зависит от следующих
факторов:
степени вариации
единиц генеральной совокупности;
объема выборки;
выбранных схем
отбора (бесповторный отбор дает меньшую
величину ошибки);
уровня
доверительной вероятности.
Если объем выборки
больше 30, то значение t
определяется по таблице нормального
распределения, если меньше
по таблице распределения Стьюдента
(Приложение
1).
Приведем некоторые
значения коэффициента доверия из таблицы
нормального распределения.
![]()
Доверительный
интервал для среднего значения признака
и для доли в генеральной
совокупности
устанавливается следующим образом:
![]()
Итак, определение
границ генеральной средней и доли
состоит из следующих этапов:
нахождение в
выборке среднего значения признака
(или доли);
определение
в соответствии с выбранной схемой отбора
и вида выборки;
задание
доверительной вероятности Р
и определение коэффициента доверия t
по
соответствующей таблице;
вычисление
предельной ошибки выборки ;
построение
доверительного интервала для средней
(или доли).
Ошибки выборки
при различных видах отбора
1. Собственно
случайная и механическая выборка.
Средняя
ошибка собственно случайной и механической
выборки находятся по формулам,
представленным в табл. 11.1.
Таблица 1
Формулы для
расчета средней ошибки
собственно
случайной и механической выборки ()

где
2
дисперсия
признака в выборочной совокупности.
Пример 2. Для
изучения уровня фондоотдачи было
проведено выборочное обследование 90
предприятий из 225 методом случайной
повторной выборки, в результате которого
получены данные, представленные в
таблице.

В рассматриваемом
примере имеем 40%-ную выборку (90 : 225
0,4, или 40%). Определим ее предельную ошибку
и границы для среднего значения признака
в генеральной совокупности по шагам
алгоритма:
1. По результатам
выборочного обследования рассчитаем
среднее значение и дисперсию в выборочной
совокупности:
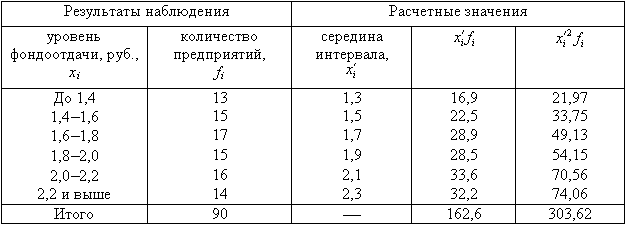
Выборочная средняя
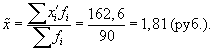
Выборочная
дисперсия изучаемого признака
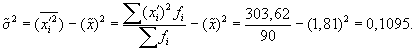
2. Определяем
среднюю ошибку повторной случайной
выборки
![]()
3. Зададим
вероятность, на уровне которой будем
говорить о величине предельной ошибки
выборки. Чаще всего она принимается
равной 0,999; 0,997; 0,954.
Для наших данных
определим предельную ошибку выборки,
например, с вероятностью 0,954. По таблице
значений вероятности функции нормального
распределения (см. выдержку из нее,
приведенную в Приложении 1) находим
величину коэффициента доверия t,
соответствующего вероятности 0,954. При
вероятности 0,954 коэффициент t
равен 2.
4. Предельная
ошибка выборки с вероятностью 0,954 равна
![]()
5. Найдем доверительные
границы для среднего значения уровня
фондоотдачи в генеральной совокупности
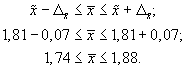
Таким образом, в
954 случаях из 1000 среднее значение
фондоотдачи будет не выше 1,88 руб. и не
ниже 1,74 руб.
Выше была
использована повторная схема случайного
отбора. Посмотрим, изменятся ли результаты
обследования, если предположить, что
отбор осуществлялся по схеме бесповторного
отбора. В этом случае расчет средней
ошибки проводится по формуле
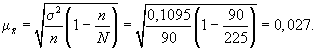
Тогда при вероятности
равной 0,954 величина предельной ошибки
выборки составит:
![]()
Доверительные
границы для среднего значения признака
при бесповторном случайном отборе будут
иметь следующие значения:
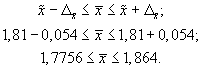
Сравнив результаты
двух схем отбора, можно сделать вывод
о том, что применение бесповторной
случайной выборки дает более точные
результаты по сравнению с применением
повторного отбора при одной и той же
доверительной вероятности. При этом,
чем больше объем выборки, тем существеннее
сужаются границы значений средней при
переходе от одной схемы отбора к другой.
По данным примера
определим, в каких границах находится
доля предприятий с уровнем фондоотдачи,
не превышающим значения 2,0 руб., в
генеральной совокупности:
1) рассчитаем
выборочную долю.
Количество
предприятий в выборке с уровнем
фондоотдачи, не превышающим значения
2,0 руб., составляет 60 единиц. Тогда
m
60, n
90, w
m/n
60 : 90
0,667;
2) рассчитаем
дисперсию доли в выборочной совокупности
w2
w(1
w)
0,667(1
0,667)
0,222;
3) средняя ошибка
выборки при использовании повторной
схемы отбора составит
![]()
Если предположить,
что была использована бесповторная
схема отбора, то средняя ошибка выборки
с учетом поправки на конечность
совокупности составит
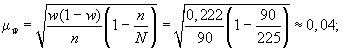
4) зададим
доверительную вероятность и определим
предельную ошибку выборки.
При значении
вероятности Р
0,997 по таблице нормального распределения
получаем значение для коэффициента
доверия t
3 (см. выдержку из нее, приведенную в
Приложении 1):
![]()
5) установим границы
для генеральной доли с вероятностью
0,997:

Таким образом, с
вероятностью 0,997 можно утверждать, что
в генеральной совокупности доля
предприятий с уровнем фондоотдачи, не
превышающим значения 2,0 руб., не меньше,
чем 54,7%, и не больше 78,7%.
2. Типическая
выборка. При
типической выборке генеральная
совокупность объектов разбита на k
групп, тогда
N1
N2
…
Ni
…
Nk
N.
Объем извлекаемых
из каждой типической группы единиц
зависит от принятого способа отбора;
их общее количество образует необходимый
объем выборки
n1
n2
…
ni
…
nk
n.
Существуют
следующие два способа организации
отбора внутри типической группы:
пропорциональной объему типических
групп и пропорциональной степени
колеблемости значений признака у единиц
наблюдения в группах. Рассмотрим первый
из них, как наиболее часто используемый.
Отбор, пропорциональный
объему типических групп, предполагает,
что в каждой из них будет отобрано
следующее число единиц совокупности:
![]()
где ni
количество извлекаемых единиц для
выборки из i-й
типической группы;
n
общий объем выборки;
Ni
количество единиц генеральной
совокупности, составивших i-ю
типическую группу;
N
общее количество единиц генеральной
совокупности.
Отбор единиц
внутри групп происходит в виде случайной
или механической выборки.
Формулы для
оценивания средней ошибки выборки для
среднего и доли представлены в табл.
11.2.
Таблица 2
Формулы для
расчета средней ошибки выборки ()
при использовании типического отбора,
пропорционального объему типических
групп
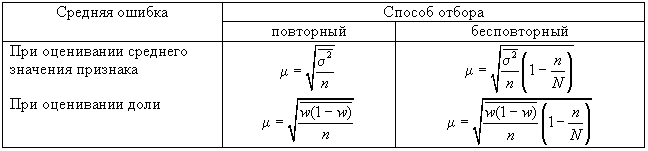
Здесь
![]()
средняя из групповых дисперсий типических
групп.
Пример 3. В
одном из московских вузов проведено
выборочное обследование студентов с
целью определения показателя средней
посещаемости вузовской библиотеки
одним студентом за семестр. Для этого
была использована 5%-ная бесповторная
типическая выборка, типические группы
которой соответствуют номеру курса.
При отборе, пропорциональном объему
типических групп, получены следующие
данные:
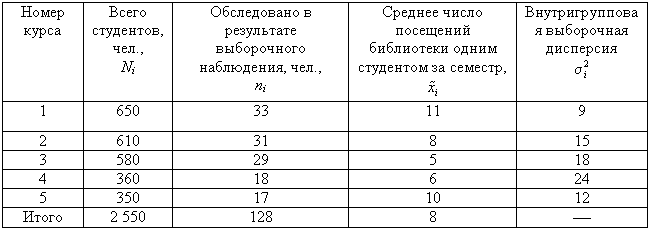
Число студентов,
которое необходимо обследовать на
каждом курсе, рассчитаем следующим
образом:
общий объем
выборочной совокупности:
![]()
количество
единиц, отобранных из каждой типической
группы:
![]()
аналогично для
других групп:
п2
31 (чел.);
п3
29 (чел.);
п4
18 (чел.);
п5
17 (чел.).
Проведем необходимые
расчеты.
1. Выборочная
средняя, исходя из значений средних
типических групп, составит:
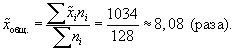
2. Средняя из
внутригрупповых дисперсий
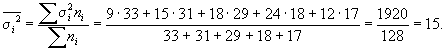
3. Средняя ошибка
выборки:
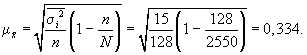
С вероятностью
0,954 находим предельную ошибку выборки:
![]()
4. Доверительные
границы для среднего значения признака
в генеральной совокупности:
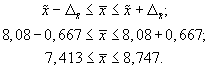
Таким образом, с
вероятностью 0,954 можно утверждать, что
один студент за семестр посещает
вузовскую библиотеку в среднем от семи
до девяти раз.
3.
Малая выборка. В
связи с небольшим объемом выборочной
совокупности
те формулы для определения ошибок
выборки,
которые использовались нами ранее при
«больших» выборках, становятся
неподходящими и требуют корректировки.
Среднюю ошибку
малой выборки
определяют по формуле
![]()
Предельная
ошибка малой выборки:
![]()
Распределение
значений выборочных средних всегда
имеет нормальный закон распределения
(или приближается к нему) при п
100, независимо от характера распределения
генеральной
совокупности.
Однако в случае малых выборок действует
иной закон распределения
распределение Стьюдента.
В этом случае коэффициент доверия
находится по таблице t-распределения
Стьюдента в зависимости от величины
доверительной вероятности Р
и объема выборки п.
В Приложении
1
приводится фрагмент таблицы t-распределения
Стьюдента, представленной в виде
зависимости доверительной вероятности
от объема выборки и коэффициента доверия
t.
Пример 4.
Предположим,
что выборочное обследование восьми
студентов академии показало, что на
подготовку к контрольной работе по
статистике они затратили следующее
количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4;
6,6.
Оценим выборочные
средние затраты времени и построим
доверительный интервал для среднего
значения признака в генеральной
совокупности, приняв доверительную
вероятность равной 0,95.
1. Среднее значение
признака в выборке равно
![]()
2. Значение среднего
квадратического отклонения составляет
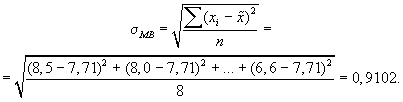
3. Средняя ошибка
выборки:
![]()
4. Значение
коэффициента доверия t
2,365 для п
8 и Р
0,95 (Приложение 1).
5. Предельная
ошибка выборки:
![]()
6. Доверительный
интервал для среднего значения признака
в генеральной совокупности:
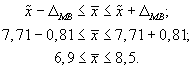
То есть с вероятностью
0,95 можно утверждать, что затраты времени
студента на подготовку к контрольной
работе находятся в пределах от 6,9 до 8,5
ч.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ( )
)
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки ( ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп

Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Содержание
- Экспресс-подготовка к онлайн-тестированию:
- Сдаешь тесты самостоятельно?
- Статистика Тесты с ответами Тема 1-2
- «Выборочное наблюдение»
- «Статистика населения и рынка труда»
- Статистическое наблюдение
- Тест № 3
- Тест № 4
- Статистическая отчетность — это
- Тест № 5
- Тема: Абсолютные и относительные величины
- Тест № 2
- Тест № 3
- Тест № 4
- Тест № 5
- Тест №1
- Формула «» является:
- а) средней арифметической простой;
- Тема: Ряды динамики
- Тест № 1
- Тема: Выборочное наблюдение
- Тема: Индексы
- К теме № 9
- Тест № 1
- К теме № 15
- Тест № 1
- Тест № 2
- Тема: Статистика рынка труда
- Тест № 1
- Тест № 2
Экспресс-подготовка к онлайн-тестированию:
для студентов дистанционного обучения, при устройстве на работу, прохождении аттестаций

Сдаешь тесты самостоятельно?
Закажи скайп-консультацию и узнай все секреты успешной сдачи экзаменов онлайн!

Статистика Тесты с ответами Тема 1-2
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 1 Предмет, метод и задачи статистики
Статистика – это…
вид научно-практической деятельности, направленной только на обработку информации
вид научно-практической деятельности, направленной только на получение информации, характеризующей количественные закономерности жизни общества
+вид научно-практической деятельности, направленной на получение, обработку, анализ и хранение информации, характеризующей количественные закономерности жизни общества во всём ее многообразии в неразрывной связи с её качественным содержанием
Статистика – это вид научно-практической деятельности, направленной на получение, обработку, анализ и хранение информации, характеризующей количественные закономерности жизни общества во всём ее многообразии в неразрывной связи с её…
Статистическая совокупность бывает:
первичной и вторичной
однородной и комбинированной
структурной и аналитической
+однородной и разнородной
Что является особенностью статистического исследования?
в нем изучаются только неварьирующие признаки
в нем изучаются как варьирующие, так и неварьирующие признаки
+в нем изучаются только варьирующие признаки
в нем изучаются не только варьирующие признаки
Друзья, более 600 собак Воронежского приюта Дора очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение. Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка . По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович)
Заполните пропуски:
Статистическая совокупность – это множество единиц изучаемого явления, объединенных качественной (1), определенной (2), (3) состояний отдельных единиц и наличием (4).
___________ состоит в изучении размеров и количественных соотношений массовых общественных явлений в конкретных условиях места и времени, а так же числовое выражение проявляющихся в них закономерностей.
Статистической называется закономерность.
выявленная на основе случайного наблюдения за объектами
+выявленная на основе массового наблюдения, то есть проявляющаяся лишь в большой массе явлений через преодоление свойственной её единичным элементам случайности
выявленная на основе единичного наблюдения и проявляющаяся лишь в большой массе явлений через преодоление несвойственной её элементам случайности
На какие группы делятся признаки по характеру отображения свойств единиц изучаемой совокупности?
имеющие непосредственное качественное выражение
не имеющие непосредственного стоимостного выражения
имеющие непосредственное стоимостное выражение
не имеющие непосредственного качественного выражения
+не имеющие непосредственного количественного выражения
+имеющие непосредственное количественное выражение
Понятие, которое отражает наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира — это.
Заполните пропуски:
Статистическое наблюдение – это (1) статистики, который заключается в сборе первичного статистического (2), в научно организованной регистрации всех существенных (3), относящихся к рассматриваемому (4).
Тема 2. Статистическое наблюдение. Источники статистической информации
Что представляет собой «наблюдение основного массива»
наблюдение за величинами «среднего» размера
наблюдение малозначительных величин
наблюдение за важнейшей единицей совокупности
наблюдение основной единицы совокупности
+наблюдение за совокупностью за исключением малозначительных величин
Что предполагает наблюдение основного массива?
включение в состав совокупности малозначимых единиц
исключение из состава совокупности малозначимых единиц и исследование исключенной части
включение в состав совокупности малозначимых единиц и исследование всей совокупности
исключение из состава совокупности значимых единиц и исследование оставшейся части
+исключение из состава совокупности малозначимых единиц и исследование основной ее части
Какую цель преследует «монографическое наблюдение»
изучение минимально-возможной единицы совокупности
+изучение важнейшей для исследователя единицы совокупности
изучение минимально допустимой единицы совокупности
изучение наибольшей единицы совокупности
изучение минимальной единицы совокупности
Каким образом проводится «выборочное наблюдение»
заданным отбором единиц совокупности в необходимом количестве при ошибке репрезентативности
+случайным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки
случайным отбором нескольких единиц совокупности
случайным отбором нескольких единиц совокупности в необходимом количестве
заданным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки
Как расшифровывается понятие «место статистического наблюдения»
адрес представителя статистического органа, проводящего сбор статистических данных
место обработки статистических данных
+место сбора статистических данных
адрес статистического органа
адрес местного органа власти, на территории которого проводится статистическое наблюдение
Как организуется «почтовый способ» проведения наблюдения
необходимые сведения тайно собираются непосредственно лицами-регистраторами
необходимые сведения запрашиваются и передаются через «почтовый ящик»
необходимые сведения по распоряжению руководящих органов собираются непосредственно лицами-регистраторами
необходимые сведения запрашиваются и передаются непосредственно из рук в руки
+необходимые сведения запрашиваются и передаются при помощи соответствующих органов связи
Что представляет собой понятие «объект наблюдения»
совокупность единиц наблюдения, имеющая наименьший удельный вес в генеральной совокупности
+определенная совокупность единиц наблюдения, выбранная согласно поставленной цели, для исследования
определенная генеральная совокупность
определенная совокупность единиц наблюдения
совокупность единиц наблюдения, имеющая наибольший удельный вес в совокупности
Как организуется «экспедиционный способ наблюдения»
лица-регистраторы собирают по почте заполненные регистрируемыми лицами формуляры наблюдений
лица-регистраторы на месте проведения наблюдения собирают заполненные регистрируемыми лицами формуляры наблюдений
лица-регистраторы собирают в статистических органах заполненные регистрируемыми лицами формуляры наблюдений
регистрируемые лица самостоятельно заполняют формуляр и отправляют его в статистические органы
+лица-регистраторы на месте проведения наблюдения сами получают необходимые сведения и заполняют формуляр наблюдений
Что такое «критический момент» при проведении статистического наблюдения?
определенное число статистических единиц наблюдения
+определенная дата, на которую регистрируются все сведения
календарные сроки проведения наблюдения
любое число статистических единиц наблюдения
срок статистического наблюдения
Кумулята – это __________ изображение статистического ряда накопленных данных полученной информации
Источник
«Выборочное наблюдение»
121. По результатам выборочного обследования жилищных условий населения доля людей, не обеспеченных жильем в соответствии с социальными нормами, составила 10%, а средняя ошибка выборки — 0,1%. С вероятностью 0,954 (коэффициент доверия t=2) доля людей, не обеспеченных жильем, в генеральной совокупности находится в пределах:
• 9,8–10,2%
122. Под выборочным наблюдением понимают .
• несплошное наблюдение части единиц совокупности, отобранных случайным способом
123. Преимущества выборочного наблюдения по сравнению со сплошным наблюдением:
• более низкие материальные затраты
• возможность провести исследования по более широкой программе
• снижение трудовых затрат за счет уменьшения объема обработки первичной информации
124. При проведении выборочного наблюдения определяют:
• численность выборки, при которой предельная ошибка не превысит допустимого уровня
125. Репрезентативность результатов выборочного наблюдения зависит от .
• вариации признака и объема выборки
126. Средняя площадь, приходящаяся на одного жителя, в выборке составила 19 кв.м., а средняя ошибка выборки – 0,23 кв.м. Коэффициент доверия t=2 (при вероятности 0,954). Средняя площадь (с точностью до 0,01 кв.м.) в расчете на одного жителя в генеральной совокупности находится в пределах __________________ кв.м.
• 18,54–19,46
127. Статистическое наблюдение, при котором обследуется научно отобранная часть совокупности, называется:
• выборочным наблюдением
128. Укажите метод отбора, при котором сохраняется вероятность попадания единицы генеральной совокупности в выборку:
• повторный
«Статистика населения и рынка труда»
129. В РФ в 2001 году: среднегодовая численность населения в возрасте 15-72 года равнялась 110,4 млн. чел., численность занятых в экономике — 64664 тыс. чел., численность безработных — 6303 тыс. чел. Уровень экономической активности населения = .
• 64,3%
130. Выберите правильное определение маятниковой миграции:
• периодическое перемещение населения из одного населенного пункта в другой и обратно, связанное с работой или учебой
131. Имеются следующие данные о численности населения населенного пункта за год (чел.): средняя годовая численность населения: 242350, число родившихся: 3380, доля женщин в возрасте 15-49 лет в общей численности населения города: 28%. Специальный коэффициент рождаемости = __________________ промилле (с точностью до 0,1 промилле).
• 49,8
132. Имеются следующие данные о численности населения населенного пункта за год (чел.): численность населения на начало года: 241400, на конец года: 243300, число родившихся: 3380, число умерших: 680, прибыло на постоянное жительство: 1800, убыло в другие населенные пункты: 600. Коэффициент общего прироста численности населения = __________________ промилле (с точностью до 1 промилле).
• 8
133. Имеются следующие данные о численности населения населенного пункта за год (чел.): численность населения на начало года: 241400, численность населения на конец года: 243300, прибыло на постоянное жительство: 1800, убыло в другие населенные пункты: 600. Коэффициент механического прироста населения = __________________ промилле (с точностью до 1 промилле).
• 5
134. Имеются следующие данные о численности населения населенного пункта за год (чел.): численность населения на начало года: 241400, численность населения на конец года: 243300, число родившихся: 3380. Общий коэффициент рождаемости = __________________ промилле (с точностью до 1 промилле).
• 14
135. Имеются следующие данные о численности населения населенного пункта за год (чел.): численность населения на начало года: 241400, численность населения на конец года: 243300, число умерших: 2680. Общий коэффициент смертности = __________________ промилле (с точностью до 1 промилле).
• 11
Источник
Статистическое наблюдение

Тема: Статистическое наблюдение
Объект статистического наблюдения — это
а) единица наблюдения;
б) статистическая совокупность;
в) единица статистической совокупности;
г) отчетная единица.
Правильный ответ: б
Субъект, от которого поступают данные в ходе статистического наблюдения, называется:
а) единица наблюдения;
б) единица статистической совокупности;
в) отчетная единица.
Правильный ответ: в
Тест № 3
Перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения, называется:
б) программа наблюдения;
в) инструментарий наблюдения.
Правильный ответ: б
Тест № 4
Статистическая отчетность — это
а) вид статистического наблюдения;
б) способ статистического наблюдения;
в) форма статистического наблюдения.
Правильный ответ: в
Тест № 5
Расхождение между расчетными значениями и действительным значением изучаемых величин называется:
а) ошибкой наблюдения;
б) ошибкой регистрации;
в) ошибкой репрезентативности.
Правильный ответ: а
Тема: Сводка и группировка статистических данных.
Какой вид группировок представляет распределение предприятий по организационно-правовым формам собственности:
1.Группировка промышленных предприятий по формам собственности является примером группировки:
в) типологической; (ответ)
2. К дискретным признакам группировок относится:
б) численность населения страны;
в) число членов семьи; (ответ)
г) прибыль банка.
3. К атрибутивным признакам группировок относится:
а) прибыль предприятия;
б) пол человека; (ответ)
в) разряд работы;
Основанием группировки может быть:
а) количественный признак;
б) качественный признак;
в) как количественный признак, так и качественный признак.
Правильный ответ: в
К атрибутивным группировочным признакам относятся:
б) возраст человека;
в) среднедушевой доход семьи.
г) правильного ответа нет
Правильный ответ: а
Операция по образованию новых групп на основе ранее построенной группировки называется:
а) вторичной группировкой;
б) комбинационной группировкой;
в) многомерной группировкой.
Правильный ответ: а
Подлежащее статистической таблицы это:
а) объект исследования;
б) система показателей, характеризующих объект исследования;
в) сводная числовая характеристика совокупности.
Правильный ответ: б
По характеру разработки сказуемого различают статистические таблицы:
Правильный ответ: а
Какой вид таблицы применяется для оформления группировки по двум признакам взятым в их сочетании:
Правильный ответ: в
Тема: Абсолютные и относительные величины
К какому виду по временному фактору относятся показатель «Объем производства товаров и услуг»?
Правильный ответ: б
Чему равна относительная величина расчетного задания по продаже продукции, если относительная величина выполнения расчетного задания равна 104, 1%, а прирост продажи продукции по сравнению с прошлым годом составил 7,5%:
4. Показатели обеспеченности населения учреждениями здравоохранения торговли – это относительная величина:
б) интенсивности; (ответ)
Тест № 2
Соотношение одного и того же абсолютного показателя, характеризующего разные объекты, называется относительной величиной:
Правильный ответ: д
Тест № 3
Правильный ответ: г
Тест № 4
Показатель «Соотношение собственных и заемных средств предприятия» называется относительной величиной:
Правильный ответ: в
Тест № 5
Коммерческая фирма рассчитывала в 2007 г. по сравнению с 2006г. увеличить оборот на 20,5%. Выполнение расчетного задания составило 102,4%. Чему будет равна относительная величина динамики оборота?
Правильный ответ: в
Тема: Ряды распределения
6. Имеется ряд распределения рабочих по тарифному разряду: 2(8 чел.чел.) 4(17 чел.) 5(9 чел.чел.). Вид данного ряда:
в) дискретный; (ответ)
7. Для ряда распределения рабочих по тарифному разряду: 2(8 чел.чел.) 4(17 чел.) 5(9 чел.чел.) определить моду:
8. Для ряда распределения рабочих по тарифному разряду: 2(8 чел.чел.) 4(17 чел.) 5(9 чел.чел.) определить медиану:
Тема: Средние величины
Для вычисления показателя средней убыточности за ряд лет используется формула:
*а) средней арифметической
б) средней гармонической
в) средней геометрической
Изменится ли средняя величина, если все веса увеличить в два раза:
а) увеличиться в 2 раза;
в) изменится в 4 раза.
г) уменьшится в 2 раза
Можно ли для одного соотношения вычислять среднюю различными формами:
в) можно, если наложит дополнительные условия;
г) можно для определенных совокупностей
Как изменяется средняя гармоническая величина, если все варианты уменьшить в 2 раза, а все веса увеличить в 2 раза:
б) увеличится в 2 раза;
*г) уменьшится в 2 раза
5. Средняя величина признака равна 20, а коэффициент вариации – 25%.
Дисперсия признака равна:
Изменится ли средняя величина, если все варианты уменьшить на 5 единиц:
*1. уменьшится на 5 единиц;
2. уменьшится на определенное значение, зависящее от веса вариант;
4. увеличится на 5 единиц.
Тест №1
Формула « » является:
» является:
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней гармонической простой;
г) средней гармонической взвешенной;
д) средней квадратической простой;
е) средней квадратической взвешенной.
Правильный ответ: г
Тема: Показатели вариации
Чему равен коэффициент вариации, если средняя величина признака равна 22 рубля, а дисперсия 36:
9. Средний квадрат индивидуальных значений признака равен 625, дисперсия – 400. Средняя равна:
Коэффициент детерминации представляет собой долю:
*а) межгрупповой дисперсии в общей
б) межгрупповой дисперсии в остаточной
в) дисперсии теоретических значений в общей дисперсии
Тема: Ряды динамики
Тест № 1
Ряд динамики характеризует:
а) изменение характеристики совокупности в пространстве;
б) изменение характеристики совокупности во времени;
в) структуру совокупности по какому-либо признаку.
Правильный ответ: б
Если сравниваются смежные уровни ряда динамики, показатели называются:
Правильный ответ: б
Может ли темп роста быть отрицательной величиной?
б) может, в случае снижения показателя.
Правильный ответ: а
13. Средний уровень интервального ряда динамики с равными временными промежутками исчисляется по формуле средней:
а) арифметической простой; (ответ)
б) арифметической взвешенной;
в) гармонической простой;
г) гармонической взвешенной.
14. . Средний уровень интервального ряда динамики с неравными временными промежутками исчисляется по формуле средней:
а) арифметической простой;
б) арифметической взвешенной; (ответ)
в) гармонической простой;
г) гармонической взвешенной.
Средний уровень интервального ряда динамики определяется как:
а) средняя арифметическая;
б) средняя гармоническая;
в) средняя хронологическая.
Правильный ответ: а
Средний темп роста определяется по формуле:
а) средней арифметической;
б) средней гармонической;
в) средней геометрической.
Правильный ответ: в
15. Для выявления основной тенденции развития явления используется:
а) аналитическое выравнивание; (ответ)
б) индексный метод;
в) метод плывущей средней;
г) корреляционный анализ.
Основная тенденция представляет собой изменение ряда динамики:
а) равномерно повторяющиеся через определенные промежутки внутри ряда;
б) определяющее какое-то общее направление развития.
Правильный ответ: б
Тема: Выборочное наблюдение
Под выборочным наблюдением понимают:
а) обследование наиболее крупных единиц изучаемой совокупности
б) сплошное наблюдение всех единиц совокупности
*в) несплошное наблюдение части единиц совокупности, отобранных случайным способом
г) несплошное наблюдение части единиц совокупности
Выборочный метод наблюдения основан на:
а) случайном отборе единиц совокупности;
б) обследовании самых существенных единиц совокупности;
в) обследовании отдельных единиц совокупности, обычно представителей каких-либо новых типов явлений;
г) изучении всех единиц совокупности.
Средняя ошибка выборки зависит от:
а) доверительной вероятности утверждения;
б) вариации значений признаков выборочной совокупности;
в) значения модального интервала
Для равных значений предельная ошибка выборки больше при:
а) повторном отборе;
б) бесповторном отборе.
При определении средней ошибки выборки для серийного отбора рассчитывается:
а) общая дисперсия;
б) межгрупповая дисперсия;
в) средняя из групповых дисперсий.
Тема: Индексы
К теме № 9
Тест № 1
Индекс цен Пааше определяется по формуле:
а)  ;
;
б)  ;
;
в)  .
.
Правильный ответ: б
Если индекс переменного состава равен 128%, а индекс постоянного состава 105%, то индекс структурных сдвигов равен:
Правильный ответ: в
10. Известно, что индекс постоянного состава равен 102,5%, а индекс структурных сдвигов – 100,6%. Индекс переменного состава равен:
11. Агрегатный индекс цен Паше строится:
а) с весами текущего периода; (ответ)
б) с весами базисного периода;
в) без использования весов;
г) нет правильного ответа.
12. Физический объем продукции снизился на 20%, а производственные затраты увеличились на 6%. Индекс себестоимости единицы продукции
Как изменился товарооборот в отчетном периоде по сравнению с базисным, если цены увеличились на 10%, а количество проданного товара снизилось на 20% :
Правильный ответ: а
Если себестоимость продукции в отчетном периоде по сравнению с базисным увеличилась на 10%, а количество произведенной продукции снизилось на 7 процентов, то индекс издержек на производство будет равен:
Правильный ответ: б
По какой из перечисленных формул рассчитывается индекс переменного состава:
а) 
б) 
*в) 
Чему будет равен индекс структурных сдвигов, если индекс переменного состава равен 97,8% ,а индекс фиксированного состава 109,5%:
Тема: Статистика населения
К теме № 15
Тест № 1
Что является объектом наблюдения при проведении переписи населения?
в) постоянное население;
г) все население страны;
д) опрашиваемые граждане страны.
Правильный ответ: г
Тест № 2
Коэффициент роста населения менее единицы:
а) численность населения растет;
б) численность населения сокращается;
в) численность населения остается на прежнем уровне.
Правильный ответ: б
21. Определите коэффициент миграции, если коэффициент общего прироста (убыли) – 2%, коэффициент естественной убыли – 4%.
а) 0; б) 2,0; в) 6,0; г) -2,0.
а) безработные; (ответ)
б) подростки до 16 лет;
в) служители культов;
г) студенты дневных отделений вузов.
«Общий коэффициент брачности» относиться к показателям, характеризующим:
а) естественное движение населения;
б) механическое движение населения.
Правильный ответ: а
Какой вид средней применяется для расчета среднегодовой численности населения (известна численность на начало и конец года)?
а) средней арифметической простой;
б) средней арифметической взвешенной;
в) средней хронологической;
г) средней гармонической;
д) средней геометрической.
Правильный ответ: а
23.Среднегодовая численность населения в РФ составила 145 200 тыс. чел., занято в экономике 65766 тыс. чел., численность безработных – 6153 тыс. чел. Определите коэффициент занятости населения, %:
а) 8,5; б) 1,2; в) 0,453; г) нет правильного ответа.
Какой вид средней применяется при определении среднемесячной численности населения за квартал, если известна численность на 1.01, 1.02, 1.03, 1.04?
а) средней арифметической;
б) средней хронологической;
в) средней гармонической;
г) средней геометрической.
Правильный ответ: б
Тема: Статистика рынка труда
Тест № 1
«Экономически активное население» — это:
б) население в трудоспособном возрасте;
г) занятые и безработные.
Правильный ответ: г
Тест № 2
Уровень экономически активного населения определяется как отношение численности экономически активного населения:
а) к средней численности населения;
б) к занятому населению.
Правильный ответ: а
Уровень безработицы определяется как отношение численности безработных:
а) к общей численности населения;
б) к численности экономически активного населения;
в) к численности занятых.
Правильный ответ: б
Выберите формулу расчета средней численности зарегистрированных безработных, если имеются данные об их числе на несколько равноотстоящих дат:
а)  ;
;
б)  ;
;
в)  .
.
Правильный ответ: б
Во сколько раз измениться производительность труда, если выпуск продукции увеличился в 4 раза, а численность работающих – в 2 раза?
Правильный ответ: б
Тема: Баланс активов и пассивов
и статистика национального богатства
Эффективность использования основных фондов характеризует показатель:
б) коэффициент обновления;
в) коэффициент ликвидности;
Укажите, какие показатели характеризуют оборачиваемость оборотных средств:
*а) длительность одного оборота;
в) коэффициент ликвидности;
Стоимость воспроизводства основных фондов характеризует:
*а) полная восстановительная стоимость;
б) остаточная восстановительная стоимость;
в) полная первоначальная стоимость;
г) остаточная первоначальная стоимость.
Укажите, какие из перечисленных элементов относятся к материальным основным фондам:
*а) машины и оборудование;
17. Какой из перечисленных видов экономических активов не относится к национальному богатству:
а) основные фонды;
б) человеческий капитал; (ответ)
г) непроизведенные материальные активы;
18. Что отражает оценка основных фондов по полной восстановительной стоимости:
а) фактическую стоимость основных фондов в момент их ввода в эксплуатацию;
б) стоимость воспроизводства основных фондов в данное время; (ответ)
г) стоимость на конец года.
Укажите, что входит в состав основных фондов:
б) компьютерное программное обеспечение.
в) незавершенное производство;
д) правильного ответа нет
Правильный ответ: б
Эффективность использования основных фондов характеризует показатель:
б) коэффициент обновления;
д) коэффициент годности.
Правильный ответ: г
Как измениться фондоотдача, если выпуск продукции увеличился на 7%, а стоимость основных производственных фондов вырастет на 10%?
Правильный ответ: б
Тема: Статистическое изучение рынка товаров и услуг.
Для изучения скорости развития рынка товаров и услуг используют:
2. степенные средние;
3. структурные средние;
4. показатели динамического ряда.*
Для изучения сезонных колебаний спроса и предложения используют:
1. индекс физического объема товарооборота;
2. индекс сезонности;*
3. показатели динамического ряда;
4. хронологические средние
Укажите показатели, характеризующие состояние рынка товаров и услуг:
4. правильного ответа нет
Тема: Статистика производительности труда
Во сколько раз измениться производительность труда, если выпуск продукции увеличился в 4 раза, а численность работающих – в 2 раза?
К ТЕМЕ: Статистическое изучение предпринимательства
Показатель продукции, используемый при расчете коэффициента оборачиваемости оборотных средств предприятия:
б) объем продукции (работ, услуг);
г) валовой выпуск.
При расчете индекса физического объема промышленной продукции используется формула:
а)  ;
;
б)  ;
;
в)  .
.
а) прибыль, рентабельность производства;
б) фондовооруженность труда;
в) коэффициент оборачиваемости, средняя продолжительность одного оборота;
г) фондоотдача, фондоемкость продукции.
К ТЕМЕ: Статистическое изучение доходов, потребления и социальной защиты населения
Относительное изменение реального располагаемого дохода ( IРРД) определяется по формуле(ам):
где IРД — индекс номинальных располагаемых доходов;
IР— сводный индекс потребительских цен.
где IРД — индекс номинальных располагаемых доходов;
IД — индекс-дефлятор ВВП.
где IРД — индекс номинальных располагаемых доходов;
Id— индекс-дефлятор ВВП.
Наибольший удельный вес в структуре доходов населения в РФ имеет:
в) доходы от собственности.
Фактическое конечное потребление имеют следующие сектора экономики:
а) домашние хозяйства, органы государственного управления, некоммерческие организации, обслуживающие домашние хозяйства;
б) домашние хозяйства, органы государственного управления;
в) все сектора национальной экономики.
Индекс развития человеческого потенциала относится к показателям:
а) концентрации доходов населения;
б) обобщающим показателям уровня жизни населения;
в) расходов населения.
Тема: Статистическое изучение инвестиций
Доходность государственных облигаций составляет 20%, премия за риск оцениваемого пакета ценных бумаг – 10%, коэффициент β=0,5. Стоит ли рассматривать пакет акций, доходность которого составляет 30%?
б) отчетность таможенных органов;
в) отчетность участников внешнеэкономической деятельности.
В РФ в настоящее время используется:
а) общая система учета торговли;
б) специальная система учета торговли.
Относительное изменение средних контрактных цен под влиянием изменений в географической структуре экспорта и импорта товаров определяется по формуле(ам):
а)  ;
;
б)  ;
;
в)  .
.
В стоимость импорта товара по данным таможенной статистики включаются:
а) затраты, связанные с производством и доставкой товара до границы экспортирующей страны;
б) затраты, связанные с производством и доставкой товара до границы страны-импортера без оплаты таможенных платежей;
в) затраты, связанные с производством и доставкой товара до границы страны-импортера, включая оплату таможенных платежей.
Стоимостная оценка экспорта и импорта товаров производится по:
а) таможенной стоимости;
б) статистической стоимости;
в) фактурной стоимости.
Тема: Основы высших финансово-экономических вычислений и статистический анализ информации
Укажите формулу для определения наращенной суммы на основе простых процентов:
1.  *
*
2. 
3. 
4.  ,
,
где S – наращенная сумма,
P – сумма представленная в кредит;
t — число дней функционирования сделки;
K – временная база;
Определите период времени, по окончании которого процентный доход сравняется с величиной вклада, если ставка процентов сложная и равна 7%:
3) всегда будет меньше;
5) все ответы неверны.
Укажите формулу для определения наращенной суммы аннуитета:
1)  *
*
2) 
3) 
4)  .
.
Величина текущей доходности облигации рассчитывается:
а) как отношение дохода, полученного за определенный период, к величине рыночной цены облигации
б) как отношение рыночной цены в конкретный момент на определенном рынке к номинальной цене облигации;
в) произведение величин номинальной стоимости облигации и купонной ставки;
г) назначается в момент эмиссии и фиксируется.
Источник
Тест № 16
Под выборочным наблюдением понимают:
а) обследование наиболее крупных единиц изучаемой совокупности
б) сплошное наблюдение всех единиц совокупности
(ответ)в) несплошное наблюдение части единиц совокупности, отобранных случайным способом
г) несплошное наблюдение части единиц совокупности
Тест №1
Выборочный метод наблюдения основан на:
а) случайном отборе единиц совокупности;
б) обследовании самых существенных единиц совокупности;
в) обследовании отдельных единиц совокупности, обычно представителей каких-либо новых типов явлений;
г) изучении всех единиц совокупности.
Ответ: а).
Тест №2
Средняя ошибка выборки зависит от:
а) доверительной вероятности утверждения;
б) вариации значений признаков выборочной совокупности;
в) значения модального интервала
Ответ: б)
Тест №3
Для равных значений предельная ошибка выборки больше при:
а) повторном отборе;
б) бесповторном отборе.
Ответ: а).
Тест №4
При определении средней ошибки выборки для серийного отбора рассчитывается:
а) общая дисперсия;
б) межгрупповая дисперсия;
в) средняя из групповых дисперсий.
Ответ: б).
