Для расчета полной прогнозной величины ошибок необходимо знать

Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе  программных продуктов для прогнозирования продаж и управления запасами.

В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.

Статистические методы

Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.

В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно  к показателям средних ошибок прогнозирования.

К ним относятся:

MAPE – средняя абсолютная ошибка в процентах

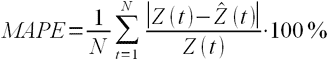
где Z(t) – фактическое значение временного ряда, а   – прогнозное.

Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE. 

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

                                                                                                  .

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

ME – средняя ошибка

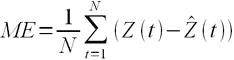
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).

MSE – среднеквадратичная ошибка

.

RMSE – квадратный корень из среднеквадратичной ошибки

.

.

SD – стандартное отклонение

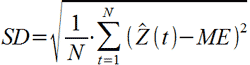
где ME – есть средняя ошибка, определенная по формуле выше.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>

Связь точности и ошибки прогнозирования

В начале этого обсуждения разберемся с определениями.

Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.  Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.

Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев. 

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)

Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:

где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:

Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:

В таком случае для тех же примеров ошибка рассчитается иначе:

Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.   

Визуальный метод – графический

Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее  сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.  

По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.

Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.  

Использование формул ошибки прогнозирования на практике

Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами  — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз  в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.

Пример расчета такой оценки Вы сможете увидеть в файле Excel.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.  

Для чего используется ошибка прогнозирования

В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.

Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.

В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.

Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».

Источник: сайт http://uppravuk.net/  

Open Source Content Management

Nav view search

Навигация

Искать

Main Menu

Измерение ошибок и выбор метода прогнозирования

В ходе процесса прогнозирования неизбежно возникают ошибки прогноза. Под ошибкой прогноза понимают расхождение между прогнозом и действительностью. Хотя в прогнозировании считается, что, до тех пор, пока значение прогноза находится в доверительных границах, эти расхождения не являются ошибкой.

Ошибки прогноза могут возникать по разным причинам и иметь различные источники. Их можно разделить на систематические, возникающие из-за погрешности измерения, и случайные. К источникам систематических ошибок относятся недостаточное количество прямых переменных, использование некорректной зависимости между переменными, применение неверной трендовой линии, ошибочный сдвиг сезонного спроса и наличие необнаруженного тренда во временных рядах. К случайным ошибкам относятся те ошибки, которые нельзя объяснить используемой моделью прогноза.

Измерение ошибок прогноза производится с помощью таких показателей, как среднее абсолютное отклонение, среднеквадратическое отклонение, средняя абсолютная относительная ошибка и средняя относительная ошибка.

Среднее абсолютное отклонение (МАD) представляет собой среднее значение ошибки в прогнозе, которое измеряет разброс прогнозируемых значений от ожидаемых. МАD вычисляют как разность между действительным и прогнозируемым спросом без учета знака, по следующей формуле:

(3.16)

где t – номер периода;

А – текущий спрос данного периода;

F – прогнозируемый спрос данного периода;

n – общее количество периодов.

Определение среднеквадратического отклонения (MSE) также основано на вычислении отклонений от средней арифметической, однако при ее вычислении используют не абсолютные величины, а квадраты величин отклонений. Она определяется по формуле:

(3.17)

Показатель MSE позволяет выявить отдельные большие отклонения от фактических данных. На основе MSE можно отобрать такие способы прогнозирования, которые стабильно дают приемлемые средние ошибки, и отсеять такие способы, которые характеризуются, как правило, малыми ошибками, но допускающие иногда очень большую погрешность.

Средняя абсолютная относительная ошибка (МАРЕ) применяется в том случае, если для определения показателя общей ошибки удобнее использовать не абсолютные, а относительные величины.

(3.18)

В случае, когда требуется оценить, насколько смещенными (т.е. завышенными или заниженными) являются результаты прогнозирования, то можно использовать показатель средней относительной ошибки МРЕ.

(3.19)

Если показатель МРЕ близок к нулю, то смещения нет. Если он отрицательный, то имеет место завышение прогнозных оценок; если положительный, то оценки будут заниженными.

При сравнении двух и более методов прогнозирования, чем меньше рассмотренные выше показатели, тем более точный прогноз.

Выбор метода прогнозирования зависит от временных и затратных факторов. При нехватке времени и средств целесообразно использовать простые и дешевые методы прогнозирования, такие как модели на основе скользящих средних или экспоненциальное сглаживание. Для проверки надежности какого-либо метода прогнозирования можно использовать разные методы измерения ошибок прогноза.

Источник

Методы оценки качества прогноза

Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R 2 ) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )

В статьях о методах прогнозирования при оценке полученной модели я постоянно использовал такие аббревиатуры или обозначения.

• R 2
• MSE
• MAPE
• MAD
• Bias

Попробую объяснить, что я имел в виду.

Остатки

Суровые MSE и R 2

Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле

где n-количество наблюдений.

Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.

Вторая абстрактная величина это R 2 — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле:

где Var(Y) — дисперсия исходных данных.

Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу.

MAPE и MAD для сравнения моделей

Статистические методы оценки моделей вроде MSE и R 2 , к сожалению, трудно интерпретировать, поэтому светлые головы придумали облегченные, но удобные для сравнения коэффициенты.

Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.

MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE).

где Y — значение исходного ряда.

Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.

Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.

Можете попробовать это сами в Excel и Numbers

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?

Источник

Оценка точности и надежности прогнозов

Важным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов.

Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными ( 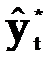) и фактическими (у_t) значениями исследуемого показателя. Данный подход возможен только в двух случаях:

а) период упреждения известен, уже закончился, и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя;

б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени, за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования.

В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза.

Полученные таким образом ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду.

В случае если, ретроспективное прогнозирование осуществляется по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков.

Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:

Аналитические показатели точности прогнозапозволяют количественно определить величину ошибки прогноза. К ним относятся:

Абсолютная ошибка прогноза (D * ) определяется как разность между эмпирическими и прогнозными значениями признака и вычисляется по формуле:

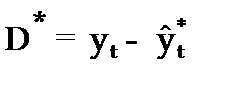, (3.54)

у_t–фактическое значение признака;

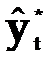–прогнозное значение признака.

Относительная ошибка прогноза (d * _отн) может быть определена как отношение абсолютной ошибки прогноза (D * ):

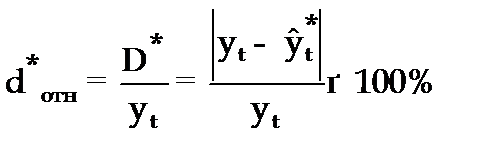(3.55)

— к прогнозному значению признака ( )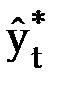

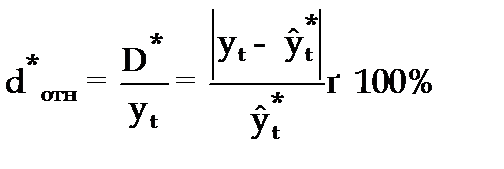(3.56)

Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели.

Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (К_к), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле:

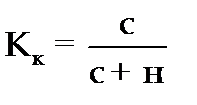. (3.57)

Значение К_к = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяется в пределах от 0 до 1.

Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков.

Средним показателем точности прогнозаявляется средняя абсолютная ошибка прогноза ( 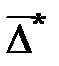), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:

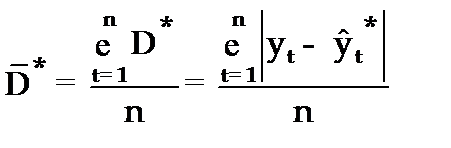, (3.58)

n–длина временного ряда.

Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.

Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле:

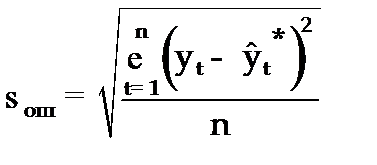. (3.59)

Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение:

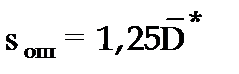. (3.60)

Недостатками средней абсолютной и средней квадратической ошибок прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений.

Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида:

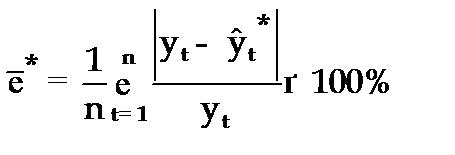. (3.61)

Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам. Интерпретация оценки точности прогноза на основе данного показателя представлена в следующей таблице:

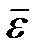,%	Интерпретация точности
50	Высокая Хорошая Удовлетворительная Не удовлетворительная

В качествесравнительного показателя точности прогнозаиспользуетсякоэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:

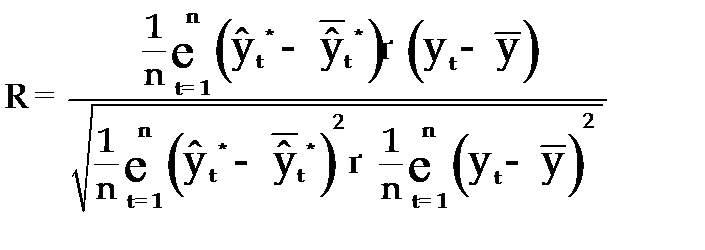, (3.62)

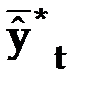– средний уровень ряда динамики прогнозных оценок.

Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.

Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях:

1. Коэффициент несоответствия (КН₁), определяемый как отношение средней квадратической ошибки к квадрату фактических значений признака:

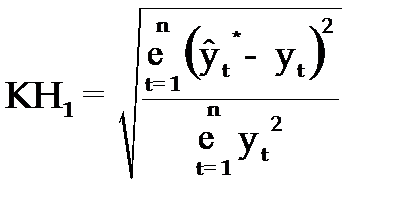. (3.63)

КН = 0, если 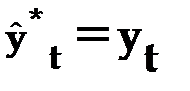, то есть полное совпадение фактических и прогнозных значений признака.

КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов.

КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет.

2.Коэффициент несоответствия (КН₂), определяется как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период:

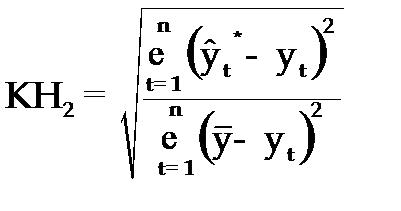, (3.64)

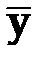–средний уровень исходного ряда динамики.

3.Коэффициент несоответствия (КН₃), определяемый как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда:

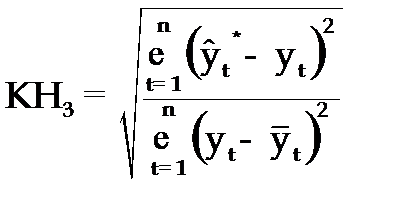, (3.65)

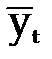–теоретические уровни временного ряда, полученные по модели тренда.

Контрольные вопросы к разделу III

1. Охарактеризуйте статистическое прогнозирование как составную часть общей теории прогностики.

2. Сформулируйте задачи статистического прогнозирования.

3. Дайте понятие объекта прогнозирования.

4. Перечислите основные понятия и термины, употребляемые в экономической прогностике.

5. Охарактеризуйте модели по сложности, масштабности и степени информационного обеспечения.

6. Раскройте содержание основных показателей точности прогнозов.

7. Раскройте сущность точечного и интервального прогнозов.

8. Как осуществляется предварительный анализ рядов динамики?

9. Раскройте содержание понятия объективизации прогнозов.

10. Перечислите простейшие методы прогнозирования динамики. Раскройте их сущность.

11. Охарактеризуйте метод прогнозирования на основе экстраполяции трендов.

12. Охарактеризуйте методы прогнозирования на основе кривых роста.

13. Охарактеризуйте метод простого экспоненциального сглаживания.

14. Охарактеризуйте метод гармонических весов.

15. Как достигается точность и надежность прогнозов на основе рядов динамики?

Источник

Аудиторская
выборка— это применение аудиторских
процедур менее чем ко всем элементам
одной статьи отчетности или группы
одно­типных операций. Она дает
возможность аудитору получить и оценить
аудиторские доказательства в отношении
некоторых характеристик элементов,
отобранных для того, чтобы сформировать
или помочь сформировать выводы, касающиеся
генеральной совокупности, из которой
произведена выборка.

В отношении
изучаемой совокупности в аудите различают
понятиягенеральной совокупности,
элементов выборки и стратифи­кации.

Генеральная
совокупность представляет
собой полный набор элементов, из
которых аудитор отбирает совокупность
и в отношении которой он хочет сделать
выводы. Она должна быть надлежащей с
точки зрения цели про­цедуры
выборки, а также полной.

Элементы выборки
— индивидуальные элементы, отражаемые
в учете и составляющие генеральную
совокупность. Это могут быть натуральные
объекты (напри­мер,
однотипные первичные учетные документы)
или показатели в денежном выра­жении.

Аудитор
может подразделить генеральную
совокупность на стра­ты,
т.е. подмножества. В таком случае каждая
страта проверяется отдельно. Процесс
деления генеральной совокупности на
страты, каж­дая
из которых представляет собой группу
элементов выборки со сход­ными
характеристиками, называетсястратификацией. При стратифи­кации
аудитору необходимо обеспечить, чтобы
каждый элемент выбор­ки
мог быть включен только в одну страту.

Ошибки, различаемые в аудиторской выборке

Риск выборки
возникает, когда вывод аудитора,
сделанныйна основе
отобранной совокупности, отличается
от вывода, который мог быть сделан, если
к генеральной совокупности в целом были
бы приме­нены идентичных процедур
аудита.

Математическим
дополнением указанных рисков являются
так называемые уровни
доверия,
например:

высокому
риску соответствует низкий уровень
доверия;

среднему
риску соответствует средний уровень
доверия;

низкому
риску соответствует высокий уровень
доверия.

Риск, не связанный
с использованием аудиторской выборки,
является следстви­ем
факторов, которые приводят аудитора к
ошибочному выводу по
любым причинам, кроме тех, которые
связаны с объемом выборки (т.е.
числом отбираемых для проверки элементов).

Различают
следующие виды отбора элементов:

1.
представительная (репрезентативная) —
элементы ее генераль­ной совокупности
имеют равную вероятность быть отобранными;

2.
непредставительная (нерепрезентативная)
— элементы
ее гене­ральной
совокупности не имеют равную вероятность
быть отобран­ными. Аудитор полагается
на свое профессиональное суждение при
отборе элементов.

Различают следу­ющие
методы отбора элементов (аудитор
может произвести):

1. Отбор всех
   элементов (сплошная проверка)— не
   применяют при проведении тестов средств
   внутреннего контроля, его используют
   в отношении аудиторских про­цедур
   проверок по существу.

2. Отбор специфических
   (определенных) элементов— предполагает
   отбор специфических элементов.

Раз­личают
специфические элементы наибольшей
стоимости и ключевые элементы.

1. Отбор отдельных
   элементов (формирование аудиторской
   выборки)
   — представляет собой отбор элементов
   для построе­ния
   представительной выборки.

Прежде
чем отобрать элементы, необ­ходимо
определить объем выборки.

Выбор
метода или сочетания методов отбора
элементов зависит от
обстоятельств проверки, в частности
аудиторского риска и эффек­тивности
аудита.

Факторы,
влияющие на объем выборки:

Выборка
является основой тестирования средств
внутреннего кон­троля
и процедур проверки по существу.

Факторы, влияющие
на объем отобранной совокупности

для
тестирования средств внутреннего
контроля:

Число элементов
выборки, которая состоит из элементов,осно­ванных
на сальдо счетов,
определяют по следующей формуле:

ЭВ = ( (ОС – ЭН –
ЭК) * КП) / 0,75УС

где
ОС — общий объем проверяемой
совокупности в стоимостном (денеж­ном)
выражении;

ЭН
— суммарное стоимостное (денежное)
выражение элементов наи­большей
стоимости (превышающих планируемый
уровень существенности);

ЭК
— суммарное стоимостное (денежное)
выражение ключевых элементов
(существенны качественно и количественно);

КП — коэффициент
проверки;

УС — уровень
существенности.

Значения коэффициента
проверки, используемого при определе­нии
элементов выборки в зависимости от
состояния систем бухгал­терского
учета и внутреннего контроля аудируемого
лица.Значение КП:
0,7 (когда не выявлены ошибки по счетам
БУ, а оценка СВК отвечает необходимым
требованиям); 2 (обнаружены ошибки по
счетам БУ, а СВК отвечает необходимым
требованиям); 3 (выявлены потенциальные
ошибки по счетам БУ и нет доверия к СВК).

Факторы, влияющие
на объем отобранной совокупности

для
проверки по существу:

При
определении элементов
выборки для отбора по номеру докумен­та
используется следующая формула (при
условии, что наибольшие и
ключевые значения в изучаемой совокупности
отсутствуют):

ЭВ = (ГС * КП) / УС

где ГС — общее
число документов генеральной совокупности.

В этом случае
аудируемое лицо должно обеспечить
выполнение требования обязательного
присвоения номера всем первичным учетным
документам.

Выборка может
быть отобрана следующими методами:

1. Бессистемный
отбор– проводится без применения
какой-либо систематизации, его используют
в нерепрезентативной выборке, где
произвольно отбираются и оцениваются
какие-либо особо важные позиции, как
правило, на основаниипрофессионального
суждения аудитора, его опыта и интуиции.

2. Случайный метод
—используетсястатистическаявыборка, базирующаяся на теории
вероятностей, при использовании которой
должны соблюдаться репрезентативность
и принцип случайности выборки. При его
применении достаточно высока уверенность,
что все элементы множества отобраны с
одинаковой вероятностью.

Построение выборки
случайным отбором проводится с
использованием таблицы или генератора
случайных чисел. Номер документа
элементов, попавших в выборку случайным
отбором, определяют по формуле:

НД =
(ЗК — ЗН) * СЧ + ЗН

где
ЗК — значение конечное, т.е. номер
последнего документа генеральное
совокупности;

ЗН
— значение начальное, т.е. номер первого
документа генеральной совокупности;

СЧ
— случайное число.

Числа берут из
таблицы случайных чисел. Первое число
выбира­ют случайно, а следующие числа
— по порядку, т.е. по столбцу или строке.

2) Систематический
метод отбора состоит в выборе элементов
из генеральной совокупности через
определенный интервал между двумя
отборами.

Интервал определяют
по следующей формуле:

ИНТ
= (ЗК – ЗН) / ЭВ или ИНТ = ЗК / (ЭВ – 1)

где
ЭВ — число элементов выборки без учета
элементов наибольшей сто­имости,
т.е. ключевых элементов.

Для
построения статистической выборки с
использованием интервала стартовая
точка, т.е. первый номер документа,
попавшего в выборку,
определяется случайным отбором по
формуле:

СТ = ИНТ * СЧ + ЗН

Номера других
документов, попавших в выборку, вычисляют
по следующей формуле:

НД = СТ + ИНТ * (а-1)

где
а
— порядковый
номер элемента выборки

Для любой
выборки аудитор обязан:

— анализировать
каждую ошибку, попавшую в выборку;

— экстраполировать
полученные при выборке результаты на
всю проверяемую совокупность;

— оценивать риск
выборки.

Полная
прогнозная величина ошибки определяется
по формуле:

ОШп = Ошв * ( (ОС –
ЭН – ЭК) / СЭВ) + ОШн + ОШк

где
ОШ_В
— фактическая величина ошибок, выявленная
при выборке;

ОС —
общий объем проверяемой совокупности;

ЭН — сумма стоимости
элементов наибольшей стоимости;

ЭК —
сумма стоимости ключевых элементов
(т.е. имеющих большую вероятность
наличия искажений);

СЭВ
— суммарная стоимость элементов выборки;

ОШн
— фактическая величина ошибок при
проверке элементов наиболь­шей
стоимости;

ОШк
— фактическая величина ошибок при
проверке ключевых элементов.

В зависимости от
соотношения величины полной прогнозной
ошибки и уровня существенности возможны
различные действия ауди­тора

Зависимость
действий аудитора от величины полной
прогнозной ошибки*

Анализ ошибок,
выявленных при проверке выборки,
позволяет определить тип ошибки и
причины их возникновения, что будет
способствовать их устранению в
последующем.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #