Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Общий вид аддитивной модели следующий:
![]() . (2.14)
. (2.14)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (![]() ), сезонной (
), сезонной (![]() ) и случайной (
) и случайной (![]() ) компонент.
) компонент.
Общий вид мультипликативной модели выглядит так:
![]() . (2.15)
. (2.15)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (![]() ), сезонной (
), сезонной (![]() ) и случайной (
) и случайной (![]() ) компонент.
) компонент.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений ![]() ,
, ![]() и
и ![]() для каждого уровня ряда.
для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты ![]() .
.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (![]() ) в аддитивной или (
) в аддитивной или (![]() ) в мультипликативной модели.
) в мультипликативной модели.
4) Аналитическое выравнивание уровней (![]() ) или (
) или (![]() ) и расчет значений
) и расчет значений ![]() с использованием полученного уравнения тренда.
с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений (![]() ) или (
) или (![]() ).
).
6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок ![]() для анализа взаимосвязи исходного ряда и других временных рядов.
для анализа взаимосвязи исходного ряда и других временных рядов.
Методику построения аддитивной модели рассмотрим в данном разделе методического пособия.
Пример. Построение аддитивной модели временного ряда. Обратимся к данным об объеме правонарушений на таможне за четыре года, представленным в табл. 2.1.
Как видно из табл. 2.1, данный временной ряд содержит сезонные колебания периодичностью 4, т. к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 2.2).
Таблица 2.1
|
Год |
Квартал |
|
Количество возбужденных дел, |
|
1999 |
I |
1 |
375 |
|
II |
2 |
371 |
|
|
III |
3 |
869 |
|
|
IV |
4 |
1015 |
|
|
2000 |
I |
5 |
357 |
|
II |
6 |
471 |
|
|
III |
7 |
992 |
|
|
IV |
8 |
1020 |
|
|
2001 |
I |
9 |
390 |
|
II |
10 |
355 |
|
|
III |
11 |
992 |
|
|
IV |
12 |
905 |
|
|
2002 |
I |
13 |
461 |
|
II |
14 |
454 |
|
|
III |
15 |
920 |
|
|
IV |
16 |
927 |
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.2). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.2).
Таблица 2.2
|
№ квартала,
|
Количество правонарушений,
|
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
375 |
– |
– |
– |
– |
|
2 |
371 |
2630 |
657,5 |
– |
– |
|
3 |
869 |
2612 |
653 |
655,25 |
213,75 |
|
4 |
1015 |
2712 |
678 |
665,5 |
349,5 |
|
5 |
357 |
2835 |
708,75 |
693,75 |
-336,75 |
|
6 |
471 |
2840 |
710 |
709,375 |
-238,375 |
|
7 |
992 |
2873 |
718,25 |
714,125 |
277,875 |
|
8 |
1020 |
2757 |
689,25 |
703,75 |
316,25 |
|
9 |
390 |
2757 |
689,25 |
689,25 |
-299,25 |
|
10 |
355 |
2642 |
660,5 |
674,875 |
-319,875 |
|
11 |
992 |
2713 |
678,25 |
669,375 |
322,625 |
|
12 |
905 |
2812 |
703 |
690,625 |
214,375 |
|
13 |
461 |
2740 |
685 |
694 |
-233 |
|
14 |
454 |
2762 |
690,5 |
687,75 |
-233,75 |
|
15 |
920 |
– |
– |
– |
– |
|
16 |
927 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 2.2). Используем эти оценки для расчета значений сезонной компоненты ![]() (табл. 2.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты
(табл. 2.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты ![]() . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 2.3

Для данной модели имеем:
![]() .
.
Корректирующий коэффициент: ![]() .
.
Рассчитываем скорректированные значения сезонной компоненты (![]() ) и заносим полученные данные в таблицу 6.6.
) и заносим полученные данные в таблицу 6.6.
Проверим равенство нулю суммы значений сезонной компоненты:
![]() .
.
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины ![]() (гр. 4 табл. 2.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 2.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту ![]() данной модели. Для этого проведем аналитическое выравнивание ряда (
данной модели. Для этого проведем аналитическое выравнивание ряда (![]() ) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
![]() .
.
Подставляя в это уравнение значения ![]() , найдем уровни
, найдем уровни ![]() для каждого момента времени (гр. 5 табл. 2.4).
для каждого момента времени (гр. 5 табл. 2.4).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням ![]() значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 2.4).
значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 2.4).
Таблица 2.4
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
375 |
-292,448 |
667,448 |
672,700 |
380,252 |
-5,252 |
27,584 |
|
2 |
371 |
-266,781 |
637,781 |
673,624 |
406,843 |
-35,843 |
1284,721 |
|
3 |
869 |
268,636 |
600,364 |
674,547 |
943,183 |
-74,183 |
5503,117 |
|
4 |
1015 |
290,593 |
724,407 |
675,470 |
966,063 |
48,937 |
2394,830 |
|
5 |
357 |
-292,448 |
649,448 |
676,394 |
383,946 |
-26,946 |
726,087 |
|
6 |
471 |
-266,781 |
737,781 |
677,317 |
410,536 |
60,464 |
3655,895 |
|
7 |
992 |
268,636 |
723,364 |
678,240 |
946,876 |
45,124 |
2036,175 |
|
8 |
1020 |
290,593 |
729,407 |
679,163 |
969,756 |
50,244 |
2524,460 |
|
9 |
390 |
-292,448 |
682,448 |
680,087 |
387,639 |
2,361 |
5,574 |
|
10 |
355 |
-266,781 |
621,781 |
681,010 |
414,229 |
-59,229 |
3508,074 |
|
11 |
992 |
268,636 |
723,364 |
681,933 |
950,569 |
41,431 |
1716,528 |
|
12 |
905 |
290,593 |
614,407 |
682,857 |
973,450 |
-68,450 |
4685,403 |
|
13 |
461 |
-292,448 |
753,448 |
683,780 |
391,332 |
69,668 |
4853,630 |
|
14 |
454 |
-266,781 |
720,781 |
684,703 |
417,922 |
36,078 |
1301,622 |
|
15 |
920 |
268,636 |
651,364 |
685,627 |
954,263 |
-34,263 |
1173,953 |
|
16 |
927 |
290,593 |
636,407 |
686,550 |
977,143 |
-50,143 |
2514,320 |
На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Рис. 28. График фактических уровней временного ряда
И теоретических, полученных по аддитивной модели.
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
 .
.
Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.
Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года. Прогнозное значение ![]() уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
![]() .
.
Получим
![]() ;
;
![]() .
.
Значения сезонных компонент за соответствующие кварталы равны: ![]() и
и ![]() . Таким образом,
. Таким образом,
![]() ;
;
![]() .
.
Т. е. в первые два квартала 2003 г. следовало ожидать порядка 395 и 422 правонарушений соответственно. Построение мультипликативной модели проводится по той же схеме, что и построение аддитивной модели.
Вопросы для самопроверки
1. В каких случаях для прогнозирования применяют методы прямой экстраполяции?
2. Когда для прогнозирования можно использовать модель тренда?
3. Какие модели трендов обычно используются при прогнозировании в экономике?
4. Перечислите этапы прогнозирования экономических показателей с применением моделей тренда.
5. Что понимают под адекватностью и точностью модели прогнозировании? Как можно проверить адекватность и точность модели прогнозирования?
6. Поясните, почему при прогнозировании наряду с точечным прогнозом рассчитывают и интервальный прогноз?
7. Что такое коэффициент автокорреляции? Как он рассчитывается и что он показывает?
8. Для чего используется критерий Дарбина-Уотсона в моделях временных рядов?
9. Что такое коррелограмма?
10. Поясните технологию расчета точечного интервального прогнозов при использовании моделей тренда.
| < Предыдущая | Следующая > |
|---|
Автокорреляционная функция и аддитивная модель временного ряда
Краткая теория
При
наличии во временном ряде тенденции и циклических колебаний значения каждого
последующего уровня ряда зависят от предыдущих.
Корреляционную зависимость между последовательными уровнями временного ряда
называют автокорреляцией уровней ряда. Количественно ее можно измерить с
помощью линейного коэффициента корреляции между уровнями исходного временного ряда
и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Число
периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент
автокорреляции, уменьшается. Некоторые авторы считают целесообразным для
обеспечения статистической достоверности коэффициентов автокорреляции
использовать правило – максимальный лаг должен быть не больше
.
Отметим
два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии
с линейным коэффициентом корреляции и таким образом характеризует тесноту
только линейной связи текущего и предыдущего уровней ряда. Поэтому по
коэффициенту автокорреляции можно судить о наличии линейной (или близкой к
линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную
тенденцию (например, параболу второго порядка или экспоненту), коэффициент
автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых,
по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или
убывающей тенденции в уровнях ряда. Большинство временных рядов экономических
данных содержит положительную автокорреляцию уровней, однако при этом могут
иметь убывающую тенденцию.
Последовательность
коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют
автокорреляционной функцией временного рада. График зависимости ее значений от
величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ
автокорреляционной функции и коррелограммы позволяет
определить лаг, при котором автокорреляция наиболее высокая, а
следовательно, и лаг, при котором связь между текущим и предыдущими уровнями
ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если
наиболее высоким оказался коэффициент автокорреляции первого порядка,
исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка
, ряд содержит
циклические колебания с периодичностью в
моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно
сделать одно из двух предположений относительно структуры этого ряда: либо ряд
не содержит тенденции и циклических колебаний, либо ряд содержит сильную
нелинейную тенденцию, для выявления которой нужно провести дополнительный
анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию
целесообразно использовать для выявления во временном ряде наличия или
отсутствия трендовой компоненты (
)
и
циклической (сезонной) компоненты (
).
Существует несколько подходов к
анализу структуры временных рядов, содержащих сезонные или циклические
колебания. Простейший подход — расчет значений сезонной компоненты методом
скользящей средней и построение аддитивной или мультипликативной модели
временного ряда. Общий вид аддитивной модели следующий:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
сумма трендовой
,
сезонной
и случайной
компонент. Общий вид
мультипликативный модели выглядит так:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
произведение трендовой
,
сезонной
и случайной
компонент. Выбор одной из двух моделей
осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда
колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в
которой значения сезонной компоненты предполагаются постоянными для различных
циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят
мультипликативную модель временного ряда, которая ставит уровни ряда в
зависимость от значений сезонной компоненты.
Построение аддитивной и
мультипликативной моделей сводится к расчету значений
и
для каждого уровня ряда.
Процесс построения
модели включает в себя следующие шаги.
1. Выравнивание
исходного ряда методом скользящей средней.
2. Расчет значений
сезонной компоненты
.
3. Устранение сезонной
компоненты из исходных уровней ряда и получение выравненных данных
в аддитивной или
в мультипликативной модели.
4. Аналитическое
выравнивание уровней
или
и расчет значений
с использованием полученного уравнения тренда.
5. Расчет полученных по
модели значений
или
.
6. Расчет абсолютных
и/или относительных ошибок.
Если полученные
значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни
ряда и в дальнейшем использовать временной ряд ошибок
для анализа взаимосвязи исходного ряда и
других временных рядов.
Пример решения задачи
Задача
Имеются
условные данные об объемах потребления электроэнергии
жителями региона за 16 кварталов.
Требуется:
1.
Построить автокорреляционную функцию и сделать вывод о наличии сезонных
колебаний.
2.
Построить аддитивную модель временного ряда (для нечетных вариантов) или
мультипликативную модель временного ряда (для четных вариантов).
3.
Сделать прогноз на 2 квартала вперед.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
1) Построим поле корреляции:
Поле корреляции
Уже
исходя из графика видно, что значения
образуют пилообразную фигуру. Рассчитаем несколько
последовательных коэффициентов автокорреляции. Для этого составляем первую
вспомогательную таблицу:
Следует
заметить. что среднее
значение получается путем деления не на 16, а на 15, так как у нас теперь на
одно наблюдение меньше.
Коэффициент
автокорреляции первого порядка:
Составляем
вспомогательную таблицу для расчета коэффициента автокорреляции второго
порядка:
Следовательно:
Аналогично
находим коэффициенты автокорреляции более высоких порядков, а все полученные
значения заносим в сводную таблицу:
Коэффициенты автокорреляции
| Лаг | Коэффициент автокорреляции уровней |
| 1 | 0.180 |
| 2 | -0.542 |
| 3 | 0.129 |
| 4 | 0.980 |
| 5 | 0.987 |
| 6 | -0.686 |
| 7 | 0.019 |
| 8 | 0.958 |
| 9 | 0.117 |
| 10 | -0.707 |
| 11 | -0.086 |
| 12 | 0.937 |
Коррелограмма
Анализ
коррелограммы и графика исходных уровней временного
ряда позволяет сделать выводы о наличии в изучаемом временном ряде сезонных
колебаний периодичностью в четыре квартала.
2) Проведем выравнивание исходных уровней ряда
методом скользящей средней. Для этого:
Просуммируем
уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент
времени и определим условные годовые объемы потребления электроэнергии.
Разделив
полученные суммы на 4, найдем скользящие средние. Полученные таким образом
выровненные значения уже не содержат сезонной компоненты.
Приведем
эти значения в соответствие с фактическими моментами времени, для чего найдем
средние значения из двух последовательных скользящих средних – центрированные
скользящие средние.
Расчет сезонной компоненты
| Итого за четыре квартала | Скользящая средняя за четыре квартала |
Центрированая скользящая средняя |
Оценка сезонной компоненты |
||
| 1 | 5.5 | — | — | — | — |
| 2 | 4.8 | 24.4 | 6.1 | — | — |
| 3 | 5.1 | 26 | 6.5 | 6.300 | -1.200 |
| 4 | 9 | 26.1 | 6.525 | 6.513 | 2.488 |
| 5 | 7.1 | 27.1 | 6.775 | 6.650 | 0.450 |
| 6 | 4.9 | 28.1 | 7.025 | 6.900 | -2.000 |
| 7 | 6.1 | 29.2 | 7.3 | 7.163 | -1.063 |
| 8 | 10 | 29.8 | 7.45 | 7.375 | 2.625 |
| 9 | 8.2 | 30.2 | 7.55 | 7.500 | 0.700 |
| 10 | 5.5 | 31.2 | 7.8 | 7.675 | -2.175 |
| 11 | 6.5 | 31.9 | 7.975 | 7.888 | -1.388 |
| 12 | 11 | 32.9 | 8.225 | 8.100 | 2.900 |
| 13 | 8.9 | 33.7 | 8.425 | 8.325 | 0.575 |
| 14 | 6.5 | 33.9 | 8.475 | 8.450 | -1.950 |
| 15 | 7.3 | — | — | — | — |
| 16 | 11.2 | — | — | — | — |
Найдем
оценки сезонной компоненты как разность между фактическими уровнями ряда и
центрированными скользящими среднеми. Используем эти оценки для расчета
значений сезонной компоненты
. Для этого найдем средние
за каждый квартал (по всем годам) оценки сезонной компоненты
:
В моделях
с сезонной компонентой обычно предполагается, что сезонные воздействия за
период взаимопогашаются. В аддитивной модели это выражается в том, что сумма
значений сезонной компоненты по всем кварталам должны быть равна нулю.
Для данной
модели имеем:
Корректирующий
коэффициент:
Рассчитываем
скорректированные значения сезонной компоненты
и заносим полученные данные в таблицу.
Проверим
равенство нулю суммы значений сезонной компоненты:
Исключим влияние сезонной компоненты, вычитая ее
значения из каждого уровня исходного временного ряда. Получим величины
. Эти значения
рассчитываются за каждый момент времени и содержат только тенденцию и случайную
компоненту.
Определим
компоненту
данной модели. Для этого проведем
аналитическое выравнивание ряда
с помощью линейного тренда. Результаты
аналитического выравнивания следующие:
Подставляя
в это уравнение значения
, найдем уровни
для каждого момента времени
Найлем
значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к
уровням
значения сезонной компоненты для
соответствующих кварталов.
На одном
графике отложим фактические значения уровней временного ряда и теоретические,
полученные по аддитивной модели.
Фактические и теоретические уровни
Для оценки
качества построенной модели применим сумму квадратов полученных абсолютных
ошибок:
Следовательно,
можно сказать, что аддитивная модель объясняет 99.3% общей вариации уровней
временного ряда.
3)
Прогнозное значение
уровня временного ряда в аддитивной модели
есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты
воспользуемся уравнением тренда:
Получим:
Значения
сезонных компонент за соответствующие кварталы равны:
Таким
образом:
Шаг 4.
Определим компоненту
![]()
данной модели. Для этого проведем
аналитическое выравнивание ряда (![]() )
)
с помощью линейного тренда. Результаты
аналитического выравнивания следующие:
![]() .
.
Подставляя в это
уравнение значения
![]() ,
,
найдем уровни
![]()
для каждого момента времени (гр. 5 табл.
4.7).
Шаг 5.
Найдем значения уровней ряда, полученные
по аддитивной модели. Для этого прибавим
к уровням
![]()
значения сезонной компоненты для
соответствующих кварталов (гр. 6 табл.
4.7).
На одном графике
отложим фактические значения уровней
временного ряда и теоретические,
полученные по аддитивной модели.

Рис. 4.6.
Для оценки качества
построенной модели применим сумму
квадратов полученных абсолютных ошибок.
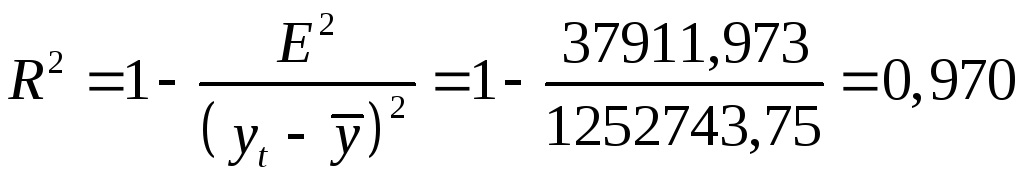 .
.
Следовательно,
можно сказать, что аддитивная модель
объясняет 97% общей вариации уровней
временного ряда количества правонарушений
по кварталам за 4 года.
Шаг 6.
Прогнозирование по аддитивной модели.
Предположим, что по нашему примеру
необходимо дать прогноз об общем объеме
правонарушений на I
и II
кварталы 2003 года. Прогнозное значение
![]()
уровня временного ряда в аддитивной
модели есть сумма трендовой и сезонной
компонент. Для определения трендовой
компоненты воспользуемся уравнением
тренда
![]() .
.
Получим
![]() ;
;
![]() .
.
Значения сезонных
компонент за соответствующие кварталы
равны:
![]()
и
![]() .
.
Таким образом,
![]() ;
;
![]() .
.
Т.е. в первые два
квартала 2003 г. следовало ожидать порядка
395 и 422 правонарушений соответственно.
Построение
мультипликативной модели рассмотрим
на данных предыдущего примера.
Шаг 1.
Методика, применяемая на этом шаге,
полностью совпадает с методикой
построения аддитивной модели.
Таблица 4.8
|
№ квартала, |
Количество |
Итого за |
Скользящая |
Центрированная |
Оценка |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
375 |
– |
– |
– |
– |
|
2 |
371 |
2630 |
657,5 |
– |
– |
|
3 |
869 |
2612 |
653 |
655,25 |
1,3262 |
|
4 |
1015 |
2712 |
678 |
665,5 |
1,5252 |
|
5 |
357 |
2835 |
708,75 |
693,75 |
0,5146 |
|
6 |
471 |
2840 |
710 |
709,375 |
0,6640 |
|
7 |
992 |
2873 |
718,25 |
714,125 |
1,3891 |
|
8 |
1020 |
2757 |
689,25 |
703,75 |
1,4494 |
|
9 |
390 |
2757 |
689,25 |
689,25 |
0,5658 |
|
10 |
355 |
2642 |
660,5 |
674,875 |
0,5260 |
|
11 |
992 |
2713 |
678,25 |
669,375 |
1,4820 |
|
12 |
905 |
2812 |
703 |
690,625 |
1,3104 |
|
13 |
461 |
2740 |
685 |
694 |
0,6643 |
|
14 |
454 |
2762 |
690,5 |
687,75 |
0,6601 |
|
15 |
920 |
– |
– |
– |
– |
|
16 |
927 |
– |
– |
– |
– |
Шаг 2.
Найдем оценки сезонной компоненты как
частное от деления фактических уровней
ряда на центрированные скользящие
средние (гр. 6 табл. 4.8). Эти оценки
используются для расчета сезонной
компоненты
![]()
(табл. 4.9). Для этого найдем средние за
каждый квартал оценки сезонной компоненты
![]() .
.
Так же как и в аддитивной модели считается,
что сезонные воздействия за период
взаимопогашаются. В мультипликативной
модели это выражается в том, что сумма
значений сезонной компоненты по всем
кварталам должна быть равна числу
периодов в цикле. В нашем случае число
периодов одного цикла равно 4.
Таблица 4.9
|
Показатели |
Год |
№ квартала, |
|||
|
I |
II |
III |
IV |
||
|
1999 |
– |
– |
1,3262 |
1,5252 |
|
|
2000 |
0,5146 |
0,6640 |
1,3891 |
1,4494 |
|
|
2001 |
0,5658 |
0,5260 |
1,4820 |
1,3104 |
|
|
2002 |
0,6643 |
0,6601 |
– |
– |
|
|
Всего |
1,7447 |
1,8501 |
4,1973 |
4,2850 |
|
|
Средняя |
0,5816 |
0,6167 |
1,3991 |
1,4283 |
|
|
Скорректированная |
0,5779 |
0,6128 |
1,3901 |
1,4192 |
Имеем
![]() .
.
Определяем
корректирующий коэффициент:
![]() .
.
Скорректированные
значения сезонной компоненты
![]()
получаются при умножении ее средней
оценки
![]()
на корректирующий коэффициент
![]() .
.
Проверяем условие
равенство 4 суммы значений сезонной
компоненты:
![]() .
.
Шаг 3.
Разделим каждый уровень исходного ряда
на соответствующие значения сезонной
компоненты. В результате получим величины
![]()
(гр. 4 табл. 4.10), которые содержат только
тенденцию и случайную компоненту.
Таблица 4.10
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
375 |
0,5779 |
648,9012 |
654,9173 |
378,4767 |
0,9908 |
|
2 |
371 |
0,6128 |
605,4178 |
658,1982 |
403,3439 |
0,9198 |
|
3 |
869 |
1,3901 |
625,1349 |
661,4791 |
919,5221 |
0,9451 |
|
4 |
1015 |
1,4192 |
715,1917 |
664,7600 |
943,4274 |
1,0759 |
|
5 |
357 |
0,5779 |
617,7539 |
668,0409 |
386,0608 |
0,9247 |
|
6 |
471 |
0,6128 |
768,6031 |
671,3218 |
411,3860 |
1,1449 |
|
7 |
992 |
1,3901 |
713,6177 |
674,6027 |
937,7652 |
1,0578 |
|
8 |
1020 |
1,4192 |
718,7148 |
677,8836 |
962,0524 |
1,0602 |
|
9 |
390 |
0,5779 |
674,8572 |
681,1645 |
393,6450 |
0,9907 |
|
10 |
355 |
0,6128 |
579,3081 |
684,4454 |
419,4281 |
0,8464 |
|
11 |
992 |
1,3901 |
713,6177 |
687,7263 |
956,0083 |
1,0377 |
|
12 |
905 |
1,4192 |
637,6832 |
691,0072 |
980,6774 |
0,9228 |
|
13 |
461 |
0,5779 |
797,7159 |
694,2881 |
401,2291 |
1,1490 |
|
14 |
454 |
0,6128 |
740,8616 |
697,5690 |
427,4703 |
1,0621 |
|
15 |
920 |
1,3901 |
661,8229 |
700,8499 |
974,2515 |
0,9443 |
|
16 |
927 |
1,4192 |
653,1849 |
704,1308 |
999,3024 |
0,9277 |
Шаг 4.
Определим компоненту
![]()
в мультипликативной модели. Для этого
рассчитаем параметры линейного тренда,
используя уровни
![]() .
.
В результате получим уравнение тренда:
![]() .
.
Подставляя в это
уравнение значения
![]() ,
,
найдем уровни
![]()
для каждого момента времени (гр. 5 табл.
4.10).
Шаг 5.
Найдем уровни ряда, умножив значения
![]()
на соответствующие значения сезонной
компоненты (гр. 6 табл. 4.10). На одном
графике откладываем фактические значения
уровней временного ряда и теоретические,
полученные по мультипликативной модели.
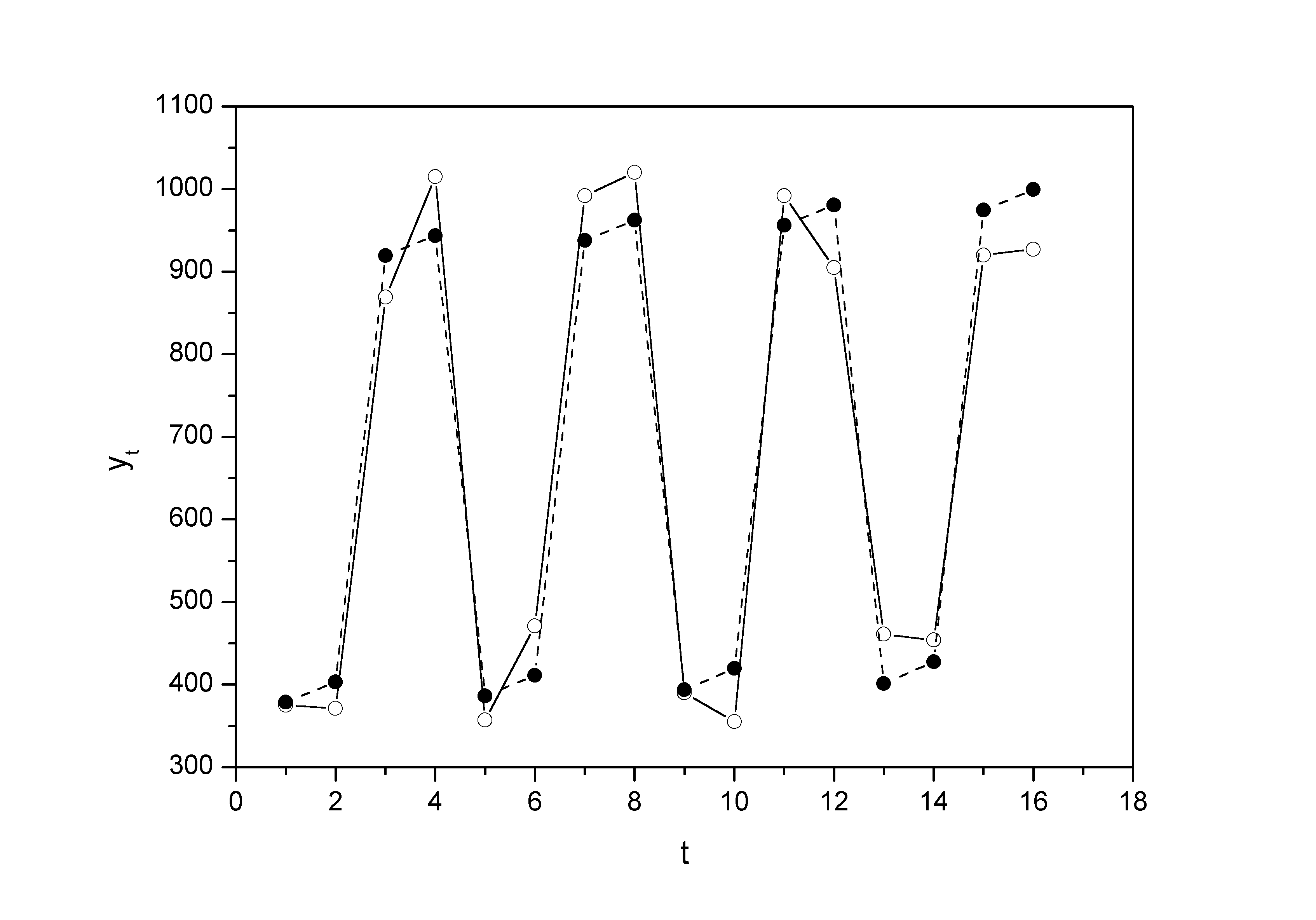
Рис. 4.7.
Расчет ошибки в
мультипликативной модели производится
по формуле:
![]() .
.
Для сравнения
мультипликативной модели и других
моделей временного ряда можно, по
аналогии с аддитивной моделью, использовать
сумму квадратов абсолютных ошибок
![]() :
:
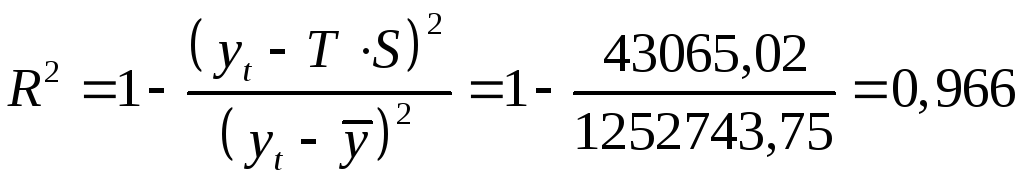 .
.
Сравнивая показатели
детерминации аддитивной и мультипликативной
моделей, делаем вывод, что они примерно
одинаково аппроксимируют исходные
данные.
Шаг 6.
Прогнозирование по мультипликативной
модели. Если предположить, что по нашему
примеру необходимо дать прогноз об
общем объеме правонарушений на I
и II
кварталы 2003 года, прогнозное значение
![]()
уровня временного ряда в мультипликативной
модели есть произведение трендовой и
сезонной компонент. Для определения
трендовой компоненты воспользуемся
уравнением тренда
![]() .
.
Получим
![]() ;
;
![]() .
.
Значения сезонных
компонент за соответствующие кварталы
равны:
![]()
и
![]() .
.
Таким образом
![]() ;
;
![]() .
.
Т.е. в первые два
квартала 2003 г. следовало ожидать порядка
409 и 436 правонарушений соответственно.
Таким образом,
аддитивная и мультипликативная модели
дают примерно одинаковый результат по
прогнозу.
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Имеются условные данные об объемах потребления электроэнергии yt жителями региона за 16 кварталов.
| t | yt | t | yt |
|---|---|---|---|
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение:
1. Рассчитаем коэффициент автокорреляции уровней ряда первого порядка, то есть между соседними уровнями ряда yt и yt-1 (лаг = 1), и измерим тесноту связи между объёмом потребления электроэнергии в текущем и предыдущем году.
Для этого составим таблицу расчётных данных.
Расчёт коэффициента автокорреляции первого порядка для временного ряда объемов потребления электроэнергии жителями региона:
| t | yt | yt-1 | 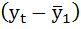 |
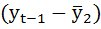 |
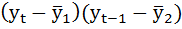 |
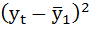 |
 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | — | — | — | — | — | — |
| 2 | 4,7 | 5,6 | -2,827 | -1,547 | 4,371911 | 7,990044 | 2,392178 |
| 3 | 5,2 | 4,7 | -2,327 | -2,447 | 5,692578 | 5,413378 | 5,986178 |
| 4 | 9,1 | 5,2 | 1,573 | -1,947 | -3,06276 | 2,475378 | 3,789511 |
| 5 | 7 | 9,1 | -0,527 | 1,953 | -1,02876 | 0,277378 | 3,815511 |
| 6 | 5,1 | 7 | -2,427 | -0,147 | 0,355911 | 5,888711 | 0,021511 |
| 7 | 6 | 5,1 | -1,527 | -2,047 | 3,124578 | 2,330711 | 4,188844 |
| 8 | 10,2 | 6 | 2,673 | -1,147 | -3,06542 | 7,146711 | 1,314844 |
| 9 | 8,2 | 10,2 | 0,673 | 3,053 | 2,055911 | 0,453378 | 9,322844 |
| 10 | 5,6 | 8,2 | -1,927 | 1,053 | -2,02942 | 3,712044 | 1,109511 |
| 11 | 6,4 | 5,6 | -1,127 | -1,547 | 1,742578 | 1,269378 | 2,392178 |
| 12 | 10,8 | 6,4 | 3,273 | -0,747 | -2,44409 | 10,71471 | 0,557511 |
| 13 | 9,1 | 10,8 | 1,573 | 3,653 | 5,747911 | 2,475378 | 13,34684 |
| 14 | 6,7 | 9,1 | -0,827 | 1,953 | -1,61476 | 0,683378 | 3,815511 |
| 15 | 7,5 | 6,7 | -0,027 | -0,447 | 0,011911 | 0,000711 | 0,199511 |
| 16 | 11,3 | 7,5 | 3,773 | 0,353 | 1,333244 | 14,23804 | 0,124844 |
| Итого | 112,9 | 107,2 | — | — | 11,19133 | 65,06933 | 52,37733 |
Рассчитаем выборочные средние:
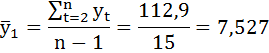
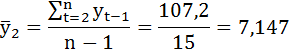
Определим коэффициент автокорреляции уровней ряда первого порядка:
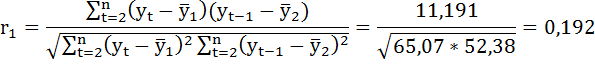
Полученное значение свидетельствует об очень слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Рассчитаем коэффициент автокорреляции 2-го порядка.
| t | yt | yt-2 | 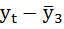 |
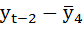 |
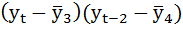 |
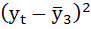 |
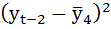 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | — | — | — | — | — | — |
| 2 | 4,7 | — | — | — | — | — | — |
| 3 | 5,2 | 5,6 | -2,529 | -1,521 | 3,847041 | 6,393673 | 2,314745 |
| 4 | 9,1 | 4,7 | 1,371 | -2,421 | -3,32082 | 1,880816 | 5,863316 |
| 5 | 7 | 5,2 | -0,729 | -1,921 | 1,399898 | 0,530816 | 3,691888 |
| 6 | 5,1 | 9,1 | -2,629 | 1,979 | -5,20082 | 6,909388 | 3,914745 |
| 7 | 6 | 7 | -1,729 | -0,121 | 0,209898 | 2,987959 | 0,014745 |
| 8 | 10,2 | 5,1 | 2,471 | -2,021 | -4,99582 | 6,107959 | 4,086173 |
| 9 | 8,2 | 6 | 0,471 | -1,121 | -0,52867 | 0,222245 | 1,257602 |
| 10 | 5,6 | 10,2 | -2,129 | 3,079 | -6,55296 | 4,530816 | 9,477602 |
| 11 | 6,4 | 8,2 | -1,329 | 1,079 | -1,43296 | 1,765102 | 1,163316 |
| 12 | 10,8 | 5,6 | 3,071 | -1,521 | -4,67296 | 9,433673 | 2,314745 |
| 13 | 9,1 | 6,4 | 1,371 | -0,721 | -0,98939 | 1,880816 | 0,520459 |
| 14 | 6,7 | 10,8 | -1,029 | 3,679 | -3,78367 | 1,057959 | 13,53189 |
| 15 | 7,5 | 9,1 | -0,229 | 1,979 | -0,45224 | 0,052245 | 3,914745 |
| 16 | 11,3 | 6,7 | 3,571 | -0,421 | -1,5051 | 12,7551 | 0,177602 |
| Итого | 108,2 | 99,7 | — | — | -27,9786 | 56,50857 | 52,24357 |
Выборочные средние:
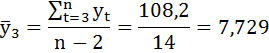
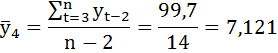
Коэффициент автокорреляции уровней ряда первого порядка:
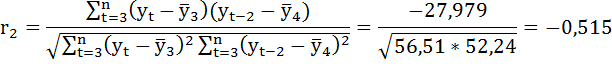
Продолжив расчёты аналогичным образом, получим автокорреляционную функцию этого ряда. Её значения приведены в таблице:
| Лаг | Коэффициент автокорреляции уровней |
|---|---|
| 1 | 0,1917 |
| 2 | -0,5149 |
| 3 | 0,1272 |
| 4 | 0,9862 |
| 5 | 0,1448 |
| 6 | -0,6487 |
| 7 | -0,00647 |
| 8 | 0,9632 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в 4 квартала.
2. Построим аддитивную модель временного ряда.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр. 3);
2) разделив полученные суммы на 4, найдём скользящие средние (гр. 4). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5).
Расчёт оценок сезонной компоненты в аддитивной модели
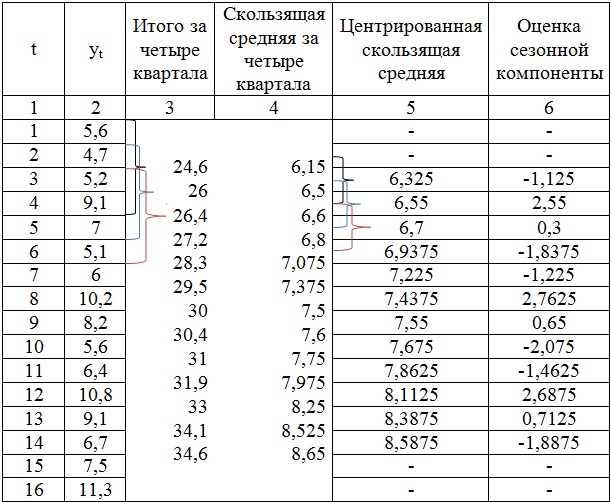
Шаг 2. Рассчитаем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчёт значений сезонной компоненты:
| Показатели | Год | № квартала, i | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| 1 | — | — | -1,125 | 2,55 | |
| 2 | 0,3 | -1,8375 | -1,225 | 2,7625 | |
| 3 | 0,65 | -2,075 | -1,4625 | 2,6875 | |
| 4 | 0,7125 | -1,8875 | — | — | |
| Итого за i-й квартал | 1,6625 | -5,8 | -3,8125 | 8 | |
Средняя оценка сезонной компоненты для i-го квартала, 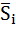 |
0,554167 | -1,93333 | -1,27083 | 2,666667 | |
| Скорректированная сезонная компонента, Si | 0,55 | -1,9375 | -1,275 | 2,6625 |
Для данной модели имеем:
0,554167 + ( -1,93333) + (-1,27083) + 2,666667 = 0,016667
Определим корректирующий коэффициент:
k = 0,016667 / 4 = 0,004167
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
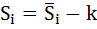
Проверим условие равенство нулю суммы значений сезонной компоненты:
0,55 + (-1,9375) + (-1,275) + 2,6625 = 0
Таким образом, получены следующие значения сезонной компоненты:
I квартал: S1 = 0,55;
II квартал: S2 = -1,9375;
III квартал: S3 = -1,275;
IV квартал: S4 = 2,6625.
Занесём полученные значения в таблицу для соответствующих кварталов каждого года (гр. 3).
| t | yt | Si | T + E = yt – Si | T | T + S | E = yt – (T + S) | E2 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,6 | 0,55 | 5,05 | 5,8588235 | 6,408824 | -0,80882 | 0,654196 |
| 2 | 4,7 | -1,9375 | 6,6375 | 6,0651471 | 4,127647 | 0,572353 | 0,327588 |
| 3 | 5,2 | -1,275 | 6,475 | 6,2714706 | 4,996471 | 0,203529 | 0,041424 |
| 4 | 9,1 | 2,6625 | 6,4375 | 6,4777941 | 9,140294 | -0,04029 | 0,001624 |
| 5 | 7 | 0,55 | 6,45 | 6,6841176 | 7,234118 | -0,23412 | 0,054811 |
| 6 | 5,1 | -1,9375 | 7,0375 | 6,8904412 | 4,952941 | 0,147059 | 0,021626 |
| 7 | 6 | -1,275 | 7,275 | 7,0967647 | 5,821765 | 0,178235 | 0,031768 |
| 8 | 10,2 | 2,6625 | 7,5375 | 7,3030882 | 9,965588 | 0,234412 | 0,054949 |
| 9 | 8,2 | 0,55 | 7,65 | 7,5094118 | 8,059412 | 0,140588 | 0,019765 |
| 10 | 5,6 | -1,9375 | 7,5375 | 7,7157353 | 5,778235 | -0,17824 | 0,031768 |
| 11 | 6,4 | -1,275 | 7,675 | 7,9220588 | 6,647059 | -0,24706 | 0,061038 |
| 12 | 10,8 | 2,6625 | 8,1375 | 8,1283824 | 10,79088 | 0,009118 | 8,31E-05 |
| 13 | 9,1 | 0,55 | 8,55 | 8,3347059 | 8,884706 | 0,215294 | 0,046352 |
| 14 | 6,7 | -1,9375 | 8,6375 | 8,5410294 | 6,603529 | 0,096471 | 0,009307 |
| 15 | 7,5 | -1,275 | 8,775 | 8,7473529 | 7,472353 | 0,027647 | 0,000764 |
| 16 | 11,3 | 2,6625 | 8,6375 | 8,9536765 | 11,61618 | -0,31618 | 0,099968 |
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y — S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 5,6525 + 0,206 * t
Подставляя в это уравнение значения t = 1,…,16, найдем уровни T для каждого момента времени (гр. 5 табл.).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Коэффициент детерминации.
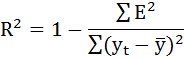
| t | yt | Е2 | 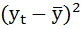 |
|---|---|---|---|
| 1 | 5,6 | 0,654196 | 3,262539 |
| 2 | 4,7 | 0,327588 | 7,323789 |
| 3 | 5,2 | 0,041424 | 4,867539 |
| 4 | 9,1 | 0,001624 | 2,868789 |
| 5 | 7 | 0,054811 | 0,165039 |
| 6 | 5,1 | 0,021626 | 5,318789 |
| 7 | 6 | 0,031768 | 1,977539 |
| 8 | 10,2 | 0,054949 | 7,805039 |
| 9 | 8,2 | 0,019765 | 0,630039 |
| 10 | 5,6 | 0,031768 | 3,262539 |
| 11 | 6,4 | 0,061038 | 1,012539 |
| 12 | 10,8 | 8,31E-05 | 11,51754 |
| 13 | 9,1 | 0,046352 | 2,868789 |
| 14 | 6,7 | 0,009307 | 0,498789 |
| 15 | 7,5 | 0,000764 | 0,008789 |
| 16 | 11,3 | 0,099968 | 15,16129 |
| Итого | 118,5 | 1,457029 | 68,549 |
Рассчитаем коэффициент детерминации.
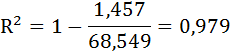
Следовательно, можно сказать, что аддитивная модель объясняет 97,9% общей вариации уровней временного ряда.
Далее необходимо провести проверку адекватности модели данным наблюдения. Воспользуемся F-критерием Фишера:
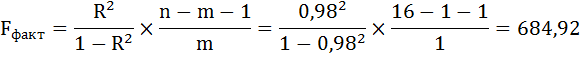
где m — количество факторов в уравнении тренда (m=1).
Табличное значение F-критерия Фишера при уровне значимости α = 0,05,
k1 = m = 1, k2 = n — m — 1 = 14,
Fтабл = 4,60
Поскольку F > Fтабл, то уравнение статистически значимо, надёжно.
Шаг 6. Прогнозирование по аддитивной модели.
Прогнозное значение Ft уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:
T = 5,6525 + 0,206 × t
Прогноз на 1 период:
T17 = 5,6525 + 0,206 × 17 = 9,16
Значение сезонного компонента за соответствующий период равно:
S1 = 0,55
Таким образом,
F17 = T17 + S1 = 9,16 + 0,55 = 9,71
Прогноз на 2 период:
T18 = 5,6525 + 0,206 × 18 = 9,366
Значение сезонной компоненты за соответствующий период равно:
S2 = – 1,9375
Таким образом, прогнозное значение на 2 квартала вперёд составит:
F18 = T18 + S2 = 9,366 – 1,9375 = 7,429
|
t |
yt |
Si |
T = |
T |
T |
E |
E2 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
52 |
0,188 |
51,813 |
47,938 |
48,125 |
3,875 |
15,016 |
|
2 |
66 |
16,771 |
49,229 |
50,546 |
67,317 |
-1,317 |
1,734 |
|
3 |
50 |
3,354 |
46,646 |
53,154 |
56,508 |
-6,508 |
42,358 |
|
4 |
30 |
-20,313 |
50,313 |
55,763 |
35,450 |
-5,450 |
29,703 |
|
5 |
62 |
0,188 |
61,813 |
58,371 |
58,558 |
3,442 |
11,845 |
|
6 |
75 |
16,771 |
58,229 |
60,979 |
77,750 |
-2,750 |
7,563 |
|
7 |
68 |
3,354 |
64,646 |
63,588 |
66,942 |
1,058 |
1,120 |
|
8 |
48 |
-20,313 |
68,313 |
66,196 |
45,883 |
2,117 |
4,480 |
|
9 |
72 |
0,188 |
71,813 |
68,804 |
68,992 |
3,008 |
9,050 |
|
10 |
96 |
16,771 |
79,229 |
71,413 |
88,183 |
7,817 |
61,100 |
|
11 |
83 |
3,354 |
79,646 |
74,021 |
77,375 |
5,625 |
31,641 |
|
12 |
58 |
-20,313 |
78,313 |
76,629 |
56,317 |
1,683 |
2,834 |
|
13 |
72 |
0,188 |
71,813 |
79,238 |
79,425 |
-7,425 |
55,131 |
|
14 |
94 |
16,771 |
77,229 |
81,846 |
98,617 |
-4,617 |
21,314 |
|
15 |
90 |
3,354 |
86,646 |
84,454 |
87,808 |
2,192 |
4,803 |
|
16 |
64 |
-20,313 |
84,313 |
87,063 |
66,750 |
-2,750 |
7,563 |
|
Сумма |
0 |
315,253 |
Шаг
6.Найдем значения уровней ряда,
полученные по аддитивной модели. Для
этого прибавим к уровнямTзначения сезонной компоненты. Графически
значения (T+S)
представлены на рисунке 3.2.
Шаг
7. Для аддитивной модели расчет
абсолютной ошибки производится по
формулеE=Y– (T+S).
Численные
значения абсолютных ошибок приведены
в таблице 3.6 столбец 7.
Для
оценки качества построения модели или
для выбора наилучшей модели можно
применять сумму квадратов полученных
абсолютных ошибок. Для данной аддитивной
модели сумма квадратов абсолютных
ошибок: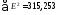 .
.
По отношению к общей сумме квадратов
отклонений уровней ряда от его среднего
уровня ,
,
эта величина составляет 6,5%:

Следовательно,
можно сказать, что аддитивная модель
объясняет 100 – 6,5 = 93,5 % общей вариации
уровней временного ряда товарооборота
компании за последние 16 кварталов.

Рис.
3.2. Товарооборот компании
5.
Построиммультипликативную модельвременного ряда
Y=TּSּE.
Шаг
1ишаг 2мультипликативной модели
полностью совпадает с шагом 1 и 2 аддитивной
модели.
Шаг
3. Найдем оценки сезонной компоненты
какчастноеот деления фактических
уровней (таблица 3.7 столбец 2) ряда на
центрированные скользящие средние
(таблица 3.7 столбец 5). Полученные оценки
запишем в таблицу 3.7 столбец 6.
Построим
новую таблицу 3.8. Последовательно занесем
полученные в таблице 3.7 оценки сезонной
компоненты в строки таблицы 3.8. Просуммируем
по каждому кварталу и найдем средние
за каждый квартал оценки сезонной
компоненты –
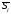 .
.
Взаимопогашаемость
сезонных колебаний в мультипликативной
модели выражается в том, что сумма
значений сезонной компоненты должна
быть равна числу периодов в цикле. В
нашем случае число периодов одного
цикла (года) равно 4 (четыре квартала).
Имеем:
1,004 + 1,226 + 1,038 + 0,673 = 3,942.
Т.
к. сумма не равна четырем, ее нужно
корректировать. Рассчитаем корректирующий
коэффициент k:k= 4 / 3,942 = 1,015.
Определим
скорректированные значения сезонной
компоненты, умножив ее средние оценки
на корректирующий коэффициент k.
Таблица
3.7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Имеются условные данные об объемах потребления электроэнергии yt жителями региона за 16 кварталов.
| t | yt | t | yt |
|---|---|---|---|
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение:
1. Рассчитаем коэффициент автокорреляции уровней ряда первого порядка, то есть между соседними уровнями ряда yt и yt-1 (лаг = 1), и измерим тесноту связи между объёмом потребления электроэнергии в текущем и предыдущем году.
Для этого составим таблицу расчётных данных.
Расчёт коэффициента автокорреляции первого порядка для временного ряда объемов потребления электроэнергии жителями региона:
| t | yt | yt-1 | 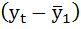 |
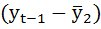 |
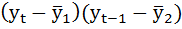 |
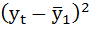 |
 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | — | — | — | — | — | — |
| 2 | 4,7 | 5,6 | -2,827 | -1,547 | 4,371911 | 7,990044 | 2,392178 |
| 3 | 5,2 | 4,7 | -2,327 | -2,447 | 5,692578 | 5,413378 | 5,986178 |
| 4 | 9,1 | 5,2 | 1,573 | -1,947 | -3,06276 | 2,475378 | 3,789511 |
| 5 | 7 | 9,1 | -0,527 | 1,953 | -1,02876 | 0,277378 | 3,815511 |
| 6 | 5,1 | 7 | -2,427 | -0,147 | 0,355911 | 5,888711 | 0,021511 |
| 7 | 6 | 5,1 | -1,527 | -2,047 | 3,124578 | 2,330711 | 4,188844 |
| 8 | 10,2 | 6 | 2,673 | -1,147 | -3,06542 | 7,146711 | 1,314844 |
| 9 | 8,2 | 10,2 | 0,673 | 3,053 | 2,055911 | 0,453378 | 9,322844 |
| 10 | 5,6 | 8,2 | -1,927 | 1,053 | -2,02942 | 3,712044 | 1,109511 |
| 11 | 6,4 | 5,6 | -1,127 | -1,547 | 1,742578 | 1,269378 | 2,392178 |
| 12 | 10,8 | 6,4 | 3,273 | -0,747 | -2,44409 | 10,71471 | 0,557511 |
| 13 | 9,1 | 10,8 | 1,573 | 3,653 | 5,747911 | 2,475378 | 13,34684 |
| 14 | 6,7 | 9,1 | -0,827 | 1,953 | -1,61476 | 0,683378 | 3,815511 |
| 15 | 7,5 | 6,7 | -0,027 | -0,447 | 0,011911 | 0,000711 | 0,199511 |
| 16 | 11,3 | 7,5 | 3,773 | 0,353 | 1,333244 | 14,23804 | 0,124844 |
| Итого | 112,9 | 107,2 | — | — | 11,19133 | 65,06933 | 52,37733 |
Рассчитаем выборочные средние:
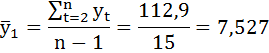
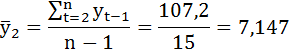
Определим коэффициент автокорреляции уровней ряда первого порядка:
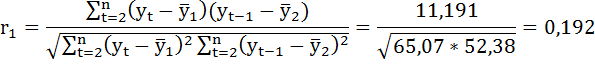
Полученное значение свидетельствует об очень слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Рассчитаем коэффициент автокорреляции 2-го порядка.
| t | yt | yt-2 | 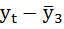 |
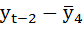 |
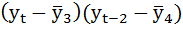 |
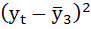 |
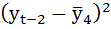 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | — | — | — | — | — | — |
| 2 | 4,7 | — | — | — | — | — | — |
| 3 | 5,2 | 5,6 | -2,529 | -1,521 | 3,847041 | 6,393673 | 2,314745 |
| 4 | 9,1 | 4,7 | 1,371 | -2,421 | -3,32082 | 1,880816 | 5,863316 |
| 5 | 7 | 5,2 | -0,729 | -1,921 | 1,399898 | 0,530816 | 3,691888 |
| 6 | 5,1 | 9,1 | -2,629 | 1,979 | -5,20082 | 6,909388 | 3,914745 |
| 7 | 6 | 7 | -1,729 | -0,121 | 0,209898 | 2,987959 | 0,014745 |
| 8 | 10,2 | 5,1 | 2,471 | -2,021 | -4,99582 | 6,107959 | 4,086173 |
| 9 | 8,2 | 6 | 0,471 | -1,121 | -0,52867 | 0,222245 | 1,257602 |
| 10 | 5,6 | 10,2 | -2,129 | 3,079 | -6,55296 | 4,530816 | 9,477602 |
| 11 | 6,4 | 8,2 | -1,329 | 1,079 | -1,43296 | 1,765102 | 1,163316 |
| 12 | 10,8 | 5,6 | 3,071 | -1,521 | -4,67296 | 9,433673 | 2,314745 |
| 13 | 9,1 | 6,4 | 1,371 | -0,721 | -0,98939 | 1,880816 | 0,520459 |
| 14 | 6,7 | 10,8 | -1,029 | 3,679 | -3,78367 | 1,057959 | 13,53189 |
| 15 | 7,5 | 9,1 | -0,229 | 1,979 | -0,45224 | 0,052245 | 3,914745 |
| 16 | 11,3 | 6,7 | 3,571 | -0,421 | -1,5051 | 12,7551 | 0,177602 |
| Итого | 108,2 | 99,7 | — | — | -27,9786 | 56,50857 | 52,24357 |
Выборочные средние:
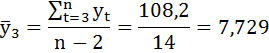
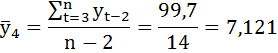
Коэффициент автокорреляции уровней ряда первого порядка:
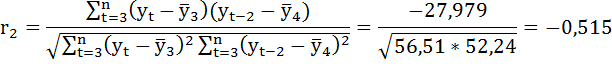
Продолжив расчёты аналогичным образом, получим автокорреляционную функцию этого ряда. Её значения приведены в таблице:
| Лаг | Коэффициент автокорреляции уровней |
|---|---|
| 1 | 0,1917 |
| 2 | -0,5149 |
| 3 | 0,1272 |
| 4 | 0,9862 |
| 5 | 0,1448 |
| 6 | -0,6487 |
| 7 | -0,00647 |
| 8 | 0,9632 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в 4 квартала.
2. Построим аддитивную модель временного ряда.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр. 3);
2) разделив полученные суммы на 4, найдём скользящие средние (гр. 4). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5).
Расчёт оценок сезонной компоненты в аддитивной модели

Шаг 2. Рассчитаем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчёт значений сезонной компоненты:
| Показатели | Год | № квартала, i | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| 1 | — | — | -1,125 | 2,55 | |
| 2 | 0,3 | -1,8375 | -1,225 | 2,7625 | |
| 3 | 0,65 | -2,075 | -1,4625 | 2,6875 | |
| 4 | 0,7125 | -1,8875 | — | — | |
| Итого за i-й квартал | 1,6625 | -5,8 | -3,8125 | 8 | |
Средняя оценка сезонной компоненты для i-го квартала, 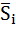 |
0,554167 | -1,93333 | -1,27083 | 2,666667 | |
| Скорректированная сезонная компонента, Si | 0,55 | -1,9375 | -1,275 | 2,6625 |
Для данной модели имеем:
0,554167 + ( -1,93333) + (-1,27083) + 2,666667 = 0,016667
Определим корректирующий коэффициент:
k = 0,016667 / 4 = 0,004167
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
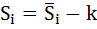
Проверим условие равенство нулю суммы значений сезонной компоненты:
0,55 + (-1,9375) + (-1,275) + 2,6625 = 0
Таким образом, получены следующие значения сезонной компоненты:
I квартал: S1 = 0,55;
II квартал: S2 = -1,9375;
III квартал: S3 = -1,275;
IV квартал: S4 = 2,6625.
Занесём полученные значения в таблицу для соответствующих кварталов каждого года (гр. 3).
| t | yt | Si | T + E = yt – Si | T | T + S | E = yt – (T + S) | E2 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,6 | 0,55 | 5,05 | 5,8588235 | 6,408824 | -0,80882 | 0,654196 |
| 2 | 4,7 | -1,9375 | 6,6375 | 6,0651471 | 4,127647 | 0,572353 | 0,327588 |
| 3 | 5,2 | -1,275 | 6,475 | 6,2714706 | 4,996471 | 0,203529 | 0,041424 |
| 4 | 9,1 | 2,6625 | 6,4375 | 6,4777941 | 9,140294 | -0,04029 | 0,001624 |
| 5 | 7 | 0,55 | 6,45 | 6,6841176 | 7,234118 | -0,23412 | 0,054811 |
| 6 | 5,1 | -1,9375 | 7,0375 | 6,8904412 | 4,952941 | 0,147059 | 0,021626 |
| 7 | 6 | -1,275 | 7,275 | 7,0967647 | 5,821765 | 0,178235 | 0,031768 |
| 8 | 10,2 | 2,6625 | 7,5375 | 7,3030882 | 9,965588 | 0,234412 | 0,054949 |
| 9 | 8,2 | 0,55 | 7,65 | 7,5094118 | 8,059412 | 0,140588 | 0,019765 |
| 10 | 5,6 | -1,9375 | 7,5375 | 7,7157353 | 5,778235 | -0,17824 | 0,031768 |
| 11 | 6,4 | -1,275 | 7,675 | 7,9220588 | 6,647059 | -0,24706 | 0,061038 |
| 12 | 10,8 | 2,6625 | 8,1375 | 8,1283824 | 10,79088 | 0,009118 | 8,31E-05 |
| 13 | 9,1 | 0,55 | 8,55 | 8,3347059 | 8,884706 | 0,215294 | 0,046352 |
| 14 | 6,7 | -1,9375 | 8,6375 | 8,5410294 | 6,603529 | 0,096471 | 0,009307 |
| 15 | 7,5 | -1,275 | 8,775 | 8,7473529 | 7,472353 | 0,027647 | 0,000764 |
| 16 | 11,3 | 2,6625 | 8,6375 | 8,9536765 | 11,61618 | -0,31618 | 0,099968 |
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y — S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 5,6525 + 0,206 * t
Подставляя в это уравнение значения t = 1,…,16, найдем уровни T для каждого момента времени (гр. 5 табл.).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Коэффициент детерминации.
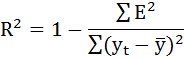
| t | yt | Е2 | 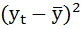 |
|---|---|---|---|
| 1 | 5,6 | 0,654196 | 3,262539 |
| 2 | 4,7 | 0,327588 | 7,323789 |
| 3 | 5,2 | 0,041424 | 4,867539 |
| 4 | 9,1 | 0,001624 | 2,868789 |
| 5 | 7 | 0,054811 | 0,165039 |
| 6 | 5,1 | 0,021626 | 5,318789 |
| 7 | 6 | 0,031768 | 1,977539 |
| 8 | 10,2 | 0,054949 | 7,805039 |
| 9 | 8,2 | 0,019765 | 0,630039 |
| 10 | 5,6 | 0,031768 | 3,262539 |
| 11 | 6,4 | 0,061038 | 1,012539 |
| 12 | 10,8 | 8,31E-05 | 11,51754 |
| 13 | 9,1 | 0,046352 | 2,868789 |
| 14 | 6,7 | 0,009307 | 0,498789 |
| 15 | 7,5 | 0,000764 | 0,008789 |
| 16 | 11,3 | 0,099968 | 15,16129 |
| Итого | 118,5 | 1,457029 | 68,549 |
Рассчитаем коэффициент детерминации.
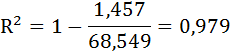
Следовательно, можно сказать, что аддитивная модель объясняет 97,9% общей вариации уровней временного ряда.
Далее необходимо провести проверку адекватности модели данным наблюдения. Воспользуемся F-критерием Фишера:
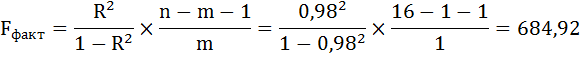
где m — количество факторов в уравнении тренда (m=1).
Табличное значение F-критерия Фишера при уровне значимости α = 0,05,
k1 = m = 1, k2 = n — m — 1 = 14,
Fтабл = 4,60
Поскольку F > Fтабл, то уравнение статистически значимо, надёжно.
Шаг 6. Прогнозирование по аддитивной модели.
Прогнозное значение Ft уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:
T = 5,6525 + 0,206 × t
Прогноз на 1 период:
T17 = 5,6525 + 0,206 × 17 = 9,16
Значение сезонного компонента за соответствующий период равно:
S1 = 0,55
Таким образом,
F17 = T17 + S1 = 9,16 + 0,55 = 9,71
Прогноз на 2 период:
T18 = 5,6525 + 0,206 × 18 = 9,366
Значение сезонной компоненты за соответствующий период равно:
S2 = – 1,9375
Таким образом, прогнозное значение на 2 квартала вперёд составит:
F18 = T18 + S2 = 9,366 – 1,9375 = 7,429
Автокорреляционная функция и аддитивная модель временного ряда
Краткая теория
При
наличии во временном ряде тенденции и циклических колебаний значения каждого
последующего уровня ряда зависят от предыдущих.
Корреляционную зависимость между последовательными уровнями временного ряда
называют автокорреляцией уровней ряда. Количественно ее можно измерить с
помощью линейного коэффициента корреляции между уровнями исходного временного ряда
и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Число
периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент
автокорреляции, уменьшается. Некоторые авторы считают целесообразным для
обеспечения статистической достоверности коэффициентов автокорреляции
использовать правило – максимальный лаг должен быть не больше
.
Отметим
два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии
с линейным коэффициентом корреляции и таким образом характеризует тесноту
только линейной связи текущего и предыдущего уровней ряда. Поэтому по
коэффициенту автокорреляции можно судить о наличии линейной (или близкой к
линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную
тенденцию (например, параболу второго порядка или экспоненту), коэффициент
автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых,
по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или
убывающей тенденции в уровнях ряда. Большинство временных рядов экономических
данных содержит положительную автокорреляцию уровней, однако при этом могут
иметь убывающую тенденцию.
Последовательность
коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют
автокорреляционной функцией временного рада. График зависимости ее значений от
величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ
автокорреляционной функции и коррелограммы позволяет
определить лаг, при котором автокорреляция наиболее высокая, а
следовательно, и лаг, при котором связь между текущим и предыдущими уровнями
ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если
наиболее высоким оказался коэффициент автокорреляции первого порядка,
исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался
коэффициент автокорреляции порядка
, ряд содержит
циклические колебания с периодичностью в
моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно
сделать одно из двух предположений относительно структуры этого ряда: либо ряд
не содержит тенденции и циклических колебаний, либо ряд содержит сильную
нелинейную тенденцию, для выявления которой нужно провести дополнительный
анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию
целесообразно использовать для выявления во временном ряде наличия или
отсутствия трендовой компоненты (
)
и
циклической (сезонной) компоненты (
).
Существует несколько подходов к
анализу структуры временных рядов, содержащих сезонные или циклические
колебания. Простейший подход — расчет значений сезонной компоненты методом
скользящей средней и построение аддитивной или мультипликативной модели
временного ряда. Общий вид аддитивной модели следующий:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
сумма трендовой
,
сезонной
и случайной
компонент. Общий вид
мультипликативный модели выглядит так:
Эта модель
предполагает, что каждый уровень временного ряда может быть представлен как
произведение трендовой
,
сезонной
и случайной
компонент. Выбор одной из двух моделей
осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда
колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в
которой значения сезонной компоненты предполагаются постоянными для различных
циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят
мультипликативную модель временного ряда, которая ставит уровни ряда в
зависимость от значений сезонной компоненты.
Построение аддитивной и
мультипликативной моделей сводится к расчету значений
и
для каждого уровня ряда.
Процесс построения
модели включает в себя следующие шаги.
1. Выравнивание
исходного ряда методом скользящей средней.
2. Расчет значений
сезонной компоненты
.
3. Устранение сезонной
компоненты из исходных уровней ряда и получение выравненных данных
в аддитивной или
в мультипликативной модели.
4. Аналитическое
выравнивание уровней
или
и расчет значений
с использованием полученного уравнения тренда.
5. Расчет полученных по
модели значений
или
.
6. Расчет абсолютных
и/или относительных ошибок.
Если полученные
значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни
ряда и в дальнейшем использовать временной ряд ошибок
для анализа взаимосвязи исходного ряда и
других временных рядов.
Пример решения задачи
Задача
Имеются
условные данные об объемах потребления электроэнергии
жителями региона за 16 кварталов.
Требуется:
1.
Построить автокорреляционную функцию и сделать вывод о наличии сезонных
колебаний.
2.
Построить аддитивную модель временного ряда (для нечетных вариантов) или
мультипликативную модель временного ряда (для четных вариантов).
3.
Сделать прогноз на 2 квартала вперед.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1) Построим поле корреляции:
Поле корреляции
Уже
исходя из графика видно, что значения
образуют пилообразную фигуру. Рассчитаем несколько
последовательных коэффициентов автокорреляции. Для этого составляем первую
вспомогательную таблицу:
Следует
заметить. что среднее
значение получается путем деления не на 16, а на 15, так как у нас теперь на
одно наблюдение меньше.
Коэффициент
автокорреляции первого порядка:
Составляем
вспомогательную таблицу для расчета коэффициента автокорреляции второго
порядка:
Следовательно:
Аналогично
находим коэффициенты автокорреляции более высоких порядков, а все полученные
значения заносим в сводную таблицу:
Коэффициенты автокорреляции
| Лаг |
Коэффициент автокорреляции уровней |
| 1 | 0.180 |
| 2 | -0.542 |
| 3 | 0.129 |
| 4 | 0.980 |
| 5 | 0.987 |
| 6 | -0.686 |
| 7 | 0.019 |
| 8 | 0.958 |
| 9 | 0.117 |
| 10 | -0.707 |
| 11 | -0.086 |
| 12 | 0.937 |
Коррелограмма
Анализ
коррелограммы и графика исходных уровней временного
ряда позволяет сделать выводы о наличии в изучаемом временном ряде сезонных
колебаний периодичностью в четыре квартала.
2) Проведем выравнивание исходных уровней ряда
методом скользящей средней. Для этого:
Просуммируем
уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент
времени и определим условные годовые объемы потребления электроэнергии.
Разделив
полученные суммы на 4, найдем скользящие средние. Полученные таким образом
выровненные значения уже не содержат сезонной компоненты.
Приведем
эти значения в соответствие с фактическими моментами времени, для чего найдем
средние значения из двух последовательных скользящих средних – центрированные
скользящие средние.
Расчет сезонной компоненты
|
|
|
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированая скользящая средняя |
Оценка сезонной компоненты |
| 1 | 5.5 | — | — | — | — |
| 2 | 4.8 | 24.4 | 6.1 | — | — |
| 3 | 5.1 | 26 | 6.5 | 6.300 | -1.200 |
| 4 | 9 | 26.1 | 6.525 | 6.513 | 2.488 |
| 5 | 7.1 | 27.1 | 6.775 | 6.650 | 0.450 |
| 6 | 4.9 | 28.1 | 7.025 | 6.900 | -2.000 |
| 7 | 6.1 | 29.2 | 7.3 | 7.163 | -1.063 |
| 8 | 10 | 29.8 | 7.45 | 7.375 | 2.625 |
| 9 | 8.2 | 30.2 | 7.55 | 7.500 | 0.700 |
| 10 | 5.5 | 31.2 | 7.8 | 7.675 | -2.175 |
| 11 | 6.5 | 31.9 | 7.975 | 7.888 | -1.388 |
| 12 | 11 | 32.9 | 8.225 | 8.100 | 2.900 |
| 13 | 8.9 | 33.7 | 8.425 | 8.325 | 0.575 |
| 14 | 6.5 | 33.9 | 8.475 | 8.450 | -1.950 |
| 15 | 7.3 | — | — | — | — |
| 16 | 11.2 | — | — | — | — |
Найдем
оценки сезонной компоненты как разность между фактическими уровнями ряда и
центрированными скользящими среднеми. Используем эти оценки для расчета
значений сезонной компоненты
. Для этого найдем средние
за каждый квартал (по всем годам) оценки сезонной компоненты
:
В моделях
с сезонной компонентой обычно предполагается, что сезонные воздействия за
период взаимопогашаются. В аддитивной модели это выражается в том, что сумма
значений сезонной компоненты по всем кварталам должны быть равна нулю.
Для данной
модели имеем:
Корректирующий
коэффициент:
Рассчитываем
скорректированные значения сезонной компоненты
и заносим полученные данные в таблицу.
Проверим
равенство нулю суммы значений сезонной компоненты:
Исключим влияние сезонной компоненты, вычитая ее
значения из каждого уровня исходного временного ряда. Получим величины
. Эти значения
рассчитываются за каждый момент времени и содержат только тенденцию и случайную
компоненту.
Определим
компоненту
данной модели. Для этого проведем
аналитическое выравнивание ряда
с помощью линейного тренда. Результаты
аналитического выравнивания следующие:
Подставляя
в это уравнение значения
, найдем уровни
для каждого момента времени
Найлем
значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к
уровням
значения сезонной компоненты для
соответствующих кварталов.
На одном
графике отложим фактические значения уровней временного ряда и теоретические,
полученные по аддитивной модели.
Фактические и теоретические уровни
Для оценки
качества построенной модели применим сумму квадратов полученных абсолютных
ошибок:
Следовательно,
можно сказать, что аддитивная модель объясняет 99.3% общей вариации уровней
временного ряда.
3)
Прогнозное значение
уровня временного ряда в аддитивной модели
есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты
воспользуемся уравнением тренда:
Получим:
Значения
сезонных компонент за соответствующие кварталы равны:
Таким
образом:
Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Общий вид аддитивной модели следующий:
![]() . (2.14)
. (2.14)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (![]() ), сезонной (
), сезонной (![]() ) и случайной (
) и случайной (![]() ) компонент.
) компонент.
Общий вид мультипликативной модели выглядит так:
![]() . (2.15)
. (2.15)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (![]() ), сезонной (
), сезонной (![]() ) и случайной (
) и случайной (![]() ) компонент.
) компонент.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений ![]() ,
, ![]() и
и ![]() для каждого уровня ряда.
для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты ![]() .
.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (![]() ) в аддитивной или (
) в аддитивной или (![]() ) в мультипликативной модели.
) в мультипликативной модели.
4) Аналитическое выравнивание уровней (![]() ) или (
) или (![]() ) и расчет значений
) и расчет значений ![]() с использованием полученного уравнения тренда.
с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений (![]() ) или (
) или (![]() ).
).
6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок ![]() для анализа взаимосвязи исходного ряда и других временных рядов.
для анализа взаимосвязи исходного ряда и других временных рядов.
Методику построения аддитивной модели рассмотрим в данном разделе методического пособия.
Пример. Построение аддитивной модели временного ряда. Обратимся к данным об объеме правонарушений на таможне за четыре года, представленным в табл. 2.1.
Как видно из табл. 2.1, данный временной ряд содержит сезонные колебания периодичностью 4, т. к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 2.2).
Таблица 2.1
|
Год |
Квартал |
|
Количество возбужденных дел, |
|
1999 |
I |
1 |
375 |
|
II |
2 |
371 |
|
|
III |
3 |
869 |
|
|
IV |
4 |
1015 |
|
|
2000 |
I |
5 |
357 |
|
II |
6 |
471 |
|
|
III |
7 |
992 |
|
|
IV |
8 |
1020 |
|
|
2001 |
I |
9 |
390 |
|
II |
10 |
355 |
|
|
III |
11 |
992 |
|
|
IV |
12 |
905 |
|
|
2002 |
I |
13 |
461 |
|
II |
14 |
454 |
|
|
III |
15 |
920 |
|
|
IV |
16 |
927 |
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.2). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.2).
Таблица 2.2
|
№ квартала,
|
Количество правонарушений,
|
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
375 |
– |
– |
– |
– |
|
2 |
371 |
2630 |
657,5 |
– |
– |
|
3 |
869 |
2612 |
653 |
655,25 |
213,75 |
|
4 |
1015 |
2712 |
678 |
665,5 |
349,5 |
|
5 |
357 |
2835 |
708,75 |
693,75 |
-336,75 |
|
6 |
471 |
2840 |
710 |
709,375 |
-238,375 |
|
7 |
992 |
2873 |
718,25 |
714,125 |
277,875 |
|
8 |
1020 |
2757 |
689,25 |
703,75 |
316,25 |
|
9 |
390 |
2757 |
689,25 |
689,25 |
-299,25 |
|
10 |
355 |
2642 |
660,5 |
674,875 |
-319,875 |
|
11 |
992 |
2713 |
678,25 |
669,375 |
322,625 |
|
12 |
905 |
2812 |
703 |
690,625 |
214,375 |
|
13 |
461 |
2740 |
685 |
694 |
-233 |
|
14 |
454 |
2762 |
690,5 |
687,75 |
-233,75 |
|
15 |
920 |
– |
– |
– |
– |
|
16 |
927 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 2.2). Используем эти оценки для расчета значений сезонной компоненты ![]() (табл. 2.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты
(табл. 2.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты ![]() . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 2.3

Для данной модели имеем:
![]() .
.
Корректирующий коэффициент: ![]() .
.
Рассчитываем скорректированные значения сезонной компоненты (![]() ) и заносим полученные данные в таблицу 6.6.
) и заносим полученные данные в таблицу 6.6.
Проверим равенство нулю суммы значений сезонной компоненты:
![]() .
.
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины ![]() (гр. 4 табл. 2.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 2.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту ![]() данной модели. Для этого проведем аналитическое выравнивание ряда (
данной модели. Для этого проведем аналитическое выравнивание ряда (![]() ) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
![]() .
.
Подставляя в это уравнение значения ![]() , найдем уровни
, найдем уровни ![]() для каждого момента времени (гр. 5 табл. 2.4).
для каждого момента времени (гр. 5 табл. 2.4).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням ![]() значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 2.4).
значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 2.4).
Таблица 2.4
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
375 |
-292,448 |
667,448 |
672,700 |
380,252 |
-5,252 |
27,584 |
|
2 |
371 |
-266,781 |
637,781 |
673,624 |
406,843 |
-35,843 |
1284,721 |
|
3 |
869 |
268,636 |
600,364 |
674,547 |
943,183 |
-74,183 |
5503,117 |
|
4 |
1015 |
290,593 |
724,407 |
675,470 |
966,063 |
48,937 |
2394,830 |
|
5 |
357 |
-292,448 |
649,448 |
676,394 |
383,946 |
-26,946 |
726,087 |
|
6 |
471 |
-266,781 |
737,781 |
677,317 |
410,536 |
60,464 |
3655,895 |
|
7 |
992 |
268,636 |
723,364 |
678,240 |
946,876 |
45,124 |
2036,175 |
|
8 |
1020 |
290,593 |
729,407 |
679,163 |
969,756 |
50,244 |
2524,460 |
|
9 |
390 |
-292,448 |
682,448 |
680,087 |
387,639 |
2,361 |
5,574 |
|
10 |
355 |
-266,781 |
621,781 |
681,010 |
414,229 |
-59,229 |
3508,074 |
|
11 |
992 |
268,636 |
723,364 |
681,933 |
950,569 |
41,431 |
1716,528 |
|
12 |
905 |
290,593 |
614,407 |
682,857 |
973,450 |
-68,450 |
4685,403 |
|
13 |
461 |
-292,448 |
753,448 |
683,780 |
391,332 |
69,668 |
4853,630 |
|
14 |
454 |
-266,781 |
720,781 |
684,703 |
417,922 |
36,078 |
1301,622 |
|
15 |
920 |
268,636 |
651,364 |
685,627 |
954,263 |
-34,263 |
1173,953 |
|
16 |
927 |
290,593 |
636,407 |
686,550 |
977,143 |
-50,143 |
2514,320 |
На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Рис. 28. График фактических уровней временного ряда
И теоретических, полученных по аддитивной модели.
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
 .
.
Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.
Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года. Прогнозное значение ![]() уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
![]() .
.
Получим
![]() ;
;
![]() .
.
Значения сезонных компонент за соответствующие кварталы равны: ![]() и
и ![]() . Таким образом,
. Таким образом,
![]() ;
;
![]() .
.
Т. е. в первые два квартала 2003 г. следовало ожидать порядка 395 и 422 правонарушений соответственно. Построение мультипликативной модели проводится по той же схеме, что и построение аддитивной модели.
Вопросы для самопроверки
1. В каких случаях для прогнозирования применяют методы прямой экстраполяции?
2. Когда для прогнозирования можно использовать модель тренда?
3. Какие модели трендов обычно используются при прогнозировании в экономике?
4. Перечислите этапы прогнозирования экономических показателей с применением моделей тренда.
5. Что понимают под адекватностью и точностью модели прогнозировании? Как можно проверить адекватность и точность модели прогнозирования?
6. Поясните, почему при прогнозировании наряду с точечным прогнозом рассчитывают и интервальный прогноз?
7. Что такое коэффициент автокорреляции? Как он рассчитывается и что он показывает?
8. Для чего используется критерий Дарбина-Уотсона в моделях временных рядов?
9. Что такое коррелограмма?
10. Поясните технологию расчета точечного интервального прогнозов при использовании моделей тренда.
| < Предыдущая | Следующая > |
|---|
