Основными
характеристиками помехоустойчивых
кодов являются: длина кода n,
его основание m,
общее число кодовых комбинаций N,
число разрешенных кодовых комбинаций
Nр,
избыточность кода Ки
и минимальное кодовое расстояние dmin.
Длина
кода2
n
– это
число символов в кодовой комбинации.
Например, комбинация 11010 состоит из пяти
символов, следовательно, n=5.
Если все кодовые комбинации содержат
одинаковое число символов, то код
называется равномерным.
В неравномерных
кодах длина кодовых комбинаций может
быть разной.
Основание
кода m
– это число различных символов в коде.
Для двоичных кодов символами являются
1 и 0, поэтому m=2.
Число
кодовых комбинаций
для равномерного кода равно N=mn.
Например, для равномерного двоичного
кода, имеющего длину n=6,
число различных кодовых комбинаций
равно N=26=64.
Число
разрешенных кодовых комбинаций Nр
– это количество кодовых комбинаций
кода, используемых для передачи сообщений.
Для помехоустойчивых кодов Nр<N.
Оставшиеся кодовые комбинации N—Nр
называют запрещенными.
Если Nр=N,
то код является безызбыточным. Для
разделимых кодов Nр=2
k.
Избыточность
кода Ки
в общем случае определяется выражением
![]() .
.
(5.1)
и
показывает, какая доля длины кодовой
комбинации не используется для передачи
информации, а используется для повышения
помехоустойчивости кода. Для разделимых
кодов
![]() ,
,
(5.2)
где
величина k/n
называется относительной
скоростью кода.
Кодовое
расстояние d(А,В)
– это число позиций, в которых две
кодовые комбинации А
и В
отличаются друг от друга. Например, если
А=01101,
В=10111,то
d(А,В)=3.
Кодовое расстояние между комбинациями
А
и В
может быть найдено в результате сложения
по модулю 2 одноименных разрядов
комбинаций, а именно
![]() ,
,
(5.3)
где
ai
и
bi
– i-е
разряды кодовых комбинаций A
и
B;
символ
обозначает сложение по модулю 2. Например,
чтобы получить кодовое расстояние между
комбинациями 1101011 и 0111101 достаточно
подсчитать число единиц в сумме этих
комбинаций по модулю 2:

Кодовое
расстояние между различными комбинациями
конкретного кода может быть различным.
Так, для первичных кодов (приложения 1,
2) это расстояние для различных пар
кодовых комбинаций может принимать
значения от единицы до величины длины
кода.
Минимальное
кодовое расстояние dmin
–
это минимальное расстояние между
разрешенными кодовыми комбинациями
данного кода. Минимальное кодовое
расстояние является основной
характеристикой корректирующей
способности кода. В первичных
(безызбыточных) кодах все комбинации
являются разрешенными, поэтому минимальное
кодовое расстояние для них равно единице
(dmin
=
1).
Такие коды не способны обнаруживать и
исправлять ошибки. Для того чтобы код
обладал корректирующими способностями,
его минимальное кодовое расстояние
должно быть не менее двух (dmin
2).
Для
обнаружения всех ошибок кратностью3
s
и менее, минимальное кодовое расстояние
должно удовлетворять условию
dmin
s
+1
. (5.4)
Если
код используется для исправления ошибок
кратности не более t,
то минимальное кодовое расстояние
должно иметь значение
dmin
2t
+1
. (5.5)
Например,
из (5.4) и (5.5) следует, что для обнаружения
однократных ошибок (s
=
1) требуется код с dmin
=
2, а для того чтобы исправить такие
ошибки, требуется код с кодовым расстоянием
dmin
=
3.
Для
обнаружения s
ошибок и исправления t
ошибок должно выполняться условие
dmin
s
+ t
+1 . (5.6)
Таким
образом, задача построения кода с
заданной корректирующей способностью
сводится к обеспечению необходимого
кодового расстояния. Увеличение dmin
приводит к росту избыточности кода. При
этом желательно, чтобы число проверочных
символов r
было минимальным. В настоящее время
известен ряд верхних и нижних границ,
которые устанавливают связь между
кодовым расстоянием и числом проверочных
символов. Сведения о границах для
кодового расстояния будут приведены
позже в процессе оценки качества приема
кодированных сообщений.
Соседние файлы в папке Лекции. СИСТЕМЫ И СЕТИ
- #
- #
- #
- #
- #
- #
- #
Страница 18 из 46
Число используемых символов (или букв в кодовом алфавите) определяет основание кода т. По значению т коды подразделяются на двузначные (двоичные, бинарные) при т=2, трехзначные (т = 3) и многозначные (т>3). Число разрядов п в кодовых комбинациях определяет длину кода. Если длина всех кодовых слов одинакова (п = const), то код называется равномерным.
Емкость кода — число комбинаций (кодовых слов) из общего числа N = тn используемых для передачи сообщений. Эти комбинации называются рабочими Np. Закон Np=f(n,m), по которому составляются рабочие комбинации, и является кодом.
Избыточность кода, коэффициент избыточности.
Из всех возможных кодовых комбинаций N=тn для передачи сообщений используется лишь некоторая часть (Np< N). Остальные же избыточные комбинации служат для целей проверки правильности прохождения кодированного сигнала. Если вместо посланной кодовой комбинации принята кодовая комбинация, не входящая в число Np, то это означает, что в процессе передачи произошла ошибка.
Принятая искаженная комбинация анализируется. Результатом анализа может явиться сигнал ошибки (защитное действие) либо восстановление посланного сигнала (исправление ошибки). Таким образом, способность кодов обнаруживать (или исправлять) ошибки связана с их избыточностью. Избыточность кодов характеризуется коэффициентом избыточности
![]() (3.1)
(3.1)
Значение Kиз лежит в пределах 0 < Киз < 1. Код, у которого используются все возможные комбинации в качестве рабочих (Np = N), называется без избыточным непомехозащищенным кодом. Для такого кода Киз =0.
Кодовое расстояние d между двумя кодовыми комбинациями (кодовыми векторами) равно числу одноименных разрядов с отличными символами. Для двузначных кодов кодовое расстояние определяется как вес (т. е. число единиц) суммы по модулю 2 двух кодовых комбинаций. Например, d между комбинациями 0110111 и 1101010 равно 5, поскольку сумма по модулю 2 1011101 имеет вес, равный 5.
Кодовое расстояние играет важную роль при рассмотрении помехозащищенности кодов. Оно характеризует, насколько одна рабочая комбинация удалена от другой. Чем больше d, тем труднее при прочих равных условиях помехам исказить посланную комбинацию так, чтобы она превратилась в другую рабочую комбинацию, т. е. чтобы было принято ложное сообщение.
Таблица 3.1. Матрица кодовых расстояний d. .
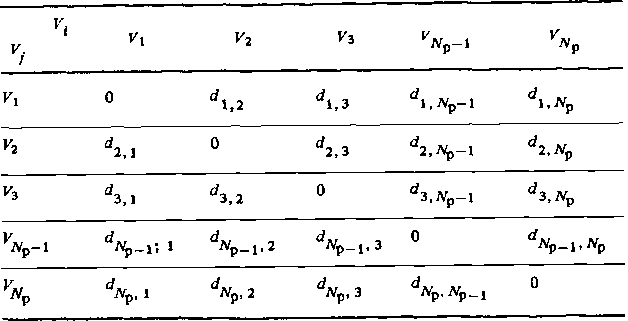
В теории помехозащищенных кодов помехи характеризуются кратностью помех, указывающей число символов кода, которые помеха способна исказить (в двузначных кодах 0 заменить 1 и наоборот). Так, однократная помеха искажает один разряд кодовой комбинации, двукратная — два и т. д.
Если вероятность однократной помехи обозначить р, то для симметричного двоичного канала без памяти вероятность двукратной помехи составит р2, трехкратной -р3 и т. д. Ясно, что при такой модели канала наибольшую опасность имеют однократные помехи, поскольку они наиболее вероятны.
Для характеристики помехозащищенности кода в целом существует понятие минимального кодового расстояния d . — минимально-
го расстояния между любыми парами кодовых векторов, входящих в данный код.
Совокупность кодовых расстояний между всеми рабочими векторами кода Nр образует матрицу кодовых расстояний (табл. 3.1). Минимальное кодовое расстояние определяется из этой матрицы:
![]()
Величина dmin характеризует минимальную кратность помехи, которая может привести к не обнаруживаемым ошибкам (т. е. к приему ложных сообщений). Так, при dmin = 1 уже однократная помеха, т. е. помеха, искажающая всего один бит в кодовой комбинации, приводит к ложному сообщению. Следует подчеркнуть, что в избыточных кодах не все искажения кратности dmin вызывают ложные сообщения.
Однако dmin характеризует ту наименьшую кратность помехи, которая достаточна для появления ложных сообщений.
Зависимость между кодовым расстоянием и кратностью обнаруживаемых и исправляемых ошибок.
Чем большим кодовым расстоянием обладает код, тем он имеет большую потенциальную помехозащищенность. Для обнаружения всех ошибок кратности до r минимальное кодовое расстояние должно быть равно
dmin=r+i· (3-2)
Выполнение условия (3.2) означает, что любая помеха кратности до r не сможет перевести одну рабочую комбинацию в другую, т. е. не сможет образовать ложного сообщения, а переводит рабочую комбинацию в область запрещенных, которые приемник может просто обнаружить и запретить их исполнение.
Существуют коды, которые позволяют не только обнаруживать ошибки, но и исправлять их и тем самым восстанавливать исходные кодовые комбинации, искаженные при передаче. Для исправления ошибок кратности s минимальное кодовое расстояние должно быть увеличено по сравнению с расстоянием, определяемым по формуле (3-2):
![]() (3-3)
(3-3)
При этом кодовые комбинации с ошибками кратности до s как бы группируются вокруг соответствующей рабочей комбинации, образуя группу кодовых векторов, удаленных от данной рабочей комбинации на меньшие расстояния, чем от любых других. Это обстоятельство и используется для исправления ошибок кратности не более s: принятая кодовая комбинация расшифровывается как рабочая, если отстоит от рабочей на расстоянии, не превышающем s.
Для исправления s-кратных и обнаружения r-кратных ошибок необходимо выполнение следующего условия:
![]() (3.4) причем r > s.
(3.4) причем r > s.
Коды, позволяющие обнаруживать (исправлять) ошибки, называются также корректирующими (самокорректирующими).
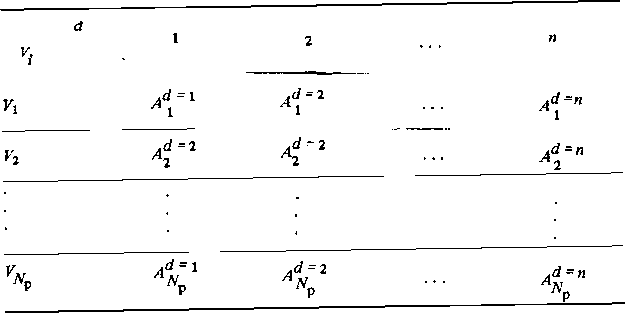
Таблица 3.2. Распределение кодовых векторов d по кодовым расстояниям А.
Распределение рабочих кодовых комбинаций по кодовым расстояниям.
Матрица кодовых расстояний (табл. 3.1) позволяет определить для всех рабочих векторов Vi, i = 1, 2, . . ., Np, числа кодовых векторов, удаленных от данного на расстояния d = 1,2, . . ., п. Эти числа А представляют собой распределение i -го рабочего вектора по кодовым расстояниям в ансамбле рабочих кодов (табл. 3.2). Минимальное значение d в этом распределении равно dmin, максимальное может достигать числа разрядов п (если все разряды кодовых комбинаций инверсны). Если все кодовые векторы имеют одинаковое распределение кодовых расстояний
![]()
то такой код является симметричным. Для характеристики симметричного кода, очевидно, достаточно иметь распределение![]() для одного любого кодового вектора.
для одного любого кодового вектора.
Распределение кодовых векторов по кодовым расстояниям позволяет более детально (по сравнению с известной величиной dmin) охарактеризовать потенциальную помехозащищенность кода. Зная это распределение, можно определить, от какого количества ошибок той или иной кратности защищен данный код. Для этого необходимо вычислить коэффициенты не обнаруживаемых (ложных) переходов одной рабочей комбинации в другие под влиянием помех заданной кратности.
Для простейших кодов существуют формулы для вычисления
Однако в общем случае эти вычисления производятся с помощью несложных программ на ЭВМ.
Коэффициент ложных переходов определяется следующим образом:
![]()
(3.5)
где
![]()
— число рабочих векторов, отстоящих от данного рабочего
![]()
вектора на расстоянии d;![]() — суммарное число возможных кодовых векторов той же разрядности п, отстоящих от данного рабочего вектора на расстоянии d.
— суммарное число возможных кодовых векторов той же разрядности п, отстоящих от данного рабочего вектора на расстоянии d.
Величина![]() для всех двузначных кодов определяется числом сочетаний из числа разрядов n по d:
для всех двузначных кодов определяется числом сочетаний из числа разрядов n по d:
![]()
Рабочий вектор под воздействием d-кратной помехи может перейти в множество![]() векторов, причем если он попадет в подмножество
векторов, причем если он попадет в подмножество
![]() этого множества, то будет принято ложное сообщение. Коэффициент
этого множества, то будет принято ложное сообщение. Коэффициент![]() и характеризует долю ложных переходов под влиянием d-кратной помехи.
и характеризует долю ложных переходов под влиянием d-кратной помехи.
Для симметричных кодов, как было отмечено, существует единое распределение .![]() для кода в целом. Поэтому подсчет
для кода в целом. Поэтому подсчет![]() для таких кодов производится непосредственно по выражению (3.5).
для таких кодов производится непосредственно по выражению (3.5).
Для несимметричных кодов можно определить лишь среднее значение![]() , для чего определяется
, для чего определяется![]() для каждого из Np векторов в отдельности (i=1,2,…, Np) и затем производится усреднение по всем рабочим кодовым векторам:
для каждого из Np векторов в отдельности (i=1,2,…, Np) и затем производится усреднение по всем рабочим кодовым векторам:
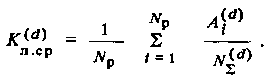 (3.6)
(3.6)
Понятие о минимальном кодовом расстоянии
Одним из основных понятий, на котором базируется любая теория помехоустойчивого
кодирования, является понятие о кодовом расстоянии вообще и о минимальном
кодовом расстоянии в частности.
Пример. Допустим, m = 8, и сообщения
закодированы простым неизбыточным двоичным кодом. Тогда из выражения M
= 2n = 2m следует m
= n = 3. Список рабочих комбинаций имеет следующий вид:

Изобразим так называемую геометрическую модель кода, вводя систему координат
из трех осей, каждая из которых отображает один из разрядов. Модель кода
– куб (рис.25). Каждая кодовая комбинация отображается одной из вершин
куба. Будем называть ребро кубы, определяющее две соседние кодовые комбинации,
одним кодовым переходом и рассматривать как единичное расстояние
между двумя соседними кодовыми комбинациями. Кодовым расстоянием
между парой любых кодовых комбинаций будем называть минимальное число ребер
(кодовых переходов), разделяющих эти комбинации:
![]()
кодовых переходов ![]() .
.
Например,
![]()

Рис. 25 Геометрическая модель двоичного трехразрядного кода
Понятие минимального кодового расстояния характеризует код в целом.
Минимальным кодовым расстоянием dmin
является минимум среди всех кодовых расстояний данного кода, то есть определяется
по всем возможным парам кодовых комбинаций данного кода
![]()
Для рассматриваемого кода dmin= 1. Учитывая, что рассматриваемый код по построению является неизбыточным,
можно утверждать, что любой неизбыточный код имеет dmin= 1 и наоборот, если dmin= 1, код является неизбыточным.
Из геометрической модели кода видно, что любая, даже одиночная, ошибка
не может быть обнаружена кодом с dmin= 1, так как любая кодовая комбинация, в которой произошла ошибка,
переместившись на один кодовый переход, совпадет с соседней кодовой комбинацией
и будет разрешенной.
Для построения простейшего избыточного кода, который может обнаруживать
одну ошибку (r = 1) нужно отобрать рабочие
комбинации на расстоянии
![]()
В рассматриваемом коде можно выбрать следующие комбинации:

где MРАБ
– число рабочих комбинаций.
Избыточность полученного кода
![]() .
.
Если требуется обнаруживать две ошибки (r =
2), то рабочих комбинаций будет только две (например, 000 и 111), минимальное
кодовое расстояние в этом случае dmin
= 3, избыточность
![]() .
.
Если r = 3, dmin≥ 4, что невозможно обеспечить в рассматриваемом
коде, так как кодовое расстояние
![]() .
.
Если бы сообщения кодировались неизбыточным кодом, то для получения
четырех кодовых комбинаций потребовалось бы m =
2 информационных элементов.
В двоичных кодах кодовое расстояние между любыми двумя комбинациями
можно определить как число отличающихся разрядов.
В общем случае в кодах, используемых в режиме обнаружения ошибок кратности
r должно обеспечиваться минимальное кодовое
расстояние
dmin ≥ r + 1. (4)
Определим минимальное кодовое расстояние в кодах, работающих в режиме
исправления s ошибок.
Для исправления s ошибок нужно, очевидно,
искаженную кодовую комбинацию bi
отождествить с комбинацией ai, которая
является рабочей и из которой bi
получилась в результате s искажений. Такое
отождествление производится на базе критерия правдоподобия, под которым
понимается
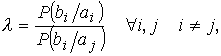
где P(bi / ai) – вероятность образования bi из
ai;
P(ai / bi) – вероятность образования ai из
bi.
λ сравнивается с некоторым
пороговым значением, чаще всего с единицей. Если λ > 1,
то выносится решение о том, что bi
получилось из ai. Если λ < 1,
то выносится решение о том, что bi
нельзя отождествлять с ai.
Значения условных вероятностей, необходимых для вычисления λ,
нельзя установить непосредственно, но можно воспользоваться связью между
ними и соответствующими кодовыми расстояниями. Из факта уменьшения вероятности
появления ошибки при увеличении ее кратности следует:
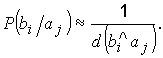
Кодовое расстояние между bi и
ai равно
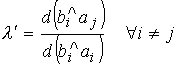 .
.
Если ![]() , то bi
, то bi
получилось из aj, так как ai
ближе к bi, чем ai.
Если ![]() , то bi
, то bi
получилось из ai.
Геометрически этот результат можно интерпретировать следующим образом:
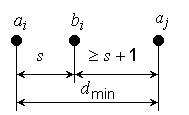
Минимальное расстояние кода, работающего в режиме исправления s
ошибок,
dmin ≥ 2s + 1. (5)
По аналогии можно утверждать, что код, способный обнаруживать r
ошибок и исправлять s из них, должен иметь
минимальное кодовое расстояние
dmin ≥ r + s + 1 (r ≥
s). (6)
Выражения (5) и (6) не противоречат друг другу, так как прежде чем исправлять
ошибку, ее надо сначала обнаружить
Можно показать, что для исправления e ошибок
стирания нужно обеспечить минимальное кодовое расстояние
dmin ≥ e + 1. (7)
В общем случае для обнаружения r ошибок
трансформации, исправления s из них и для исправления
e ошибок стирания нужно обеспечить минимальное
кодовое расстояние
dmin ≥ r + s + e + 1 (r ≥
s). (8)
Выражения (4) — (7) вытекают из (8).
Число обнаруживаемых или исправляемых ошибок.
При применении двоичных кодов учитывают
только дискретные искажения, при которых
единица переходит в нуль (1 → 0) или нуль
переходит в единицу (0 → 1). Переход 1 →
0 или 0 → 1 только в одном элементе кодовой
комбинации называют единичной ошибкой
(единичным искажением). В общем случае
под кратностью ошибки подразумевают
число позиций кодовой комбинации, на
которых под действием помехи одни
символы оказались заменёнными на другие.
Возможны двукратные (t= 2) и многократные (t> 2) искажения элементов в кодовой
комбинации в пределах 0 <t<n.
Минимальное кодовое расстояние является
основным параметром, характеризующим
корректирующие способности данного
кода. Если код используется только для
обнаружения ошибок кратностью t0,
то необходимо и достаточно, чтобы
минимальное кодовое расстояние было
равно
dmin
> t0
+ 1. (13.10)
В этом случае никакая комбинация из t0ошибок не может перевести одну разрешённую
кодовую комбинацию в другую разрешённую.
Таким образом, условие обнаружения всех
ошибок кратностьюt0можно записать в виде:
t0≤ dmin — 1. (13.11)
Чтобы можно было исправить все ошибки
кратностью tии менее, необходимо иметь минимальное
расстояние, удовлетворяющее условию:
![]() . (13.12)
. (13.12)
В этом случае любая кодовая комбинация
с числом ошибок tиотличается от каждой разрешённой
комбинации не менее чем вtи+ 1 позициях. Если условие (13.12) не выполнено,
возможен случай, когда ошибки кратностиtисказят переданную
комбинацию так, что она станет ближе к
одной из разрешённых комбинаций, чем к
переданной или даже перейдёт в другую
разрешённую комбинацию. В соответствии
с этим, условие исправления всех ошибок
кратностью не болееtиможно записать в виде:
tи
≤(dmin
— 1) / 2 . (13.13)
Из (13.10) и (13.12) следует, что если код
исправляет все ошибки кратностью tи,
то число ошибок, которые он может
обнаружить, равноt0= 2∙tи. Следует
отметить, что соотношения (13.10) и (13.12)
устанавливают лишь гарантированное
минимальное число обнаруживаемых или
исправляемых ошибок при заданномdminи не ограничивают возможность обнаружения
ошибок большей кратности. Например,
простейший код с проверкой на чётность
сdmin= 2 позволяет обнаруживать не только
одиночные ошибки, но и любое нечётное
число ошибок в пределахt0<n.
Корректирующие возможности кодов.
Вопрос о минимально необходимой
избыточности, при которой код обладает
нужными корректирующими свойствами,
является одним из важнейших в теории
кодирования. Этот вопрос до сих пор не
получил полного решения. В настоящее
время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают
связь между максимально возможным
минимальным расстоянием корректирующего
кода и его избыточностью.
Так, граница Плоткинадаёт верхнюю
границу кодового расстоянияdminпри заданном числе разрядовnв
кодовой комбинации и числе информационных
разрядовm, и для
двоичных кодов:
![]() (13.14)
(13.14)
или
![]() при
при![]() . (13.15)
. (13.15)
Верхняя граница Хеммингаустанавливает
максимально возможное число разрешённых
кодовых комбинаций (2m)
любого помехоустойчивого кода при
заданных значенияхnиdmin:
 , (13.16)
, (13.16)
где
![]() —
—
число сочетаний изnэлементов поiэлементам.
Отсюда можно получить выражение для
оценки числа проверочных символов:
 . (13.17)
. (13.17)
Для значений (dmin/n)
≤ 0,3 разница между границей Хемминга и
границей Плоткина сравнительно невелика.
Граница Варшамова-Гильбертадля
больших значенийnопределяет нижнюю
границу для числа проверочных разрядов,
необходимого для обеспечения заданного
кодового расстояния:
 . (13.18)
. (13.18)
Отметим, что для некоторых частных
случаев Хемминг получил простые
соотношения, позволяющие определить
необходимое число проверочных символов:
![]() дляdmin= 3,
дляdmin= 3,
![]() дляdmin= 4.
дляdmin= 4.
Блочные коды с dmin= 3 и 4 в литературе обычно называют кодами
Хемминга.
Все приведенные выше оценки дают
представление о верхней границе числаdminпри фиксированных значенияхnиmили оценку снизу числа проверочных
символовkпри заданныхmиdmin.
Существующие методы построения избыточных
кодов решают в основном задачу нахождения
такого алгоритма кодирования и
декодирования, который позволял бы
наиболее просто построить и реализовать
код с заданным значением dmin.
Поэтому различные корректирующие коды
при одинаковыхdminсравниваются по сложности кодирующего
и декодирующего устройств. Этот критерий
является в ряде случаев определяющим
при выборе того или иного кода.
Соседние файлы в папке ЛБ_3
- #
- #
14.04.2015937 б70KodHemmig.m
- #
14.04.20150 б62ЛБ_3.exe
Оценка корректирующей способности блокового (n, k) кода
Кодовое (хемминговое) расстояние — число несовпадающих разрядов двух кодовых комбинаций.
Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.
Кратность ошибки (r) — число искаженных символов кодовой комбинации.
Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.
Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.
Доля обнаруживаемых ошибок 2k(2n-2k)/(2k2n) = 1 — 2k—n
Число кодовых комбинаций: любых 2n , разрешенных 2к, запрещенных 2n — 2k .
 Число вариантов передачи кода 2к 2n. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2k(2n-2k).
Число вариантов передачи кода 2к 2n. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2k(2n-2k).
Рекомендуемые материалы
Доля исправляемых ошибок среди обнаруживаемых 2k(2n—k-1)/2k(2n-2k)=2—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к переданной разрешенной комбинации. Число таких случаев 2k(2n-k-1).
 Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве. Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:
Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве. Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:
Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».
d ³ r + 1 для обнаружения ошибки кратности r,
d ³ 2s + 1 для исправления ошибки кратности s,
d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности r и s.
Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний Сnr . При s = 1 (исправление ошибки кратности 1) должно выполняться условие 2n—k-1 > Cn1 = n, при s = 2 — условие 2n—k-1 > Cn1+ Cn2, в общем случае – условие

Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
������� ������� RFpro.ru:
���������� ������
���������������� ������� �� ���� Linux x64 � Windows x64
�������� ������� RFPRO.RU
�������� �������� ��������� � ���� ��������
|
������� ��������� ������� ������: ���������� �������: 4281 � �������� ������� » |
������ ����� ������: ���������� �������: 3222 � �������� ������� » |
lamed ������: ���������� �������: 2339 � �������� ������� » |
/ ����� � ����������� / ������ � ������������ ����� / �����������
| ����� �������: | 185 |
| ���� ������: | 21.04.2010, 19:00 |
| ������������� ��������: | ���������� �.�., ������������ |
| ����������� / ���������: | 176 / 144 |
| �������� / �������: | 3 / 5 |
������ № 177866: ������� ������� �����, ��������� ��������! ������� ���������� «������ �������� ���������� � ��������». �������� ���������� ������ ����� ������: ���������� ����������� ������� ����������, ����������� ��� ����������� ������� ������. ������…
������ № 177867: ������� ������� �����, ��������� ��������! ������� ���������� «������ �������� ���������� � ��������». �������� ���������� ������ ����� ������: ��������� ��� �������-���� ��� ����� ��������� A, B, C, D, E, F, ������������ � �������������…
������ № 177870: ������������, ��������� ��������. ����������, ����������, ��� � qBasic ��������� ��������� ���������� Y = ( ∑{i=0…n} xi ) / (n+1) ������� �������…
������ № 177866:
������� ������� �����, ��������� ��������!
������� ���������� «������ �������� ���������� � ��������». �������� ���������� ������ ����� ������: ���������� ����������� ������� ����������, ����������� ��� ����������� ������� ������. ������ ����� ��������� ����� ��������� ���, ��� �������� dmin=7?
� ���������, ��������.
���������: 16.04.2010, 11:00
������ �����: ������ �������� ����������, ����������
����� �������: 2
�������� ������� »
�������� F®ost, ������� ��������� :
������������, ������ �������� ����������.
����������� ������� ���������� — ��������, ������������ ������������������ ���� � ���������� � ���� ������������. ����������� ������� ����������� ������������ �������������� �������� �����. � ����� ������ ��� ����������� r ������ ����������� ������� ����������
d0=r+1=3+1=4.
� ����� ������, ����� ���������� ��� �������� ������������ ������ ���������� r, ������ ����������� �������
dmin>r+1.
�� �������, dmin=7, ������ r+1=6<7, ���������
������ r=6-1=5.
——
�� ������� � ������, �� �������� � �������
����� ��������: F®ost, ������� ���������
����� ���������: 16.04.2010, 11:19
����� ������: 260844
��������, �����
���.: 375292792018
�����������: ������� ���������������
�����: ��. �.�������, 13, �. �����, ��������
����� �����: ������� ���������������
������ ������: 5
����������� � ������:
��������� �� ������.
�������!!!
� ���������, ��������.
| ��� ����� �����? ����������, ������������� �������� �� ���! ��� ������� ����� �������� «�������»? |
|
�� ����� 1151 (������) | ��� ������ » |
|
|
�������� coremaster1, 8-� ����� :
������������, ������ �������� ����������.
��� � ����������� ������� ����������� d �������� ������������ d — 1 ������ � ���������� (d — 1)/2 ������.
��� ����������� �ң� ������ ������� ���������� ������ ���� �� ����� 4.
��� ������� ���� � dmin = 7 ����� ���������� (7 — 1)/2 = 3 ������.
����� ��������: coremaster1, 8-� �����
����� ���������: 16.04.2010, 11:49
����� ������: 260845
������ ������: 5
����������� � ������:
�������!!!
�������!
� ���������, ��������.
| ��� ����� �����? ����������, ������������� �������� �� ���! ��� ������� ����� �������� «�������»? |
|
�� ����� 1151 (������) | ��� ������ » |
|
|
������ № 177867:
������� ������� �����, ��������� ��������!
������� ���������� «������ �������� ���������� � ��������». �������� ���������� ������ ����� ������: ��������� ��� �������-���� ��� ����� ��������� A, B, C, D, E, F, ������������ � ������������� 0.4; 0.25; 0.15; 0.1; 0.05; 0.05. ��������� ������� ����� ������� ���������� � �������� �� � ��������� ���������.
� ���������, ��������.
���������: 16.04.2010, 11:10
������ �����: ������ �������� ����������, ����������
����� �������: 2
�������� ������� »
�������� F®ost, ������� ��������� :
������������, ������ �������� ����������.
���� ����� ������� ������������ ��������� ��������� �������� �� �� ����������� �� ������. ����� ����������� ��������� ����:
�) ������ �������� ������� �� ��� ����� (������� �� ������ � ������ �������) ���, ����� ����� ������ ����� ������ (������� �� ∑1 � ∑2) ���� ����� ��� �������� �����. � ������, ����� ������� ��������� ������� �� �������, ������� ����� ������� ������ ���� ����������;
�) ������� ����������� ������ ����� ������������ 1, �������
����������� ������ ����� ������������ 0;
�) ����������� ������ �����: ���� ��� �������� ������ ���� ������, ������ � ��� �������������, – ���������, ��� ��� ��� �� �������� ��������, � ����������� ������� � ���� �) ��� ���������� ���� ������ �����. ���� �������� ������ ������, ��������� � ���� �) � ��������� ����������� � ������ ������ ��� � ��������������� ������������� �������;
�) ����������� ������ �����: ���� ��� �������� ������ ���� ������, ������ � ��� ����
��������� � ����������� ��������� � ����������� ������ (��� �). ���� �������� ������ ������, ��������� � ���� �) � ��������� ����������� �� ������ ������ ��� � ��������������� �������;
�) ������������� ���������� ������: ���� �� ���� – ��� ��������, ������ �������������. ���� ���, – ����������� ��� �).
��������� � ���������� ����:
1 ����.
∑1=�+�=0,65
∑2=�+D+E+F=0,35
��� ���������:
�=1
B=1
C=0
D=0
E=0
F=0
2 ����.
∑1=�=0,4
∑2=�=0,25
�=11
B=10
C=0
D=0
E=0
F=0
3
����.
∑1=�=0,15
∑2=D+E+F=0,2
�=11
B=10
C=01
D=00
E=00
F=00
4 ����.
∑1=D=0,1
∑2=E+F=0,1
�=11
B=10
C=01
D=001
E=000
F=000
5 ����.
∑1=E=0,05
∑2=F=0,05
�=11
B=10
C=01
D=001
E=0001
F=0000
��� � ���� ��� ������-���� ��� ���������.
��������� ������� ����� ������� ���������� (�����
�������� ������������ ����) �� �������:
l�� = 0,4*2 + 0,25*2 + 0,15*2 + 0,1*3 + 0,05*4 + 0,05*4 = 2,3.
——
�� ������� � ������, �� �������� � �������
����� ��������: F®ost, ������� ���������
����� ���������: 16.04.2010, 12:04
����� ������: 260846
��������, �����
���.: 375292792018
�����������: ������� ���������������
�����: ��. �.�������, 13, �. �����, ��������
����� �����: ������� ���������������
������ ������: 5
����������� � ������:
�������!!!
��� ������� �� ������ � �� �������� ��������.
� ���������, ��������.
| ��� ����� �����? ����������, ������������� �������� �� ���! ��� ������� ����� �������� «�������»? |
|
�� ����� 1151 (������) | ��� ������ » |
|
|
�������� coremaster1, 8-� ����� :
������������, ������ �������� ����������.
������ ���������� ���� �������-���� ��������� �� �������. � ������� ������� ��������� ����������� ������ ��������.
�������� ������ ����� ��������� ������� ����������:
A: 1
B: 01
C: 001
D: 0001
E: 00001
F: 00000
������� ����� ������� ����������: 1*0.4 + 2*0.25 + 3*0.15 + 4*0.1 + 5*0.05 + 5*0.05 = 2.25
�������� ���������: -[0.4*log2(0.4) + 0.25*log2(0.25) + 0.15*log2(0.15) + 0.1*log2(0.1) + 2*0.05*log2(0.05)]
= 2.20 ���
����� ��������: coremaster1, 8-� �����
����� ���������: 16.04.2010, 14:06
����� ������: 260852
������ ������: 5
����������� � ������:
�������!!!
��������� �� ������� ������ � �� ��������.
� ���������, ��������.
| ��� ����� �����? ����������, ������������� �������� �� ���! ��� ������� ����� �������� «�������»? |
|
�� ����� 1151 (������) | ��� ������ » |
|
|
������ № 177870:
������������, ��������� ��������. ����������, ����������, ��� � qBasic ��������� ��������� ����������
Y = ( ∑{i=0…n} xi ) / (n+1)
������� �������
���������: 16.04.2010, 13:40
������ �����: Ushastik1985, ����������
����� �������: 1
�������� ������� »
�������� ������ ����� ����������, ��������� :
������������, Ushastik1985.
��������, ���:
���:
'������� �����
CLS
'������ n
INPUT "n = ", n
'������ ������ (� 0)
DIM x(n)
'��������� �������� �����
Y = 0
'���� �� ���� ��������� �������
FOR i = 0 TO n
'������� ����������� x(i)=, ����� � ������� - ����� ��� ��������� ����������,
'� ����� - ����� �� ���� �������� �� ��������� ������
PRINT "x("; i; ") = ";
'������ x(i)
INPUT "",x (i)
'������������
Y = Y + x(i)
'�� ������ ����� �� i
NEXT
'�������� ����� �� n+1
Y = Y / (n + 1)
'������� ���������
PRINT "Y = ";Y
'�������� ������� �� �������
a$ = INKEY$ '
——
�����!
����� ��������: ������ ����� ����������, ���������
����� ���������: 16.04.2010, 14:39
����� ������: 260853
�������, ����������
���.: +380957525051
ICQ # 234137952
Mail.ru-�����: igorlyskov@mail.ru
������� Skype: igorlyskov
������ ������: 5
| ��� ����� �����? ����������, ������������� �������� �� ���! ��� ������� ����� �������� «�������»? |
|
�� ����� 1151 (������) | ��� ������ » |
|
|
������� ������ »
��� ����� ����� ���� ������ �� ���� ������� ��������!
������ ������ ��������� ���� �������� »
������� «�������» ��������, ������� ����� ���!
��������� ���-��������� � ������ #thank �����_������
�� �������� ����� 1151 (������)
����� ������ � ���������� ����� ��� ������ ����� ������� ������.
������ ������ ������� »
* ��������� ������ ���-��������� �� 7.15 ���. � ������� �� ��������� ������� �����.
(������ ������ �������)
** ��� ��������� ����� ������ ������ ��� ������ #thank ������ ��������� ���������, �������� �������� �� ������������.
*** ����� ������� ��������-������ ������ ������������� �� ����� ������������ �� ������ �� ����������� ��������.
