— Нарисовать структурную схему кодера и декодера, исправляющего ошибку.
— Определить проверочный код для передаваемой кодовой комбинации 1011.
— Исправить ошибку, допущенную в четвертом элементе принятой кодовой комбинации.
Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока. Поясним идею проверки на чётность на примере простейшего корректи-рующего кода, который так и называется кодом с проверкой на чётность иликодом с проверкой по паритету (равенству).В таком коде к кодовым комбинациям безизбыточного первичного двоич-ного k — разрядного кода добавляется один дополнительный разряд (символпроверки на чётность, называемый проверочным, или контрольным). Если чис-ло символов “1” исходной кодовой комбинации чётное, то в дополнительномразряде формируют контрольный символ 0, а если число символов “1” нечёт-ное, то в дополнительном разряде формируют символ 1. В результате общеечисло символов “1” в любой передаваемой кодовой комбинации всегда будет чётным.Таким образом, правило формирования проверочного символа сводится кследующему:
Помехоустойчивое кодирование
r1 = i1 ⊕ i2 ⊕ . ⊕ ik ,
где i — соответствующий информационный символ (0 или 1), k — общее их числоа под операцией «⊕» здесь и далее понимается сложение по mod2. Очевидно,что добавление дополнительного разряда увеличивает общее число возмож-ных комбинаций вдвое по сравнению с числом комбинаций исходного первич-ного кода, а условие чётности разделяет все комбинации на разрешённые инеразрешённые. Код с проверкой на чётность позволяет обнаруживать одиноч-ную ошибку при приёме кодовой комбинации, так как такая ошибка нарушаетусловие чётности, переводя разрешённую комбинацию в запрещённую.Критерием правильности принятой комбинации является равенство нулюрезультата S суммирования по mod 2 всех n символов кода, включая провероч-ный символ r1. При наличии одиночной ошибки S принимает значение 1:
S = r1 ⊕ i1 ⊕ i2 ⊕ . . . ⊕ ik = 0 — ошибки нет
1444424443 = 1 — однократная ошибка. n
Этот код является (k +1, k) — кодом, или (n, n -1) — кодом. Минимальное рас-стояние кода равно двум (d min = 2), и, следовательно, никакие ошибки не могутбыть исправлены. Простой код с проверкой на чётность может использоватьсятолько для обнаружения (но не исправления) однократных ошибок.Увеличивая число дополнительных проверочных разрядов и формируя поопределённым правилам проверочные символы r, равные 0 или 1, можно уси-лить корректирующие свойства кода так, чтобы он позволял не только обнару-живать, но и исправлять ошибки. На этом и основано построение кодов Хем-минга.Коды Хемминга. Рассмотрим эти коды, позволяющие исправлять одиноч-ную ошибку, с помощью непосредственного описания. Для каждого числа про-верочных символов r = 3,4,5… существует классический код Хемминга с марки-ровкой (n,k) = (2r–1, 2r–1 –r) , (3.20)
При других значениях числа информационных символов k получаются такназываемые усечённые (укороченные) коды Хемминга. Так, для международно-го телеграфного кода МТК-2 , имеющего 5 информационных символов, потре-буется использование корректирующего кода (9,5), являющегося усечённым отклассического кода Хемминга (15,11), так как число символов в этом кодеуменьшается (укорачивается) на 6. Для примера рассмотрим классический кодХемминга (7,4), который можно сформировать и описать с помощью кодера,представленного на рис.3.2. В простейшем варианте при заданных четырёх(k=4) информационных символах (i1, i2, i3, i4) будем полагать, что они сгруппиро-ваны в начале кодового слова, хотя это и не обязательно. Дополним эти ин-формационные символы тремя проверочными символами (r = 3), задавая ихследующими равенствами проверки на чётность, которые определяются соот-ветствующими алгоритмами [3,5]:
Циклический код (15,11) Часть 1
где знак ⊕ означает сложение по модулю 2.
В соответствии с этим алгоритмом определения значений проверочныхсимволов ri ниже выписаны все возможные 16 кодовых слов (7,4) — кода Хем-минга.
На рис. 3.3 приведена схема декодера для (7,4) — кода Хемминга, на входкоторого поступает кодовое слово
V = ( i1′, i2′, i3′, i4′, r1′, r2′, r3′)
Апостроф означает, что любой символ слова может быть искажён помехой вканале передачи.
В декодере в режиме исправления ошибок строится последовательность:
s1 = r1′ ⊕ i1′ ⊕ i2′ ⊕ i3′;
s2 = r2′ ⊕ i2′ ⊕ i3′ ⊕ i4′;
s3 = r3′ ⊕ i1′ ⊕ i2′ ⊕ i4′. Трёхсимвольная последовательность ( s1, s2, s3 ) называется синдромом.
Термин «синдром» используется и в медицине, где он обозначает сочетаниепризнаков, характерных для определённого заболевания. В данном случаесиндром S = (s1, s2, s3 ) представляет собой сочетание результатов проверкина чётность соответствующих символов кодовой группы и характеризует опре-делённую конфигурацию ошибок (шумовой вектор).
Кодовые слова (7,4) — кода Хемминга.
Источник: studopedia.ru
Кодер и декодер кода Хэмминга на VB.NET

Данный кодер легко переписать таким образом, чтобы он работал не с битовыми массивами типа BitArray(), а с байтами: на вход получал 11-разрядное число (от 0 до 0x7FF) и выдавал 2 закодированных байта:
Public Shared Function Encode_15_11(ByVal numberToEncode As Integer) As Byte() Dim enc As BitArray = Hamming.Encode_15_11(New BitArray()) Dim encBytes(1) As Byte enc.CopyTo(encBytes, 0) Return encBytes End Function
3 Декодер кода Хэмминга (15, 11), написанный на VB.NET
Теперь пора поговорить о декодере. Декодер получает на вход 2 байта закодированных данных и возвращает 11 бит декодированных данных, которые распределены по двум байтам. Если в кодер были переданы 8 бит данных, то нас будет интересовать только первый байт, полученный с декодера.
Код декодера Хэмминга (15, 11) на VB.NET (разворачивается)
»’ »’ Декодер кода (15, 11). »’ »’ Входные данные, 16 бит (2 байта). »’ Выходные данные – 10 бит.
»’ »’ Размещение проверочных и информационных бит в кодовом слове: »’ »’ |15|14|13|12|11|10|09|08|07|06|05|04|03|02|01|00| »’ code_word| L| K| I| H| G| F| E| P| D| C| B| P| A| P| P| X| »’ out_data | | | | | | L| K| I| H| G| F| E| D| C| B| A| »’ »’ A,B,C,D,E,F,G,H,I,K,L – биты данных информационного слова; »’ P – проверочный бит; »’ X – бит, равный 0 (не используется). »’ »’ Кодовое слово дополняется одним битом, чтобы длина была равна степени двойки. Сейчас этот бит никак не используется. »’ Можно его использовать как бит четности и получить так называемый дополненный код Хэмминга.
Здесь этого не сделано. »’ Public Shared Function Decode_15_11(ByVal b As Byte()) As Integer Dim codeWord As New BitArray(b) ’16 бит входных данных ‘Весь процесс декодирования – это сложение по модулю два бит информационного слова, по весу полученных единиц в результате – получение позиции ошибки. Dim syndrome As New BitArray(4) ‘Вычисление первого проверочного символа из полученного кодового слова и далее сравнение его с полученным. syndrome(0) = codeWord(3) Xor codeWord(5) Xor codeWord(7) Xor codeWord(9) Xor codeWord(11) Xor codeWord(13) Xor codeWord(15) Xor codeWord(1) ‘Вычисление второго проверочного символа из полученного кодового слова и далее сравнение его с полученным. syndrome(1) = codeWord(3) Xor codeWord(6) Xor codeWord(7) Xor codeWord(10) Xor codeWord(11) Xor codeWord(14) Xor codeWord(15) Xor codeWord(2) ‘Вычисление третьего проверочного символа из полученного кодового слова и далее сравнение его с полученным. syndrome(2) = codeWord(5) Xor codeWord(6) Xor codeWord(7) Xor codeWord(12) Xor codeWord(13) Xor codeWord(14) Xor codeWord(15) Xor codeWord(4) ‘Вычисление четвёртого проверочного символа из полученного кодового слова и далее сравнение его с полученным. syndrome(3) = codeWord(9) Xor codeWord(10) Xor codeWord(11) Xor codeWord(12) Xor codeWord(13) Xor codeWord(14) Xor codeWord(15) Xor codeWord(8) ‘Вычисление по синдрому позиции ошибки.
Это просто ПЗУ или дешифратор. ‘Если смотреть на синдром как на число — то это и есть номер позиции ошибки. ‘Синдром равен 0 — ошибки нет. ‘Поскольку на выход модуля передаются только биты данных — не все варианты перечислены, нет смысла исправлять проверочные биты. Dim syn As Integer = (Convert.ToInt32(syndrome(3)) ) Case 5 ‘позиция 5 correction = New BitArray() Case 6 ‘позиция 6 correction = New BitArray() Case 7 ‘позиция 7 correction = New BitArray() Case 9 ‘позиция 9 correction = New BitArray() Case 10 ‘позиция 10 correction = New BitArray() Case 11 ‘позиция 11 correction = New BitArray() Case 12 ‘позиция 12 correction = New BitArray() Case 13 ‘позиция 13 correction = New BitArray() Case 14 ‘позиция 14 correction = New BitArray() Case 15 ‘позиция 15 correction = New BitArray() Case Else ‘Если синдром равен 0 или указывает на ошибку в проверочном символе «P» — коррекция информационных символов не требуется. ‘Мы инициализировали correction() нулями (correction = New BitArray(11)), поэтому ничего делать не нужно.
End Select ‘Результат декодирования с учетом коррекции (11 бит выходных данных): Dim outData As New BitArray(11) outData(0) = codeWord(3) Xor correction(0) outData(1) = codeWord(5) Xor correction(1) outData(2) = codeWord(6) Xor correction(2) outData(3) = codeWord(7) Xor correction(3) outData(4) = codeWord(9) Xor correction(4) outData(5) = codeWord(10) Xor correction(5) outData(6) = codeWord(11) Xor correction(6) outData(7) = codeWord(12) Xor correction(7) outData(8) = codeWord(13) Xor correction(8) outData(9) = codeWord(14) Xor correction(9) outData(10) = codeWord(15) Xor correction(10) Dim masks(31) As Integer masks(0) = BitVector32.CreateMask() For i As Integer = 1 To 31 masks(i) = BitVector32.CreateMask(masks(i — 1)) Next Dim v As New BitVector32 For i As Integer = 0 To 10 v(masks(i)) = outData(i) Next Dim decoded As Integer = v.Data Return decoded End Function
Для быстрой проверки кодировщика и декодировщика кода Хэмминга (15, 11), используя вышеописанные классы, я написал две программы. Первая – кодер Хэмминга . Вводите 11-разрядное число (от 0 до 0x7FF или 2047), и на выходе получаем 16-разрядное число, представленное в виде двух байтов.
Вторая программа – декодер кода Хмминга (15, 11) .

Легко убедиться, что если мы внесём битовую ошибку при декодировании, то декодер восстановит исходное закодированное число.
Обе программы работают под ОС Windows и требуют .NET версии 3.5 . Выкладываю описанные программы.
Скачать кодер и декодер кода Хэмминга (15, 11)
- Скачать кодер и декодер кода Хэмминга (15, 11) с Depositfiles.com
- Скачать кодер и декодер кода Хэмминга (15, 11) c Up-4ever.com
Источник: soltau.ru
Изучение кодеров и декодеров Хэмминга
В блочных кодах непрерывная информационная последовательность делится на блоки — сообщения длиной k символов. Кодер преобразует блоки информации в более длинные двоичные последовательности, состоящие из n символов, которые называются кодовыми словами. Символы (n-k), добавляющиеся к каждому блоку информации, называются избыточными.
Код называется линейным, если сумма по модулю 2 двух кодовых комбинаций также является кодовой комбинацией этого кода.
Важным качеством линейных блочных кодов является систематичность. Систематический код содержит неизменную информационную часть длиной k символов и избыточную длиной (n-k) символов. Блочный код, обладающий свойствами линейности и систематичности, называется линейным блочным систематическим кодом и обозначается как (n-k).
Коды Хэмминга относятся к линейным систематическим кодам, в которых проверочные разряды (избыточные символы) формируются линейным преобразованием (суммированием по модулю 2) информационных разрядов (символы сообщения). Данные коды имеют кодовое расстояние d0=3 и d0=4.
данного типа связано с кодовым расстоянием следующим выражением:
Таким образом, с учетом кодового расстояния, коды Хэмминга позволяют исправлять только одну ошибку.
В зависимости от количества информационных и проверочных разрядов в кодовых словах выделяют коды Хемминга (7,4), (9,5), (11, 7), (15, 11). Обозначение кода (7, 4) означает, что длина кодового слова равна 7 бит, а длина сообщения 4.
Следовательно, число проверочных разрядов r в коде равно 3. По аналогии рассматриваются другие типы кодов.
«Синдром» определяется как сумма по модулю 2 принятых приемником проверочных разрядов bi кода Хэмминга и заново вычисленных проверочных разрядов b*i по принятым информационным элементам кода. При этом проверочные разряды b*i рассчитываются по тем же самым выражениям, которые использовались при расчете bi.
Если в результате суммирования по модулю 2 элементов bi и b*i «синдром» равен нулю, то ошибки в кодовой комбинации отсутствуют, при наличии ошибки в составе «синдрома» появятся единицы.
Двоичное число «синдрома» представляет собой условный номер (в десятичной системе) разряда в коде, где произошла ошибка. В таблице 1 приведены числа, представляющие синдром, для кода Хэмминга (7,4).

Если ошибка происходит в одном из проверочных элементов, то в составе «синдрома» будет только одна единица, например, при возникновении ошибки в разряде b1 ей будет соответствовать двоичный код «синдрома» 100 (десятичное число 4). Появление большего числа единиц в «синдроме» будет связано с ошибками в информационной части кода. В таблице условные номера присваиваются информационным элементам в порядке возрастания двоичного числа «синдрома».
Используя приведенную таблицу, определяются выражения для расчёта элементов проверочной группы bi. Например, в двоичном коде «синдрома» элемента b1 единица присутствует в разряде C1, поэтому в выражение для его расчёта будут входить только те информационные элементы кода, у которых в разряде С1 «синдрома» также находится единица. Такими информационными элементами являются a2 a3 и а4. По аналогии определяются формулы для расчёта b2 и b3.
Таким образом, выражения для расчета проверочной группы кода Хэмминга (7, 4) имеют вид:

Приведенные соотношения можно компактно отобразить в виде проверочной матрицы Н:

По аналогии строится таблица, проверочная матрица и выводятся выражения для расчета проверочной группы кодов Хэмминга (9, 5), (11,7), (15,11).
Аппаратная реализация кодера Хэмминга может быть представлена в соответствии со структурной схемой, приведённой на рис. 2.

Кодер включает в себя входной и выходной регистры, логическую схему и систему управления. На вход устройства поступает информационная последовательность от источника сообщения, которая записывается во входной регистр. В логической схеме рассчитываются элементы проверочной группы, согласно выражениям, полученным на основе анализа «синдрома». После этого информационная и проверочная кодовые группы записываются в выходной регистр. Система управления реализует заданный алгоритм кодирования информации.
Структура декодера Хэмминга приведена на рис. 3. Она включает в себя входной и выходной регистры, логическую схему и схему сравнения, дешифратор и схему исправления ошибок. Код Хэмминга поступает во входной регистр, где выполняется его преобразование из последовательной формы в параллельную.
Логическая схема рассчитывает элементы проверочной группы b*i по принятым информационным элементам. Схема сравнения вычисляет «синдром». В случае ненулевого «синдрома» дешифратор выполняет преобразование его двоичного кода в десятичный, соответствующий номеру разряда кода в котором произошла ошибка, а схема исправления ошибок инвертирует данный разряд. В выходной регистр записывается декодированная кодовая последовательность. Система управления реализует заданный алгоритм декодирования информации.

Выполнение работы
1. Составим таблицы синдромов для кодов Хэмминга (7,4), (9,5), (11,7), (15,11):

2. Получим выражения для расчета элементов проверочных групп для кодов Хэмминга (7,4), (9,5), (11,7), (15,11):
3. На элементах ИСКЛ-ИЛИ построим структуры кодеров и проверим прохождение сигналов:
4. На стенде подадим на вход кодера (7,4) построенный код, проверим эпюры работы декодера в контрольных точках.
Введем ошибку в код (7,4), и подадим полученный код на вход декодера, приведем эпюры. Убедимся, что декодер исправил ошибку.
Код без ошибки Код с ошибкой во 2 разряде
Источник: studbooks.net
Где ошибка? Код Хэмминга (15,11)
Ввожу 11-битовое кодовое слово, умножаю его на порождающую матрицу, получаю закодированное слово, затем ввожу это закодированное слово и он пишет, что есть ошибка, хотя такого быть не должно. Где ошибка в коде найти не могу.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.IO; namespace ConsoleApplication1 { class Test { static void Main() { char[] data = new char[11]; int[] encoded = new int[15]; int[] edata = new int[15]; int[] syndrome = new int[12]; int[,] hmatrix = new int[4, 15]{{1,0,0,0,1,0,0,1,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,0,1,0,1,1,0,1,1}, {0,0,1,0,0,1,1,1,0,0,1,1,1,0,1}, {1,0,0,1,0,0,1,0,1,1,0,1,1,1,1}}; char[,] gmatrix = new char[11, 15] { { ‘1’, ‘1’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘0’, ‘1’, ‘1’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘0’, ‘0’, ‘1’, ‘1’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘1’, ‘0’, ‘1’, ‘1’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘0’, ‘1’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘1’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘1’, ‘1’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’ }, { ‘0’, ‘1’, ‘1’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’ }, { ‘1’, ‘0’, ‘1’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’, ‘0’ }, { ‘1’, ‘1’, ‘0’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’, ‘0’ }, { ‘1’, ‘1’, ‘1’, ‘1’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘1’ }}; int i, j; Console.Write(«nКод Хэмминга. КодированиеnnВведите 11-битовое слово: n»); for (int d = 0; d 11; d++) { data[d] = Convert.ToChar(Console.ReadLine()); } //Console.Write(«nGenerator matrix entern»); /* for(i=0;i <11;i++) for(j=0;j <15;j++) Console.Write(«,»,i,j); gmatrix[i,j]=Convert.ToChar(Console.ReadLine()); > Console.WriteLine(); > */ Console.Write(«nПорождающая матрицаn»); for (i = 0; i 11; i++) for (j = 0; j 15; j++) { Console.Write(» t Console.WriteLine(); } Console.WriteLine(«nКодированные данныеn»); for (i = 0; i 15; i++) for (j = 0; j 11; j++) encoded[i] += ((data[j] — 0) * (gmatrix[j, i] — 0)); encoded[i] = encoded[i] % 2; Console.Write(» Console.Write(«nКод Хэмминга. ДекодированиеnnВведите кодированные данные : n»); for (i = 0; i 15; i++) edata[i] = Convert.ToChar(Console.ReadLine()); for (i = 0; i 4; i++) { for (j = 0; j 15; j++) syndrome[i] += (edata[j] * hmatrix[i, j]); syndrome[i] = syndrome[i] % 2; } for (j = 0; j 15; j++) if ((syndrome[0] == hmatrix[0, j]) (syndrome[1] == hmatrix[1, j]) (syndrome[2] == hmatrix[2, j]) (syndrome[3] == hmatrix[3, j])) break; if (j == 15) Console.Write(«nОшибок нетn»); else «, 0); else if (edata[j] == 49) Console.Write(» Console.ReadKey(); } } }
Добавлено через 54 минуты
Например я ввожу 10100101111. Получаю закодированное слово 100010100101111. Ввожу 100010100101111 и он пишет, что ошибка находится в 4 бите. Такого быть не должно.
Добавлено через 19 минут
Хэлпаните как-нибудь уже
Источник: www.cyberforum.ru
Коды Хэмминга
позволяют
исправлять одиночную ошибку в блоке.
Для каждого числа проверочных символов
![]() существует классический код Хэмминга
существует классический код Хэмминга
с маркировкой
![]() ,
,
(8.57)
т.е. — (7,4), (15, 11),
(31, 26) …
При других значениях
числа информационных символов т
получаются
так называемые усеченные
(или
укороченные)
коды Хэмминга.
Так, для
международного телеграфного кода
МТК-2, имеющего 5 информационных символов,
потребуется использование
корректирующего кода (9,5), являющегося
усеченным от классического кода Хэмминга
(15,11), так как число символов в этом коде
уменьшается (укорачивается) на 6. Для
примера рассмотрим код Хэмминга (7,4).
В простейшем
варианте при заданных четырех (т=4)
информационных символах
![]() будем полагать, что они сгруппированы
будем полагать, что они сгруппированы
в начале кодового слова, хотя это и не
обязательно. Дополним эти информационные
символы тремя проверочными символами
(![]() ),
),
задавая их следующими равенствами
проверки на четность, которые определяются
соответствующими алгоритмами. Известно,
что кодовое расстояние равно минимальному
числу проверок, в которые входит
информационный символ, плюс 1. В
рассматриваемом коде![]() .
.
Следовательно,
каждый информационный символ должен
входить минимум в две проверки. Определим
правило формирования проверочных
символов следующим образом:
 (8.58)
(8.58)
В соответствии с
этим алгоритмом определения значений
проверочных символов
![]() в табл. 8.13 приведены все возможные 16
в табл. 8.13 приведены все возможные 16
кодовых слов кода Хэмминга (7,4).
Таблица 8.13. Кодовые
комбинации кода Хэмминга (7,4)
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Составим производящую
матрицу
![]() в канонической форме
в канонической форме
![]() или
или
![]() (табл.8.14).
(табл.8.14).
Таблица 8.14.
Производящая матрица
![]() в канонической форме
в канонической форме
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
 ,
,

Составим проверочную
матрицу
 .
.
Транспонированная
проверочная матрица будет иметь вид
 .
.
Предположим, что
на вход декодера для (7,4)-кода Хэмминга
поступает кодовое слово
![]() .
.
Апостроф означает,
что любой символ слова может быть искажен
помехой в канале связи и возникает
ошибка
![]() .
.
В декодере в режиме
исправления ошибок строится
последовательность:
![]() (8.59)
(8.59)
где
![]() – результат декодирования (синдром),
– результат декодирования (синдром),
который в данном случае является
трехсимвольным.
Символы синдрома
можно так же получить с использованием
следующей процедуры
 (8.60)
(8.60)
В данном случае
синдром
![]() представляет собой сочетание результатов
представляет собой сочетание результатов
проверки на четность соответствующих
символов кодовой группы и характеризует
определенную конфигурацию ошибок(вектор
ошибок).
Число возможных
синдромов определяется выражением
![]() .
.
(8.61)
При числе проверочных
символов
![]() имеется восемь возможных синдромов (23
имеется восемь возможных синдромов (23
= 8). Нулевой синдром (000) указывает на то,
что ошибки при приеме отсутствуют
или не обнаружены. Всякому ненулевому
синдрому соответствует определенная
конфигурация ошибок, которая и
исправляется. Классические коды
Хэмминга
имеют число синдромов, точно равное их
необходимому числу, позволяют исправить
все однократные ошибки в любом
информативном и проверочном символах
и включают один нулевой синдром. Такие
коды называются плотноупакованными.
Для рассматриваемого
кода (7,4) в табл. 8.15 представлены ненулевые
синдромы и соответствующие конфигурации
ошибок.
Таблица 8.15. Ненулевые
синдромы и соответствующие конфигурации
ошибок для кода (7,4)
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфи-гурация |
0000001 |
0000010 |
0001000 |
0000100 |
1000000 |
0010000 |
0100000 |
|
Ошиб- ка |
|
|
|
|
|
|
|
Для определения
и исправления искаженного разряда можно
использовать матрицу одиночных ошибок,
состоящую из единичной матрицы размерности
![]() ,
,
к которой приписывается транспонированная
проверочная матрица.
![]() .
.
При определении
синдрома в проверочной матрице находится
комбинация синдрома. Искаженный разряд
– это разряд в данной строке, в которой
стоит «1». Искаженный разряд исправляем
посредством сложения строки в матрице
ошибок полученной комбинации.
Пример. Для кода
(7,4) задана комбинация
![]() .
.
Составляется
матрица одиночных ошибок

Под воздействием
помех принята комбинация
![]() — искажен третий разряд.
— искажен третий разряд.
Определяем синдром
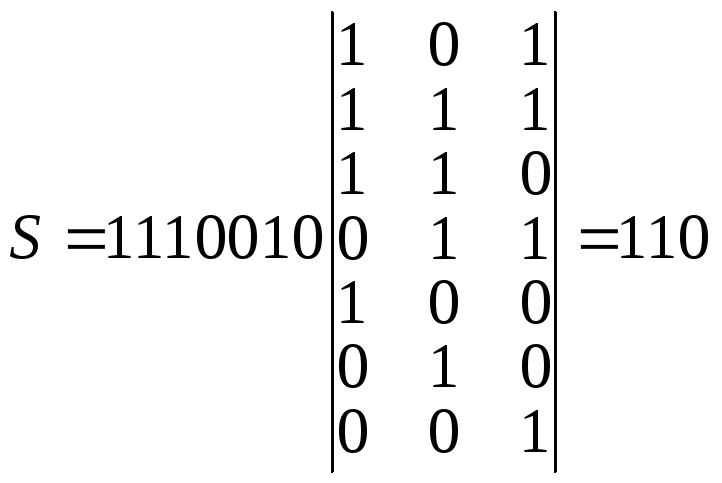
В проверочной
матрице находим комбинацию 110.

Прибавляем третью
строку единичной матрицы к полученной
комбинации
![]() .
.
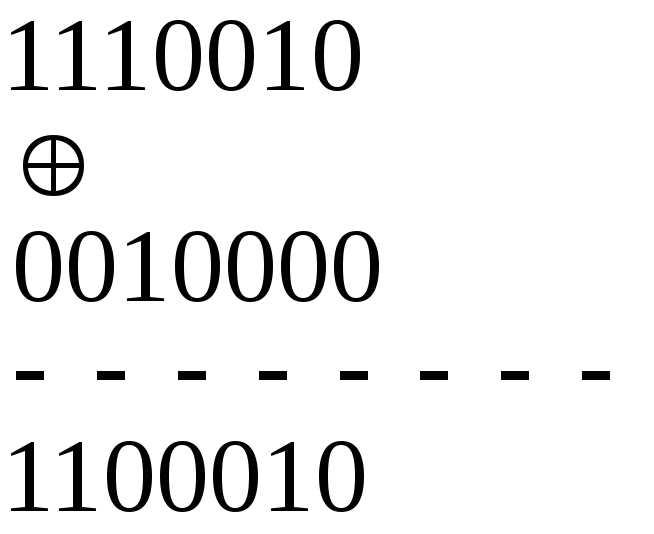
Сообщение исправлено.
Таким образом, код
(7,4) позволяет исправить все одиночные
ошибки. Простая проверка показывает,
что каждая из ошибок имеет свой
единственный синдром. При этом
возможно создание такого цифрового
корректора ошибок (дешифратора
синдрома), который по соответствующему
синдрому исправляет соответствующий
символ в принятой кодовой группе. После
внесения исправления проверочные
символы
![]() на выход декодера не выводятся. Две или
на выход декодера не выводятся. Две или
более ошибок превышают возможности
корректирующего кода Хэмминга, и декодер
будет ошибаться. Это означает, что он
будет вносить неправильные исправления
и выдавать искаженные информационные
символы.
Идея построения
подобного корректирующего кода,
естественно, не меняется при
перестановке позиций символов в кодовых
словах. Все такие варианты также
называются кодами Хэмминга (7,4). Часто
проверочные разряды располагают не в
начале или конце информационных разрядов,
а в определенных местах. Рассмотрим
методику построения такого кода на
примере кода (7,4). Переведем
номера разрядов в двоичную систему
счисления и поставим им в соответствие
проверочные и информационные разряды
(табл.8.16).
Таблица 8.16.
Места расположения информационных и
проверочных разрядов и формирование
проверочных разрядов для кода Хэмминга
(7,4)
|
№ разряда |
№ разряда |
Места |
|
1 |
001 |
|
|
2 |
010 |
|
|
3 |
011 |
|
|
4 |
100 |
|
|
5 |
101 |
|
|
6 |
110 |
|
|
7 |
111 |
|
Т.е. 1-й проверочный
разряд
![]() расположен там, где номер разряда имеет
расположен там, где номер разряда имеет
только одну 1 и к тому же на 1-м месте. Ему
соответствует разряд под номером 1.
Второй проверочный разряд![]() расположен там, где номер разряда имеет
расположен там, где номер разряда имеет
так же только одну 1 и к тому же на 2-м
месте. Ему соответствует разряд под
номером 2. Третий проверочный разряд![]() расположен там, где номер разряда имеет
расположен там, где номер разряда имеет
так же только одну 1 и к тому же на 3-м
месте. Ему соответствует разряд под
номером 4. Оставшиеся разряды 3-й, 5-й, 6-й
и 7-й заполняем информациоными разрядами.
Выпишем разряды,
у которых
первый разряд равен 1:
![]() = 1, 3, 5, 7.
= 1, 3, 5, 7.
Выпишем разряды,
у которых
второй разряд равен 1:
![]() = 2, 3, 6, 7.
= 2, 3, 6, 7.
Выпишем разряды,
у которых
третий разряд равен 1:
![]() = 4, 5, 6, 7.
= 4, 5, 6, 7.
Для
получения первого проверочного разряда
суммируем все разряды первой строки
![]() ,
,
кроме первого, т.е. 3, 5 и 7.
![]() .
.
Для
получения второго проверочного разряда
суммируем все разряды второй строки
![]() ,
,
кроме первого, т.е. 3, 6, 7:
![]() .
.
Для
получения третьего проверочного разряда
суммируем все разряды третьей строки
![]() ,
,
кроме первого, т.е. 5, 6, 7:
![]() .
.
При этом синдром
укажет номер искаженного разряда. Так,
если синдром равен
![]() 0
0
1 1, то искажен третий разряд. Ему
соответствует 1-й информационный символ.
Усеченные коды
являются неплотно
упакованными,
так как число
синдромов у них превышает необходимое.
Так, в коде (9,5) при четырех проверочных
символах число синдромов будет равно
24
=16, в то время как необходимо всего 10.
Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).
Рассмотрим методику
формирования проверочных разрядов на
примере усеченного кода (9,5). В коде (9,5)
имеется 9 разрядов, 5 из которых являются
информационными. Пронумеруем разряды
в десятичной и двоичной системе счисления
(табл.8.17). Номерам разрядов в двоичной
системе будут соответствовать синдромы.
Таблица 8.17. Места
расположения информационных и проверочных
разрядов и формирование проверочных
разрядов для кода Хэмминга (9,5)

Расположим
проверочные разряды на тех позициях,
которым соответствуют номера разрядов
в двоичной системе с одной единицей, а
именно
![]() расположим на 1-м месте (№ разряда в
расположим на 1-м месте (№ разряда в
двоичной системе – 0001),![]() на 2-м (0010),
на 2-м (0010),![]() на 4-м (0100) и
на 4-м (0100) и![]() на 8-м (1000). Информационные разряды
на 8-м (1000). Информационные разряды
расположим на оставшихся местах.
Проверочный разряд![]() получим суммированием информационных
получим суммированием информационных
разрядов, которым соответствует номер
с единицей в 1- разряде двоичной системы
счисления![]() .
.
Проверочный разряд![]() получим суммированием информационных
получим суммированием информационных
разрядов, которым соответствует номер
с единицей во 2- разряде двоичной системы![]() .
.
Аналогично![]() и
и![]() .
.
Для формирования разряда![]() остался один информационный разряд
остался один информационный разряд![]() ,
,
что характерно для усеченных кодов.
Чтобы не было простого дублирования
информационного разряда для формирования![]() возьмем еще какой-нибудь разряд, например,
возьмем еще какой-нибудь разряд, например,![]() ,
,
который также можно исключить из
формирования![]() .
.
Тогда![]() ,
,
а![]() .
.
Если же мы исключили![]() из
из![]() и ввели в
и ввели в![]() ,
,
то его номер также должен быть изменен.
Поэтому теперь![]() соответствует номер 1110. Рассмотрим
соответствует номер 1110. Рассмотрим
пример. Необходимо закодировать сообщение
1 1 0 1 0.
Имеется 5
информационных разрядов
![]() :
:
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
Рассчитаем
количество проверочных разрядов
Маркировка кода
Хэмминга
![]() .
.
Необходимо, чтобы
выполнялось условие:
![]() ,
,![]() – число полученных разрядов.
– число полученных разрядов.
Если
принять
![]() ,
,
23
=8;
тогда
![]() =8-1=7;
=8-1=7;![]() 7-5=2.
7-5=2.
22
< 7+1
![]() неравенство
неравенство
не выполняется.
Примем
![]() ,
,
24
=16;
тогда
![]() =16-1=15;
=16-1=15;![]() 15-5=10.
15-5=10.
210
≥ 15+1
![]() неравенство
неравенство
выполняется.
24
≥
![]() +1,
+1,![]() =4+5=9.
=4+5=9.
Получен
код (9,5).
Получим
проверочные разряды
1
1 0 1 0
![]() =1+1+0=0;
=1+1+0=0;
![]() =1+0+1=0;
=1+0+1=0;
![]() =1+0+1=0;
=1+0+1=0;
![]() =1+0=1.
=1+0=1.
Закодированное
сообщение будет иметь вид:
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
Проверочные разряды
можно также получить при помощи
суммирования номеров ненулевых
информационных разрядов в двоичной
системе. Для данного примера ненулевыми
информационными разрядами являются
![]() ,
,![]() и
и![]() .
.
Им соответствуют номера разрядов 0 0 1
1, 0 1 0 1 и 1 1 1 0 соответственно. Просуммируем
эти номера и получим проверочные разряды
(табл. 8.18).
Таблица 8.18. Правило
формирования проверочных разрядов
|
Разряд |
№ разряда |
|
|
0 |
|
|
0 |
|
|
1 |
|
Сумма |
1 |
|
Проверочные |
|
Пусть под воздействием
помех в данной комбинации исказился
7=й разряд, т.е.
![]() 0
0
0 1 0 1 00
1 0. Определяем
синдром:
![]()
![]() =0+1+1+0=0;
=0+1+1+0=0;
![]() =0+1+0+0=1;
=0+1+0+0=1;
![]() =0+1+0+0=1;
=0+1+0+0=1;
![]() =1+0+0=1.
=1+0+0=1.
Получен
синдром
![]() 1
1
1 1 0.
Смотрим
в таблицу 8.17 и ищем синдром 1 1 1 0 и
определяем, что ему соответствует 7-й
разряд. Исправляем 7-й разряд 0 0 1 0 1 0 1
1 0. Сообщение исправлено. Исключаем
проверочные символы: 1 1 0 1 0.
Расширенные коды
Хэмминга
получают в
результате дополнения кодов с
![]() общей проверкой каждой из кодовых
общей проверкой каждой из кодовых
комбинаций на четность, т.е. еще одним
проверочным символом. Это позволяет
увеличить минимальное кодовое расстояние
до![]() .
.
За показатель
помехоустойчивости кода Хэмминга примем
вероятность приёма кодовой комбинации
с ошибками.
Расчёт вероятности
ошибки произведём для семиэлементного
кода, считая искажения символов в кодовых
комбинациях равновероятными и
независимыми.
Приём с ошибкой
при применении кода Хемминга с исправлением
одиночной ошибки будет в том случае,
если искажено более одного символа. В
соответствии с этим вероятность искажения
кодовой комбинации равна
![]() ,
,
(8.62)
где
![]() — вероятность отсутствия искажений;
— вероятность отсутствия искажений;
![]() —
—
вероятность возникновения одной ошибки.
Соседние файлы в папке Пособие ТЕЗ_рус12
- #
- #
- #
- #
- #
- #
- #
- #
- #
I have a sequence of bits
$$
111011011110
$$
and need to detect two errors(without correction) using Hamming codes. Hamming codes contain a control bit in each $2^n$ position. Hence I should put this control bits in their positions.
$$
0010110011011110
$$
I’ve found a simple explanation of how to count the code for a sequence of bits. It says that each control bit responds for the following bits using these rules: First control bit responds for $2^n$ position and each following bit through $2^n$ . So the first bit responds for the first, third, fifth and etc. bits. The second control bit responds for 2nd, 3rd, 6th, 7th, 10th, 11th and etc. bits. Third control bit(which is on the 4th position) responds for 4th, 5th, 6th, 7th, 12th, 13th etc. bits. And so on. The value of each of the controls bits is counted as a modulo sum of the bits, which this control bit responds for.
Here is an illustration of what I mean:

Assuming this rule is right, the last 16th bit(after control bits addition) is not under the responsibility of any of the control bits.
So the question is: How can I detect double error(only detect, not correct) for the given sequence of bits using the Hamming code?
I have a sequence of bits
$$
111011011110
$$
and need to detect two errors(without correction) using Hamming codes. Hamming codes contain a control bit in each $2^n$ position. Hence I should put this control bits in their positions.
$$
0010110011011110
$$
I’ve found a simple explanation of how to count the code for a sequence of bits. It says that each control bit responds for the following bits using these rules: First control bit responds for $2^n$ position and each following bit through $2^n$ . So the first bit responds for the first, third, fifth and etc. bits. The second control bit responds for 2nd, 3rd, 6th, 7th, 10th, 11th and etc. bits. Third control bit(which is on the 4th position) responds for 4th, 5th, 6th, 7th, 12th, 13th etc. bits. And so on. The value of each of the controls bits is counted as a modulo sum of the bits, which this control bit responds for.
Here is an illustration of what I mean:

Assuming this rule is right, the last 16th bit(after control bits addition) is not under the responsibility of any of the control bits.
So the question is: How can I detect double error(only detect, not correct) for the given sequence of bits using the Hamming code?
Коды Хемминга позволяют закодировать исходное сообщение таким образом, чтобы после передачи его по зашумлённым каналам связи (например, по радиоканалу) и искажениям в принятой информации, можно было восстановить исходное сообщение.
1Что такое код Хэмминга
Код Хэмминга добавляет к сообщению (информационные разряды) некоторое количество избыточной информации (проверочные разряды), сформированной определённым образом. Сообщение с добавленной проверочной информацией называется «кодовый символ» или «кодовое слово». Параметры кода указываются, например, так: (7, 4). Это означает, что длина кодового слова равна 7 битам, а длина сообщения – 4 бита. В зависимости от количества информационных и проверочных разрядов в кодовых словах существуют коды Хэмминга (7,4), (9,5), (11, 7), (15, 11), (31, 26), (63, 57) и т. д.
Общий вид формулы, по которой определяются виды кодов Хэмминга по соотношению числа информационных символов к проверочным: (2x − 1, 2x − x − 1), где x – натуральное число.
Чтобы восстановить закодированное сообщение, оно подвергается декодированию. При этом есть вероятность, что исходное сообщение нельзя будет восстановить, в случае превышения числом ошибок корректирующей способности кода. Однако помехоустойчивость закодированной информации всё равно выше, чем у незакодированной.
Из-за своей простоты, кодирование кодом Хемминга получило широкое распространение. Оно применяется, например, в беспроводной технологии WiFi, в системах хранения данных (RAID-массивах), в некоторых типах микросхем памяти, в схемотехнике и т.д.
Хорошая статья, описывающая принцип работы кода Хэмминга, есть, например, на Хабре.
2Кодер кода Хэмминга (15, 11), написанный на VB.NET
Напишем кодировщик, который будет получать на вход 11 бит данных, кодировать их и возвращать 15 бит выходной информации. Если на вход пришло больше 11-ти бит данных, генерируется исключение. Если данных меньше 11-ти бит (например, 1 байт – 8 бит), то число дополняется нулями в старших разрядах до 11-ти бит и далее кодируется обычным образом. Возвращает кодер 16 бит (кодовое слово).
Код кодера Хэмминга (15, 11) на VB.NET (разворачивается)
''' <summary>
''' Кодирует 11 бит информации кодом Хэмминга (15, 11).
''' Входные данные – 11 бит, выходные – 16 бит.
''' </summary>
''' <param name="dataIn">Входные данные, не более 11-ти бит.</param>
''' <remarks>
''' Размещение проверочных и информационных бит в кодовом слове:
'''
''' |15|14|13|12|11|10|09|08|07|06|05|04|03|02|01|00|
''' in_data | | | | | | L| K| I| H| G| F| E| D| C| B| A|
''' code_word| L| K| I| H| G| F| E| P| D| C| B| P| A| P| P| X|
'''
''' A,B,C,D,E,F,G,H,I,K,L – биты данных информационного слова;
''' P – проверочный бит;
''' X – бит, равный 0 (не используется).
''' Кодовое слово дополняется одним битом, чтобы длина была равна степени двойки. Сейчас этот бит никак не используется.
''' Можно его использовать как бит чётности и получить так называемый дополненный код Хэмминга. Здесь этого не сделано.
''' </remarks>
Public Shared Function Encode_15_11(ByVal b As BitArray) As BitArray
'Можно также добавить проверку на длину передаваемой битовой последовательности:
'If (b.Count > 11) Then
' Throw New ArgumentException("Входная последовательность длиннее 11-ти битов.")
'End If
Dim preDataIn As New BitArray(11)
For i As Integer = 0 To 10
If (b.Count > i) Then
preDataIn(i) = b(i)
Else
Exit For
End If
Next
Dim dataIn As New BitArray(preDataIn)
'Весь процесс кодирования – это сложение по модулю два бит информационного слова.
Dim codeWord As New BitArray(16)
'Младший разряд не используется. Можно добавить в него проверку на чётность.
codeWord(0) = False
'Вычисление первого проверочного символа:
codeWord(1) = dataIn(0) Xor dataIn(1) Xor dataIn(3) Xor dataIn(4) Xor dataIn(6) Xor dataIn(8) Xor dataIn(10)
'Вычисление второго проверочного символа:
codeWord(2) = dataIn(0) Xor dataIn(2) Xor dataIn(3) Xor dataIn(5) Xor dataIn(6) Xor dataIn(9) Xor dataIn(10)
'Вычисление третьего проверочного символа:
codeWord(4) = dataIn(1) Xor dataIn(2) Xor dataIn(3) Xor dataIn(7) Xor dataIn(8) Xor dataIn(9) Xor dataIn(10)
'Вычисление четвертого проверочного символа:
codeWord(8) = dataIn(4) Xor dataIn(5) Xor dataIn(6) Xor dataIn(7) Xor dataIn(8) Xor dataIn(9) Xor dataIn(10)
'Информационные символы:
codeWord(3) = dataIn(0)
codeWord(5) = dataIn(1)
codeWord(6) = dataIn(2)
codeWord(7) = dataIn(3)
codeWord(9) = dataIn(4)
codeWord(10) = dataIn(5)
codeWord(11) = dataIn(6)
codeWord(12) = dataIn(7)
codeWord(13) = dataIn(8)
codeWord(14) = dataIn(9)
codeWord(15) = dataIn(10)
Return codeWord
End Function
Данный кодер легко переписать таким образом, чтобы он работал не с битовыми массивами типа BitArray(), а с байтами: на вход получал 11-разрядное число (от 0 до 0x7FF) и выдавал 2 закодированных байта:
Public Shared Function Encode_15_11(ByVal numberToEncode As Integer) As Byte()
Dim enc As BitArray = Hamming.Encode_15_11(New BitArray({numberToEncode}))
Dim encBytes(1) As Byte
enc.CopyTo(encBytes, 0)
Return encBytes
End Function
3Декодер кода Хэмминга (15, 11), написанный на VB.NET
Теперь пора поговорить о декодере. Декодер получает на вход 2 байта закодированных данных и возвращает 11 бит декодированных данных, которые распределены по двум байтам. Если в кодер были переданы 8 бит данных, то нас будет интересовать только первый байт, полученный с декодера.
Код декодера Хэмминга (15, 11) на VB.NET (разворачивается)
''' <summary>
''' Декодер кода (15, 11).
''' </summary>
''' <param name="b">Входные данные, 16 бит (2 байта).</param>
''' <returns>Выходные данные – 10 бит.</returns>
''' <remarks>
''' Размещение проверочных и информационных бит в кодовом слове:
'''
''' |15|14|13|12|11|10|09|08|07|06|05|04|03|02|01|00|
''' code_word| L| K| I| H| G| F| E| P| D| C| B| P| A| P| P| X|
''' out_data | | | | | | L| K| I| H| G| F| E| D| C| B| A|
'''
''' A,B,C,D,E,F,G,H,I,K,L – биты данных информационного слова;
''' P – проверочный бит;
''' X – бит, равный 0 (не используется).
'''
''' Кодовое слово дополняется одним битом, чтобы длина была равна степени двойки. Сейчас этот бит никак не используется.
''' Можно его использовать как бит четности и получить так называемый дополненный код Хэмминга. Здесь этого не сделано.
''' </remarks>
Public Shared Function Decode_15_11(ByVal b As Byte()) As Integer
Dim codeWord As New BitArray(b) '16 бит входных данных
'Весь процесс декодирования – это сложение по модулю два бит информационного слова, по весу полученных единиц в результате – получение позиции ошибки.
Dim syndrome As New BitArray(4)
'Вычисление первого проверочного символа из полученного кодового слова и далее сравнение его с полученным.
syndrome(0) = codeWord(3) Xor codeWord(5) Xor codeWord(7) Xor codeWord(9) Xor codeWord(11) Xor codeWord(13) Xor codeWord(15) Xor codeWord(1)
'Вычисление второго проверочного символа из полученного кодового слова и далее сравнение его с полученным.
syndrome(1) = codeWord(3) Xor codeWord(6) Xor codeWord(7) Xor codeWord(10) Xor codeWord(11) Xor codeWord(14) Xor codeWord(15) Xor codeWord(2)
'Вычисление третьего проверочного символа из полученного кодового слова и далее сравнение его с полученным.
syndrome(2) = codeWord(5) Xor codeWord(6) Xor codeWord(7) Xor codeWord(12) Xor codeWord(13) Xor codeWord(14) Xor codeWord(15) Xor codeWord(4)
'Вычисление четвёртого проверочного символа из полученного кодового слова и далее сравнение его с полученным.
syndrome(3) = codeWord(9) Xor codeWord(10) Xor codeWord(11) Xor codeWord(12) Xor codeWord(13) Xor codeWord(14) Xor codeWord(15) Xor codeWord(8)
'Вычисление по синдрому позиции ошибки. Это просто ПЗУ или дешифратор.
'Если смотреть на синдром как на число - то это и есть номер позиции ошибки.
'Синдром равен 0 - ошибки нет.
'Поскольку на выход модуля передаются только биты данных - не все варианты перечислены, нет смысла исправлять проверочные биты.
Dim syn As Integer = (Convert.ToInt32(syndrome(3)) << 3) Or (Convert.ToInt32(syndrome(2)) << 2) Or (Convert.ToInt32(syndrome(1)) << 1) Or Convert.ToInt32(syndrome(0))
' |15|14|13|12|11|10|09|08|07|06|05|04|03|02|01|00|
'code_word| L| K| I| H| G| F| E| P| D| C| B| P| A| P| P| X|
'Синдромы ошибок в информационных битах, позиции в кодовом слове 3,5,6,7,9,10,11,12,13,14,15:
Dim correction As New BitArray(11)
Select Case syn
Case 3 'позиция 3
correction = New BitArray({True, False, False, False, False, False, False, False, False, False, False})
Case 5 'позиция 5
correction = New BitArray({False, True, False, False, False, False, False, False, False, False, False})
Case 6 'позиция 6
correction = New BitArray({False, False, True, False, False, False, False, False, False, False, False})
Case 7 'позиция 7
correction = New BitArray({False, False, False, True, False, False, False, False, False, False, False})
Case 9 'позиция 9
correction = New BitArray({False, False, False, False, True, False, False, False, False, False, False})
Case 10 'позиция 10
correction = New BitArray({False, False, False, False, False, True, False, False, False, False, False})
Case 11 'позиция 11
correction = New BitArray({False, False, False, False, False, False, True, False, False, False, False})
Case 12 'позиция 12
correction = New BitArray({False, False, False, False, False, False, False, True, False, False, False})
Case 13 'позиция 13
correction = New BitArray({False, False, False, False, False, False, False, False, True, False, False})
Case 14 'позиция 14
correction = New BitArray({False, False, False, False, False, False, False, False, False, True, False})
Case 15 'позиция 15
correction = New BitArray({False, False, False, False, False, False, False, False, False, False, True})
Case Else
'Если синдром равен 0 или указывает на ошибку в проверочном символе "P" - коррекция информационных символов не требуется.
'Мы инициализировали correction() нулями (correction = New BitArray(11)), поэтому ничего делать не нужно.
End Select
'Результат декодирования с учетом коррекции (11 бит выходных данных):
Dim outData As New BitArray(11)
outData(0) = codeWord(3) Xor correction(0)
outData(1) = codeWord(5) Xor correction(1)
outData(2) = codeWord(6) Xor correction(2)
outData(3) = codeWord(7) Xor correction(3)
outData(4) = codeWord(9) Xor correction(4)
outData(5) = codeWord(10) Xor correction(5)
outData(6) = codeWord(11) Xor correction(6)
outData(7) = codeWord(12) Xor correction(7)
outData(8) = codeWord(13) Xor correction(8)
outData(9) = codeWord(14) Xor correction(9)
outData(10) = codeWord(15) Xor correction(10)
Dim masks(31) As Integer
masks(0) = BitVector32.CreateMask()
For i As Integer = 1 To 31
masks(i) = BitVector32.CreateMask(masks(i - 1))
Next
Dim v As New BitVector32
For i As Integer = 0 To 10
v(masks(i)) = outData(i)
Next
Dim decoded As Integer = v.Data
Return decoded
End Function
Для быстрой проверки кодировщика и декодировщика кода Хэмминга (15, 11), используя вышеописанные классы, я написал две программы. Первая – кодер Хэмминга. Вводите 11-разрядное число (от 0 до 0x7FF или 2047), и на выходе получаем 16-разрядное число, представленное в виде двух байтов.

Вторая программа – декодер кода Хмминга (15, 11).

Легко убедиться, что если мы внесём битовую ошибку при декодировании, то декодер восстановит исходное закодированное число.
Обе программы работают под ОС Windows и требуют .NET версии 3.5. Выкладываю описанные программы.
Скачать кодер и декодер кода Хэмминга (15, 11)
- Скачать кодер и декодер кода Хэмминга (15, 11) с Depositfiles.com
- Скачать кодер и декодер кода Хэмминга (15, 11) c Up-4ever.com
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.IO; namespace ConsoleApplication1 { class Test { static void Main() { char[] data = new char[11]; int[] encoded = new int[15]; int[] edata = new int[15]; int[] syndrome = new int[12]; int[,] hmatrix = new int[4, 15]{{1,0,0,0,1,0,0,1,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,0,1,0,1,1,0,1,1}, {0,0,1,0,0,1,1,1,0,0,1,1,1,0,1}, {1,0,0,1,0,0,1,0,1,1,0,1,1,1,1}}; char[,] gmatrix = new char[11, 15] { { '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0' }, { '0', '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0' }, { '0', '0', '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0' }, { '1', '0', '1', '1', '0', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0' }, { '0', '1', '0', '1', '0', '0', '0', '0', '1', '0', '0', '0', '0', '0', '0' }, { '1', '0', '0', '1', '0', '0', '0', '0', '0', '1', '0', '0', '0', '0', '0' }, { '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0', '0', '0' }, { '0', '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0', '0' }, { '1', '0', '1', '1', '0', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0' }, { '1', '1', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '1', '0' }, { '1', '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '1' }}; int i, j; Console.Write("nКод Хэмминга. КодированиеnnВведите 11-битовое слово: n"); for (int d = 0; d < 11; d++) { data[d] = Convert.ToChar(Console.ReadLine()); } //Console.Write("nGenerator matrix entern"); /* for(i=0;i<11;i++){ for(j=0;j<15;j++){ Console.Write("{0},{1}",i,j); gmatrix[i,j]=Convert.ToChar(Console.ReadLine()); } Console.WriteLine(); } */ Console.Write("nПорождающая матрицаn"); for (i = 0; i < 11; i++) { for (j = 0; j < 15; j++) { Console.Write("{0} t|", gmatrix[i, j]); } Console.WriteLine(); } Console.WriteLine("nКодированные данныеn"); for (i = 0; i < 15; i++) { for (j = 0; j < 11; j++) encoded[i] += ((data[j] - 0) * (gmatrix[j, i] - 0)); encoded[i] = encoded[i] % 2; Console.Write("{0} |", encoded[i]); } Console.Write("nКод Хэмминга. ДекодированиеnnВведите кодированные данные : n"); for (i = 0; i < 15; i++) edata[i] = Convert.ToChar(Console.ReadLine()); for (i = 0; i < 4; i++) { for (j = 0; j < 15; j++) syndrome[i] += (edata[j] * hmatrix[i, j]); syndrome[i] = syndrome[i] % 2; } for (j = 0; j < 15; j++) if ((syndrome[0] == hmatrix[0, j]) && (syndrome[1] == hmatrix[1, j]) && (syndrome[2] == hmatrix[2, j]) && (syndrome[3] == hmatrix[3, j])) break; if (j == 15) Console.Write("nОшибок нетn"); else { Console.Write("nОшибка получена в {0} бите данныхn", j + 1); edata[j] = 0; Console.Write("nДанные должны быть такими : "); for (j = 0; j < 15; j++) if (edata[j] == 48) Console.Write("{0} |", 0); else if (edata[j] == 49) Console.Write("{0} |", 1); else Console.Write("{0} |", edata[j]); } Console.ReadKey(); } } } |
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
-

coshmarik
New Member
- Публикаций:
-
0
- Регистрация:
- 30 апр 2010
- Сообщения:
- 7
Добрый день!
Помогите, пожалуйста!
Нигде не могу найти описание кода Хемминга 15/11.
Заранее большое спасибо! -

OLS
New Member
- Публикаций:
-
0
- Регистрация:
- 8 янв 2005
- Сообщения:
- 322
- Адрес:
- Russia
Считаем биты в сообщениях с единицы, обозначим «p» — исходное сообщение, «с» — кодированное (т.е. в нашем случае нумерация — p1..p11, c1..c15).
Все биты кодированного сообщения, номера которых — точная степень двойки (c1, c2, c4, c8) — контрольные, остальные — это биты сообщения (т.е. c3<-p1, c5<-p2, c6<-p3, c7<-p4, c9<-p5, далее — без пропусков).
Каждый контрольный бит отвечает за чётность суммы группы бит, в номерах каждого из которых этот бит поднят.
Т.е.чтобы определить, какие контрольные биты контролируют бит кодированного сообщения в позиции k надо разложить k по степеням двойки: если k = 11 = 8 + 2 + 1, то этот бит контролируется c1, c2 и c8.В итоге контрольные биты для Hamming(15,11) вычисляются как
c1 <- c3+c5+c7+c9+c11+c13+c15
c2 <- c3+c6+c7+c10+c11+c14+c15
c4 <- c5+c6+c7+c12+c13+c14+c15
c8 <- c9+c10+c11+c12+c13+c14+c15Поскольку код Хемминга интересен именно тем, что определение позиции, содержащей искажение, определяется
суммированием позиций «нарушенных» контрольных бит, то работать удобнее именно с этой нумерацией, и не доводить ее до нумерации по исходному сообщению. -

coshmarik
New Member
- Публикаций:
-
0
- Регистрация:
- 30 апр 2010
- Сообщения:
- 7
Очень-очень большое спасибо!!!
-

Dr.Golova
New Member
- Публикаций:
-
0
- Регистрация:
- 7 сен 2002
- Сообщения:
- 348
А теперь хочется узнать про XOR таблицы, кои используются во всех современных архиваторах для восстановления данных. Это вроде не совсем коды хемминга — тут нужен некий брутфорс узлов, с вероятностным успехом. или не?
-

persicum
New Member
- Публикаций:
-
0
- Регистрация:
- 2 фев 2007
- Сообщения:
- 947
Dr.Golova
вроде в архиваторах везде простой КСОР с весами
1 1 1 1 … На этот счет есть статья з0мби доходчивая…А вот quickpar и iceecc юзают таблицы для КСОРа с 16битными весами,
это гораздо круче.То бишь архиваторы исправляют однократные ошибки на срез, а quickpar соответственно 65536 кратные.
А в проге persicum’s CRC32 веса так ващще 32битные и исправляет она миллионнократные ошибки.
-

persicum
New Member
- Публикаций:
-
0
- Регистрация:
- 2 фев 2007
- Сообщения:
- 947
Вопщем, в программах формула такая:
w1*byte1 XOR w2*byte2 XOR w3*byte3… = parity1
и т.д.В архиваторах веса просто единицы, а в специализированных прогах- вовсе не единицы.
Нулей в весах нет, в отличие от кодов хэмминга… -

Aoizora
Active Member
- Публикаций:
-
0
- Регистрация:
- 29 янв 2017
- Сообщения:
- 281
Древний тред, нашел его, пока искал реализации кода Хэмминга (15, 11). Нормальных реализаций нет, пришлось писать свою
 Все матрицы расчитывал вручную на бумаге
Все матрицы расчитывал вручную на бумаге-
typedef uint16_t hamming_word;
-
inline uint8_t sum_bits(hamming_word n)
-
hamming_word make_error(const hamming_word n, std::size_t position)
-
return n ^ 1 << position;
-
hamming_word hamming_encode(hamming_word i)
-
constexpr std::size_t matrix_cols = 15;
-
uint16_t g[matrix_cols] = {0b10000000000,
-
for (std::size_t col = 0; col < matrix_cols; ++col)
-
result |= sum_bits(i & g[col]); // Умножение двоичных векторов и сумма бит по модулю 2
-
uint8_t syndrome(hamming_word codeword)
-
constexpr std::size_t matrix_rows = 4;
-
hamming_word syndrome = 0;
-
uint16_t h[matrix_rows] = { 0b111101011001000,
-
for (std::size_t row = 0; row < matrix_rows; ++row)
-
syndrome |= sum_bits(codeword & h[row]);
-
hamming_word hamming_error_correct(hamming_word i)
-
const uint8_t syndrome_to_bit[16] = {UINT8_MAX, 0, 1, 4, 2, 8, 5, 10, 8, 14, 9, 7, 6, 13, 11, 12 };
-
return i ^ 1 << syndrome_to_bit[syndrome(i)];
-
hamming_word hamming_decode(hamming_word i)
-
uint8_t data = hamming_error_correct(i);
-
return data >> 4 & 0x7FF;
-
std::map<hamming_word, uint8_t> syndrome_map;
-
for (int i = 0; i < 15; i++)
-
syndrome_map[i] = syndrome(1 << i);
-
for (auto it : syndrome_map)
-
std::cout << (int)it.second << «=>» << std::dec << (int)it.first << std::endl;

My preferred approach is algebraic. Note that I prefer to construct the parity check matrix first, and then deduce a matrix for the code, using exactly the same trick as rschwieb. (My parity check matrix is the transpose of his.) Constructing the parity check matrix first has some advantages IMHO, such as yielding directly immediately that the code is cyclic.
Construct the field with 16 elements as $mathbf{F}_{2}[alpha]$, with $alpha$ a primitive element, so that the powers $1, alpha, dots, alpha^{14}$ are distinct.
Now write the element $1, alpha, dots, alpha^{14}$ as column vectors with respect to the basis $1, alpha, alpha^2, alpha^3$ of $mathbf{F}_{2}[alpha]$ as a vector space over $mathbf{F}_{2}$. So
$$
1 mapsto begin{bmatrix}0\0\0\1end{bmatrix},quad
alpha mapsto begin{bmatrix}0\0\1\0end{bmatrix},quad
alpha^2 mapsto begin{bmatrix}0\1\0\0end{bmatrix},quad
alpha^3 mapsto begin{bmatrix}1\0\0\0end{bmatrix},quad
alpha^4 mapsto begin{bmatrix}a_3\a_2\a_1\a_0end{bmatrix},quad
text{etc,}
$$
where $x^4+a_3 x^3 + a_2 x^2 + a_1 x + a_0$ is the minimal polynomial of $alpha$ over $mathbf{F}_{2}$.
Then these column vectors are the columns, written right-to-left, of the parity check matrix.
Erno Lancaster edited this adding
This uses the fact that the Hamming code is the set of all polynomials of degree $< 15$ with $alpha$ as a root. In other words, a Hamming code is also a $t = 1$ BCH code.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.IO; namespace ConsoleApplication1 { class Test { static void Main() { char[] data = new char[11]; int[] encoded = new int[15]; int[] edata = new int[15]; int[] syndrome = new int[12]; int[,] hmatrix = new int[4, 15]{{1,0,0,0,1,0,0,1,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,0,1,0,1,1,0,1,1}, {0,0,1,0,0,1,1,1,0,0,1,1,1,0,1}, {1,0,0,1,0,0,1,0,1,1,0,1,1,1,1}}; char[,] gmatrix = new char[11, 15] { { '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0' }, { '0', '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0' }, { '0', '0', '1', '1', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0' }, { '1', '0', '1', '1', '0', '0', '0', '1', '0', '0', '0', '0', '0', '0', '0' }, { '0', '1', '0', '1', '0', '0', '0', '0', '1', '0', '0', '0', '0', '0', '0' }, { '1', '0', '0', '1', '0', '0', '0', '0', '0', '1', '0', '0', '0', '0', '0' }, { '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0', '0', '0' }, { '0', '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0', '0' }, { '1', '0', '1', '1', '0', '0', '0', '0', '0', '0', '0', '0', '1', '0', '0' }, { '1', '1', '0', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '1', '0' }, { '1', '1', '1', '1', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '1' }}; int i, j; Console.Write("nКод Хэмминга. КодированиеnnВведите 11-битовое слово: n"); for (int d = 0; d < 11; d++) { data[d] = Convert.ToChar(Console.ReadLine()); } //Console.Write("nGenerator matrix entern"); /* for(i=0;i<11;i++){ for(j=0;j<15;j++){ Console.Write("{0},{1}",i,j); gmatrix[i,j]=Convert.ToChar(Console.ReadLine()); } Console.WriteLine(); } */ Console.Write("nПорождающая матрицаn"); for (i = 0; i < 11; i++) { for (j = 0; j < 15; j++) { Console.Write("{0} t|", gmatrix[i, j]); } Console.WriteLine(); } Console.WriteLine("nКодированные данныеn"); for (i = 0; i < 15; i++) { for (j = 0; j < 11; j++) encoded[i] += ((data[j] - 0) * (gmatrix[j, i] - 0)); encoded[i] = encoded[i] % 2; Console.Write("{0} |", encoded[i]); } Console.Write("nКод Хэмминга. ДекодированиеnnВведите кодированные данные : n"); for (i = 0; i < 15; i++) edata[i] = Convert.ToChar(Console.ReadLine()); for (i = 0; i < 4; i++) { for (j = 0; j < 15; j++) syndrome[i] += (edata[j] * hmatrix[i, j]); syndrome[i] = syndrome[i] % 2; } for (j = 0; j < 15; j++) if ((syndrome[0] == hmatrix[0, j]) && (syndrome[1] == hmatrix[1, j]) && (syndrome[2] == hmatrix[2, j]) && (syndrome[3] == hmatrix[3, j])) break; if (j == 15) Console.Write("nОшибок нетn"); else { Console.Write("nОшибка получена в {0} бите данныхn", j + 1); edata[j] = 0; Console.Write("nДанные должны быть такими : "); for (j = 0; j < 15; j++) if (edata[j] == 48) Console.Write("{0} |", 0); else if (edata[j] == 49) Console.Write("{0} |", 1); else Console.Write("{0} |", edata[j]); } Console.ReadKey(); } } } |
