1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
разность
сумма квадратов
разности
квадрат разности
сумма разности
квадратов
Решение:
Одним из типов
эконометрических моделей является
уравнение регрессии, которое может быть
записано в виде математического выражения
![]() ,
,
гдеy
– зависимая переменная; xj
– независимая переменная (j
= 1,…, k;
k
– количество независимых переменных);
f
– тип функциональной зависимости
(математическая функция);
![]() –
–
случайные факторы. При этом![]() ,
,
тогда![]() ,
,
где![]() –
–
фактическое значение зависимой
переменной,![]() –
–
расчетное значение зависимой переменной,![]() –
–
ошибка модели. Выразим значение![]() :
:![]() .
.
Поэтому правильный ответ – «разность».
2. Величина называется …
случайной
составляющей
оценкой параметра
значением параметра
переменной
Решение:
Величина
![]() называется
называется
случайной составляющей, или возмущением,
и включает в себя влияние факторов,
неучтенных в модели, ошибок выборки и
ошибок измерения.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
ошибку модели
величину коэффициента
регрессии
значение свободного
члена уравнения
нулевое значение
независимой переменной
Решение:
Одним из типов
эконометрических моделей является
уравнение регрессии, которое может быть
записано в виде математического выражения
![]() ,
,
гдеy
– зависимая переменная; xj
– независимая переменная (j
= 1,…, k;
k
– количество независимых переменных);
f
– тип функциональной зависимости
(математическая функция);
![]() –
–
случайные факторы. При этом![]() ,
,
тогда![]() ,
,
где![]() –
–
фактическое значение зависимой
переменной,![]() –
–
расчетное значение зависимой переменной,![]() –
–
ошибка модели. Поэтому правильный ответ
– «ошибку модели».
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
0,8
![]()
![]()
Решение:
Коэффициент
детерминации
 равен
равен
доле дисперсии, объясненной регрессией,
в общей дисперсии. Следовательно,![]()
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков.
минимизации
суммы квадратов
равенства нулю
суммы квадратов
минимизации модулей
равенства нулю
Решение:
При методе наименьших
квадратов параметры уравнения парной
линейной регрессии
![]() определяются
определяются
из условия минимизации суммы квадратов
остатков![]() .
.
Тема 6: Предпосылки мнк, методы их проверки
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина
– Уотсона
тест Уайта
критерий Гольдфельда
– Квандта
тест Парка
Решение:
Для обнаружения
автокорреляции остатков используется
расчет статистик Дарбина – Уотсона.
Тест Уайта, критерий Гольдфельда –
Квандта, тест Парка применяются для
обнаружения гетероскедастичности
остатков.
2. Известно, что
коэффициент автокорреляции остатков
первого порядка
равен –0,3. Также даны критические
значения статистики Дарбина – Уотсона
для заданного количества параметров
при неизвестном и количестве наблюдений
![]() ,
,![]() .
.
По данным характеристикам можно сделать
вывод о том, что …
автокорреляция
остатков отсутствует
статистика Дарбина
– Уотсона попадает в зону неопределенности
есть положительная
автокорреляция остатков
есть отрицательная
автокорреляция остатков
Решение:
Дано, что коэффициент
автокорреляции остатков первого порядка
равен –0,3,
![]() .
.
Рассчитаем статистику Дарбина – Уотсона
по формуле![]() .
.
Нам известны критические значения
статистики Дарбина – Уотсона для
заданного количества параметров при
неизвестном и количестве наблюдений![]() ,
,![]() ,
,
которые разбивают отрезок от 0 до 4 на
пять частей.
В интервале [0;
0,82] есть положительная автокорреляция
остатков;
в интервале (0,82;
1,32] – зона неопределенности;
в интервале (1,32;
2,68] нет автокорреляции остатков;
в интервале (2,68;
3,12] – зона неопределенности;
в интервале (3,12;
4] есть отрицательная автокорреляция
остатков.
В нашем случае
значение статистики Дарбина–Уотсона
d=2,6 попадает в интервал (1,32; 2,68]. Значит,
можно сделать вывод, что нет автокорреляции
остатков.
3. Значение
критерия Дарбина – Уотсона можно
приблизительно
рассчитать по формуле
![]() ,
,
где![]() –
–
значение коэффициента автокорреляции
остатков модели. Минимальная величина
значения![]() будет
будет
наблюдаться при ________ автокорреляции
остатков.
положительной
отрицательной
нулевой
бесконечно малой
Решение:
Значение коэффициента
автокорреляции остатков модели
![]() рассчитывается
рассчитывается
по аналогии с парным коэффициентом
автокорреляции и изменяется в таких же
пределах, то есть от –1 до +1. Подставим
эти граничные значения в формулу для
расчета значения критерия Дарбина –
Уотсона: если![]() ,
,
то![]() ;
;
если![]() ,
,
то![]() .
.
Поэтому значение![]() меняется
меняется
от 0 до 4. Минимальное значение![]() равно
равно
0 для случая, когда![]() ,
,
то есть для положительной автокорреляции
остатков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение 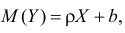
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии  неизвестны, неизвестна и величина коэффициента корреляции
неизвестны, неизвестна и величина коэффициента корреляции 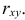 Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений:
Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений: 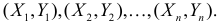 Эти результаты могут служить источником информации о неизвестных значениях
Эти результаты могут служить источником информации о неизвестных значениях 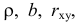 надо только уметь эту информацию извлечь оттуда.
надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии 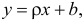 как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для
как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для  можно принять те их значения, при которых имеет минимум функция
можно принять те их значения, при которых имеет минимум функция 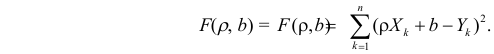
Такие значения  , согласно необходимым условиям экстремума, находятся из системы уравнений:
, согласно необходимым условиям экстремума, находятся из системы уравнений:
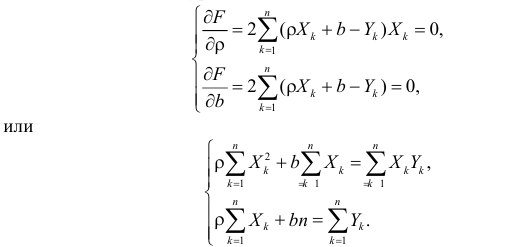
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.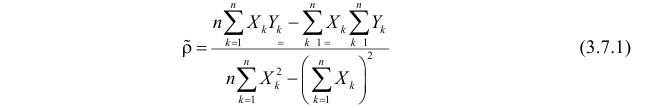
и
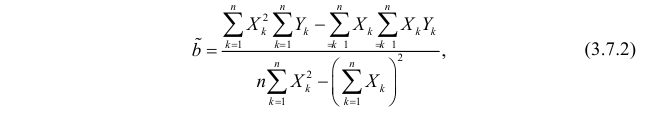
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 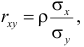 где
где 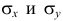 средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через
средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через 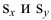 оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку
оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку 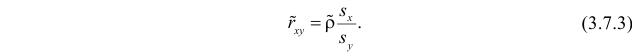
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 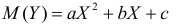 оценки параметров
оценки параметров 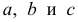 находятся из условия минимума функции
находятся из условия минимума функции
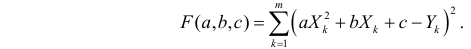
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X 
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
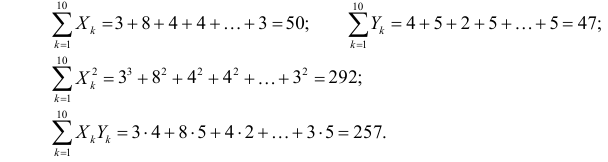
По формулам (3.7.1) и (3.7.2) получим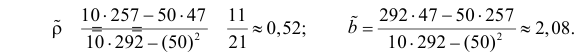
Итак, оценка линии регрессии имеет вид 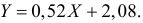 Так как
Так как 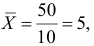 то по формуле (3.1.3)
то по формуле (3.1.3)
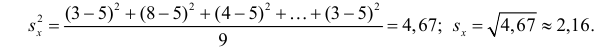
Аналогично, 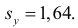 Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину
Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину 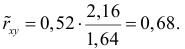
Ответ. 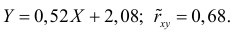
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 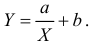 Найти оценки параметров
Найти оценки параметров 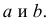
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 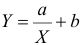 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)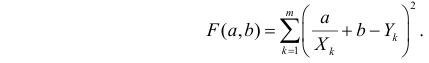
Необходимые условия экстремума приводят к системе из двух уравнений: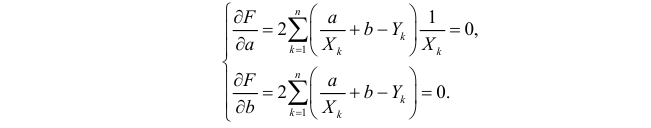
Откуда
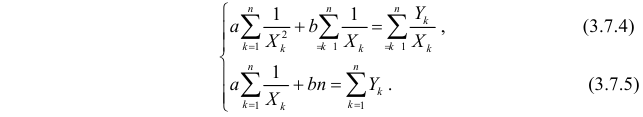
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров 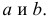
На основе опытных данных вычисляем: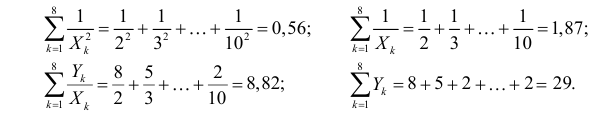
В итоге получаем систему уравнений (?????) и (?????) в виде 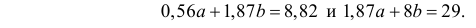
Эта система имеет решения 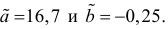
Ответ. 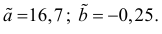
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 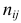 равно числу наблюдений, для которых X находится в интервале
равно числу наблюдений, для которых X находится в интервале 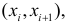 а Y – в интервале
а Y – в интервале 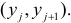 Через
Через 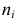 обозначено число наблюдений, при которых
обозначено число наблюдений, при которых 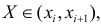 а Y произвольно. Число наблюдений, при которых
а Y произвольно. Число наблюдений, при которых 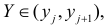 а X произвольно, обозначено через
а X произвольно, обозначено через 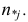
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 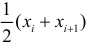 и
и 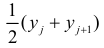 наблюдались
наблюдались 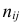 раз.
раз.
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.

Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 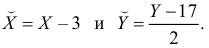 Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 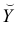 при фиксированных значениях
при фиксированных значениях 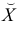 :
:
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).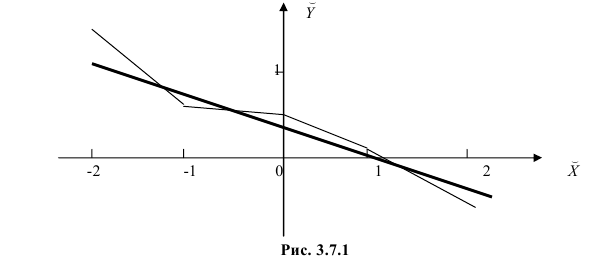
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33): 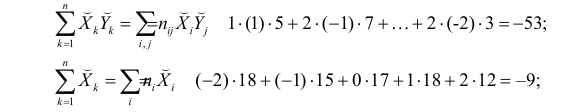
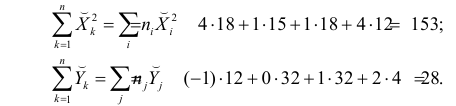
Тогда
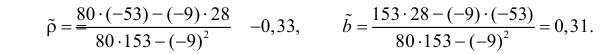
В новом масштабе оценка линии регрессии имеет вид 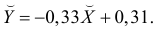 График этой прямой линии изображен на рис. 3.7.1.
График этой прямой линии изображен на рис. 3.7.1.
Для оценки 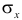 по корреляционной таблице можно воспользоваться формулой (3.1.3):
по корреляционной таблице можно воспользоваться формулой (3.1.3):
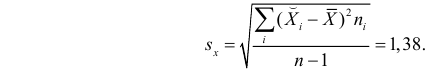
Подобным же образом можно оценить 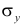 величиной
величиной 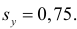 Тогда оценкой коэффициента корреляции может служить величина
Тогда оценкой коэффициента корреляции может служить величина 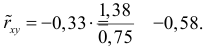
Вернемся к старому масштабу:
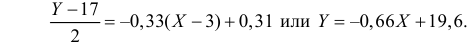
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ. 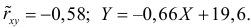
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 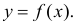 Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то
Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то 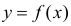 играет роль линии регрессии и все свойства линии регрессии приложимы к
играет роль линии регрессии и все свойства линии регрессии приложимы к 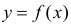 . В частности,
. В частности, 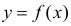 обычно находят по методу наименьших квадратов.
обычно находят по методу наименьших квадратов.
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
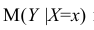 можно представить в виде
можно представить в виде 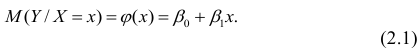
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 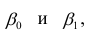 называемые коэффициентами регрессии, а также
называемые коэффициентами регрессии, а также 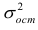 — остаточная дисперсия.
— остаточная дисперсия.
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей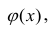 которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости
которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости 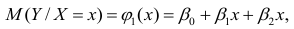
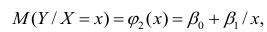
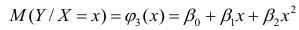 линейны относительно параметров
линейны относительно параметров 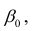
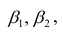 хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости
хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости 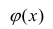 выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
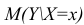 можно представить в виде (2.1).
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 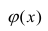 линейна и по оцениваемым параметрам, и
линейна и по оцениваемым параметрам, и
по переменным. Оценки параметров модели (2.1) 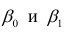 обозначил
обозначил 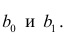 Оценку остаточной дисперсии
Оценку остаточной дисперсии 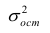 обозначим
обозначим 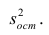 Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии
Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии 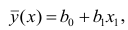 коэффициенты которого
коэффициенты которого 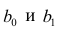 находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака
находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака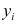 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 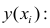
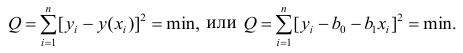
Составим систему нормальных уравнений: первое уравнение
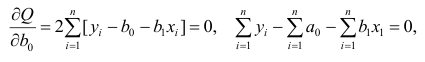
откуда 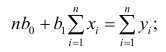
второе уравнение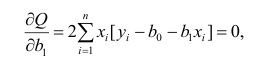
откуда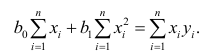
Итак,
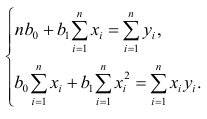
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно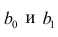 найдём оценки параметров
найдём оценки параметров 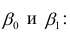
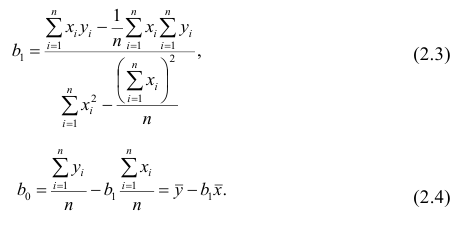
Остаётся получить оценку параметра 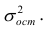 . Имеем
. Имеем
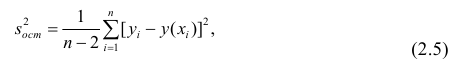
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы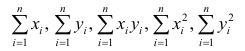 заменяют на
заменяют на
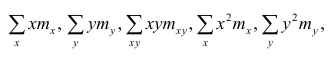
где 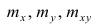 — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
— частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
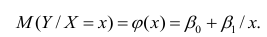
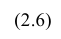
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
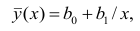
где 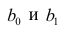 —оценки коэффициентов регрессии
—оценки коэффициентов регрессии 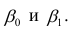
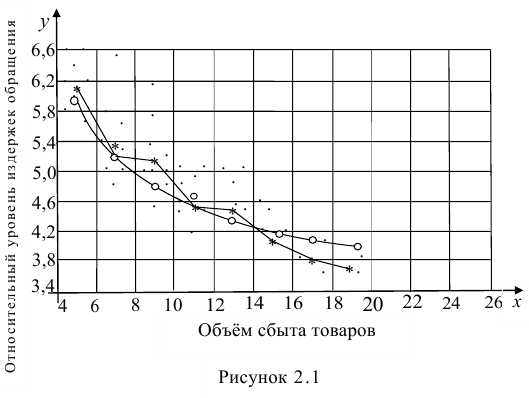
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
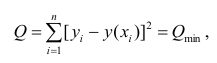
или
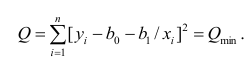
Дифференцируя последнее равенство по 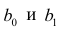 и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
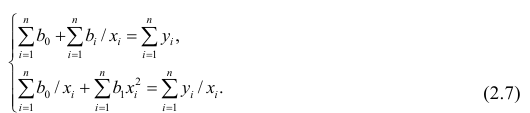
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
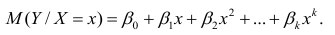
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
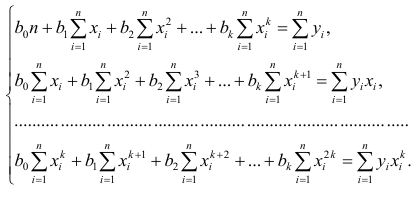
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 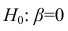 статистика
статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 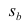 — оценка среднеквадратического отклонения
— оценка среднеквадратического отклонения
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение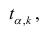 удовлетворяющее условию
удовлетворяющее условию 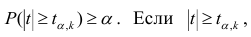 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При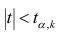 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
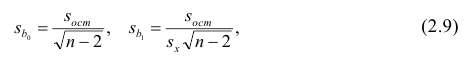
где 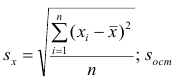 — оценка остаточной дисперсии, вычисляемая по
— оценка остаточной дисперсии, вычисляемая по
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
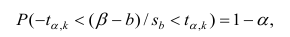
где а — уровень значимости, находим

Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 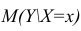 является условное среднее
является условное среднее 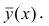 Кроме точечной оценки для
Кроме точечной оценки для 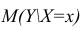 можно
можно
построить доверительный интервал в точке 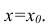
Известно, что 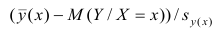 имеет распределение
имеет распределение
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания 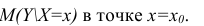
Оценку дисперсии условного среднего вычисляют по формуле
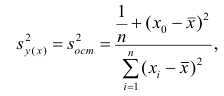
или для интервального ряда
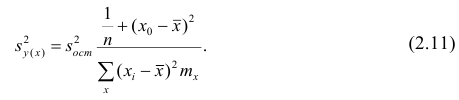
Доверительный интервал находят из условия
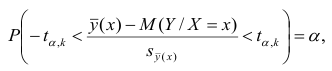
где а — уровень значимости. Отсюда
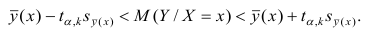
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
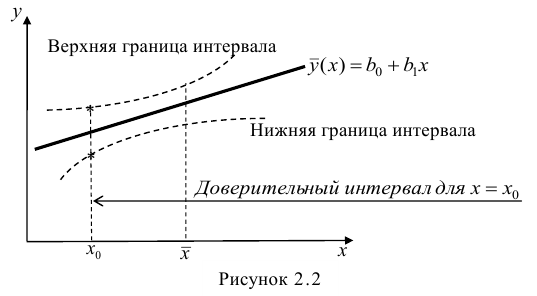
Из рис. 2.2 видно, что в точке 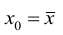 границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 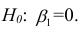 Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением
Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением 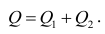 — Общая сумма квадратов отклонений результативного признака
— Общая сумма квадратов отклонений результативного признака
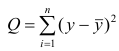 разлагается на
разлагается на 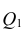 (сумму, характеризующую влияние признака
(сумму, характеризующую влияние признака
X) и 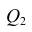 (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
(остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
Для проверки нулевой гипотезы вычисляют статистику 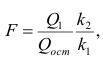 которая имеет распределение Фишера-Снедекора с А
которая имеет распределение Фишера-Снедекора с А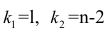 степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы
степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы 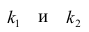 находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение
находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение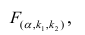 удовлетворяющее условию
удовлетворяющее условию 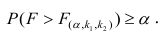 . Если
. Если 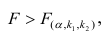 нулевую гипотезу отвергают, уравнение считают значимым. Если
нулевую гипотезу отвергают, уравнение считают значимым. Если 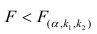 то нет оснований отвергать нулевую гипотезу.
то нет оснований отвергать нулевую гипотезу.
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 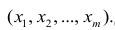 Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним
Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним 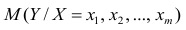 и постоянной дисперсией
и постоянной дисперсией 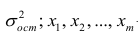 — линейно независимые векторы
— линейно независимые векторы 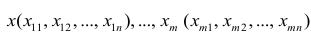 . Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
. Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
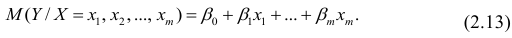
Оценке подлежат параметры 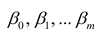 и остаточная дисперсия.
и остаточная дисперсия.
Заменив параметры их оценками, запишем уравнение регрессии
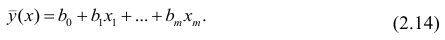
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 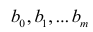 является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:
является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

Как и в двумерном случае, составляют систему нормальных уравнений
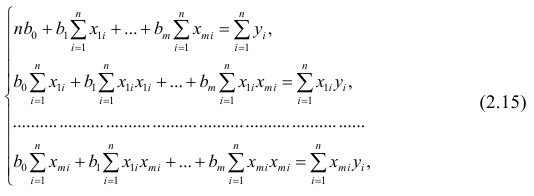
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 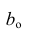 через остальные параметры:
через остальные параметры:
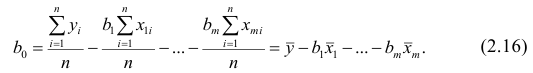
Подставим в остальные уравнения системы вместо 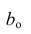 полученное выражение:
полученное выражение:
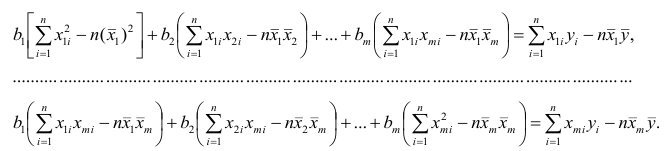
Пусть С — матрица коэффициентов при неизвестных параметрах 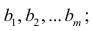
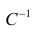 — матрица, обратная матрице С;
— матрица, обратная матрице С; 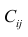 — элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы
— элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы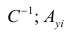 — выражение
— выражение
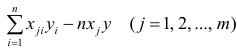 . Тогда, используя формулы линейной алгебры,
. Тогда, используя формулы линейной алгебры,
запишем окончательные выражения для параметров:
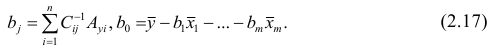
Оценкой остаточной дисперсии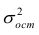 является
является
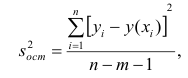
где 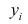 — измеренное значение результативного признака;
— измеренное значение результативного признака;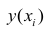 значение результативного признака, вычисленное по уравнению регрессий.
значение результативного признака, вычисленное по уравнению регрессий.
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику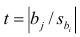 вычисляют для каждого j-го коэффициента регрессии
вычисляют для каждого j-го коэффициента регрессии
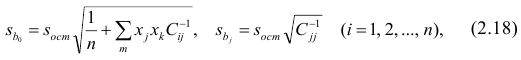
где 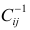 —элемент обратной матрицы, стоящий на пересечении i-й строки и j-
—элемент обратной матрицы, стоящий на пересечении i-й строки и j-
го столбца;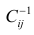 —диагональный элемент обратной матрицы.
—диагональный элемент обратной матрицы.
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 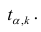 Если
Если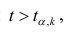 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если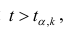 то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: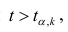
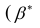 — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики
— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 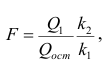 , где
, где 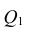 — сумма квадратов, характеризующая влияние признаков X;
— сумма квадратов, характеризующая влияние признаков X; 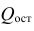 — остаточная сумма квадратов, характеризующая влияние неучтённых факторов;
— остаточная сумма квадратов, характеризующая влияние неучтённых факторов; 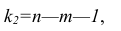
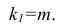 Для уровня значимости а и числа степеней свободы
Для уровня значимости а и числа степеней свободы 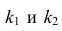 по табл. 3 приложений находят критическое значение
по табл. 3 приложений находят критическое значение 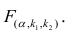 Если
Если 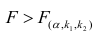 то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При
то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 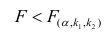 нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 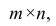 аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений
аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений 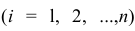 столбцы — признакам
столбцы — признакам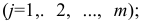 таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных
таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных 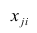 переходят к переменным
переходят к переменным 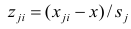 В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
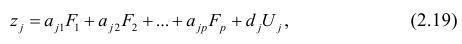
где 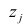 -j-й признак (величина случайная);
-j-й признак (величина случайная); 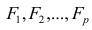 — общие факторы (величины случайные, имеющие нормальный закон распределения);
— общие факторы (величины случайные, имеющие нормальный закон распределения); 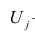 — характерный фактор;
— характерный фактор; 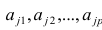 — факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);
— факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);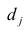 — нагрузка характерного фактора.
— нагрузка характерного фактора.
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 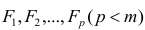 и характерного фактора
и характерного фактора 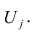
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков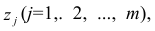 , т.е.
, т.е.
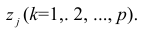
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы 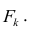
Факторные нагрузки 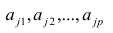 . характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
. характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
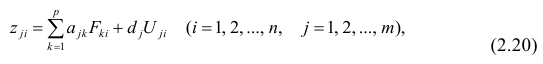
где 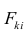 значение k-го фактора для i-го объекта.
значение k-го фактора для i-го объекта.
Дисперсию признака 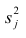 можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность
можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность 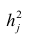 и часть, обусловленную действием j-го характера фактора, характерность
и часть, обусловленную действием j-го характера фактора, характерность 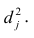 Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака
Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака 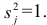 Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
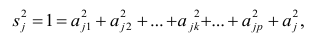
где 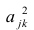 —доля дисперсии признака
—доля дисперсии признака 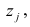 приходящаяся на k-й фактор.
приходящаяся на k-й фактор.
Полный вклад k-го фактора в суммарную дисперсию признаков
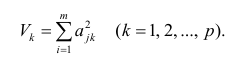
Вклад общих факторов в суммарную дисперсию 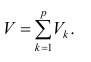
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
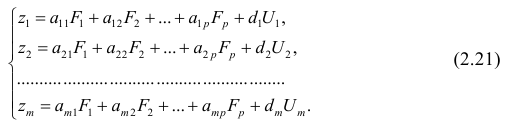
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
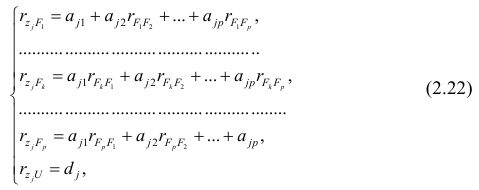
где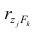 — выборочный коэффициент корреляции между j-м параметром и к-
— выборочный коэффициент корреляции между j-м параметром и к-
м фактором;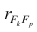 — коэффициент корреляции между к-м и р-м факторами.
— коэффициент корреляции между к-м и р-м факторами.
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
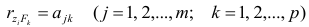 , т.е. коэффициенты отображения равны
, т.е. коэффициенты отображения равны
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам: 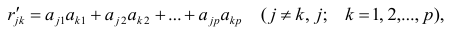
где 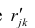 —вычисленный по отображению коэффициент корреляции между j-м
—вычисленный по отображению коэффициент корреляции между j-м
и к-м признаком. Остаточный коэффициент корреляции
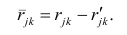
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
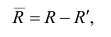
где 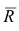 — матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
— матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
Результаты факторного анализа удобно представить в виде табл. 2.10.

Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
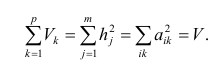
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции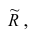 у которой на главной диагонали стоят значения общностей
у которой на главной диагонали стоят значения общностей 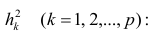 :
: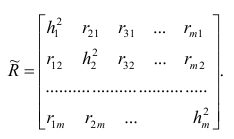
Редуцированная и полная матрицы связаны соотношением

где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 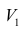 должен быть найден при условии
должен быть найден при условии
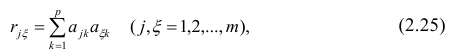
где 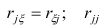 —общность
—общность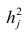 параметра
параметра
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора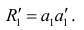 Имея эту матрицу, получают первую матрицу остатков:
Имея эту матрицу, получают первую матрицу остатков: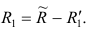
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 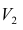 находят из условия
находят из условия
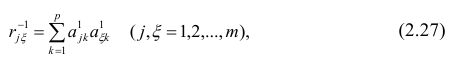
где 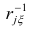 — коэффициент корреляции из первой матрицы остатков;
— коэффициент корреляции из первой матрицы остатков; 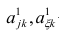 — факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков:
— факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков: 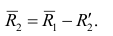
Факторный анализ учитывает суммарную общность. Исходная суммарная общность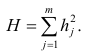 Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на
Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на 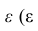 — наперёд заданное малое число).
— наперёд заданное малое число).
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных 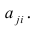
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
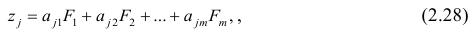
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 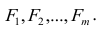 По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
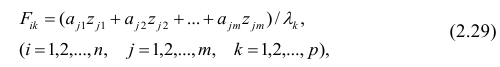
где 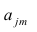 — элементы факторного решения:
— элементы факторного решения: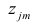 — исходные переменные;
— исходные переменные; 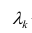 .— k-е собственное значение; р — количество оставленных главных
.— k-е собственное значение; р — количество оставленных главных
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента 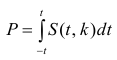
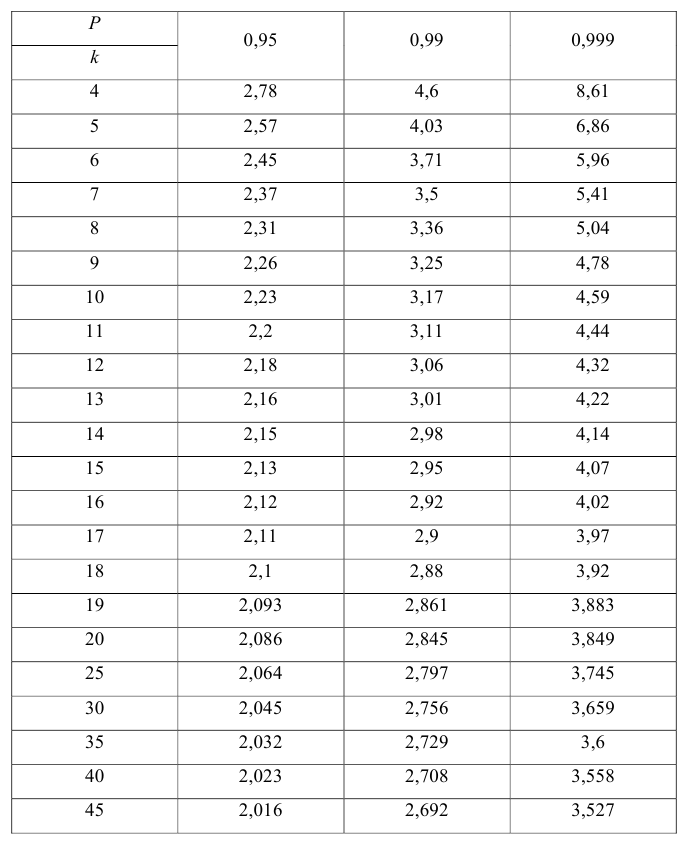
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 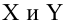 связаны линейной корреляционной зависимостью
связаны линейной корреляционной зависимостью 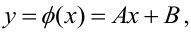 для отыскания которой проведено
для отыскания которой проведено 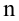 независимых измерений
независимых измерений 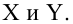
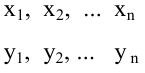
Диаграмма рассеяния (разброса, рассеивания)
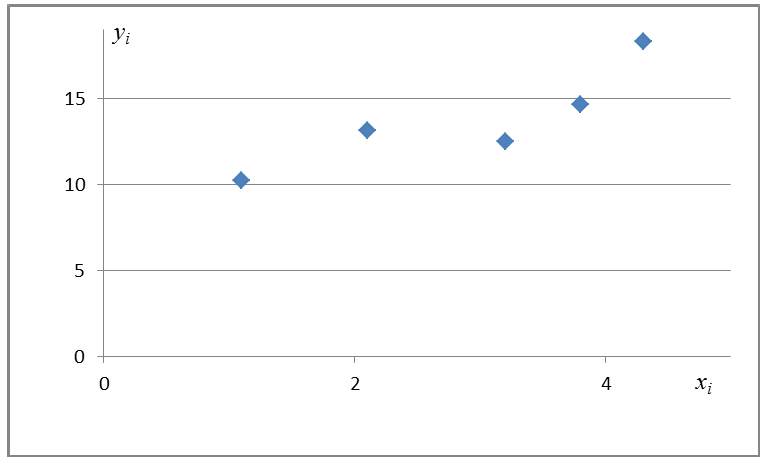
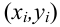 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Выборочное уравнение прямой линии регрессии 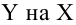 имеет вид
имеет вид
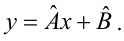
Задача: подобрать 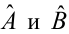 таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой
таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой 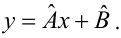
Для того, что бы провести прямую 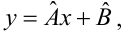 воспользуемся МНК. Потребуем,
воспользуемся МНК. Потребуем,
чтобы 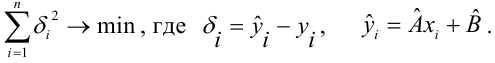
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
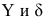 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.- Дисперсия
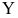 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения. - Результаты наблюдений
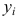 в разных точках независимы.
в разных точках независимы. - Входные переменные
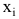 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 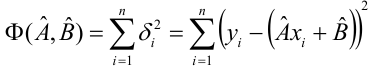 и найдём её минимальное значение
и найдём её минимальное значение
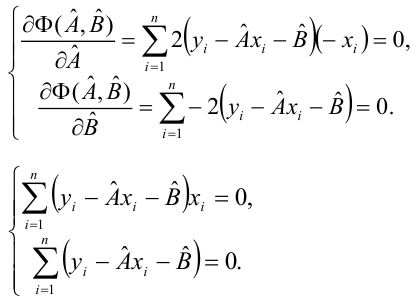
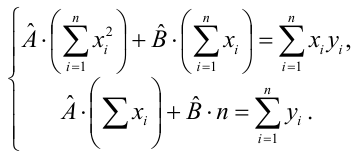
Решив систему, получим искомые значения 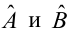
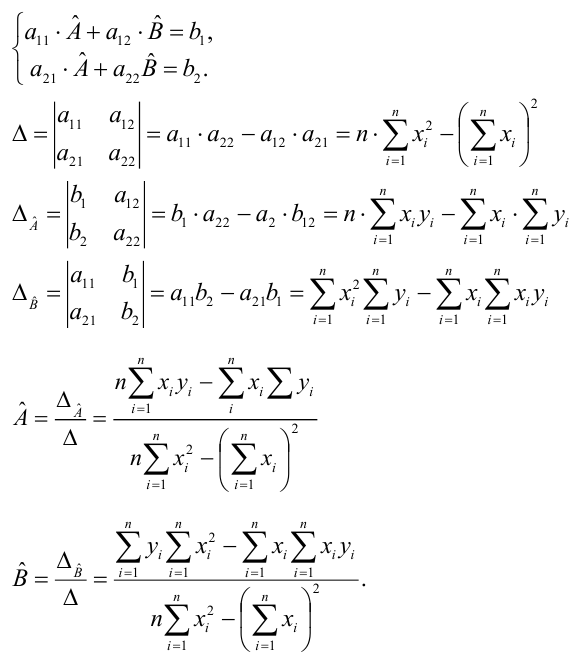
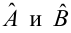 является несмещенными оценками истинных значений коэффициентов
является несмещенными оценками истинных значений коэффициентов 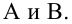
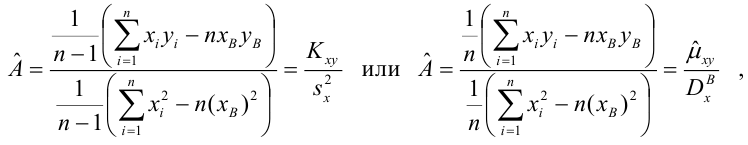 где
где
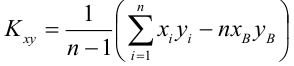 несмещенная оценка корреляционного момента (ковариации),
несмещенная оценка корреляционного момента (ковариации),
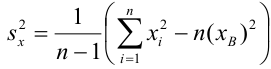 несмещенная оценка дисперсии
несмещенная оценка дисперсии 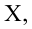
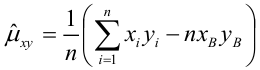 выборочная ковариация,
выборочная ковариация,
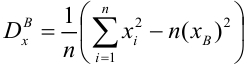 выборочная дисперсия
выборочная дисперсия 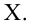
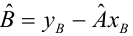
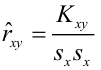 — выборочный коэффициент корреляции
— выборочный коэффициент корреляции
Коэффициент детерминации
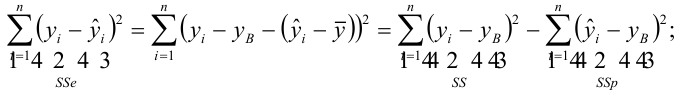
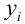 — наблюдаемое экспериментальное значение
— наблюдаемое экспериментальное значение 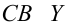 при
при 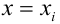
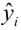 — предсказанное значение
— предсказанное значение 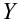 удовлетворяющее уравнению регрессии
удовлетворяющее уравнению регрессии
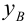 — средневыборочное значение
— средневыборочное значение 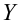
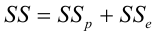
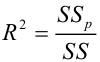 — коэффициент детерминации, доля изменчивости
— коэффициент детерминации, доля изменчивости 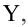 объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии
объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии 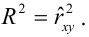
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
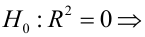 регрессия незначима
регрессия незначима
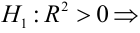 регрессия значима
регрессия значима
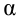 — уровень значимости
— уровень значимости
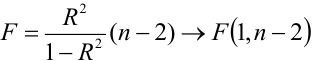 — статистический критерий
— статистический критерий
Критическая область — правосторонняя; 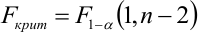
Если 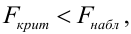 то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
Мощность статистического критерия. Функция мощности
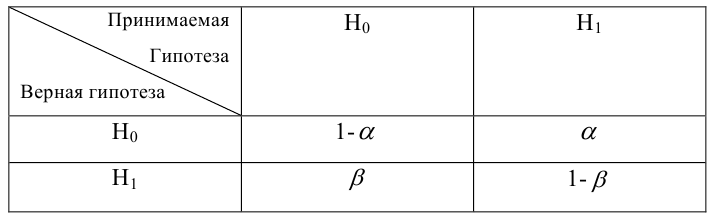
Определение. Мощностью критерия 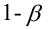 называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода 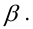
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 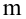 и дисперсией
и дисперсией 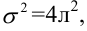 проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
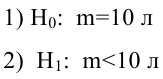
3) Уровень значимости 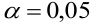
4) Статистический критерий
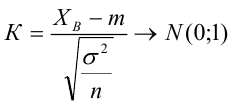
5) Критическая область — левосторонняя
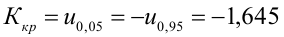
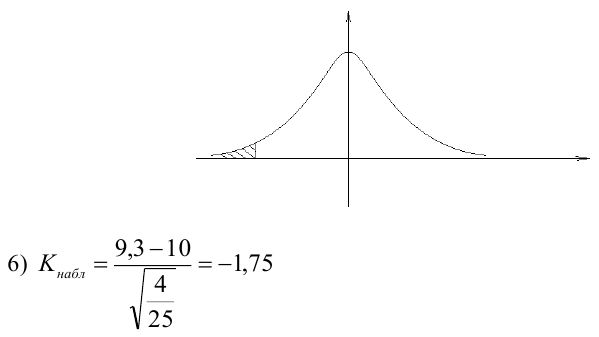
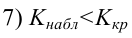 следовательно
следовательно 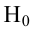 отвергается на уровне значимости
отвергается на уровне значимости 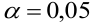
Пример:
В условиях примера 1 предположим, что наряду с 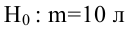 рассматривается конкурирующая гипотеза
рассматривается конкурирующая гипотеза 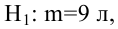 а критическая область задана неравенством
а критическая область задана неравенством 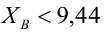 Найти вероятность ошибок I рода и II рода.
Найти вероятность ошибок I рода и II рода.
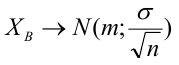
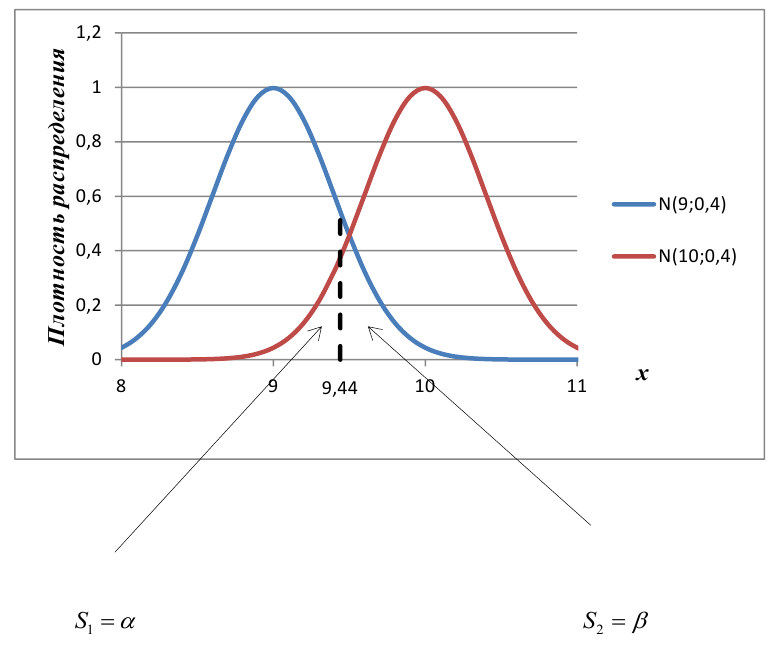
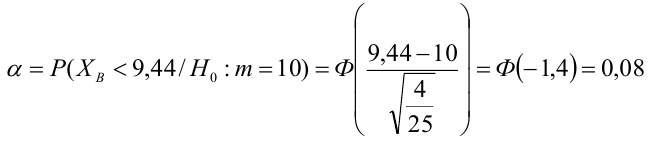
 автомобилей имеют меньший расход топлива)
автомобилей имеют меньший расход топлива)
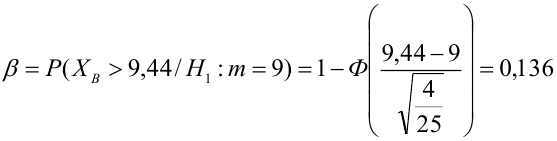
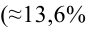 автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
Определение. Пусть проверяется 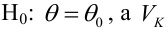 — критическая область критерия с заданным уровнем значимости
— критическая область критерия с заданным уровнем значимости 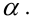 Функцией мощности критерия
Функцией мощности критерия 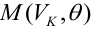 называется вероятность отклонения
называется вероятность отклонения 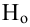 как функция параметра
как функция параметра 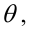 т.е.
т.е.
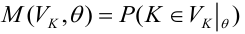
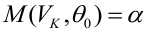 — ошибка 1-ого рода
— ошибка 1-ого рода
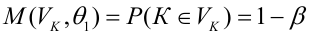 — мощность критерия
— мощность критерия
Пример:
Построить график функции мощности из примера 2 для 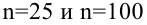
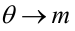
 попадает в критическую область.
попадает в критическую область.
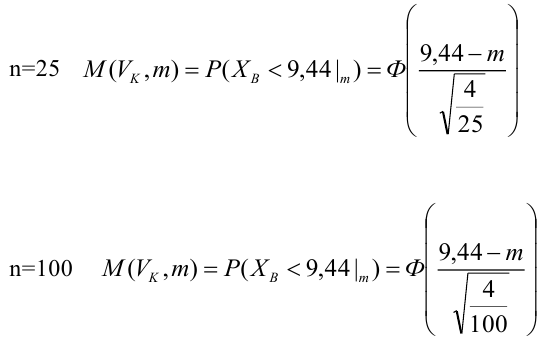
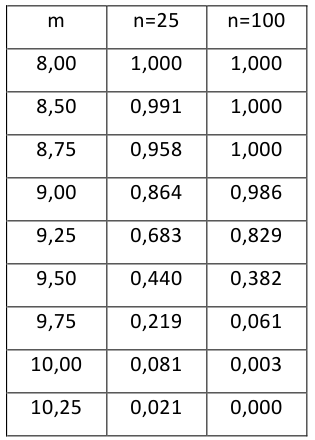
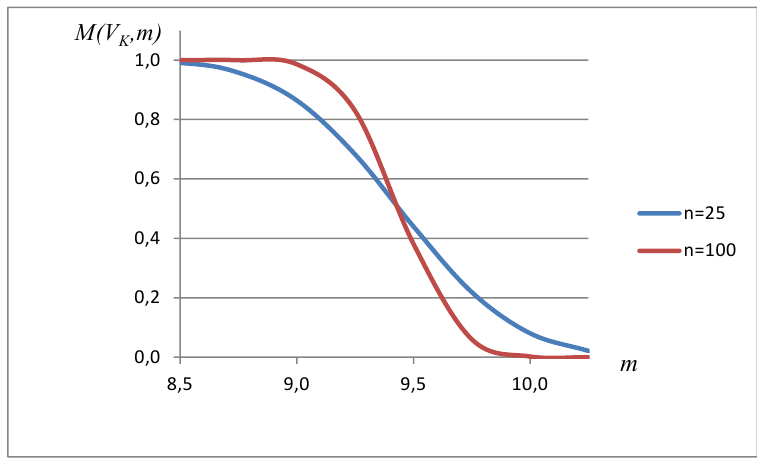
Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить 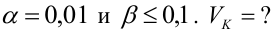
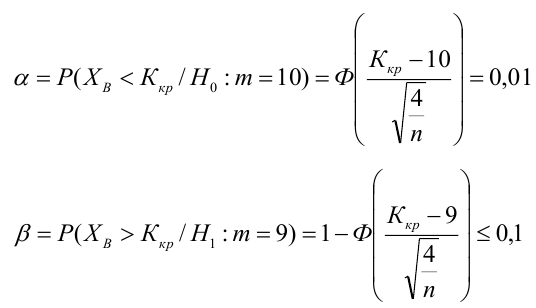
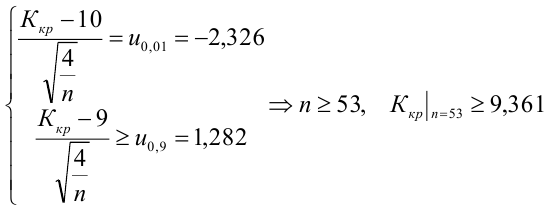
Лемма Неймана-Пирсона.
При проверке простой гипотезы 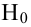 против простой альтернативной гипотезы
против простой альтернативной гипотезы 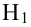 наилучшая критическая область (НКО) критерия заданного уровня значимости
наилучшая критическая область (НКО) критерия заданного уровня значимости 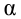 состоит из точек выборочного пространства (выборок объема
состоит из точек выборочного пространства (выборок объема 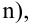 для которых справедливо неравенство:
для которых справедливо неравенство:
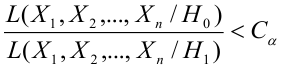
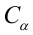 — константа, зависящая от
— константа, зависящая от 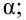
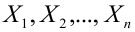 — элементы выборки;
— элементы выборки;
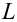 — функция правдоподобия при условии, что соответствующая гипотеза верна.
— функция правдоподобия при условии, что соответствующая гипотеза верна.
Пример:
Случайная величина 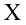 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 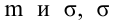 известно. Найти НКО для проверки
известно. Найти НКО для проверки 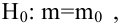 против
против 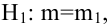 причем
причем 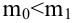
Решение:
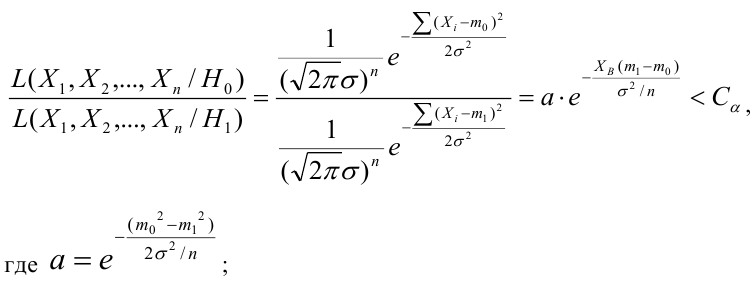
Ошибка первого рода: 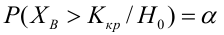
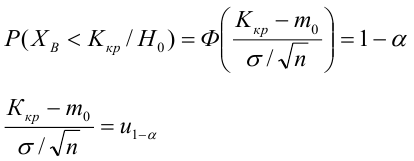
НКО: 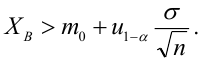
Пример:
Для зависимости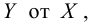 заданной корреляционной табл. 13, найти оценки параметров
заданной корреляционной табл. 13, найти оценки параметров 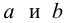 уравнения линейной регрессии
уравнения линейной регрессии 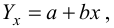 остаточную дисперсию; выяснить значимость уравнения регрессии при
остаточную дисперсию; выяснить значимость уравнения регрессии при 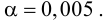
Решение. Воспользуемся предыдущими результатами
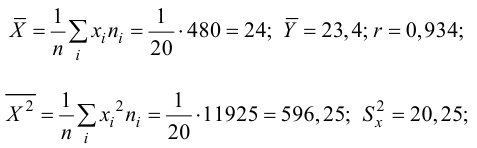
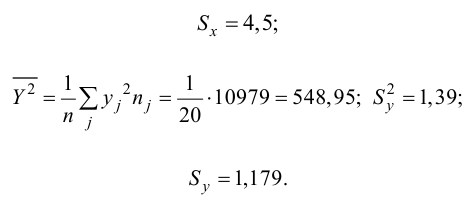
Согласно формуле (24), уравнение регрессии будет иметь вид 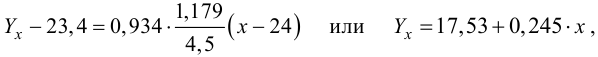 тогда
тогда 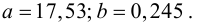
Для выяснения значимости уравнения регрессии вычислим суммы 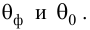 Составим расчетную таблицу:
Составим расчетную таблицу:
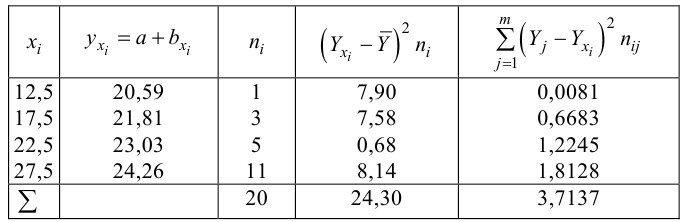
Из (27) и (28) по данным таблицы получим 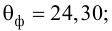
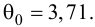
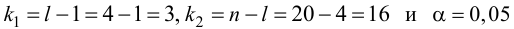 по табл. П7 находим
по табл. П7 находим 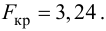
Вычислим статистику
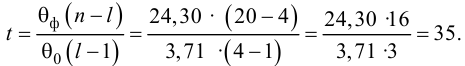
Так как 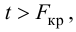 то уравнение регрессии значимо. Остаточная дисперсия равна
то уравнение регрессии значимо. Остаточная дисперсия равна 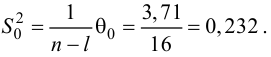
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Экономическая интерпретация параметров модели
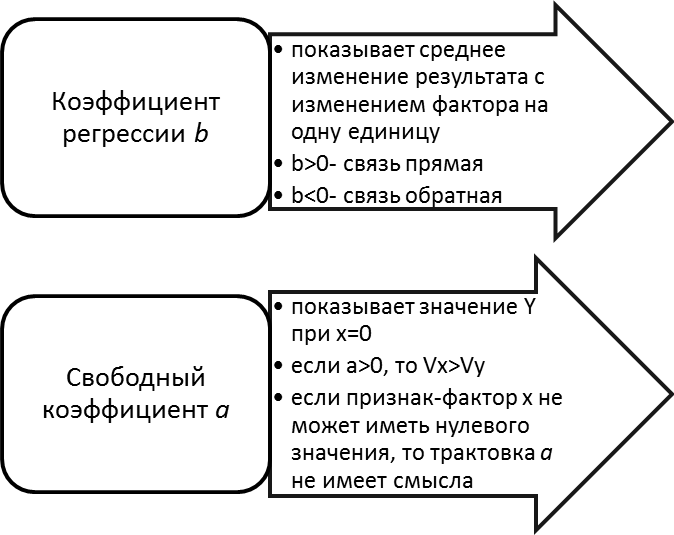
Рис. 4.1. Интерпретация параметров модели
Коэффициенты корреляции и детерминации в линейной модели парной регрессии. Если все точки лежат на построенной прямой, то регрессия Y на Х «идеально» объясняет поведение зависимой переменной. Обычно поведение Y лишь частично объясняется влиянием переменной Х.
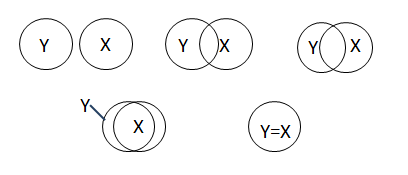
Рис. 4.2. Диаграмма Венна
Линейный коэффициент парной корреляции:
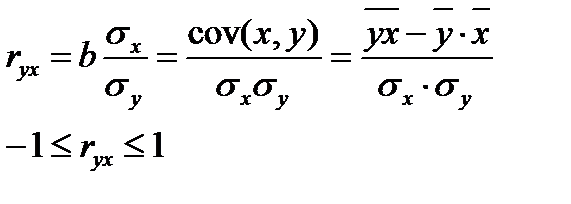
Если b>0, то ryx>0; если b 2 – остаточная дисперсия на одну степень свободы;
t – случайная величина, имеющая распределение Стьюдента с заданной вероятностью.
Вопросы и задания для самоконтроля
1. Каков экономический смысл коэффициента регрессии?
2. Какой смысл может иметь свободный коэффициент уравнения регрессии?
3. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?
4. Каков статистический смысл коэффициента детерминации?
5. Как записывается баланс для сумм квадратов отклонений результативного признака?
6. Что происходит, когда общая СКО равна остаточной? В каком случае общая СКО равна факторной?
7. Что такое число степеней свободы? Чему равны числа степеней свободы для различных СКО в парной регрессии?
8. Как используется F-статистика в регрессионном анализе?
9. Как F-статистика связана с коэффициентом детерминации в парной регрессии?
10. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?
11. В чем суть предсказания индивидуальных значений зависимой переменной?
Задача 1. Пусть имеется следующая модель парной регрессии, построенная по 20 наблюдениям: 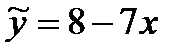 . При этом
. При этом 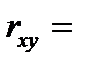 — 0,5.
— 0,5.
Задание: построить доверительный интервал для коэффициента регрессии в этой модели с вероятностями 0,9 и 0,95.
Задача 2. Анализируется зависимость между доходами горожан (X), имеющими индивидуальные домовладения, и рыночной стоимостью их домов (Y). По случайной выборке из 120 горожан данной категории получены результаты:
 27343;
27343; 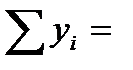 115870;
115870; 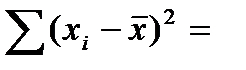 75200;
75200;
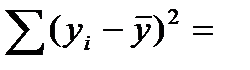 1620340;
1620340;  250431.
250431.
Задание: найти оценку коэффициента регрессии 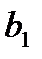 и построить 95% доверительный интервал для коэффициента регрессии.
и построить 95% доверительный интервал для коэффициента регрессии.
Качество регрессионной модели. Нелинейная регрессия
Значимость уравнения регрессии еще не означает, что выбранная модель достаточно правильно (адекватно) описывает исследуемое экономическое явление. Применение неадекватной модели для целей анализа и прогнозирования может приводить к неоправданно большим ошибкам. Если модель адекватна, то остатки регрессии представляют собой независимые нормально распределенные случайные величины с одинаковой дисперсией. В случае неадекватности модели остатки содержат также и систематическую составляющую, а закон их распределения отличается от нормального. Проверка адекватности регрессионной модели рассматривается в § 3.8.
Обычно в начале исследуется линейная модель, для которой после оценки параметров и проверки значимости уравнения регрессии определяется коэффициент детерминации и оценивается точность.
Коэффициент детерминации R 2 рассчитывается по формуле
 . . |
(2.19) |
Его значение показывает долю вариации результата Y, обусловленную вариацией фактора X. К примеру, если R 2 =0,856, то это означает, что 85,6 % вариации результата Y вызвано вариацией фактора X, а соответственно 14,4 % ( 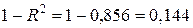 ) — неучтенными и случайными факторами. Коэффициент детерминации принимает значения в интервале от 0 до 1. Чем ближе R 2 к единице, тем лучше модель объясняет вариацию Y, а уравнение регрессии аппроксимирует фактические данные.
) — неучтенными и случайными факторами. Коэффициент детерминации принимает значения в интервале от 0 до 1. Чем ближе R 2 к единице, тем лучше модель объясняет вариацию Y, а уравнение регрессии аппроксимирует фактические данные.
Заметим, что для линейной парной модели коэффициент детерминации равен квадрату коэффициента корреляции: 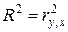 , а стандартная ошибка регрессии Sрег связана с R 2 соотношением
, а стандартная ошибка регрессии Sрег связана с R 2 соотношением
 , , |
(2.20) |
где Sy — стандартное отклонение зависимой переменной Y в исходных данных.
Коэффициент детерминации и F–статистика Фишера (см. § 2.3) связаны между собой соотношением
 , , |
(2.21) |
где n — число наблюдений; m — число оцениваемых параметров регрессионной модели, включая свободный коэффициент b0.
В случае парной линейной регрессии m=2 и
 . . |
(2.22) |
Точность модели, т.е. близость линии регрессии к фактическим данным,характеризует средняя относительная ошибка аппроксимации
 . . |
(2.23) |
Если Еотн не превышает 10 %, то считается, что модель имеет высокую точность, при  точность модели хорошая, при
точность модели хорошая, при  — удовлетворительная, а при
— удовлетворительная, а при 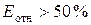 — неудовлетворительная.
— неудовлетворительная.
Средняя относительная ошибка аппроксимации Еотн связана со стандартной ошибкой регрессии Sрег приближенным соотношением
 . . |
(2.24) |
Расхождение между формулами (2.23) и (2.24) обычно незначительное, особенно при достаточно большом объеме наблюдений (  ).
).
После анализа качества линейной модели переходят к исследованию нелинейных моделей, коэффициент детерминации и средняя относительная ошибка аппроксимации которых, определяются по тем же самым формулам и имеют тот же смысл, что и для линейной модели. Наиболее часто на практике используются нелинейные модели, приведенные в табл. 2.2.
Значимость нелинейного уравнения регрессии проверяется по F‑критерию Фишера. Лучшей считается модель, имеющая наибольший коэффициент детерминации R 2 . При незначительных расхождениях в значениях R 2 предпочтение отдается более простой модели. Если модель предполагается использовать для целей анализа, то ее параметры должны иметь содержательную экономическую интерпретацию. Интерпретация параметров степенной, показательной и логарифмической регрессий рассматривается в приведенных ниже примерах.
| Таблица | 2.2 |
| Часто используемые на практике нелинейные модели |
| Форма связи | Модель | Уравнение регрессии |
| 1. Степенная | 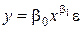 |
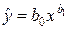 |
| 2. Показательная |  |
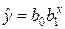 |
| 3. Экспоненциальная (другой вид показательной связи) |  |
 |
| 4. Логарифмическая | 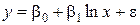 |
 |
| 5. Гиперболическая |  |
 |
| 6. Полиноминальная разных степеней (q — степень полинома) |  |
 |
Решение типовых задач
Пример 2.1
По десяти однородным предприятиям имеется информация, характеризующая зависимость объема выпускаемой продукции (результативная переменная Y, млн. руб.) от объема капиталовложений (фактор X, млн. руб.):
| Предприятие | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Y | ||||||||||
| X |
1. Рассчитать парный коэффициент корреляции между переменными Y и X и проверить его статистическую значимость (уровень значимости a=0,05).
2. Найти параметры уравнения линейной регрессии Y по X и дать их экономическую интерпретацию.
3. Вычислить коэффициент детерминации R 2 и пояснить его смысл.
4. Проверить статистическую значимость уравнения регрессии по F-критерию Фишера (a=0,05).
5. Определить стандартную ошибку регрессии и оценить точность модели с помощью средней относительной ошибки аппроксимации.
6. Построитьдоверительные интервалы для истинных параметров b0 и b1 регрессионной модели и проверить статистическую значимость коэффициентов уравнения регрессии по t-критерию Стьюдента (a=0,05).
7. Спрогнозировать с доверительной вероятностью 0,9 значение показателя Y, если прогнозное значения фактора Х составит 80 % от максимального значения в исходных данных.
8. Изобразить графически результаты моделирования и прогнозирования.
1. Для определения парного коэффициента корреляции ry,x между переменными Y и X в EXCEL может быть использована любая из встроенных функций «КОРРЕЛ» или «ПИРСОН». Использование встроенных функций EXCEL рассмотрено в § 5.4.
Коэффициент корреляции имеет значение
 .
.
Критическое значение коэффициента корреляции для уровня значимости a=0,05 и числа степеней свободы  составляет rкр=0,632, где n=10 — число пар значений переменных. Видно, что коэффициент корреляции превышает по абсолютной величине критическое значение и следовательно является статистически значимым. Положительное значение коэффициента корреляции свидетельствует о прямой связи между переменными Y и X, а превышение им по абсолютной величине 0,8 — о тесной линейной связи.
составляет rкр=0,632, где n=10 — число пар значений переменных. Видно, что коэффициент корреляции превышает по абсолютной величине критическое значение и следовательно является статистически значимым. Положительное значение коэффициента корреляции свидетельствует о прямой связи между переменными Y и X, а превышение им по абсолютной величине 0,8 — о тесной линейной связи.
2. Линейная модель парной регрессии Y по X и уравнение регрессии соответственно имеют вид:
 ;
;
 .
.
Коэффициенты уравнения регрессии определяем с помощью встроенных функций «ОТРЕЗОК» и «НАКЛОН» соответственно. Они имеют значения:
 млн. руб.;
млн. руб.;
 .
.
Окончательно уравнение регрессии —
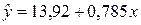 .
.
Значение свободного коэффициента b0 показывает, что при нулевом объеме капиталовложений X объем выпускаемой продукции Y будет составлять в среднем 13,92 млн. руб. Значение углового коэффициента b1=0,785 показывает, что при увеличении объема капиталовложений на 1 млн. руб. объем выпускаемой продукции возрастает в среднем на 0,785 млн. руб.
3. Коэффициент детерминации R 2 парной линейной регрессии определяется с помощью встроенной функции EXCEL «КВПИРСОН». Получим:
 .
.
Значение R 2 показывает, что линейная модель объясняет 86,9 % вариации Y. Другими словами, 86,9 % вариации объема выпускаемой продукции Y обусловлена вариацией объема капиталовложений X.
4. Для проверки статистической значимости уравнения регрессии F‑статистику Фишера определимчерез коэффициент детерминации по формуле (2.22):
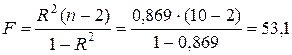 .
.
Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии)  и знаменателя (остатка)
и знаменателя (остатка)  составляет Fтаб=5,32. Так как F-статистика превышает табличное значение F-критерия, то это свидетельствует о статистической значимости уравнения регрессии в целом.
составляет Fтаб=5,32. Так как F-статистика превышает табличное значение F-критерия, то это свидетельствует о статистической значимости уравнения регрессии в целом.
5. Стандартная ошибка линейной парной регрессии Sрег (см. § 2.2) определяется с помощью встроенной функции EXCEL «СТОШYX». Имеем:
 млн. руб.
млн. руб.
Среднюю относительную ошибку аппроксимации Еотн рассчитаем по приближенной формуле
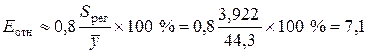 %,
%,
где  млн. руб. — средний объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ».
млн. руб. — средний объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ».
Значение Еотн показывает, что предсказанные уравнением регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,1 %. Так как средняя относительная ошибка аппроксимации меньше 10 %, то это свидетельствует о высокой точности линейной модели.
6. Для определения интервальных оценок истинных параметров b0 и b1 регрессионной модели рассчитаем стандартные ошибки коэффициентов уравнения регрессии:
 млн. руб.;
млн. руб.;
 ,
,
где  млн. руб. — стандартное отклонение переменной X в исходных данных, определяемое с помощью встроенной функции «СТАНДОТКЛОН»;
млн. руб. — стандартное отклонение переменной X в исходных данных, определяемое с помощью встроенной функции «СТАНДОТКЛОН»;  — сумма квадратов значений переменной X в исходных данных (функция «СУММКВ»).
— сумма квадратов значений переменной X в исходных данных (функция «СУММКВ»).
Доверительный интервал, «накрывающий» с заданной надежностью 0,95 неизвестное значение параметра b0 модели, имеет вид:
 млн. руб.,
млн. руб.,
где tтаб=2,306 — табличное значение t-критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка линейной парной регрессии  .
.
Таким образом, с доверительной вероятностью 95 % истинное значение параметра b0 будет находиться в интервале от 3,89 до 23,95 млн. руб. Так как нижняя и верхняя границы доверительного интервала имеют одинаковый знак, то коэффициент b0 уравнения регрессии признается статистически значимым на уровне значимости a=0,05.
Доверительный интервал для параметра b1 модели имеет вид:
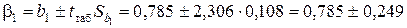 .
.
Это означает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y с вероятностью 95 % возрастает в среднем на величину, заключенную в интервале от 0,536 до 1,034 млн. руб. Один и тот же знак доверительных границ свидетельствует о статистической значимости коэффициента b1 и уравнения регрессии в целом на уровне a=0,05.
7. Спрогнозируем объем выпускаемой продукции Y, если прогнозное значение x0 объема капиталовложений X составит 80 % от своего максимального значения в исходных данных xmax=59 млн. руб.:
 млн. руб.
млн. руб.
Среднее прогнозируемое значение объема выпускаемой продукции (точечный прогноз) равно
 млн. руб.
млн. руб.
Точечный прогноз можно рассчитать и с помощью встроенной функции «ПРЕДСКАЗ».
Стандартная ошибка прогноза фактического значенияобъема выпускаемой продукции y0 рассчитывается по формуле
 млн. руб.,
млн. руб.,
где 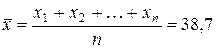 млн. руб. — средний объем капиталовложений, определенный с помощью встроенной функции «СРЗНАЧ».
млн. руб. — средний объем капиталовложений, определенный с помощью встроенной функции «СРЗНАЧ».
Интервальный прогноз фактического значения объема выпускаемой продукции y0 с надежностью g=0,9 (уровень значимости a=0,1) имеет вид:
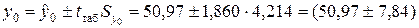 млн. руб.,
млн. руб.,
где tтаб=1,860 — табличное значение t-критерия Стьюдента при уровне значимости a=0,1 и числе степеней свободы  .
.
Объем выпускаемой продукции с вероятностью 90 % будет находиться в интервале от 43,13 до 58,81 млн. руб.
8. График, на котором изображены фактические и предсказанные уравнением регрессии значения Y, строим с помощью надстройки «Мастер диаграмм» EXCEL (рис. 2.5). Данная надстройка позволяет построить линии нескольких видов регрессии (линейной, степенной, логарифмической, экспоненциальной и полиноминальной), определить их уравнение и коэффициент детерминации. Использование «Мастера диаграмм» рассмотрено в § 5.1.

рис. 2.5. Линия линейной парной регрессии и точки прогноза
Пример 2.2
Используя исходные данные предыдущего примера, выполнить следующие действия:
1. С помощью табличного процессора EXCEL построить уравнения линейной, логарифмической, степенной и показательной регрессий Y по X. Для указанных регрессий:
· привести графики их линий;
· дать экономическую интерпретацию параметрам уравнений;
· найти коэффициенты детерминации;
· проверить статистическую значимость уравнений по F-критерию Фишера;
· оценить точность моделей с помощью средней относительной ошибки аппроксимации.
2. Сравнить построенные модели между собой и выбрать лучшую из них для целей анализа и прогнозирования.
1. Линейную, степенную, логарифмическую и показательную регрессии строим с помощью «Мастера диаграмм» EXCEL. Линейная и степенная регрессии показаны на рис. 2.6, логарифмическая и показательная — на рис. 2.7. На графиках приводятся не только линии регрессии, но также их уравнения и коэффициенты детерминации (см. § 5.1).

рис. 2.6. Линии линейной и степенной регрессий

рис. 2.7. Линии логарифмической и показательной регрессий
Рассмотрим последовательно каждую модель.
1) Уравнение линейной регрессии имеет вид:
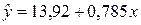 .
.
Угловой коэффициент b1=0,785 является показателем среднего абсолютного прироста. Его значение показывает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y возрастает в среднем на 0,785 млн. руб.
Коэффициент детерминации R 2 =0,869 показывает, что линейная модель объясняет 89,8 % вариации объема выпускаемой продукции Y.
F-статистика Фишера линейной модели определяем через коэффициент детерминации R 2 по формуле
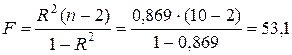 .
.
Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии)  и знаменателя (остатка)
и знаменателя (остатка)  составляет Fтаб=5,32. Так как F-статистика превышает табличное значение, то это свидетельствует о статистической значимости уравнения линейной регрессии в целом.
составляет Fтаб=5,32. Так как F-статистика превышает табличное значение, то это свидетельствует о статистической значимости уравнения линейной регрессии в целом.
Следует заметить, что табличное значение F-критерия Фишера одинаково как для линейной, так и для всех нелинейных моделей, которые здесь строятся (Fтаб=5,32).
Стандартная ошибка линейной регрессии рассчитывается по формуле
 млн. руб.,
млн. руб.,
где  млн. руб. — стандартное отклонение переменной X в исходных данных, определенное с помощью встроенной функции «СТАНДОТКЛОН».
млн. руб. — стандартное отклонение переменной X в исходных данных, определенное с помощью встроенной функции «СТАНДОТКЛОН».
Среднюю относительную ошибку аппроксимации определяем по приближенной формуле
 %,
%,
где 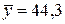 млн. руб. — средний объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ».
млн. руб. — средний объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ».
Предсказанные уравнением линейной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,1 %.
2) Уравнение степенной регрессии выглядит следующим образом:
 .
.
Показатель степени b1=0,721 является средним коэффициентом эластичности. Его значение показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции Y возрастает в среднем на 0,721 %.
Коэффициент детерминации R 2 =0,873 показывает, что степенная модель объясняет 87,3 % вариации объема выпускаемой продукции Y.
F-статистика степенной модели

также превышает табличное значение F-критерия Фишера (Fтаб=5,32), что указывает на статистическую значимость уравнения степенной регрессии.
Стандартную ошибку и среднюю относительную ошибку аппроксимации нелинейных регрессий будем определять по тем же самым формулам, что и для линейной модели. Для степенной регрессии они равны:
 млн. руб.;
млн. руб.;
 %.
%.
Предсказанные уравнением степенной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,0 %.
3) Уравнение логарифмической регрессии имеет вид:
 .
.
Значение параметра b1=29,9 показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции Y возрастает в среднем на  млн. руб.
млн. руб.
Коэффициент детерминации R 2 =0,898 показывает, что логарифмическая модель объясняет 89,8 % вариации объема выпускаемой продукции Y.
F-статистика Фишера логарифмической модели равна

и превышает табличное значение F-критерия Фишера (Fтаб=5,32). Это свидетельствует о статистической значимости уравнения регрессии.
Стандартная ошибка логарифмической регрессии составляет
 млн. руб.
млн. руб.
Средняя относительная ошибка аппроксимации имеет значение
 %.
%.
Предсказанные уравнением логарифмической регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 6,2 %.
4) Уравнение показательной регрессии определяется через экспоненциальную регрессию:
 ,
,
где е=2,718… — основание натуральных логарифмов;  — функция экспоненты (в EXCEL встроенная функция «EXP»).
— функция экспоненты (в EXCEL встроенная функция «EXP»).
Параметр b1=1,019 показательной регрессии 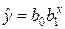 является средним коэффициентом роста. Его значение показывает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпуска продукции Y возрастает в среднем в 1,019 раза, т.е. на 1,9 %.
является средним коэффициентом роста. Его значение показывает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпуска продукции Y возрастает в среднем в 1,019 раза, т.е. на 1,9 %.
Заметим, что параметр b1 экспоненциальной регрессии  , умноженный на 100, является средним темпом прироста, выраженным в процентах. Данный вывод вытекает из приближенного соотношения
, умноженный на 100, является средним темпом прироста, выраженным в процентах. Данный вывод вытекает из приближенного соотношения  , при относительно малых значениях a (
, при относительно малых значениях a (  ).
).
Уравнения показательной и экспоненциальной регрессии являются эквивалентными.
Коэффициент детерминации R 2 =0,821 показывает, что показательная модель объясняет 82,1 % вариации объема выпускаемой продукции Y.
F-статистика показательной модели

превышает табличное значение F-критерия Фишера (Fтаб=5,32), что свидетельствует о статистической значимости уравнения регрессии.
Стандартная ошибка показательной регрессии
 млн. руб.
млн. руб.
Средняя относительная ошибка аппроксимации
 %.
%.
Предсказанные уравнением показательной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 8,3 %.
2. Сравнивая между собой коэффициенты детерминации R 2 четырех моделей, можно придти к выводу, что лучшей из них является логарифмическая модель, так как она имеет самое большое значение R 2 . Эту модель и целесообразно использовать в качестве рабочей для анализа и прогнозирования изменения объема выпускаемой продукции Y в зависимости от изменения объема капиталовложений X.
Заметим, что при выборе лучшей модели из четырех рассмотренных для целей анализа параметр b1 должен иметь содержательную интерпретацию. Так, если бы переменные X и Y были относительными величинами и измерялись в процентах, то корректная интерпретация параметра b1 нелинейных моделей оказалась бы затруднительной. В этом случае для прогнозирования следовало бы выбрать модель с большим R 2 , а для целей анализа — линейную модель.
Пример 2.3
В магазине исследуется зависимость количества реализованных за день упаковок шампуня (Y, шт.) от цены одной упаковки (X, руб.). Имеется информация по одиннадцати наименованиям шампуня:
| Шампунь | А | Б | В | Г | Д | Е | Ж | З | И | К | Л |
| Y | |||||||||||
| X |
Выполнить те же самые действия, что и в предыдущем примере.
1. Линейную, степенную, логарифмическую и показательную регрессии строим с помощью «Мастера диаграмм» EXCEL. Линейная и степенная регрессии показаны на рис. 2.8, логарифмическая и показательная — на рис. 2.9.
Используя формулы предыдущего примера, рассчитаем для каждой модели коэффициент детерминации R 2 , F-статистику Фишера, стандартную ошибку регрессии Sрег и среднюю относительную ошибку аппроксимации Eотн (  шт.; Sy=13,631 шт.). Полученные результаты сведены в табл. 2.3.
шт.; Sy=13,631 шт.). Полученные результаты сведены в табл. 2.3.

рис. 2.8. Линии линейной и степенной регрессий

рис. 2.9. Линии логарифмической и показательной регрессий
| Таблица | 2.3 |
| Сводная таблица результатов моделирования |
| Модель | Уравнение регрессии | R 2 | F | Sрег, шт. | Eотн, % |
| 1. Линейная |  |
0,788 | 33,45 | 6,62 | 11,8 |
| 2. Степенная |  |
0,857 | 53,94 | 5,43 | 9,7 |
| 3. Логарифмическая |  |
0,834 | 45,22 | 5,86 | 10,4 |
| 4. Показательная (экспоненциальная) |  ( (  ) ) |
0,825 | 42,43 | 6,01 | 10,7 |
Очевидно, что между переменными X и Y имеется обратная статистическая связь. На это указывают отрицательные значения параметра b1 линейного, степенного и логарифмического уравнений регрессии, а также меньшее единицы значение параметра b1 показательного уравнения. Все уравнения регрессии статистически значимы на уровне значимости a=0,05 (  ;
;  ; Fтаб=5,12).
; Fтаб=5,12).
Угловой коэффициент b1=–0,933 линейной регрессии показывает, что при увеличении цены шампуня X на 1 руб. количество проданных упаковок Y уменьшается в среднем на 0,933 шт. Линейная модель объясняет 78,8 % вариации Y (R 2 =0,788). Предсказанные уравнением регрессии значения Y отличаются от фактических значений в среднем на 11,8 %.
Показатель степени b1=–0,888 степенной регрессии показывает, что при увеличении цены X на 1 % число реализованных упаковок Y уменьшается в среднем на 0,888 %. Степенная модель объясняет 85,7 % вариации Y. Предсказанные уравнением регрессии значения Y отличаются от фактических в среднем на 9,7 %.
Значение параметра b1=39,6 логарифмической регрессии показывает, что при увеличении цены единицы продукции X на 1 % количество проданных упаковок Y уменьшается в среднем на  шт. Логарифмическая модель объясняет 83,4 % вариации Y. Средняя погрешность предсказания составляет 10,4 %.
шт. Логарифмическая модель объясняет 83,4 % вариации Y. Средняя погрешность предсказания составляет 10,4 %.
Значение основания степени b1=0,979 показательной регрессии показывает, что при увеличении цены X на 1 руб. объем реализации Y составит в среднем 97,9 % от первоначального значения, или, другими словами, уменьшится на 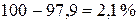 . Это же значение получается, если умножить на 100 параметр «–0,021» экспоненциальной регрессии (см. табл. 2.3). Показательная модель объясняет 82,5 % вариации Y. Предсказанные уравнением регрессии значения Y отличаются от фактических в среднем на 10,7 %.
. Это же значение получается, если умножить на 100 параметр «–0,021» экспоненциальной регрессии (см. табл. 2.3). Показательная модель объясняет 82,5 % вариации Y. Предсказанные уравнением регрессии значения Y отличаются от фактических в среднем на 10,7 %.
2. Сравнивая между собой коэффициенты детерминации R 2 четырех построенных моделей, приходим к выводу, что лучшей является степенная модель, имеющая наибольший R 2 . Эту модель и целесообразно использовать в качестве рабочей для анализа и прогнозирования изменения объема реализации Y от изменения цены единицы продукции X.
Контрольные задания
Используя приведенные ниже данные, выполнить расчеты в соответствии с заданием к примерам 2.1 и 2.2. В вариантах 1 – 5 между переменными присутствует прямая связь, в вариантах 6 – 10 — обратная связь.
Вариант 1(прямая связь)
Вариант 2(прямая связь)
Вариант 3(прямая связь)
Вариант 4(прямая связь)
Вариант 5(прямая связь)
Вариант 6(обратная связь)
Вариант 7(обратная связь)
Вариант 8(обратная связь)
Вариант 9(обратная связь)
Вариант 10(обратная связь)
Тестовые вопросы для самоконтроля
Из перечня предлагаемых ответов на вопрос только один является правильным. Правильные ответы приведены на с. 151. Числовые данные тестов можно использовать как исходные для рассмотренных в § 2.7 примеров.
По десяти интернет-брокерам в секции фондового рынка имеются данные, характеризующие зависимость годового торгового оборота (Y, млрд. руб.) от средней ставки маржинального кредитования (X, % годовых):
| Компания | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Y | 30,82 | 30,8 | 25,14 | 14,1 | 12,73 | 10,8 | 9,74 | 8,42 | 7,65 | |
| X | 16,5 |
Парный коэффициент линейной корреляции между переменными Y и X имеет значение ry,x=–0,451.
Охарактеризовать линейную связь между торговым оборотом Y и средней ставкой маржинального кредитования X, если критическое значение коэффициента корреляции на уровне значимости a=0,05 составляет rкр=0,632.
а) Линейная связь статистически значимая.
б) Линейная связь статистически незначимая.
в) Линейная связь тесная.
г) Линейная связь прямая функциональная.
д) Линейная связь обратная функциональная.
По семи целлюлозно-бумажным компаниям имеются данные, характеризующие зависимость объема выпускаемой продукции (Y, млн. долл. США) от производственной мощности (X, тыс. тонн целлюлозы в год), по итогам года:
| Компания | А | Б | В | Г | Д | Е | Ж |
| Y | |||||||
| X |
Стандартные отклонения переменных Y и X и парный коэффициент корреляции между ними имеют соответственно значения: Sy=344 млн. долл. США, Sx=824 тыс. тонн, ry,x=0,988.
На сколько в среднем увеличивается объем выпускаемой продукции Y при росте производственной мощности X на одну тысячу тонн целлюлозы в год?
а) На 0,344 млн. долл.
б) На 0,824 млн. долл.
в) На 0,412 млн. долл.
г) На 0,988 млн. долл.
д) На 0,280 млн. долл.
Исследуется связь между официальными курсами доллара США (Y, руб./USD) и евро (X, руб./EUR), установленными Центральным банком Российской Федерации. Имеются данные за десять последовательных дней:
| День | ||||||||||
| Y | 28,11 | 27,97 | 27,97 | 28,01 | 27,98 | 28,12 | 28,19 | 28,13 | 28,09 | 28,07 |
| X | 36,59 | 36,46 | 36,56 | 36,47 | 36,28 | 36,13 | 35,98 | 35,97 | 36,00 | 36,13 |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:
 .
.
Суммы квадратов отклонений зависимой переменной Y от своего среднего значения составляют:
· обусловленная регрессией — SSрег=0,0240;
Рассчитать F-статистику и проверить статистическую значимость уравнения регрессии, если табличное значение F‑критерия Фишера на уровне значимости a=0,05 составляет Fтаб=5,32.
а) F=6,17; уравнение регрессии статистически значимо.
б) F=0,77; уравнение регрессии статистически незначимо.
в) F=1,77; уравнение регрессии статистически незначимо.
г) F=2,54; уравнение регрессии статистически незначимо.
д) F=14,17; уравнение регрессии статистически значимо.
По девяти из наиболее прибыльных компаний региона имеются данные, характеризующие зависимость чистой прибыли (Y, млн. руб.) от объема реализации (X, млн. руб.) по итогам одного года:
| Компания | А | Б | В | Г | Д | Е | Ж | З | И |
| Y | |||||||||
| X |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:
 .
.
Коэффициент детерминациисоставляет R 2 =0,540.
Рассчитать F-статистику и проверить статистическую значимость уравнения регрессии на уровне a=0,05, если табличное значение F‑критерия Фишера составляет Fтаб=5,59.
а) F=0,73; уравнение регрессии статистически незначимо.
б) F=1,17; уравнение регрессии статистически незначимо.
в) F=3,91; уравнение регрессии статистически значимо.
г) F=8,22; уравнение регрессии статистически значимо.
д) F=22,6; уравнение регрессии статистически значимо.
По восьми крупнейшим западным банкам-консультантам на рынке M&A (сопровождение сделок по слияниям и поглощениям) имеются данные, характеризующие зависимость размера комиссионных (Y, млн. долл. США) от объема сделок (X, млрд. долл. США), по итогам трех кварталов года:
| Банк | А | Б | В | Г | Д | Е | Ж | З |
| Y | ||||||||
| X | 305,5 | 265,7 | 240,4 | 149,3 | 101,6 | 114,6 | 122,2 |
Уравнение линейной регрессии Y по X имеет вид:
 .
.
Стандартные ошибки коэффициентов уравнения составляют:
· свободного коэффициента —  млн. долл.;
млн. долл.;
· углового коэффициента —  млн. долл./млрд. долл.
млн. долл./млрд. долл.
Проверить статистическую значимость уравнения регрессии на уровне значимости a=0,05 для чего рассчитать соответствующую t-статистику. Табличное значение t‑критерия Стьюдента составляет tтаб=2,447.
а) t=0,892; уравнение регрессии статистически незначимо.
б) t=2,510; уравнение регрессии статистически значимо.
в) t=1,121; уравнение регрессии статистически незначимо.
г) t=3,404; уравнение регрессии статистически значимо.
д) t=3,816; уравнение регрессии статистически значимо.
По семи оценочным компаниям имеются данные, характеризующие зависимость совокупной выручки за полугодие (Y, тыс. руб.) от количества специалистов-оценщиков (X, чел.):
| Компания | А | Б | В | Г | Д | Е | Ж |
| Y | |||||||
| X |
С помощью «Мастера диаграмм» EXCEL были получены уравнения линейной, степенной, показательной и логарифмической регрессий Y по X, и для каждой модели определен коэффициент детерминации R 2 :
· линейная:  ; R 2 =0,877;
; R 2 =0,877;
· степенная:  ; R 2 =0,858;
; R 2 =0,858;
· показательная:  ; R 2 =0,939;
; R 2 =0,939;
· логарифмическая:  ; R 2 =0,780.
; R 2 =0,780.
Какая из моделей лучше характеризует вариацию совокупной выручки Y?
Исследуется связь между ценой нефти марки Urals (Y, долл. США/баррель) и ценой нефти марки Brent (X, долл./баррель) по итогам торгов на Международной нефтяной бирже за десять торговых дней:
| День | ||||||||||
| Y | 39,91 | 41,18 | 40,38 | 39,4 | 39,44 | 39,54 | 40,04 | 38,42 | 38,49 | 39,81 |
| X | 44,8 | 45,87 | 44,64 | 43,65 | 43,38 | 43,69 | 43,05 | 42,93 | 42,98 | 44,42 |
Было получено уравнение линейной регрессии Y по X:
 .
.
Дать правильную экономическую интерпретацию угловому коэффициенту b1=0,715 уравнения регрессии.
Угловой коэффициент b1=0,715 уравнения регрессии показывает, что …
а) … 71,5 % вариации цены нефти Urals объясняется вариацией цены нефти Brent.
б) … с ростом цены нефти Brent на один процент цена нефти Urals возрастает в среднем на 0,715 %.
в) … с ростом цены нефти Brent на один процент цена нефти Urals возрастает в среднем на 0,715 долл./баррель.
г) … с ростом цены барреля нефти Brent на один доллар цена барреля нефти Urals возрастает в среднем на 0,715 %.
д) … с ростом цены барреля нефти Brent на один доллар цена барреля нефти Urals возрастает в среднем на 0,715 доллара.
Исследуется зависимость месячного торгового оборота универсального магазина (Y, млн. руб.) от размера торговых площадей (X, м 2 ). Имеются данные по восьми универмагам города:
| Магазин | А | Б | В | Г | Д | Е | Ж | З |
| Y | ||||||||
| X |
Было получено уравнение степенной регрессии Y по X:
 .
.
Дать правильную экономическую интерпретацию показателю степени b1=0,552 в уравнении регрессии.
Показатель степени b1=0,552 в уравнении регрессии показывает, что …
а) … 55,2 % вариации торгового оборота объясняется вариацией размера торговых площадей.
б) … с увеличением размера торговых площадей на один процент торговый оборот возрастает в среднем на 0,552 %.
в) … с увеличением размера торговых площадей на один процент торговый оборот возрастает в среднем на 0,552 млн. руб.
г) … с увеличением размера торговых площадей на один квадратный метр торговый оборот возрастает в среднем на 0,552 %.
д) … с увеличением размера торговых площадей на один квадратный метр торговый оборот возрастает в среднем на 0,552 млн. руб.
По девяти туристическим агентствам города исследуется зависимость месячного торгового оборота (Y, тыс. долл. США) от количества менеджеров по туризму (X, чел.):
| Турагентство | А | Б | В | Г | Д | Е | Ж | З | И |
| Y | |||||||||
| X |
Было получено уравнение показательной регрессии Y по X:
 .
.
Дать правильную экономическую интерпретацию основанию степени b1=1,076 в уравнении регрессии.
Основание степени b1=1,076 в уравнении регрессии показывает, что …
а) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем в 1,076 раз, т.е. на 7,6 %.
б) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем на 1,076 %.
в) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем на 1,076 тыс. руб.
г) … с увеличением численности менеджеров по туризму на один процент торговый оборот возрастает в среднем в 1,076 раз, т.е. на 7,6 %.
д) … 1,076 % вариации торгового оборота объясняется вариацией численности менеджеров по туризму.
Исследуется связь между учетной ценой Банка России на аффинированное золото (Y, руб./г) и ценой золота на мировых рынках (X, долл. за тройскую унцию) по данным за десять последовательных дней:
| День | ||||||||||
| Y | 390,38 | 391,74 | 393,61 | 378,8 | 377,01 | 381,28 | 383,09 | 372,84 | 374,48 | 381,19 |
| X | 438,9 | 441,1 | 422,2 | 422,5 | 423,3 | 426,8 | 415,9 | 418,85 | 427,1 |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:
 .
.
Построить интервальный прогноз учетной цены Банка России на аффинированное золото y0 с надежностью 90 % при цене золота x0=410 долл. за тройскую унцию, если стандартная ошибка прогноза фактического значения Y при этом составляет  руб./г, а табличное значение t-критерия Стьюдента — tтаб=1,86.
руб./г, а табличное значение t-критерия Стьюдента — tтаб=1,86.
С вероятностью 0,9 учетная цена золота будет находиться в интервале …
Дать экономическую интерпретацию параметров уравнения
Все эти эффекты затрудняют и без того сложную задачу интерпретации коэффициентов регрессии или вообще делают невозможным ее решение без привлечения новых способов обработки и дополнительной информации. В этих условиях нельзя применять уравнение регрессии и для прогноза значений переменной у. В то же время если уравнение регрессии предполагается использовать для целей прогноза значений переменной у только в точках, близких к значениям объясняющих переменных х(1 . . х из матрицы данных X, то оно может оказаться вполне удовлетворительным независимо от степени связи между предсказывающими переменными качество уравнения регрессии определяется значением коэффициента множественной корреляции Ry.x между переменной у и переменными X (хотя при этом может быть необходимо принять некоторые предосторожности чисто вычислительного характера). Таким образом, последствия мультиколлинеарности тем серьезнее, чем больше информации мы хотим получить из имеющейся совокупности наблюдений. [c.254]
Более правильной на первый взгляд кажется интерпретация коэффициента регрессии а как обусловленная фактором Xi часть интенсивности совместного влияния всех факторов. Коэффициент регрессии а, показывает, на сколько единиц изменяется результативный показатель У в случае изменения факторного показателя Xi на единицу при изменении других факторных показателей аналогично их изменению в условиях исследуемого эксперимента (в рамках исследуемой статистической совокупности наблюдений). Данная интерпретация как будто вообще устраняет проблему применяемости модели — каждая модель по данному формальному подходу имеет содержательную интерпретацию и, следовательно, ее можно применять в процессе принятия решений в качестве истинного отображения реальных связей. Подобное мнение опровергается практикой статистического моделирования. Формальная интерпретация интенсивности влияния отдельных факторов часто противоречит здравому смыслу и практическому опыту субъекта управления. Это означает, что интерпретация коэффициентов регрессии не отражает их сущности. [c.122]
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т.е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии, который говорит о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается. [c.121]
Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию значений коэффициента корреляции можно представить следующим образом. [c.123]
Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно О или 1 . Однако в эконометрической практике почти всегда используются фиктивные переменные типа 0—1 , так как при этом интерпретация полученных результатов выглядит наиболее просто. Так, если бы в модели (5.2) в качестве фиктивной выбрали переменную Zj, принимающую значения z,i=4 (для работников-мужчин) и 2/2=1 (для женщин), то коэффициент регрессии оц при этой переменной равнялся бы 1/(4— 1), т. е. одной трети среднего изменения заработной платы у мужчин. [c.117]
Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать Л=3 значения z,-i=l при наличии начального образования, гд=2 — среднего и г,з=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят (k—l) бинарных переменных. [c.117]
Дайте интерпретацию коэффициента эластичности данной модели регрессии. [c.36]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию их параметров и доверительных интервалов для коэффициентов регрессии. [c.84]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию его параметров и доверительных интервалов для коэффициентов регрессии на примере одного из факторных признаков. [c.85]
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, —10 0, то эффективность данной ценной бумаги повышаться при росте эффективности рынка. При Р хь, хв. Между собой они причинно не связаны. В соответствии с нормами технических условий из общей массы выделялись годные приборы и анализировалась как вся масса приборов, так и годные. Это позволило попытаться уловить различие во взаимосвязи параметров приборов до и после их отбраковки. Эмпирические корреляционные отношения рассчитывались только для годных приборов, поскольку разброс параметров для всей совокупности приборов был настолько велик, что подсчитывать корреляционные отношения не имело смысла. Доверительные интервалы ввиду большого объема выборки подсчитывались по формуле [37]. Сравнение парных коэффициентов корреляции с эмпирическими отношениями использовалось для проверки линейности связи между параметрами. Эмпирическому корреляционному отношению приписывается тот знак, который имеет парный коэффициент корреляции. Связь считается линейной, если корреляционное отношение попадает в доверительный интервал для парного коэффициента корреляции. Может показаться, что мы противоречим высказанному выше утверждению о том, что не существует формальных методов, позволяющих определить форму связи. Однако в данном случае мы говорим не об определении формы связи с целью, например, нахождения параметров уравнения регрессии и дальнейшей интерпретации или экстраполяции в каком-либо виде. Единственная наша забота состоит в том, чтобы парные коэффициенты корреляции (или иные оценки тесноты связи) были действительными характеристиками связи. В табл. 94 приведены в первой строке каждой клетки — парный коэф- [c.188]
Построенное уравнение регрессии в любом случае требует определенной интерпретации и анализа. Интерпретация требует словесного описания полученных результатов с трактовкой найденных коэффициентов, с тем чтобы построенная зависимость стала понятной человеку, не являющемуся специалистом в эконометрическом анализе. В нашем примере коэффициент b>i может трактоваться как предельная [c.106]
Интерпретация коэффициента регрессии как углового коэффициента в линейном уравнении для нелинейной зависимости не годится. Определить изменение У при изменении X на единицу можно с помощью производной (простой или частной), взятой по соответствующему фактору X. Так, для степенного уравнения У = а0Ха производная по X равна [c.136]
При интерпретации коэффициентов регрессии следует иметь в виду, что чем меньше индекс браузинга (зависимая переменная), тем сильнее покупатели склонны демонстрировать поведение, с магазина без определенной Два предиктора с [c.669]
Кроме того, при интерпретации коэффициентов множественной рефессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии у = —1,09 + 0,364у2 + 1,192л , показывает, что с ростом х на единицу у возрастает в среднем на 1,192 ед. при неизменном уровне значения у2. Между тем в соответствии с системой одновременных уравнений переменная у2 не может быть неизменной, ибо она в свою очередь зависит от yt. [c.199]
Значения -коэффициента заключены в интервале [—
источники:
http://lektsii.org/3-35810.html
http://economy-ru.info/info/15194/
В вторегрессионной схеме первого порядка зависимость между последовательными случайными членами описывается формулой u k+1 = ________, где а ρ – константа, ε k+1 – новый случайный член:
−1 +1 + k k ρu ε
+1 − k k ρu ε
k +1 ρε
+1 + k k u ρε
+1 + k k ρu ε
Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
сумма квадратов разности
разность
сумма разности квадратов
квадрат разности
Параметры множественной регрессии ?1, ?2,…?м показывают _________ соответствующих экономических факторов:
1) степень влияния
2) случайность
3) уровень независимости
4) непостоянство
5) цикличность
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного ряда, содержащего периодические колебания в 4 момента, получены значения сезонных компонент: S1 = 2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256. Известны значения компонент: T5 = 20,6 и E5 = 0,4. Рассчитайте значение уровня временного ряда y5.
0,83
17,2
23,1
33
Если две переменные независимы, то их теоретическая ковариация равна:
1) ?
2) 0
3) 2
4) 1
5) -1
Критерий Дарбина-Уотсона –метод обнаружения _________ с помощью статистики Дарбина-Уотсона:
1) гетероскедастичности ошибки
2) сезонных колебаний
3) мультиколлинеарности
4) автокорреляции
5) гомоскедастичности
Стандартные отклонения коэффициентов регрессии обратно пропорциональны величи-
не _________, где n – число наблюдений:
1) n
2) n2
3) n3
4) n
5) n4
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
первого, второго, третьего и последующих порядков
факторов, формирующих уровень ряда
между трендовой, сезонной и случайной компонентами
между несколькими временными рядами
При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
применить обычный метод наименьших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, рассчитанные теоретические значения, и получить структурные коэффициенты модели
на основе коэффициентов приведенной формы модели получить теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений
для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
преобразовать структурную форму модели в приведенную форму модели
для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
Линия регрессии _______ через точку (, ):
может пройти или не пройти
всегда проходит
x y
несколько раз проходит
_ __
никогда не проходит
может пройти
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно …
1,3
6,51
9,35
10,65
Если записать типы эконометрических моделей в следующем порядке:1) точно идентифицируемая система одновременных уравнений,2) сверхидентифицируемая система одновременных уравнений,3) уравнение множественной регрессии,4) уравнение множественной регрессии при автокорреляции остатков,то методы, применяемые для нахождения параметров соответствующих типов эконометрических моделей, будут расположены в следующем порядке
метод наименьших квадратов
косвенный метод наименьших квадратов
обобщенный метод наименьших квадратов
двухшаговый метод наименьших квадратов
Число степеней свободы для уравнения m-мерной регрессии при достаточном числе
наблюдений n составляет:
1) n/m
2) n-m
3) n-m+1
4) n-m-1
5) m-1
Значения t-статистики для фиктивных переменных незначимо отличается от:
1) 1
2) 0
3) -1
4) ?
5) 2
Из перечисленного: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3) конкретные значения переменных ? критические значения статистики Дарбина-Уотсона зависят от:
1) 3
2) 1, 2
3) 1, 2, 3
4) 1, 3
5) 2
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение  . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
увеличится на 1,67
уменьшится на (-1,67)
изменится на 0,003
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид  , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная (  – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии:  , где
, где  – стоимость основных фондов (тыс. руб.);
– стоимость основных фондов (тыс. руб.);  – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
на 1 тыс. руб. … уменьшится на 10,8 тыс. руб
на 1 тыс. руб. … увеличится на 10,8%
на 1% … увеличится на 10,8%
Решение:
В уравнении множественной линейной регрессии  , параметр
, параметр  показывает среднее изменение результата y при увеличении фактора
показывает среднее изменение результата y при увеличении фактора  на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением
на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением  , параметр
, параметр  равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …


Решение:
Коэффициент детерминации  равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (  ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
 . Значит,
. Значит, 
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1):  . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
Решение:
Эконометрическая модель линейного уравнения парной регрессии имеет вид:  , где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения;
, где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле  . Если
. Если  , то
, то  ; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … к общей
Решение:
F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
сумма квадратов разности
сумма разности квадратов
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);  – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Выразим значение
– ошибка модели. Выразим значение  :
:  . Поэтому правильный ответ – «разность».
. Поэтому правильный ответ – «разность».
2. Величина 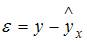 называется …
называется …
Решение:
Величина  называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
величину коэффициента регрессии
значение свободного члена уравнения
нулевое значение независимой переменной
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);  – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Поэтому правильный ответ – «ошибку модели».
– ошибка модели. Поэтому правильный ответ – «ошибку модели».
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …


Решение:
Коэффициент детерминации  равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно, 
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия ______ остатков
определяются из условия ______ остатков  .
.
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение  . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
увеличится на 1,67
уменьшится на (-1,67)
изменится на 0,003
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид  , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная (  – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии:  , где
, где  – стоимость основных фондов (тыс. руб.);
– стоимость основных фондов (тыс. руб.);  – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
на 1 тыс. руб. … уменьшится на 10,8 тыс. руб
на 1 тыс. руб. … увеличится на 10,8%
на 1% … увеличится на 10,8%
Решение:
В уравнении множественной линейной регрессии  , параметр
, параметр  показывает среднее изменение результата y при увеличении фактора
показывает среднее изменение результата y при увеличении фактора  на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением
на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением  , параметр
, параметр  равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …


Решение:
Коэффициент детерминации  равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( 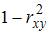 ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
 . Значит,
. Значит, 
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1):  . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
Решение:
Эконометрическая модель линейного уравнения парной регрессии имеет вид:  , где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения;
, где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле  . Если
. Если  , то
, то  ; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … к общей
Решение:
F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
сумма квадратов разности
сумма разности квадратов
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);  – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Выразим значение
– ошибка модели. Выразим значение  :
:  . Поэтому правильный ответ – «разность».
. Поэтому правильный ответ – «разность».
2. Величина  называется …
называется …
Решение:
Величина  называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
величину коэффициента регрессии
значение свободного члена уравнения
нулевое значение независимой переменной
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция);  – случайные факторы. При этом
– случайные факторы. При этом  , тогда
, тогда  , где
, где  – фактическое значение зависимой переменной,
– фактическое значение зависимой переменной,  – расчетное значение зависимой переменной,
– расчетное значение зависимой переменной,  – ошибка модели. Поэтому правильный ответ – «ошибку модели».
– ошибка модели. Поэтому правильный ответ – «ошибку модели».
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …


Решение:
Коэффициент детерминации  равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно, 
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия ______ остатков
определяются из условия ______ остатков  .
.
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
увеличится на 1,67
уменьшится на (-1,67)
изменится на 0,003
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид , где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
на 1 тыс. руб. … уменьшится на 10,8 тыс. руб
на 1 тыс. руб. … увеличится на 10,8%
на 1% … увеличится на 10,8%
Решение:
В уравнении множественной линейной регрессии , параметр показывает среднее изменение результата y при увеличении фактора на одну единицу, при условии, что все остальные переменные останутся на постоянном уровне. В нашем случае, объем промышленного производства y характеризуется следующим уравнением , параметр равен 10,8, следовательно, при увеличении объема основных фондов на 1 тыс. руб. объем промышленного производства увеличится на 10,8 тыс. руб. при постоянной численности занятых.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
Решение:
Коэффициент детерминации равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
. Значит,
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
Решение:
Эконометрическая модель линейного уравнения парной регрессии имеет вид: , где y – зависимая переменная, x – независимая переменная; a, b – параметры уравнения; – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение параметра а может быть рассчитано по формуле . Если , то ; в таком случае говорят, что среднее значение переменной y, не зависящее от величины переменной х, равно значению параметра а. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет 10,75 рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … к общей
Решение:
F-статистика рассчитывается как отношение факторной дисперсии на одну степень свободы к остаточной дисперсии на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
сумма квадратов разности
сумма разности квадратов
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); – случайные факторы. При этом , тогда , где – фактическое значение зависимой переменной, – расчетное значение зависимой переменной, – ошибка модели. Выразим значение : . Поэтому правильный ответ – «разность».
2. Величина называется …
Решение:
Величина называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
величину коэффициента регрессии
значение свободного члена уравнения
нулевое значение независимой переменной
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); f – тип функциональной зависимости (математическая функция); – случайные факторы. При этом , тогда , где – фактическое значение зависимой переменной, – расчетное значение зависимой переменной, – ошибка модели. Поэтому правильный ответ – «ошибку модели».
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
Решение:
Коэффициент детерминации равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
Минимизации суммы квадратов
равенства нулю суммы квадратов
Решение:
При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия минимизации суммы квадратов остатков .
Тема 6: Предпосылки МНК, методы их проверки
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
критерий Гольдфельда – Квандта
Решение:
Для обнаружения автокорреляции остатков используется расчет статистик Дарбина – Уотсона. Тест Уайта, критерий Гольдфельда – Квандта, тест Парка применяются для обнаружения гетероскедастичности остатков.
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
статистика Дарбина – Уотсона попадает в зону неопределенности
есть положительная автокорреляция остатков
есть отрицательная автокорреляция остатков
Решение:
Дано, что коэффициент автокорреляции остатков первого порядка равен –0,3, . Рассчитаем статистику Дарбина – Уотсона по формуле . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , , которые разбивают отрезок от 0 до 4 на пять частей.
В интервале [0; 0,82] есть положительная автокорреляция остатков;
в интервале (0,82; 1,32] – зона неопределенности;
в интервале (1,32; 2,68] нет автокорреляции остатков;
в интервале (2,68; 3,12] – зона неопределенности;
в интервале (3,12; 4] есть отрицательная автокорреляция остатков.
В нашем случае значение статистики Дарбина–Уотсона d=2,6 попадает в интервал (1,32; 2,68]. Значит, можно сделать вывод, что нет автокорреляции остатков.
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
Решение:
Значение коэффициента автокорреляции остатков модели рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если , то ; если , то . Поэтому значение меняется от 0 до 4. Минимальное значение равно 0 для случая, когда , то есть для положительной автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
нулевая средняя величина
Решение:
Условия, необходимые для несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК.
Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:
– случайный характер остатков;
– нулевая средняя величина остатков, не зависящая от ;
– отсутствие автокорреляции остатков;
– подчинение остатков нормальному закону распределения.
Гетероскедатичность остатков не является предпосылкой МНК.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
Решение:
Значение коэффициента автокорреляции остатков модели рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если , то ; если , то . Поэтому значение меняется от 0 до 4. Максимальное значение равно 4 для случая, когда , то есть для отрицательной автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка параметра называется несмещенной, если математическое ожидание »; где – истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка параметра называется несмещенной, если математическое ожидание »; где – истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание в том случае, если .
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
дисперсия остатков минимальная
точность оценок выборки увеличивается с увеличением объема выборки
дисперсия остатков не зависит от величины
Решение:
Несмещенность оценок параметров регрессии означает, что математическое ожидание остатков равно нулю.
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
нормальном законе распределения
Решение:
Оценка называется несмещенной, если математическое ожидание остатков равно нулю. Если оценка параметров регрессии является смещенной, то математическое ожидание остатков отличается от нуля, и при большом количестве выборочных оцениваний остатки будут накапливаться.
Нарушается предпосылка о нулевой средней величине остатков.
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
математическое ожидание остатков равно нулю
дисперсия остатков минимальная
дисперсия остатков не зависит от величины
Решение:
Состоятельность оценок параметров регрессии означает, что точность оценок выборки увеличивается с увеличением объема выборки.
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
гомоскедастичными и некоррелированными
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений минимальна. Отклонение , посчитанное для i-го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК о автокоррелированности и гетероскедастичности остатков, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Правильный вариант ответа – «автокоррелированными и/или гетероскедастичными».
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
Решение:
При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется вместо традиционного метода наименьших квадратов применять обобщенный метод наименьших квадратов.
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников .
После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
на работника при увеличении фондовооруженности труда на единицу при неизменном уровне производительности труда
на единицу продукции при увеличении фондоемкости продукции на единицу при неизменном уровне трудоемкости продукции
на единицу продукции при увеличении трудоемкости продукции на единицу при неизменном уровне фондоемкости продукции
Решение:
Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников: .
Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Новая модель имеет дело с новыми переменными: – объем затрат на одного работника, – производительность труда, – фондовооруженность труда. В новой модели коэффициент регрессии показывает среднее изменение затрат на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда .
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
дисперсия остатков не является постоянной величиной
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений минимальна. Отклонение , посчитанное для i-го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю.
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .
Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
фондоемкости продукции при неизменном уровне трудоемкости продукции
трудоемкости продукции при неизменном уровне фондоемкости продукции
фондовооруженности труда при неизменном уровне производительности труда производительности труда при неизменном уровне фондовооруженности труда
Решение:
Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .
После применения обобщенного метода наименьших квадратов новая модель приняла вид . Новая модель имеет дело с новыми переменными – затраты на единицу продукции, – фондоемкость продукции, – трудоемкость продукции. В новой модели параметр показывает среднее изменение затрат на единицу продукции с увеличением на единицу фондоемкости продукции при неизменном уровне трудоемкости продукции .
Тема 9: Оценка тесноты связи
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
Решение:
Заданная регрессионная модель вида – это линейное уравнение парной регрессии, для которого показателем тесноты связи между переменными и является парный коэффициент линейной корреляции.
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
Решение:
Коэффициент корреляции для парной линейной регрессии в общем случае изменяется в пределах [–1, 1]. Однако так как значение коэффициента регрессии отрицательное, то и значение коэффициента корреляции для уравнения тоже будет отрицательным, значит, самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии будет [–1; 0].
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
Решение:
Показатель множественной корреляции изменяется в пределах [0; 1]. Однако величина индекса множественной корреляции должна быть больше максимального парного индекса корреляции или равна ему Следовательно, самым коротким интервалом изменения показателя множественной корреляции будет [0,7; 1].
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
Решение:
Графическое отображение совокупности точек с координатами на плоскости для зависимости от называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».


Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
http://poisk-ru.ru/s16312t6.html
http://zdamsam.ru/b12887.html
Ошибкой спецификации эконометрической модели уравнения регрессии является …
- расчет показателей качества модели
- использование парной регрессии вместо множественной
- оценка параметров при помощи МНК
- учет случайных факторов
Тип вопроса: Вопрос с одним правильными вариантом
Ответ на этот вопрос уже получили: 345 раз(а)
Помогли ответы? Ставь лайк 👍
Вопрос задал(а): Анонимный пользователь, 09 Январь 2017 в 20:42
На вопрос ответил(а): Астафьева Любовь, 09 Январь 2017 в 20:42
