Для чего нужен анализ ошибок

In linguistics, according to J. Richard et al., (2002), an error is the use of a word, speech act or grammatical items in such a way that it seems imperfect and significant of an incomplete learning (184). It is considered by Norrish (1983, p. 7) as a systematic deviation which happens when a learner has not learnt something, and consistently gets it wrong. However, the attempts made to put the error into context have always gone hand in hand with either [language learning and second-language acquisition] processe, Hendrickson (1987:357) mentioned that errors are ‘signals’ that indicate an actual learning process taking place and that the learner has not yet mastered or shown a well-structured [linguistic competence|competence] in the target language.

All the definitions seeme to stress either on the systematic deviations triggered in the language learning process, or its indications of the actual situation of the language learner themselves, which will later help monitoring, be it an applied linguist or particularly the language teacher to solve the problem, respecting one of the approaches argued in the Error Analysis (Anefnaf 2017). The occurrence of errors doesn’t only indicate that the learner has not learned something yet, but also it gives the linguist the idea of whether the teaching method applied was effective or it needs to be changed.

According to Corder (1976), errors signify three things: first to the teacher, in that the learner tells the teacher, if they have undertaken a systematic analysis, how far towards that goal the learner has progressed and, consequently, what remains for them to learn; second, they provide the researcher with evidence of how language is learned or acquired, and what strategies or procedures the learner is employing in their discovery of the language; third, (and in a sense this is their most important aspect) they are indispensable to the learner himself/herself, because the making of errors can be regarded as a device the learner uses in order to learn (p. 167). The occurrence of errors is merely a sign of ‘the present inadequacy of our teaching methods’(Corder 1976, p. 163).

There have been two schools of thought when it comes to error analysis and philosophy; the first one, according to Corder (1967) linked the error commitment with the teaching method, arguing that if the teaching method was adequate, the errors would not be committed; the second, believed that we live in an imperfect world and that error correction is something real and the applied linguist cannot do without it no matter what teaching approach they may use.

Errors vs. mistakes[edit]

Chomsky (1965) made a distinguishing explanation of competence and performance on which, later on, the identification of mistakes and errors will be possible, Chomsky stated that ‘’We thus make a fundamental distinction between competence (the speaker-hearer’s knowledge of his language) and performance (the actual use of language in concrete situations)’’ ( 1956, p. 4). In other words, errors are thought of as indications of an incomplete learning, and that the speaker or hearer has not yet accumulated a satisfied language knowledge which can enable them to avoid linguistics misuse. Relating knowledge with competence was significant enough to represent that the competence of the speaker is judged by means of errors that concern the amount of linguistic data they have been exposed to, however, performance which is the actual use of language does not represent the language knowledge that the speaker has. According to J. Richard et al (2002), people may have the competence to produce an infinitely long sentence but when they actually attempt to use this knowledge (to “perform”) there are many reasons why they restrict the number of adjectives, adverbs, and clauses in any one sentence (2002, 392).

The actual state of the speaker somehow involves and influences the speaker’s performance by either causing a good performance or mistakes. Thus, it is quite obvious that there is some kind of interrelationship between competence and performance; somehow, a speaker can perform well if they have had already satisfied linguistic knowledge. As a support to this, Corder (1967) mentioned that mistakes are of no significance to “the process of language learning’’ (P. 167).

Error analysis approach[edit]

Before the rise of error analysis approach, contrastive analysis had been the dominant approach used in dealing and conceptualizing the learners’ errors in the 1950s, this approach had often gone hand in hand with concept of L1 Interference and precisely the interlingual effect (Anefnaf Z. 2017), it claimed that the main cause of committing errors in the process of second language learning is the L1, in other words, the linguistic background of the language learners badly affects the production in the target language or second language.

X. Fang and J. Xue-mei (2007) pointed out that contrastive analysis hypothesis claimed that the principal barrier to second language acquisition is the interference of the first language system with the second language system and that a scientific, structural comparison of the two languages in question would enable people to predict and describe which are problems and which are not. Error analysis approach overwhelmed and announced the decline of the Contrastive Analysis which was only effective in phonology; and, according to J. Richard et al. (2002), EA developed as a branch of Linguistics in the 1960s and it came to light to argue that the mother tongue was not the main and the only source of the errors committed by the learners. In addition, Hashim, A. (1999) mentioned that the language effect is more complex and these errors can be caused even by the target language itself and by the applied communicative strategies as well as the type and quality of the second language instructions.

The aim of EA according to J. Richard et al. (2002) is, first, to identify strategies which learners use in language learning, in terms of the approaches and strategies used in both of teaching and learning. Second, to try to identify the causes of learners’ errors, that is, investigating the motives behind committing such errors as the first attempt to eradicate them. Third, to obtain information on common difficulties in Language Learning, as an aid to teaching or in the preparation of the teaching materials,

The two major causes of error, coined by the error analysis approach, are the Interlingual error which is an error made by the Learner’s Linguistic background and Native language interference, and the Intralingual error which is the error committed by the learners when they misuse some Target Language rules, considering that the error cause lies within and between the target language itself and the Learners false application of certain target language rules.

Error analysis in SLA was established in the 1960s by Corder and colleagues.^[1] Error analysis (EA) was an alternative to contrastive analysis, an approach influenced by behaviorism through which applied linguists sought to use the formal distinctions between the learners’ first and second languages to predict errors. Error analysis showed that contrastive analysis was unable to predict a great majority of errors, although its more valuable aspects have been incorporated into the study of language transfer. A key finding of error analysis has been that many learner errors are produced by learners making faulty inferences about the rules of the new language.

Error analysts distinguish between errors, which are systematic, and mistakes, which are not. They often seek to develop a typology of errors. Error can be classified according to basic type: omissive, additive, substitutive or related to word order. They can be classified by how apparent they are: overt errors such as «I angry» are obvious even out of context, whereas covert errors are evident only in context. Closely related to this is the classification according to domain, the breadth of context which the analyst must examine, and extent, the breadth of the utterance which must be changed in order to fix the error. Errors may also be classified according to the level of language: phonological errors, vocabulary or lexical errors, syntactic errors, and so on. They may be assessed according to the degree to which they interfere with communication: global errors make an utterance difficult to understand, while local errors do not. In the above example, «I angry» would be a local error, since the meaning is apparent.

From the beginning, error analysis was beset with methodological problems. In particular, the above typologies are problematic: from linguistic data alone, it is often impossible to reliably determine what kind of error a learner is making. Also, error analysis can deal effectively only with learner production (speaking and writing) and not with learner reception (listening and reading). Furthermore, it cannot account for learner use of communicative strategies such as avoidance, in which learners simply do not use a form with which they are uncomfortable. For these reasons, although error analysis is still used to investigate specific questions in SLA, the quest for an overarching theory of learner errors has largely been abandoned. In the mid-1970s, Corder and others moved on to a more wide-ranging approach to learner language, known as interlanguage.

Error analysis is closely related to the study of error treatment in language teaching. Today, the study of errors is particularly relevant for focus on form teaching methodology.

In second language acquisition, error analysis studies the types and causes of language errors. Errors are classified^[2] according to:

• modality (i.e., level of proficiency in speaking, writing, reading, listening)
• linguistic levels (i.e., pronunciation, grammar, vocabulary, style)
• form (e.g., omission, insertion, substitution)
• type (systematic errors/errors in competence vs. occasional errors/errors in performance)
• cause (e.g., interference, interlanguage)
• norm vs. system

Types of errors[edit]

Linguists have always been attempting to describe the types of errors committed by the language learners, and that is exactly the best way to start with, as it helps out the applied linguist to identify where the problem lies. According to Dulay et al. (1982) errors take place when the learner change the surface structure in a particularly systematic manner (p. 150), thus, the error, no matter what form and type it is, represent a damage at the level of the target language production.

Errors have been classified by J. Richard et al. (2002) into two categories. The Interlingual Error and the Intralingual Error, those two elements refer respectively to the negative influence of both the speaker’s native language, and the target language itself.

Interlingual error is caused by the interference of the native language L1 (also known as interference, linguistic interference, and crosslinguistic influence), whereby the learner tends to use their linguistic knowledge of L1 on some Linguistic features in the target language, however, it often leads to making errors. The example, provided by J. Richard et al. (2002) ‘’ the incorrect French sentence Elle regarde les (“She sees them”), produced according to the word order of English, instead of the correct French sentence Elle les regarde (Literally, “She them sees”). (P. 267) shows the type of errors aroused by the negative effect of the native language interference.

Intralingual error is an error that takes place due to a particular misuse of a particular rule of the target language, it is, in fact, quite the opposite of Interlingual error, it puts the target language into focus, the target language in this perspective is thought of as an error cause. Furthermore, J. Richard, et al. (2002) consider it as one which results from ‘’faulty or partial’’ learning of the target language. (p.267) thus the intralingual error is classified as follow:

Overgeneralizations: in linguistics, overgeneralizations error occur when the speaker applies a grammatical rule in cases where it doesn’t apply. Richard et al, (2002) mentioned that they are caused ‘’by extension of target language rules to inappropriate context.’’ (P.185). this kind of errors have been committed while dealing with regular and irregular verbs, as well as the application of plural forms. E.g. (Tooth == Tooths rather than teeth) and (he goes == he goed rather than went).

Simplifications: they result from learners producing simpler linguistic forms than those found in the target language, in other words, learners attempt to be linguistically creative and produce their own poetic sentences/utterances, they may actually be successful in doing it, but it is not necessary the case, Corder (as cited in Mahmoud 2014:276) mentioned that learners do not have the complex system which they could simplify. This kind of errors is committed through both of Omission and addition of some linguistic elements at the level of either the Spelling or grammar. A. Mahmoud (2014) provided examples based on a research conducted on written English of Arabic-speaking second year University students:

1. Spelling: omission of silent letters:
   • no (= know) * dout (= doubt) * weit (weight)
2. Grammar:
   1. Omission:
      • We wait ^ the bus all the time.
      • He was ^ clever and has ^ understanding father.
   2. Addition:
      • Students are do their researches every semester.
      • Both the boys and the girls they can study together.

Developmental errors: this kind of errors is somehow part of the overgeneralizations, (this later is subtitled into Natural and developmental learning stage errors), D.E are results of normal pattern of development, such as (come = comed) and (break = breaked), D.E indicates that the learner has started developing their linguistic knowledge and fail to reproduce the rules they have lately been exposed to in target language learning.

Induced errors: as known as transfer of training, errors caused by misleading teaching examples, teachers, sometimes, unconditionally, explain a rule without highlighting the exceptions or the intended message they would want to convey. J. Richard et al. (2002) provided an example that occurs at the level of teaching prepositions and particularly ‘’ at ‘’ where the teacher may hold up a box and say ‘’ I am looking at the box ‘’, the students may understand that ‘’ at ‘’ means ‘’ under ‘’, they may later utter ‘’ the cat is at the table ‘’ instead of the cat is under the table.

Errors of avoidance: these errors occur when the learner fail to apply certain target language rules just because they are thought of to be too difficult.

Errors of overproduction: in the early stages of language learning, learners are supposed to have not yet acquired and accumulated a satisfied linguistic knowledge which can enable them to use the finite rules of the target language in order to produce infinite structures, most of the time, beginners overproduce, in such a way, they frequently repeat a particular structure.

Steps[edit]

According to linguist Corder, the following are the steps in any typical EA research:^[3]

1. collecting samples of learner language
2. identifying the errors
3. describing the errors
4. explaining the errors
5. evaluating/correcting the errors

collection of errors:
the nature and quantity of errors is likely to vary depending on whether the data consist of natural, spontaneous language use or careful, elicited language use.

Corder (1973) distinguished two kinds of elicitation:clinical and experimental elicitation.
clinical elicitation involves getting the informant to produce data of any sort, for example by means of general interview or writing a composition.
experimental elicitation involves the use of special instrument to elicit data containing the linguistic features such as a series of pictures which had been designed to elicit specific features.

Bibliography[edit]

• Anefnaf. Z ( 2017) English Learning: Linguistic flaws, Sais Faculty of Arts and Humanities, USMBA, Retrieved from https://www.academia.edu/33999467/English_Learning_in_Morocco_Linguistic_Flaws
• Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press. P. 4
• Corder, Pit. (1967). the significance of learner’s errors. International Review of Applied Linguistics, 161-170
• Dulay, H., Burt, M., & Krashen, S.D. (1982). Language two. New York: Oxford University Press. p. 150
• Edje, J (1989). Mistakes and Correction. London: Longman. P. 26
• Fang, X. & Xue-mei, J. (2007). Error analysis and the EFL classroom teaching: US-China education review, 4(9), pp. 10–14.
• Hashim, A. (1999). Crosslinguistic influence in the written English of Malay undergraduates: Journal of Modern Languages, 12, (1), pp. 59–76.
• Hendrickson, J.M. (1987). Error correction in foreign language teaching: Recent theory, research, and practice. In M.H. Long & J.C. Richards (Eds.), Methodology in TESOL: A book of readings. Boston: Heinle & Heinle. p. 357
• Norrish, J. (1983). Language learners and their errors. London: Macmillan Press. P. 7
• Richards, J. C. & Schmidt, R. (2002). Dictionary of language teaching and applied linguistics (3rd Ed.). London: Longman.
• Richards J. C., & Rodgers T. S.(2001). Approaches and Methods in Language Teaching. (2nd edition), Cambridge University Press: Cambridge, UK. P. 153

See also[edit]

• Error (linguistics)
• Error treatment (linguistics)
• Second language acquisition

References[edit]

In linguistics, according to J. Richard et al., (2002), an error is the use of a word, speech act or grammatical items in such a way that it seems imperfect and significant of an incomplete learning (184). It is considered by Norrish (1983, p. 7) as a systematic deviation which happens when a learner has not learnt something, and consistently gets it wrong. However, the attempts made to put the error into context have always gone hand in hand with either [language learning and second-language acquisition] processe, Hendrickson (1987:357) mentioned that errors are ‘signals’ that indicate an actual learning process taking place and that the learner has not yet mastered or shown a well-structured [linguistic competence|competence] in the target language.

All the definitions seeme to stress either on the systematic deviations triggered in the language learning process, or its indications of the actual situation of the language learner themselves, which will later help monitoring, be it an applied linguist or particularly the language teacher to solve the problem, respecting one of the approaches argued in the Error Analysis (Anefnaf 2017). The occurrence of errors doesn’t only indicate that the learner has not learned something yet, but also it gives the linguist the idea of whether the teaching method applied was effective or it needs to be changed.

According to Corder (1976), errors signify three things: first to the teacher, in that the learner tells the teacher, if they have undertaken a systematic analysis, how far towards that goal the learner has progressed and, consequently, what remains for them to learn; second, they provide the researcher with evidence of how language is learned or acquired, and what strategies or procedures the learner is employing in their discovery of the language; third, (and in a sense this is their most important aspect) they are indispensable to the learner himself/herself, because the making of errors can be regarded as a device the learner uses in order to learn (p. 167). The occurrence of errors is merely a sign of ‘the present inadequacy of our teaching methods’(Corder 1976, p. 163).

There have been two schools of thought when it comes to error analysis and philosophy; the first one, according to Corder (1967) linked the error commitment with the teaching method, arguing that if the teaching method was adequate, the errors would not be committed; the second, believed that we live in an imperfect world and that error correction is something real and the applied linguist cannot do without it no matter what teaching approach they may use.

Errors vs. mistakes[edit]

Chomsky (1965) made a distinguishing explanation of competence and performance on which, later on, the identification of mistakes and errors will be possible, Chomsky stated that ‘’We thus make a fundamental distinction between competence (the speaker-hearer’s knowledge of his language) and performance (the actual use of language in concrete situations)’’ ( 1956, p. 4). In other words, errors are thought of as indications of an incomplete learning, and that the speaker or hearer has not yet accumulated a satisfied language knowledge which can enable them to avoid linguistics misuse. Relating knowledge with competence was significant enough to represent that the competence of the speaker is judged by means of errors that concern the amount of linguistic data they have been exposed to, however, performance which is the actual use of language does not represent the language knowledge that the speaker has. According to J. Richard et al (2002), people may have the competence to produce an infinitely long sentence but when they actually attempt to use this knowledge (to “perform”) there are many reasons why they restrict the number of adjectives, adverbs, and clauses in any one sentence (2002, 392).

The actual state of the speaker somehow involves and influences the speaker’s performance by either causing a good performance or mistakes. Thus, it is quite obvious that there is some kind of interrelationship between competence and performance; somehow, a speaker can perform well if they have had already satisfied linguistic knowledge. As a support to this, Corder (1967) mentioned that mistakes are of no significance to “the process of language learning’’ (P. 167).

Error analysis approach[edit]

Before the rise of error analysis approach, contrastive analysis had been the dominant approach used in dealing and conceptualizing the learners’ errors in the 1950s, this approach had often gone hand in hand with concept of L1 Interference and precisely the interlingual effect (Anefnaf Z. 2017), it claimed that the main cause of committing errors in the process of second language learning is the L1, in other words, the linguistic background of the language learners badly affects the production in the target language or second language.

X. Fang and J. Xue-mei (2007) pointed out that contrastive analysis hypothesis claimed that the principal barrier to second language acquisition is the interference of the first language system with the second language system and that a scientific, structural comparison of the two languages in question would enable people to predict and describe which are problems and which are not. Error analysis approach overwhelmed and announced the decline of the Contrastive Analysis which was only effective in phonology; and, according to J. Richard et al. (2002), EA developed as a branch of Linguistics in the 1960s and it came to light to argue that the mother tongue was not the main and the only source of the errors committed by the learners. In addition, Hashim, A. (1999) mentioned that the language effect is more complex and these errors can be caused even by the target language itself and by the applied communicative strategies as well as the type and quality of the second language instructions.

The aim of EA according to J. Richard et al. (2002) is, first, to identify strategies which learners use in language learning, in terms of the approaches and strategies used in both of teaching and learning. Second, to try to identify the causes of learners’ errors, that is, investigating the motives behind committing such errors as the first attempt to eradicate them. Third, to obtain information on common difficulties in Language Learning, as an aid to teaching or in the preparation of the teaching materials,

The two major causes of error, coined by the error analysis approach, are the Interlingual error which is an error made by the Learner’s Linguistic background and Native language interference, and the Intralingual error which is the error committed by the learners when they misuse some Target Language rules, considering that the error cause lies within and between the target language itself and the Learners false application of certain target language rules.

Error analysis in SLA was established in the 1960s by Corder and colleagues.^[1] Error analysis (EA) was an alternative to contrastive analysis, an approach influenced by behaviorism through which applied linguists sought to use the formal distinctions between the learners’ first and second languages to predict errors. Error analysis showed that contrastive analysis was unable to predict a great majority of errors, although its more valuable aspects have been incorporated into the study of language transfer. A key finding of error analysis has been that many learner errors are produced by learners making faulty inferences about the rules of the new language.

Error analysts distinguish between errors, which are systematic, and mistakes, which are not. They often seek to develop a typology of errors. Error can be classified according to basic type: omissive, additive, substitutive or related to word order. They can be classified by how apparent they are: overt errors such as «I angry» are obvious even out of context, whereas covert errors are evident only in context. Closely related to this is the classification according to domain, the breadth of context which the analyst must examine, and extent, the breadth of the utterance which must be changed in order to fix the error. Errors may also be classified according to the level of language: phonological errors, vocabulary or lexical errors, syntactic errors, and so on. They may be assessed according to the degree to which they interfere with communication: global errors make an utterance difficult to understand, while local errors do not. In the above example, «I angry» would be a local error, since the meaning is apparent.

From the beginning, error analysis was beset with methodological problems. In particular, the above typologies are problematic: from linguistic data alone, it is often impossible to reliably determine what kind of error a learner is making. Also, error analysis can deal effectively only with learner production (speaking and writing) and not with learner reception (listening and reading). Furthermore, it cannot account for learner use of communicative strategies such as avoidance, in which learners simply do not use a form with which they are uncomfortable. For these reasons, although error analysis is still used to investigate specific questions in SLA, the quest for an overarching theory of learner errors has largely been abandoned. In the mid-1970s, Corder and others moved on to a more wide-ranging approach to learner language, known as interlanguage.

Error analysis is closely related to the study of error treatment in language teaching. Today, the study of errors is particularly relevant for focus on form teaching methodology.

In second language acquisition, error analysis studies the types and causes of language errors. Errors are classified^[2] according to:

• modality (i.e., level of proficiency in speaking, writing, reading, listening)
• linguistic levels (i.e., pronunciation, grammar, vocabulary, style)
• form (e.g., omission, insertion, substitution)
• type (systematic errors/errors in competence vs. occasional errors/errors in performance)
• cause (e.g., interference, interlanguage)
• norm vs. system

Types of errors[edit]

Linguists have always been attempting to describe the types of errors committed by the language learners, and that is exactly the best way to start with, as it helps out the applied linguist to identify where the problem lies. According to Dulay et al. (1982) errors take place when the learner change the surface structure in a particularly systematic manner (p. 150), thus, the error, no matter what form and type it is, represent a damage at the level of the target language production.

Errors have been classified by J. Richard et al. (2002) into two categories. The Interlingual Error and the Intralingual Error, those two elements refer respectively to the negative influence of both the speaker’s native language, and the target language itself.

Interlingual error is caused by the interference of the native language L1 (also known as interference, linguistic interference, and crosslinguistic influence), whereby the learner tends to use their linguistic knowledge of L1 on some Linguistic features in the target language, however, it often leads to making errors. The example, provided by J. Richard et al. (2002) ‘’ the incorrect French sentence Elle regarde les (“She sees them”), produced according to the word order of English, instead of the correct French sentence Elle les regarde (Literally, “She them sees”). (P. 267) shows the type of errors aroused by the negative effect of the native language interference.

Intralingual error is an error that takes place due to a particular misuse of a particular rule of the target language, it is, in fact, quite the opposite of Interlingual error, it puts the target language into focus, the target language in this perspective is thought of as an error cause. Furthermore, J. Richard, et al. (2002) consider it as one which results from ‘’faulty or partial’’ learning of the target language. (p.267) thus the intralingual error is classified as follow:

Overgeneralizations: in linguistics, overgeneralizations error occur when the speaker applies a grammatical rule in cases where it doesn’t apply. Richard et al, (2002) mentioned that they are caused ‘’by extension of target language rules to inappropriate context.’’ (P.185). this kind of errors have been committed while dealing with regular and irregular verbs, as well as the application of plural forms. E.g. (Tooth == Tooths rather than teeth) and (he goes == he goed rather than went).

Simplifications: they result from learners producing simpler linguistic forms than those found in the target language, in other words, learners attempt to be linguistically creative and produce their own poetic sentences/utterances, they may actually be successful in doing it, but it is not necessary the case, Corder (as cited in Mahmoud 2014:276) mentioned that learners do not have the complex system which they could simplify. This kind of errors is committed through both of Omission and addition of some linguistic elements at the level of either the Spelling or grammar. A. Mahmoud (2014) provided examples based on a research conducted on written English of Arabic-speaking second year University students:

1. Spelling: omission of silent letters:
   • no (= know) * dout (= doubt) * weit (weight)
2. Grammar:
   1. Omission:
      • We wait ^ the bus all the time.
      • He was ^ clever and has ^ understanding father.
   2. Addition:
      • Students are do their researches every semester.
      • Both the boys and the girls they can study together.

Developmental errors: this kind of errors is somehow part of the overgeneralizations, (this later is subtitled into Natural and developmental learning stage errors), D.E are results of normal pattern of development, such as (come = comed) and (break = breaked), D.E indicates that the learner has started developing their linguistic knowledge and fail to reproduce the rules they have lately been exposed to in target language learning.

Induced errors: as known as transfer of training, errors caused by misleading teaching examples, teachers, sometimes, unconditionally, explain a rule without highlighting the exceptions or the intended message they would want to convey. J. Richard et al. (2002) provided an example that occurs at the level of teaching prepositions and particularly ‘’ at ‘’ where the teacher may hold up a box and say ‘’ I am looking at the box ‘’, the students may understand that ‘’ at ‘’ means ‘’ under ‘’, they may later utter ‘’ the cat is at the table ‘’ instead of the cat is under the table.

Errors of avoidance: these errors occur when the learner fail to apply certain target language rules just because they are thought of to be too difficult.

Errors of overproduction: in the early stages of language learning, learners are supposed to have not yet acquired and accumulated a satisfied linguistic knowledge which can enable them to use the finite rules of the target language in order to produce infinite structures, most of the time, beginners overproduce, in such a way, they frequently repeat a particular structure.

Steps[edit]

According to linguist Corder, the following are the steps in any typical EA research:^[3]

1. collecting samples of learner language
2. identifying the errors
3. describing the errors
4. explaining the errors
5. evaluating/correcting the errors

collection of errors:
the nature and quantity of errors is likely to vary depending on whether the data consist of natural, spontaneous language use or careful, elicited language use.

Corder (1973) distinguished two kinds of elicitation:clinical and experimental elicitation.
clinical elicitation involves getting the informant to produce data of any sort, for example by means of general interview or writing a composition.
experimental elicitation involves the use of special instrument to elicit data containing the linguistic features such as a series of pictures which had been designed to elicit specific features.

Bibliography[edit]

• Anefnaf. Z ( 2017) English Learning: Linguistic flaws, Sais Faculty of Arts and Humanities, USMBA, Retrieved from https://www.academia.edu/33999467/English_Learning_in_Morocco_Linguistic_Flaws
• Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press. P. 4
• Corder, Pit. (1967). the significance of learner’s errors. International Review of Applied Linguistics, 161-170
• Dulay, H., Burt, M., & Krashen, S.D. (1982). Language two. New York: Oxford University Press. p. 150
• Edje, J (1989). Mistakes and Correction. London: Longman. P. 26
• Fang, X. & Xue-mei, J. (2007). Error analysis and the EFL classroom teaching: US-China education review, 4(9), pp. 10–14.
• Hashim, A. (1999). Crosslinguistic influence in the written English of Malay undergraduates: Journal of Modern Languages, 12, (1), pp. 59–76.
• Hendrickson, J.M. (1987). Error correction in foreign language teaching: Recent theory, research, and practice. In M.H. Long & J.C. Richards (Eds.), Methodology in TESOL: A book of readings. Boston: Heinle & Heinle. p. 357
• Norrish, J. (1983). Language learners and their errors. London: Macmillan Press. P. 7
• Richards, J. C. & Schmidt, R. (2002). Dictionary of language teaching and applied linguistics (3rd Ed.). London: Longman.
• Richards J. C., & Rodgers T. S.(2001). Approaches and Methods in Language Teaching. (2nd edition), Cambridge University Press: Cambridge, UK. P. 153

See also[edit]

• Error (linguistics)
• Error treatment (linguistics)
• Second language acquisition

References[edit]

Как сделать анализ ошибок, чтобы сделать все ваши модели лучше

  Перевод

  Ссылка на автора

Введение

Существует множество способов улучшить готовые модели машинного обучения. Есть вещи, которые вы можете сделать как с моделями, так и с данными, чтобы получить лучшие результаты, чем со стандартной версией модели scikit-learn. Существует разработка функций, настройка гиперпараметров и выбор правильной функции стоимости. Если мы углубимся в глубокое обучение, то подойдем к идеям сетевых архитектур, трансферного обучения и многим другим. Как ученый, работающий с данными, это одни из первых и самых важных вещей, которые вы узнаете о построении моделей. Такие инструменты, как случайный поиск и поиск по сетке, должны быть в наборе инструментов каждого ученого, чтобы помочь оптимизировать этот процесс и построить наилучшую возможную модель.

Когда вы работаете над проектом, большинство людей делают все то, что я изложил выше, а затем, с помощью перекрестной проверки или разделения теста поезда, получают некоторую метрику оценки. Эти шаги повторяются до тех пор, пока не будет получена наилучшая возможная метрическая оценка, и модель не будет признана достойной использования. Это ни в коем случае не плохой путь. Обычно это приводит к отличным моделям, которые обеспечивают ценность так, как они должны. Однако, приложив немного дополнительных усилий, вы сможете сделать каждую модель, которую вы когда-либо построите, лучше. Мы можем сделать это с помощью анализа ошибок.

Анализ ошибок

Что это такое?

При построении модели вы можете сделать это случайно или намеренно. Случайный подход к построению модели заманчиво. Это требует меньше усилий и все же приносит результаты. Случайный подход был бы в том случае, когда после каждой итерации модели вы решаете попробовать что-то новое, чтобы сделать это лучше, не задумываясь о том, почему. Это просто так: идея пришла вам в голову, которая может улучшить счет Ф1, так почему бы не попробовать? Это легко и работает.

Преднамеренный подход к построению модели использует анализ ошибок. Анализ ошибок требует от вас копаться в результатах вашей модели после каждой итерации. Вы просматриваете данные и прогнозы на уровне наблюдений и формируете гипотезы о том, почему ваша модель не оправдалась при определенных прогнозах. Затем вы проверяете свою гипотезу, изменяя модель таким образом, чтобы исправить эту ошибку, и начинаете следующую итерацию. Каждая итерация моделирования занимает больше времени с анализом ошибок, но окончательные результаты лучше и, скорее всего, будут быстрее.

Правильный способ сделать анализ ошибок

Не существует установленного способа выполнения анализа ошибок. Это исследовательский и требует творчества и знаний в области. При этом я собираюсь рассказать вам о шагах, которые я обычно делаю, когда делаю это. Надеемся, что это даст вам отправную точку, чтобы найти отличные идеи от ошибок в вашей модели.

Типы
ошибок: лексическая (недопустимые
символы)

синтаксическая
(в синтаксическом анализаторе)

семантическая
(происходит на этапе семантического
анализа; пример – несоответствие типа
операнда конкретной операции)

логическая
(возникает во время выполнения; пример
— зацикливание)

Обработчик
ошибок должен:

Точно
определить место и тип ошибки,быстро
восстановиться после ошибки для
продолжения анализа

эффективно
работать при анализе корректных программ

Выделяют
несколько стратегий действия после
обнаружения ошибок:

режим
паники транслятор
пропускает символы из входной строки
до обнаружения символа из синхронизирующего
множества Недостатки:Пропускаемое
множество символов может быть очень
большим, Появление цепной реакции,
позднее проявление ошибки

уровень
фразы Недостатки:Для
каждого случая необходимо писать свою
процедуру ошибок

продукции
ошибок Добавляется
ошибочная ситуация, тогда синтаксический
анализатор обнаруживает ошибку,
локализует ее, восстанавливается и
работает дальше.
Недостатки:Описывает
только ограниченные и ранее известные
типы ошибок

глобальная
коррекция необходимо
минимально видоизменить программу,
чтобы она преобразовалась в синтаксически
корректную Недостатки:Сложность
реализации

20 Семантика языка, методы описания и анализа.

• Фаза
  контроля типов

• Идентификация.
  Работа с таблицами

• Идентификация.
  Работа с типами

• Причины
  использования промежуточных языков в
  компиляторах

• Различные
  формы представления промежуточных
  языков (ПЯ) в компиляторах:

  • Атрибутивные
    деревья разбора

  • Прямая
    и обратная польские записи

  • Триады/тетрады

  • RTL

На
этапе семантического анализа можно:

Проверить
соответствие типов

Проверить
управление (различных переходов)

Проверить
единственность (чтобы один раз объявлялась
переменная или функция)

Проверить
имена (чтобы имя встречалось определенное
количество раз)

Сравнение
может быть статическим
(на этапе трансляции) и динамическим
(во время выполнения).

Приведение
типов

Расширяющее
(short
-> long)

Сужающее
(long
-> short)

Формализм
атрибутных грамматик оказался очень
удобным средством для описания семантики
языков программирования

21 Понятие атрибутивные грамматики

входит
в раздел синтаксически управляемые
грамматики.

Для
каждого символа грамматики вводится
атрибут val

Вместе
с правилами грамматики записываются
семантические правила, которые вычисляют
значение этих атрибутов.Процесс
построения дерева разбора, а затем
вычисления атрибутов (нетерминал к
терминалу) и называется синтаксически
управляемой трансляцией

Атрибутивная
грамматика содержит:Синтаксические
правила. Для каждого элемента грамматики
– множество атрибутов.Для каждого
правила – множество семантических
правил

Атрибуты
бывают:Синтезируемые.Наследуемые

Семантическая
часть правила состоит из локальных
объявлений и семантических действий.
В качестве семантических действий
допускаются как атрибутные присваивания,
так и составные операторы.

Метка
в семантической части правила привязывает
выполнение оператора к обходу дерева
разбора сверху-вниз слева направо.
Конструкция i : оператор означает,
что оператор должен быть выполнен сразу
после обхода i-й компоненты правой части.
Конструкция i E : оператор
означает, что оператор должен быть
выполнен, только если порождение i-й
компоненты правой части пусто. Конструкция
i A : оператор означает, что
оператор должен быть выполнен после
разбора каждого повторения i-й компоненты
правой части (имеется в виду конструкция
повторения).

Для математики популярная поговорка «умные люди учатся на чужих ошибках» практически не работает, так как ошибка в большинстве случаев является необходимой и полезной, ведь она позволяет определить пробелы в знаниях школьника и своевременно их устранить. Главное – правильно относится к ошибке и ее правильно ее использовать.

Тем более обидно получать глупые ошибки, которые вызваны невнимательностью обучающихся, пропусками переменных, случайными потерями знаков, скобок и другими различными ляпами.

Для того чтобы снизить вероятность ошибок, необходимо использовать различные методики предупреждения типичных ошибок, что будет в итоге способствовать повышению уровня математической подготовки школьников.

Разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания

Организация работы обучающихся, направленной на анализ и исправление допущенных недочетов называется работой над ошибками. Ее основной целью является разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания. Правильно организованная работа обучающихся обеспечивает:

• дифференцированный подход к обучению;

• является профилактикой будущих ошибок;

• позволяет своевременно ликвидировать пробелы в знаниях и навыках детей;

• формирует умение систематизировать и обобщать, закреплять полученные знания.

Грамотный, творческий подход учителя к организации работы над ошибками создает условия для развития адекватного отношения обучающегося к ошибкам, умение работать с ними.

Можно говорить о том, что, после проведения работы над ошибками итоговая оценка отражает действительный уровень усвоения знаний и умений обучающихся. Существует практика, когда некоторые учителя практикуют выставление оценок за каждую проведенную работу. При этом, часто бывает, что после работы над ошибками, отметка за проверяемую работу повышается (как правило на один бал).

Обычно, работа над ошибками проводится в классе, под руководством учителя, но может проводиться и дома, возможно, под контролем родителей. Если учитель считает возможным дать выполнение работы над ошибками в качестве домашнего задания, он должен убедиться, что все обучающиеся знают и помнят основной алгоритм действий по выполнению работы. Целесообразно, каждому ребенку выдать памятку с порядком выполнения действий. Кроме этого, необходимо предварительно, на уроке провести общий анализ допущенных ошибок.

В классе, работу над ошибками проводят, как правило, после контрольных, самостоятельных или творческих работ. Работе над ошибками может быть посвящен, как весь урок, так и его часть. Это зависит от характера и количества видов ошибок, от уровня самостоятельности обучающихся и т.п. По усмотрению учителя возможны: фронтальная, групповая, парная, индивидуальная работа.

Основные этапы и формы организации работы над ошибками на уроке

При работе на уроке выделяют несколько основных этапов:

• консультация;

• коррекция знаний и умений;

• диагностика результатов;

• оценочная деятельность.

По усмотрению учителя возможны: фронтальная, групповая, индивидуальная работа.

Рассмотрим несколько вариантов проведения работы над ошибками

В начале урока, после проведения общего анализа проверенной работы, учитель просит поднять руку тех обучающихся, которые допустили ошибки при выполнении первого задания. К доске приглашается один из обучающихся, который будет выполнять и комментировать аналогичное задание у доски. Обучающийся определяется либо по его желанию, либо по решению учителя. Остальные обучающиеся выполняют работу у себя в тетрадях. Затем все самостоятельно решают задание проверочной работы. Таким образом, дети прорешивая аналогичное задание, прорабатывают ошибки, допущенные не только ими самими, но и остальными обучающимися. Такой подход целесообразен, когда в данном задании большинство обучающихся допустили ошибки.

Следующая форма работы используется, когда один, или несколько обучающихся допустили ошибки в задании, которое большинство обучающихся выполнили правильно. При данной форме организации урока один обучающийся выполняет работу над своими ошибками у доски, остальные обучающиеся исправляют свои недочеты в тетрадях или выполняют индивидуальные задания. С одной стороны, этот метод позволяет экономить время, затрачиваемое на данную деятельность, с другой — учитель не может контролировать деятельность других детей. Для исправления возникшей ситуации, нужно обеспечить каждому обучающемуся возможность обратиться к учителю за помощью, за консультацией.

Бывают ситуации, когда часть обучающихся выполнила проверочную работу на «отлично», т.е. возникает необходимость организовать деятельность этих обучающихся, и, одновременно организовать выполнение работы над ошибками остальными обучающимися. В этом случае, есть несколько вариантов организации работы на уроке.

Во-первых, «отличникам» можно предложить выполнение индивидуальных заданий повышенного или углубленного уровней, творческие задания, работу по подготовке, например, информационного сообщения к следующему уроку. С остальными обучающимися проводится работа над ошибками.

Во-вторых, обучающихся, показавших высокий уровень усвоения учебного материала, можно привлечь к консультированию других детей. В этом случае возможна организация групповой и (или) парной работы.

Имеют место случаи, когда педагог, в целях экономии времени, выделяет только типичные ошибки, допущенные обучающимися при выполнении проверочной работы, и на уроке проводят работу только таким видом ошибок. В этом случае работа организовывается фронтально, анализ и исправление типичных ошибок и недочетов выполняет весь класс вместе. При этом у доски работают обучающиеся по желанию, по очереди или по решению учителя, в зависимости от того, кто какие ошибки допустил.

Алгоритм действий по выполнению работы над ошибками

Алгоритм действий по проведению работы над ошибками определяется учителем самостоятельно, исходя из особенностей класса, общего уровня обученности и т.д.

Например, алгоритм действий обучающегося может выглядеть следующим образом:

1. просмотреть всю работу, обратить внимание на исправления учителя;
2. найти ошибку, выписать задание, в котором она допущена, проанализировать причину ее возникновения:

• ошибка в вычислении – перерешать;

• ошибка в применении формулы (правила, закона) — вспомнить нужную формулу (правило, закон) по данной теме, применить при решении;

• ошибка в построении рисунка – повторить материал в учебнике и выполнить рисунок правильно;

1. решить аналогичное задание

Памятка-помощник

В практике работы некоторых учителей встречается использование памяток, которые изготавливаются педагогом и раздаются каждому обучающемуся. Памятки могут быть индивидуальными. Работа с памятками выполняется под контролем педагога.

В памятке пронумерованы и записаны основные группы ошибок в виде:

Тема «….».

Примеры.

1.  
2.  
3. …

Если учитель планирует проводить работу над ошибками, с использованием памяток, то при проверке работы на полях тетради, напротив задания, в котором допущена ошибка, ставится номер, соответствующего задания в памятке. Это не только облегчает работу обучающихся, но и совершенствует систему обучения. Обучающийся неоднократно обращается к данной памятке, что способствует лучшему запоминанию учебного материала.

Проверка и подведение итогов работы над ошибками

В конце работы над ошибками необходимо провести проверку. Существует несколько форм ее организации.

• самопроверка;

• парная работа;

• групповая работа, когда «сильные» обучающиеся выступают в роли консультантов;

• фронтальная работа со всем классом.

Во всех случаях, необходимо обеспечить возможность каждому обучающемуся консультирования и помощи учителя, если возникают трудности.

В конце работы над ошибками, как и в конце любого урока, необходимо провести рефлексию. Дети анализируют свои ошибки, отмечают, как изменились собственные умения, отмечают моменты, которые остались не понятны, говорят о том, что вызвало трудности и высказывают свои предложения.

Следует отметить, что проведение работы над ошибками является обязательным и систематическим действием после каждой контрольной и проверочной работы. При этом необходимо обращать внимание и прорабатывать все ошибки, допущенные обучающимися, тщательно проводить отбор задач и примеров для отработки знаний и умений, для закрепления пройденного материала.

Превентивная деятельность учителя по предупреждению ошибок

Большая часть ошибок, допускаемых обучающимися, не связана с отсутствием или наличием знаний, хотя, конечно, доведение до уровня автоматизма ряда вычислительных операций позволяет существенно снизить вероятность появления ошибок. Однако при этом необходимо, чтобы обучающийся все равно руководствовался нужными правилами и постоянно сохранял концентрацию внимания.

Знание определенных правил нужно и для того, чтобы обучающийся мог проверить правильность решения и дать его обоснование. В тоже время многие школьники воспринимают курс алгебры в качестве набора правил, которые абсолютно не связаны между собой, поэтому они заучиваются исключительно для решения какой-то конкретной задачи, а по истечению незначительного промежутка времени просто забываются. В этой связи требуется организовывать процесс обучения правилам с использованием приемов, которые активизируют рефлексивную деятельность школьников по предупреждению и исправлению ошибок, возникающих при формальном усвоении правил.

Если процесс поиска и исправления ошибок сделать максимально поучительным для обучающихся, то анализ ошибок может стать эффективным средством для развития познавательного интереса к математике.

Наиболее распространенными ошибками являются:

• незнание или непонимание правил, формул и определений;

• неправильное применение формул или неумение правильно применять определения и правила;

• совершение вычислительных ошибок;

• невнимательное чтение условий задачи;

• отказ от использования свойств фигур при решении геометрических задач;

• неправильное раскрытие скобок;

• совершение логических ошибок при решении текстовых задач;

• применение формул сокращенного умножения.

К основным причинам совершения ошибок по математике относят:

• пропуски уроков, в результате чего появляются пробелы в знаниях;

• поверхностное изучение нового материала;

• повышенная усталость, вызванная чрезмерной нагрузкой или недостаточным сном, в результате чего понижается скорость мышления и снижается уровень внимания;

• неаккуратный почерк, из-за чего учитель часто не понимает, что написал обучающийся;

• скорость работы. При этом на появление ошибок влияет как высокая скорость работы, из-за которой обучающийся просто не стремиться вникнуть в суть задания, так и медленная. В последнем случае замедленная скорость мыслительных операций не позволяет обучающемуся в полной мере контролировать себя, а из-за «зависания» нужная информация просто удаляется из «оперативной памяти»;

• полное либо кратковременное переключение внимания с одной деятельности на другую;

• низкая мотивация, в результате которой теряется внимание и появляются ошибки.

Объяснение и предупреждение ошибок

Для предупреждения ошибок и сведения их к минимуму используются следующие профилактические мероприятия и действия:

• постоянный разбор наиболее распространенных ошибок в классе;

• предлагаемые обучающимся письменные задания должны быть максимально удобны для восприятия, то есть грамотно сформулированными и понятными;

• подбор заданий и упражнений, которые будут вызывать у детей интерес и повышенное внимание;

• учитель должен при объяснении нового материала стараться предугадать возможные ошибки обучающихся и разработать систему заданий, которые позволят правильно усвоить новые понятия;

• использование правил удобных для запоминания и исключающих двойную их трактовку.

Кроме того, учитель математики должен помнить, что систематическое и планомерное повторение является основным инструментом для ликвидации пробелов знаний.

Также рекомендуется при объяснении нового материала активно применять определения и теоремы, которые изучались ранее. Так, при изучении темы «Теоремы сложения» целесообразно организовать повторение ряда теоретических вопросов:

1. Изменение тригонометрических функций при возрастании и убывании аргумента.

2. Четные и нечетные функции.

3. Таблицы значений тригонометрических функций.

4. Знаки тригонометрических функций.

Дополнительно выполняются следующие задания:

1. Необходимо определить четность и нечестность тригонометрических функций:

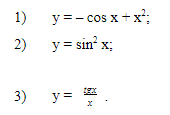
1. Найдите область определения функции y = x2 – 6x + 10.

2. Определите, при каких значениях x, функции y = sin x и y = cos x принимают одинаковые значения?

Перед тем как приступить к изучению темы «Первообразная и интеграл», следует повторить все формулы дифференцирования. После этого обучающиеся выполняют самостоятельную работу (время решения – 10-15 минут), во время которой школьникам предлагаются карточки-задания, где «опущены» один-два компонента из формулы дифференцирования, а также приведены две функции, производные которых необходимо найти.

Затем проводиться проверка работы и анализ совершенных ошибок, что необходимо для выявления пробелов в знаниях и проведения работы по их устранению.

Список литературы:

1. Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
2. Амонашвили Ш.А. Воспитательная и образовательная функции оценки обучения школьников: Экспериментальное педагогическое исследование. – М.: Педагогика, 1984. – 296 с.
3. Бабанский Ю.К. Педагогика. М.: Просвещение, 1983.
4. Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
5. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
6. Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
7. Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
8. Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
9. Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
10. Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
11. Действующие учебники и учебные пособия по математике для средней школы.
12. Журналы «Математика в школе» за 1970-1990 гг.
13. Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
14. Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
15. Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
16. Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
17. Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
18. Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
19. Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
20. Рогановский, Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
21. Селевко, Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
22. Столяр, А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
23. Темербекова, А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
24. Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
25. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
26. Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
27. Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
28. Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
29. Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.

1