Доверительный интервал
Доверительный
интервал – это отрезок на оси значений
оцениваемой характеристики случайной
величины (например, математического
ожидания), который с заданной вероятностью
накрывает неизвестное значение
оцениваемой характеристики.
Доверительная
вероятность
– это вероятность того, что неизвестное
значение оцениваемой характеристики
окажется внутри доверительного интервала.
Точки на оси,
ограничивающие доверительный интервал,
называются доверительными
границами.
Чем шире доверительный
интервал, тем больше доверительная
вероятность.
Для того чтобы по
заданной доверительной вероятности
установить границы доверительного
интервала необходимо иметь плотность
распределения или закон распределения
статистики, применяемой для оценивания
неизвестного значения характеристики
случайной величины.
Однако известно,
что при объёме выборки большем 25
распределение любой статистики очень
близко к нормальному распределению.
Границы доверительного
интервала устанавливают так, чтобы в
его пределах оказались значения
оцениваемой характеристики, наиболее
близкие к среднему значению плотности
распределения или закона распределения,
а «хвосты», содержащие достаточно
удалённые и, как правило, маловероятные
значения, оказались вне границ. Причём
суммы вероятностей значений в каждом
из «хвостов» должны быть равными друг
другу.
Если оценка среднего
![]()
имеет нормальное или близкое к нормальному
распределение, то границы доверительного
интервала могут быть определены прямо
через величину среднеквадратической
ошибки оценки
![]() ,
,
на основании свойств нормального
распределения. Делается это следующим
образом.
Пусть вычислены
оценка среднего
![]()
и её среднеквадратическая ошибка
![]() .
.
Истинное неизвестное математическое
ожидание случайной величины будет
находиться в доверительном интервале
от
![]() –
–![]() до
до
![]() +
+![]() с доверительной вероятностью 0,682 .
с доверительной вероятностью 0,682 .
Если выбрать
доверительный интервал вдвое шире, т.е.
по двукратной
ошибке,
его границами будут значения от
![]() –2
–2![]() до
до
![]() +2
+2![]() .
.
Доверительная вероятность при таком
интервале составляет 0,955, т.е. больше,
чем при предыдущем интервале, определённом
пооднократной
ошибке.
Доверительная
вероятность в пределах трёхкратной
ошибки,
т.е. от
![]() –3
–3![]() до
до
![]() +3
+3![]() ,
,
будет 0,997 , а значит, практически все
выборочные данные, 99,7 %, попадут в
этот интервал. Это свойство нормального
распределения носит название «правило
трёх сигм».
Чем больше
доверительная вероятность, тем выше
надёжность результата. Однако при этом
увеличивается и доверительный интервал,
который желательно иметь как можно уже.
Помимо
задания доверительного интервала по
одно-, двух- и трёхкратной ошибке
существует ещё один способ задания: по
доверительной вероятности. Обычно
используются следующие значения
доверительной вероятности: 0,90 ,
0,95 и 0,99. Ширины доверительного
интервала в этом случае составляют
соответственно 1,65![]() , 1,96
, 1,96![]() и 2,58
и 2,58![]() от выборочного среднего
от выборочного среднего
![]() .
.
А вероятности ошибки: 0,10 , 0,05 и 0,01 (10 %,
5 % и 1 %).
Результатом
оценивания является:
-
либо значение
оценки неизвестной характеристики
случайной величины (например, её
математического ожидания) и
среднеквадратическая ошибка оценки
 ;
; -
либо две границы
доверительного интервала, накрывающего
неизвестное значение интересующей
характеристики случайной величины с
заданной (указываемой) доверительной
вероятностью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 — alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA — Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } &= 0.45 pm 1.65{0.30 over sqrt {100}} &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
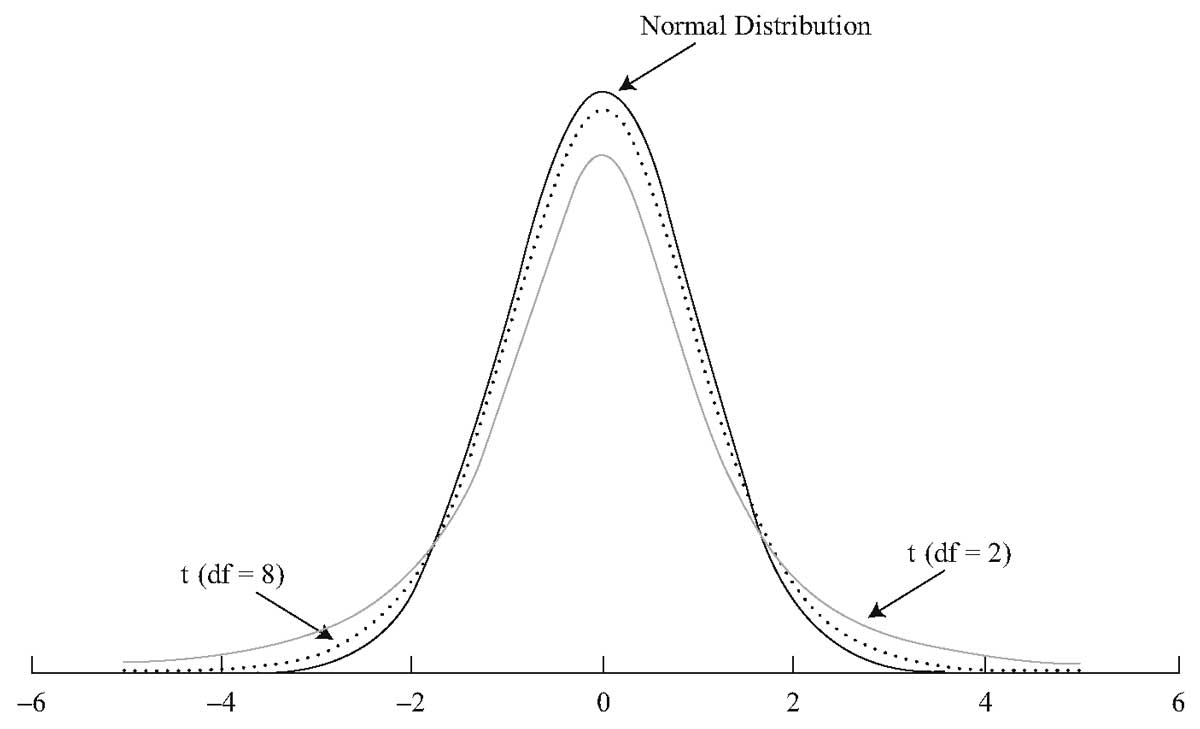 Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) — это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } &= 0.45 pm 1.66{0.30 over sqrt {100}} &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
Таблица 3. Основы для расчета факторов надежности.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Выборка. Типы выборок. Расчет ошибки выборки
Калькуляторы
Калькулятор расчета ошибки и размера выборки
Калькулятор расчета статистической значимости различий
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих
определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и
времени. Примеры генеральных совокупностей
- Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
- Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
- Юридические лица России (2,2 млн. на начало 2005 года)
- Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и
т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей
генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на
всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и
нерепрезентативной для разных генеральных совокупностей.
Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население
Москвы. - Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать
москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках
соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от
ошибки никак не зависит от размера выборки.
Пример:
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой
всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера
выборки. Чем больше размер выборки, тем она ниже.
Пример:
Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной
вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об
ошибке выборки, подразумевают именно статистическую ошибку.
Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих
результаты исследования в определенную сторону.
Пример:
- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни.
Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например,
дома). - Проблема респондентов, отказывающихся отвечать на вопросы
анкеты (доля «отказников» в Москве, для разных опросов,
колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот
или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов,
наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата
рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер
генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы
(страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются
случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности,
типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60
лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для
каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны
попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной
совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки
используются в маркетинговых исследованиях достаточно
часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег,
знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за
исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда
необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход,
респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения
и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство
интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром –
активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает
проблема выбора признака и определения его типичного значения.
Курс лекций по теории статистики
Более подробную информацию по выборочным наблюдениям можно получить просмотрев видеокурс по теории статистики:
Выборочное наблюдение Способы формирование выборки
Специальные виды отбора
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям:
Доверительная вероятность
Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по
выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятность
Ошибка выборки (доверительный интервал)
Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное
истинное значение оцениваемого параметра распределения.
Доля признака
Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют,
необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Калькулятор расчета статистической значимости различий
Калькулятор позволяет проверить есть ли статистически значимая разница между долями признака, полученными из
независимых выборок.
Например, если до начала рекламной кампании марку знали 55% респондентов, а по окончании – 60% — есть ли между этими
долями статистически значимая разница, или же эта разница укладывается в ошибку выборки?
Примечание. Эта процедура может законно использоваться, только если обе выборки удовлетворяют следующему условию:
произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, должны быть не меньше 5.
Оставить свои комментарии по затронутой теме Вы можете на наших страницах в Facebook и Вконтакте.
При перепечатке материалов ссылка на маркетинговое агентство обязательна
FDF Group © 2023
Разработка сайта — Монохром
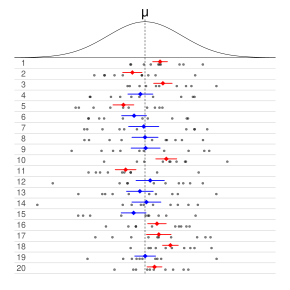
Each row of points is a sample from the same normal distribution. The colored lines are 50% confidence intervals for the mean, μ. At the center of each interval is the sample mean, marked with a diamond. The blue intervals contain the population mean, and the red ones do not.
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated confidence level; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used.[1][2] The confidence level represents the long-run proportion of CIs (at the given confidence level) that theoretically contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter’s true value.[3]
Factors affecting the width of the CI include the sample size, the variability in the sample, and the confidence level.[4] All else being the same, a larger sample produces a narrower confidence interval, greater variability in the sample produces a wider confidence interval, and a higher confidence level produces a wider confidence interval.[5]
Definition[edit]
Let X be a random sample from a probability distribution with statistical parameter θ, which is a quantity to be estimated, and φ, representing quantities that are not of immediate interest. A confidence interval for the parameter θ, with confidence level or coefficient γ, is an interval 


The number γ, whose typical value is close to but not greater than 1, is sometimes given in the form 


It is important for the bounds 

Approximate confidence intervals[edit]
In many applications, confidence intervals that have exactly the required confidence level are hard to construct, but approximate intervals can be computed. The rule for constructing the interval may be accepted as providing a confidence interval at level 
to an acceptable level of approximation. Alternatively, some authors[6] simply require that
which is useful if the probabilities are only partially identified or imprecise, and also when dealing with discrete distributions. Confidence limits of form
and
are called conservative;[7](p 210) accordingly, one speaks of conservative confidence intervals and, in general, regions.
Desired properties[edit]
When applying standard statistical procedures, there will often be standard ways of constructing confidence intervals. These will have been devised so as to meet certain desirable properties, which will hold given that the assumptions on which the procedure relies are true. These desirable properties may be described as: validity, optimality, and invariance.
Of the three, «validity» is most important, followed closely by «optimality». «Invariance» may be considered as a property of the method of derivation of a confidence interval, rather than of the rule for constructing the interval. In non-standard applications, these same desirable properties would be sought:
Validity[edit]
This means that the nominal coverage probability (confidence level) of the confidence interval should hold, either exactly or to a good approximation.
Optimality[edit]
This means that the rule for constructing the confidence interval should make as much use of the information in the data-set as possible.
Recall that one could throw away half of a dataset and still be able to derive a valid confidence interval. One way of assessing optimality is by the length of the interval so that a rule for constructing a confidence interval is judged better than another if it leads to intervals whose lengths are typically shorter.
Invariance[edit]
In many applications, the quantity being estimated might not be tightly defined as such.
For example, a survey might result in an estimate of the median income in a population, but it might equally be considered as providing an estimate of the logarithm of the median income, given that this is a common scale for presenting graphical results. It would be desirable that the method used for constructing a confidence interval for the median income would give equivalent results when applied to constructing a confidence interval for the logarithm of the median income: Specifically the values at the ends of the latter interval would be the logarithms of the values at the ends of former interval.
Methods of derivation[edit]
For non-standard applications, there are several routes that might be taken to derive a rule for the construction of confidence intervals. Established rules for standard procedures might be justified or explained via several of these routes. Typically a rule for constructing confidence intervals is closely tied to a particular way of finding a point estimate of the quantity being considered.
Summary statistics[edit]
This is closely related to the method of moments for estimation. A simple example arises where the quantity to be estimated is the population mean, in which case a natural estimate is the sample mean. Similarly, the sample variance can be used to estimate the population variance. A confidence interval for the true mean can be constructed centered on the sample mean with a width which is a multiple of the square root of the sample variance.
Likelihood theory[edit]
Estimates can be constructed using the maximum likelihood principle, the likelihood theory for this provides two ways of constructing confidence intervals or confidence regions for the estimates.
Estimating equations[edit]
The estimation approach here can be considered as both a generalization of the method of moments and a generalization of the maximum likelihood approach. There are corresponding generalizations of the results of maximum likelihood theory that allow confidence intervals to be constructed based on estimates derived from estimating equations.[citation needed]
Hypothesis testing[edit]
If hypothesis tests are available for general values of a parameter, then confidence intervals/regions can be constructed by including in the 100 p % confidence region all those points for which the hypothesis test of the null hypothesis that the true value is the given value is not rejected at a significance level of (1 − p) .[7](§ 7.2 (iii))
Bootstrapping[edit]
In situations where the distributional assumptions for the above methods are uncertain or violated, resampling methods allow construction of confidence intervals or prediction intervals. The observed data distribution and the internal correlations are used as the surrogate for the correlations in the wider population.
Central limit theorem[edit]
The central limit theorem is a refinement of the law of large numbers. For a large number of independent identically distributed random variables 



Example[edit]
Suppose {X1, …, Xn} is an independent sample from a normally distributed population with unknown parameters mean μ and variance σ2. Let
Where X is the sample mean, and S2 is the sample variance. Then
has a Student’s t distribution with n − 1 degrees of freedom.[8] Note that the distribution of T does not depend on the values of the unobservable parameters μ and σ2; i.e., it is a pivotal quantity. Suppose we wanted to calculate a 95% confidence interval for μ. Then, denoting c as the 97.5th percentile of this distribution,
Note that «97.5th» and «0.95» are correct in the preceding expressions. There is a 2.5% chance that 





Consequently,
and we have a theoretical (stochastic) 95% confidence interval for μ.
After observing the sample we find values x for X and s for S, from which we compute the confidence interval

In this bar chart, the top ends of the brown bars indicate observed means and the red line segments («error bars») represent the confidence intervals around them. Although the error bars are shown as symmetric around the means, that is not always the case. In most graphs, the error bars do not represent confidence intervals (e.g., they often represent standard errors or standard deviations)
Interpretation[edit]
Various interpretations of a confidence interval can be given (taking the 95% confidence interval as an example in the following).
- The confidence interval can be expressed in terms of a long-run frequency in repeated samples (or in resampling): «Were this procedure to be repeated on numerous samples, the proportion of calculated 95% confidence intervals that encompassed the true value of the population parameter would tend toward 95%.»[9]
- The confidence interval can be expressed in terms of probability with respect to a single theoretical (yet to be realized) sample: «There is a 95% probability that the 95% confidence interval calculated from a given future sample will cover the true value of the population parameter.» [10] This essentially reframes the «repeated samples» interpretation as a probability rather than a frequency. See Neyman construction.
- The confidence interval can be expressed in terms of statistical significance, e.g.: «The 95% confidence interval represents values that are not statistically significantly different from the point estimate at the .05 level«.[11]

Interpretation of the 95% confidence interval in terms of statistical significance.
Common misunderstandings[edit]
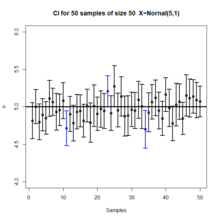
Plot of 50 confidence intervals from 50 samples generated from a normal distribution.
See also: § Counterexamples
Confidence intervals and levels are frequently misunderstood, and published studies have shown that even professional scientists often misinterpret them.[12][13][14][15][16][17]
- A 95% confidence level does not mean that for a given realized interval there is a 95% probability that the population parameter lies within the interval (i.e., a 95% probability that the interval covers the population parameter).[18] According to the strict frequentist interpretation, once an interval is calculated, this interval either covers the parameter value or it does not; it is no longer a matter of probability. The 95% probability relates to the reliability of the estimation procedure, not to a specific calculated interval.[19] Neyman himself (the original proponent of confidence intervals) made this point in his original paper:[10]
It will be noticed that in the above description, the probability statements refer to the problems of estimation with which the statistician will be concerned in the future. In fact, I have repeatedly stated that the frequency of correct results will tend to α. Consider now the case when a sample is already drawn, and the calculations have given [particular limits]. Can we say that in this particular case the probability of the true value [falling between these limits] is equal to α? The answer is obviously in the negative. The parameter is an unknown constant, and no probability statement concerning its value may be made…
- Deborah Mayo expands on this further as follows:[20]
It must be stressed, however, that having seen the value [of the data], Neyman–Pearson theory never permits one to conclude that the specific confidence interval formed covers the true value of 0 with either (1 − α)100% probability or (1 − α)100% degree of confidence. Seidenfeld’s remark seems rooted in a (not uncommon) desire for Neyman–Pearson confidence intervals to provide something which they cannot legitimately provide; namely, a measure of the degree of probability, belief, or support that an unknown parameter value lies in a specific interval. Following Savage (1962), the probability that a parameter lies in a specific interval may be referred to as a measure of final precision. While a measure of final precision may seem desirable, and while confidence levels are often (wrongly) interpreted as providing such a measure, no such interpretation is warranted. Admittedly, such a misinterpretation is encouraged by the word ‘confidence’.
- A 95% confidence level does not mean that 95% of the sample data lie within the confidence interval.
- A confidence interval is not a definitive range of plausible values for the sample parameter, though it is often heuristically taken as a range of plausible values.
- A particular confidence level of 95% calculated from an experiment does not mean that there is a 95% probability of a sample parameter from a repeat of the experiment falling within this interval.[16]
Counterexamples[edit]
Since confidence interval theory was proposed, a number of counter-examples to the theory have been developed to show how the interpretation of confidence intervals can be problematic, at least if one interprets them naïvely.
Confidence procedure for uniform location[edit]
Welch[21] presented an example which clearly shows the difference between the theory of confidence intervals and other theories of interval estimation (including Fisher’s fiducial intervals and objective Bayesian intervals). Robinson[22] called this example «[p]ossibly the best known counterexample for Neyman’s version of confidence interval theory.» To Welch, it showed the superiority of confidence interval theory; to critics of the theory, it shows a deficiency. Here we present a simplified version.
Suppose that 

A fiducial or objective Bayesian argument can be used to derive the interval estimate
which is also a 50% confidence procedure. Welch showed that the first confidence procedure dominates the second, according to desiderata from confidence interval theory; for every 


However, when 

Moreover, when the first procedure generates a very short interval, this indicates that 
The two counter-intuitive properties of the first procedure—100% coverage when 

This counter-example is used to argue against naïve interpretations of confidence intervals. If a confidence procedure is asserted to have properties beyond that of the nominal coverage (such as relation to precision, or a relationship with Bayesian inference), those properties must be proved; they do not follow from the fact that a procedure is a confidence procedure.
Confidence procedure for ω2[edit]
Steiger[24] suggested a number of confidence procedures for common effect size measures in ANOVA. Morey et al.[18] point out that several of these confidence procedures, including the one for ω2, have the property that as the F statistic becomes increasingly small—indicating misfit with all possible values of ω2—the confidence interval shrinks and can even contain only the single value ω2 = 0; that is, the CI is infinitesimally narrow (this occurs when 

This behavior is consistent with the relationship between the confidence procedure and significance testing: as F becomes so small that the group means are much closer together than we would expect by chance, a significance test might indicate rejection for most or all values of ω2. Hence the interval will be very narrow or even empty (or, by a convention suggested by Steiger, containing only 0). However, this does not indicate that the estimate of ω2 is very precise. In a sense, it indicates the opposite: that the trustworthiness of the results themselves may be in doubt. This is contrary to the common interpretation of confidence intervals that they reveal the precision of the estimate.
History[edit]
Confidence intervals were introduced by Jerzy Neyman in 1937.[25] Statisticians quickly took to the idea, but adoption by scientists was more gradual. Some authors in medical journals promoted confidence intervals as early as the 1970s. Despite this, confidence intervals were rarely used until the following decade, when they quickly became standard.[26] By the late 1980s, medical journals began to require the reporting of confidence intervals.[27]
See also[edit]
- CLs upper limits (particle physics)
- 68–95–99.7 rule
- Confidence band, an interval estimate for a curve
- Confidence distribution
- Confidence region, a higher dimensional generalization
- Credence (statistics)
- Credible interval, a Bayesian alternative for interval estimation
- Cumulative distribution function-based nonparametric confidence interval
- Error bar – Graphical representations of the variability of data
- Estimation statistics – Data analysis approach in frequentist statistics
- Margin of error, the CI halfwidth
- p-value – Function of the observed sample results
- Prediction interval, an interval estimate for a random variable
- Probable error
- Robust confidence intervals
Confidence interval for specific distributions[edit]
- Confidence interval for binomial distribution
- Confidence interval for exponent of the power law distribution
- Confidence interval for mean of the exponential distribution
- Confidence interval for mean of the Poisson distribution
- Confidence intervals for mean and variance of the normal distribution
References[edit]
- ^ Zar, Jerrold H. (199). Biostatistical Analysis (4th ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 43–45. ISBN 978-0130815422. OCLC 39498633.
- ^ a b c Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). «A Modern Introduction to Probability and Statistics». Springer Texts in Statistics. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN 1431-875X.
- ^ Illowsky, Barbara. Introductory statistics. Dean, Susan L., 1945-, Illowsky, Barbara., OpenStax College. Houston, Texas. ISBN 978-1-947172-05-0. OCLC 899241574.
- ^ Hazra, Avijit (October 2017). «Using the confidence interval confidently». Journal of Thoracic Disease. 9 (10): 4125–4130. doi:10.21037/jtd.2017.09.14. ISSN 2072-1439. PMC 5723800. PMID 29268424.
- ^ Khare, Vikas; Nema, Savita; Baredar, Prashant (2020). Ocean Energy Modeling and Simulation with Big Data Computational Intelligence for System Optimization and Grid Integration. ISBN 978-0-12-818905-4. OCLC 1153294021.
- ^ Roussas, George G. (1997). A Course in Mathematical Statistics (2nd ed.). Academic Press. p. 397.
- ^ a b Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall.
- ^ Rees. D.G. (2001) Essential Statistics, 4th Edition, Chapman and Hall/CRC. ISBN 1-58488-007-4 (Section 9.5)
- ^ Cox D.R., Hinkley D.V. (1974) Theoretical Statistics, Chapman & Hall, p49, p209
- ^ a b Neyman, J. (1937). «Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability». Philosophical Transactions of the Royal Society A. 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. doi:10.1098/rsta.1937.0005. JSTOR 91337.
- ^ Cox D.R., Hinkley D.V. (1974) Theoretical Statistics, Chapman & Hall, pp 214, 225, 233
- ^ Kalinowski, Pawel (2010). «Identifying Misconceptions about Confidence Intervals» (PDF). Retrieved 2021-12-22.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2014-09-16.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Hoekstra, R., R. D. Morey, J. N. Rouder, and E-J. Wagenmakers, 2014. Robust misinterpretation of confidence intervals. Psychonomic Bulletin Review, in press. [1]
- ^ Scientists’ grasp of confidence intervals doesn’t inspire confidence, Science News, July 3, 2014
- ^ a b Greenland, Sander; Senn, Stephen J.; Rothman, Kenneth J.; Carlin, John B.; Poole, Charles; Goodman, Steven N.; Altman, Douglas G. (April 2016). «Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations». European Journal of Epidemiology. 31 (4): 337–350. doi:10.1007/s10654-016-0149-3. ISSN 0393-2990. PMC 4877414. PMID 27209009.
- ^ Helske, Jouni; Helske, Satu; Cooper, Matthew; Ynnerman, Anders; Besancon, Lonni (2021-08-01). «Can Visualization Alleviate Dichotomous Thinking? Effects of Visual Representations on the Cliff Effect». IEEE Transactions on Visualization and Computer Graphics. Institute of Electrical and Electronics Engineers (IEEE). 27 (8): 3397–3409. arXiv:2002.07671. doi:10.1109/tvcg.2021.3073466. ISSN 1077-2626. PMID 33856998. S2CID 233230810.
- ^ a b Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). «The Fallacy of Placing Confidence in Confidence Intervals». Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
- ^ «1.3.5.2. Confidence Limits for the Mean». nist.gov. Archived from the original on 2008-02-05. Retrieved 2014-09-16.
- ^ Mayo, D. G. (1981) «In defence of the Neyman–Pearson theory of confidence intervals», Philosophy of Science, 48 (2), 269–280. JSTOR 187185
- ^ Welch, B. L. (1939). «On Confidence Limits and Sufficiency, with Particular Reference to Parameters of Location». The Annals of Mathematical Statistics. 10 (1): 58–69. doi:10.1214/aoms/1177732246. JSTOR 2235987.
- ^ Robinson, G. K. (1975). «Some Counterexamples to the Theory of Confidence Intervals». Biometrika. 62 (1): 155–161. doi:10.2307/2334498. JSTOR 2334498.
- ^ Pratt, J. W. (1961). «Book Review: Testing Statistical Hypotheses. by E. L. Lehmann». Journal of the American Statistical Association. 56 (293): 163–167. doi:10.1080/01621459.1961.10482103. JSTOR 2282344.
- ^ Steiger, J. H. (2004). «Beyond the F test: Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis». Psychological Methods. 9 (2): 164–182. doi:10.1037/1082-989x.9.2.164. PMID 15137887.
- ^ [Neyman, J., 1937. Outline of a theory of statistical estimation based on the classical theory of probability. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 236(767), pp.333-380]
- ^ Altman, Douglas G. (1991). «Statistics in medical journals: Developments in the 1980s». Statistics in Medicine. 10 (12): 1897–1913. doi:10.1002/sim.4780101206. ISSN 1097-0258. PMID 1805317.
- ^ Sandercock, Peter A.G. (2015). «Short History of Confidence Intervals». Stroke. Ovid Technologies (Wolters Kluwer Health). 46 (8): e184-7. doi:10.1161/strokeaha.115.007750. ISSN 0039-2499. PMID 26106115.
Bibliography[edit]
- Fisher, R.A. (1956) Statistical Methods and Scientific Inference. Oliver and Boyd, Edinburgh. (See p. 32.)
- Freund, J.E. (1962) Mathematical Statistics Prentice Hall, Englewood Cliffs, NJ. (See pp. 227–228.)
- Hacking, I. (1965) Logic of Statistical Inference. Cambridge University Press, Cambridge. ISBN 0-521-05165-7
- Keeping, E.S. (1962) Introduction to Statistical Inference. D. Van Nostrand, Princeton, NJ.
- Kiefer, J. (1977). «Conditional Confidence Statements and Confidence Estimators (with discussion)». Journal of the American Statistical Association. 72 (360a): 789–827. doi:10.1080/01621459.1977.10479956. JSTOR 2286460.
- Mayo, D. G. (1981) «In defence of the Neyman–Pearson theory of confidence intervals», Philosophy of Science, 48 (2), 269–280. JSTOR 187185
- Neyman, J. (1937) «Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability» Philosophical Transactions of the Royal Society of London A, 236, 333–380. (Seminal work.)
- Robinson, G.K. (1975). «Some Counterexamples to the Theory of Confidence Intervals». Biometrika. 62 (1): 155–161. doi:10.1093/biomet/62.1.155. JSTOR 2334498.
- Savage, L. J. (1962), The Foundations of Statistical Inference. Methuen, London.
- Smithson, M. (2003) Confidence intervals. Quantitative Applications in the Social Sciences Series, No. 140. Belmont, CA: SAGE Publications. ISBN 978-0-7619-2499-9.
- Mehta, S. (2014) Statistics Topics ISBN 978-1-4992-7353-3
- «Confidence estimation», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). «The fallacy of placing confidence in confidence intervals». Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
External links[edit]
- The Exploratory Software for Confidence Intervals tutorial programs that run under Excel
- Confidence interval calculators for R-Squares, Regression Coefficients, and Regression Intercepts
- Weisstein, Eric W. «Confidence Interval». MathWorld.
- CAUSEweb.org Many resources for teaching statistics including Confidence Intervals.
- An interactive introduction to Confidence Intervals
- Confidence Intervals: Confidence Level, Sample Size, and Margin of Error by Eric Schulz, the Wolfram Demonstrations Project.
- Confidence Intervals in Public Health. Straightforward description with examples and what to do about small sample sizes or rates near 0.

Each row of points is a sample from the same normal distribution. The colored lines are 50% confidence intervals for the mean, μ. At the center of each interval is the sample mean, marked with a diamond. The blue intervals contain the population mean, and the red ones do not.
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated confidence level; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used.[1][2] The confidence level represents the long-run proportion of CIs (at the given confidence level) that theoretically contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter’s true value.[3]
Factors affecting the width of the CI include the sample size, the variability in the sample, and the confidence level.[4] All else being the same, a larger sample produces a narrower confidence interval, greater variability in the sample produces a wider confidence interval, and a higher confidence level produces a wider confidence interval.[5]
Definition[edit]
Let X be a random sample from a probability distribution with statistical parameter θ, which is a quantity to be estimated, and φ, representing quantities that are not of immediate interest. A confidence interval for the parameter θ, with confidence level or coefficient γ, is an interval 


The number γ, whose typical value is close to but not greater than 1, is sometimes given in the form 


It is important for the bounds 

Approximate confidence intervals[edit]
In many applications, confidence intervals that have exactly the required confidence level are hard to construct, but approximate intervals can be computed. The rule for constructing the interval may be accepted as providing a confidence interval at level 
to an acceptable level of approximation. Alternatively, some authors[6] simply require that
which is useful if the probabilities are only partially identified or imprecise, and also when dealing with discrete distributions. Confidence limits of form
and
are called conservative;[7](p 210) accordingly, one speaks of conservative confidence intervals and, in general, regions.
Desired properties[edit]
When applying standard statistical procedures, there will often be standard ways of constructing confidence intervals. These will have been devised so as to meet certain desirable properties, which will hold given that the assumptions on which the procedure relies are true. These desirable properties may be described as: validity, optimality, and invariance.
Of the three, «validity» is most important, followed closely by «optimality». «Invariance» may be considered as a property of the method of derivation of a confidence interval, rather than of the rule for constructing the interval. In non-standard applications, these same desirable properties would be sought:
Validity[edit]
This means that the nominal coverage probability (confidence level) of the confidence interval should hold, either exactly or to a good approximation.
Optimality[edit]
This means that the rule for constructing the confidence interval should make as much use of the information in the data-set as possible.
Recall that one could throw away half of a dataset and still be able to derive a valid confidence interval. One way of assessing optimality is by the length of the interval so that a rule for constructing a confidence interval is judged better than another if it leads to intervals whose lengths are typically shorter.
Invariance[edit]
In many applications, the quantity being estimated might not be tightly defined as such.
For example, a survey might result in an estimate of the median income in a population, but it might equally be considered as providing an estimate of the logarithm of the median income, given that this is a common scale for presenting graphical results. It would be desirable that the method used for constructing a confidence interval for the median income would give equivalent results when applied to constructing a confidence interval for the logarithm of the median income: Specifically the values at the ends of the latter interval would be the logarithms of the values at the ends of former interval.
Methods of derivation[edit]
For non-standard applications, there are several routes that might be taken to derive a rule for the construction of confidence intervals. Established rules for standard procedures might be justified or explained via several of these routes. Typically a rule for constructing confidence intervals is closely tied to a particular way of finding a point estimate of the quantity being considered.
Summary statistics[edit]
This is closely related to the method of moments for estimation. A simple example arises where the quantity to be estimated is the population mean, in which case a natural estimate is the sample mean. Similarly, the sample variance can be used to estimate the population variance. A confidence interval for the true mean can be constructed centered on the sample mean with a width which is a multiple of the square root of the sample variance.
Likelihood theory[edit]
Estimates can be constructed using the maximum likelihood principle, the likelihood theory for this provides two ways of constructing confidence intervals or confidence regions for the estimates.
Estimating equations[edit]
The estimation approach here can be considered as both a generalization of the method of moments and a generalization of the maximum likelihood approach. There are corresponding generalizations of the results of maximum likelihood theory that allow confidence intervals to be constructed based on estimates derived from estimating equations.[citation needed]
Hypothesis testing[edit]
If hypothesis tests are available for general values of a parameter, then confidence intervals/regions can be constructed by including in the 100 p % confidence region all those points for which the hypothesis test of the null hypothesis that the true value is the given value is not rejected at a significance level of (1 − p) .[7](§ 7.2 (iii))
Bootstrapping[edit]
In situations where the distributional assumptions for the above methods are uncertain or violated, resampling methods allow construction of confidence intervals or prediction intervals. The observed data distribution and the internal correlations are used as the surrogate for the correlations in the wider population.
Central limit theorem[edit]
The central limit theorem is a refinement of the law of large numbers. For a large number of independent identically distributed random variables 



Example[edit]
Suppose {X1, …, Xn} is an independent sample from a normally distributed population with unknown parameters mean μ and variance σ2. Let
Where X is the sample mean, and S2 is the sample variance. Then
has a Student’s t distribution with n − 1 degrees of freedom.[8] Note that the distribution of T does not depend on the values of the unobservable parameters μ and σ2; i.e., it is a pivotal quantity. Suppose we wanted to calculate a 95% confidence interval for μ. Then, denoting c as the 97.5th percentile of this distribution,
Note that «97.5th» and «0.95» are correct in the preceding expressions. There is a 2.5% chance that 





Consequently,
and we have a theoretical (stochastic) 95% confidence interval for μ.
After observing the sample we find values x for X and s for S, from which we compute the confidence interval

In this bar chart, the top ends of the brown bars indicate observed means and the red line segments («error bars») represent the confidence intervals around them. Although the error bars are shown as symmetric around the means, that is not always the case. In most graphs, the error bars do not represent confidence intervals (e.g., they often represent standard errors or standard deviations)
Interpretation[edit]
Various interpretations of a confidence interval can be given (taking the 95% confidence interval as an example in the following).
- The confidence interval can be expressed in terms of a long-run frequency in repeated samples (or in resampling): «Were this procedure to be repeated on numerous samples, the proportion of calculated 95% confidence intervals that encompassed the true value of the population parameter would tend toward 95%.»[9]
- The confidence interval can be expressed in terms of probability with respect to a single theoretical (yet to be realized) sample: «There is a 95% probability that the 95% confidence interval calculated from a given future sample will cover the true value of the population parameter.» [10] This essentially reframes the «repeated samples» interpretation as a probability rather than a frequency. See Neyman construction.
- The confidence interval can be expressed in terms of statistical significance, e.g.: «The 95% confidence interval represents values that are not statistically significantly different from the point estimate at the .05 level«.[11]

Interpretation of the 95% confidence interval in terms of statistical significance.
Common misunderstandings[edit]

Plot of 50 confidence intervals from 50 samples generated from a normal distribution.
See also: § Counterexamples
Confidence intervals and levels are frequently misunderstood, and published studies have shown that even professional scientists often misinterpret them.[12][13][14][15][16][17]
- A 95% confidence level does not mean that for a given realized interval there is a 95% probability that the population parameter lies within the interval (i.e., a 95% probability that the interval covers the population parameter).[18] According to the strict frequentist interpretation, once an interval is calculated, this interval either covers the parameter value or it does not; it is no longer a matter of probability. The 95% probability relates to the reliability of the estimation procedure, not to a specific calculated interval.[19] Neyman himself (the original proponent of confidence intervals) made this point in his original paper:[10]
It will be noticed that in the above description, the probability statements refer to the problems of estimation with which the statistician will be concerned in the future. In fact, I have repeatedly stated that the frequency of correct results will tend to α. Consider now the case when a sample is already drawn, and the calculations have given [particular limits]. Can we say that in this particular case the probability of the true value [falling between these limits] is equal to α? The answer is obviously in the negative. The parameter is an unknown constant, and no probability statement concerning its value may be made…
- Deborah Mayo expands on this further as follows:[20]
It must be stressed, however, that having seen the value [of the data], Neyman–Pearson theory never permits one to conclude that the specific confidence interval formed covers the true value of 0 with either (1 − α)100% probability or (1 − α)100% degree of confidence. Seidenfeld’s remark seems rooted in a (not uncommon) desire for Neyman–Pearson confidence intervals to provide something which they cannot legitimately provide; namely, a measure of the degree of probability, belief, or support that an unknown parameter value lies in a specific interval. Following Savage (1962), the probability that a parameter lies in a specific interval may be referred to as a measure of final precision. While a measure of final precision may seem desirable, and while confidence levels are often (wrongly) interpreted as providing such a measure, no such interpretation is warranted. Admittedly, such a misinterpretation is encouraged by the word ‘confidence’.
- A 95% confidence level does not mean that 95% of the sample data lie within the confidence interval.
- A confidence interval is not a definitive range of plausible values for the sample parameter, though it is often heuristically taken as a range of plausible values.
- A particular confidence level of 95% calculated from an experiment does not mean that there is a 95% probability of a sample parameter from a repeat of the experiment falling within this interval.[16]
Counterexamples[edit]
Since confidence interval theory was proposed, a number of counter-examples to the theory have been developed to show how the interpretation of confidence intervals can be problematic, at least if one interprets them naïvely.
Confidence procedure for uniform location[edit]
Welch[21] presented an example which clearly shows the difference between the theory of confidence intervals and other theories of interval estimation (including Fisher’s fiducial intervals and objective Bayesian intervals). Robinson[22] called this example «[p]ossibly the best known counterexample for Neyman’s version of confidence interval theory.» To Welch, it showed the superiority of confidence interval theory; to critics of the theory, it shows a deficiency. Here we present a simplified version.
Suppose that 

A fiducial or objective Bayesian argument can be used to derive the interval estimate
which is also a 50% confidence procedure. Welch showed that the first confidence procedure dominates the second, according to desiderata from confidence interval theory; for every 


However, when 

Moreover, when the first procedure generates a very short interval, this indicates that 
The two counter-intuitive properties of the first procedure—100% coverage when 

This counter-example is used to argue against naïve interpretations of confidence intervals. If a confidence procedure is asserted to have properties beyond that of the nominal coverage (such as relation to precision, or a relationship with Bayesian inference), those properties must be proved; they do not follow from the fact that a procedure is a confidence procedure.
Confidence procedure for ω2[edit]
Steiger[24] suggested a number of confidence procedures for common effect size measures in ANOVA. Morey et al.[18] point out that several of these confidence procedures, including the one for ω2, have the property that as the F statistic becomes increasingly small—indicating misfit with all possible values of ω2—the confidence interval shrinks and can even contain only the single value ω2 = 0; that is, the CI is infinitesimally narrow (this occurs when 

This behavior is consistent with the relationship between the confidence procedure and significance testing: as F becomes so small that the group means are much closer together than we would expect by chance, a significance test might indicate rejection for most or all values of ω2. Hence the interval will be very narrow or even empty (or, by a convention suggested by Steiger, containing only 0). However, this does not indicate that the estimate of ω2 is very precise. In a sense, it indicates the opposite: that the trustworthiness of the results themselves may be in doubt. This is contrary to the common interpretation of confidence intervals that they reveal the precision of the estimate.
History[edit]
Confidence intervals were introduced by Jerzy Neyman in 1937.[25] Statisticians quickly took to the idea, but adoption by scientists was more gradual. Some authors in medical journals promoted confidence intervals as early as the 1970s. Despite this, confidence intervals were rarely used until the following decade, when they quickly became standard.[26] By the late 1980s, medical journals began to require the reporting of confidence intervals.[27]
See also[edit]
- CLs upper limits (particle physics)
- 68–95–99.7 rule
- Confidence band, an interval estimate for a curve
- Confidence distribution
- Confidence region, a higher dimensional generalization
- Credence (statistics)
- Credible interval, a Bayesian alternative for interval estimation
- Cumulative distribution function-based nonparametric confidence interval
- Error bar – Graphical representations of the variability of data
- Estimation statistics – Data analysis approach in frequentist statistics
- Margin of error, the CI halfwidth
- p-value – Function of the observed sample results
- Prediction interval, an interval estimate for a random variable
- Probable error
- Robust confidence intervals
Confidence interval for specific distributions[edit]
- Confidence interval for binomial distribution
- Confidence interval for exponent of the power law distribution
- Confidence interval for mean of the exponential distribution
- Confidence interval for mean of the Poisson distribution
- Confidence intervals for mean and variance of the normal distribution
References[edit]
- ^ Zar, Jerrold H. (199). Biostatistical Analysis (4th ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 43–45. ISBN 978-0130815422. OCLC 39498633.
- ^ a b c Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). «A Modern Introduction to Probability and Statistics». Springer Texts in Statistics. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN 1431-875X.
- ^ Illowsky, Barbara. Introductory statistics. Dean, Susan L., 1945-, Illowsky, Barbara., OpenStax College. Houston, Texas. ISBN 978-1-947172-05-0. OCLC 899241574.
- ^ Hazra, Avijit (October 2017). «Using the confidence interval confidently». Journal of Thoracic Disease. 9 (10): 4125–4130. doi:10.21037/jtd.2017.09.14. ISSN 2072-1439. PMC 5723800. PMID 29268424.
- ^ Khare, Vikas; Nema, Savita; Baredar, Prashant (2020). Ocean Energy Modeling and Simulation with Big Data Computational Intelligence for System Optimization and Grid Integration. ISBN 978-0-12-818905-4. OCLC 1153294021.
- ^ Roussas, George G. (1997). A Course in Mathematical Statistics (2nd ed.). Academic Press. p. 397.
- ^ a b Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall.
- ^ Rees. D.G. (2001) Essential Statistics, 4th Edition, Chapman and Hall/CRC. ISBN 1-58488-007-4 (Section 9.5)
- ^ Cox D.R., Hinkley D.V. (1974) Theoretical Statistics, Chapman & Hall, p49, p209
- ^ a b Neyman, J. (1937). «Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability». Philosophical Transactions of the Royal Society A. 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. doi:10.1098/rsta.1937.0005. JSTOR 91337.
- ^ Cox D.R., Hinkley D.V. (1974) Theoretical Statistics, Chapman & Hall, pp 214, 225, 233
- ^ Kalinowski, Pawel (2010). «Identifying Misconceptions about Confidence Intervals» (PDF). Retrieved 2021-12-22.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2014-09-16.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Hoekstra, R., R. D. Morey, J. N. Rouder, and E-J. Wagenmakers, 2014. Robust misinterpretation of confidence intervals. Psychonomic Bulletin Review, in press. [1]
- ^ Scientists’ grasp of confidence intervals doesn’t inspire confidence, Science News, July 3, 2014
- ^ a b Greenland, Sander; Senn, Stephen J.; Rothman, Kenneth J.; Carlin, John B.; Poole, Charles; Goodman, Steven N.; Altman, Douglas G. (April 2016). «Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations». European Journal of Epidemiology. 31 (4): 337–350. doi:10.1007/s10654-016-0149-3. ISSN 0393-2990. PMC 4877414. PMID 27209009.
- ^ Helske, Jouni; Helske, Satu; Cooper, Matthew; Ynnerman, Anders; Besancon, Lonni (2021-08-01). «Can Visualization Alleviate Dichotomous Thinking? Effects of Visual Representations on the Cliff Effect». IEEE Transactions on Visualization and Computer Graphics. Institute of Electrical and Electronics Engineers (IEEE). 27 (8): 3397–3409. arXiv:2002.07671. doi:10.1109/tvcg.2021.3073466. ISSN 1077-2626. PMID 33856998. S2CID 233230810.
- ^ a b Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). «The Fallacy of Placing Confidence in Confidence Intervals». Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
- ^ «1.3.5.2. Confidence Limits for the Mean». nist.gov. Archived from the original on 2008-02-05. Retrieved 2014-09-16.
- ^ Mayo, D. G. (1981) «In defence of the Neyman–Pearson theory of confidence intervals», Philosophy of Science, 48 (2), 269–280. JSTOR 187185
- ^ Welch, B. L. (1939). «On Confidence Limits and Sufficiency, with Particular Reference to Parameters of Location». The Annals of Mathematical Statistics. 10 (1): 58–69. doi:10.1214/aoms/1177732246. JSTOR 2235987.
- ^ Robinson, G. K. (1975). «Some Counterexamples to the Theory of Confidence Intervals». Biometrika. 62 (1): 155–161. doi:10.2307/2334498. JSTOR 2334498.
- ^ Pratt, J. W. (1961). «Book Review: Testing Statistical Hypotheses. by E. L. Lehmann». Journal of the American Statistical Association. 56 (293): 163–167. doi:10.1080/01621459.1961.10482103. JSTOR 2282344.
- ^ Steiger, J. H. (2004). «Beyond the F test: Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis». Psychological Methods. 9 (2): 164–182. doi:10.1037/1082-989x.9.2.164. PMID 15137887.
- ^ [Neyman, J., 1937. Outline of a theory of statistical estimation based on the classical theory of probability. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 236(767), pp.333-380]
- ^ Altman, Douglas G. (1991). «Statistics in medical journals: Developments in the 1980s». Statistics in Medicine. 10 (12): 1897–1913. doi:10.1002/sim.4780101206. ISSN 1097-0258. PMID 1805317.
- ^ Sandercock, Peter A.G. (2015). «Short History of Confidence Intervals». Stroke. Ovid Technologies (Wolters Kluwer Health). 46 (8): e184-7. doi:10.1161/strokeaha.115.007750. ISSN 0039-2499. PMID 26106115.
Bibliography[edit]
- Fisher, R.A. (1956) Statistical Methods and Scientific Inference. Oliver and Boyd, Edinburgh. (See p. 32.)
- Freund, J.E. (1962) Mathematical Statistics Prentice Hall, Englewood Cliffs, NJ. (See pp. 227–228.)
- Hacking, I. (1965) Logic of Statistical Inference. Cambridge University Press, Cambridge. ISBN 0-521-05165-7
- Keeping, E.S. (1962) Introduction to Statistical Inference. D. Van Nostrand, Princeton, NJ.
- Kiefer, J. (1977). «Conditional Confidence Statements and Confidence Estimators (with discussion)». Journal of the American Statistical Association. 72 (360a): 789–827. doi:10.1080/01621459.1977.10479956. JSTOR 2286460.
- Mayo, D. G. (1981) «In defence of the Neyman–Pearson theory of confidence intervals», Philosophy of Science, 48 (2), 269–280. JSTOR 187185
- Neyman, J. (1937) «Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability» Philosophical Transactions of the Royal Society of London A, 236, 333–380. (Seminal work.)
- Robinson, G.K. (1975). «Some Counterexamples to the Theory of Confidence Intervals». Biometrika. 62 (1): 155–161. doi:10.1093/biomet/62.1.155. JSTOR 2334498.
- Savage, L. J. (1962), The Foundations of Statistical Inference. Methuen, London.
- Smithson, M. (2003) Confidence intervals. Quantitative Applications in the Social Sciences Series, No. 140. Belmont, CA: SAGE Publications. ISBN 978-0-7619-2499-9.
- Mehta, S. (2014) Statistics Topics ISBN 978-1-4992-7353-3
- «Confidence estimation», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). «The fallacy of placing confidence in confidence intervals». Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.
External links[edit]
- The Exploratory Software for Confidence Intervals tutorial programs that run under Excel
- Confidence interval calculators for R-Squares, Regression Coefficients, and Regression Intercepts
- Weisstein, Eric W. «Confidence Interval». MathWorld.
- CAUSEweb.org Many resources for teaching statistics including Confidence Intervals.
- An interactive introduction to Confidence Intervals
- Confidence Intervals: Confidence Level, Sample Size, and Margin of Error by Eric Schulz, the Wolfram Demonstrations Project.
- Confidence Intervals in Public Health. Straightforward description with examples and what to do about small sample sizes or rates near 0.
Погрешность и доверительный интервал: в чем разница?
17 авг. 2022 г.
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
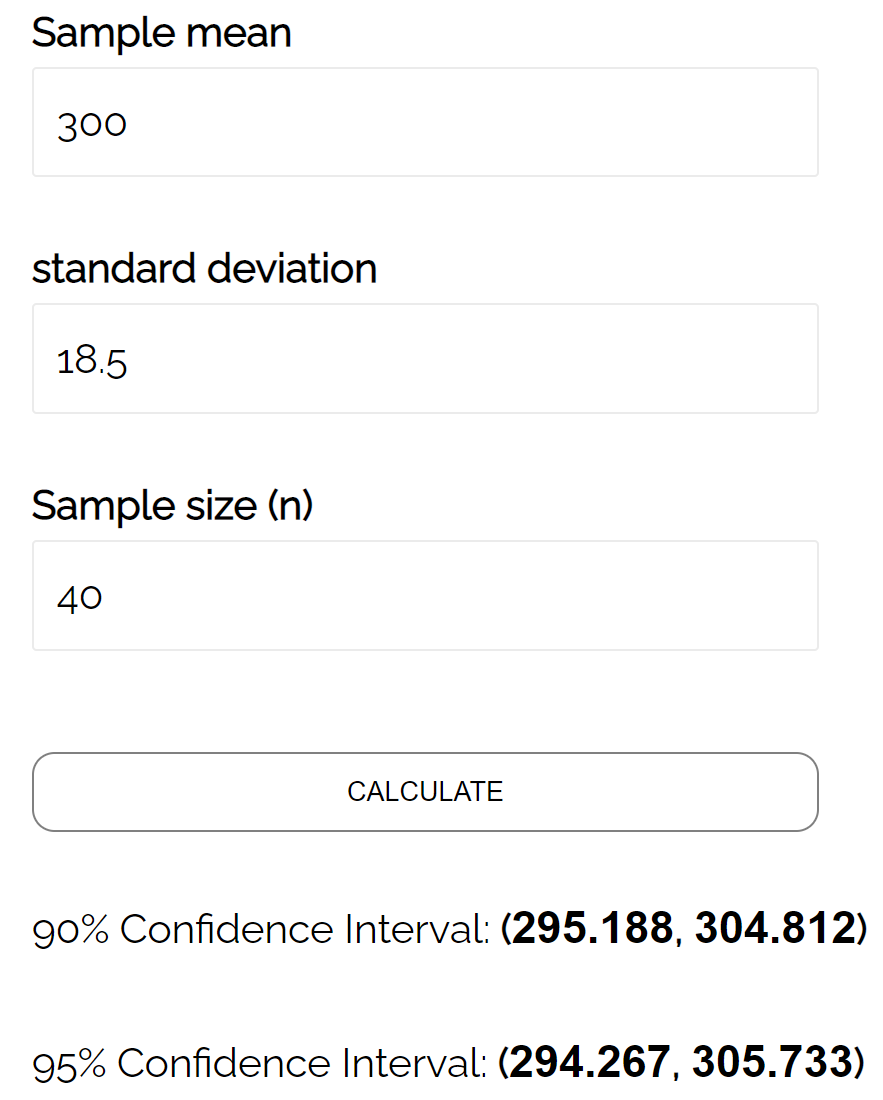
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:

95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 — alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA — Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
 Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) — это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.
Доверительный интервал
Что такое доверительный интервал:
Это оценка диапазона, используемого в статистике, который содержит параметр совокупности. Этот неизвестный параметр популяции находится в выборочной модели, рассчитанной на основе собранных данных .
Пример: среднее значение выборки x̅ может соответствовать или не соответствовать истинному среднему значению для населения µ. Для этого можно рассмотреть диапазон выборочных средств, в которых может содержаться это среднее значение. Чем длиннее этот интервал, тем больше вероятность этого.
Доверительный интервал выражается в процентах, обозначенных уровнем достоверности, причем 90%, 95% и 99% являются наиболее указанными. Например, на изображении ниже мы имеем 90% доверительный интервал между его верхним и нижним пределами (a и -a ).
 Пример 90% доверительного интервала между его верхним (а) и нижним (-а) пределами.
Пример 90% доверительного интервала между его верхним (а) и нижним (-а) пределами.
Доверительный интервал является одним из наиболее важных понятий в рамках проверки гипотез в статистике, поскольку он используется в качестве меры неопределенности. Термин был введен польским математиком и статистиком Ежи Нейманом в 1937 году.
Какова актуальность доверительного интервала?
Доверительный интервал важен для указания границы неопределенности (или неточности) в сравнении с выполненными расчетами. Этот расчет использует выборку исследования для оценки фактического размера результата в исходной популяции.
Расчет доверительного интервала — это стратегия, которая учитывает выборку ошибок. Размер результата вашего исследования и ваш доверительный интервал характеризуют предполагаемые значения для исходной популяции.
Чем уже доверительный интервал, тем больше вероятность того, что процент исследуемой совокупности представляет реальное число исходной совокупности, что дает большую уверенность в отношении результата исследуемого объекта.
Как интерпретировать доверительный интервал?
Правильная интерпретация доверительного интервала, вероятно, является наиболее сложным аспектом этой статистической концепции. Примером наиболее распространенной интерпретации концепции является следующее:
Существует 95% вероятность того, что в будущем истинное значение параметра совокупности (например, среднее значение) попадет в диапазон X (нижний предел) и Y (верхний предел).
Таким образом, доверительный интервал интерпретируется следующим образом: он на 95% уверен, что интервал между X (нижняя граница) и Y (верхняя граница) содержит истинное значение параметра совокупности.
Было бы совершенно неверно утверждать, что: существует 95% вероятность того, что интервал между X (нижняя граница) и Y (верхняя граница) содержит реальное значение параметра совокупности.
Вышеприведенное утверждение является наиболее распространенным заблуждением о доверительном интервале. После расчета статистического диапазона он может содержать только параметр совокупности или нет.
Тем не менее, интервалы могут варьироваться между выборками, в то время как истинный параметр популяции одинаков независимо от выборки.
Следовательно, доверительный интервал доверительного интервала может быть сделан только в случае, когда доверительные интервалы пересчитываются для количества выборок.
Этапы расчета доверительного интервала
Диапазон рассчитывается с использованием следующих шагов:
- Соберите пример данных: n ;
- Рассчитать среднее значение выборки x̅;
- Определить, является ли стандартное отклонение популяции ( σ ) известным или неизвестным;
- Если стандартное отклонение популяции известно, z- точка может использоваться для соответствующего уровня достоверности;
- Если стандартное отклонение популяции неизвестно, мы можем использовать статистику t для соответствующего уровня достоверности;
- Таким образом, нижний и верхний пределы доверительного интервала находятся по следующим формулам:
а) Стандартное отклонение известной популяции :

Формула для расчета стандартного отклонения известной совокупности.
б) стандартное отклонение неизвестной популяции :

Формула для расчета стандартного отклонения неизвестной популяции.
Практический пример доверительного интервала
Клиническое исследование оценило связь между наличием астмы и риском развития обструктивного апноэ сна у взрослых.
Некоторые взрослые были случайным образом набраны из списка государственных служащих, за которыми следили в течение четырех лет.
Участники с астмой, по сравнению с теми, у кого нет, имели более высокий риск развития апноэ через четыре года.
При проведении клинических исследований, подобных этому примеру, подмножество интересующей группы населения обычно привлекается для повышения эффективности исследования (меньше затрат и меньше времени).
Эта подгруппа лиц, изучаемая популяция, состоит из тех, кто соответствует критериям включения и согласен участвовать в исследовании, как показано на рисунке ниже.
 Пояснительная графика населения, изученного на примере.
Пояснительная графика населения, изученного на примере.
Затем исследование завершается и рассчитывается величина эффекта (например, средняя разница или относительный риск ), чтобы ответить на вопрос исследования.
Этот процесс, называемый выводом, включает использование данных, собранных у исследуемой совокупности, для оценки величины фактического воздействия на представляющую интерес совокупность, то есть совокупность происхождения.
В приведенном примере исследователи набрали случайную выборку государственных служащих (исходная популяция), которые имели право и согласились участвовать в исследовании (исследуемая популяция), и сообщили, что астма увеличивает риск развития апноэ в исследуемой популяции.
Чтобы учесть ошибку выборки из-за набора только подгруппы представляющего интерес населения, они также рассчитали 95% доверительный интервал (около оценки) от 1, 06 до 1, 82, что указывает на вероятность 95 %, что истинный относительный риск в исходной популяции будет между 1, 06 и 1, 82 .
Доверительный интервал для среднего
Когда у человека есть информация о стандартном отклонении населения, он может рассчитать доверительный интервал для среднего или среднего значения этого населения.
Когда измеряемая статистическая характеристика (например, доход, IQ, цена, рост, количество или вес) является числовой, в большинстве случаев оценивается, что найдено среднее значение для населения.
Таким образом, мы пытаемся найти среднее значение популяции ( μ ), используя среднее значение выборки ( x̅ ), с пределом погрешности. Результат этого расчета называется доверительным интервалом для среднего населения .
Когда стандартное отклонение популяции известно, формула для доверительного интервала (CI) для среднего значения популяции:

где:
- х̅ — среднее значение по выборке;
- σ — стандартное отклонение населения;
- n — размер выборки;
- Ζ * представляет подходящее значение стандартного нормального распределения для желаемого уровня достоверности.
Ниже приведены значения для различных уровней достоверности ( Ζ * ):
| Уровень доверия | Значение Z * — |
|---|---|
| 80% | 1:28 |
| 90% | 1.645 (обычный) |
| 95% | 1, 96 |
| 98% | 2:33 |
| 99% | 2:58 |
В таблице выше приведены значения z * для предоставленных уровней достоверности. Обратите внимание, что эти значения получены из стандартного нормального распределения (Z-).
Область между каждым значением z * и отрицательным значением этого значения является (приблизительным) процентом достоверности. Например, область между z * = 1, 28 и z = -1, 28 составляет приблизительно 0, 80. Следовательно, эта таблица также может быть расширена до других доверительных процентов. В таблице указаны только наиболее часто используемые проценты доверия.
Смотрите также значение гипотезы.
Доверительный интервал – интервал значений, в пределах которого, как можно надеяться, находится параметр генеральной совокупности.
Наша надежда выражается доверительной вероятностью – вероятность, с которой доверительный интервал «захватит» истинное значение параметра генеральной совокупности. Чем выше доверительная вероятность, тем шире доверительный интервал. Значение доверительной вероятности выбирает сам исследователь. Обычно это 0,9; 0,95; 0,99.
Если статистическая оценка параметра закона распределения случайной величины ![]() характеризуется двумя числами – концами интервала, то такая оценка называется интервальной.
характеризуется двумя числами – концами интервала, то такая оценка называется интервальной.
Интервал ![]() , в который попадает оцениваемый параметр
, в который попадает оцениваемый параметр ![]() с заданной надежностью
с заданной надежностью ![]() (вероятностью), называется доверительным интервалом, а вероятность
(вероятностью), называется доверительным интервалом, а вероятность ![]() — доверительной вероятностью или уровнем надежности. Число
— доверительной вероятностью или уровнем надежности. Число ![]() называется уровнем значимости.
называется уровнем значимости.
Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.
Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции. Если мы установим больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он «накрывает» неизвестное среднее популяции, и наоборот.
Доверительный интервал применяется в случае сравнительно небольшого объема выборки, когда предполагается, что надежность точечной оценки может быть невысокой.
Доверительный интервал симметричен относительно оценки ![]() истинного значения параметра
истинного значения параметра ![]() и имеет вид
и имеет вид ![]() , где
, где ![]() — предельная ошибка выборки (наибольшее отклонение выборочного значения параметра от его истинного значения). Это означает, что неравенства
— предельная ошибка выборки (наибольшее отклонение выборочного значения параметра от его истинного значения). Это означает, что неравенства ![]() выполняются с вероятностью
выполняются с вероятностью ![]() .
.
Для доверительного интервала ![]() половина его длины
половина его длины ![]() называется точностью интервального оценивания.
называется точностью интервального оценивания.
Если выполняется соотношение ![]() , то число
, то число ![]() называется точностью, а число
называется точностью, а число ![]() — надежностью оценки
— надежностью оценки ![]() генеральной числовой характеристики
генеральной числовой характеристики ![]() .
.
2. Доверительный интервал для оценки генеральной средней
Рассмотрим построение доверительного интервала для оценки математического ожидания.
Пусть ![]() — выборка объема
— выборка объема ![]() из генеральной совокупности объема
из генеральной совокупности объема ![]() ;
; ![]() — выборочное среднее;
— выборочное среднее; ![]() — выборочное среднее квадратическое отклонение.
— выборочное среднее квадратическое отклонение.
Доверительный интервал уровня надежности ![]() для математического ожидания (генеральной средней)
для математического ожидания (генеральной средней) ![]() имеет вид
имеет вид
![]() ,
,
где ![]() — предельная ошибка выборки, которая зависит от объема выборки
— предельная ошибка выборки, которая зависит от объема выборки ![]() , доверительной вероятности
, доверительной вероятности ![]() и равна половине доверительного интервала.
и равна половине доверительного интервала.
Интервальной оценкой с надежностью ![]() генеральной средней
генеральной средней ![]() в случае нормального распределения генеральной совокупности при неизвестном среднем квадратическом отклонении
в случае нормального распределения генеральной совокупности при неизвестном среднем квадратическом отклонении ![]() служит доверительный интервал:
служит доверительный интервал:
![]()
где ![]() — выборочное среднее;
— выборочное среднее; ![]() — исправленное выборочное среднее квадратическое отклонение;
— исправленное выборочное среднее квадратическое отклонение; ![]() — параметр, который находится по таблице распределения Стьюдента для (
— параметр, который находится по таблице распределения Стьюдента для (![]() ) степеней свободы и доверительной вероятности
) степеней свободы и доверительной вероятности ![]() .
.
Интервальной оценкой с надежностью ![]() генеральной средней
генеральной средней ![]() в случае нормального распределения генеральной совокупности при известном среднем квадратическом отклонении
в случае нормального распределения генеральной совокупности при известном среднем квадратическом отклонении ![]() служит доверительный интервал:
служит доверительный интервал:
![]()
где ![]() — выборочное среднее;
— выборочное среднее; ![]() — выборочное среднее квадратическое отклонение;
— выборочное среднее квадратическое отклонение; ![]() — значение аргумента функции Лапласа
— значение аргумента функции Лапласа ![]() , при котором
, при котором ![]() ;
; ![]() — объем выборки.
— объем выборки.
Выводы. Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится «истинное» (неизвестное) среднее значение признака.
Хорошо известно, например, что чем «неопределенней» прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным.
Пример. Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины, если известны ее среднее квадратическое отклонение ![]() , выборочная средняя
, выборочная средняя ![]() и объем выборки
и объем выборки ![]() .
.
Воспользуемся формулой ![]() . Значение
. Значение ![]() найдем по таблице значений функции Лапласа
найдем по таблице значений функции Лапласа  , с учетом того, что
, с учетом того, что ![]() , т.е.
, т.е. ![]() . Находим по таблице для значения функции
. Находим по таблице для значения функции ![]() значение аргумента
значение аргумента ![]() . Получим доверительный интервал:
. Получим доверительный интервал:
![]() ; или
; или ![]() .
.
Тестовые задания
1. Длина доверительного интервала уменьшается с увеличением:
1) выборочных значений 2) объема выборки
3) доверительной вероятности 4) выборочного среднего
2. Длина доверительного интервала с увеличением объема выборки:
1) уменьшается; 2) увеличивается;
3) не изменяется; 4) колеблется.
3. Длина доверительного интервала с увеличением доверительной вероятности:
1) изменяется, 2) уменьшается,
3) увеличивается, 4) постоянна.
4. Отметьте два правильных ответа. Символы ![]() и
и ![]() в формуле доверительного интервала означают:
в формуле доверительного интервала означают:
1) оценка параметра; 2) доверительный интервал;
3) объем выборки; 4) доверительная вероятность.
Ответы. 1. 2). 2. 1 3. 2). 4. 4) и 3).
контрольные Вопросы
-
Что понимается под термином «интервальная оценка параметра распределения»?
-
Дайте определение доверительного интервала.
-
Что такое точность оценки и надежность оценки?
-
Что называется доверительной вероятностью? Какие значения она принимает?
-
Как изменится длина доверительного интервала, если увеличить: 1) объем выборки, 2) доверительную вероятность? Ответ обоснуйте.
-
Запишите формулу для нахождения доверительного интервала математического ожидания нормально распределенной случайной величины, если генеральная дисперсия: 1) известна; 2) неизвестна.
Часть 3. проверка статистических гипотез
Тема 1. Основные понятия теории принятия статистического решения
1. Нулевая и альтернативная статистические гипотезы
Статистической гипотезой называется такое предположение о виде или свойствах генерального или выборочного распределений, которое можно проверить статистическими методами на основе имеющейся выборки.
Сущность проверки статистической гипотезы заключается в том, чтобы установить:
-
согласуются ли экспериментальные данные и выдвинутая гипотеза;
-
допустимо ли отнести расхождение между гипотезой и результатом статистического анализа экспериментальных данных за счет случайных причин.
По содержанию статистические гипотезы подразделяются на виды:
-
о законе распределения генеральной совокупности (например, гипотеза о том, что количество ошибок внимания у младших школьников имеет равномерное распределение);
-
о числовых значениях параметров случайной величины (например, гипотеза о том, что среднее количество правильных ответов студентов контрольной группы на десять тестовых вопросов по теме равно восьми);
-
об однородности выборок (т.е. принадлежности их одной и той же генеральной совокупности);
-
о виде модели, описывающей статистическую зависимость между несколькими признаками (например, предположение о том, что связь между успешностью обучения математики
 и показателем невербального интеллекта учащихся
и показателем невербального интеллекта учащихся  линейная, прямо пропорциональная).
линейная, прямо пропорциональная).
Проверяемую гипотезу обычно называют нулевой гипотезой и обозначают ![]() . В психологии принято считать, что
. В психологии принято считать, что ![]() – это гипотеза о сходстве, т.е. об отсутствии различий. Другими словами, это предположение о том, что все события, интересующие исследователя, произошли случайно, естественным образом. Обозначается нулевая гипотеза как
– это гипотеза о сходстве, т.е. об отсутствии различий. Другими словами, это предположение о том, что все события, интересующие исследователя, произошли случайно, естественным образом. Обозначается нулевая гипотеза как ![]() .
.
Пример. Пусть исследователь сопоставляет значения некоторого признака развитости интеллекта (например, уровень вербального мышления) у двух групп подростков — из полных семей (первая группа) и неполных семей (вторая группа). Обозначим через ![]() и
и ![]() случайные величины, показывающие значения признака (уровня вербального мышления). Тогда нулевая гипотеза означает предположение, что различий в показателе интеллекта у двух групп подростков.
случайные величины, показывающие значения признака (уровня вербального мышления). Тогда нулевая гипотеза означает предположение, что различий в показателе интеллекта у двух групп подростков.
Гипотезе ![]() может быть противопоставлена альтернативная, или конкурирующая, гипотеза
может быть противопоставлена альтернативная, или конкурирующая, гипотеза ![]() , являющаяся логическим отрицанием
, являющаяся логическим отрицанием ![]() . В паре они составляют две возможности выбора, осуществляемого в задачах проверки статистических гипотез. В альтернативной гипотезе
. В паре они составляют две возможности выбора, осуществляемого в задачах проверки статистических гипотез. В альтернативной гипотезе ![]() предполагается, что события, интересующие исследователя, случайным образом произойти не могли, и имело место воздействие некоторого фактора.
предполагается, что события, интересующие исследователя, случайным образом произойти не могли, и имело место воздействие некоторого фактора.
Если нулевая гипотеза ![]() говорит о «сходстве», то альтернативная гипотеза
говорит о «сходстве», то альтернативная гипотеза ![]() – гипотеза «о различии », точнее, о значимости различий. Например, альтернативная гипотеза о том, что контрольные и экспериментальные группы различаются между собой по каким-либо значимым характеристикам.
– гипотеза «о различии », точнее, о значимости различий. Например, альтернативная гипотеза о том, что контрольные и экспериментальные группы различаются между собой по каким-либо значимым характеристикам.










![{displaystyle left[{bar {x}}-{frac {cs}{sqrt {n}}},{bar {x}}+{frac {cs}{sqrt {n}}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a90d533cc8ae393c6949495405824f49865b80)
![{displaystyle {bar {X}}pm {begin{cases}{dfrac {|X_{1}-X_{2}|}{2}}&{text{if }}|X_{1}-X_{2}|<1/2[8pt]{dfrac {1-|X_{1}-X_{2}|}{2}}&{text{if }}|X_{1}-X_{2}|geq 1/2.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80260117bd9ee1f05d0928e0b5697663a297ecbc)

