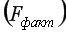15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
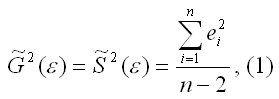
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
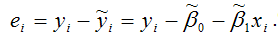
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
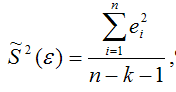
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
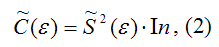
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
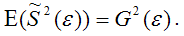
Доказательство. Примем без доказательства справедливость следующих равенств:
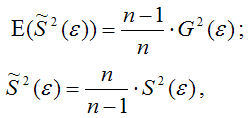
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
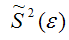
– выборочная оценка дисперсии случайной ошибки.
Тогда:
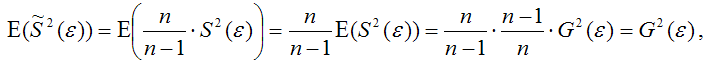
т. е.
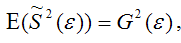
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
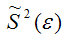
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
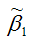
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
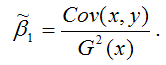
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
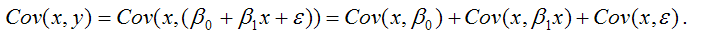
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
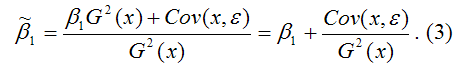
Таким образом, МНК-оценка
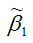
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
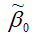
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
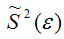
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Пример 9.1. По 15 сельскохозяйственным предприятиям (табл. 9.1) известны:  – количество техники на единицу посевной площади (ед/га) и
– количество техники на единицу посевной площади (ед/га) и  – объем выращенной продукции (тыс. ден. ед.). Необходимо:
– объем выращенной продукции (тыс. ден. ед.). Необходимо:
1) определить зависимость  от
от 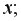
2) построить корреляционные поля и график уравнения линейной регрессии на
на 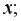
3) сделать вывод о качестве модели и рассчитать прогнозное значение 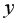 при прогнозном значении
при прогнозном значении 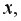 составляющем 112% от среднего уровня.
составляющем 112% от среднего уровня.
Таблица 9.1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
x |
2,97 |
1,65 |
9,02 |
4,95 |
3,63 |
6,38 |
3,3 |
7,81 |
1,32 |
11,44 |
5,39 |
5,72 |
12,65 |
10,34 |
7,15 |
|
y |
121 |
77 |
341 |
132 |
82,5 |
187 |
110 |
198 |
33 |
484 |
209 |
165 |
429 |
341 |
253 |
Решение:
1) В Excel составим вспомогательную таблицу 9.2.
Таблица 9.2
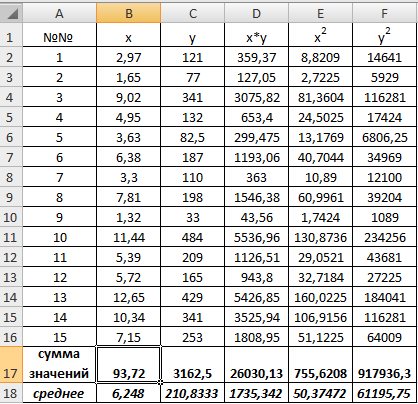
Рис. 9.1. Таблица для расчета промежуточных значений
Вычислим количество измерений 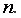 Для этого в ячейку В19 поместим =СЧЁТ(A2:A16).
Для этого в ячейку В19 поместим =СЧЁТ(A2:A16).
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех  (ячейка В17) и
(ячейка В17) и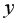 (ячейка С17).
(ячейка С17).
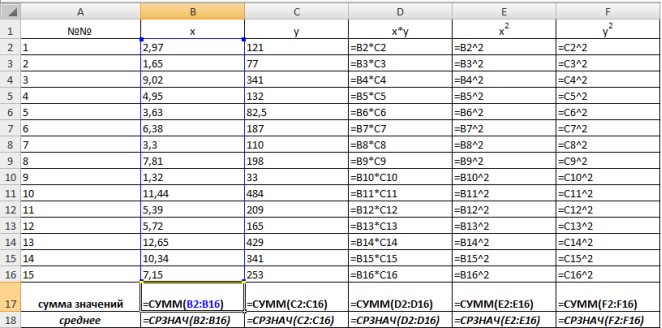
Рис. 9.2. Расчет суммы значений и средних
Для вычисления средних значений используем встроенную функцию MS Excel СРЗНАЧ(), в скобках указывается диапазон значений для определения средней. Таким образом, средний объем выращенной продукции по 15 хозяйствамсоставляет 210,833 тыс.ден. ед., а средние количество техники – 6,248ед/га.
Для заполнения столбцов D, E, Fвведем формулувычисления произведения: в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
Для вычисления выборочной ковариациимежду 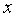 и
и 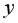 используем формулу
используем формулу 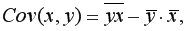 т.е. в ячейку B21 поместим =D18-B18*C18 и получим 418,055 (рис. 9.3).
т.е. в ячейку B21 поместим =D18-B18*C18 и получим 418,055 (рис. 9.3).
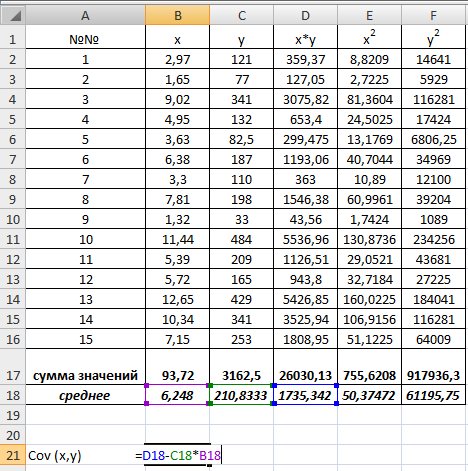
Рис. 9.3. Вычисление 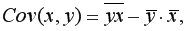
Выборочную дисперсиюдля  найдем по формуле
найдем по формуле 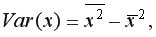 для этого в ячейку B22 поместим =E18-B18^2 (^- знак указывающий возведение в степень) и получим 11,337. Аналогично определяем
для этого в ячейку B22 поместим =E18-B18^2 (^- знак указывающий возведение в степень) и получим 11,337. Аналогично определяем 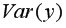 =16745,05556 (рис. 9.4)
=16745,05556 (рис. 9.4)
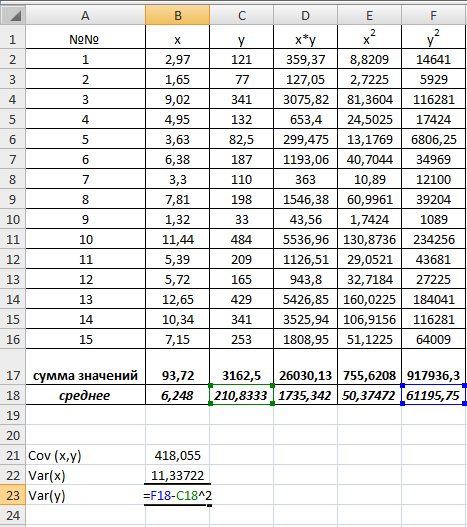
Рис. 9.4. Вычисление Var(x) и Var (y)
Далее используя стандартную функцию MS Excel «КОРРЕЛ» вычисляем значение линейного коэффициента корреляции для нашей задачи функция будет иметь вид «=КОРРЕЛ(B2:B16;C2:C16)», а значение rxy=0,96. Полученное значение коэффициента корреляции указывает на прямую и сильную связь наличия техники и объемов выращенной продукции.
Находим выборочный коэффициент линейной регрессии 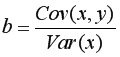 =36,87; параметр
=36,87; параметр 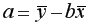 =-17,78. Значит, уравнение парной линейной регрессии имеет вид
=-17,78. Значит, уравнение парной линейной регрессии имеет вид 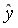 =-17,78+36,87
=-17,78+36,87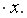
Коэффициент 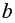 показывает, что при увеличении количества техники на 1 ед/га объем выращенной продукции
показывает, что при увеличении количества техники на 1 ед/га объем выращенной продукции 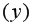 в среднем увеличится на 36,875 тыс. ден. ед. (рис. 9.5)
в среднем увеличится на 36,875 тыс. ден. ед. (рис. 9.5)
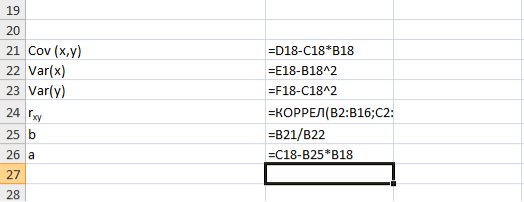
Рис. 9.5. Расчет параметров уравнения регрессии.
Таким образом, уравнение регрессии будет иметь вид: 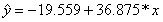 .
.
Подставляем в полученное уравнение фактические значения x (количество техники) находим теоретические значения объемов выращенной продукции (рис. 9.6).
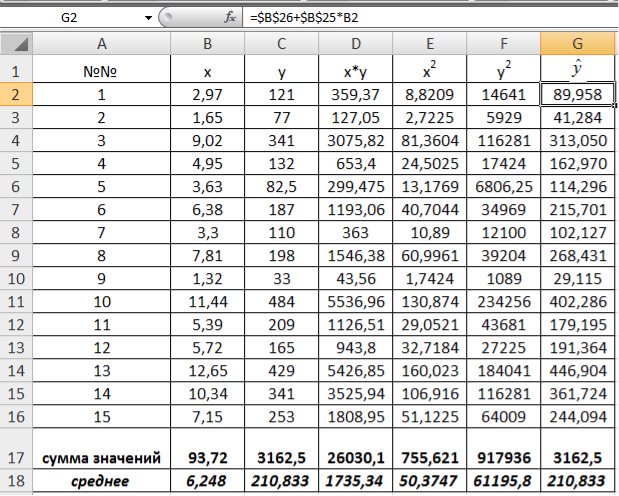
Рис. 9.6. Расчет теоретических значений объемов выращенной продукции
Используя Мастер диаграмм строим корреляционные поля (выделяя столбцы со значениями  и
и  ) и уравнение линейной регрессии (выделяя столбцы со значениями
) и уравнение линейной регрессии (выделяя столбцы со значениями  и
и  ). Выбираем тип диаграммы – Точечная В полученной диаграмме заполняем нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим график представленный на рис. 9.7.
). Выбираем тип диаграммы – Точечная В полученной диаграмме заполняем нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим график представленный на рис. 9.7.
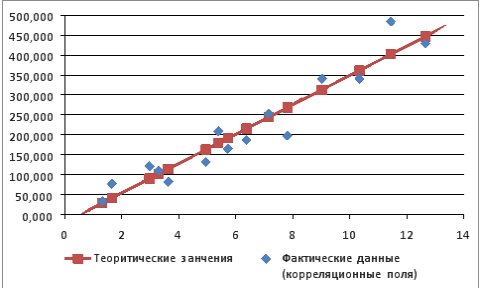
Рис. 9.7. График зависимости объема выращенной продукции от количества техники
Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации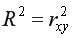 =0,92, который показывает, что изменение затрат на выпуск продукции
=0,92, который показывает, что изменение затрат на выпуск продукции 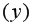 на 92% объясняется изменением объема произведенной продукции
на 92% объясняется изменением объема произведенной продукции 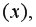 а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;
а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим разность фактического и теоретического значений 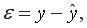 а в столбце I – выражение
а в столбце I – выражение 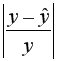 . Обращаем Ваше внимание, что для вычисления значения по модулю используется стандартная функция MS Excel «ABS». При умножении среднего значения (ячейка I18) на 100% получим
. Обращаем Ваше внимание, что для вычисления значения по модулю используется стандартная функция MS Excel «ABS». При умножении среднего значения (ячейка I18) на 100% получим 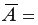 18,2%. Следовательно, в среднем теоретические значения
18,2%. Следовательно, в среднем теоретические значения отклоняются от фактических
отклоняются от фактических 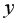 на 18,2%(рис. 1.8).
на 18,2%(рис. 1.8).
С помощью 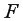 -критерия Фишераоценим значимость уравнения регрессии в целом:
-критерия Фишераоценим значимость уравнения регрессии в целом: 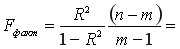 150,74.
150,74.
На уровне значимости 0,05 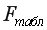 =4,67 определяем c помощью встроенной статистической функции FРАСПОБР (рис. 1.9). При этом необходимо помнить, что «Степени_свободы1» это знаменатель
=4,67 определяем c помощью встроенной статистической функции FРАСПОБР (рис. 1.9). При этом необходимо помнить, что «Степени_свободы1» это знаменатель 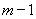 , а «Степени_свободы2» – числитель
, а «Степени_свободы2» – числитель 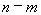 , где
, где 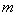 – число параметров в уравнении регрессии (у нас 2), n – число исходных пар значений (у нас 15).
– число параметров в уравнении регрессии (у нас 2), n – число исходных пар значений (у нас 15).
Так как 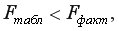 то уравнение регрессии значимо при
то уравнение регрессии значимо при 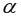 =0,05.
=0,05.
Рис. 9.8. Определение коэффициента детерминации и средней ошибки апроксимации
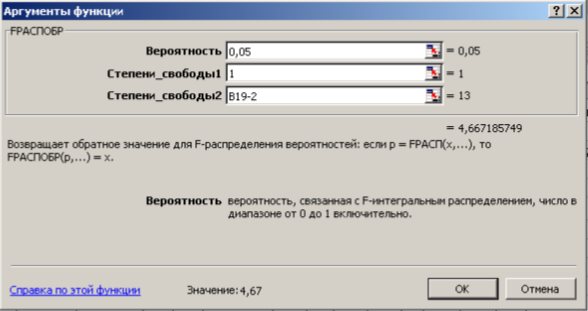
Рис. 9.9. Диалоговое окно функции FРАСПОБР
Далее определяем средний коэффициент эластичности по формуле.  Найденное
Найденное 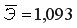 показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1,093%.
показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1,093%.
Рассчитаем прогнозное значение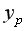 путем подстановки в уравнение регрессии
путем подстановки в уравнение регрессии 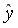 =-19,559+36,8746
=-19,559+36,8746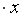 прогнозного значения фактора
прогнозного значения фактора 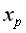 =
=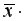 1,12=6,248*1,12=6,9978. Получим
1,12=6,248*1,12=6,9978. Получим 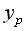 =238,48. Следовательно, при количестве техники в количестве 6,9978ед/гаобъем выпущенной продукции составит 238,48 тыс. ден. ед.
=238,48. Следовательно, при количестве техники в количестве 6,9978ед/гаобъем выпущенной продукции составит 238,48 тыс. ден. ед.
Найдем остаточную дисперсию, для этого вычислим сумму квадратов разности фактического и теоретического значений. 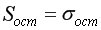 =39,166 поместив следующую формулу =КОРЕНЬ(J17/(B19-2))в ячейку H21 (рис. 9.10).
=39,166 поместив следующую формулу =КОРЕНЬ(J17/(B19-2))в ячейку H21 (рис. 9.10).
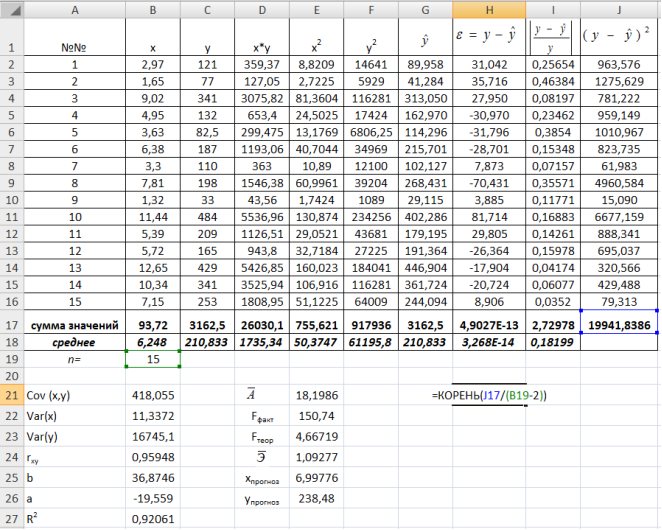
Рис. 9.10. Определение остаточной дисперсии
Средняя стандартная ошибка прогноза:
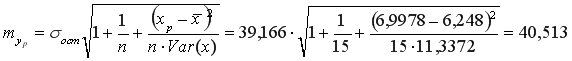
На уровне значимости 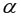 =0,05 с помощью встроенной статистической функции СТЬЮДРАСПОБР определим
=0,05 с помощью встроенной статистической функции СТЬЮДРАСПОБР определим 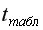 =2,1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать
=2,1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать 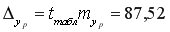 .
.
Доверительный интервал прогноза:
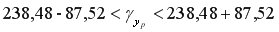 или
или 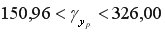 .
.
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 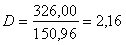 раза. Это произошло за счет малого объема наблюдений.
раза. Это произошло за счет малого объема наблюдений.
Необходимо отменить, что в MS Excel встроены статистические функции позволяющие значительно снизить количество промежуточных вычислений, например (рис. 9.11.):
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.
Выборочная ковариация между 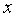 и
и 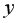 находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.
находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.
Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).
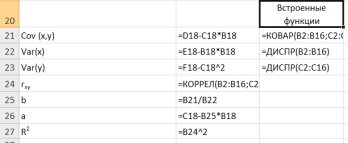
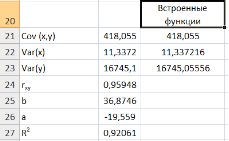
Рис.9.11. Вычисление показателей встроенными функциями MSExcel
Параметры линейной регрессии 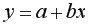 в Excel можно определить несколькими способами.
в Excel можно определить несколькими способами.
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций  среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 9.12):
среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 9.12):
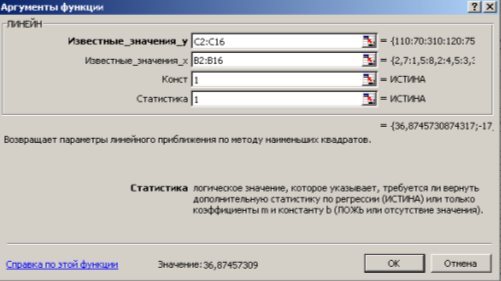
Рис. 9.12. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+ <SHIFT>+ <ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 9.3):
Таблица 9.3
|
Значение коэффициента |
Значение коэффициента |
|
Среднеквадратическое |
Среднеквадратическое |
|
Коэффициент |
Среднеквадратическое |
|
|
Число степеней свободы |
|
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
|
36,87457 |
-19,55899932 |
|
3,003392 |
21,316623 |
|
0,920606 |
39,16615351 |
|
150,7405 |
13 |
|
231234 |
19941,83855 |
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню (через кнопку Microsoft Office получить доступ к параметрам MS Excel) в диалоговом окне «Параметры MSExcel» выбрать команду «Надстройки» и справа выбрать надстройку Пакета анализа далее нажать кнопку «Перейти» (рис. 9.13). В открывшемся диалоговом окне поставить галочку напротив «Пакет анализа» и нажать «ОК» (рис. 9.14).
На вкладке «Данные» в группе «Анализ» появится доступ к установленной надстройке. (рис. 9.15).
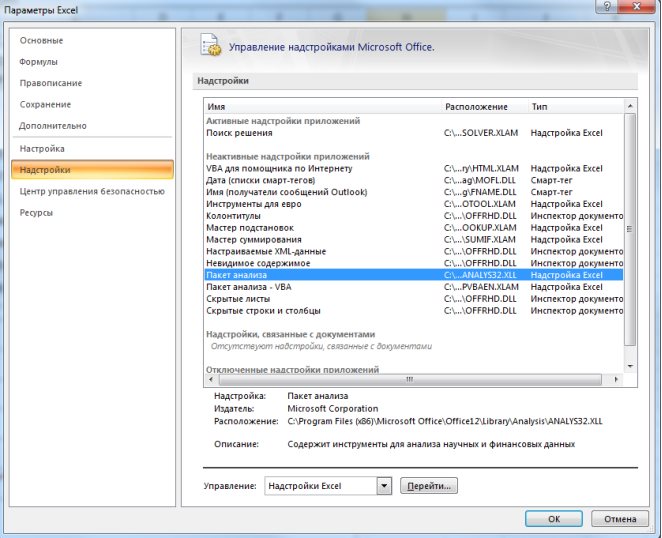
Рис. 9.13. Включение надстроек в MSExcel
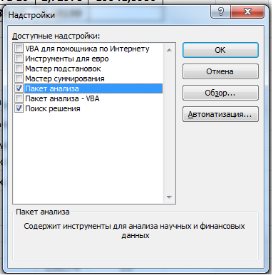
Рис. 9.14. Диалоговое окно «Надстройки»

Рис. 9.15. Надстройка «Анализ данных» на ленте MSExcel 2007.
2. Выбрать на «Данные» в группе «Анализ» выбираем команду Анализ данных в открывшемся диалоговом окне выбрать инструмент анализа «Регрессия» и нажать «ОК» (рис. 9.16):
Рис. 9.16. Диалоговое окно «Анализ данных»
В появившемся диалоговом окне (рис. 9.17) заполнить поля:
Входной интервалY – диапазон, содержащий данные результативного признака Y;
Входной интервалX– диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Рис. 9.17. Диалоговое окно «Регрессия»
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне.
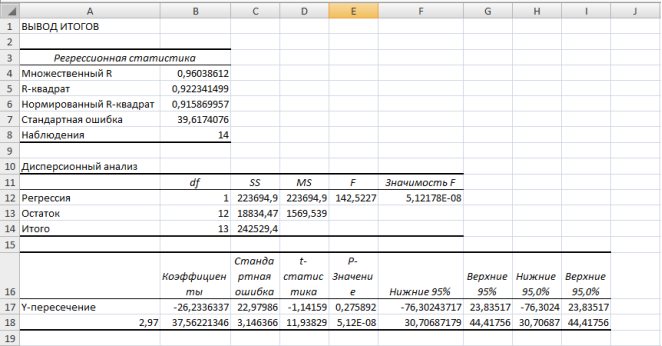
Рис. 9.18. Результаты применения инструмента Регрессия
В MSExcel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в ленте выбрать «Макет» и в группе анализ выбрать команду «Линия тренда» (рис. 9.19.). В выпадающем пункте меню выбрать «Дополнительные параметры линии тренда».

Рис. 1.19. Лента
2. В появившемся диалоговом окне выбрать фактические значения, затем откроется диалоговое окно «Формат линии тренда» (рис. 9.20.) в котором выбирается вид линии тренда и устанавливаются соответствующие параметры.
Рис. 9.20. Диалоговое окно «Формат линии тренда»
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину (рис.9.21).
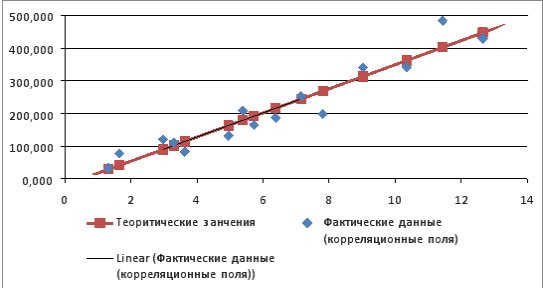
Рис. 9.21. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 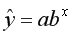 с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
В предыдущем параграфе мы научились описывать облако точек некоторой прямой, не делая никаких предположений по поводу природы анализируемых данных. Иными словами, мы не предполагали никакой конкретной модели, описывающей процесс порождения наших данных. Для дальнейшего продвижения, однако, это будет нам необходимо.
Вернемся к нашему примеру с квартирами. Естественно ожидать, что на цену квартиры (y) влияет её площадь (x), а также прочие факторы, например, удаленность квартиры от метро, этаж, наличие балкона и так далее. Обозначим эти прочие факторы переменной (varepsilon ). С учетом этих соображений естественно предположить следующую модель цены квартиры:
( {y}_i = {β}_1 + {β}_2 {x}_i + {ε}_i , i = 1,2 , … , n ).
Здесь — площадь i-ой квартиры в квадратных метрах, — цена i-ой квартиры в миллионах рублей, — прочие факторы, которые оказывают влияние на цену квартиры (y_i). Переменную (varepsilon ) принято называть случайной ошибкой модели. Буквой n будем обозначать число наблюдений в доступной нам выборке.
В целом такая модель выглядит достаточно разумно. Если бы мы знали точные значения коэффициентов (beta _1) и (beta _2), мы могли бы использовать её в практических целях. Например, зная, что (beta _2=0,3), строительная компания могла бы учитывать при планировании продаж, что один дополнительный квадратный метр площади квартиры оценивается рынком в 0,3 млн рублей. К сожалению, на практике значения параметров (beta _1) и (beta _2) нам не известны, зато мы можем собрать статистические данные и получить их (приблизительные) оценки.
Здесь уместно подчеркнуть важное различие между
- параметрами (beta _k) (без «крышек») в выражении (y_i=beta _1+beta _2x_i+varepsilon _i),
- и их оценками (widehat {beta _k})(c «крышками») в выражении .
Это различие состоит в том, что и — это некоторые истинные значения параметров модели, которые на практике никогда не известны исследователю. Все, что исследователь в силах сделать — собрать данные и эти значения оценить приближенно. — это оценки истинных значений, которые мы получаем, используя наши выборочные данные. Так как (widehat {beta _1}text{и}widehat {beta _2}) рассчитываются на основе случайной выборки, то они являются случайными величинами.
Естественно, мы хотим, чтобы оценки были близки к истинным значениям оцениваемых параметров. Поэтому нам важно знать: при каких условиях мы можем доверять этим оценкам, то есть рассчитывать на то, что результат использования МНК будет близок к истине? Эти условия называют предпосылками классической линейной модели парной регрессии.
Предпосылки классической линейной модели парной регрессии (КЛМПР):
- Модель линейна по параметрам и корректно специфицирована
(y_i=beta _1+beta _2x_i+varepsilon _i,i=1,2,{dots},n.) - (x_1,x_2,{dots},x_n) — детерминированные (неслучайные) величины, не все одинаковые.
- Математическое ожидание случайных ошибок равно нулю
(Evarepsilon _i=0). - Дисперсия случайной ошибки одинакова для всех наблюдений (mathit{var}left(varepsilon _iright)=sigma ^2).
- Случайные ошибки, относящиеся к разным наблюдениям, взаимно независимы.
- Случайные ошибки имеют нормальное распределение (varepsilon _iNleft(0,sigma ^2right)).
Мы обсудили выше соображения, исходя из которых может быть сформулирована предпосылка №1. Как мы увидим в дальнейшем, правильная спецификация подразумевает в первую очередь отсутствие среди прочих факторов других переменных, которые одновременно влияют на y и коррелируют с x. Нарушение этого требования приводит к серьезным проблемам, которые мы осветим в конце данной главы.
Предпосылка №2 касается двух важных аспектов. Во-первых, мы предполагаем, что регрессоры (x_i) являются неслучайными величинами. Это техническое предположение, которое упростит некоторые выкладки в этом разделе. Обратите внимание, что (varepsilon _i) в отличие от регрессоров являются случайными величинами, а следовательно, и (y_i) тоже случайны, так как представляют собой сумму неслучайной компоненты (beta _1+beta _2x_i) и случайной величины (varepsilon _i). В терминах нашего примера с квартирами про эту предпосылку можно думать так: представим, что вы собрали случайную выборку из 100 квартир площадью 30 м2, 100 квартир площадью 35 м2 и 100 квартир площадью 40 м2. Если вы соберете другую выборку из трехсот квартир с такими же площадями, то значения регрессоров (x_i) останутся теми же самыми, а вот значения объясняемой переменной (y_i) поменяются, поэтому в данном примере разумно думать про регрессоры как про неслучайные величины, а про величины (y_i) — как про случайные.
Во-вторых, в рамках предпосылки №2 мы предполагаем, что не все значения регрессоров одинаковы. Нетрудно понять, зачем нужно это предположение, если взглянуть на формулу оценки коэффициента
(widehat {beta _2}=frac{widehat {mathit{Cov}}left(x,yright)}{widehat {mathit{Var}}left(xright)}). Обратите внимание, что в знаменателе этой формулы стоит выборочная дисперсия переменной x, но если все значения этой переменной в выборке будут одинаковы, то эта дисперсия окажется равной нулю, и из-за этого мы не сможем рассчитать МНК-оценку (widehat {beta _2}).
Предпосылка №3 говорит о том, что прочие факторы могут приводить к отклонению (y_i) от величины (beta _1+beta _2x_i) как вверх, так и вниз, но в среднем эти отклонения компенсируют друг друга.
Предпосылка №4 требует, чтобы разброс случайных ошибок в среднем был постоянен для всех наблюдений. Её смысл удобно пояснить, используя картинку. Посмотрите на рисунки 2.3а и 2.3б. В первом случае предпосылка о постоянстве дисперсии случайной ошибки выполнена, а во втором — нет, так как разброс точек вокруг линии регрессии растет по мере увеличения объясняющей переменной, следовательно, мы можем заключить, что дисперсия случайной ошибки не является одинаковой для всех наблюдений. Ситуация, когда предпосылка №4 выполнена (то есть ситуация, соответствующая рисунку 2.3а) называется гомоскедастичностью случайных ошибок. Альтернативная ситуация называется гетероскедастичностью случайных ошибок.
Рисунок 2.3а. Гомоскедастичность случайных ошибок
Рисунок 2.3б. Гетероскедастичность случайных ошибок
Из предпосылки №5 следует, что случайные ошибки, относящиеся к разным наблюдениям, не коррелированы друг с другом: (mathit{cov}left(varepsilon _i,varepsilon _jright)=0) при (i{neq}j).
Предпосылка №6 не требуется для обеспечения хороших свойств оценок коэффициентов (обратите внимание, что ниже, в формулировке теоремы Гаусса — Маркова, она не фигурирует), однако будет полезна для тестирования гипотез и построения доверительных интервалов.
Теорема Гаусса — Маркова. Если выполнены предпосылки 1-5 классической линейной модели парной регрессии, то МНК-оценки коэффициентов (widehat {beta _1}text{и}widehat {beta _2}) будут:
(а) несмещенными,
(б) эффективными в классе всех несмещенных и линейных по y оценок1.
Напомним, что оценка называется несмещенной, если её математическое ожидание совпадает с истинным значением оцениваемого параметра: (Ewidehat {beta _2}=beta _2). Свойство эффективности означает, что оценка характеризуется минимальной дисперсией среди всех альтернативных оценок в данном классе, то есть является «наиболее точной» оценкой интересующего нас параметра. Линейность по y означает, что мы рассматриваем все оценки, которые могут быть представлены в виде линейной комбинации значений объясняемой переменной, то есть записаны в виде (sum _{i=1}^nc_i{ast}y_i).
Если переформулировать свойства несмещенности и эффективности нестрого, то можно сказать, что при выполнении предпосылок 1-5 МНК-оценки параметров окажутся хорошими: они будут «в среднем правильными» и наиболее точными. Теорема Гаусса — Маркова дает нам важную мотивацию для того, чтобы оценивать параметры нашей модели именно методом наименьших квадратов, а не каким-то альтернативным способом.
Лирическое отступление о предпосылках
Каждый раз, когда я рассказываю студентам об этой теореме, в моей голове разыгрывается примерно такой диалог между двумя эконометристами (назовем их Филипп и Дима).
Дима: Реалистичны ли предпосылки КЛМПР?
Филипп: Не очень. Например, в реальных исследованиях на пространственных данных ты почти всегда будешь сталкиваться с нарушением требования постоянства дисперсии случайной ошибки (нарушением предпосылки №4). Во многих прикладных исследованиях также окажется более целесообразным думать про регрессоры как про случайные, а не детерминированные случайные величины (это отклонение от предпосылки №2). На нормальность случайных ошибок (предпосылка №6) я бы тоже не рассчитывал…
Дима: Зачем же тогда мы её изучаем? Давайте сразу перейдем к более реалистичной модели.
Филипп: Мы начинаем с КЛМПР, так как это самая простая модель, на примере которой мы можем обсудить ряд важных эконометрических идей и при этом не погрязнуть в технических трудностях. В последующих главах мы будем постепенно отказываться от предпосылок КЛМПР и в результате получим набор моделей и методов, которые хорошо подходят для реальных исследований на живых данных. Кроме того, мы научимся проверять выполнение тех или иных предположений КЛМПР, чтобы понять, когда стоит их использовать, а когда — нет.
В частности, последствия нарушения предпосылки №3 читателю предлагается проанализировать уже в этом параграфе, в одном из заданий для самостоятельного решения.
- Несмещенность и эффективность — это свойства оценок при фиксированном объеме выборки (при фиксированном n). Во многих случаях удобно также использовать асимптотические свойства оценок, то есть свойства, которые имеют место при (nrightarrow {infty}) (например, состоятельность). Об асимптотических свойствах МНК-оценок мы подробно поговорим в одной из последующих глав. ↵

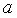
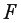 -статистика
-статистика