,
—
уравнение регрессии,
—
случайная ошибка (с ограничениями).
;
;
—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.
Предположим,
что оценка σ2
связана с
суммой квадратов остатков регрессии
Вычислим:
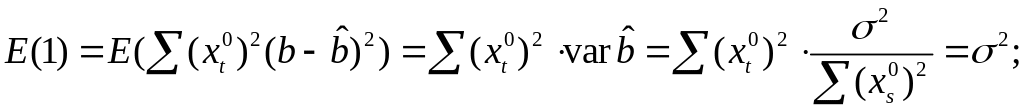
Используя,
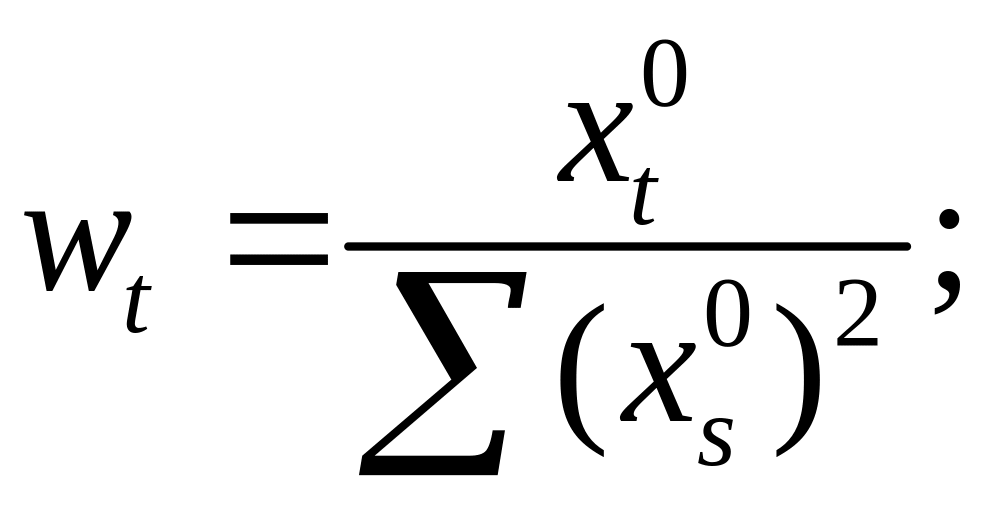
получим
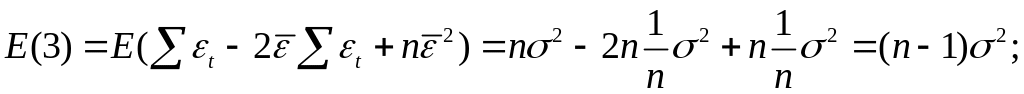
где
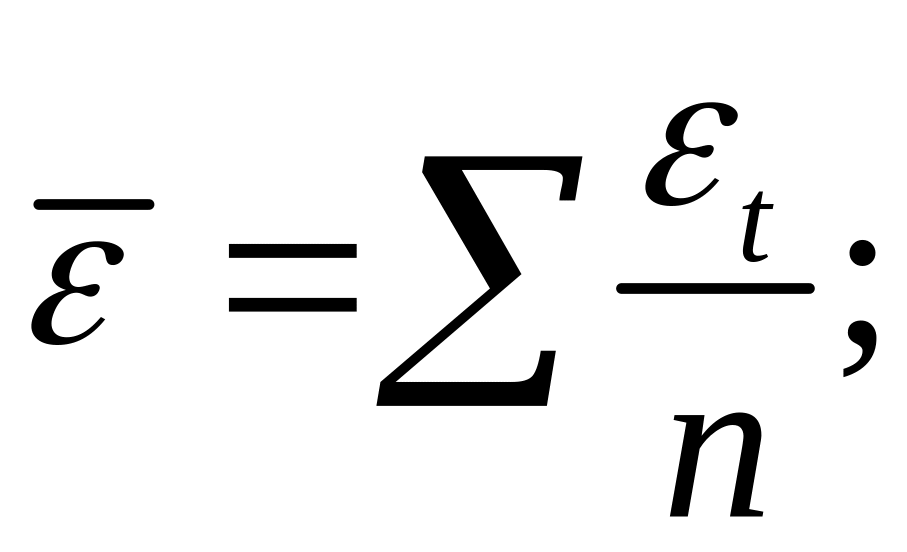
Таким образом
откуда следует,
что
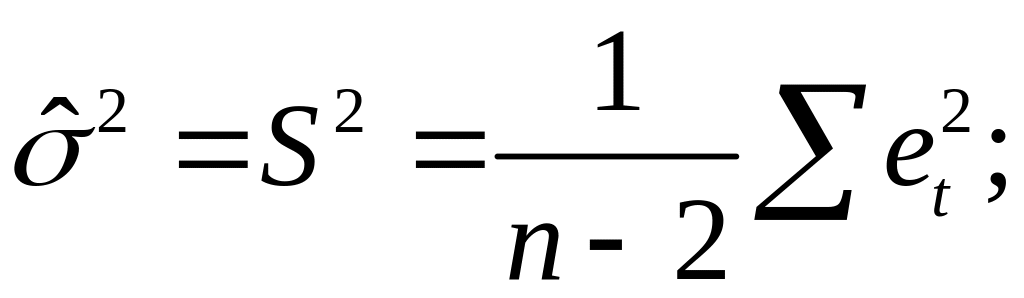
является
несмещенной оценкой дисперсии ошибок
σ2.
12. Оценка существенности параметров линейной регрессии и корреляции
Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.
При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра Sb
рассчитывается
по формуле
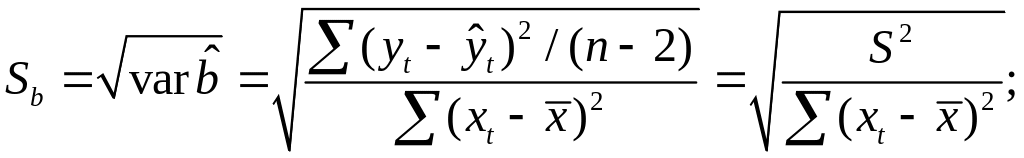
где S2
— остаточная
дисперсия на одну степень свободы.
Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.
Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: tb=b/Sb
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если tb>tкр,
коэф-т b значим и
его нельзя заменить 0.
Доверительный
интервал для коэф-та регрессии опр-ся
как
.
Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.
Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции Sr=mr(заменить):
О
тсюда
фактическое значение
Данная формула
свидетельствует, что в парной лин.
регрессии
tr2=F
=>tr2=
tb2
.
Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.
13. Интервалы прогноза по линейному уравнению регрессии
Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.
Этот прогноз
осущ-ся путем подстановки знач. фактора
х=хk
в ур-ние
регрессии
.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.
,
где
—
стандартная ошибка оценки
.
Получим данную
оценку для лин. регрессии
.
Подставим это
выражение в ур-ие
.
Отсюда следует,
что стандартная ошибка
зависит от
ошибки
и ошибки
коэффициента b,
т.е.
.
В курсе мат. стат.
получено:
=S2/n,где
S2
– оценка дисперсии рез-ого признака.
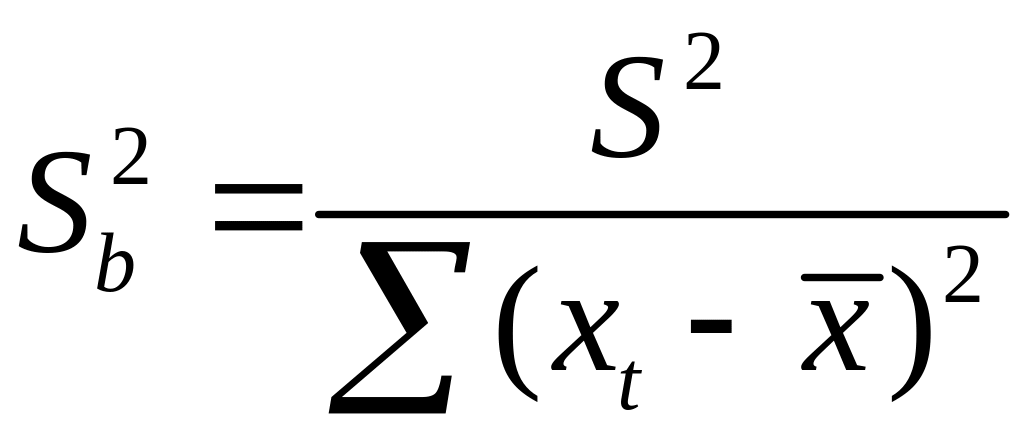
;Получим
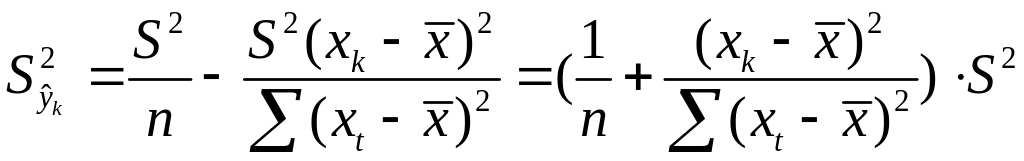
Откуд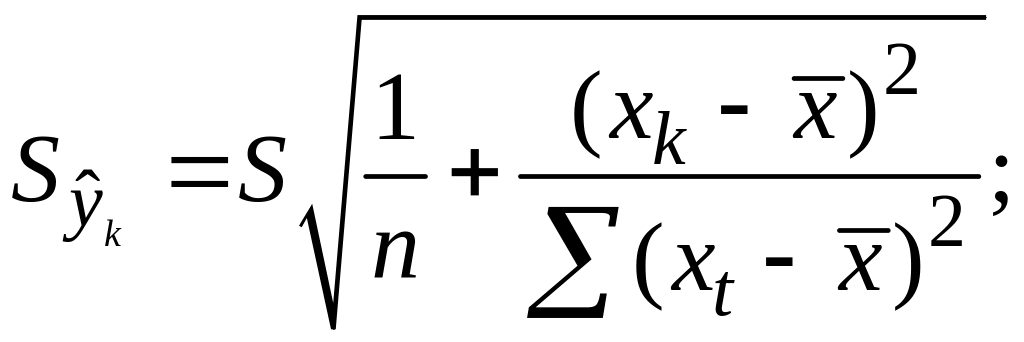
Где t=1,…n
– номера измерений, xk
не обязано совпадать с одним из xt.
Видно, что величина
стандартной ошибки xk
зависит от
.
Она достигает
мин. при xк=
и возрастает
по мере того, как «удаляется» от
в любом
направлении.
Т.е.
.
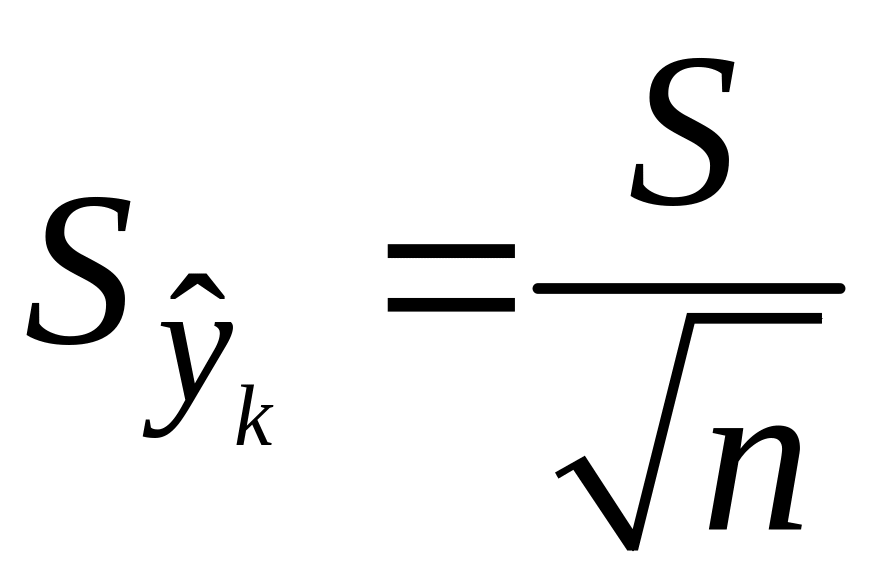
Можно строить
интервальные оценки рез-ого признака
при заданном xк
, которые
определяются как
,
где
—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.
На графике
доверительные границы для
представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.
Фактические знач.
yk
варьируют
около ср. знач.
на величину случ. ошибки ε, дисперсия
кот. оценивается как S2
, поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку
так и случ.ошибку S.
Средняя ошибка
прогнозного индив.значения составит
.
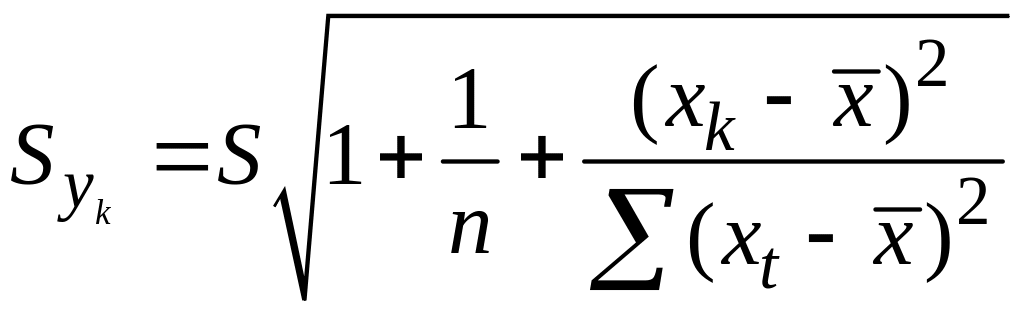
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
You are quite right. In the context of linear regression, or of any other model that can yield predictions on one variable (response) from values of other variables (predictors), we usually have a set of observations, that is, points where we observed the actual response and the predictors. Given a model, for each observation we can compute the predicted value (from model and predictors) and the actual value. The error is the difference between predicted and observed value.
Since we have a set of observations, we have a set of errors and therefore we can compute its variance. Furthermore, if observations are seen as a random variable, we can estimate its variance.
That is error variance.
Colman’s definition is equivalent to this one, but from another point of view.
In our set of observations, we can compute variance of the response. If we have a model, we can explain part of the variance of the response from the variance of predictors. The part we can’t explain is error variance — the same error variance explained above.
And to summarize: Please have a look at the page of Corman’s book and notice that just before «error variance» there is the definition of «error variable». A short definition of error variance is that it is the variance of the error variable.
You are quite right. In the context of linear regression, or of any other model that can yield predictions on one variable (response) from values of other variables (predictors), we usually have a set of observations, that is, points where we observed the actual response and the predictors. Given a model, for each observation we can compute the predicted value (from model and predictors) and the actual value. The error is the difference between predicted and observed value.
Since we have a set of observations, we have a set of errors and therefore we can compute its variance. Furthermore, if observations are seen as a random variable, we can estimate its variance.
That is error variance.
Colman’s definition is equivalent to this one, but from another point of view.
In our set of observations, we can compute variance of the response. If we have a model, we can explain part of the variance of the response from the variance of predictors. The part we can’t explain is error variance — the same error variance explained above.
And to summarize: Please have a look at the page of Corman’s book and notice that just before «error variance» there is the definition of «error variable». A short definition of error variance is that it is the variance of the error variable.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
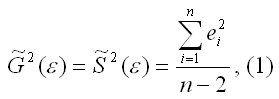
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
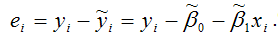
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
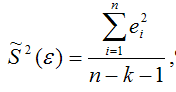
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
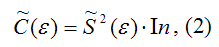
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
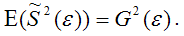
Доказательство. Примем без доказательства справедливость следующих равенств:
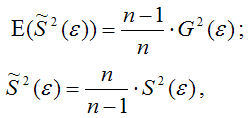
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
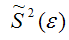
– выборочная оценка дисперсии случайной ошибки.
Тогда:
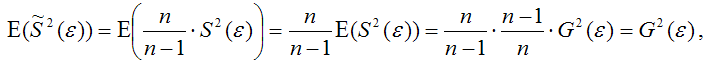
т. е.
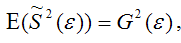
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
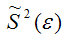
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
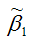
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
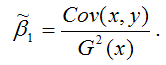
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
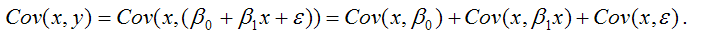
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
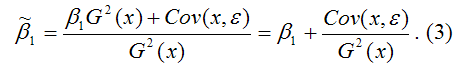
Таким образом, МНК-оценка
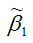
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
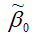
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
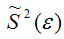
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
[c.85]
Основные положения теории Шарпа. Коэффициенты регрессии. Измерение ожидаемой доходности и риска портфеля. Дисперсия ошибок. Определение весов ценных бумаг в модели Шарпа. Нахождение оптимального портфеля. Сравнительный анализ методов Г. Марковица и В. Шарпа.
[c.335]
Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями.
[c.19]
Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров (п дисперсий ошибок регрессии а ) с помощью п наблюдений.
[c.161]
Решение. Предположим, что дисперсии ошибок о, связаны уравнением регрессии
[c.163]
Вспомним, что наиболее часто употребляемые процедуры устранения гетероскедастичности так или иначе были основаны на предположении, что дисперсия ошибок регрессии ст2 является функцией от каких-то регрессоров. Если а2 существенно зависит от регрессора Z, а при спецификации модели регрессор Z не был включен в модель, стандартные процедуры могут не привести к устранению гетероскедастичности.
[c.250]
В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений X должна быть приблизительно равна необъясненной дисперсии для больших значений X, то есть должно быть справедливым следующее равенство [c.125]
Чем ближе к единице отношение / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = Sl / S2 подчиняется F -распределению
[c.125]
Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора X и отклика 7. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией.
[c.126]
Пятая часть полностью посвящена приложению матричного дифференциального исчисления к линейной регрессионной модели. Она содержит исчерпывающее изложение проблемы оценивания, связанной с неслучайной частью модели при различных предположениях о рангах и других ограничениях. Кроме того, она содержит ряд параграфов, связанных со стохастической частью модели, например оценивание дисперсии ошибок и прогноз ошибок. Включен также небольшой параграф, посвященный анализу чувствительности. Вводная глава содержит необходимые предварительные сведения из теории вероятностей и математической статистики.
[c.16]
Дисперсия ошибок прогноза в задаче (3.6) — (3.7) достигает минимума в точке , являющейся основанием перпендикуляра, опущенного из точки т] на подпространство Q, определяемое равенством (3.7). Соотношение (3.10) эквивалентно равенству
[c.309]
Ограничение (а) не вызывает претензий. Условие (б) также естественно. Ясно, что механизм сглаживания и прогноза, при котором математическое ожидание или дисперсия ошибок фильтрации или интенсивность искусственного рассеивания достаточно велики, вряд ли рационален и тем более не может быть признан оптимальным.
[c.320]
Задача прогнозирования по минимуму дисперсии ошибок при различных статистических характеристиках входных случайных процессов и ошибок измерений подробно обсуждалась в литературе. Имеются и стандартные аналоговые устройства и программы для ЦВМ, реализующие соответствующие схемы. Экстремальная задача, к которой сводится вычисление характеристик генераторов случайных шумов, несомненно, проще исходной вариационной задачи.
[c.334]
Матрица корреляции k j R регулируемых ошибок прогноза, оптимального в смысле показателя качества R( k ), может быть получена из корреляционной матрицы kff a ошибок прогноза, оптимальных в смысле минимума дисперсии ошибок в каждой координате в каждый момент времени, по следующей формуле [c.339]
Из (1.14), в частности, следует, что коэффициент корреляции признаков, на которые наложены ошибки измерения, всегда меньше по абсолютной величине, чем коэффициент корреляции исходных признаков. Другими словами, ошибки измерения всегда ослабляют исследуемую корреляционную связь между исходными переменными, и это искажение тем меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих исходных переменных. Формула (1.14) позволяет скорректировать искаженное значение коэффициента корреляции для этого нужно либо знать разрешающие характеристики измерительных приборов (и, следовательно, величины дисперсий ошибок а и а ), либо провести дополнительное исследование по их выявлению.
[c.73]
Пример 7.4 ]. Известно, что дисперсия о2, вызванная ошибками измерения, при некоторых видах количественного анализа составляет 0,5. Если заменить измерительный прибор и произвести 10-кратное измерение одного и того же стандартного образца, а затем подсчитать дисперсию, то она составит s2 = 0,25. Может показаться, что дисперсия ошибок измерения изменилась, превысив 5%-ный уровень значимости. Так ли это [c.128]
Теорема Гаусса-Маркова. Оценка дисперсии ошибок сг2
[c.41]
Оценка дисперсии ошибок а2
[c.43]
Формулы (2.11), (2.13) дают дисперсии оценок о, Ь коэффициентов регрессии в том случае, если а2 известно. На практике, как правило, дисперсия ошибок а2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а, Ь. В этом случае вместо дисперсий оценок о, b мы можем получить лишь оценки дисперсий о, 6, заменив а2 на s2 из (2.15) в (2.11), (2.13), (2.14) [c.45]
Распределение оценки дисперсии ошибок s2
[c.47]
Так как оценка дисперсии ошибок s2 является функцией от остатков регрессии et, то для того чтобы доказать независимость s2 и (2,6), достаточно доказать независимость et и (2,6). Оценки 2, 6 так же, как и остатки регрессии et, являются линейными функциями ошибок t (см. (2.4а), (2.46), (2.20)) и поэтому имеют совместное нормальное распределение. Известно (приложение МС, п. 4, N4), что два случайных вектора, имеющие совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость s2 и (а, 6), нам достаточно доказать некоррелированность et и (2,6).
[c.48]
Значение Д2 увеличилось по сравнению с первой регрессией. Переход к удельным данным приводит к уменьшению дисперсии ошибок модели.
[c.58]
Пусть SML = Y et/ n и OLS — ] et/ (n — 1 — оценки методов максимального правдоподобия и наименьших квадратов для дисперсии ошибок <т2 в классической модели парной регрессии Yt =
[c.62]
Оценка дисперсии ошибок а1. Распределение s2
[c.72]
Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]
Тест ранговой корреляции Спирмена использует наиболее общие предположения о зависимости дисперсий ошибок регрессии от значений регрессоров [c.158]
Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.
[c.161]
Наиболее простой и часто употребляемый тест на гетероске-дастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е.
[c.161]
Другим недостатком тестов Уайта и Глейзера является то, что факт невыявления ими гетероскедастичности, вообще говоря, не означает ее отсутствия. В самом деле, принимая гипотезу Щ, мы принимаем лишь тот факт, что отсутствует определенного вида зависимость дисперсий ошибок регрессии от значений регрессоров.
[c.166]
Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить.
[c.57]
Доказано (см., например, [37]), что приведенную задачу оптимального стохастического управления можно разделить на две задачу сглаживания и лрогноза по минимуму дисперсии ошибок и задачу оптимального детерминированного управления. При более сложном критерии качества управления и при дополнительных ограничениях на переменные состояния и управляющие параметры такое разделение не всегда удается я, его, по-видимому, не всегда целесообразно производить.
[c.44]
Здесь Paaa(tt, » ) — система функций веса, минимизирующих дисперсию ошибок За(/г-) прогноза W (ti, т) — тождественно не равные нулю функ-22 339
[c.339]
В ходе анализа финансовых данных любой ряд динамики, будь то процентные ставки или цены на финансовые активы, можно разбить на две компоненты, одна из которых изменяется случайным образом, а другая подчиняется определенному закону. Колебания финансовых переменных значительно изменяются во времени бурные периоды с высокой волатильностью переменных сменяют спокойные периоды и наоборот. В некоторых случаях вола-тильность играет ключевую роль в ценообразовании на финансовые активы. В частности, курсы акций напрямую зависят от ожидаемой волатильности доходов корпораций. Все финансовые учреждения без исключения стремятся адекватно оценить волатильность в целях успешного управления рисками. В свое время Трюгве Хаавельмо, нобелевский лауреат по экономике 1989 г., предложил рассматривать изменение экономических переменных как однородный стохастический (случайный) процесс. Вплоть до 1980-х гг. экономисты для анализа финансовых рынков применяли статистические методы, предполагавшие постоянную волатильность во времени. В 1982 г. Роберт Ингл развил новую эконометрическую концепцию, позволяющую анализировать периоды с разной волатильностью. Он ввел кластеризацию данных и условную дисперсию ошибок, которая завесит от времени. Свою разработку Ингл назвал авторегрессионной гетероскедастической моделью , с ее помощью можно точно описать множество временных рядов, встречающихся в экономике. Метод Ингла сегодня применяется финансовыми аналитиками в целях оценки финансовых активов и портфельных рисков.
[c.197]
Отметим, что оценки максимального правдоподобия параметров а, 6 совпадают с оценками метода наименьших квадратов OML = SOLS, ML OLS- Это легко видеть из того, что уравнения (2.37а) и (2.376) совпадают с соответствующими уравнениями метода наименьших квадратов (2.2). Оценка максимального правдоподобия для <т2 не совпадает с
несмещенной оценкой дисперсии ошибок. Таким образом, с = ((п — 2)/n)<7OLS является смещенной, но тем не менее состоятельной оценкой <т2.
[c.57]
В этом разделе мы рассмотрим частный случай обобщенной регрессионной модели, а именно, модель с гетероскедастичностъю, Это означает, что ошибки некоррелированы, но имеют непостоянные дисперсии. (Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной.) Как уже отмечалось, Гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.
[c.168]
В качестве введения в материал гл. 8 и 9 рассмотрим сейчас некоторые характеристики ошибок оценивания. Оценку величины 
обозначим через 
т. е. с помощью символа 
Величина 
это оценка 
построенная по наблюдению на конечном интервале времени или по конечному числу выборочных точек.
Предположим, что оценка 
(хотя бы умозрительно) может быть получена многократно путем повторения эксперимента или выполнения определенной программы измерений. Тогда принципе можно оценить математическое ожидание 
обозначаемое 
Например, если эксперимент повторяется многократно и дает оценки 
то
Это математическое ожидание может совпасть или не совпасть с истинным значением 
. В случае совпадения оценка 
называется несмещенной. В противном случае оценка называется смещенной. Смещение оценки, обозначаемое 
равно математическому ожиданию оценки минус истинное значение параметра:
Следовательно, смещение оценки — это систематическая ошибка, которая всегда имеет одну и ту же абсолютную величину и один и тот же знак, если измерения проводятся при неизменных условиях.
Дисперсия оценки, обозначаемая 
определяется как математическое ожидание квадрата разности между оценкой и ее средним значением. Формально
Дисперсия характеризует случайную ошибку оценки, т. е. ту часть общей ошибки, которая не является систематической и может иметь разные знаки и разные абсолютные значения от измерения к измерению.
Суммарная ошибка оценивания характеризуется средним квадратом ошибки, который определяется как математическое ожидание квадрата разности между оценкой и ее истинным значением. Средний квадрат ошибки оценки 
равен
Легко проверить, что
Иначе говоря, средний квадрат ошибки равен сумме дисперсии и квадрата смещения. Если смещение равно нулю или пренебрежимо мало, то средний квадрат ошибки и дисперсия совпадают.
Рис. 1.18 иллюстрирует смысл смещения (систематической ошибки) и дисперсии (случайной ошибки) на примере пристрелки двух винтовок. Рис. 1.18, а показывает, что винтовка А обладает большим смещением и малой случайной ошибкой. Рис. 1.18, б показывает, что винтовка 
имеет малое смещение, но большую случайную ошибку. Очевидно, из винтовки А никогда нельзя попасть в цель, в то время как из винтовки 
можно случайно поразить ее. Однако большинство стрелков предпочтет винтовку А, поскольку систематическую ошибку можно исключить (если известно, что она есть) путем регулировки прицела винтовки, а случайную ошибку устранить нельзя. Следовательно, винтовка А потенциально имеет меньший средний квадрат ошибки.
Рис. 1.18. Случайные и систематические ошибки при стрельбе из винтовки по мишени: а — винтовка А, большая систематическая ошибка и малая случайная ошибка; б — винтовка Б, малая систематическая ошибка и большая случайная ошибка.
Наконец, важной величиной является нормированная среднеквадратичная ошибка оценки, обозначаемая 
Эта безразмерная ошибка равна квадратному корню из среднего квадрата ошибки, деленному на истинное значение параметра (разумеется, в предположении, что оно не равно нулю). Формально
На практике стараются уменьшить нормированную среднеквадратичную ошибку в максимально возможной степени. В этом случае появляется уверенность в том, что произвольная оценка 
близка к истинному значению 
,
—
уравнение регрессии,
—
случайная ошибка (с ограничениями).
;
;
—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.
Предположим,
что оценка σ2
связана с
суммой квадратов остатков регрессии
Вычислим:
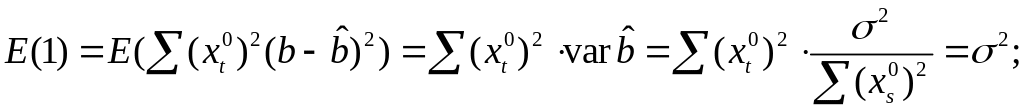
Используя,
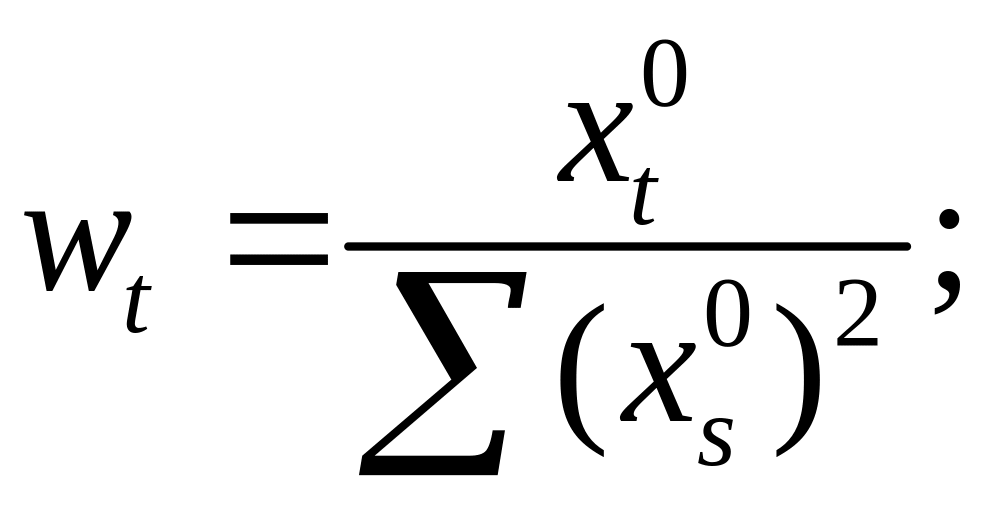
получим
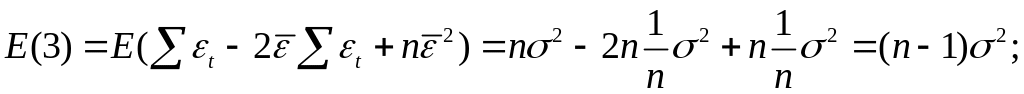
где
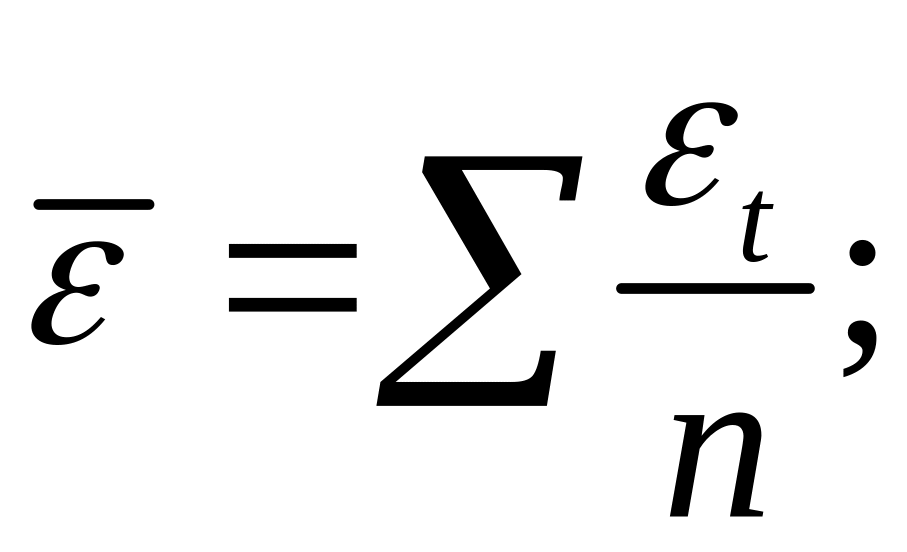
Таким образом
откуда следует,
что
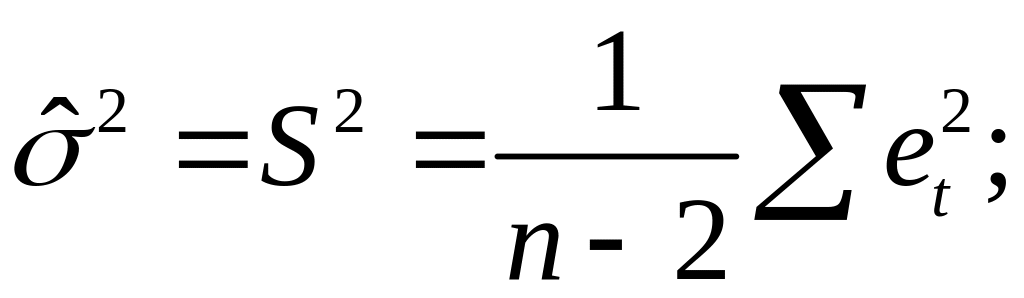
является
несмещенной оценкой дисперсии ошибок
σ2.
12. Оценка существенности параметров линейной регрессии и корреляции
Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.
При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра Sb
рассчитывается
по формуле
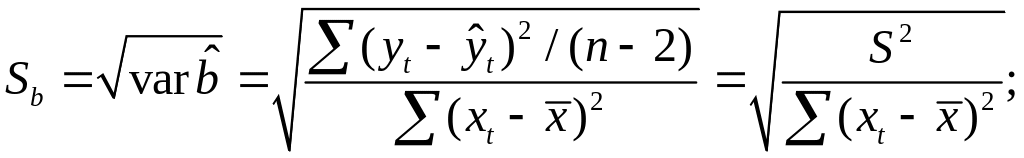
где S2
— остаточная
дисперсия на одну степень свободы.
Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.
Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: tb=b/Sb
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если tb>tкр,
коэф-т b значим и
его нельзя заменить 0.
Доверительный
интервал для коэф-та регрессии опр-ся
как
.
Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.
Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции Sr=mr(заменить):
О
тсюда
фактическое значение
Данная формула
свидетельствует, что в парной лин.
регрессии
tr2=F
=>tr2=
tb2
.
Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.
13. Интервалы прогноза по линейному уравнению регрессии
Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.
Этот прогноз
осущ-ся путем подстановки знач. фактора
х=хk
в ур-ние
регрессии
.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.
,
где
—
стандартная ошибка оценки
.
Получим данную
оценку для лин. регрессии
.
Подставим это
выражение в ур-ие
.
Отсюда следует,
что стандартная ошибка
зависит от
ошибки
и ошибки
коэффициента b,
т.е.
.
В курсе мат. стат.
получено:
=S2/n,где
S2
– оценка дисперсии рез-ого признака.
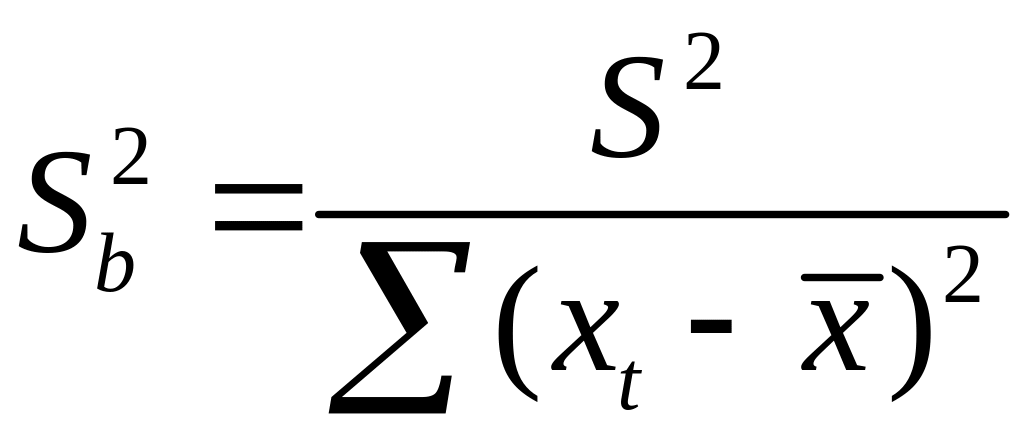
;Получим
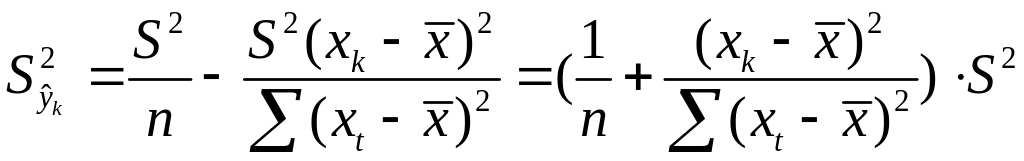
Откуд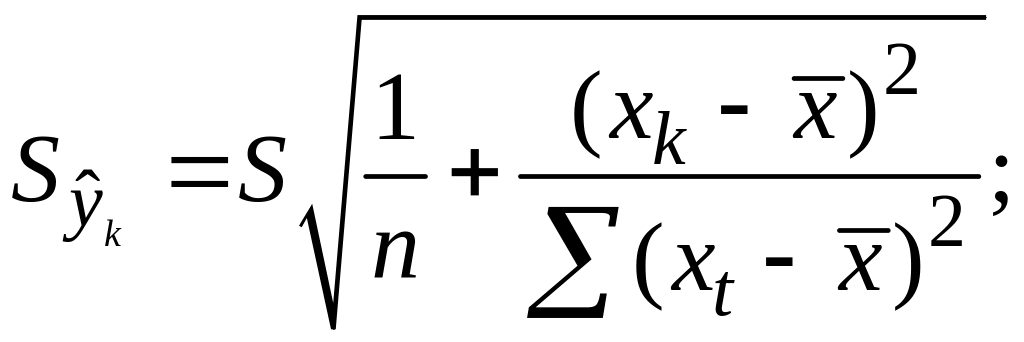
Где t=1,…n
– номера измерений, xk
не обязано совпадать с одним из xt.
Видно, что величина
стандартной ошибки xk
зависит от
.
Она достигает
мин. при xк=
и возрастает
по мере того, как «удаляется» от
в любом
направлении.
Т.е.
.
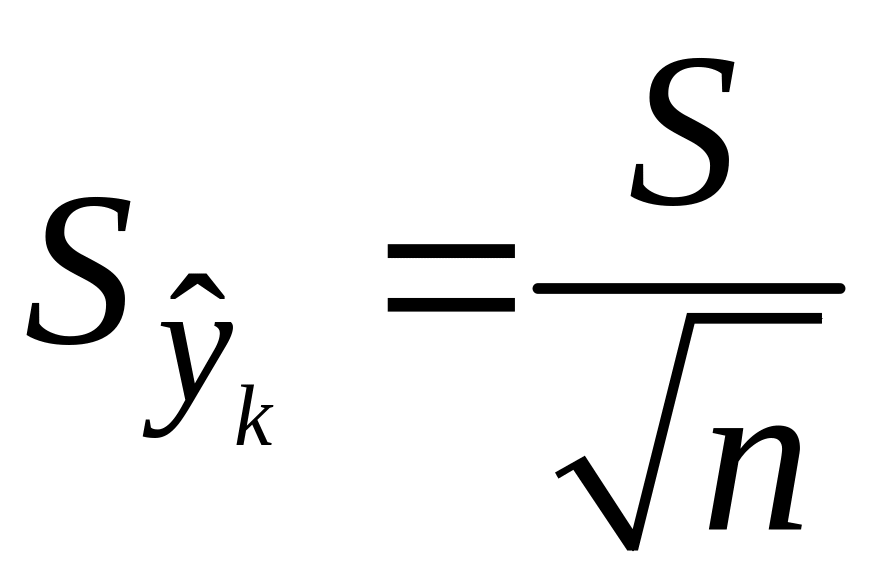
Можно строить
интервальные оценки рез-ого признака
при заданном xк
, которые
определяются как
,
где
—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.
На графике
доверительные границы для
представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.
Фактические знач.
yk
варьируют
около ср. знач.
на величину случ. ошибки ε, дисперсия
кот. оценивается как S2
, поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку
так и случ.ошибку S.
Средняя ошибка
прогнозного индив.значения составит
.
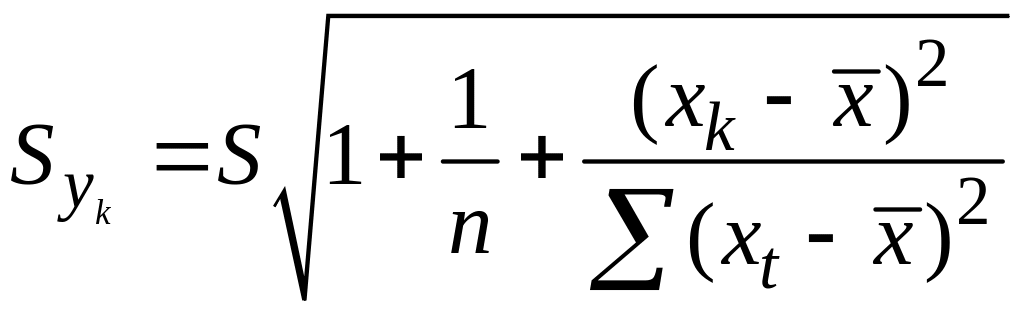
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
You are quite right. In the context of linear regression, or of any other model that can yield predictions on one variable (response) from values of other variables (predictors), we usually have a set of observations, that is, points where we observed the actual response and the predictors. Given a model, for each observation we can compute the predicted value (from model and predictors) and the actual value. The error is the difference between predicted and observed value.
Since we have a set of observations, we have a set of errors and therefore we can compute its variance. Furthermore, if observations are seen as a random variable, we can estimate its variance.
That is error variance.
Colman’s definition is equivalent to this one, but from another point of view.
In our set of observations, we can compute variance of the response. If we have a model, we can explain part of the variance of the response from the variance of predictors. The part we can’t explain is error variance — the same error variance explained above.
And to summarize: Please have a look at the page of Corman’s book and notice that just before «error variance» there is the definition of «error variable». A short definition of error variance is that it is the variance of the error variable.
Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.
Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.
Функции оценки
В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.
Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция
Точечная оценка
Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:
Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.
Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.
Функция оценки
Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.
Смещение и дисперсия
Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.
Смещение
Смещение определяется следующим
образом:
где ожидаемое значение E(θˆm) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.
Оценщик θˆm называется несмещенным, если bias(θˆm)=0, что подразумевает что E(θˆm) = θ.
Дисперсия и Стандартная ошибка
Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.
Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.
Давайте теперь рассмотрим некоторые обычно используемые функции оценки.
Оценка Максимального Правдоподобия (MLE)
Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.
Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение Pdata(x). Пусть Pmodel(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, Pmodel(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность Pdata(x).
Оценка максимального правдоподобия для θ определяется как:
Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:
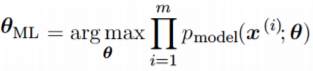
Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.
В итоге, получаем:
Два важных свойства: сходимость и
эффективность
Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.
Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.
Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.
Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.
Максимальная апостериорная (MAP) оценка
Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):
где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.
Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.
Функции потерь
В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.
До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.
Давайте рассмотрим некоторые часто используемые функции потерь.
Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.
где y(i) – фактический ожидаемый результат, а ŷ(i) – прогноз модели.
Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.
Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.
Получение MSE из MLE
Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).
Можно смоделировать модель
линейной регрессии следующим образом:
мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.
Вернемся к логарифмической вероятности, определенной ранее:
где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:
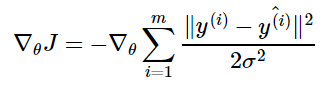
Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.
Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.
Кросс-энтропия определяется как:
где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.
Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели
Бинарная классификация
В случае бинарной классификации (M=2),
формула имеет вид:
При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.
Визуализация
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.
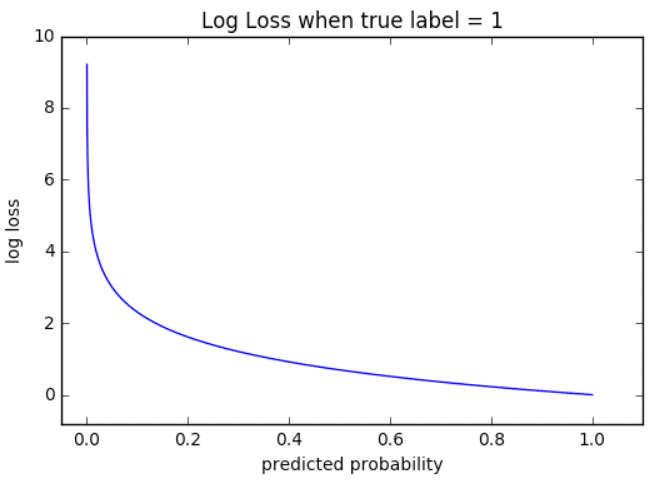
Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!
Мульти-классовая классификация
В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.
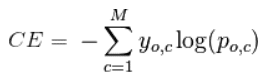
Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.
Задачи ML и соответствующие функции потерь
Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:
Задача регрессии
Задача, когда
вы прогнозируете вещественное число.
• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).
Задача бинарной классификации
Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.
• Конфигурация выходного
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
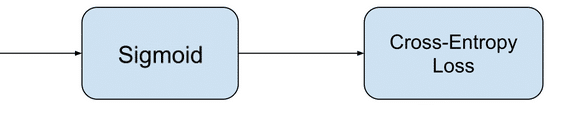
Задача мульти-классовой классификации
Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.
• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.
Оптимизаторы
Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.
Но как именно это делается? Используя оптимизаторы.
Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.
Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.
Градиентный Спуск
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:
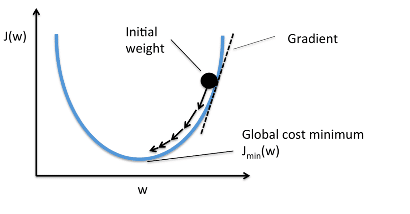
Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение Jmin. Нам нужно найти способ достичь
этого минимального значения.
В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.
Повторяем до достижения минимума:
{
}
В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.
Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели Wj, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.
Есть три способа сделать градиентный спуск:
Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.
Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.
Вот некоторые другие часто
используемые Оптимизаторы:
Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.
Адаград
Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.
Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.
RMSprop
RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.
Адам
Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.
Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.
Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:
# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')или
# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')Спасибо за проявленный интерес!
Ссылки:
[1] https://www.deeplearningbook.org/contents/ml.html
[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/
[3] https://blog.algorithmia.com/introduction-to-optimizers/
[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/
[5] https://blog.algorithmia.com/introduction-to-loss-functions/
[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/
[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html
[8] https://rohanvarma.me/Loss-Functions/
[9] http://blog.christianperone.com/2019/01/mle/
Дисперсия — ошибка
Cтраница 1
Дисперсия ошибки в 5 ( sft t) падает пропорционально nk, однако при этом увеличивается время, затрачиваемое на измерение.
[1]
Дисперсия ошибки б2 при других значениях fep и 7 должна оказаться больше.
[3]
Дисперсия ошибки с ростом k возрастает.
[5]
Дисперсия ошибки будет тем меньше, чем уже полоса ( больше постоянная времени) фильтра. Величина ошибки, обусловленная дробовым эффектом, весьма мала.
[6]
Дисперсии ошибок в системах с ВР рассмотренных типов выражаются одинаковыми формулами. Эти формулы справедливы для помех малого уровня.
[7]
Дисперсия ошибки регулирования служит критерием качества АСР при случайных входных сигналах.
[8]
Дисперсия ошибки выходного параметра является наиболее простой вероятностной характеристикой как с точки зрения вычисления, так и с точки зрения определения оптимальной конструкции. Однако эта характеристика в общем случае не отражает всех особенностей ошибки выходного параметра.
[9]
Если дисперсия ошибок в экспериментальных данных является постоянной, то весовые коэффициенты принимаются равными единице. Если же эта дисперсия является переменной величиной, зависящей от номера экспериментального значения функции, то весовые коэффициенты выбираются равными величинам, обратным к величинам дисперсий.
[10]
Следовательно дисперсия ошибок регрессии не постоянна.
[11]
Зависимость дисперсии ошибки от изменения амплитуды гармонической компоненты оказывается весьма слабой.
[12]
Вычисление Дисперсии ошибки по формуле, аналогичной ( 22 — 9), где 5Ш выражается формулой ( 22 — 6), может привести к противоречию в случае некоторых типов фильтров, так как спектральная плотность растет так же быстро, как падает частотная характеристика системы Ф ( / ш) 2 и интеграл ( 22 — 9) расходится.
[13]
Вычисление дисперсии ошибки ИСП в соответствии с ( 3 — 94) при известных выражениях для Ф ( / со, 0) и 8 ( ш) аналогично вычислению дисперсии ошибки непрерывных линейных систем и не вызывает принципиальных трудностей.
[14]
Выразить дисперсию ошибки оптимальной динамической системы через спектра иные плотности 5И (), Sv ( t), иг / С0) ( ( 0 — полезный сигнал, V ( f) — помеха), если передаточная функция оптимальной системы L ( to), а N — оператор, результат применения которого к функции U ( t) система должна вырабатывать с наименьшей ошибкой.
[15]
Страницы:
1
2
3
4