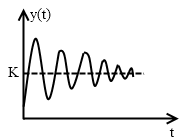
Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:
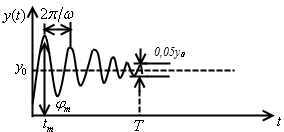
Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
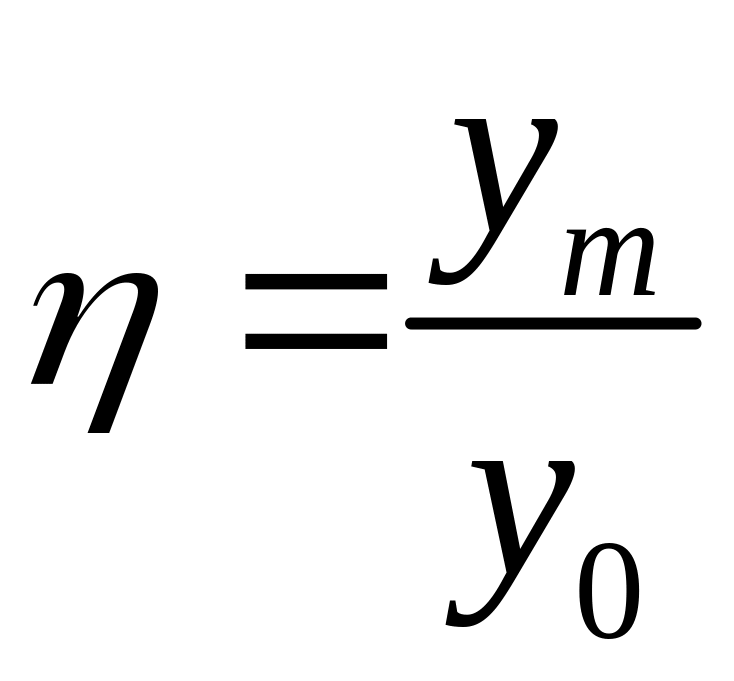
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
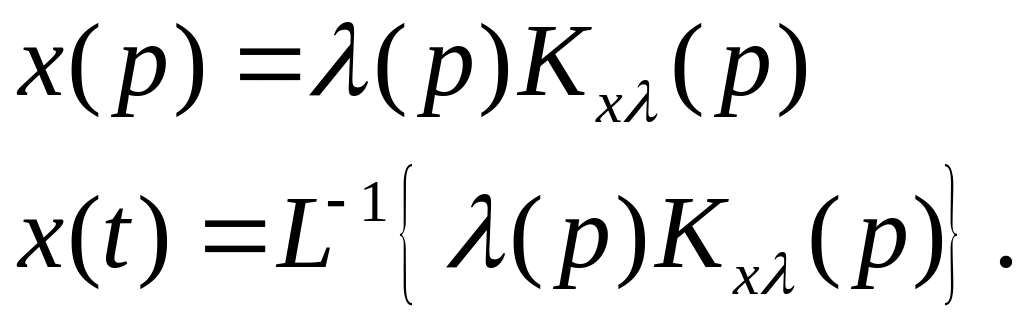
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:
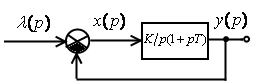

;
![]()
— характеристический полином;
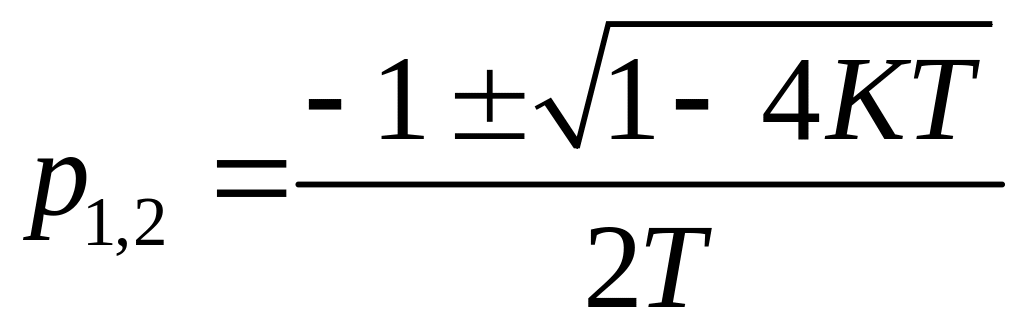
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
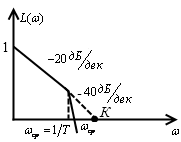
![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
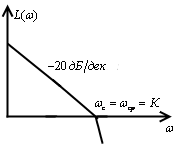
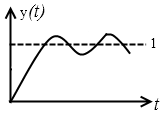
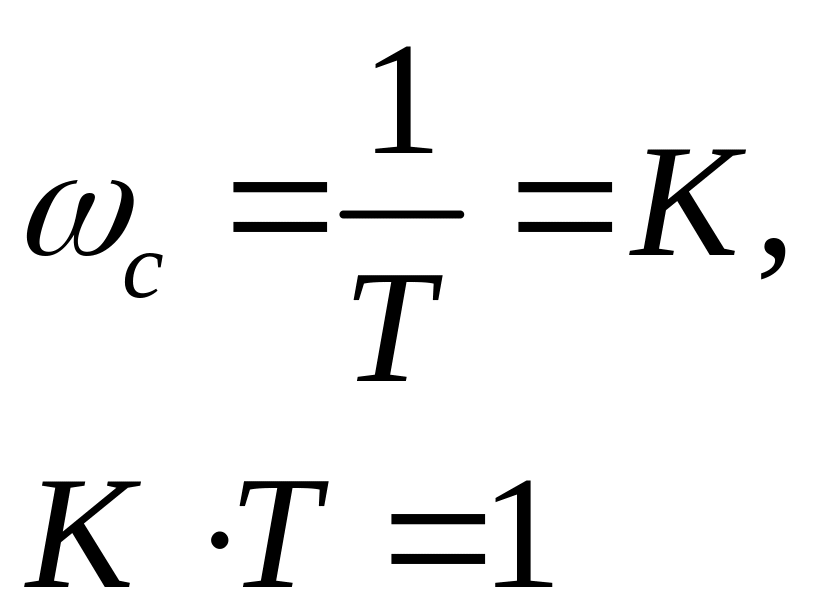
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:
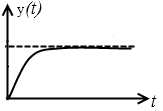
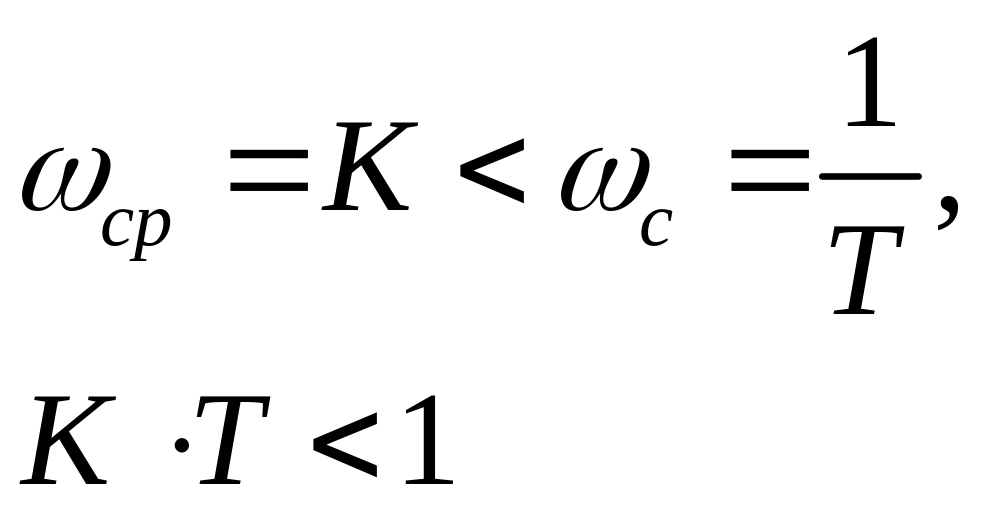
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
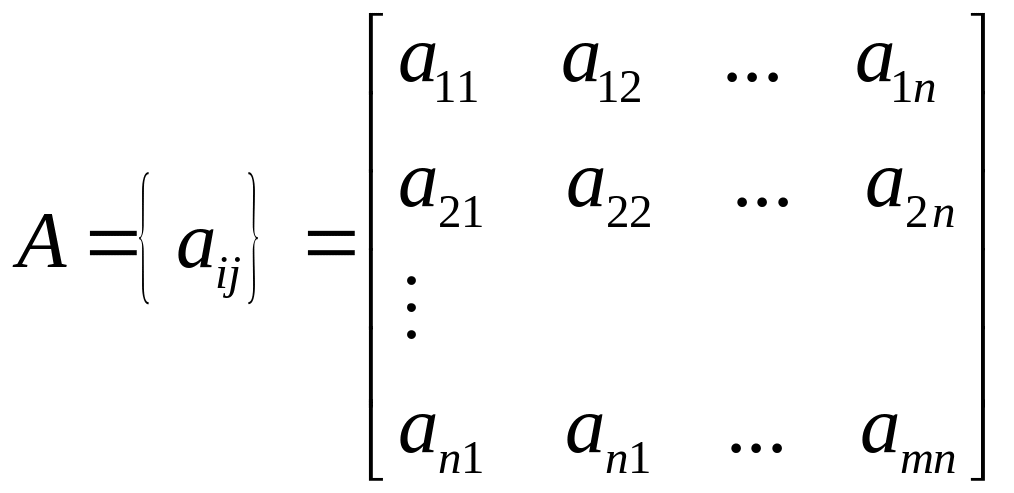
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
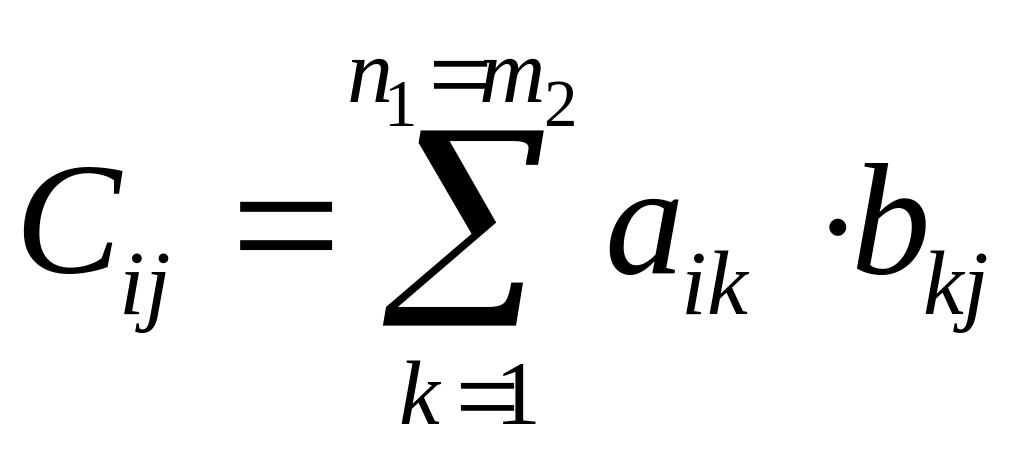
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
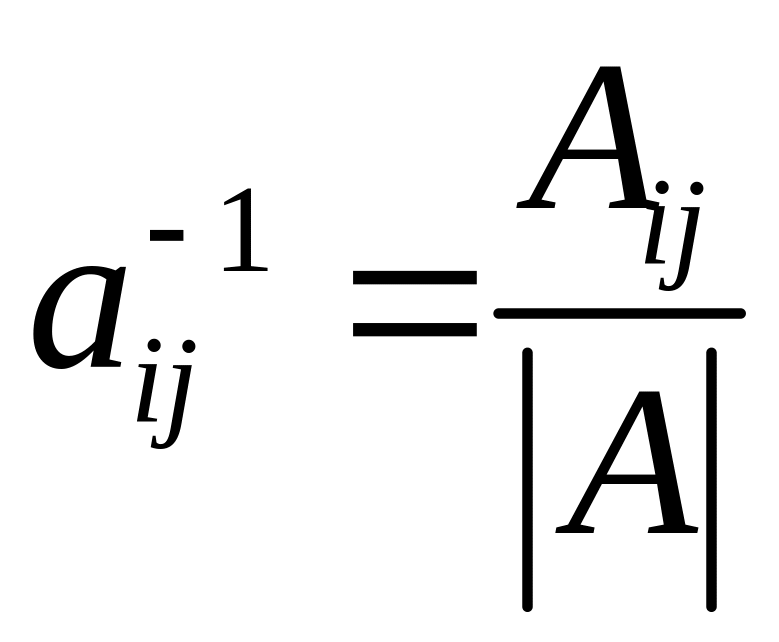
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
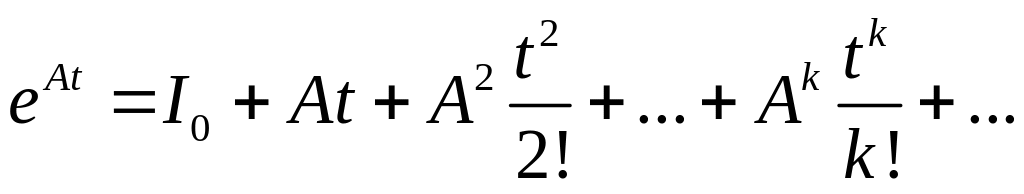
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = 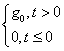 , g(p) =
, g(p) = ![]() ;
;
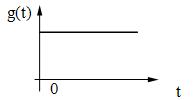
б) линейное воздействие: g(t) = ![]() t , t > 0
t , t > 0
; ![]() ;
;
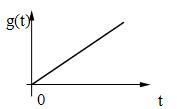
в) квадратичное воздействие:
![]() /2 , t > 0 ;
/2 , t > 0 ;
g(p) = ![]() .
.
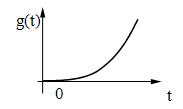
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
![]() , t > 0.
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если ![]() , то
, то ![]() и для g(t) = g0
и для g(t) = g0
получим ![]() .
.
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
![]() ,
,
где Res
x(p)
– вычет функции x(p)
в точке a.
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
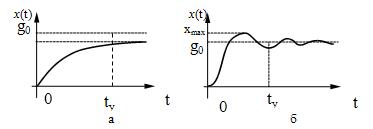
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза ![]() . Для оценки качества системы
. Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением ![]() .
.
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования ![]() .
.
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме ![]() . В зависимости от
. В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: ![]() .
.
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
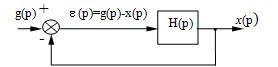
Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда ![]() или e (p) = He(p)g(p)
или e (p) = He(p)g(p)
, где He(p) = ![]() называется передаточной функцией
называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
![]() ,
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
![]() .
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
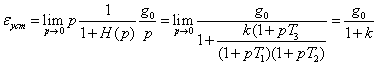 .
.
Предположим теперь, что входное
воздействие изменяется линейно ![]() t или
t или ![]() .
.
Тогда ![]() . Соответствующие входные воздействия и
. Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
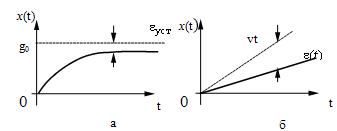
Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с ![]() .
.
Для ступенчатого воздействия g(t) = g0
или g(p) = ![]() получим
получим
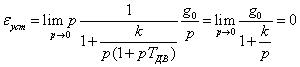 .
.
При линейном входном воздействии
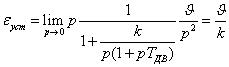 .
.
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
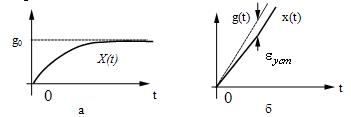
Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, ![]() . При ступенчатом
. При ступенчатом
воздействии 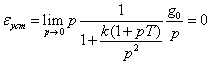 .
.
При линейном 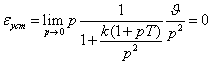 .
.
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
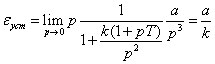 .
.
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии ![]() . Наконец, в системах с астатизмом
. Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
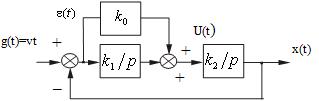
Рис.
25
Пусть входной сигнал системы управления
изменяется линейно: ![]()
![]() t. Как было
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= ![]() t , то на
t , то на
входе второго интегратора должен быть сигнал ![]() . Действительно, при нулевом
. Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора ![]() . Первый интегратор
. Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:

Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
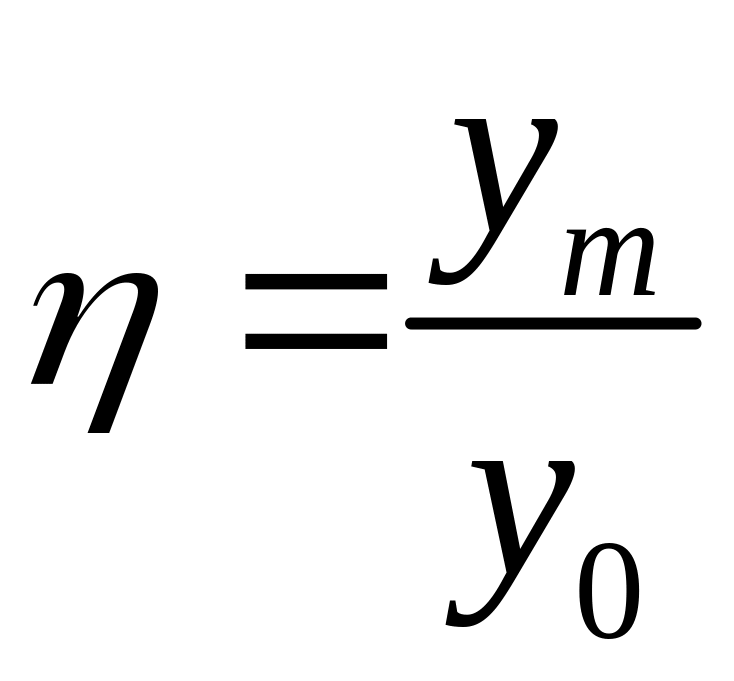
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
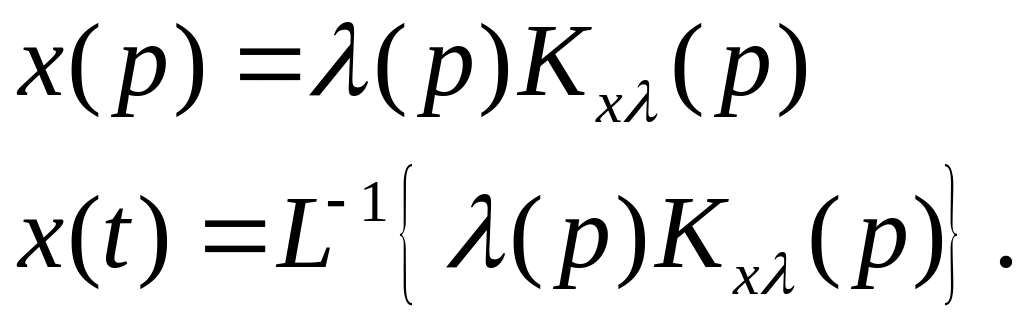
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:


;
![]()
— характеристический полином;
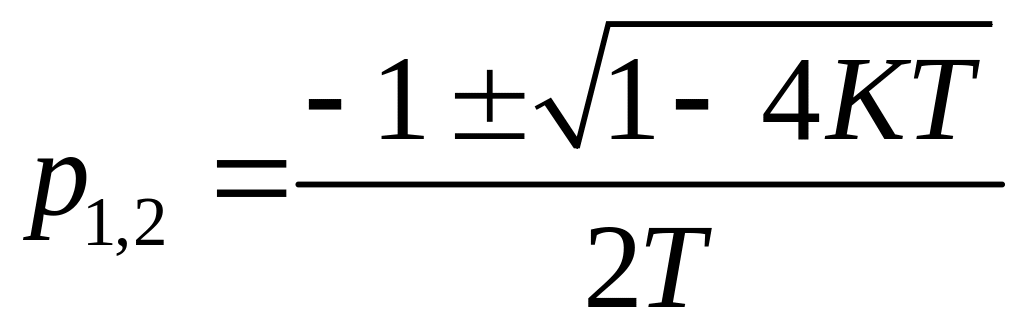
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
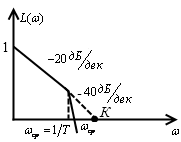

![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
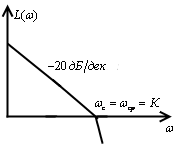

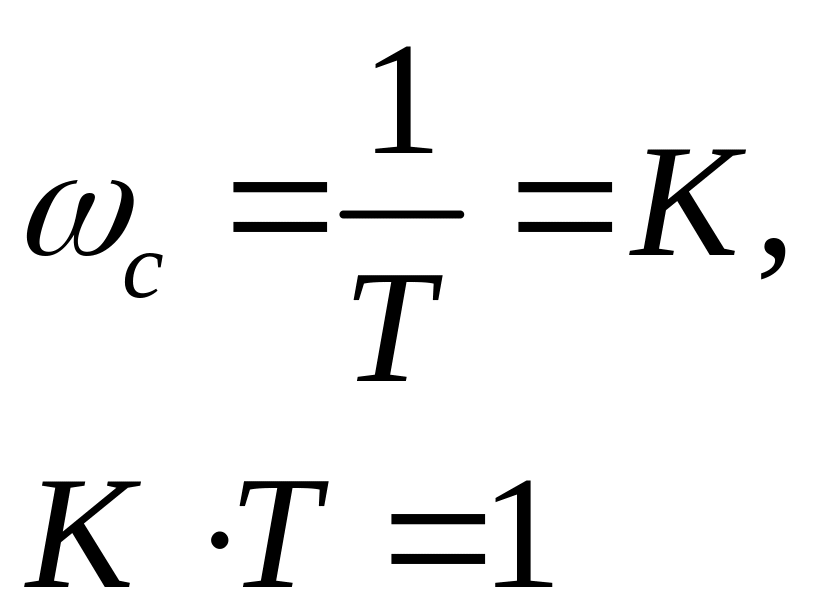
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:

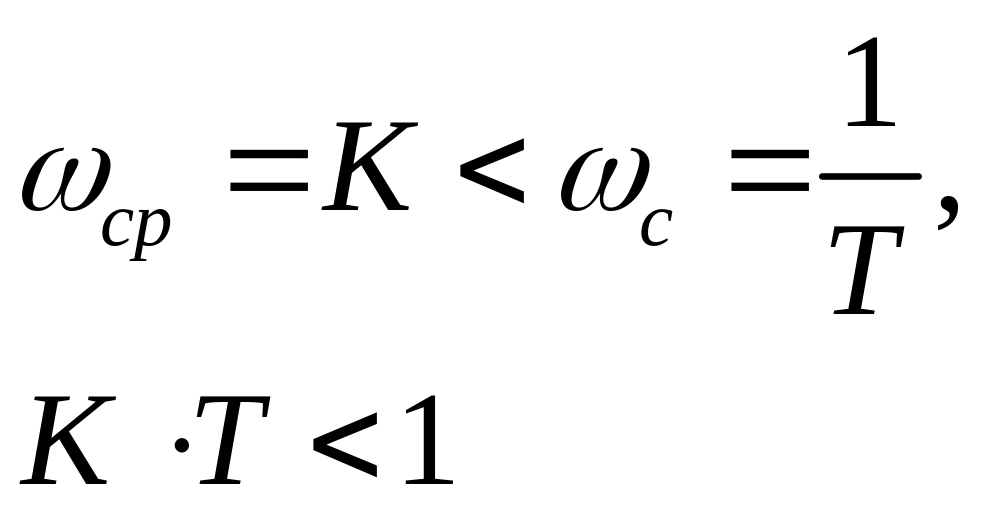
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
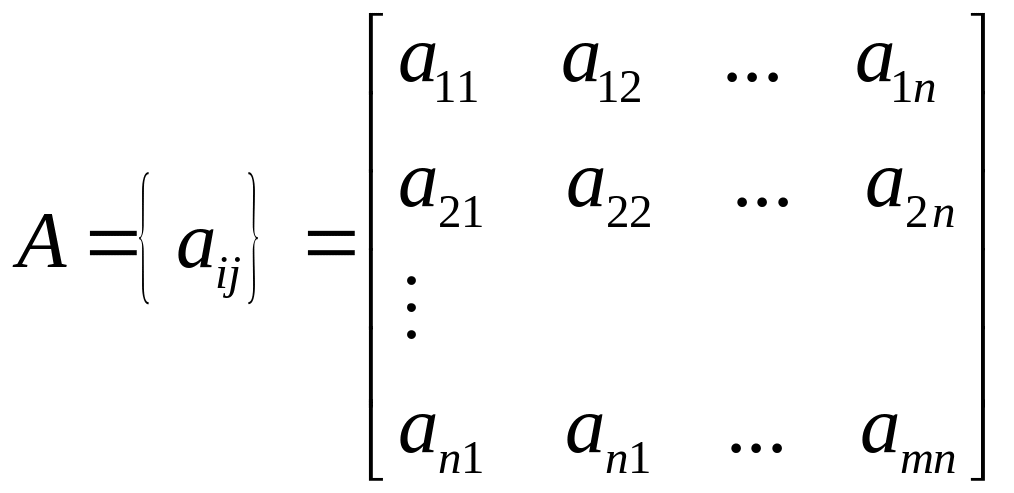
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
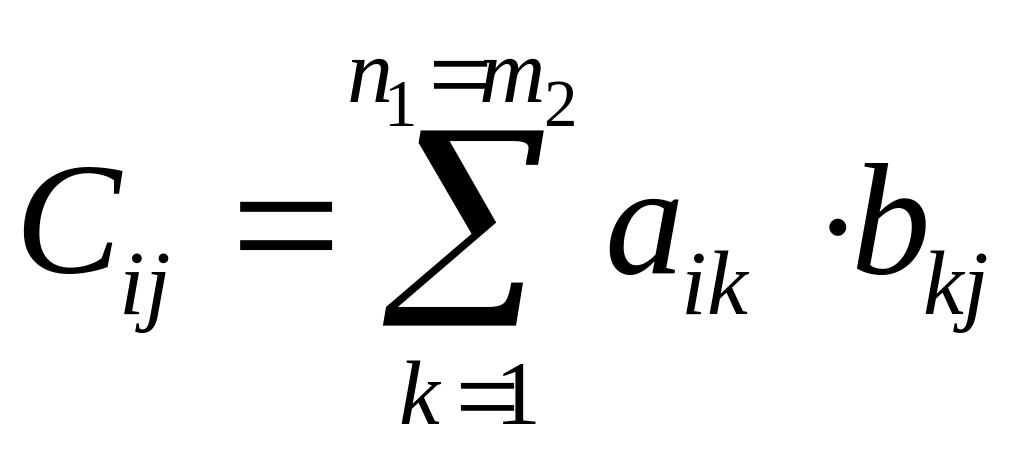
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
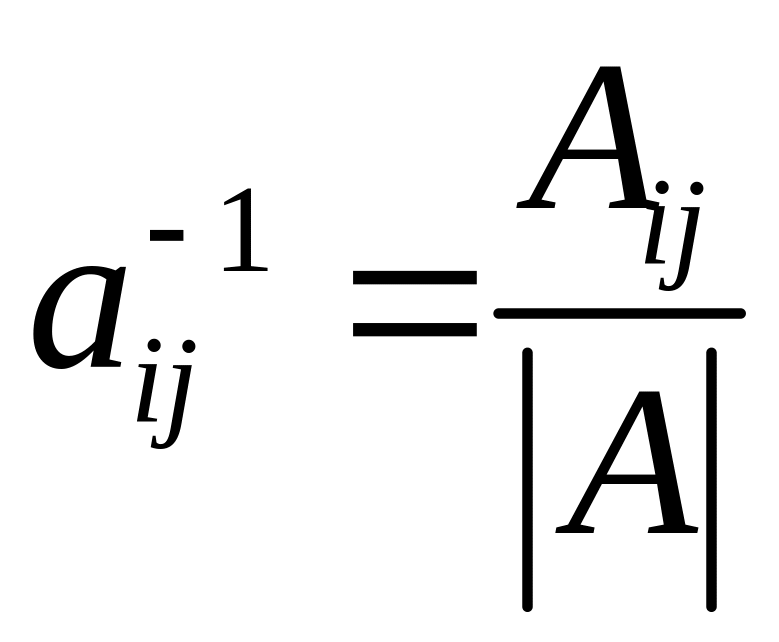
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
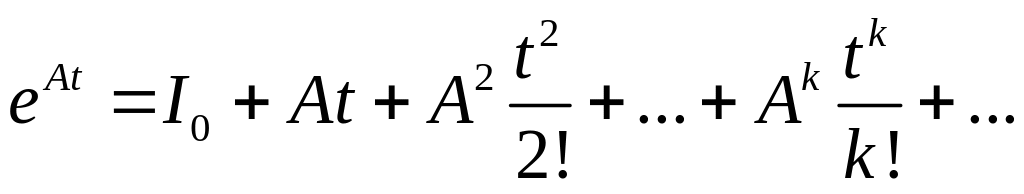
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = 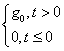 , g(p) =
, g(p) = ![]() ;
;
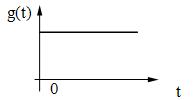
б) линейное воздействие: g(t) = ![]() t , t > 0
t , t > 0
; ![]() ;
;
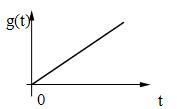
в) квадратичное воздействие:
![]() /2 , t > 0 ;
/2 , t > 0 ;
g(p) = ![]() .
.

В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
![]() , t > 0.
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если ![]() , то
, то ![]() и для g(t) = g0
и для g(t) = g0
получим ![]() .
.
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
![]() ,
,
где Res
x(p)
– вычет функции x(p)
в точке a.
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
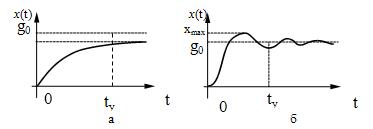
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза ![]() . Для оценки качества системы
. Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением ![]() .
.
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования ![]() .
.
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме ![]() . В зависимости от
. В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: ![]() .
.
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).

Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда ![]() или e (p) = He(p)g(p)
или e (p) = He(p)g(p)
, где He(p) = ![]() называется передаточной функцией
называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
![]() ,
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
![]() .
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
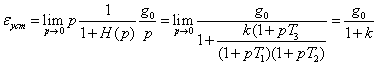 .
.
Предположим теперь, что входное
воздействие изменяется линейно ![]() t или
t или ![]() .
.
Тогда ![]() . Соответствующие входные воздействия и
. Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.

Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с ![]() .
.
Для ступенчатого воздействия g(t) = g0
или g(p) = ![]() получим
получим
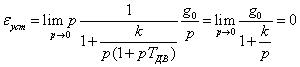 .
.
При линейном входном воздействии
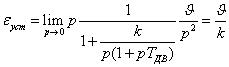 .
.
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.

Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, ![]() . При ступенчатом
. При ступенчатом
воздействии 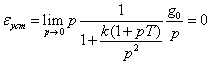 .
.
При линейном 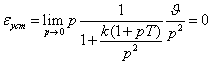 .
.
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
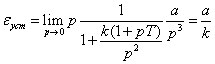 .
.
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии ![]() . Наконец, в системах с астатизмом
. Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)

Рис.
25
Пусть входной сигнал системы управления
изменяется линейно: ![]()
![]() t. Как было
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= ![]() t , то на
t , то на
входе второго интегратора должен быть сигнал ![]() . Действительно, при нулевом
. Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора ![]() . Первый интегратор
. Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Если подать на вход системы единичный
скачёк, то переходный процесс, как
правило, имеет следующий вид:

Качество переходного процесса
характеризуется параметрами:
1. максимальное перерегулирование
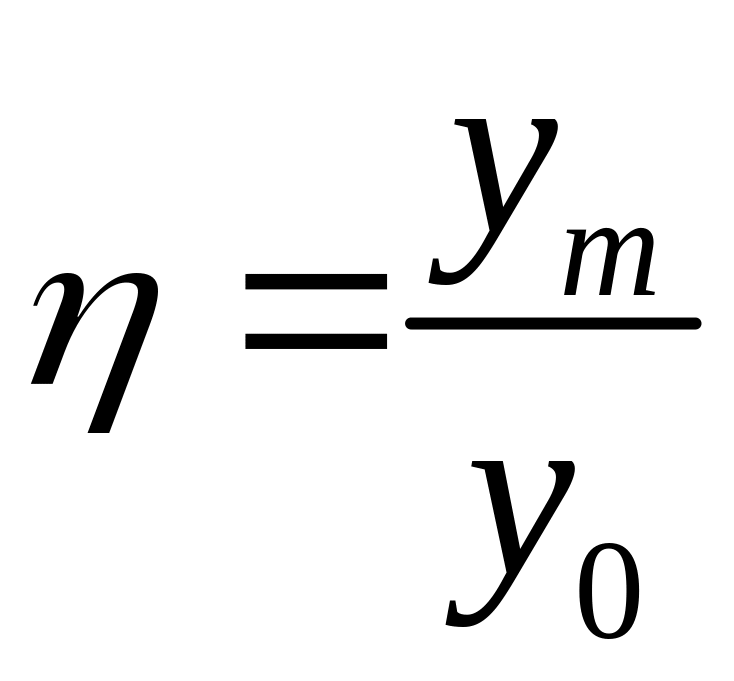
;
2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
![]()
;
3. время достижения первого
максимума
![]()
;
4. частота автоколебаний
;
В литературе приводятся выражения для
этих параметров для типичных передаточных
функций.
Ошибку регулирования в переходном
режиме можно определить, решая
дифференциальное уравнение или используя
преобразования Лапласа.
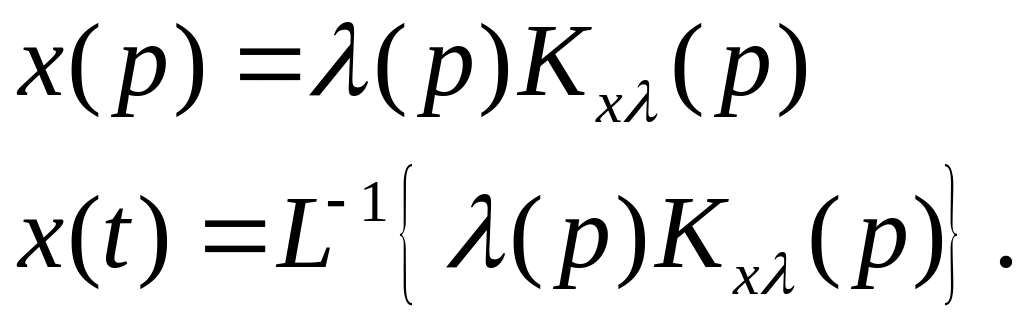
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой
системы:


;
![]()
— характеристический полином;
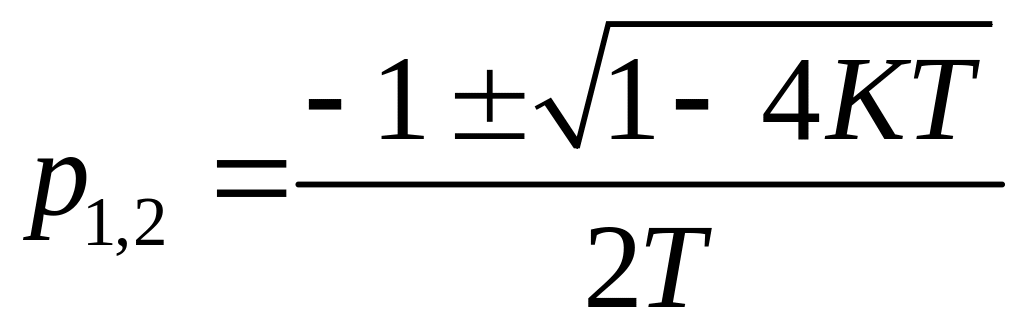
— корни характеристического
полинома.
Если корни действительны
![]()
,
то выходной сигнал определяется
выражением
![]()
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
![]()
![]()
,
то выходной сигнал определяется
выражение
![]()
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
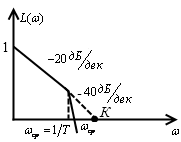

![]()
,
![]()
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
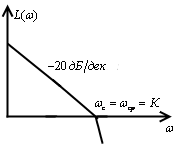

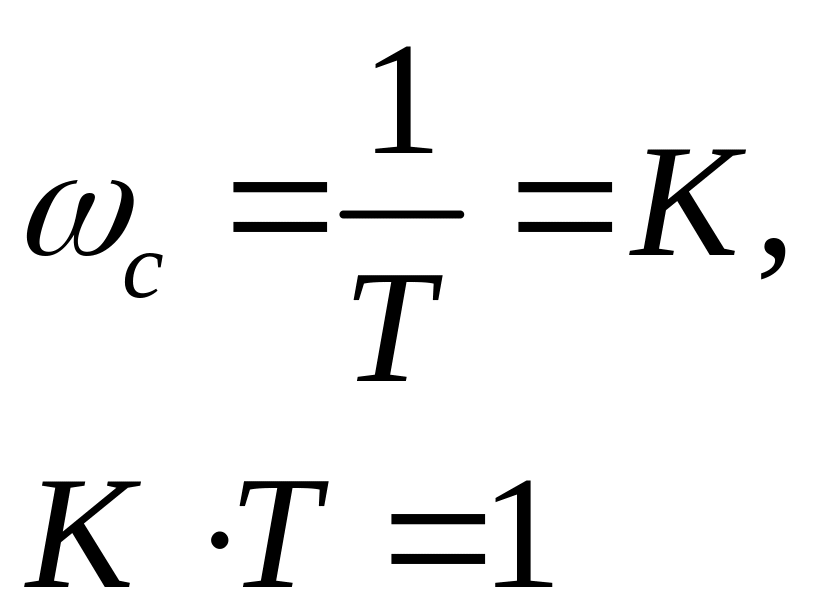
Корни комплексно сопряжённые, на частота
колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:

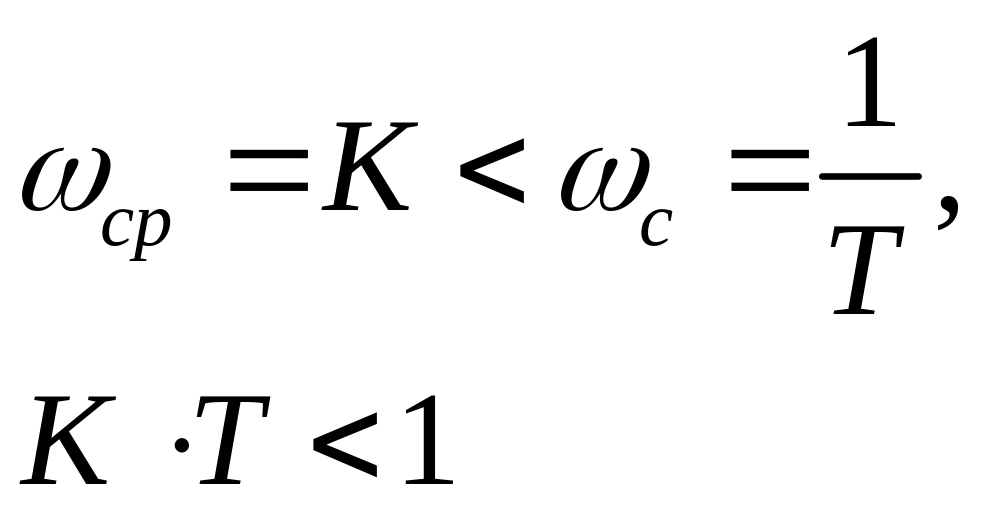
Пусть
![]()
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
![]()
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний
предназначен для решения дифференциальных
уравнений с помощью ЭВМ. Сущность этого
метода состоит в замене скалярного
дифференциального уравнения матричным
дифференциальным уравнением первого
порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
![]()
строк
и
![]()
столбцов,
вида:
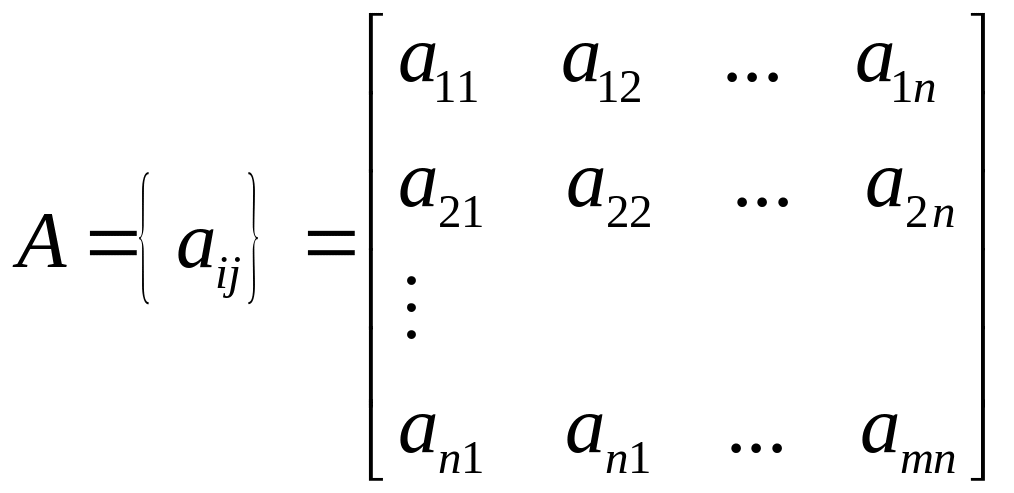
,
где i
– номер строки,
j – номер
столбца.
Матрицу, состоящую из одного столбца,
называют вектор-столбец, а из одной
строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
![]()
и
![]()
одинакового размера
![]()
называют матрицу
![]()
,
элементы которой равны сумме элементов
исходной матрицы
![]()
.
Теорема умножения матриц.
Произведение матрицы
размером
![]()
на матрицу
размера
![]()
называют матрицу, равной
с элементами (произведение взаимно если
![]()
)
:
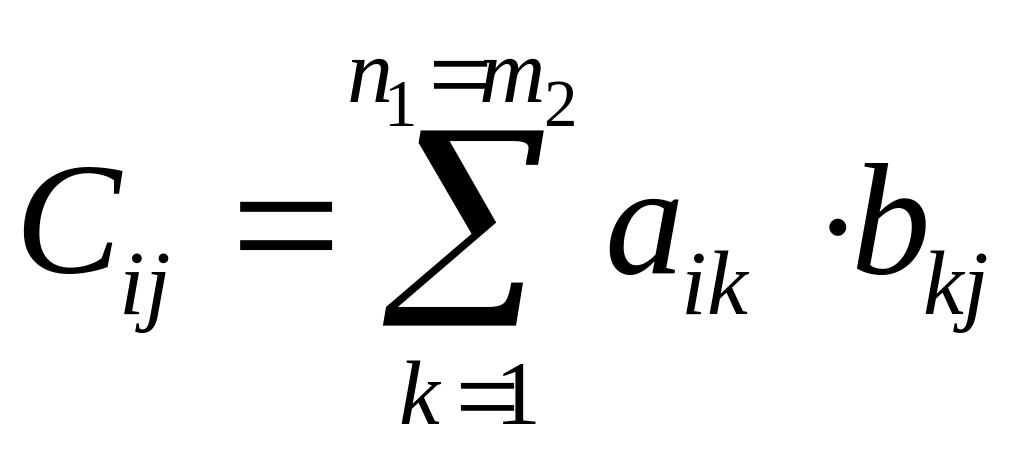
.
Теорема обращения матрицы.
Матрица
![]()
является обратной матрице
,
если выполняется условие
![]()
— единичная матрица размером

.
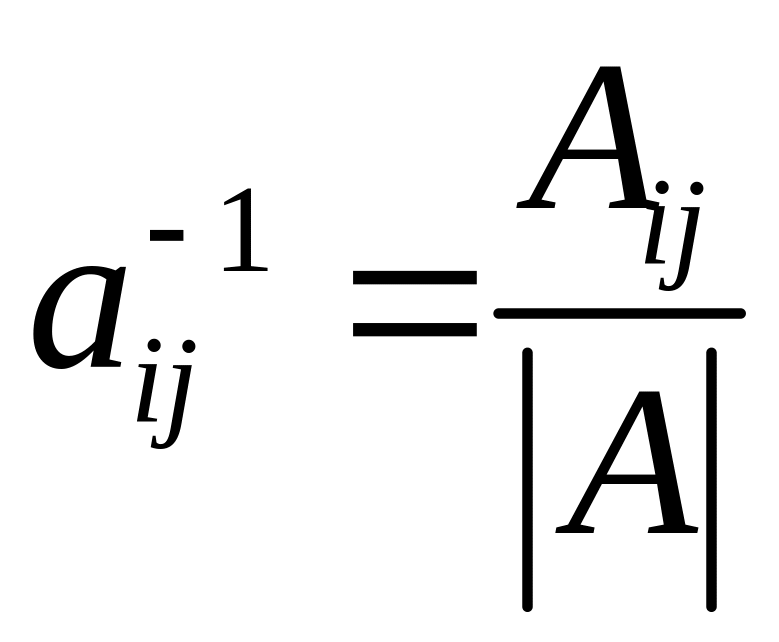
,
где
![]()
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
![]()
— алгебраическое дополнение аргумента,
где
![]()
— минор, равный определителю
![]()
порядка полученному из определителя
вычёркиванием
![]()
строки и
![]()
столбца.
Пример №1.

.
Теорема дифференцирования
и интегрирования матриц.
Для нахождения производной или интеграла
от матрицы по скалярному аргументу
необходимо вычислить их для каждого
элемента матрицы.
Матричной экспонентой называют
матрицу
![]()
,
где
— матрица,
![]()
— скалярный аргумент,
определяющейся бесконечным рядом
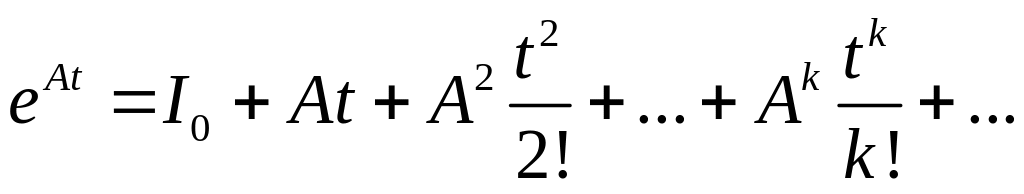
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Динамическая ошибка
Cтраница 3
Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]
Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]
Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]
Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]
Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]
Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]
Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]
Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]
Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]
Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]
Страницы:
1
2
3
4
Постановка задачи. Критерии качества переходных процессов
Любая система автоматического регулирования, для того чтобы удовлетворять своему назначению, прежде всего, должна быть устойчивой. Однако устойчивость является необходимым, но недостаточным условием технической пригодности системы регулирования. Помимо устойчивости, к переходному процессу предъявляются требования, обуславливающие его так называемые показатели.
Качество функционирования АСР оценивается прямыми показателями оценки качества переходных процессов в замкнутой АСР. К ним относятся:
Соответственно основными критериями качества системы управления являются:
1) Устойчивость системы;
2) Максимальная динамическая ошибка
3) Статическая ошибка;
4) Время регулирования ;
5) Величина перерегулирования;
6) Степень затухания переходного процесса;
7) Степень колебательности.
Как всякая динамическая система, САУ может находиться в одном из двух режимов — стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются критериями качества переходного процесса.
Существуют три группы критериев качества: корневые, интегральные и частотные.
Группа корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции САУ. В частном случае, когда нулей нет, качество переходного процесса определяется только полюсами.
Переходный процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.
Интегральными критериями качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Такие критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки. Применяются интегральные критерии обычно в теории оптимальных систем.
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик.
Рассмотрим некоторые критерии качества работы САУ:
1) Статическая ошибка (имеет место только в П — регуляторе) — это отклонение регулируемого параметра от заданного в установившемся режиме (точность системы);

.
Если в числителе передаточной функции системы нет свободного члена, то статическая ошибка равна нулю;
2) Динамическая ошибка — это максимальное рассогласование между заданной и текущей траекторией в переходном режиме;
3) Время регулирования — это время, в течение которого переходный процесс войдет в зону допустимой погрешности регулирования , где определяется следующим образом:

.
4)Величина перерегулирования — определяется как отношение амплитуды второй полуволны к первой

.
5)Степень затухания

учитывая, что
.
C данным критерием тесно связан еще один параметр-степень колебательности системы

;
Данные критерии взаимосвязаны следующими соотношениями:

.
Проведя небольшой анализ приведенных соотношений, можно выделить два крайних состояния системы:
а) апериодический процесс , ;
б) незатухающие колебания , .
Часто в расчетах применяют , .
Все системы регулирования рассчитываются с заданным значением либо , либо . Система регулирования считается настроенной оптимально, если она удовлетворяет двум или трем показателям качества. Например, максимальная динамическая ошибка, степень затухания, время регулирования удовлетворяют заданным значениям.
